The coronavirus disease 2019 (COVID-2019), a newly emerging disease in China, posed a public health emergency of China. Wuhan is the most serious affected city. Some measures have been taken to control the transmission of COVID-19. From Jan. 23rd, 2020, gradually increasing medical resources (such as health workforce, protective clothing, essential medicines) were sent to Wuhan from other provinces, and the government has established the hospitals to quarantine and treat infected individuals. Under the condition of sufficient medical resources in Wuhan, late-stage of epidemic showed a downward trend. Assessing the effectiveness of medical resources is of great significance for the future response to similar disease. Based on the transmission mechanisms of COVID-19 and epidemic characteristics of Wuhan, by using time-dependent rates for some parameters, we establish a dynamical model to reflect the changes of medical resources on transmission of COVID-19 in Wuhan. Our model is applied to simulate the reported data on cumulative and new confirmed cases in Wuhan from Jan. 23rd to Mar. 6th, 2020. We estimate the basic reproduction number R0 = 2.71, which determines whether the disease will eventually die out or not under the absence of effective control measures. Moreover, we calculate the effective daily reproduction ratio Re(t), which is used to measure the 'daily reproduction number'. We obtain that Re(t) drops less than 1 since Feb. 8th. Our results show that delayed opening the 'Fire God Hill' hospital will greatly increase the magnitude of the outbreak. This shows that the government's timely establishment of hospitals and effective quarantine via quick detection prevent a larger outbreak.
Citation: Liping Wang, Jing Wang, Hongyong Zhao, Yangyang Shi, Kai Wang, Peng Wu, Lei Shi. Modelling and assessing the effects of medical resources on transmission of novel coronavirus (COVID-19) in Wuhan, China[J]. Mathematical Biosciences and Engineering, 2020, 17(4): 2936-2949. doi: 10.3934/mbe.2020165
| [1] | Tao Chen, Zhiming Li, Ge Zhang . Analysis of a COVID-19 model with media coverage and limited resources. Mathematical Biosciences and Engineering, 2024, 21(4): 5283-5307. doi: 10.3934/mbe.2024233 |
| [2] | Chayu Yang, Jin Wang . A mathematical model for the novel coronavirus epidemic in Wuhan, China. Mathematical Biosciences and Engineering, 2020, 17(3): 2708-2724. doi: 10.3934/mbe.2020148 |
| [3] | Weike Zhou, Aili Wang, Fan Xia, Yanni Xiao, Sanyi Tang . Effects of media reporting on mitigating spread of COVID-19 in the early phase of the outbreak. Mathematical Biosciences and Engineering, 2020, 17(3): 2693-2707. doi: 10.3934/mbe.2020147 |
| [4] | Dipo Aldila, Meksianis Z. Ndii, Brenda M. Samiadji . Optimal control on COVID-19 eradication program in Indonesia under the effect of community awareness. Mathematical Biosciences and Engineering, 2020, 17(6): 6355-6389. doi: 10.3934/mbe.2020335 |
| [5] | Kai Wang, Zhenzhen Lu, Xiaomeng Wang, Hui Li, Huling Li, Dandan Lin, Yongli Cai, Xing Feng, Yateng Song, Zhiwei Feng, Weidong Ji, Xiaoyan Wang, Yi Yin, Lei Wang, Zhihang Peng . Current trends and future prediction of novel coronavirus disease (COVID-19) epidemic in China: a dynamical modeling analysis. Mathematical Biosciences and Engineering, 2020, 17(4): 3052-3061. doi: 10.3934/mbe.2020173 |
| [6] | Sha He, Sanyi Tang, Libin Rong . A discrete stochastic model of the COVID-19 outbreak: Forecast and control. Mathematical Biosciences and Engineering, 2020, 17(4): 2792-2804. doi: 10.3934/mbe.2020153 |
| [7] | Süleyman Cengizci, Aslıhan Dursun Cengizci, Ömür Uğur . A mathematical model for human-to-human transmission of COVID-19: a case study for Turkey's data. Mathematical Biosciences and Engineering, 2021, 18(6): 9787-9805. doi: 10.3934/mbe.2021480 |
| [8] | Ming-Tao Li, Gui-Quan Sun, Juan Zhang, Yu Zhao, Xin Pei, Li Li, Yong Wang, Wen-Yi Zhang, Zi-Ke Zhang, Zhen Jin . Analysis of COVID-19 transmission in Shanxi Province with discrete time imported cases. Mathematical Biosciences and Engineering, 2020, 17(4): 3710-3720. doi: 10.3934/mbe.2020208 |
| [9] | Damilola Olabode, Jordan Culp, Allison Fisher, Angela Tower, Dylan Hull-Nye, Xueying Wang . Deterministic and stochastic models for the epidemic dynamics of COVID-19 in Wuhan, China. Mathematical Biosciences and Engineering, 2021, 18(1): 950-967. doi: 10.3934/mbe.2021050 |
| [10] | Yue Deng, Siming Xing, Meixia Zhu, Jinzhi Lei . Impact of insufficient detection in COVID-19 outbreaks. Mathematical Biosciences and Engineering, 2021, 18(6): 9727-9742. doi: 10.3934/mbe.2021476 |
The coronavirus disease 2019 (COVID-2019), a newly emerging disease in China, posed a public health emergency of China. Wuhan is the most serious affected city. Some measures have been taken to control the transmission of COVID-19. From Jan. 23rd, 2020, gradually increasing medical resources (such as health workforce, protective clothing, essential medicines) were sent to Wuhan from other provinces, and the government has established the hospitals to quarantine and treat infected individuals. Under the condition of sufficient medical resources in Wuhan, late-stage of epidemic showed a downward trend. Assessing the effectiveness of medical resources is of great significance for the future response to similar disease. Based on the transmission mechanisms of COVID-19 and epidemic characteristics of Wuhan, by using time-dependent rates for some parameters, we establish a dynamical model to reflect the changes of medical resources on transmission of COVID-19 in Wuhan. Our model is applied to simulate the reported data on cumulative and new confirmed cases in Wuhan from Jan. 23rd to Mar. 6th, 2020. We estimate the basic reproduction number R0 = 2.71, which determines whether the disease will eventually die out or not under the absence of effective control measures. Moreover, we calculate the effective daily reproduction ratio Re(t), which is used to measure the 'daily reproduction number'. We obtain that Re(t) drops less than 1 since Feb. 8th. Our results show that delayed opening the 'Fire God Hill' hospital will greatly increase the magnitude of the outbreak. This shows that the government's timely establishment of hospitals and effective quarantine via quick detection prevent a larger outbreak.
Wuhan, the capital city of the Hubei province in China, is the focus of global attention because of the outbreak of a febrile respiratory disease caused by novel coronavirus. On Dec. 12nd, 2019, a pneumonia case of unknown etiology was reported in Wuhan, associated with the Huanan Seafood Wholesale Market where there was also sale of live wild animals. On Dec. 31st, 2019, Chinese authorities alerted the World Health Organization (WHO) on the outbreak of pneumonia of unknown aetiology. Subsequently, Chinese authorities isolated a novel strain of coronavirus on Jan. 7th, 2020 [1]. On Feb. 11st, WHO named a novel coronavirus as COVID-19 [2]. In the early stages, little was known about the COVID-19. Due to an annual spring migration in China, COVID-19 spread rapidly from Wuhan to almost every province in China, to reach various countries including Japan, Thailand, South Korea, Philippines, Singapore, Mexico, Italy and the United States of America. As of Jan. 29th, cumulative 7711 confirmed cases with 170 deaths were reported in China. The size of the outbreak prompted the WHO to declare the outbreak of COVID-19 as a ''Public Health Emergency of International Concern" on Jan. 30th, 2020 [3].
Based on transmission mechanisms and routes of COVID-19, some researchers try to use mathematical models to study rapid spread of COVID-19 [4,5,6,7,8,9,10,11]. However, there are very few models to investigate the effects of medical resources on transmission dynamics of COVID-19. For rapid spread of COVID-19 in China, Wuhan is the most serious affected city. In China, a regional university teaching hospital is usually equipped with 500-1000 beds, with only a small portion for isolation purpose [12]. When the infection started in districts of Wuhan, the available medical resources of the health system (health workforce, hospital beds, protective clothing, essential medicines, and the like) sufficed for diagnosing and treating the infected cases. As the number of infections keeps increasing rapidly, the medical resources proved incapable of treating the emerging cases in a timely way. In response to this situation, public health decision-and policy-makers took timely measures. After Wuhan was sealed off on Jan. 23rd, 2020, gradually increasing COVID-19 detecting kits and health workforces were sent to Wuhan from other provinces in succession. Government started setting up some hospitals for infected cases. On Feb. 4th, the 'Fire God Hill' hospital began to receive confirmed cases. Later, Feb. 8th, the 'Thunder God Hill' hospital also began to receive confirmed cases. Up to Feb. 28th, about sixteen the 'Mobile Field' hospitals had been gradually built to provide adequate hospital beds with infected individuals for diagnosis and treatment. Under the condition of sufficient medical resources in Wuhan, late-stage of epidemic showed a downward trend. Therefore, the medical resources can be considered as one of the main reasons for the transmission and control of COVID-19 in Wuhan.
The main purpose of this paper is to build a time-dependent model of COVID-19 to study the effects of medical resources on transmission of COVID-19 in Wuhan. In this paper, we first establish a model and use our model to fit the cumulative and new confirmed cases in Wuhan for the period from Jan. 23rd to Mar. 6th, 2020. Our model will allow us to estimate the basic reproduction number and effective daily reproduction ratio. Lastly, we assess the effects of medical resources on transmission of COVID-19 in Wuhan.
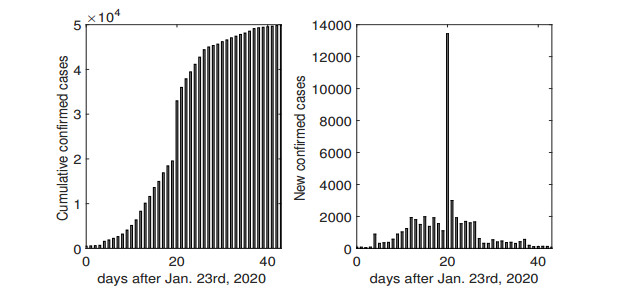
This study is based on daily reported cases extracted from the National Health Commission of the People's Republic of China [13] and the Health Commission of Hubei Province [14]. The data contain suspected cases, new confirmed cases, cumulative confirmed cases, hospitalized cases and death cases due to COVID-19 infection. Although the data do not include patient level information, they provide the best available data on the outbreak of COVID-19. On Jan. 23rd, 2020, Chinese government announced to seal off Wuhan from all outside contact to stop the spread of COVID-19. Hence, we choose Jan. 23rd, 2020 as the initial observation date and use the daily reported cumulative and new confirmed cases (see Figure 1) in Wuhan from Jan. 23rd to Mar. 6th, 2020 to do our study.
The main purpose in this work is to investigate the effects of medical resources which include effective quarantine via quick detection of post-stage exposed individuals, contact rates and hospitalization rates of infected individuals. Up to Feb. 28th, about sixteen the 'Mobile Field' hospitals and two 'Hill' hospitals had been gradually built to provide adequate hospital beds with infected individuals for diagnosis and treatment. The first hospital to be built was 'Fire God Hill', which began to receive confirmed cases on Feb. 4th. Thus, we can treat the opening time of the 'Fire God Hill' hospital (Feb. 4th) as the initial time for hospital intervention.
Based on transmission mechanisms and routes of COVID-19, we draw a flow diagram shown in Figure 2. We divide the total number of individuals at time t, denoted by Nh(t), into seven categories: susceptible S(t), pre-stage exposed E1(t), post-stage exposed E2(t), infected with mild symptoms I1(t), infected with serious symptoms I2(t), hospitalized H(t) and recovered R(t) individuals. So, Nh(t)=S(t)+E1(t)+E2(t)+I1(t)+I2(t)+H(t)+R(t). Assume that hospitalized individuals H(t) are isolated and are unable to contact with susceptible individuals S(t). We also capture the fact that post-stage exposed individuals have infectious ability. So, infectious individuals include E2(t), I1(t) and I2(t).
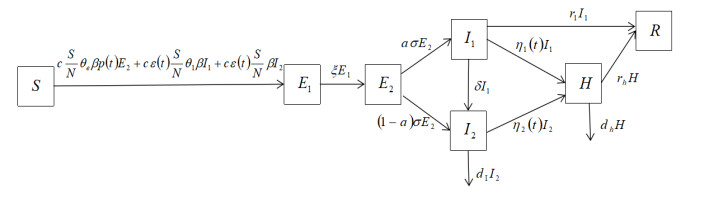
Susceptible individuals can be infected with COVID-19 via effective contact with post-stage exposed individuals E2 at a rate cSNθeβp(t)E2. c represents the mean number of an infectious individual contacting with others in unit time. cSN represents the mean number of an infectious individual contacting with susceptible individuals in unit time. β represents transmission probability from infectious individuals with serious symptoms I2 to susceptible individuals per contact. θe (0<θe<1) accounts for reduction in transmissibility of post-stage exposed individuals compare to I2. So, cSNθeβ represents the mean number of a post-stage exposed individual contacting and infecting susceptible individuals in unit time under the absence of effective control measures. Let q(t) be a proportion, and it indicates that effective quarantine via quick detection of post-stage exposed individuals is adopted to keep the quarantined population from infecting others. So, the other unquarantined proportion 1−q(t) of the post-stage exposed individuals is infectious. Here, we set p(t)=1−q(t). Then p(t) represents the unquarantined proportion of post-stage exposed individuals. From Jan. 23rd, 2020, gradually increasing COVID-19 detecting kits were sent to Wuhan from other provinces. It implies that the unquarantined proportion p(t) would gradually decrease. According to the idea of modeling in [10,11], in our study, we use the following form p(t) to represent the exponential decay of the unquarantined proportion of the post-stage exposed individuals due to effective quarantine via quick detection,
| p(t)={p0,0≤t≤τ1,(p0−p1)e−m0(t−τ1)+p1,τ1<t<τ2,(p0−p1)e−m0(t−τ1)e−m1(t−τ2)+p1,t≥τ2. | (2.1) |
Here, p0 represents initial unquarantined proportion of post-stage exposed individuals. p1 represents the minimum proportion under the current control strategies. Deservedly, we have p(0)=p0 and limt→+∞p(t)=p1 with p1<p0. τ1 represents the time for sealing off the city. In this study, since Wuhan was sealed off on Jan. 23rd and we choose Jan. 23rd as the initial observation date, we can treat τ1 as 0. τ2 represents the time for opening the 'Fire God Hill' hospital. Since 'Fire God Hill' hospital was opened on Feb. 4th, we can treat τ2 as 12. Obviously, τ1<τ2. When τ1<t<τ2, p(t)=(p0−p1)e−m0(t−τ1)+p1 represents the exponential decay at a rate m0 of unquarantined proportion due to sealing off the city. When t≥τ2, on the basis of e−m0(t−τ1), we add the exponential decay at a rate m1 of unquarantined proportion due to opening the 'Fire God Hill' hospital e−m1(t−τ2).
Susceptible individuals can also be infected with COVID-19 via effective contact with infected individuals at a rate cϵ(t)SNθ1I1+cϵ(t)SNI2, in which θ1 (0<θ1<1) accounts for reduction in transmissibility of infected individuals with mild symptoms compare to individuals with serious symptoms. After the 'Fire God Hill' hospital was opened on Feb. 4th, infected individuals would be arranged for hospitalization in succession. It implies that contact rate of infected individuals to susceptible individuals would gradually decrease. According to the idea of modeling in [10,11], we use ϵ(t) to represent the exponential decay of contact rate of infected individuals to susceptible individuals due to opening the 'Fire God Hill' hospital with the following form
| ϵ(t)={1,0≤t<τ2,(1−ϵ1)e−m2(t−τ2)+ϵ1,t≥τ2. | (2.2) |
Here, ϵ1 represents the minimum proportion of contact rate of infected individuals to susceptible individuals under the measure of opening the 'Fire God Hill' hospital. Obviously, limt→+∞ϵ(t)=ϵ1. m2 represents the exponential decreasing rate of contact rate of infected individuals to susceptible individuals due to opening the 'Fire God Hill' hospital.
Susceptible individuals are infected with COVID-19 and move into pre-stage exposed class E1 with mean duration of 1ξ days, later, enter into post-stage exposed class. Then individuals enter into infected class with mild symptoms I1 at a proportion a, and into infected class with serious symptoms I2 at a proportion 1−a over post-stage exposed period 1σ. The infected class with mild symptoms may recover through medication or self-immunity at a rate r1, and may also be serious and enters to I2 at a rate δ. If medical resources are adequate, then I1 and I2 can be admitted to hospital at rates η1(t) and η2(t), respectively. I2 without recovery will die at a rate dI. The hospitalized individual either recovers at a rate rh or dies at a rate dh.
After the 'Fire God Hill' hospital was opened on Feb. 4th, 2020, infected individuals would be arranged for hospitalization in succession. It implies that hospitalization rate η1(t) and η2(t) would gradually increase. According to the idea of modeling in [10], we use the following forms to represent the raises of hospitalization rate due to opening the 'Fire God Hill' hospital, respectively,
| η1(t)={η10,0≤t<τ2,1(1η10−1η11)e−m3(t−τ2)+1η11,t≥τ2, | (2.3) |
and
| η2(t)={η20,0≤t<τ2,1(1η20−1η21)e−m3(t−τ2)+1η21,t≥τ2, | (2.4) |
in which η10 and η20 represent the average hospitalization rates of infectious individuals with mild symptoms and serious symptoms between Jan. 23rd and Feb. 3rd, 2020. η11 and η21 represent maximum hospitalization rates with limt→+∞η1(t)=η11 and limt→+∞η2(t)=η21. m3 represents the exponential decreasing rate of period of arranged for hospitalization of infected individuals.
In view of the above analysis, we formulate a COVID-19 model with medical resources as follows
| {dSdt=−cSNθeβp(t)E2−cϵ(t)SNθ1βI1−cϵ(t)SNβI2,dE1dt=cSNθeβp(t)E2+cϵ(t)SNθ1βI1+cϵ(t)SNβI2−ξE1,dE2dt=ξE1−σE2,dI1dt=aσE2−δI1−η1(t)I1−r1I1,dI2dt=(1−a)σE2+δI1−η2(t)I2−dII2,dHdt=η1(t)I1+η2(t)I2−rhH−dhH,dRdt=r1I1+rhH. | (2.5) |
In this section, we first apply model (2.5) to fit the cumulative and new confirmed cases from Jan. 23rd to Mar. 6th, 2020 in Wuhan and estimate unknown parameters. Then, based on the parameters, the basic reproduction number and effective daily reproduction ratio are estimated. Later, we will assess the effects of medical resources on transmission of COVID-19.
Let X(t) be theoretic cumulative confirmed cases and its change with time is determined by dX(t)dt=σE2, Y(t) be theoretic new confirmed cases and its change with time is determined by Y(t)=X(t)−X(t−1). Let ˉX(t) and ˉY(t) is reported cumulative and new confirmed cases in day t, respectively. About 9 million are living in the city after sealing off the city. We can set the initial number of susceptible individuals S(0)=9,000,000. The reported cumulative and new confirmed cases on Jan. 23rd are 495 and 70, respectively. So, X(0)=495 and Y(0)=70. Based on reported data from websites [14], we can set I1(0)=495⋅a and I2(0)=495⋅(1−a). Then, we set H(0)=η10I1(0)+η20I2(0) and R(0)=r1I1(0). Because the numbers of the initial pre-stage exposed population E1(0) cannot be obtained directly, its value can be estimated as a parameter. Then, we derive E2(0)=ξE1(0). Next, the least-square estimation is used to calculate the parameter values to minimize the objective functions
| J1=1nn∑t=1(X(t)−ˉX(t))2,J2=1nn∑t=1(Y(t)−ˉY(t))2, |
in which n is the number of reported data. In our model, take day as the unit time. So n = 44. By applying method of random simulation and running 1000 simulations, the values of parameter are given in Table 1.
| Parameter | Description | Value | Source |
| c | Contact rate (Day−1) | 13.8 | Assumption |
| β | Transmission probability of I2 per contact (Dimensionless) | 0.036 | Estimation |
| 1ξ | Pre-stage exposed period (Day) | 1.52 | Estimation |
| 1σ | Post-stage exposed period (Day) | 6.67 | Estimation |
| a | Proportion of post-stage exposed class entering I1 compartment (Dimensionless) | 0.8 | Calculation [14] |
| δ | Transition rate from infectious cases with mild symptoms to infectious cases with serious symptoms (Day−1) | 0.2 | Estimation |
| η10 | Average hospitalization rate of infectious cases with mild symptoms between Jan. 23rd and Feb. 3rd (Day−1) | 0.31 | Assumption |
| η11 | Maximum hospitalization rate of infectious cases with mild symptoms (Day−1) | 0.93 | Estimation |
| η20 | Average hospitalization rate of infectious cases with serious symptoms between Jan. 23rd and Feb. 3rd (Day−1) | 0.7 | Assumption |
| η21 | Maximum hospitalization rate of infectious cases with serious symptoms (Day−1) | 0.98 | Estimation |
| r1 | Recovery rate of infectious cases with mild symptoms (Day−1) | 112.5 | [12] |
| rh | Recovery rate of hospitalized cases (Day−1) | 0.05 | Estimation |
| dI | Disease-related death rate of infectious cases with serious symptoms (Day−1) | 0.055 | Assumption [13] |
| dh | Disease-related death rate of hospitalized cases (Day−1) | 0.049 | Assumption [13] |
| p0 | The initial unquarantined proportion of post-stage exposed individuals (Dimensionless) | 0.76 | Estimation |
| p1 | The minimum unquarantined proportion of post-stage exposed individuals (Dimensionless) | 0.00608 | Estimation |
| θe | Modification parameter or infectious reduction factor (Dimensionless) | 0.72 | Estimation |
| θ1 | Modification parameter or infectious reduction factor (Dimensionless) | 0.87 | Estimation |
| m0 | The exponential decreasing rate of the unquarantined proportion of E2 due to sealing off the city (Dimensionless) | 0.02 | Estimation |
| m1 | The exponential decreasing rate of the unquarantined proportion of E2 due to opening the 'Fire God Hill' hospital (Dimensionless) | 0.19 | Estimation |
| m2 | The exponential decreasing rate of contact rate of I1 and I2 to S due to opening the 'Fire God Hill' hospital (Dimensionless) | 0.22 | Estimation |
| m3 | The exponential decreasing rate of period of arranged for hospitalization of I1 and I2 (Dimensionless) | 0.3 | Estimation |
| ϵ1 | Minimum proportion of contact rate of I1 and I2 to S due to opening the 'Fire God Hill' hospital (Dimensionless) | 0.1 | Estimation |
| τ1 | The time for sealing off the city (Dimensionless) | 0 | Calculation |
| τ2 | The time for opening the 'Fire God Hill' hospital (Dimensionless) | 12 | Calculation |
| E1(0) | The initial number of pre-stage exposed individuals (Dimensionless) | 1800 | Estimation |
Through some rational assumptions and parameter estimations, fitting curves of cumulative and new confirmed cases using model (2.5) are shown in Figures 3 and 4. Figures 3 and 4 indicate that our model (2.5) provides well fit to the reported data from Jan. 23rd to Mar. 6th, 2020 in Wuhan. From Figure 3, in the early stages, disease grows rapidly. The possible reason is the lack of medical resources. With the opening of the 'Fire God Hill' hospital and other the 'Mobile Field' hospitals in succession, later, new confirmed cases drop rapidly (Figure 4).
Now, we give a risk index: the basic reproduction number R0. The value of R0 determines whether the disease will eventually die out or not under the absence of effective control measures. To be specific, if R0>1, then the disease will break out. Conversely, if R0<1, then the disease will die out. R0 can be calculated under conditions: p(t)≡p0, ϵ(t)≡1, η1(t)≡η10 and η2(t)≡η20. By using the next generation matrix, we can calculate R0, the spectral radius of the next generation matrix [15,16] given by
| R0=RE+RI1+RI2, | (3.1) |
where
| RE=βcθep0σ,RI1=βcθ1aδ+η10+r1,RI2=βc((1−a)+aδδ+η10+r1)1η20+dI. |
Biologically, R0 represents the number of secondary infections produced by an infected individual during its average infectious lifetime in a completely susceptible population. Susceptible individuals acquire infection with COVID-19 by an effective contact with either post-stage exposed E2, or infected with mild symptoms I1, or infected with serious symptoms I2 individuals. Thus, R0 consists of three parts: RE,RI1 and RI2. Firstly, the number of new infectious individuals produced by a post-stage exposed individual E2 via effective contact with susceptible individuals at a rate βcθep0 during its average infectious lifetime 1σ is βcθep0σ. Secondly, a indicates the proportion that an individual in the E2 class will become I1. 1δ+η10+r1 represents the average infectious lifetime of I1. So, the number of new infectious individuals generated by an infected individual with mild symptoms I1 during its average infectious lifetime is given by θ1βc⋅a⋅1δ+η10+r1. Lastly, the number of new infectious individuals generated by an infected individual with serious symptoms I2 consists of two parts. The first path is given by the product of the infection rate βc, the proportion that E2 becomes I2 class (1−a), and the average infectious duration of an individual in the I2 class 1η20+dI. The second path is given by the product of the infection rate βc, the proportion that E2 becomes I1 class a, the proportion that I1 becomes I2 class δδ+η10+r1, and the average infectious duration of an individual in the I2 class 1η20+dI.
We estimate that the value of R0 is 2.71. It is contributed by post-stage exposed individuals RE = 1.81, contributed by infected individuals with mild symptoms RI1=0.59, contributed by infected individuals with serious symptoms RI2= 0.31. This suggests that transmission of post-stage exposed individuals is main factor of an outbreak of COVID-19. However, the effects of transmission of infected individuals on the spread of COVID-19 cannot be neglected.
Based on the definition of the effective daily reproduction ratio in [10,11], which is used to measure the 'daily reproduction number', the number of new infectious individuals induced by a single infectious individual during its infectious period per day. In this paper, the effective daily reproduction ratio is calculated by
| Re(t)=(βcθep(t)σ+βθ1acϵ(t)δ+η1(t)+r1+βcϵ(t)((1−a)+aδδ+η1(t)+r1)1η2(t)+dI)S(t)N(t). | (3.2) |
The effective daily reproduction ratio can be simulated and shown in Figure 5. Re(0) is a risk index of the initial transmissibility of COVID-19 on Jan. 23rd. We know that Re(0)=R0. From Figure 5, under the scenario sealing off the city, the effective daily reproduction ratio begins to decrease and drops to 2.33 as of Feb. 4th. After the 'Fire God Hill' hospital was opened on Feb. 4th, 2020, infected individuals would be arranged for hospitalization in succession. It makes infected individuals quarantine, thereby reduces contact rate. Under the combination of the restrictive measures, including sealing off the city and opening the 'Fire God Hill' hospital, the effective daily reproduction ratio declines rapidly and drops less than 1 since Feb. 8th. As of Mar. 6th, it drops to 0.06, and the epidemic will gradually die off.
In this part, we will examine the effects of opening the 'Fire God Hill' hospital later on cumulative and new confirmed cases, and the effects of the exponential decreasing rates of unquarantined proportion of E2, the contact rate of I1 and I2 to S, and the period of arranged for hospitalization of infected individuals due to opening the 'Fire God Hill' hospital on cumulative confirmed cases.
Firstly, we consider different values of the time for opening the 'Fire God Hill' hospital: τ2 = 12, 13, 14, 15, 16, 17. From Figure 6(A), if the 'Fire God Hill' hospital is opened 1 day delay (i.e., τ2=13), then the number of cumulative confirmed cases in Wuhan will be about 30% higher than the real reported cases (49, 871) by Mar. 6th. If the 'Fire God Hill' hospital is opened 5 day delay (i.e., τ2=17), then the number of cumulative confirmed cases in Wuhan will be about 80.1% higher than the real data by Mar. 6th. It implies that delayed opening the 'Fire God Hill' hospital will greatly increase the magnitude of the outbreak. From Figure 6(B), if the 'Fire God Hill' hospital is opened later, the inflection point of the epidemic will appear later and the peak will be increased. This implies that the government's timely establishment of hospitals prevent a larger outbreak.
Next, we examine the effects of the exponential decreasing rates of unquarantined proportion of E2, the contact rate of I1 and I2 to S, and the period of arranged for hospitalization of infected individuals due to opening the 'Fire God Hill' hospital on cumulative confirmed cases. For this purpose, we choose different exponential decreasing rates m1,m2 and m3, respectively. Figure 7 shows that the larger the strength of quarantine is, the smaller the number of cumulative confirmed cases is. The results shown in Figures 8 and 9 indicate the larger the strength of acceptance patients is, the smaller the number of cumulative confirmed cases is. It suggests that effective quarantine via quick detection and adequate number of available hospital beds will effectively reduce the number of cases of COVID-19.
Based on the transmission mechanisms of COVID-19 and epidemic characteristics of Wuhan, we build a time-dependent mathematical model of COVID-19 to focus on investigating the effects of medical resources on transmission of COVID-19. We apply our model to fit the cumulative and new confirmed cases in Wuhan from Jan. 23rd to Mar. 6th, 2020 and get reasonable match. The basic reproduction number is estimated R0= 2.71. Li et al. [17] estimated the basic reproduction number of COVID-19 to be 2.2 (95% CI, 1.4–3.9). Zhao et al. estimated range of the basic reproduction number R0 from 3.30 (95% CI: 2.73–3.96) to 5.47 (95% CI: 4.16–7.10) based on the early outbreak data following the exponential growth in [19]. Later, in [18], they also estimated R0 at 2.56 (95% CI: 2.49–2.63) through modelling the epidemic curve of COVID-19 cases, from Dec. 1st, 2019 to Jan. 24th, 2020. Other studies have shown that the range of the basic reproductive number is about 2–3. In this study, our estimate is reasonable.
Due to variation in the control strategies with the time, we calculate the effective daily reproduction ratio Re(t), which is used to measure the 'daily reproduction number'. From Jan. 23rd, the effective daily reproduction ratio begins to decrease from 2.71 to 2.33 as of Feb. 4th. After the 'Fire God Hill' hospital was opened on Feb. 4th, it declines rapidly and drops less than 1 since Feb. 8th. As of Mar. 6th, it drops to 0.06, the epidemic will gradually die off.
Our results show that opening the 'Fire God Hill' hospital delay will greatly increase the magnitude of the outbreak and disappear later the inflection point of the epidemic. Moreover, effective quarantine via quick detection and adequate number of available hospital beds will effectively reduce the number of cases of COVID-19. By establishing mathematical model, our results are basically consistent with the current government decision-making. We suggest that other countries may make the similar measures for this disease.
We are very grateful to anonymous referees and editor for careful reading and helpful suggestions which led to an improvement of our original manuscript. The work is supported by the National Natural Science Foundation of China (Nos 11971013, 11571170).
The authors declare there is no conflict of interest.
| [1] |
W. Tan, X. Zhao, X. Ma, W. Wang, P. Niu, W. Xu, et al., A novel coronavirus genome identified in a cluster of pneumonia cases-Wuhan, China 2019-2020, China CDC Weekly, 2 (2020), 61-62. doi: 10.46234/ccdcw2020.017

|
| [2] | E. Martin, Update: 'A bit chaotic.' Christening of new coronavirus and its disease name create confusion. Sciencemag, 2020. Available from: https://www.sciencemag.org/news/2020/02/bit-chaotic-christening-new-coronavirus-and-its-disease-name-create-confusion. |
| [3] | World Health Organization, Novel Coronavirus, 2020. Available from: https://www.who.int/new-sroom/detail/30-01-2020-statement-on-the-second-meeting-of-the-international-health-regulations-(2005)-emergency-committee-regarding-the-outbreak-of-novel-coronavirus-(2019-ncov). |
| [4] | T. Chen, J. Rui, Q. Wang, Z. Zhao, J. A. Cui, L. Yin, A mathematical model for simulating the transmission of Wuhan novel Coronavirus, bioRxiv, (2020). |
| [5] |
B. Tang, X. Wang, Q. Li, N. L. Bragazzi, S. Tang, Y. Xiao, et al., Estimation of the transmission risk of the 2019-nCoV and its implication for public health interventions, J. Clin. Med., 9 (2020), 462. doi: 10.3390/jcm9020462

|
| [6] | P. Shao, Y. Shan, Beware of asymptomatic transmission: Study on 2019-nCoV prevention and control measures based on extended SEIR model, bioRxiv, (2020). |
| [7] | M. Shen, Z. Peng, Y. Xiao, L. Zhang, Modelling the epidemic trend of the 2019 novel coronavirus outbreak in China, bioRxiv, (2020). |
| [8] | S. Funk, R. M. Eggo, Early dynamics of transmission and control of 2019-nCoV: a mathematical modelling study, medRxiv, (2020). |
| [9] | B. J. Quilty, S. Clifford, Effectiveness of airport screening at detecting travellers infected with novel coronavirus (2019-nCoV), Euro. Surveill., 25 (2020). |
| [10] |
B. Tang, N. L. Bragazzi, Q. Li, S. Tang, Y. Xiao, J. Wu, An updated estimation of the risk of transmission of the novel coronavirus (2019-nCov), Infect. Disease Model., 5 (2020), 248-255. doi: 10.1016/j.idm.2020.02.001

|
| [11] | M. Shen, Z. Peng, Y. Xiao, L. Zhang, Modelling the epidemic trend of the 2019 novel coronavirus outbreak in China, bioRxiv, (2020). |
| [12] | W. Ming, J. Huang, C. J. Zhang, Breaking down of healthcare system: Mathematical modelling for controlling the novel coronavirus (2019-nCoV) outbreak in Wuhan, China, bioRxiv, (2020). |
| [13] | National Health Commission of the People's Republic of China. Update on pneumonia in new coronavirus, 2020. Available from: http://www.nhc.gov.cn/xcs/xxgzbd/gzbd index.shtml. |
| [14] | Health Commission of Hubei Province. Update on pneumonia in new coronavirus, 2020. Available from: http://wjw.hubei.gov.cn/fbjd/tzgg/. |
| [15] | O. Diekmann, J. A. P. Heesterbeek, J. A. Metz, On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations, J. Math. Biol., 28 (1990), 365-382. |
| [16] |
P. Van den Driessche, J. Watmough, Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission, Math. Biosci., 180 (2002), 29-48. doi: 10.1016/S0025-5564(02)00108-6

|
| [17] | Q. Li, X. Guan, P. Wu, X. Wang, L. Zhou, Y. Tong, et al., Early transmission dynamics in Wuhan, China, of novel coronavirus-infected pneumonia, N. Engl. J. Med., (2020). |
| [18] |
S. Zhao, S. S. Musa, Q. Lin, J. Ran, G. Yang, W. Wang, et al., Estimating the unreported number of novel coronavirus (2019-nCoV) cases in China in the first half of January 2020: A data-driven modelling analysis of the early outbreak, J. Clin. Med., 9 (2020), 388. doi: 10.3390/jcm9020388

|
| [19] |
S. Zhao, Q. Lin, J. Ran, S. S. Musa, G. Yang, W. Wang, et al., Preliminary estimation of the basic reproduction number of novel coronavirus (2019-nCoV) in China, from 2019 to 2020: A data-driven analysis in the early phase of the outbreak, Int. J. Infect. Dis., 92 (2020), 214-217. doi: 10.1016/j.ijid.2020.01.050

|
| 1. | 雪萍 王, An Epidemic Model of COVID-19 Incorporating Both the Latent and the Asymptomatic Infectious, 2020, 09, 2324-7991, 700, 10.12677/AAM.2020.95083 | |
| 2. | Wei Wei, Bowen Duan, Min Zuo, Quanmin Zhu, An extended state observer based U-model control of the COVID-19, 2021, 00190578, 10.1016/j.isatra.2021.02.039 | |
| 3. | Nao Yamamoto, Bohan Jiang, Haiyan Wang, Quantifying compliance with COVID-19 mitigation policies in the US: A mathematical modeling study, 2021, 6, 24680427, 503, 10.1016/j.idm.2021.02.004 | |
| 4. | Bootan Rahman, Evar Sadraddin, Annamaria Porreca, The basic reproduction number of SARS‐CoV‐2 in Wuhan is about to die out, how about the rest of the World?, 2020, 30, 1052-9276, 10.1002/rmv.2111 | |
| 5. | Xiaolong Chen, Ruijie Wang, Dan Yang, Jiajun Xian, Qing Li, Chenquan Gan, Effects of the Awareness-Driven Individual Resource Allocation on the Epidemic Dynamics, 2020, 2020, 1099-0526, 1, 10.1155/2020/8861493 | |
| 6. | Guo-Rong Xing, Ming-Tao Li, Li Li, Gui-Quan Sun, The Impact of Population Migration on the Spread of COVID-19: A Case Study of Guangdong Province and Hunan Province in China, 2020, 8, 2296-424X, 10.3389/fphy.2020.587483 | |
| 7. | Jinhu Xu, Yan Geng, Dimitri Volchenkov, Dynamics of a Diffusive Multigroup SVIR Model with Nonlinear Incidence, 2020, 2020, 1099-0526, 1, 10.1155/2020/8847023 | |
| 8. | Nitin K Kamboj, Sangeeta Sharma, Sandeep Sharma, 2021, Chapter 16, 978-981-33-6263-5, 309, 10.1007/978-981-33-6264-2_16 | |
| 9. | Gauri Bhuju, Ganga Ram Phaijoo, Dil Bahadur Gurung, Modeling Transmission Dynamics of COVID-19 in Nepal, 2020, 08, 2327-4352, 2167, 10.4236/jamp.2020.810162 | |
| 10. | Linhe Zhu, Wenshan Liu, Zhengdi Zhang, Interplay between epidemic and information spreading on multiplex networks, 2021, 188, 03784754, 268, 10.1016/j.matcom.2021.04.017 | |
| 11. | Khagendra Adhikari, Ramesh Gautam, Anjana Pokharel, Kedar Nath Uprety, Naveen K. Vaidya, Transmission dynamics of COVID-19 in Nepal: Mathematical model uncovering effective controls, 2021, 521, 00225193, 110680, 10.1016/j.jtbi.2021.110680 | |
| 12. | Yanjun Zhao, Huilai Li, Wenxuan Li, Yang Wang, Global stability of a SEIR epidemic model with infectious force in latent period and infected period under discontinuous treatment strategy, 2021, 14, 1793-5245, 2150034, 10.1142/S1793524521500340 | |
| 13. | Jinhu Xu, Global dynamics for an SVEIR epidemic model with diffusion and nonlinear incidence rate, 2022, 2022, 1687-2770, 10.1186/s13661-022-01660-8 | |
| 14. | Mario Santana-Cibrian, Manuel A. Acuña-Zegarra, Marco Tulio Angulo, Andreu Comas-García, Esteban A. Hernández-Vargas, Jorge X. Velasco-Hernandez, 2022, Chapter 16, 978-3-030-72833-5, 543, 10.1007/978-3-030-72834-2_16 | |
| 15. | Sarita Bugalia, Jai Prakash Tripathi, Hao Wang, Mathematical modeling of intervention and low medical resource availability with delays: Applications to COVID-19 outbreaks in Spain and Italy, 2021, 18, 1551-0018, 5865, 10.3934/mbe.2021295 | |
| 16. | Vanshika Aggarwal, Geeta Arora, Homan Emadifar, Faraidun K. Hamasalh, Masoumeh Khademi, Sania Qureshi, Numerical Simulation to Predict COVID-19 Cases in Punjab, 2022, 2022, 1748-6718, 1, 10.1155/2022/7546393 | |
| 17. | M. A. El Safty, Samirah Al Zahrani, M. K. El-Bably, M. El Sayed, Soft -Rough Set and Its Applications in Decision Making of Coronavirus, 2022, 70, 1546-2226, 267, 10.32604/cmc.2022.019345 | |
| 18. | Shengtao Wang, Yan Li, Ximei Wang, Yuanyuan Zhang, Yiyi Yuan, Yong Li, Giulia Morsica, The Impact of Lockdown, Patient Classification, and the Large-Scale Case Screening on the Spread of the Coronavirus Disease 2019 (COVID-19) in Hubei, 2022, 2022, 2314-6141, 1, 10.1155/2022/8920117 | |
| 19. | Yujie Sheng, Jing-An Cui, Songbai Guo, The modeling and analysis of the COVID-19 pandemic with vaccination and isolation: a case study of Italy, 2023, 20, 1551-0018, 5966, 10.3934/mbe.2023258 | |
| 20. | Orwa Al-Abdulla, Agneta Kallström, Camilo Valderrama, Jussi Kauhanen, Simulation of the Progression of the COVID-19 Outbreak in Northwest Syria Using a Basic and Adjusted SIR Model, 2022, 2, 2813-0227, 44, 10.3390/zoonoticdis2020006 | |
| 21. | Indrajit Ghosh, Tanujit Chakraborty, An integrated deterministic–stochastic approach for forecasting the long-term trajectories of COVID-19, 2021, 12, 1793-9623, 2141001, 10.1142/S1793962321410014 | |
| 22. | Yan Liu, Qiuyan Yu, Haoyu Wen, Fang Shi, Fang Wang, Yudi Zhao, Qiumian Hong, Chuanhua Yu, What matters: non-pharmaceutical interventions for COVID-19 in Europe, 2022, 11, 2047-2994, 10.1186/s13756-021-01039-x | |
| 23. | M. El Sayed, M. A. El Safty, M. K. El-Bably, Topological approach for decision-making of COVID-19 infection via a nano-topology model, 2021, 6, 2473-6988, 7872, 10.3934/math.2021457 | |
| 24. | Yuanchen He, Yinzi Chen, Lin Yang, Ying Zhou, Run Ye, Xiling Wang, Ka Chun Chong, The impact of multi-level interventions on the second-wave SARS-CoV-2 transmission in China, 2022, 17, 1932-6203, e0274590, 10.1371/journal.pone.0274590 | |
| 25. | Youming Guo, Tingting Li, Modeling and dynamic analysis of novel coronavirus pneumonia (COVID-19) in China, 2022, 68, 1598-5865, 2641, 10.1007/s12190-021-01611-z | |
| 26. | 2023, 9780443186790, 229, 10.1016/B978-0-44-318679-0.00013-2 | |
| 27. | Jingli Ren, Haiyan Wang, 2023, 9780443186790, 173, 10.1016/B978-0-44-318679-0.00012-0 | |
| 28. | Jinxing Guan, Yang Zhao, Yongyue Wei, Sipeng Shen, Dongfang You, Ruyang Zhang, Theis Lange, Feng Chen, Transmission dynamics model and the coronavirus disease 2019 epidemic: applications and challenges, 2022, 2, 2749-9642, 89, 10.1515/mr-2021-0022 | |
| 29. | S. A. Alblowi, M. El Sayed, M. A. El Safty, Decision Making Based on Fuzzy Soft Sets and Its Application in COVID-19, 2021, 30, 1079-8587, 961, 10.32604/iasc.2021.018242 | |
| 30. | Yanjun Zhao, Wenxuan Li, Yang Wang, 2023, 9780323995573, 323, 10.1016/B978-0-32-399557-3.00017-X | |
| 31. | Yong Zhou, Yiming Ding, Minrui Guo, Path analysis method in an epidemic model and stability analysis, 2023, 11, 2296-424X, 10.3389/fphy.2023.1158814 | |
| 32. | Silu Chen, Jiangping Chen, Tianyou Cheng, Gang Xu, An Improved SEIR Model Considering Contact Restrictions to Simulate the COVID-19 Epidemic in Wuhan, 2022, 1556-5068, 10.2139/ssrn.4105112 | |
| 33. | Elhadi E. Elamir, M. El Sayed, A.N. Al Qarni, M.A. El Safty, Decision-making to limit epidemics spread based on fuzzy-soft and topological spaces, 2023, 74, 11100168, 725, 10.1016/j.aej.2023.05.045 | |
| 34. | Lei Shi, Ziang Chen, Peng Wu, Spatial and temporal dynamics of COVID-19 with nonlocal dispersal in heterogeneous environment: Modeling, analysis and simulation, 2023, 174, 09600779, 113891, 10.1016/j.chaos.2023.113891 | |
| 35. | Huayan Pei, Ying Ding, Guanghui Yan, Impact of information adoption and the resulted self-protective actions on epidemic spreading in awareness-disease coupled multiplex networks, 2024, 97, 1434-6028, 10.1140/epjb/s10051-024-00693-5 | |
| 36. | Jing Wang, Hongyong Zhao, Threshold dynamics and regional optimal control of a malaria model with spatial heterogeneity and ivermectin therapy, 2024, 125, 0307904X, 591, 10.1016/j.apm.2023.09.006 | |
| 37. | Lu Lan, Gao Qisheng, Zhan Chenglin, Influence Mechanism Analysis of the Spatial Evolution of Inter-Provincial Population Flow in China Based on Epidemic Prevention and Control, 2023, 42, 0167-5923, 10.1007/s11113-023-09780-4 | |
| 38. | Kamlesh Sarkar, Xiang-Sheng Wang, Data Fixing by Data Fitting: Estimating the Unreported Cases During the Early COVID-19 Outbreak in Hubei, China, 2024, 20, 1927-5129, 92, 10.29169/1927-5129.2024.20.09 | |
| 39. | Peng Wu, Zhaosheng Feng, Global dynamics of a space-age structured covid-19 model coupling within-host infection and between-host transmission, 2024, 131, 10075704, 107801, 10.1016/j.cnsns.2023.107801 | |
| 40. | Hui Yang, Zhaojian Wang, Ying Zhang, Man Xu, Yushu Wang, Yi Zhang, Xuefeng Liu, Zhuoling An, Zhaohui Tong, Clinical characteristics and factors for serious outcomes among outpatients infected with the Omicron subvariant BF.7, 2023, 95, 0146-6615, 10.1002/jmv.28977 | |
| 41. | Berend H. H. Beishuizen, Mart L Stein, Joeri S Buis, Alma Tostmann, Caroline Green, James Duggan, Máire A Connolly, Chantal P Rovers, Aura Timen, Identifying essential resource parameters for pandemic preparedness and response: an international Delphi study within the EU PANDEM-2 project, 2024, 14, 2044-6055, e079609, 10.1136/bmjopen-2023-079609 | |
| 42. | Yicheng Hao, Yantao Luo, Zhidong Teng, Role of limited medical resources in an epidemic model with media report and general birth rate, 2025, 10, 24680427, 522, 10.1016/j.idm.2025.01.001 | |
| 43. | Alphonse Houssou Hounye, Xiaogao Pan, Yuqi Zhao, Cong Cao, Jiaoju Wang, Abidi Mimi Venunye, Li Xiong, Xiangping Chai, Muzhou Hou, Significance of supervision sampling in control of communicable respiratory disease simulated by a new model during different stages of the disease, 2025, 15, 2045-2322, 10.1038/s41598-025-86739-9 | |
| 44. | Jing Wang, Hongyong Zhao, Regional optimization problem for a general reaction–diffusion malaria model with temperature and rainfall, 2025, 09473580, 101198, 10.1016/j.ejcon.2025.101198 |
| Parameter | Description | Value | Source |
| c | Contact rate (Day−1) | 13.8 | Assumption |
| β | Transmission probability of I2 per contact (Dimensionless) | 0.036 | Estimation |
| 1ξ | Pre-stage exposed period (Day) | 1.52 | Estimation |
| 1σ | Post-stage exposed period (Day) | 6.67 | Estimation |
| a | Proportion of post-stage exposed class entering I1 compartment (Dimensionless) | 0.8 | Calculation [14] |
| δ | Transition rate from infectious cases with mild symptoms to infectious cases with serious symptoms (Day−1) | 0.2 | Estimation |
| η10 | Average hospitalization rate of infectious cases with mild symptoms between Jan. 23rd and Feb. 3rd (Day−1) | 0.31 | Assumption |
| η11 | Maximum hospitalization rate of infectious cases with mild symptoms (Day−1) | 0.93 | Estimation |
| η20 | Average hospitalization rate of infectious cases with serious symptoms between Jan. 23rd and Feb. 3rd (Day−1) | 0.7 | Assumption |
| η21 | Maximum hospitalization rate of infectious cases with serious symptoms (Day−1) | 0.98 | Estimation |
| r1 | Recovery rate of infectious cases with mild symptoms (Day−1) | 112.5 | [12] |
| rh | Recovery rate of hospitalized cases (Day−1) | 0.05 | Estimation |
| dI | Disease-related death rate of infectious cases with serious symptoms (Day−1) | 0.055 | Assumption [13] |
| dh | Disease-related death rate of hospitalized cases (Day−1) | 0.049 | Assumption [13] |
| p0 | The initial unquarantined proportion of post-stage exposed individuals (Dimensionless) | 0.76 | Estimation |
| p1 | The minimum unquarantined proportion of post-stage exposed individuals (Dimensionless) | 0.00608 | Estimation |
| θe | Modification parameter or infectious reduction factor (Dimensionless) | 0.72 | Estimation |
| θ1 | Modification parameter or infectious reduction factor (Dimensionless) | 0.87 | Estimation |
| m0 | The exponential decreasing rate of the unquarantined proportion of E2 due to sealing off the city (Dimensionless) | 0.02 | Estimation |
| m1 | The exponential decreasing rate of the unquarantined proportion of E2 due to opening the 'Fire God Hill' hospital (Dimensionless) | 0.19 | Estimation |
| m2 | The exponential decreasing rate of contact rate of I1 and I2 to S due to opening the 'Fire God Hill' hospital (Dimensionless) | 0.22 | Estimation |
| m3 | The exponential decreasing rate of period of arranged for hospitalization of I1 and I2 (Dimensionless) | 0.3 | Estimation |
| ϵ1 | Minimum proportion of contact rate of I1 and I2 to S due to opening the 'Fire God Hill' hospital (Dimensionless) | 0.1 | Estimation |
| τ1 | The time for sealing off the city (Dimensionless) | 0 | Calculation |
| τ2 | The time for opening the 'Fire God Hill' hospital (Dimensionless) | 12 | Calculation |
| E1(0) | The initial number of pre-stage exposed individuals (Dimensionless) | 1800 | Estimation |
| Parameter | Description | Value | Source |
| c | Contact rate (Day−1) | 13.8 | Assumption |
| β | Transmission probability of I2 per contact (Dimensionless) | 0.036 | Estimation |
| 1ξ | Pre-stage exposed period (Day) | 1.52 | Estimation |
| 1σ | Post-stage exposed period (Day) | 6.67 | Estimation |
| a | Proportion of post-stage exposed class entering I1 compartment (Dimensionless) | 0.8 | Calculation [14] |
| δ | Transition rate from infectious cases with mild symptoms to infectious cases with serious symptoms (Day−1) | 0.2 | Estimation |
| η10 | Average hospitalization rate of infectious cases with mild symptoms between Jan. 23rd and Feb. 3rd (Day−1) | 0.31 | Assumption |
| η11 | Maximum hospitalization rate of infectious cases with mild symptoms (Day−1) | 0.93 | Estimation |
| η20 | Average hospitalization rate of infectious cases with serious symptoms between Jan. 23rd and Feb. 3rd (Day−1) | 0.7 | Assumption |
| η21 | Maximum hospitalization rate of infectious cases with serious symptoms (Day−1) | 0.98 | Estimation |
| r1 | Recovery rate of infectious cases with mild symptoms (Day−1) | 112.5 | [12] |
| rh | Recovery rate of hospitalized cases (Day−1) | 0.05 | Estimation |
| dI | Disease-related death rate of infectious cases with serious symptoms (Day−1) | 0.055 | Assumption [13] |
| dh | Disease-related death rate of hospitalized cases (Day−1) | 0.049 | Assumption [13] |
| p0 | The initial unquarantined proportion of post-stage exposed individuals (Dimensionless) | 0.76 | Estimation |
| p1 | The minimum unquarantined proportion of post-stage exposed individuals (Dimensionless) | 0.00608 | Estimation |
| θe | Modification parameter or infectious reduction factor (Dimensionless) | 0.72 | Estimation |
| θ1 | Modification parameter or infectious reduction factor (Dimensionless) | 0.87 | Estimation |
| m0 | The exponential decreasing rate of the unquarantined proportion of E2 due to sealing off the city (Dimensionless) | 0.02 | Estimation |
| m1 | The exponential decreasing rate of the unquarantined proportion of E2 due to opening the 'Fire God Hill' hospital (Dimensionless) | 0.19 | Estimation |
| m2 | The exponential decreasing rate of contact rate of I1 and I2 to S due to opening the 'Fire God Hill' hospital (Dimensionless) | 0.22 | Estimation |
| m3 | The exponential decreasing rate of period of arranged for hospitalization of I1 and I2 (Dimensionless) | 0.3 | Estimation |
| ϵ1 | Minimum proportion of contact rate of I1 and I2 to S due to opening the 'Fire God Hill' hospital (Dimensionless) | 0.1 | Estimation |
| τ1 | The time for sealing off the city (Dimensionless) | 0 | Calculation |
| τ2 | The time for opening the 'Fire God Hill' hospital (Dimensionless) | 12 | Calculation |
| E1(0) | The initial number of pre-stage exposed individuals (Dimensionless) | 1800 | Estimation |