Two-stage network data envelopment analysis production games

1.   Introduction

As a classic data-oriented mathematical programming approach ^[17], DEA (Data Envelopment Analysis), proposed by Charnes et al. ^[5], is a very useful non-parametric method to simulate the production frontier and reflect the production technology as well as measure the relative efficiency of units that consume multiple inputs to produce multiple outputs ^[23,25]. The DEA method has been extensively applied in many management decision-making fields ^[1,9,15,36].

According to DEA theory, the PPS (Production Possibility Set) is inferred from the known input and output vectors of DMUs (Decision-Making Units), and then the production technology is expressed by the frontier of the PPS. In traditional DEA models, the frontier of the PPS is often used to assess the relative efficiency of each DMU. For the inefficient DMU, the input reductions or output increases can be obtained through projecting the DMUs onto the efficient frontier of the PPS. Furthermore, the efficient frontier of the PPS can be extended outward if other DMUs with fewer inputs and more outputs are added into the PPS ^[21,31,39]. Therefore, the larger the set of input-output data is available, the more complete the description of the PPS is and the more reliable the estimation of the true efficient frontier is ^[27]. Frequently, when the organization can only use its own observed DMUs, the input reductions and output increases that can be obtained are limited and are lower than those that might be obtained if the input-output data of the observed DMUs of different organizations are pooled in order to obtain a better estimation of the PPS.

Inspired by the above characteristics of PPS, DEA production games are proposed by Lozano ^[28]. These games are expressed by the cooperative linear production models in which a set of observations (DMUs) of the production organization are employed to express the current production technology by the frontier of the PPS. Different organizations are assumed to possess their own technologies, and cooperative games arise from the possibility of pooling their available resources and (or) merging their respective technologies. Furthermore, according to the characters of these production games, the revenue of coalitions are allocated on the basis of the nucleolus and Owen set solutions. DEA production games are shown to be proper generalizations of the related linear production games, such as the Linear Production (LP) games of Owen ^[32], the Non-Centralized Linear Production (NCLP) games of Fernández et al. ^[11], and the extended Linear Transformation of Products (LTP) games of Timmer et al. ^[37].

DEA production games give answers to the problems of both cooperative manners and revenue allocation schemes among production organizations. Furthermore, the research methods of sharing resources and technologies provided in DEA production games have important practical application values. In practice, common resources, such as capital, materials, labor and information, and technologies are usually the basic and important factors for production organizations to gain revenues ^[12]. Using the resources and technologies jointly can bring more profit than using them separately ^[14]. Specifically, according to the principle of collaboration, whenever some organizations have redundant resources or lack the advanced productive technologies, pooling their resources and (or) sharing their technologies may lead to higher cooperative benefits. This creates a win-win situation of cooperation.

In view of the theoretical and application values of DEA production games, many scholars have done further research and discussion on DEA production games. Lozano et al. ^[29] proposed set-valued DEA production games for the situation of the price in which at least one output is unreliable or unavailable. Borrero et al. ^[4] established the links between the class of DEA production games and the classes of linear programming games and linear production games. Moreover, they analyzed the Owen set of DEA production games and discussed the interpretation of these allocations for different levels of the cooperation between the agents. Furthermore, for selecting the best cooperative partner (DMU), Wu et al. ^[40] considered the problem of reallocating the pooled input resources based on cooperative game theory in two scenarios, one of which was resource pooling, and the other was best-practice sharing. Hinojosa et al. ^[15] extended DEA production games to the case of fuzzy unit output prices and introduced the Preference Least Core solution concept for these fuzzy games. They obtained the fuzzy total revenue of the grand coalition and a fuzzy allocation in the preference least core by solving a single linear programming model.

Although the works mentioned above have given detailed and embedded study on DEA production games, the production organization is always regarded as a "black box" and their internal structures are ignored. With the continuous expansion of the production scale, the internal structures of the production process are becoming more and more complex. The structure of the production organization not only affects its own benefits, but also relates to the cooperation among organizations. Consequently, opening the "black box" of the production process is necessary. DEA production games with internal structure are worthy of further study and discussion.

Färe and Grosskopf ^[10] opened the "black box" and established network DEA theory. Network DEA considers the internal structures of production organizations and can provide more meaningful and informative results compared with traditional DEA ^[20]. From then on, many researchers have started to look into the internal structures and analyze the relationship among different stages ^{[6,19,20,21,24,26]}. According to the types of the structure of production process, Kao ^[19] provided a thorough classification of network DEA, in which the series process and the parallel process are two typical structures studied extensively in the literature. In the study of these two typical structures, the two-stage network structure is the simplest; hence, it is popular and has been widely researched by scholars. Yang et al. ^[41] proposed the two-level network DEA model to evaluate efficiencies of all divisions as well as all DMUs at the same time based on the weak-link approach and the maximin ratio efficiency model, respectively. Furthermore, they discussed the cross-efficiency evaluation problem in the framework of the two-level maximin network DEA model.

Recently, combining network DEA theory with game theory, and especially with cooperative game theory, is a hot research topic in the field of network DEA. The research problems mainly focus on the evaluation of efficiency for each individual stage and the decomposition of the efficiency for the overall multi-stage process, as well as the resource or cost allocation among different sub-stages ^{[2,8,18,22,30,43]}. The approaches of solving these problems can be roughly divided into two categories. One is known as the centralized approach, and the other is the decentralized (or non-cooperative) approach ^[26]. The centralized method is based on the cooperative game from the aspect of system optimization, supposing that the whole production organization is arranged by a central controller. On the contrary, from the perspective of individual optimum, the decentralized approach assumes that different stages have different priorities which are characterized by the Stackelberg or leader-follower game ^[31]. Considering a two-stage network structure, Li, Zhu, & Chen ^[22] used the DEA methodology to determine the relative efficiency by taking the internal structure and possible allocated costs into account. Moreover, they demonstrated the existence of an efficient allocation set based on a common weight, which leads all DMUs as well as their sub-stages to be simultaneously efficient. From the point of view of size, they provided an algorithm by repeatedly minimizing the maximum deviation between the efficient allocations and size allocations, thus guaranteeing the uniqueness of the final allocation. An, Wen, Ding, et al. ^[3] considered a three-stage system in which the resource sharing exists among various stages. They constructed network models to calculate the potential gains obtained after the resource pooling, and allocate the increased profits among stages based on the Shapely value. Wen et al. ^[39] explored the internal cooperation in a double-level system from the perspective of relative performance and proposed double-level DEA game models. They proved that these new games have the characters of monotone, super-additive, and have non-empty core.

In practical cases, we often encounter such problems that, in the start-up stage of a new enterprise, some shareholders invest in common resources and some invest in technologies such as knowledge and skills. The participation manners of the shareholders will affect the revenue of the enterprise. At the same time, whether the income allocation is fair or not, in return, will directly affect the stability of operation of the enterprise.

From the literature review described above, we know that the previous studies on the combination of game theory and network DEA have made much achievement, yet there is little literature on the cooperative manners among multi-stage production organizations. Therefore, we propose the two-stage network DEA (NDEA) production games so as to fill in this gap.

In this paper, we combine DEA production games with network DEA theory and focus on the series structure production process. We study the problems of the revenue of alliance in different cooperative manners, specifically resource pooling and (or) technology sharing, and consider seven types of cooperation among organizations. We also prove the properties of the proposed production games and illustrate the applicability of the proposed models by a numerical example and an empirical example. Our main contributions are as follows:

1) Formulating NDEA production games in a two-stage series environment.

2) Considering initial resources and technology sharing in each production process of the organization.

3) Establishing seven NDEA production models according to seven types of cooperation.

4) Proving the properties of two-stage DEA production games: super-additive property, totally balanced property, and having a non-empty core.

5) Allocating the coalition revenue among organizations based on the nucleolus and the Owen set.

6) Demonstrating the validity of the proposed methods by using a numerical example and an empirical application.

The rest of this paper is organized as follows: In Section 2, we introduce some basic notations for two-stage network DEA models. In Section 3, we identify seven types of cooperation by considering the cooperative manners among each corresponding stage. In Section 4, we prove the properties of the characteristic function of the proposed cooperative production games, such as the super-additive property. Furthermore, we prove that the seven NDEA production games proposed by us can be expressed as linear programming games (LPGG). Therefore, they are totally balanced games and have stable revenue allocation solutions. In Section 5, based on the nucleolus and the Owen set, a numerical example and an empirical application of 17 commercial bank branches of the China Construction Bank in the Anhui Province are presented to illustrate the applicability of the proposed approach. Finally, some conclusions are drawn in Section 6 and several issues for further research are suggested.

2.   Preliminaries

In this section, we introduce the definitions of core, the nucleolus and the Owen set. Furthermore, we give the two-stage production process and present a two-stage network DEA model with the goal of maximizing the production organization revenue.

Definition 2.1. ^[33] For a game $(N, v)$, a payoff distribution $x = ({x}_{1}, \cdots , {x}_{n})\in {\mathrm{R}}^{\mathrm{n}}$ is

● Efficient if $x\left(N\right) = v\left(N\right)$;

● Individually rational if ${x}_{i}\ge v\left(\right\{i\left\}\right)$ for all $i\in N$;

● Coalitionally rational if $x\left(S\right)\ge v\left(S\right)$ for all nonempty coalitions $S$.

The core of $(N, v)$ is the set

So, the core of $(N, v)$ is the set of all efficient and coalitionally rational payoff distributions.

Definition 2.2. ^[33] The nucleolus of an essential game $(N, v)$ is defined as follows: First, for every imputation $x$, compute all excesses. Then, select those imputations for which the maximal excesses are the smallest. If this is the case at a unique imputation, then that imputation is the nucleolus of the game. If not, then consider the second maximal excesses of the selected imputations and make a further selection by taking those imputations for which these second maximal excesses are smallest. If this happens at a unique imputation, then that is the nucleolus. Otherwise, continue with the third maximal excesses, etc., until a unique imputation is found: this is the nucleolus.

Definition 2.3. ^[38] Let $(\mathrm{A}, \;\mathrm{B}, \;\mathrm{c})\in \mathcal{L}.$ The Owen set of $(\mathrm{A}, \;\mathrm{B}, \;\mathrm{c})$ is defined as Owen $(\mathrm{A}, \;\mathrm{B}, \;\mathrm{c}): = \left\{y\mathrm{B}|y\in {\mathrm{O}}_{\mathrm{m}\mathrm{i}\mathrm{n}}(\mathrm{A}, \mathrm{B}, \mathrm{c})\right\}$.

The vectors of ${\mathrm{O}}_{\mathrm{m}\mathrm{i}\mathrm{n}}(\mathrm{A}, \mathrm{B}, \mathrm{c})$ can be seen as the shadow prices for the resources. The agents are paid for their resources according to the shadow price vector, which yields an Owen vector.

Suppose that there are $n$ independent and homogeneous organizations ${O}_{i}(i\in N = \left\{1, ..., n\right\})$ with two-stage internal structure, and each organization $i$ has $K\left(i\right) (i\in N)$ observed values, denoted as ${DMU}_{j}, j = 1, ..., K\left(i\right)$. The production process of each organization is shown in Figure 1, where $X = {({x}_{1}, {x}_{2}, ..., {x}_{m})}^{T}$ denotes the $m$ initial inputs, $Y = {({y}_{1}, {y}_{2}, ..., {y}_{s})}^{T}$ represents the $s$ intermediate products, and ${Z = ({z}_{1}, {z}_{2}, ..., {z}_{t})}^{T}$ stands for the $t$ final outputs. Specifically, ${X}_{j}\left(i\right)$, ${Y}_{j}\left(i\right)$, and ${Z}_{j}\left(i\right)$ ($j = 1, ..., K\left(i\right)$) are the observed values corresponding to the initial inputs, the intermediate products, and the final outputs of the organization ${O}_{i}$, respectively. For each organization $i\in N$, we denote $D\left(i\right) = \left\{\right({X}_{j}\left(i\right), {Y}_{j}\left(i\right), {Z}_{j}\left(i\right))\in {R}^{m}\times {R}^{s}\times {R}^{t}, j = 1, ..., K(i\left)\right\}$ as the corresponding set of recorded observations. We denote $X\left(i\right) = \left[{X}_{1}\right(i), ..., {X}_{K\left(i\right)}(i\left)\right]\in {R}^{m\times K\left(i\right)}$, $Y\left(i\right) = \left[{Y}_{1}\right(i), ..., {Y}_{K\left(i\right)}(i\left)\right]\in {R}^{s\times K\left(i\right)}$, and $Z\left(i\right) = \left[{Z}_{1}\right(i), ..., {Z}_{K\left(i\right)}(i\left)\right]\in {R}^{t\times K\left(i\right)}$. Furthermore, we use $B\left(i\right)$ to indicate the initial resource of ${O}_{i}$ ($i = 1, ..., n$), $F\left(i\right)$ to represent the number of facilities that belong to ${O}_{i}$, and ${P}_{f}\left(i\right)$ to denote the prices of the final outputs decided by the facility $f$ of ${O}_{i}$.

According to the observed $DMUs$ of each organization, we establish the network DEA model for the organization ${O}_{i}(i = 1, ..., n)$ to maximize its revenue. For simplicity, we denote the production process of the discussed organization ${O}_{i}$ as $\left({X}_{0}^{f}\right(i), {Y}_{0}^{f}(i), {Z}_{0}^{f}(i\left)\right)$ $(f = \mathrm{1, 2}, ..., F(i\left)\right)$. It can also be regarded as the prediction of the input and output of each stage under the goal of maximizing the revenue of the organization ${O}_{i}$. Based on network DEA theory, by using the current technology which is expressed by the frontier of the production possibility set (PPS), we can forecast the maximal revenue $R\left(i\right)$ of the discussed organization with resource constraint. The current technology of ${O}_{i}$ is expressed by the frontier of the PPS, which is given as

With the similar notations to that of the single-stage model ^[28], the two-stage model for the organization ${O}_{i}$ is constructed as

where ${\lambda }_{j}^{f}\left(i\right)$ and ${\mu }_{j}^{f}\left(i\right)$ represent the parameters for the first stage and the second stage of facility $f$ of ${O}_{i}$, respectively.

We assume that both stages are with variable returns to scale, which are demonstrated by the constraints $\sum _{j = 1}^{K\left(i\right)}{\lambda }_{j}^{f}\left(i\right) = 1$ and $\sum _{j = 1}^{K\left(i\right)}{\mu }_{j}^{f}\left(i\right) = 1$. Based on this linear programming model, the organization ${O}_{i}$ can plan its production process with $({X}_{0}^{f}(i), {Y}_{0}^{f}(i), {Z}_{0}^{f}(i))$ by using its own current technology, and gains maximal revenue $R\left(i\right)$ with the resource constraint $\sum _{f = 1}^{F\left(i\right)}{X}_{0}^{f}\left(i\right)\le B\left(i\right)$.

For intuition, we give the main indices, parameters, and decision variables mentioned above in Table 1.

3.   Cooperative game models for the two-stage production process

In this section, according to different cooperation manners, we identify seven distinct types of cooperation of organizations with a two-stage process.

For the $n$ independent and homogeneous organizations with two-stage structure, we consider that the organizations can cooperate with each other to form an alliance through the styles of resource-pooling and technology-sharing of each stage. We establish the cooperative game models of maximizing revenues of the coalitions to indicate seven cooperative styles, by which the maximal revenue corresponding to each alliance member is calculated. In the following, we denote coalition $S$ as a subset of $N$, which is the set of all the organizations under consideration, and propose seven types of models for coalition $S$. It should be noted that, since we assume that the intermediate product could not be disposed freely, only the initial inputs could be shared in resource-pooling. As a result, resource sharing only occurs in the first stage. It is reasonable not to consider the resource sharing of intermediate products, because for the two-stage production process, the intermediate products are only the connection products of the first and the second stages, and usually do not enter the market circulation.

We present the cooperative manner corresponding to these seven types respectively through Table 2.

For each coalition $S\subseteq N$, we denote $D\left(S\right) = {\bigcup }_{i\in S}D\left(i\right)$, $K\left(S\right) = {\sum }_{i\in S}K\left(i\right)$, $F\left(S\right) = {\sum }_{i\in S}F\left(i\right)$, and $B\left(S\right) = {\sum }_{i\in S}B\left(i\right)$. Moreover, we use $X\left(S\right) = {\bigcup }_{i\in S}X\left(i\right)\in {R}^{m\times K\left(S\right)}$, $Y\left(S\right) = {\bigcup }_{i\in S}Y\left(i\right)\in {R}^{s\times K\left(S\right)}$, and $Z\left(S\right) = {\bigcup }_{i\in S}Z\left(i\right)\in {R}^{t\times K\left(S\right)}$ to express the matrix whose columns are all the observed initial inputs, the intermediate products, and the final outputs of all the members of coalition $S$, respectively. If we denote $\left|S\right|$ to be the number of players in $S$, then we can relabel the players in $S$ as 1, 2, ..., $\left|S\right|$. Moreover, we assume that $X\left(S\right), Y\left(S\right), \;\mathrm{a}\mathrm{n}\mathrm{d}\;\;Z\left(S\right)$ are in the order in which the recorded observations of coalition $S$ are arranged.

We establish the models of maximizing revenues of coalitions corresponding to the seven types, by which the maximal revenue for each coalition is calculated. The models for the seven types are described in detail as follows:

Type 1. Only the first stage shares the resource, while the second stage keeps everything isolated. The revenue model for coalition S is presented as

In model $\left({P}_{1}\right(\mathrm{S}\left)\right)$, the objective function is to maximize the revenue of coalition S. In the constraint conditions, inequalities (1.1) and (1.2) mean that each organization ${O}_{i}$ in coalition $S$ keeps its own technology level unchanged in the first stage, but they pool their initial resource together and form an alliance, which is illustrated by inequality (1.5). Meanwhile, inequality (1.5) means that the total amount of initial resources consumed cannot exceed the total amount resulting from the pooling of resources available to coalition $S$. Furthermore, inequalities (1.3) and (1.4) imply that the second stage of each organization ${O}_{i}$ keeps its own technical level unchanged. Without loss of generality, we suppose the production processes are with variable returns to scale, and this can be seen from constraint conditions (1.6)–(1.8).

Type 2. Only the first stage shares the technology, while the second stage keeps everything isolated. The revenue model for coalition S is expressed by model $\left({P}_{2}\right(S\left)\right)$.

In the model of technology sharing, it is important to note that there will be changes in the representation of weight parameters and recorded observations compared with models that only share resources. For example, for $S = \left\{\mathrm{1, 2}\right\}$, each organization has two recorded observations and two facilities, i.e., $K\left(i\right) = 2$ and $F\left(i\right) = 2,\; \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}\;i = \mathrm{1, 2}.$ In this case, there are 4 recorded observations, and the inputs for each observation are ${X}_{1}\left(1\right), {X}_{2}\left(1\right), {X}_{1}\left(2\right),\; \;\mathrm{a}\mathrm{n}\mathrm{d}\;\;{X}_{2}\left(2\right),$ respectively. The decision constraint for organization $i$ and factory $f$ is expressed by the inequality

i.e., $\sum\limits_{h \in S} {\sum\limits_{j = 1}^{K(i)} {\lambda _j^{i, f}(h){X_j}(h)} } \leqslant X_0^f(i)$. Therefore, the model $\left({P}_{2}\right(S\left)\right)$ for the first-stage technology sharing can be expressed as

In this type, the coalition is formed by the way of technology-sharing of the first stage, which can be reflected by inequalities (2.1), (2.2), and (2.6). In this scenario the cooperating organizations share their best practices so that "all the facilities of the coalition can operate at operation points that are feasible in the expanded joint technology that results from merging their respective technologies" ^[28].

Type 3. Only the first stage shares both the resource and the technology, while the second stage keeps everything isolated. We give the revenue model for coalition S as

Comparing inequality (2.5) with (3.5), we can find the difference between the models (${P}_{2}\left(S\right)$) and (${P}_{3}\left(S\right)$). In the model (${P}_{3}\left(S\right)$), there is resource-sharing of the first stage among organizations of the alliance, but not in the model (${P}_{2}\left(S\right)$).

Type 4. Only the second stage shares the technology, while the first stage keeps everything isolated. The revenue model for the coalition S is given as

Similar to Type 2, in the model (${P}_{4}\left(S\right)$), we use inequalities (4.3), (4.4), and (4.7) to express the second stage adopting technology sharing of each organization in coalition $S$.

Type 5. The first stage only shares the resources, and the second stage only shares the technology. We use the model (${P}_{5}\left(S\right)$) to express this scenario:

In the model (${P}_{5}\left(S\right)$), from the constraints it is not difficult to see that Type 5 is a combination of Types 1 and 4. Constraint inequalities (5.1), (5.2), and (5.5) reflect that the cooperation mode of Stage 1 is resource pooling. Meanwhile, inequalities (5.3), (5.4), and (5.7) show that stage 2 cooperates in a technology-sharing manner.

Type 6. The two stages only share the technology, and keep the resources isolated. The revenue model for coalition S is given as

The constraints of the sixth model (${P}_{6}\left(S\right)$) exhibit the scenario of technical cooperation in both stages. Among them, constraints (6.1), (6.2), and (6.6) give the technology sharing in the first stage, and the similar constraints (6.3), (6.4), and (6.7) reflect the second stage. Furthermore, inequality (6.5) indicates that the initial resources are not shared.

Type 7. The first stage shares the resources, and both stages share the technology. The revenue model for coalition S is given as

This situation is the most beneficial for the coalition, because it is the most adequate way of cooperation; at the same time, it is also the most difficult to achieve since it needs to be based on a higher degree of trust and participation than any other cooperation types. Constraints (7.1), (7.2), and (7.6), as well as inequality (7.5), illustrate the technical cooperation and resource pooling between the first stages of each organization in the alliance, respectively. Technology sharing is implemented between the second stage of each member in coalition $S$, which can be expressed by inequalities (7.3), (7.4), and (7.7).

So far, under the styles of resource pooling and technology sharing, we have developed seven models of cooperative games with two-stage production processes. Then, a natural question is: what characteristics do these games have? We discuss this issue in the following section.

4.   Properties of cooperative production games

In this section, we discuss two issues: one is the basic properties of the seven NDEA production games, including the super-additive property and the relationships among the seven types of NDEA; the other is the relationship between our NDEA production games and the linear production games in the two-stage scenario, and we draw the conclusion that the NDEA production games are equivalent to the linear production games, and thus the NDEA production games are totally balanced.

4.1.   Basic properties of the seven NDEA production games

In this subsection, we show the properties of the production games proposed in Section 3. For simplicity, we denote the cooperative problems as $(N, R)$, in which the characteristic functions of the cooperative games are the revenue function $R$ of coalition $S$, and, corresponding to the seven models, $R$ can be expressed by ${R^I}(S), {R^{II}}(S), \cdots , {R^{VII}}(S),$ respectively.

It is obvious that when coalition $S$ consists of a single organization $i$, i.e., there is no cooperation among organizations, then these seven types are accordant and coincide with the situation expressed by the programming $\left({P}_{0}\right(i\left)\right)$. Furthermore, it is easy to check that the proposed cooperation game $(N, R)$ is monotonic, i.e., the larger the coalition, the more revenue it gets. This property can be expressed mathematically as

Other properties of the seven proposed DEA production games are given by the following propositions:

Proposition 1. The seven cooperative production games with two-stage processes are super-additive, i.e.,

Proof. For simplicity, we give a detailed proof for Type 1, and the other six types can be proved similarly.

For the disjoint coalitions $S{'}$ and $S{'}{'}$, we let

and

be the optimal solutions of the models $\left({P}_{1}\right(S{'}\left)\right)$ and $\left({P}_{1}\right(S{'}{'}\left)\right)$, respectively. Let organization $i$ belong to the coalition $S{'}\cup S{'}{'}$. Then, the solution $\left\{{\widetilde{\lambda }}_{j}^{f}\left(i\right), {\widetilde{\mu }}_{j}^{f}\left(i\right), {\widetilde{X}}_{0}^{f}\left(i\right), {\widetilde{Y}}_{0}^{f}\left(i\right), {\widetilde{Z}}_{0}^{f}\left(i\right)\right\}$ of the form

and

is a feasible solution to $\left({P}_{1}\right(S{'}\cup S{'}{'}\left)\right)$. Corresponding to this feasible solution, the value of the objective function for the coalition $S{'}\cup S{'}{'}$ is expressed by

According to (c), we can see that, if $i\in S{'}$, then ${[\widetilde{X}}_{0}^{f}\left(i\right), {\widetilde{Y}}_{0}^{f}\left(i\right), {\widetilde{Z}}_{0}^{f}\left(i\right)] = {\left[{X}_{0}^{f}\right(i), {Y}_{0}^{f}(i), {Z}_{0}^{f}(i\left)\right]}_{S{'}}^{*}$ is the optimal solution to the model ${(P}_{1}\left(S{'}\right))$, which means $\sum _{i\in S{'}}\sum _{f = 1}^{F\left(i\right)}{{P}_{f}\left(i\right)}^{T}{\widetilde{Z}}_{0}^{f}\left(i\right) = {R}^{I}\left(S{'}\right)$ is the optimal value of the model ${(P}_{1}\left(S{'}\right))$; meanwhile, if $i\in S{'}{'}$, then ${{[\widetilde{X}}_{0}^{f}\left(i\right), {\widetilde{Y}}_{0}^{f}\left(i\right), {\widetilde{Z}}_{0}^{f}\left(i\right)] = [{X}_{0}^{f}\left(i\right), {Y}_{0}^{f}\left(i\right), {Z}_{0}^{f}\left(i\right)]}_{S{'}{'}}^{*}$ is the optimal solution to the model $\left({P}_{1}\right(S{'}{'}\left)\right)$, and so $\sum _{i\in S{'}{'}}\sum _{f = 1}^{F\left(i\right)}{{P}_{f}\left(i\right)}^{T}{\widetilde{Z}}_{0}^{f}\left(i\right) = {R}^{I}\left(S{'}{'}\right)$ is the corresponding optimal value. As a result,

This inequality means that the game $(N, {R}^{I})$ is super-additive. The results for the other six types are analogous, and hence the proof is completed.

It should be noted that, since the the solution $\left\{{\widetilde{\lambda }}_{j}^{f}\left(i\right), {\widetilde{\mu }}_{j}^{f}\left(i\right), {\widetilde{X}}_{0}^{f}\left(i\right), {\widetilde{Y}}_{0}^{f}\left(i\right), {\widetilde{Z}}_{0}^{f}\left(i\right)\right\}$ may not be a feasible solution to the model $\left({P}_{1}\right({S}^{{'}}\bigcap {S}^{{'}{'}}\left)\right)$, as a result we cannot draw the conclusion that the seven NDEA production games have the character of convexity.

Proposition 2. There exist many relationships among the seven NDEA production games proposed by us. For any $S\subseteq N$, we have

$({\rm{i}})\; {R}^{I}\left(S\right) , {R}^{II}\left(S\right) , {R}^{III}\left(S\right) , {R}^{IV}\left(S\right) , {R}^{V}\left(S\right) , {R}^{VI}\left(S\right)\le {R}^{VII}\left(S\right) ;$

$({\rm{ii}})\; {R}^{I}\left(S\right)\le {R}^{III}\left(S\right) , {R}^{I}\left(S\right)\le {R}^{V}\left(S\right) ;$

$({\rm{iii}})\; {R}^{II}\left(S\right)\le {R}^{III}\left(S\right) , {R}^{II}\left(S\right)\le {R}^{VI}\left(S\right) ;$

$({\rm{iv}})\; {R}^{IV}\left(S\right)\le {R}^{V}\left(S\right), {R}^{IV}\left(S\right)\le {R}^{VI}\left(S\right) ;$

$({\rm{v}})\; \sum _{i\in N}R\left(i\right)\le {R}^{I}\left(N\right) , {R}^{II}\left(N\right) , {R}^{III}\left(N\right) , {R}^{IV}\left(N\right) , {R}^{V}\left(N\right) , {R}^{VI}\left(N\right)\le {R}^{VII}\left(N\right).$

Proof. According to the constraint sets of the seven NDEA production games ${(P}_{1}\left(S\right)), ({P}_{2}\left(S\right)), ..., {(P}_{7}(S\left)\right)$, we can naturally obtain the relationships of the optimal values of the seven linear programs.

Specifically, let the set of constraints for the seven linear programming models be ${T}_{1}$, ${T}_{2}$, $..., {T}_{7}$, respectively. Then, we have

Moreover, as these seven cooperative production games $(N, {R}^{I}), L = I, II, ..., VII$ are super-additive, we have

In summary, the above five groups of relationships between the seven NDEA production games have been established, and hence the proof is completed.

4.2.   The relationship between the NDEA production games and the linear production games

González-Díaz et al. ^[13] proved that the class of linear production games coincides with the class of non-negative totally balanced games. Curiel ^[7] drew the conclusion that the class of linear programming games is equivalent to the class of totally balanced games. Therefore, any non-negative totally balanced games are equivalent to the linear production games and are also equivalent to the linear programming games. Following the approach of Lozano ^[28] and Borrero et al. ^[4], we will demonstrate that the aforementioned NDEA games can be formulated as the linear programming games, and thus they are equivalent to the linear production games, and, therefore, are totally balanced games.

Owen ^[32] considered that there are $\mathrm{n}$ players who can decide whether to pool their available resources to produce some outputs, and each player $i(i\in N = \{\mathrm{1, 2}, ..., n\left\}\right)$ possesses its own resource $B\left(i\right)$. Here, each player can pool its resource together with other players' resources to form a coalition $S$ to produce the outputs ${Y}^{S}$. The main characteristics of linear production games are that there exists a linear production function with a technological matrix $A$. The market price vector $w\in {R}^{s}$ is known. The total resources available in coalition $S$ is $B\left(S\right) = \sum _{i\in S}B\left(i\right)$. Then, the maximization problem of the revenue obtained by coalition $S$ can be formulated as

An extension of linear production games is the so-called linear programming game ^[7]. These are games whose characteristic function is obtained by solving linear programming problems in which the right-hand sides in the constraints depend on the coalitions. In terms of form, the linear programming games have an additional set of equality constraints compared to linear production games, which can be expressed as

It should be noted that the matrices $A\;\mathrm{a}\mathrm{n}\mathrm{d}\;Q$ on the left-hand sides of the constraints do not change with colation $S$, and a change in alliance $S$ only affects the vectors $B\left(S\right)$ and $D\left(S\right)$ on the right-hand sides.

In order to make a game with practical meaning, the linear programming problems need to be feasible and bounded for every coalition. In the case of DEA production games with variable returns to scale, for some coalitions $S\subseteq N$ the problems may turn out to be infeasible. This happens, for example, if the resources no longer permit the recorded observations to be supported ^[4]. The rest of the results in this subsection are referred to as the subclass of DEA production games with variable returns to scale for which all the coalitions are feasible.

Proposition 3. The seven NDEA production games $(N, {R}^{L}), L = I, II, ..., VII$ proposed by us, in which all the coalitions are feasible, can be expressed as linear programming games.

Proof. First, for the seven NDEA models ${P}_{l}\left(S\right), l = \mathrm{1, 2}, ..., 7$ proposed by us, we can see that, in any optimal solution, constraint ($\mathrm{l}$.4) (the fourth constraint condition of the model ${P}_{l}\left(S\right)$), which defines the target final outputs of each facility ${Z}_{0}^{f}\left(i\right)$, holds as equality. So, we can use the left-hand side of ($\mathrm{l}$.4) to replace the ${Z}_{0}^{f}\left(i\right)$ in the objective function. Furthermore, there exists an optimal solution to the model ${P}_{l}\left(S\right) (l = \mathrm{1, 2}, ..., 7)$ for which the corresponding constraints that define the target inputs ${X}_{0}^{f}\left(i\right)$ of each facility also hold as equality, so we can use the left-hand side of ($\mathrm{l}$.1) to substitute the ${X}_{0}^{f}\left(i\right)$ in the left-hand side of ($\mathrm{l}$.5) ^[16]. Meanwhile, we can omit ${Y}_{0}^{f}\left(i\right)$ and merge ($\mathrm{l}$.2) and ($\mathrm{l}$.3) together. In this way, the simplified model will only contain variables $\mathrm{\lambda }$ and $\mathrm{\mu }$. Furthermore, for simplicity, we assume that ${P}_{f}\left(i\right) = P\in {R}^{t}$, and, taking the model $\left({P}_{1}\right(S\left)\right)$ as an example, it can be written as

As shown in the above model, the simplified model $({\widetilde{P}}_{1}(S))$ has three constraints. The first constraint is related to the initial inputs, the second constraint pertains to intermediate products, and the third constraint is the requirement that the weight coefficients sum up to 1, representing the constraint of variable returns to scale.

In order to write the games $(N, {R}^{L}), L = I, II, ..., VII$ as linear programming games, we need to establish the following stacked matrices. Based on the different collaboration scenarios between each stage, we conduct the following classification discussions for $X, Y, \;\mathrm{a}\mathrm{n}\mathrm{d}\;Z,$ as well as for the weight coefficients $\mathrm{\lambda }$ and $\mathrm{\mu }$. We refer to Section 2 for the definitions of the variables such as $X\left(N\right)$ and $X\left(i\right)$.

(1) For the initial inputs $X$, we consider the following four scenarios for the stacked matrix of $X$:

(ⅰ) The first stage shares both the resources and the technology,

(ⅱ) The first stage only shares the resources,

(ⅲ) The first stage only shares the technology,

(ⅳ) There is no collaboration in terms of resources or technology in the first stage,

(2) For the intermediate products $Y$, we consider the following two scenarios for the stacked matrix of $Y$:

(ⅰ) The stage under consideration (either the first or second stage) is with technology collaboration,

where

(ⅱ) The stage under consideration (either the first or second stage) is without technology collaboration,

where

(3) For the final outputs $Z$, we consider the following two scenarios for the stacked matrix of $Z$:

(ⅰ) There is technology collaboration in the second stage,

(ⅱ) There is no technology collaboration in the second stage,

(4) For the weight coefficients $\lambda$ and $\mu$, we consider the following four scenarios:

From the above construction of the matrices, it is not difficult to observe that the dimensions of the weight coefficients $\mathrm{\lambda }$ and $\mathrm{\mu }$ are related to the existence of technology collaboration.

(ⅰ) There is technology collaboration in the first stage,

where

(ⅱ) There is no technology collaboration in the first stage,

where

(ⅲ) There is technology collaboration in the second stage,

where

(ⅳ) There is no technology collaboration in the second stage,

where

(5) In order to ensure that the matrix on the left-hand side of the linear programming game remains unchanged, the stacked matrices constructed above include all the observed values of all the organizations. In the practical computation process, for a given coalition $S$, we must set the weight coefficients of the organizations not in coalition $S$ to 0. This requirement can be achieved by constructing the following matrix $G:$

(ⅰ) The stage under consideration (either the first or second stage) is with technology collaboration,

where

For the matrix $H$, if $j\in D\left(i\right)$, then ${h}_{ij} = 1$; $\mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}$, ${h}_{ij} = 0$.

(ⅱ) The stage under consideration (either the first or second stage) is without technology collaboration,

(6) We ensure that the sum of weight coefficients is equal to 1 by constructing the matrix $V$. For the matrix $V$, we also consider two scenarios:

(ⅰ) The stage under consideration (either the first or second stage) is with technology collaboration,

where

(ⅱ) The stage under consideration (either the first or second stage) is without technology collaboration,

where

(7) We construct three new vectors, $b\left(i\right), q\left(i\right), \;\mathrm{a}\mathrm{n}\mathrm{d}\;g\left(i\right)$, on the right-hand side.

First, let us consider the resource vector $b\left(i\right)$:

(ⅰ) There is resource collaboration in the first stage,

(ⅱ) There is no resource collaboration in the first stage,

Then, the vectors $q\left(i\right)\;\mathrm{a}\mathrm{n}\mathrm{d}\;g\left(i\right)$ are constructed as follows:

For each player $i\in N$, a vector $e\left(i\right)\in {R}^{n}$ is a standard unit vector such that ${e\left(i\right)}_{i} = 1$ and ${e\left(i\right)}_{j} = 0$ for all $j\ne i$. We denote $q\left(i\right) = M\times e\left(i\right)\in {R}^{n}$ with a sufficiently large $M$ in order not to limit the value of the corresponding $\mathrm{\lambda }$ and $\mathrm{\mu }$.

We define $g\left(i\right)\in {R}^{F\left(N\right)}$, such that ${g\left(i\right)}_{j} = 1$ if $j\in D\left(i\right)$; and ${g\left(i\right)}_{j} = 0$ otherwise:

Denote ${b}^{c}\left(S\right) = {\sum }_{i\in S}{b}^{c}\left(i\right), c = \mathrm{1, 2}$, where $c = 1$ represents resource cooperation, while $c = 2$ represents resource non-cooperation, $q\left(S\right) = {\sum }_{i\in S}q\left(i\right)$, and $g\left(S\right) = {\sum }_{i\in S}g\left(i\right)$.

For example, we consider the organizations with only one stage, $N = \{\mathrm{1, 2}, 3\}$, $S = \left\{\mathrm{1, 2}\right\}$, $K\left(i\right) = 1$, and $F\left(i\right) = 1$. If there exists technology collaboration, then

The inequality ${G}^{1}{\lambda }^{1}\le q\left(S\right)$ guarantees that ${\lambda }^{i}\left(3\right) = 0, i = \mathrm{1, 2}, 3.$ Simultaneously, by taking $M$ as a sufficiently large number, it allows ${\lambda }^{i}\left(1\right)\;\mathrm{a}\mathrm{n}\mathrm{d}\;{\lambda }^{i}\left(2\right)$ ($i = \mathrm{1, 2}, 3$) to take any values. Furthermore, the equality ${V}^{1}{\lambda }^{1} = g\left(S\right)$ guarantees that ${\lambda }^{i}\left(1\right)+{\lambda }^{i}\left(2\right)+{\lambda }^{i}\left(3\right) = 1\left(i = \mathrm{1, 2}\right)$ and ${\lambda }^{3}\left(1\right)+{\lambda }^{3}\left(2\right)+{\lambda }^{3}\left(3\right) = 0$.

Then, the models ${P}_{l}\left(S\right), l = \mathrm{1, 2}, ..., 7$ can be written as linear programming games. Taking the model ${\widetilde{P}}_{1}\left(S\right)$ for example, it can be written as

For the other models ${P}_{l}\left(S\right), l = 2, ..., 7,$ as long as we consider the cases of resource collaboration and technology collaboration, we can fill in the corresponding values of $X, Y, Z, \lambda ,\; \;\mathrm{a}\mathrm{n}\mathrm{d}\;\;\mu$ to obtain the respective forms of the linear programming games.

According to González-Díaz et al. ^[13] and Curiel ^[7], it is known that any non-negative totally balanced game is equivalent to a linear production game and is also equivalent to a linear programming game. This means that the linear production games, the linear programming games, and the totally balanced games are equivalent. In conclusion, the NDEA game belongs to the class of linear programming games, thus making it equivalent to a linear production game and, therefore, a totally balanced game.

According to Owen ^[32], Curiel ^[7], Lozano ^[28], and Borrero et al. ^[4], we can compute the dual problems of ${\hat P_l}(N)$$(l = 1, 2, \cdots , 7)$ and obtain the shadow prices corresponding to the respective constraints, denoted as ${\delta }_{1}, {\delta }_{2}, {\delta }_{3}, {\delta }_{4}, {\delta }_{5}, {\delta }_{6}, {\;\mathrm{a}\mathrm{n}\mathrm{d}\;\delta }_{7}$. Consequently, we can obtain a special core solution of the linear programming game, known as the Owen set

where, if there is resource collaboration in the first stage, $b\left(i\right) = {b}^{1}\left(i\right)$; otherwise, $b\left(i\right) = {b}^{2}\left(i\right)$.

Due to the sufficient largeness of $M$, the strict inequality constraints on $q\left(N\right)$ always hold in the optimal solution of the model ${\widehat{\mathrm{P}}}_{\mathrm{i}}\left(N\right)$. Therefore, according to the complementary slackness conditions, we have ${\mathrm{\delta }}_{3} = {\mathrm{\delta }}_{4} = \;0$. Consequently, the Owen set can be further simplified to ${u}_{i} = {\mathrm{\delta }}_{1}b\left(i\right)+{\mathrm{\delta }}_{5}g\left(i\right)+{\mathrm{\delta }}_{6}g\left(i\right), i\in N$, in which ${\mathrm{\delta }}_{1}$ represents the shadow price of the initial inputs, while ${\mathrm{\delta }}_{5}$ and ${\mathrm{\delta }}_{6}$ represent the dual variable of the constraints $\sum \lambda = 1\;\mathrm{a}\mathrm{n}\mathrm{d}\;\sum \mu = 1$, respectively.

On the other hand, Shapley ^[35] showed that a balanced game has a non-empty core. In particular, when the core is non-empty, the nucleolus, proposed by Schmeidler ^[34], always belongs to the core and it is unique. Because the seven games $(N, {R}^{L}), L = I, II, ..., VII$ are balanced, the proposed games will always have stable nucleolus allocations among organizations. In the subsequent numerical and empirical analysis, we will provide the nucleolus and Owen sets for the corresponding games, respectively.

5.   Numerical and practical examples

In order to demonstrate the validity of the proposed approach, we provide a numerical example to illustrate its effectiveness. Additionally, we apply the proposed approach to an empirical analysis of 17 branches of the China Construction Bank scattered throughout the Anhui Province.

5.1.   A numerical example

To investigate the synergy resulting from the cooperative methods of resource pooling and technology sharing on the revenue of the coalition, an example which incorporates one initial input, one intermediate product, and a single final output is employed to demonstrate the effectiveness of the suggested approach. Moreover, by making use of the essential characterizations of the nucleolus and the Owen set, the correlation between the cooperative maneuvers and the revenue allocation to each participant in the coalition is studied. We analyze the example from the five aspects given below:

1) The efficiency of two stages and the production frontiers.

Suppose that there are four organizations (A, B, C, and D) with five observed decision-making units (DMUs) each, resulting in a total of twenty DMUs. The last two columns of Table 3 present the output-oriented technical efficiencies of Stages Ⅰ and Ⅱ for these twenty DMUs, which were randomly generated. Given the technology sharing and initial resource pooling occurring between the same stages of production, this study utilizes the single-stage DEA efficiency values to evaluate the effect of each organization on the production possibility set within the same stage. The observations of each organization are then used to analyze how such entities may shift the frontier edge of the given production stage.

Table 3 offers evidence that, for Organization A, DMU1 is efficient in Stage Ⅱ, and DMU3 is revealed to be efficient in both Stages Ⅰ and Ⅱ. Additionally, Organization B boasts two technically efficient DMUs (DMU6 and DMU9) in Stage Ⅰ; in contrast, Organization C has only one DMU (DMU14) attaining efficiency in Stage Ⅱ. No technically efficient DMU is present in Organization D.

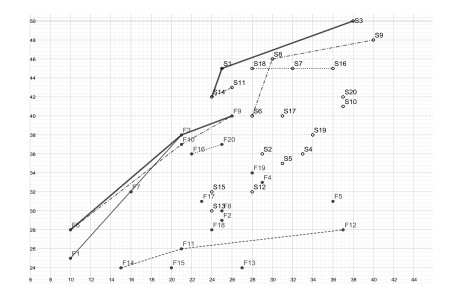
In order to gain an insight into the production capabilities of the four organizations and the entire production system, Figure 2 displays the production frontiers of the respective entities.

As depicted in production frontiers (Figure 2), the letter F represents the first stage, whereas the letter S symbolizes the second stage. Meanwhile, the numbers on the right-hand side of the symbols correspond with the respective sets of observations. When looking at the four organizations together, the two bold lines denote the leading edge of both stages Ⅰ and Ⅱ, respectively. The remaining eight thin lines exhibit the fronts of the four organizations in Stages Ⅰ and Ⅱ.

As illustrated in Figure 2, it appears that the technology of Organizations A and B is significantly more advanced than that of Organizations C and D. This observation is also consistent with the findings of Lozano ^[28], which highlights that it is not the average efficiency of the organization, but rather the specific observation points located at the edge of the organization that determine the benefits acquired by the organization from the conglomerate. This can be interpreted to imply that the extent to which a production organization is able to push the production frontier of the colation beyond its limit is a precise reflection of its contribution to the colation. Therefore, it can be seen from Figure 2 that the observation points of Organizations A and B constitute the production frontier, while the observation points of Organizations C and D are mostly located inside the frontier.

As the DEA efficiency value represents the relative technology level, we may conclude that Organization A has a relatively higher overall technology level, Organization D has a relatively lower overall technology level, Organization B has a higher technology level in the first stage, and Organization C has a higher technology level in the second stage.

2) The maximal revenue of coalitions in seven types.

For the sake of convenience, suppose the price of the final output is 1, i.e., $P = 1$ for all the outputs, each organization has three facilities, and the original inputs of resources for the four organizations are 50, 40, 70, and 80, respectively.

We first deal with the maximum revenue problem in the case where there is no cooperation among the organizations. The numerical results based on the model (${P}_{0}\left(i\right)$) are listed in Table 4.

Table 4 shows that when the organizations have certain initial resources and do not cooperate with each other, both Organizations A and B will use up their initial resources and obtain the maximum profits of 144.09 and 138.44, respectively. Meanwhile, Organizations C and D, at their current technological levels, will have the initial resource balances of 7 and 14, respectively, and correspondingly obtain the maximum profits of 129 and 135, respectively.

With a balance of initial resources, if the organizations can cooperate with each other, depending on the method of cooperation, the resources will be fully utilized or effectively saved, and the benefits will increase. So, we discuss the cases where the organizations can cooperate with each other and form coalitions of the seven types, and the maximized revenue of the corresponding fifteen coalitions are shown in Table 5.

According to the maximal revenue of coalitions in the seven types (Table 5), it is not difficult to find that, under the seven types of cooperation, the revenue of the cooperation among the organizations is not less than the sum of non-cooperation among organizations. For example, under Type 1, the revenue of the colation ABC is 416.44, while without cooperation, the sum of the revenue of Organizations A, B, and C is 144.09+138.44+129 = 411.53, and it is apparent that 416.44 > 411.53.

3) The resource surplus and revenue increase in seven cooperative types.

In order to imply the effect of saving the initial resource of these seven cooperative types, we consider the situation that all the organizations form a grand coalition (coalition ABCD), and the consumption data of resources for each organization in each type are given in Table 6. Note that, according to the hypothesis, the initial resources of a grand coalition total 240. To facilitate comparison, we denote the non-cooperative situation as Type 0, which is given in the second column in Table 6 according to the resource use and savings in Table 4.

According to the resource consumption of the organizations (Table 6), we can see that the following three types can both save resources and increase the revenue in the grand coalition: Type 2 (where only the first stage shares the technology, for the total revenue, we have 548.07 > 546.53 ( = 144.09+138.44+129+135), and for the resource surplus we have 90 > 21), Type 3 (where only the first stage shares both the technology and resources), and Type 6 (where the two stages only share the technology and keep the resources isolated). For Type 7 (where all the stages cooperate completely, the total revenue there is 595.8 > 546.53), although the original resources cannot be saved, the revenue of the grand coalition can be maximized and hence is the maximal of these seven types.

4) The revenue allocation based on the nucleolus and the Owen set.

According to Table 5, we analyze the allocation of coalition revenues among the organizations based on the basic definitions of the nucleolus and the Owen set. Since the seven NDEA production games are balanced, and the nucleolus and the Owen set are in the core, the nucleolus and the Owen set reflects the stability of the allocation scheme. Therefore, here we choose these two solution concepts as a result of the assignment. We use the R language with the CoopGame package to obtain the nucleolus, and use the proof method of Proposition 3 to calculate the Owen set, which are shown in Table 7.

For the convenience of comparison, the cooperative surplus (i.e., the negative quantity of the excess) obtained for each organization in the seven types of cooperation based on the concepts of the nucleolus and the Owen set are given in Table 8.

Among the seven types of cooperation, there is no technical cooperation in Stage Ⅱ in Types 1 to 3, and technical cooperation exists in Stage Ⅱ in Types 4 to 7. From Table 3, the second group of cooperative types (Types 4 to 7) creates more cooperative surplus than the first group (Types 1 to 3). The reason is that, under the setting of initial resource quantity, there is a relative excess of output in the first stage, so the cooperation in the second stage is particularly important.

According to Table 8, we can see that the cooperative surplus of both the nucleolus and the Owen set are relatively similar in the first group of cooperative types (Types 1 to 3) where there is no technical cooperation in Stage Ⅱ, but in the second group of cooperative types (Types 4 to 7) where technical cooperation exists in Stage Ⅱ there are some differences in cooperative surplus for the nucleolus and the Owen set.

5) Investigating each type of cooperation.

First, we investigate the first group of cooperation types (Types 1 to 3), in which the cooperation only exists in the first stage. As shown in Figure 2, the technology of Organizations A and B is relatively advanced, while Organizations C and D have abundant resources.

Type 1: There is only resource cooperation in the first stage. Comparing Type 0 with Type 1 in Table 6, we can see that Organizations A and B add 13 and 8 units of inputs, respectively, and Organizations C and D provide 7 and 14 inputs correspondingly. Organization A has more potential production capacity, and Organization D provides more input resources, so Organizations A and D receive the most cooperative surplus.

Type 2: There is only technology cooperation in the first stage. As shown in Figure 2, Organizations C and D do not create value for the alliance, so they are not assigned. Intuitively, even if Organizations C and D are relatively unadvanced, after obtaining the cutting-edge technology of Organizations A and B they can still increase the output and thus contribute to the alliance. However, Organizations C and D have two-stage production processes and have variable returns to scales, and they have excess inputs in Stage Ⅱ, so even if the technology in the first stage is improved and the output of the first stage is increased, the output of the second stage cannot increase and thus create value for the colation. Therefore, the final cooperative surplus of Organizations C and D is 0.

Type 3: There is technological cooperation and resource sharing in the first stage. Resources can flow from Organizations C and D to Organizations A and B, thus creating more revenue for the coalition. At this time, besides resource pooling, technology sharing should also be considered when discussing the contribution of Organizations A and B to the colation. The contribution of Organizations A and B is relatively greater than that in Type 1. As a result, they gain more cooperative surplus.

Next, we investigate the second group of cooperation types (Types 4 to 7), with technical cooperation in the second stage. Type 7 gains the most cooperative surplus because it has the most cooperative manner by sharing both resources and technology in the first stage.

Type 4: There is only technology cooperation in the second stage. Since the second stage can have technology cooperation, the resources of Organizations C and D are relatively fully utilized. Furthermore, in the second stage, Organizations A and D have a relatively higher technology level, and so they also play a greater role in the cooperation. In the nucleolus, Organizations A and D obtain the most cooperative surplus, while in the Owen set, Organizations C and D receive the most cooperative surplus. The difference may be due to the fact that the Owen set pays greater attention to the resources.

Type 5: There is resource pooling in the first stage and technology sharing in the second stage. From Table 8, we can see that Organization A has the most cooperative surplus in the nucleolus due to its high technology level, while Organization D has the most cooperative surplus in the Owen set because of its rich initial resources.

The distribution of cooperative surplus obtained by each organization is similar in Types 6 and 7. Organization C has a relatively high cooperative surplus in both the nucleolus and the Owen set because Organization C is rich in initial resources and has a high technology level in the second stage. On the other hand, Organization A receives the second highest cooperative surplus in the nucleolus because it has a high technology level in both stages, and Organization D obtains the second highest cooperative surplus in the Owen set due to the fact that it has the most initial resources.

To summarize, we obtain the following conclusions:

a) From the aspect of production frontiers, the specific observation points located at the edge of the organization determine the benefits acquired by the organization from the colation. These phenomena are consistent with the findings of Lozano ^[28].

b) Organization A has a relatively higher overall technology level, Organization B has a higher technology level in the first stage, Organization C performs a higher technological level in the second stage, and Organization D has a relatively lower overall technological level.

c) The cooperation of production organizations can increase the total revenue.

d) Cooperation can increase revenue, and the most gains with realized with full cooperation (Type 7).

e) The second group of cooperative types (Types 4 to 7) creates more cooperative surplus than the first group (Types 1 to 3).

f) The cooperative surplus of both the nucleolus and the Owen set are relatively similar in the first group of cooperative types (Types 1 to 3), but have some differences in the second group of cooperative types (Types 4 to 7).

5.2.   A practical example

In this subsection, we examine 17 commercial bank branches located in the Anhui Province, China, and analyze their revenue distribution among subsidiaries across different types of cooperation.

We adopt a methodology similar to that of Yang et al. ^[42] to model commercial bank activities as a two-stage network process. The first stage involves fundraising, and the second stage involves profit earning. The model includes three initial inputs: Fixed Assets (denoted as ${X}_{1}$), Employees (${X}_{2}$), and Expenditure (${X}_{3}$); two intermediate products: Credit (${Y}_{1}$) and Interbank Loans (${Y}_{2}$); and two final outputs: Loans (${Z}_{1}$) and Profit (${Z}_{2}$). All variables are measured in units of 100-thousand CNY, and specific data can be found in Table 9.

The Anhui Province comprises 17 cities: Hefei, Bengbu, Huainan, Huaibei, Maanshan, Tongling, Wuhu, Anqing, Huangshan, Fuyang, Suzhou, Chuzhou, Luan, Xuancheng, Chizhou, Chaohu, and Bozhou. Based on historical and cultural factors, the province can be divided into three regions: northern (including 6 cities), central (including 5 cities), and southern (including 6 cities). Therefore, we have divided the 17 commercial bank branches into three groups labeled as A (northern), B (central), and C (southern), respectively. In the last two columns of Table 9, we present the output-oriented technical efficiencies of Stage Ⅰ and Stage Ⅱ for these 17 commercial bank branches. As shown, Organizations A and B each have one efficient DMU in both Stage Ⅰ and Stage Ⅱ, while Organization C has two efficient DMUs in Stage Ⅰ and four efficient DMUs in Stage Ⅱ.

We now proceed to analyze the maximum benefits that the organizations can achieve in the absence of cooperation among them. For each organization, we compute its initial resources as the sum of initial inputs, and its revenue as the sum of the final outputs of its commercial bank branches. The maximum revenues of the three organizations, along with their corresponding resource balances, are presented in Table 10.

As shown in Table 10, Organization C generates the highest returns, while Organization A has the lowest revenue. Additionally, Organizations A, B, and C have excess fixed assets, while Organization C has excess expenditure. However, all organizations have fully utilized their employees.

If the three organizations cooperate with each other to form different colations, we can calculate the revenues of each colation under seven different types of cooperation. The results are presented in Table 11.

Regarding the maximal revenue of the coalitions (Table 11), we can observe that different partners and cooperation types can improve the revenue of each organization to varying degrees. In terms of initial resource utilization, we present the surplus of the three initial resources under different types of cooperation in Table 12. For comparison purposes, we also record the surplus of the initial resources of the three organizations under the condition of no cooperation as Type 0, and the details are provided in column 3 of Table 12.

Upon comparison, we observe that, under the seven cooperative modes, the surplus of the three initial resources can either be greater or smaller than the balance in the non-cooperative situations. This suggests that cooperation does not necessarily save the utilization of resources.

Specifically speaking, according to Table 12, we can see that all the cooperation types save the resources for input X1, Type 2 saves resources for input X2, while for input X3, no type of cooperation can save the resources.

We can obtain the revenue distribution results for each organization based on the nucleolus and the Owen set using the maximal revenue of the coalitions (Table 11). The assignment results are presented in Table 13.

To illustrate the value of different types of cooperation for each organization, we present the cooperative surplus of each organization in Table 14.

Based on Table 14, it can be observed that the second cooperation style (Type 2) results in the lowest excess return, whereas the seventh cooperation mode (Type 7) yields the highest cooperative surplus. The profit-earning activities are considered in the second stage, wherein Credit and Interbank Loans are utilized to generate Loans and Profit. In the second type of cooperation, only the first stage shares technology, which indicates that all the branches of commercial banks perform inadequately in profitable activities.

Furthermore, in the seventh type of cooperation, both resource pooling and technology sharing are utilized in the first stage, while only technology sharing is used in the second stage. This is identified as the most effective mode of cooperation among the seven considered. As Table 14 indicates, greater cooperation among organizations leads to greater benefits for all parties involved. Additionally, the fact that the second cooperation type results in the lowest benefits suggests that resource pooling and technology sharing in the second stage play a dominant role in the seventh cooperation mode.

It is noteworthy that the cooperative surplus of the nucleolus and the Owen set has some differences. Generally speaking, in the nucleolus, Organization B, who is with rich initial input, obtains a relatively higher cooperative surplus, while in the Owen set, Organization A, who has the second highest initial input and technology level, receives a higher cooperative surplus.

The managerial implications with related observations in the results could be re-organized as follows.

1) From the aspect of cooperation manners.

a) Different partners and cooperation types can improve the revenue of each organization to varying degrees.

b) Cooperation does not necessarily save the utilization of resources.

c) The second cooperation style (Type 2) results in the lowest excess return, whereas the seventh cooperation mode (Type 7) yields the highest cooperative surplus.

d) Greater cooperation among organizations leads to greater benefits for all parties involved.

2) From the perspective of each organization.

a) Organization A

Organization A has the second highest initial resources, whose overall technology level also ranks the second, but its performance in profit transformation is relatively poor. As a result, in the nucleolus, Organization A obtains relatively less cooperative surplus, especially under the last four types of cooperation. However, in the first three cooperation types where technology sharing is involved in the first stage, the cooperative surplus of Organization A is relatively high. In particular, in the second cooperation type where only the first stage shares technology, Organization A has the highest cooperative surplus, indicating that Organization A has a significant advantage in raising funds. Meanwhile in the Owen set, Organization A receives the highest cooperative surplus, which shows that the relative equivalence of resources and technology increases the contribution of Organization A.

b) Organization B

Organization B has more initial resources compared with Organizations A and C. Additionally, Organization B has a higher profit conversion capacity in the second stage, where the main focus is on lending money and generating profit (Loans and Profit) (Yang et al., 2011). As a result, Organization B generates more profits in the second stage, as reflected by its revenue of 202.3 in the non-cooperative situation in Table 10. Therefore, in the nucleolus, Organization B gains more cooperative surplus compared to other partners, while in the Owen set, Organization B obtains the second highest cooperative surplus.

c) Organization C

Organization C has the lowest initial resources among the three organizations. However, Table 9 shows that Organization C has relatively high efficiency values at both stages, indicating strong financing and profit-earning abilities. As a result, in the nucleolus, despite having fewer initial resources, the gap between the cooperative surplus of Organization C and the other organizations is not significant, particularly in the second cooperation type. In the Owen set, Organization C obtains relatively less cooperative surplus, which indicates that the Owen set pays more attention to the resources than the nucleolus.

Upon analyzing the commercial bank organizations with two-stage processes, i.e., financing and profit-earning, and different ways of cooperation between stages, we can extract rich management information by calculating and distributing cooperative surplus. This highlights the significance of the method proposed in this paper.

6.   Conclusions

In many managerial applications, the production process often has a multi-stage structure. In this paper, we consider the simplest form of a two-stage production organization, and suppose that the organizations can cooperate through methods of pooling the initial resource and (or) sharing the technology of each production process. Although the two-stage series production process we discuss in this paper is relatively simple, it is enough to fully reflect the internal cooperation mode. Compared with the analysis on the single-stage implemented by Lozano, the discussion on the two-stage cooperation among the organizations can bring out more helpful management information. Our proposed models can give the optimal revenue of the alliance under different cooperation types; the research conclusions can provide valuable information for managers in the selection of cooperation mode, full utilization of initial resources, and fair distribution of benefits, etc.

The main work we do in this paper is as follows:

(1) We prove that two-stage DEA production games have the super-additive property, and can be expressed as linear programming games, and hence they are equivalent to linear production games and are totally balanced. Therefore, the proposed cooperative games have a non-empty core and have that the nucleolus and the Owen set belong to the core.

(2) We discuss the influence of seven different cooperation types on the coalition revenue. Furthermore, the coalition revenue is decomposed under the two concepts of the nucleolus and the Owen set, and the distribution income of each organization reflects its resource advantages and (or) technological advantages.

(3) We use a numerical example and an empirical application of 17 commercial banks to illustrate the applicability of our proposed approach and give a detailed discussion about the relationship between the manners of cooperation and the revenue distribution.

The following conclusions can be deduced from this study:

(1) Cooperation can generate cooperative surplus. According to Table 8 and Table 14, it can be seen that almost every organization can obtain cooperative surplus based on the nucleolus and the Owen set.

(2) The higher the degree of cooperation, the higher the revenue of the coalition. Among the seven cooperation types that we discuss, the seventh cooperation mode is the most complete method, and gives each organization the most cooperative surplus.

(3) In some cases, cooperation can save resources. According to Table 6, we can see that there exist three types that can both save the resources and increase the revenue in the grand coalition. From Table 12, we see that all the cooperation types save the resources for input X1.

(4) Relative advantages and disadvantages of each organization can be obtained. By comparing the sizes of the cooperative surplus obtained by each organization, we can get the relative advantages and disadvantages of each organization in terms of the number of resources and technological level.

We would like to point out that the proposed method cannot be used for a production process with fuzzy data. Therefore, extending the proposed method to address this shortcoming is an interesting avenue in future research. Furthermore, for future studies, the production system with other types of network structure, such as parallel connection, multi-stage series connection, and mixed series parallel connection, can be considered so as to study the ways of cooperation and the scheme of resource allocation for different stages under varying production structures. Moreover, the research methods can be utilized to analyze other practical problems such as merger, acquisitions, reconstruction, and optimal partner selection for banks, insurance companies, and chain hotels, so as to supply theoretical support on resource sharing and achieving mutually beneficial win-win cooperation for the enterprises.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by National Natural Science Foundation of China (Grant No. 72001207). The authors are much grateful to the referees whose valuable suggestions helped improve this paper a lot.

Conflict of interest

The authors declare that no conflicts of interest exists in this paper.