A uniform interval-valued intuitionistic fuzzy environment: topological descriptors and their application in neural networks

1.   Introduction

Fuzzy graph theory and intuitionistic fuzzy graph theory incorporate uncertainty and imprecision into graph-based modeling, both of which are expansions of traditional graph theory. Let us examine the development of intuitionistic fuzzy graph theory from fuzzy graph theory and who was involved in its creation ^[9,29]. Fuzzy graph theory was developed as an extension of traditional graph theory to deal with circumstances where node and edge interactions are not always strictly binary (present or absent), but instead might include degrees of membership ^[37]. The roots of fuzzy graph theory were established by academics like Lotfi A. Zadeh ^[43,44], who presented the idea of fuzzy sets in 1965. Fuzzy graph theory has been introduced and improved by a number of researchers. The depiction of different levels of connectedness or interaction between nodes in a network is possible thanks to fuzzy graph theory.

As a development of fuzzy sets, Krassimir Atanassov proposed intuitionistic fuzzy sets (IFS) in the early 1980s ^[8]. Assigning non-membership, hesitation, and membership degrees to items in intuitionistic fuzzy sets allows for a more detailed portrayal of doubt and reluctance when determining membership ^[26]. To provide even more elaborate means for characterizing uncertainty in a given environment, inaccuracy in the graph structures, the concept of fuzzy graph theory and intuitionistic fuzzy sets were established ^[34]. In the theory of intuitionistic fuzzy graphs, each node and edge of a graph is warranted an intuitionistic fuzzy set with three degrees: membership, non-membership, and hesitation. Dr. Atanassov introduced the concept of intuitionistic fuzzy graph theory to the academic community, drawing on his own expertise. Published in 1992, the book "Intuitionistic Fuzzy Graphs" built the initial prototype of intuitionistic fuzzy graph theory. Atanassov's work in graph theory enabled the utilization of the concepts of IFS, which helped to better illustrate hesitant and unsure connections in graph topologies. Intuitionistic fuzzy graph theory was further developed by several scholars after this, which led to the identification of new concepts, processes, and applications in the methods of decision-making, pattern recognization, image processing, and many other fields ^[16,21].

1.1.   Topological indices in fuzzy graph theory

Topological indices are numerical values obtained from a graph's structure that provide light on its many characteristics. Topological indices are modified in both fuzzy graph theory and intuitionistic fuzzy graph theory to account for uncertainty and imprecision in the graph's edges and nodes. Let us examine the differences between these two theories' topological indices and talk about their respective weights ^[23,25,30].

1.1.1.   Fuzzy topological indices

Topological indices take into account the idea of fuzzy edges in fuzzy graph theory, where the value of membership (values between 0 and 1) is used to describe the strength of the link between nodes. Fuzzy degrees are added to conventional topological indices like degree centrality, closeness centrality, betweenness centrality, and graph invariants like the Randic index or the Zagreb indices. These indices take into consideration the ambiguity in edge connections while displaying how closely linked the central nodes are in a network ^[1,2,17].

1.1.2.   Intuitionistic fuzzy topological indices

By incorporating intuitionistic fuzzy sets, which are made up of membership, non-membership, and hesitation degrees, intuitionistic fuzzy graph theory goes beyond uncertainty. In intuitionistic fuzzy graph theory, topological indices, membership, non-membership, and hesitation degrees interact in more complicated ways for both nodes and edges. Traditional topological indices are expanded to include intuitionistic fuzzy sets, much like fuzzy graph theory does. This comprises centrality measurements, connection indices, and degree-based indices ^[3,7,35].

1.1.3.   Importance and application

In both theories, the significance of topological indices varies according to the situation and the particular issue at hand. Fuzzy graph theory and its adjusted topological indices can be adequate to capture and evaluate the underlying structure in circumstances when the interactions between nodes are ambiguous but not necessarily reluctant. Instances when hesitation is a substantial issue and uncertainty is more complex, intuitionistic fuzzy graph theory and its accompanying topological indices provide a more complete framework. The most important theory will vary depending on the application and the type of uncertainty in the graph. When dealing with networks whose connections have different degrees of strength, fuzzy graph theory is helpful; however, intuitionistic fuzzy graph theory is better applicable when both uncertainty and hesitation play important roles. Since there is ambiguity in many real-world situations to varied degrees, these theories may not be mutually incompatible. The theory and related indices that best fit the level of uncertainty in the data and are consistent with the objectives of the investigation are frequently chosen by researchers. A theory's or a collection of topological indices' significance is ultimately defined by how well it can simulate and interpret the network structure in a particular situation ^[4,5,6,36].

2.   Literature review

Invariants of intuitionistic fuzzy graph theory is interested in fuzzy graphs. Here are a few pertinent search outcomes: In ^[11], the ideas of an intuitionistic fuzzy graph's minimum intuitionistic fuzzy base and route are discussed. In ^[19], the work proposes three concepts—intuitional fuzzy threshold, intuitive fuzzy route, and intuitive fuzzy cycle—and gives a generalization of fuzzy threshold graphs. In ^[10], the smallest intuitionistic dominant vertex subset of an intuitionistic fuzzy graph is a topic that is examined. In ^[32], the idea of bipolar intuitionistic fuzzy graphs (BIFG), a fuzzy graph extension that may successfully incorporate uncertain or imprecise information, is introduced. For the purpose of identifying flood-prone areas, they suggest a decision-making model based on BIFG. In ^[24], topological indices in fuzzy graphs were defined. This provides a basis for comprehending topological indices in fuzzy graphs, although it does not specifically concentrate on uniform intuitionistic fuzzy topological indices.

Fuzzy topological invariants in uniform fuzzy graphs were given in ^[19]. This work explored three ideas related to the intuitionistic fuzzy threshold and proposed a generalization of fuzzy threshold graphs. It examined comparable ideas but did not specifically reference uniform intuitionistic fuzzy topological indices. In ^[31], the first and second fuzzy Zagreb indices, the Randic index, and the harmonic index were studied. It offered insights into fuzzy topological analysis even if it did not directly include uniform intuitionistic fuzzy topological indices. In ^{[12,15,20,27,33,45]}, as an extension of fuzzifying topology, intuitionistic fuzzifying topology was covered. These give background knowledge on fuzzy topology but do not directly handle uniform intuitionistic fuzzy topological indices. There are other environments of fuzzy indices in which topological descriptors are studied like the introduction to topological indices in neutrosophic graphs given by ^[18]. In neutrosophic graphs, which are graphs that adhere to three-valued logic, this study proposed topological indices. It explored analogous ideas in the context of fuzzy graphs, but did not particularly focus on uniform intuitionistic fuzzy topological indices. In ^[11], the ideas of an intuitionistic fuzzy graph's minimum intuitionistic fuzzy base and route were discussed. It discussed pertinent ideas in intuitionistic fuzzy graphs but did not specifically mention uniform intuitionistic fuzzy topological indices. Not only used in networking, pure mathematics graph-based modeling is available for engineering, as well, as was shown in ^{[13,28,38,40]}. For additional information on fuzzy indices and their implementation, one can refer to ^{[14,22,39,41]}. For a neural network study, one can visit ^[42].

Overall, while the search results do not directly provide literature on uniform intuitionistic fuzzy topological indices, they offer insights into related concepts in fuzzy graphs, fuzzy topological analysis, and intuitionistic fuzzy graphs. These resources can serve as a foundation for further exploration and research in uniform intuitionistic fuzzy topological indices. One can use these research articles to investigate fuzzy invariants of intuitionistic fuzzy graphs and explore the ideas of minimum intuitionistic fuzzy bases, minimal intuitionistic fuzzy thresholds, minimal intuitionistic fuzzy cycles, and minimal intuitionistic dominant vertex subsets. To construct and test various intuitionistic fuzzy graph algorithms and models, one can also utilize Python packages like NetworkX or igraph.

3.   Our proposed work and its main results

3.1.   The uniform intuitionistic fuzzy graph and its topological indices

In ^[19], authors presented some fuzzy topological invariants in the environment of uniform fuzzy graphs. Inspired by this work, we expand the concept of uniform fuzzy graphs to uniform intuitionistic fuzzy topological indices. By introducing uniform intuitionistic fuzzy topological indices (UIFTIs), the idea of traditional topological indices is generalized to fuzzy sets allowing a more flexible and detailed description of structural properties of graphs or networks. Finally, in complex systems in which structural relations present different degrees of coupling or interference, these indices are particularly useful because they express uncertainty and fuzziness in the node topology. It is appropriate to check how some superimposed indices such as first Zagreb, the second Zagreb, the harmonic, and the Randic index are related to uniform intuitionistic fuzzy topological indices.

3.1.1.   The uniform intuitionistic fuzzy graph

A uniform intuitionistic fuzzy graph is a graph where each connection between vertices is represented with two levels of uncertainty: that is, one measure of how it is connected and another measure of how it is disconnected, plus a measure of uncertainty. The term "uniform" is used to mean that these uncertain relations have some consistencies on their rules or properties in the extend of the graph. Such a type of graph is helpful to represent the conditions, where the relationships are vague or tend to be in different forms, for instance, in decision-making or complicated networks.

3.1.2.   Uniform intuitionistic fuzzy topological indices

It can be generally observed that the traditional topological indices defined and used in this work may be systematically enriched with uncertainty and imprecision uniformly by using uniform intuitionistic fuzzy topological indices. UIFTIs complement exact models within a system-oriented approach more logically, offering a more realistic and flexible way of modeling the nature of real systems by incorporating IF sights to describe degrees, distances, or other structural aspects of a system and its corresponding components. Applying UTIN: Chemoinformatics, bioinformatics, as well as complex systems analysis are among application areas that may benefit from fuzzy topological indices. Accompanying these indices, the researcher will be able to analyze and better understand the inherent contingencies into the studied systems, and perform more detailed and accurate structural and property evaluations.

3.1.3.   First Zagreb index

The first Zagreb index is known as the M1 index, which is a fundamental topological index that sums the square of degrees of all nodes in the network. Thus, the first Zagreb index may be generalized to incorporate fuzzy degrees of nodes associated with the context of UIFTIs. In this respect, the degree of a node may equivalently be deemed as an intuitionistic fuzzy set. This makes it possible to depict node connection in a more flexible manner and represents the degree of graph uncertainty. The M2 index is a conventional topological index based on near nodes' degrees that constitutes the product of pair node degrees.

3.1.4.   Second Zagreb index

As is done with the first Zagreb index, the second Zagreb index can also be generalized to fuzzy degrees giving a uniform intuitionistic fuzzy second Zagreb index. This fuzzy variation incorporates spatial relation which considers both concepts of adjacency and degree uncertainty between the node pairs.

3.1.5.   Harmonic index

The topological index called the harmonic index considers the harmonic mean of all node to node separation in the network. By defining the various distances between the nodes, it is possible to explain the concept of the harmonic index in the case of UIFTIs, which can characterized the twofold uncertainty in the graph.

3.1.6.   Randić index

The Randić index, to which is added the sum of the reciprocal square roots of the degrees of neighboring nodes, quantifies the connectivity of a network. The Randic index is the index which in fuzzy framework may get extended to embrace fuzzy degrees showing the degrees of connection between nodes.

3.2.   Uniform strong intuitionistic fuzzy

The idea of uniform strong intuitionistic fuzzy (USIF) joins the aspect of "uniformity" with strong intuitionistic fuzzy sets. Let us define these words: "Uniformity" is the even distribution of the membership values assigned to a set's elements when speaking about fuzzy sets. This results in a balanced and uniform representation since every element in the set has an equal or nearly equal value of membership.

3.3.   Strong intuitionistic fuzzy sets

Thus, in addition to membership degree, there are two additional features to consider, which are the non-membership degree and the hesitation degree, which represents the level of hesitance in the defining membership and non-membership values. They are likely to denote some specific kind of fuzzy set or fuzzy logic, which incorporates into the construct the uniformity quality together with the notion of strong intuitionistic fuzzy sets. This would mean that the membership values assigned to the set's components are not only uniformly distributed (uniform), but also within a proper intuitionist fuzzy setting taking into consideration the membership, non-membership, and degree of possibility of reluctance.

3.4.   Uniform interval-valued intuitionistic fuzzy

"Uniform interval-valued intuitionistic fuzzy (UIVIF)" refers to a specialized fuzzy set where membership, non-membership, and hesitation degrees are represented as intervals rather than precise values, providing a more flexible and nuanced way to capture uncertainty and vagueness. In this framework, the intervals for membership and non-membership functions are uniformly applied across the entire domain, ensuring consistency in the degree of uncertainty throughout. This approach is particularly useful in modeling scenarios where precise numerical values are difficult to ascertain, offering a robust method for handling imprecise information. Some of the decision-making, pattern recognition, uncertainty modeling, and other activities that require a better representation of uncertainty and imprecision may be served better with such a notion. Modifications of the conventional graph theory where both strong intuitionistic fuzzy sets, strong intuitionistic fuzzy vertices, and uniformity principles are incorporated are called the uniform strong intuitionistic fuzzy graphs (USIF graphs). This idea tries to capture the fuzziness of the graph structure and aims at having its maximal, minimal, and uncertain levels of participation for the nodes be approximately equal. Every node and edge in a USIF network is associated to an excellent intuitionistic fuzzy set that represents the degrees of membership, non-membership, and hesitation. The definition of the USIF graph's structure and the soft role of fuzzy assignments are applied to calculate the topological indices for uniform strong intuitionistic fuzzy graphs. These indices provide data regarding many structural and connectivity properties of the graph while still encompassing uncertainty and imprecision. These indices can only be computed if strong intuitionistic fuzzy sets associated with nodes and edges exist.

Examples of topological indices for uniform strong intuitionistic fuzzy graphs include the following: The overall value of the node in the graph is calculated using the strong intuitionistic fuzzy degree index. It evaluates the connectedness of a node in detail owing to the consideration of the strong membership degree and the hesitation degree. These indices are able to measure distances between nodes in terms of strong intuitionistic fuzzy sets similar to the traditional distance-based indices. With regard to the paths between nodes, they incorporate the strong membership and hesitation degrees. The degree to which nodes in a USIF network prefer to cluster together is gauged by the strong intuitionistic fuzzy clustering coefficient. To evaluate the local clustering pattern, it takes into account the strong membership, non-membership, and hesitating degrees. Applied to fuzzy sets, the concept of topological indices is elaborated by using interval-valued intuitionistic fuzzy sets to deal with uncertainty in the form of intervals in membership and non-membership functions. In uncertain conditions, this makes it possible to adjust the model more freely on each step. In order to apply the features of UIFTIs to the mathematical environment specific to fuzzy environments such as monotonicity and boundedness, enhanced techniques of calculation are used to optimize the presentation of interval-based data.

These are only a few illustrations, and research is still being done on the creation and use of topological indices for uniform strong intuitionistic fuzzy graphs. These indices are useful tools for decision-making, pattern identification, and information modeling because they offer a mechanism to assess and comprehend the structural characteristics of complex systems while taking uncertainty and imprecision into account.

3.5.   Interval-valued intuitionistic fuzzy graphs and their types

Definition 3.1. An IVIFG is of the form $G = < V, E >$ where $V = \{v_{1}, v_{2}, v_{3}, \dots, v_{n}\}$ such that $\left[\zeta_{1}^{L}(v_{i}), \zeta_{1}^{U}(v_{i})\right]\subseteq [0, 1]$ and $\left[\eta_{1}^{L}(v_{i}), \eta_{1}^{U}(v_{i})\right]\subseteq [0, 1]$ denote the value of membership and non-membership of the element $v_{i}\in V,$ respectively, where $\zeta_{1}(v_{i})^{L}$ and $\zeta_{1}^{U}(v_{i})$ represent the lower and upper bound of the membership degree of $v_{i}$, and similarly $\eta_{1}^{L}(v_{i})$ and $\eta_{1}^{U}(v_{i})$ represent the lower and upper bound of the non-membership degree of $v_{i}$. These satisfy

for every $v_{i}\in V (i = 1, 2, 3, \dots, n).$

$E\subseteq V\times V$ where $\zeta_{2}(v_{i}, v_{j}) = \left[\zeta_{2}^{L}(v_{i}, v_{j}), \zeta_{2}^{U}(v_{i}, v_{j})\right]\subseteq [0, 1]$ and $\eta_{2}(v_{i}, v_{j}) = \left[\eta_{2}^{L}(v_{i}, v_{j}), \eta_{2}^{U}(v_{i}, v_{j})\right]\subseteq [0, 1]$ denote the value of membership and non-membership of the element for every $(v_{i}, v_{j})\in E$. These satisfy the following conditions:

for every $(v_{i}, v_{j})\in E (i, j = 1, 2, 3, \dots, n).$

Note. Consider $\zeta_{1i}^{U} = \zeta_{1}^{U}(v_{i}), \; \eta_{1i}^{L} = \eta_{1}^{L}(v_{i}), \; \zeta_{2ij}^{U} = \zeta_{2}^{U}(v_{i}, v_{j})$ and $\eta_{2ij}^{L} = \eta_{2}^{L}(v_{i}, v_{j}).$

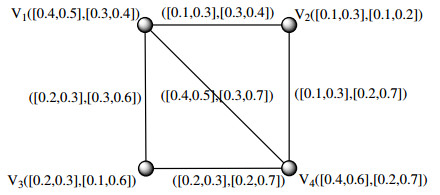
Definition 3.2. An $IVIFG = < V, E >$ is said to have a strong $IVIFG$ if $\zeta_{2ij}^{U} = \min\{\zeta_{1i}^{U}, \zeta_{1j}^{U}\}$ and $\eta_{2ij}^{L} = \max\{\eta_{1i}^{L}, \eta_{1j}^{L}\}$ for all $(v_{i}, v_{j})\in E.$ This definition is depicted in Figure 1.

Definition 3.3. A $UDMSIVIFG = < V, E >$ is said to have a uniform value of membership strong $IVIFG$ if $\zeta_{1i}^{U} = \zeta_{1j}^{U} = t, \ \zeta_{2ij}^{U} = \min(t, t) = t, \ 0\leq t \leq1,$ and $\eta_{2ij}^{L} = \max(\eta_{1i}^{L}, \eta_{1j}^{L})$ for all $(v_{i}, v_{j})\in E.$ This definition is depicted in Figure 2.

Definition 3.4. A $UDNMSIVIFG = < V, E >$ is said to have a uniform degree of non-membership strong $IVIFG$ if $\zeta_{2ij}^{U} = min(\zeta_{1i}^{U}, \zeta_{1j}^{U}), \; \eta_{1i}^{L} = \eta_{1j}^{L} = s, \; \eta_{2ij}^{L} = max(s, s) = s$, and $0 \leq s \leq 1$ for all $(v_{i}, v_{j})\in E.$ This definition is depicted in Figure 3.

Definition 3.5. A UDMNMSIVIFG $G = < V, E >$ is said to have a uniform value of membership and non-membership strong $IVIFG$ if $\zeta_{1i}^{U} = \zeta_{1j}^{U} = t$, $\zeta_{2ij}^{U} = min(t, t) = t$, $\eta_{1i}^{L} = \eta_{1j}^{L} = s$, $\eta_{2ij}^{L} = max(s, s) = s, \; 0\leq t \leq 1,$ and $0 \leq s \leq 1, \; t \neq s,$ for all $(v_{i}, v_{j})\in E.$ This definition is depicted in Figure 4.

Definition 3.6. A $TUDSIVIFG \; G = < V, E >$ is said to have a total uniform degree of strong $IVIFG$ if $\zeta_{1i}^{U} = \zeta_{1j}^{U} = \eta_{1i}^{L} = \eta_{1j}^{L} = r, \; \zeta_{2ij}^{U} = \eta_{2ij}^{L} = min\{r, r\} = max\{r, r\} = r,$ and $0 \leq r \leq 1,$ for all $(v_{i}, v_{j})\in E.$ This definition is depicted in Figure 5.

4.   Interval-valued intuitionistic fuzzy topological invariants

Definition 4.1. Let $G = < V, E >$ be an $IVIFG$, and the degree of vertex of $v_{i}$ is defined by $deg_{G}(v_{i}) = (deg_{G}^{\zeta}(v_{i}), deg_{G}^{\eta}(v_{i})),$ where $deg_{G}^{\zeta}(v_{i}) = \left(\sum \zeta_{2ij}^{U}, \sum \zeta_{2ij}^{L}\right), deg_{G}^{\eta}(v_{i}) = \left(\sum \eta_{2ij}^{U}, \sum \eta_{2ij}^{L}\right).$

Definition 4.2. Let $G = < V, E >$ be an IFG, and the sum of the value of membership and the degree of non-membership elements of adjacent vertices is taken into consideration to determine the first Zagreb index, which is provided as follows:

Definition 4.3. Let $G = < V, E >$ be an IFG, and the IF second Zagreb index is defined as

Definition 4.4. Let $G = < V, E >$ be an IFG, and the IF Randic index is defined as

Definition 4.5. Let $G = < V, E >$ be an IFG, and the IF harmonic index is defined as

4.1.   Results for a uniform degree of membership of a strong interval-valued intuitionistic fuzzy graph

Theorem 4.1. For any $UDMSIVIFG,$ the degree of a vertex $v_{i}$ is $deg_{G}(v_{i}) = (d(v_{i})\left[t, t\right], deg_{G}^{\eta}(v_{i})),$ where $d(v_{i})$ is the degree of the vertex of a crisp graph and $t$ is a uniform membership degree of $v_{i}.$

Proof. Let $G = < V, E >$ be a $UDMSIVIFG.$ Further, let the number of edges in $G$ be finite. Each edge has two $IVIF$ vertices. The membership and non-membership value of each $v_{i}\in V(G)$ is represented by $(\zeta_{1i}^{U}, \zeta_{1i}^{L}), (\eta_{1i}^{U}, \eta_{1i}^{L})$ and every edge $(v_{i}, v_{j})\in E(G)$ as $(\zeta_{2ij}^{U}, \zeta_{2ij}^{L}), (\eta_{2i}^{U}, \eta_{2i}^{L})$. The degree of the vertex is represented by $deg_{G}(v_{i}) = (deg_{G}^{\zeta}(v_{i}), deg_{G}^{\eta}(v_{i}))$, since $UDMSIVIFG$ has the same value of membership $\zeta_{1i}^{U} = \zeta_{1j}^{U} = t,$ so we get $\zeta_{2ij}^{U} = min\{t, t\} = t$ for all $i, j$, where $0\leq t \leq 1.$ As $deg_{G}^{\zeta}(v_{i})$ is the sum of the membership values of all those edges that are incident on vertex $v_{i}.$

□

Theorem 4.2. For a uniform degree of membership of a strong interval-valued intuitionistic fuzzy graph, we have

Proof. The proof of this theorem is obvious. One can get intiutionistic fuzzy topological invariants of $UDMSIVIFG$ by using Theorem 4.1. □

4.2.   Results for the uniform degree of non-membership of a strong interval-valued intuitionistic fuzzy graph

Theorem 4.3. For any $UDNMSIVIFG,$ the degree of a vertex $v_{i}$ is $deg_{G}(v_{i}) = (deg_{G}^{\zeta}(v_{i}), \left[s, s\right]d(v_{i}))$ where $d(v_{i})$ is the degree of the vertex of a crisp graph and $s$ the uniform non-membership degree of $v_{i}.$

Proof. The preceding Theorem 4.1 serves as an obvious proof for this one. □

Theorem 4.4. For a uniform degree of non-membership of a strong interval-valued intuitionistic fuzzy graph, we have

Proof. The proof of this theorem is obvious. One can get intiutionistic fuzzy topological invariants of $UDNMSIVIFG$ by using Theorem 4.3. □

4.3.   Results for the uniform degree of membership and non-membership of a strong interval-valued intuitionistic fuzzy graph

Theorem 4.5. For any UDMNMSIVIFG, the degree of a vertex $v_{i}$ is $deg_{G}(v_{i}) = \left(\left[t, t\right]d(v_{i}), \left[s, s\right]d(v_{i})\right)$, where $d(v_{i})$ is the degree of the vertex of the crisp graph, $\left[t, t\right]$ is the uniform interval-valued membership degree of $v_{i}$ and $\left[s, s\right]$ is the uniform interval-valued non-membership degree of $v_{i}.$

Proof. The preceding Theorem 4.1 serves as an obvious proof for this one. □

Theorem 4.6. For a uniform degree of membership and non-membership of a strong interval-valued intuitionistic fuzzy graph, we have

Proof. The proof of this theorem is obvious. One can get intiutionistic fuzzy topological invariants of $UDMNMSIVIFG$ by using Theorem 4.5. □

4.4.   Results for the total uniform degree of a strong interval-valued intuitionistic fuzzy graph

Theorem 4.7. For any $TUDSIVIFG$, the degree of a vertex $v_{i}$ is $deg_{G}(v_{i}) = (\left[r, r\right]d(v_{i}), \left[r, r\right]d(v_{i}))$, where $d(v_{i})$ is the degree of the vertex of the crisp graph and $r$ is a uniform interval-valued membership degree of $v_{i}.$

Proof. The preceding Theorem 4.1 serves as an obvious proof for this one. □

Theorem 4.8. For a total uniform degree of a strong interval-valued intuitionistic fuzzy graph, we have

Proof. The proof of this theorem is obvious. One can get intiutionistic fuzzy topological invariants of $TUDSIVIFG$ by using Theorem 4.7. □

5.   Application

An additional useful characteristic of the indices is the fact that UIFTIs are capable of modeling complicated, stochastic, and vague parameters and, therefore, are useful in chemical and biochemical fields of informatics. In chemical informatics, by definition, UIFTIs can be applied to supplement the molecular structure assessment, where the fuzziness of bond lengths, angles, and interactions is ideal to be described using fuzzy sets. By applying UIFTIs, researchers are also able to derive better systems for establishing QSAR and optimizing many chemical properties and reactivity indices. As for the applications in bioinformatics, one can utilize the UIFTIs for studying interactome such as PPI or gene regulatory networks. The cellular neural network will be taken into account as a cellular neural interval-valued intuitionistic fuzzy graph in this section for a set of membership and non-membership values. Through this endeavour, we will be able to discuss an analysis of interval-valued intuitionistic fuzzy topological invariants. This fuzzy intuitionistic graph will be called a uniform interval-value of membership and non-membership strong interval-valued intuitionistic fuzzy graph (UDMNMSIVIFG). We have IF topological invariants of the $UDMNMSIF$ cellular neural graph narrated from Theorem 4.6 as follows:

5.1.   Computed results of IFTIs over UDMNMSIVIFG

In this part, we will offer the computational output findings of all of the IFTIs deduced above over UDMNMSIVIFG by varying the size of the cellular neural network. This mathematical study will be useful in designing a powerful computing paradigm for complex systems with various ambiguities and fuzziness. Tables 1-6 show the computed results of IFTIs for increasing dimensions of UDMNMSIVIFG.

Now we have IF topological invariants of the $TUDSIVIFG$ cellular neural graph narrated from Theorem 4.7 as follows:

5.2.   Computed results of IFTIs over TUDSIVIFG

In this part, We will offer the computational output findings of all of the IFTIs deduced above over TUDSIVIFG by varying the size of the cellular neural network. This mathematical study will be useful in designing a powerful computing paradigm for complex systems with various ambiguities and fuzziness. Tables 7-12 show the computed results of IFTIs for increasing dimensions of TUDSIVIFG.

6.   Conclusions

Several generalized findings regarding the uniform degree of membership and non-membership of the strong interval-valued intuitionistic fuzzy graph were covered in this article. We also spoke about the findings of a strong interval-valued intuitionistic fuzzy graph's overall uniform degree. Additionally, the present section's cellular neural intuitionistic fuzzy network represents a set of membership and non-membership values. Particularly, the general Randić index, harmonic index, and first and second Zagreb indices were defined in terms of a uniform intuitionistic environment.

An intriguing and multidisciplinary study topic that combines ideas from graph theory, fuzzy logic, and neural networks is encapsulated in the this article. This interesting mix provides a wealth of prospective research topics and practical applications. Here are a few last thoughts emphasizing the importance and promise of this title.

Interdisciplinary Intersection: This term highlights the confluence of several disciplines, specifically graph theory, fuzzy logic, and neural networks. This convergence offers a distinct viewpoint that might inspire fresh ideas and uses. Incorporating Uncertainty: The phrase "uniform intuitionistic fuzzy environment" indicates that there is uncertainty and imprecision in the research. When representing real-world situations where information is frequently hazy or lacking, the use of fuzzy sets and intuitionistic fuzzy sets enables a more thorough portrayal of uncertainty. Topological Numbers: The use of the term "topological numbers" implies that the research is concerned with quantifying network structure characteristics. This may entail a number of topological indices that shed light on centrality, connectedness, and other graph-based properties. Traditional topological analysis gains a new level of complexity and depth as a result of the use of these indices in a fuzzy environment.

Neural Network Application: A practical element of the research can be seen in the use of these topological numbers in the context of neural networks. In pattern recognition and machine learning, neural networks are a common tool. The inclusion of topological data in a fuzzy environment may improve neural network comprehension and performance, thereby producing more reliable and understandable models. Real-World Relevance: The proposed study could help close the gap between theoretical ideas and practical applications. Topological analysis, along with fuzzy logic and neural networks, can be used in a variety of domains where uncertainty and complicated interactions are common, including data analysis, pattern recognition, bioinformatics, and more. Algorithm Development: The creation of algorithms that function in a consistent, intuitionistic fuzzy environment may be part of the research. The development of theoretical frameworks and practical techniques could be aided by these algorithms' ability to compute and use topological numbers effectively.

Novelty : A uniform interval-valued intuitionistic fuzzy graph (UIVIFG) contains more information on relationships and decisions compared with other fuzzy models of graphs that are useful in more complicated environments of decision-making. While a basic fuzzy graph only assigns one value to represent the strength of a relationship (membership), an intuitionistic fuzzy graph improves on this by introducing two labels: the presence and absence of relationships which may be explained on a membership and non-membership basis, respectively. The next step up is the division between the two types of fuzzy graphs; the interval-valued intuitionistic fuzzy graph not only provides a single value for membership and non-membership but a range between lower and upper bounds. This gives us four values in total: upper and lower bounds of credibility for the extent to which the relation holds or does not hold (membership and non-membership). These intervals offer more freedom, and thereby, make it easier to give a finer degree to its uncertainty and hesitating measures in connection relationships. This additional granularity therefore proves that the UIVIFG can capture more precise and broader information than any standard fuzzy graph or intuitionistic fuzzy graph. It is effective in capturing relationship systems that are not simple, or even clear-cut mutually exclusive or directly proportional; this makes its use enhance analysis and decision-making. Due to the presence of intervals, this graph could be applied in the fields of networks analysis, controls systems, and fuzzy decision theories where accuracy and depth of the data are important for receiving reliable conclusions.

Future Exploration: The title alludes to a potential direction for further investigation. New understandings about the connections between topological properties, fuzzy logic, and neural networks may be found as a result of this research. It may also encourage additional research, teamwork, and creative applications.

Finally, this section proposes a thought-provoking research strategy that unifies various fields to solve issues with uncertainty, complex systems, and machine learning. It embodies the very best of multidisciplinary study, providing the chance to develop both theoretical knowledge and real-world applications in a technological environment that is continually changing.

Author contributions

Ali Al Khabyah: Conceptualization, Methodology, Funding, Writing-Reviewing and Editing; Haseeb Ahmad: Supervision, Data curation and Writing-Original draft preparation; Ali Ahmad: Visualization, Investigation, Writing-Reviewing and Editing; Ali N. A. Koam: Funding, Writing-Reviewing and Editing, Supervision. All authors reviewed and approved the final manuscript.

Acknowledgement

The authors extend their appreciation to the Deanship of Research and Graduate Studies at King Khalid University for funding this work through the Large Research Project under Grant Number RGP2/339/45.

Conflicts of interest

The authors state that no known competing financial interest or personal relationship could have influenced any of the work reported in this paper.