Novel information measures considering the closest crisp set on fuzzy multi-attribute decision making

1.   Introduction

Since Zadeh introduced fuzzy set theory, extensive research and extension related to fuzzy sets have been pursued. Among the various generalized forms that have been proposed, Atanassov ^[1] introduced the definition of intuitionistic fuzzy sets (IFSs). This was a broader concept of fuzzy sets designed to address uncertain information. It offered a more precise characterization of such information through the triad of degree of membership, degree of nonmembership, and degree of hesitation. As an extension of IFS, Atanassov ^[2] presented an alternative definition of interval-valued intuitionistic fuzzy sets (IVIFSs), wherein the degree of membership, nonmembership, and hesitation are represented by subintervals within the range of $[0, 1]$. As a result, it can precisely capture the dynamic features. Furthermore, Xu ^[3] examined certain attributes and average operators of IVIFSs. Currently, IVIFSs have been extensively utilized in diverse areas, including quality evaluation, venture capital, and medical diagnosis ^[4,5,6,7], owing to their remarkable flexibility in managing uncertainty or ambiguity.

Information measures pertaining to IFSs and IVIFSs have garnered escalating attention due to their exceptional performance in addressing practical applications. Interested readers can to ^[8,9,10]. Axiomatic definitions of distance measures on IFSs and IVIFSs were respectively provided in ^[11,12]. Furthermore, a novel distance measure for IFSs was introduced through the utilization of line integrals ^[13]. Drawing from the relationship between distance measure and similarity measure, similarity measure has also been paid attention to by a considerable number of researchers, and numerous scholars investigated the similarity measure for IVIFSs on the basis of distance measures ^{[14,15,16,29,30,31,32]}. Fuzzy entropy was initially introduced by Zadeh, and in recent years, there has been a growing interest among scholars in exploring this concept. Interested readers are encouraged to consult references ^[17,18,19] for further details. An entropy on IVIFSs constructed based on a distance measure was proposed by Zhang et al. ^[20], and the relationship between similarity measure and entropy was investigated in the paper. Che et al. ^[21] presented a method for constructing an entropy on IVIFSs in terms of the distance function. The cross-entropy approach, originating from the information theory presented by Shannon ^[22], was later applied to decision-making problems by Ye ^[23] who developed the fuzzy cross-entropy of IVIFSs using an analogy with the intuitionistic fuzzy cross-entropy. In recent years, there has been a notable surge in the interest surrounding knowledge measures within the frameworks of IFSs and IVIFSs, as clearly demonstrated by the references ^[24,25,26]. Das et al. ^[27] employed the knowledge measures under IFSs and IVIFSs to compute the criterion weights in the decision problem, and Guo ^[28] considered both aspects of knowledge related to IVIFSs, i.e., information content and information clarity to construct a model of knowledge measure and apply it to a decision-making problem under unknown weights. In addition, some scholars have also extended IVIFS ^[33,34].

The structure of this paper is as follows: Section 2 delves into several definitions and axioms that will be utilized in the subsequent research outlined in this paper. Section 3 centers on the construction of similarity measures, knowledge measures, and entropy, all grounded in the axiomatic definition of the closest crisp set and the distance measure. Furthermore, it explores the intricate transformation relationships among these three constructs. Subsequently, we present a range of formulas for information measures, each utilizing distinct functions. In Section 4, we demonstrate the efficacy and versatility of our newly introduced methodologies by applying the proposed knowledge measure to tackle a decision-making problem and the similarity measure to address a pattern recognition problem. Lastly, in Section 5, we offer some concluding remarks on the contents of this paper.

2.   Preliminaries

In this section, we will briefly introduce some of fuzzy set theories and concepts which should be used in this paper. The $X$ in the following text is represented as: $X = (x_1, x_2, \cdots, x_n)$. Let $\mathbb{N}$ denote the set of natural numbers.

Definition 2.1. ( ^[2]) An IVIFS $\tilde{A}$ on a finite set $X$ can be defined as the following form:

where $\mu_{\tilde{A}}(x) = [\mu_{\tilde{A}}^{L}(x), \mu_{\tilde{A}}^{U}(x)]\subseteq[0, 1]$ and $\nu_{\tilde{A}}(x) = [\nu_{\tilde{A}}^{L}(x), \nu_{\tilde{A}}^{U}(x)]\subseteq[0, 1]$, which satisfies $0\leq\mu_{\tilde{A}}^{U}(x)+\nu_{\tilde{A}}^{U}(x)\leq1$, for any $x\in X$. For the interval hesitation margin $\pi_{\tilde{A}}(x) = [\pi_{\tilde{A}}^{L}(x), \pi_{\tilde{A}}^{U}(x)]\subseteq[0, 1]$, we have $\pi_{\tilde{A}}^{L}(x) = 1-\mu_{\tilde{A}}^{U}(x)-\nu_{\tilde{A}}^{U}(x)$ and $\pi_{\tilde{A}}^{U}(x) = 1-\mu_{\tilde{A}}^{L}(x)-\nu_{\tilde{A}}^{L}(x)$.

Specifically, if $\mu_{\tilde{A}}^{L}(x) = \mu_{\tilde{A}}^{U}(x)$ and $\nu_{\tilde{A}}^{L}(x) = \nu_{\tilde{A}}^{U}(x)$, then the IVIFS is reduced to an intuitionistic fuzzy set.

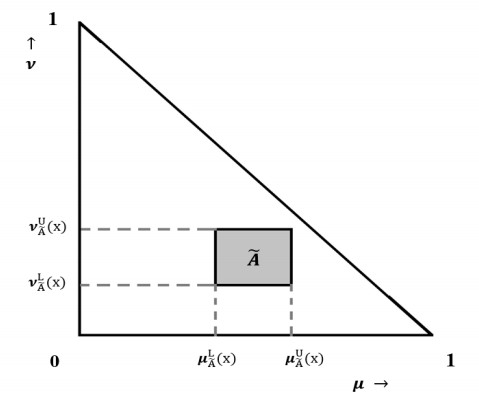
From the interval representation of membership degree and nonmembership degree of IVIFSs, it is not difficult to see that the geometric meaning of IVIFSs at a certain point is a rectangle, as shown in Figure 1. The three vertices of the triangle are denoted as $(0, 0), (1, 0), (0, 1)$, and the two sides of the triangle represent the degree of membership $\mu_{\tilde{A}}(x)$ and nonmembership $\nu_{\tilde{A}}(x)$, so that $(0, 0)$ expresses the case if $\pi_{\tilde{A}}(x) = 1$. $(1, 0)$ and $(0, 1)$ mean the two cases of the crisp sets. For the hypotenuse of the triangle, that is, the segment from $(1, 0)$ to $(0, 1)$, it corresponds to $\nu_{\tilde{A}}(x) = 1-\mu_{\tilde{A}}(x)$. Moreover, there is $0\leq\mu_{\tilde{A}}(x)+\nu_{\tilde{A}}(x)\leq1$ for an IVIFS, which also means that none of the individual vertices of the rectangle in Figure 1 can extend beyond the hypotenuse of the triangle.

For convenience, let $IVIFS\left(X\right)$ express the set of IVIFSs on $X$. Besides, we use $\mathcal{P}(X)$ to denote the set of all crisp sets defined on $X$.

Definition 2.2. ( ^[3]) For any $\tilde{A}, \tilde{B}\in IVIFS(X)$, the following relations can be defined:

(1) $\tilde{A}\subseteq\tilde{B}$ if $\mu_{\tilde{A}}^{L}(x)\leq\mu_{\tilde{B}}^{L}(x)$, $\mu_{\tilde{A}}^{U}(x)\leq\mu_{\tilde{B}}^{U}(x)$ and $\nu_{\tilde{A}}^{L}(x)\geq\nu_{\tilde{B}}^{L}(x)$, $\nu_{\tilde{A}}^{U}(x)\geq\nu_{\tilde{B}}^{U}(x)$ for any $x \in X$;

(2) $\tilde{A} = \tilde{B}$ if $\tilde{A}\subseteq\tilde{B}$ and $\tilde{A}\supseteq\tilde{B}$;

(3) The complement set $\tilde{A}^{c} = \{\langle x, \nu_{\tilde{A}}(x), \mu_{\tilde{A}}(x)\rangle|x\in X\}.$

Definition 2.3. ( ^[12]) For any $\tilde{A}, \tilde{B}, \tilde{C}\in IVIFS(X)$, a mapping $D$:$IVIFS(X) \times IVIFS(X)\rightarrow [0, 1]$ is called a distance measure on IVIFSs, and it satisfies the following properties:

$(D1)\; 0\leq D(\tilde{A}, \tilde{B})\leq 1$;

$(D2)\; D(\tilde{A}, \tilde{B}) = 0$ if $\tilde{A} = \tilde{B}$;

$(D3)\; D(\tilde{A}, \tilde{B}) = D(\tilde{B}, \tilde{A})$;

$(D4)\; D(\tilde{A}, \tilde{C})\leq D(\tilde{A}, \tilde{B})+D(\tilde{B}, \tilde{C})$;

$(D5)\; If \tilde{A} \subseteq \tilde{B}\subseteq \tilde{C}$, then $D\left(\tilde{A}, \tilde{C}\right)\geq\max{\left\{D\left(\tilde{A}, \tilde{B}\right), D\left(\tilde{B}, \tilde{C}\right)\right\}}$.

Consider $\tilde{A}, \tilde{B}\in IVIFS(X)$, where $\tilde{A} = \{\langle x, [\mu_{\tilde{A}}^{L}(x), \mu_{\tilde{A}}^{U}(x)], [\nu_{\tilde{A}}^{L}(x), \nu_{\tilde{A}}^{U}(x)]\rangle |x\in X\}$, $\tilde{B} = \{\langle x, [\mu_{\tilde{B}}^{L}(x), \mu_{\tilde{B}}^{U}(x)], [\nu_{\tilde{B}}^{L}(x), \nu_{\tilde{B}}^{U}(x)]\rangle|x\in X\}$.

For convenience, we denote:

For arbitrary $p$, the distance measure between $\tilde{A}$ and $\tilde{B}$ is presented in the following form:

where the parameter $q$ is determined by the two operations "$\ast$" and "$\star$".

When $p$ assumes different values, various distance measures can be obtained, as demonstrated in Table 1.

Definition 2.4. ( ^[28]) Let $\tilde{A}, \tilde{B}\in IVIFS(X)$, and a mapping $K$:$IVIFS(X)\rightarrow [0, 1]$ is called a knowledge measure on $IVIFS(X)$ if $K$ satisfies the following conditions:

$(K1)\; K(\tilde{A}) = 1$ if $\tilde{A}\in\mathcal{P}(X)$;

$(K2)\; K(\tilde{A}) = 0$ if $\pi_{\tilde{A}}(x) = [1, 1]$ for any $x\in X$;

$(K3)\; K(\tilde{A})\geq K(\tilde{B})$ if $\tilde{A}$ is less fuzzy than $\tilde{B}$, i.e., $\tilde{A}\subseteq\tilde{B}$ for $\mu_{\tilde{B}}^{L}(x)\leq\nu_{\tilde{B}}^{L}(x)$ and $\mu_{\tilde{B}}^{U}(x)\leq\nu_{\tilde{B}}^{U}(x)$ or $\tilde{A}\supseteq\tilde{B}$ for $\mu_{\tilde{B}}^{L}(x)\geq\nu_{\tilde{B}}^{L}(x)$ and $\mu_{\tilde{B}}^{U}(x)\geq\nu_{\tilde{B}}^{U}(x)$, for any $x\in X$;

$(K4)\; K(\tilde{A}) = K(\tilde{A}^{c})$.

Definition 2.5. ( ^[18]) Assume that the entropy is a function $E$:$IVIFS(X)\rightarrow [0, 1]$, which satisfies the nether four conditions:

$(E1)\; E(\tilde{A}) = 0$ if $\tilde{A}\in\mathcal{P}(X)$;

$(E2)\; E(\tilde{A}) = 1$ if $\mu_{\tilde{A}}(x) = \nu_{\tilde{A}}(x)$ for any $x\in X$;

$(E3)\; E(\tilde{A})\leq E(\tilde{B})$ if $\tilde{A}$ is less fuzzy than $\tilde{B}$, i.e., $\mu_{\tilde{A}}(x)\leq\mu_{\tilde{B}}(x)$ and $\nu_{\tilde{A}}(x)\geq\nu_{\tilde{B}}(x)$ for $\mu_{\tilde{B}}(x)\leq\nu_{\tilde{B}}(x)$ or $\mu_{\tilde{A}}(x)\geq\mu_{\tilde{B}}(x)$ and $\nu_{\tilde{A}}(x)\leq\nu_{\tilde{B}}(x)$ for $\mu_{\tilde{B}}(x)\geq\nu_{\tilde{B}}(x)$;

$(E4)\; E(\tilde{A}) = E(\tilde{A}^{c})$.

3.   A series of information measures of IVIFSs

Furthermore, this paper introduces the definition of the closest crisp set within the realm of IVIFSs and derives several equations pertaining to similarity measure, knowledge measure, and entropy, all grounded in the distance measure. Additionally, it delves into the methodology for converting between these measures.

3.1.   Construct a new similarity measure on IVIFSs

The extent of resemblance between two comparable entities is frequently characterized or elucidated through the utilization of similarity measure. Within this segment, we primarily introduce a novel formulation of similarity measure pertaining to IVIFSs, which relies on distance measure and the proximate crisp set denoted as $C_{\tilde{A}}$.

To this end, inspired by the concept of the closest crisp set considering intuitionistic fuzzy sets in ^[17], the notion of closest crisp set for IVIFSs is introduced.

Definition 3.1. Let $\tilde{A}\in IVIFS(X)$, and the closest crisp set to $\tilde{A}$, which is denoted by $C_{\tilde{A}}$, satisfies the following condition: If $\mu_{\tilde{A}}(x)\geq\nu_{\tilde{A}}(x)$, then $x\in C_{\tilde{A}}$; if $\mu_{\tilde{A}}(x)\ngeq\nu_{\tilde{A}}(x)$, then $x\notin C_{\tilde{A}}$.

Since any crisp set is an IVIFS with zero interval hesitation index, the closest crisp set of $\tilde{A}$ can be expressed as:

From Figure 2, it can be seen that in the left panel, $\mu_{\tilde{A}}^{L}(x) > \nu_{\tilde{A}}^{L}(x), \; \mu_{\tilde{A}}^{U}(x) > \nu_{\tilde{A}}^{U}(x)$, so that there is $x\in C_{\tilde{A}}$, or $\mu_{C_{\tilde{A}}}^{L}(x) = \mu_{C_{\tilde{A}}}^{U}(x) = 1$, $\nu_{C_{\tilde{A}}}^{L}(x) = \nu_{C_{\tilde{A}}}^{U}(x) = 0$. The opposite is true for the right panel, $\mu_{\tilde{A}}^{L}(x) < \nu_{\tilde{A}}^{L}(x), \; \mu_{\tilde{A}}^{U}(x) < \nu_{\tilde{A}}^{U}(x)$; thus, there is $x\notin C_{\tilde{A}}$, or $\mu_{C_{\tilde{A}}}^{L}(x) = \mu_{C_{\tilde{A}}}^{U}(x) = 0$, $\nu_{C_{\tilde{A}}}^{L}(x) = \nu_{C_{\tilde{A}}}^{U}(x) = 1$.

Next, a corollary is given below that presents practical properties of the closest crisp set.

Corollary 3.2. Assume that $\tilde{A}\in IVIFS(X)$, and let $C_{\tilde{A}}$ be its closest crisp set. It has the following properties:

(1) $\tilde{A}\in \mathcal{P}(X)$ if, and only if, $\tilde{A} = C_{\tilde{A}}$.

(2) If $\mu_{\tilde{A}}^{L}(x)\neq\nu_{\tilde{A}}^{L}(x), \mu_{\tilde{A}}^{U}(x)\neq\nu_{\tilde{A}}^{U}(x)$, then $C^{c}_{\tilde{A}}(x) = C_{\tilde{A}^{c}}(x)$ for any $x\in X$, where $C_{\tilde{A}^{c}}$ expresses the closest crisp set to $A^{c}$.

The preceding Corollary 3.2(2) can be elucidated more intuitively by scrutinizing Figure 3, which illustrates that the rectangular positions designated by $\tilde{A}(x)$ and $\tilde{A^{c}}(x)$ are precisely as depicted in the image when the conditions $\mu_{\tilde{A}}^{L}(x)\geq\nu_{\tilde{A}}^{L}(x)$ and $\mu_{\tilde{A}}^{U}(x)\geq\nu_{\tilde{A}}^{U}(x)$ are satisfied. Furthermore, it becomes evident that $C_{\tilde{A}}(x)$ and $C_{\tilde{A}^{c}}(x)$ occupy opposing corners, thereby establishing the equality $C^{c}_{\tilde{A}}(x) = C_{\tilde{A}^{c}}(x)$. Note here that the conditional requirement of Corollary 3.2(2) is $\mu_{\tilde{A}}^{L}(x)\neq\nu_{\tilde{A}}^{L}(x), \mu_{\tilde{A}}^{U}(x)\neq\nu_{\tilde{A}}^{U}(x)$, the reason for which is that if $\mu_{\tilde{A}}^{L}(x) = \nu_{\tilde{A}}^{L}(x), \mu_{\tilde{A}}^{U}(x) = \nu_{\tilde{A}}^{U}(x)$, as shown in Figure 4, then $\tilde{A}(x)$ and $\tilde{A}^{c}(x)$ are coincident and their closest crisp sets are the same.

Based on the proposed the closest crisp set, information measure functions are explored.

Definition 3.3. A function $f:[0, 1]^{2}\rightarrow [0, 1]$ is called a binary aggregation function, for any $x, y\in [0, 1]$, it satisfies the following conditions:

(1) $f$ is component-wise increasing;

(2) $f(0, 0) = 0$;

(3) $f(1, 1) = 1$;

(4) $f(x, y) = f(y, x)$.

Definition 3.4. ( ^[9]) Let $\tilde{A}, \tilde{B}\in IVIFS(X)$, and a mapping $S$: $IVIFS(X)\times IVIFS(X)\rightarrow [0, 1]$ is called a similarity measure on IVIFSs if $S$ satisfies the following properties:

$(S1)$ Boundary: $0\leq S(\tilde{A}, \tilde{B})\leq 1$;

$(S2)$ Symmetry: $S(\tilde{A}, \tilde{B}) = S(\tilde{B}, \tilde{A})$;

$(S3)$ Reflexivity: $S(\tilde{A}, \tilde{B}) = 1$ iff $\tilde{A} = \tilde{B}$;

$(S4)$ Complementarity: $S(\tilde{A}, \tilde{A}^{c}) = 0$ iff $\tilde{A}\in \mathcal{P}(X)$.

Theorem 3.5. Let $f:[0, 1]\times[0, 1]\rightarrow [0, 1]$ be a binary aggregation function and $D$ be an aforementioned distance in Definition 2.3 for IVIFSs. Then, for any $\tilde{A}, \tilde{B}\in IVIFS(X)$,

is a similarity measure for IVIFSs.

Proof. In the following, we will prove the proposed formula satisfies four conditions in Definition 3.4.

$(S1)$: It is clearly established.

$(S2)$: By the definition of function $f$, it can be clearly deduced that

$(S3)$: If $S(\tilde{A}, \tilde{B}) = 1$, according to the definition of $f$ and the distance measure, we can get

thus, $\tilde{A} = \tilde{B}$.

$(S4)$: If $S(\tilde{A}, \tilde{A}^{c}) = 0$, based on the definition of $f$ and the distance measure,

can be deduced. Then, $\tilde{A}\in \mathcal{P}(X)$.

With regards to Theorem 3.5, it is feasible to devise diverse formulations for calculating similarity measures on IVIFSs, leveraging various binary aggregation functions $f:[0, 1]\times[0, 1]\rightarrow [0, 1]$. By incorporating distinct functions $f$ and distance measures $D$, a range of similarity measures can be derived, as exemplified in Table 2.

3.2.   Construct a new knowledge measure and entropy on IVIFSs

The knowledge content of IVIFSs is typically characterized through knowledge measures, with entropy serving as a pivotal quantifying the uncertainty associated with fuzzy variables. In this section, we established an approach of developing similarity measures to devise knowledge measures and entropy for IVIFSs.

Theorem 3.6. Let $f$ be a function defined in Definition 3.3 and $D$ be an aforementioned distance in Definition 2.3 for IVIFSs. For any $\tilde{A}\in IVIFS(X)$,

is a knowledge measure on $IVIFS(X)$.

Proof. In the following we will show that the knowledge measure we construct satisfies the four conditions in Definition 2.4.

$(KD1)$: Let $K(\tilde{A}) = 1$, then consider the definition of the function $f$, that is, $D(\tilde{A}, C_{\tilde{A}}) = D(\tilde{A^{c}}, C_{\tilde{A}^{c}}) = 0$. Therefore, by Definition 2.3 and Corollary 3.2(1), it is easily obtained that $\tilde{A}\in \mathcal{P}(X)$.

$(KD2)$: It is not difficult to see that if $K(\tilde{A}) = 0$, then $D(\tilde{A}, C_{\tilde{A}}) = D(\tilde{A^{c}}, C_{\tilde{A}^{c}}) = 1$, and according to the definition of the distance $D$,

can be obtained. Thus, $\pi_{\tilde{A}}(x) = [1, 1]$.

$(KD3)$: Assume that $\tilde{A}\subseteq\tilde{B}$ for $\mu_{\tilde{B}}^{L}(x)\leq\nu_{\tilde{B}}^{L}(x)$ and $\mu_{\tilde{B}}^{U}(x)\leq\nu_{\tilde{B}}^{U}(x)$. It is certain that

and from the notion of the closest crisp set, it can be derived that

Therefore, let $\tilde{N} = < [0, 0], [1, 1] > ,$ and if $\tilde{N}\subseteq \tilde{A}\subseteq \tilde{B}$, then

Similarly, it is obvious that $D(\tilde{A^{c}}, C_{\tilde{A}^{c}})\leq D(\tilde{B^{c}}, C_{\tilde{B}^{c}})$. Then, by considering the function $f$ to be component-wise increasing, there is

Hence, it is easy to know that $K(\tilde{A})\geq K(\tilde{B}).$ On the other hand, assume that $\tilde{A}\supseteq\tilde{B}$ for $\mu_{\tilde{B}}^{L}(x)\geq\nu_{\tilde{B}}^{L}(x)$ and $\mu_{\tilde{B}}^{U}(x)\geq\nu_{\tilde{B}}^{U}(x)$. $K(\tilde{A})\geq K(\tilde{B})$ can also be obtained.

$(KD4)$: In order to verify $K(\tilde{A}) = K(\tilde{A}^{c})$, simply prove that

which is obvious from the definition of the function $f$.

Next, a series of knowledge measures can be obtained by using different distance measures and different expressions of function $f$. They are shown in Table 3.

Subsequently, entropy from the perspective of knowledge measures for IVIFSs will be explored.

Corollary 3.7. Let $K$ be a knowledge measure induced by the aforementioned function $f$ for IVIFSs, then for any $\tilde{A}\in IVIFS(X)$,

is an entropy for IVIFSs.

Based on Corollary 3.7, it is straightforward to deduce the existence of a distinct numerical correlation between entropy and the newly devised knowledge metric. Put simply, within the context of an IVIFS, a system with a lower entropy value may consistently possess a greater quantity of knowledge, provided that it adheres to the prescribed axioms.

By carefully examining the intricate relationship between the recently introduced knowledge measure and entropy, we can effortlessly deduce certain entropies.

Upon scrutinizing the information measures previously discussed for IVIFSs, it becomes evident that they share certain linkages, which we shall subsequently elaborate in the form of corollaries.

Corollary 3.8. Let $S$ be an aforementioned similarity measure in Theorem 3.5 for IVIFSs, and for any $\tilde{A}\in IVIFS(X)$,

is a knowledge measure for IVIFSs.

Corollary 3.9. Let $S$ be an aforementioned similarity measure in Theorem 3.5 for IVIFSs; assuming that $\tilde{A}\in IVIFS(X)$,

is an entropy for IVIFSs.

Regarding the construction method and transformation relationship of information measures, there are some important issues to be further discussed below, and these discussions pave the way for the subsequent research.

(1) Drawing upon the axiomatic definition of IVIFSs, the intricate relationship among similarity measures, knowledge measures, and the entropy of IVIFSs is comprehensively formulated in general terms, accompanied by explicit expressions. Notably, several key findings are presented in the form of theorems, which underscore the existence of a profound connection between the information measures associated with IVIFSs.

(2) Among these theorems, through the axiomatic definition of IVIFS, we can easily convert the above information measures, i.e., similarity measure, knowledge measure, and entropy, to each other. Specifically, we consider that the similarity measure and knowledge measure of IVIFS can be converted to each other, and, finally, based on the general relationship between knowledge measure and entropy, the entropy is constructed with the similarity measure, so that the larger the similarity measure, the less the amount of knowledge it contains, and the larger the entropy.

(3) The result of Corollary 3.7 in this paper shows that there is a dyadic relationship between entropy and knowledge measure, which paves the way for continuing to explore whether there is a dyadic relationship between entropy and knowledge measure for fuzzy sets and their extended forms.

4.   The applications of knowledge and similarity measures

This section employs the recently proposed knowledge measure to tackle multi-attribute decision-making (MADM) problems under conditions of unknown weights, while utilizing the novel similarity measure to address pattern recognition issues within the framework of IVIFSs. The derived outcomes are subsequently contrasted with several established measures for comprehensive analysis.

4.1.   The application of knowledge measure in investment decision

4.1.1.   An evaluation approach of MADM based on knowledge measure

In the complex process of MADM, where the weights of individual attributes remain elusive, this subsection introduces a methodology for determining these weights through the utilization of knowledge measures techniques.

Construct an MADM process that examines $m$ alternatives $\tilde{A} = \{\tilde{A}_1, \tilde{A}_2, \ldots, \tilde{A}_m\}$ using $n$ attributes $C = \{C_1, C_2, \ldots, C_n\}$. Suppose that $w = (w_1, w_2, \ldots, w_n)^{T}$ is the weight vector of attributes, where $0\leq w_j \leq 1$ and $\sum_{j = 1}^{n}w_j = 1, j = 1, 2, \ldots, n$.

The MADM problem of IVIFSs can be described in the matrix form below:

where $\tilde{a}_{ij} = \langle (x, [\mu^{ij}_{\tilde{a}L}(x), \mu^{ij}_{\tilde{a}U}(x)], [\nu^{ij}_{\tilde{a}L}(x), \nu^{ij}_{\tilde{a}U}(x)])|x\in X\rangle (i = 1, 2, \ldots, m; j = 1, 2, \ldots, n)$ indicates the assessment of an expert corresponding to attribute $C_{j}(j = 1, 2, \ldots, n)$ to evaluate the alternative $\tilde{A}_{i}(i = 1, 2, \ldots, m)$.

Step 1. By defining the knowledge measure of IVIFSs using $K_{H1}$, the knowledge measure based decision matrix $Q = (\tilde{k}_{ij})_{m\times n}$ is generated from the decision matrix $R$ above. The matrix $Q = (\tilde{k}_{ij})_{m\times n}$ is shown below.

where $\tilde{k}_{ij}$ is the knowledge measure corresponding to each $\tilde{a}_{ij}$.

Step 2. The following formula can be used to construct the attribute weights based on the knowledge measure when the attribute weights $w_j$ are completely unknown:

where $0\leq w_j \leq 1$ and $\sum_{j = 1}^{n}w_j = 1$.

Step 3. In an interval-valued intuitionistic fuzzy environment, the interval-valued intuitionistic fuzzy arithmetic mean operator ^[3] is used to calculate the weighted aggregation value of each alternative $\tilde{A}_i$ after the weights of each attribute have been determined and the operator is expressed as follows:

where $i = 1, 2, \ldots, m; j = 1, 2, \ldots, n.$ The calculated $Z_{i}$ is an IVIFS.

Step 4. In order to differentiate between the alternatives, the alternatives will be ranked below by calculating a score function for each alternative, with the following equation:

Subsequently, arrange the alternatives in a nonincreasing sequence of score function, the larger the score function of the alternative, the better the alternative is. In order to realize the whole decision-making process, Figure 5 describes a framework.

4.1.2.   Investment case

In this section, a practical case study, adapted from ^[5], will be presented to demonstrate the application of the newly introduced knowledge measure in addressing MADM problems involving unknown weights.

An investment company is about to make an investment, and the four possible choices for the investment capital are (1) $\tilde{A}_1$, a car company; (2) $\tilde{A}_2$, a food company; (3) $\tilde{A}_3$, a computer company; and (4) $\tilde{A}_4$, a branch office. The investment firm is trying to decide which of these is the best option. The following four attributes must also be taken into consideration by the investment company when making its choice: $C_1$: Risk analysis; $C_2$: Growth analysis; $C_3$: Environmental impact analysis; and $C_4$: Social and political impact analysis.

Let $w = (w_1, w_2, w_3, w_4)^{T}$ be the weight vector of the attributes, which is completely unknown. Additionally, the ratings of the alternatives over the attributes are listed in the following Table 4.

Step 1. Based on $K_{H1}$, the knowledge measure matrix is calculated as follows:

Step 2. Next, the weight of attributes are calculated by applying Eq (4.3):

Step 3. The interval-valued intuitionistic fuzzy weighted average operator can be computed by utilizing the formula presented in Eq (4.4). As a result, the combined results of the schemes are obtained as follows:

Step 4. The scoring values of the alternatives are calculated with Eq (4.5) when $\lambda = \frac{1}{2}$ as follows:

Therefore, the sorting order is $\tilde{A}_4\succ \tilde{A}_1\succ \tilde{A}_2\succ \tilde{A}_3$, and the optimal alternative is $\tilde{A}_4$. Furthermore, to underscore the practicality of the newly introduced knowledge measure in addressing the MADM problem, we contrast the derived outcomes with diverse entropy and knowledge measures. Evidently, the majority of the ranking outcomes closely align with our findings, as evident from the subsequent Table 5 and Figure 6. Notably, $\tilde{A}_4$ emerges as the optimal solution.

The aforementioned examples demonstrate the remarkable effectiveness of applying knowledge measures to tackle MADM problems that involve unknown weights. Additionally, they underscore the usefulness and practical applicability of the newly introduced knowledge measures in our daily lives.

4.1.3.   Sensitivity analysis

It is evident that the parameter $\lambda$ in Eq (4.5) can be interpreted as the weight of membership degree, and its magnitude significantly impacts the ultimate ranking of alternatives. Sensitivity analysis is performed by selecting various $\lambda$ values. Table 6 presents the score function values $\phi(Z_{i})$ and the rankings of each alternative, which are calculated based on different $\lambda$ values.

We randomly select 9 values for $\lambda$ within the interval $(0, 1)$, and it is evident that regardless of how $\lambda$ varies, the ranking of alternatives remains consistent throughout Table 6. Additionally, we will visualize the data in Figure 7, which illustrates that the ultimate ranking remains unaltered despite changes in $\lambda$. As evident from Table 6, when $\lambda > 0.5$, the score function values of the alternative solutions exhibit a substantial increase, primarily due to a greater preference for membership degree under such conditions.

To clearly demonstrate the disparities among alternative solutions as $\lambda$ escalates, consider the following definitions: $T_{1} = \phi(Z_{4})-\phi(Z_{1}), T_{2} = \phi(Z_{1})-\phi(Z_{2}), T_{3} = \phi(Z_{2})-\phi(Z_{3}).$ It can be found that with the increase of $\lambda$, the discrimination between the alternatives increases in Table 7 and Figure 8. That is to say, with the increase of $\lambda$, the score function $\phi(Z_{i})$ can better distinguish the alternatives. Therefore, the ranking results should be minimally influenced by subjective factors, which further demonstrates the stability of the method proposed in this paper.

4.1.4.   Interval-valued intuitionistic fuzzy decision support system with application to COVID-19 healthcare facilities

Novel coronavirus pneumonia (COVID-19) is an acute respiratory infectious disease caused by the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2). Since its outbreak in Pakistan, the COVID-19 situation there has garnered widespread attention. The epidemic's spread in Pakistan has exhibited certain fluctuations, with a gradual rise in confirmed cases, exerting a profound impact on public health, socioeconomic conditions, and the daily lives of citizens.

This paper refers to the example of healthcare facilities in Khyber Pakhtunkhwa, Pakistan in ^[33]. There is currently a review panel comprising three experts, $e_{1}, e_{2}$, and $e_{3}$, tasked with evaluating four hospitals $A_{l} (l = 1, 2, 3, 4)$ in Khyber Pakhtunkhwa based on four attributes: $c_{1}$: Reverse Transcription-Polymerase Chain Reaction Facilities (RT-PCR), $c_{2}$: Personal protective equipment (PPE), $c_{3}$: Shortage of Isolation Ward (SIW), $c_{4}$: Hight Qualified Staff (HQS).

Next, the specific steps of the decision-making method are as follows.

Step 1. We construct interval valued intuitionistic fuzzy decision matrices, as shown in Tables 8–10.

Step 2. By utilizing $K_{h1}$ to define the knowledge measure of IVIFSs, a decision matrix $Q^{k} (k = 1, 2, 3)$, grounded in this knowledge measure, is derived from the decision matrix. The matrix $Q^{k}(k = 1, 2, 3)$ is presented as follows.

Step 3. We assign equal weights to the three experts and aggregate their knowledge measure decision matrices into one using the formula below:

Obtain the following knowledge measure aggregation matrix $\bar{Q}$:

Step 4. Determine attribute weights by applying Eq (4.3).

Step 5. Employ Eq (4.4) to apply weights and aggregate the attributes of the alternative (Table 11).

Step 6. When $\lambda = \frac{1}{2}$, the score values by each expert to the alternative are calculated using Eq (4.5) as shown in Table 12.

Step 7. Aggregate the score values of three experts to obtain the final ranking of alternative solutions.

It is not hard to observe that $\bar{\varphi}_{2} > \bar{\varphi}_{3} > \bar{\varphi}_{4} > \bar{\varphi}_{1}$. Thus, yielding the alternative ranking result: $A_2\succ A_3\succ A_4\succ A_1$. This is consistent with the result in ^[33], which also demonstrates the effectiveness and practicality of the method proposed in this paper.

4.2.   Application of similarity measure in pattern recognition

4.2.1.   The method of pattern recognition

Suppose $X$ is a finite universe of discourse. There are $m$ patterns which are denoted by IVIFSs

and a test sample that needs to be categorized exists, which is denoted by IVIFS

The following is the recognition process:

(a) Compute the similarity measure $S(\tilde{M}_{j}, \tilde{B})$ between $\tilde{M}_{j}(j = 1, ..., m)$ and $\tilde{B}$ with $S_{H1}$ and $S_{h1}$.

(b) Sort $S(\tilde{M}_{j}, \tilde{B})$ in ascending order, where a larger value of $S(\tilde{M}_{j}, \tilde{B})$ indicates a closer proximity of $\tilde{B}$ to category $\tilde{M}_{j}$.

4.2.2.   Tackling medical diagnosis with pattern recognition methods

A diverse array of scholars have proposed numerous approaches to tackle medical diagnosis from varying perspectives. In this section, we employ pattern recognition techniques to address the medical diagnosis challenge: the collection of symptoms serves as the discourse universe, the patient functions as an unidentified test specimen, and the various diseases correspond to multiple modalities. The objective is to categorize patients into distinct groups based on their respective diseases.

Suppose $X = \{x_{1}\text{(Temperature)}, \; x_{2}\text{(Cough)}, \; x_{3} \text{(Headache)}, \; x_{4}\text{(Stomach }\; \text{pain)}\}$ is a group of symptoms and $\tilde{M} = \{\tilde{M}_{1}\text{(Viral fever)}, \; \tilde{M}_{2}\text{(Typhoid)}, \; \tilde{M}_{3}{(Pneumonia)}, \; \tilde{M}_{4}\text{(Stomach problem)}\}$ is a group of the diseases. Then, the disease-symptom matrix expressed by IVIFSs is shown in Table 13 and data is derived from ^[16].

Let the patient $B$ be expressed as:

The aim is to categorize patient $B$ into one of diseases $\tilde{M}_{1}, \tilde{M}_{2}, \tilde{M}_{3}, \tilde{M}_{4}$. We can then obtain the following results on IVIFSs, as shown in Table 14.

We may determine that there is the most similarity between $\tilde{M}_{2}$ and $B$ by taking into account the pattern recognition principle of IVIFSs, but the similarity measure $S_{1}$ is unable to determine which of $\tilde{M}_{1}$ and $\tilde{M}_{4}$ is greater. Furthermore, the newly suggested similarity measures are more practical and capable of resolving this point. In addition, by using the similarity measures $S_{H1}$ and $S_{h1}$ proposed in this paper, the same recognition results can be obtained. Hence, based on the recognition principle, we can classify patient $B$ as suffering from disease $\tilde{M}_{2}$, thereby conclusively diagnosing them with typhoid illness.

5.   Conclusions

This paper introduces the axiomatic definition of the closest crisp set for IVIFSs, along with its pertinent properties. Subsequently, leveraging the distance measure to the closest crisp set, a novel knowledge measure and entropy for IVIFSs are presented. Furthermore, several theorems are proven, and the interplay between knowledge measures and entropy is examined. Ultimately, the efficacy of the proposed method is validated through two concrete examples: The application of knowledge measures in MADM and similarity measures in pattern recognition.

In the future, we will persist in exploring the application of IVIFS information measures in other domains and strive to develop superior and more rational models for the mutual conversion of these information measures.

Author contributions

Chunfeng Suo: Writing-review & editing, supervision, project administration, funding acquisition; Le Fu: Conceptualization, Methodology, software, validation, writing-original draft, writing-review & editing; Jingxuan Chen: Software, validation, supervision, conceptualization; Xuanchen Li: Validation, writing-review. All authors have read and approved the final version of the manuscript for publication.

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This paper was supported by National Science Foundation of China (Grant Nos: 11671244, 12071271), Natural Science Foundation of Jilin Province (Grant Nos: YDZJ202201ZYTS320) and the Sixth Batch of Jilin Province Youth Science and Technology Talent Lifting Project.

Conflict of interest

The authors declare that there are no conflicts of interest in the publication of this paper.