Pythagorean hesitant fuzzy rough multi-attribute decision-making method with application to wearable health technology devices

1.   Introduction

There are numerous complementary fields, such as medical, social, and economics and management that necessitate the execution of substantial decision-making (DM), that is, determination of enterprise location, evaluation of scientific research, assessment of employees, selection of initiatives and projects, evaluation of investments, allocation of resources, and wide-ranging economic advantage classification. Prudent DM is the cornerstone of modern management and is essential for evaluating the overall effectiveness of management initiatives. Several multi-attribute DM (MADM) approaches have been implemented and their applications have been discussed in various fields of DM. For example, Gou et al. ^[1] developed two types of linguistic preference orderings for representing experts's opinions in the evaluation of resource allocation for medical health in public health emergencies, and they developed a new (Rangement Et Synthese De Ronnees Relationnelles) ORESTE method utilizing linguistic preference orderings to address MADM problems. The ORESTE method was proposed to address the actual MADM problem related to the allocation of medical health resources during public health emergencies. They analyzed the results of the ORESTE method and compared them to other existing methods in a double-hierarchy linguistic environment. Zhang et al. ^[2] introduced a novel method for comparing double hierarchy hesitant fuzzy linguistic elements (DHHFLEs). This method represents an advancement over existing comparison methods for DHHFLEs. Furthermore, they addressed a gap in the current research by proposing a cosine similarity measure for DHHFLEs, which takes a geometric perspective rather than relying solely on algebraic approaches. The proposed method is applied to solve an MADM problem in the performance evaluation of financial logistics enterprises. Gou et al. ^[3] introduced a new and comprehensive concept called the probabilistic double hierarchy linguistic term set (PDHLTS). They suggested some additional practical operations and a method to measure the distance between PDHLTSs. They enhanced the traditional (VIekriterijumsko KOmpromisno Rangiranje) VIKOR method by developing an extended probabilistic double hierarchy linguistic VIKOR method. In addition, the proposed method showcases its benefits and practicality through its application in solving a real-world MADM problem in the field of smart healthcare. Decision-makers frequently employ MADM approaches, which encompass the application of various logical methods to evaluate and prioritize a set of alternatives according to a set of interconnected criteria. Several MADM approaches employ different logical frameworks (for detailed information, see ^[4,5,6,7,8]). Typically, DMs consist of individuals who possess expertise in the particular issue being evaluated. They commonly favor the use of fuzzy numbers when conducting precise evaluations. This is because of the qualitative scoring that experts may introduce subjectivity and personal presumptions into their assessments. This implies an ambiguous and vague evaluation from the expert. Dealing with uncertainty and inaccurate information is a major difficulty. Optimal performance of traditional mathematical models often requires precise data, which is not always achievable in implementation. Rough set theory, developed by Pawlak ^[9] in the early 1980s, is a mathematical approach that addresses the challenges of dealing with vagueness and uncertainty. It acquired recognition as a widely-used framework for processing uncertain knowledge. The rough set theory stipulates a strong framework for handling uncertainty and imprecision in information. Through its emphasis on the approximation of sets using indiscernibility relations, this approach provides a distinct method for analyzing and interpreting complicated information without requiring additional details. It is often compared to fuzzy set (FS) theory, introduced by Zadeh ^[10] in 1965, and is sometimes used in combination with it as the fuzzy-rough approach, as established by Dubois and Prade ^[11]. Rough set (RS) theory has garnered global attention from numerous professionals and researchers who have made significant contributions to its advancement and practical implementations. RS theory is characterized by its overlapping nature with various other theories. However, RS theory can be perceived as a distinct discipline in its own regard. The RS theory has been widely utilized in diverse domains, particularly in research areas including artificial intelligence, cognitive sciences, machine learning, intelligent systems, inductive reasoning, pattern recognition, computational image processing, signal assessment, knowledge discovery, expert systems, data mining, knowledge discovery, feature selection and reduction, classification, clustering, decision support systems, medical diagnosis, and analyzing medical data to assist in diagnosis and treatment planning. Therefore, RS theory proves to be a valuable tool in the field of data analysis and decision support, especially in situations where data is incomplete or ambiguous. The framework enables the approximation of imprecise or incomplete information by utilizing the concepts of lower and upper approximations. Recently, there has been significant development in data analysis methods, particularly in the context of big data and the internet of things (IoT). The majority of references pertain to the stimulating works on hybrid models that are created by combining RS theory concepts within the suggested framework, which is considered a crucial element. RS theory is an emerging theory that addresses the handling of inadequate data (see ^{[12,13,14,15]} for detail information). Over the past few decades, researchers have proposed numerous generalizations and extensions of the classical RS theory. The applications of RSs in a fuzzy environment has gained significant attention in recent years. The study of Pei ^[16] focused on the challenges of approximating fuzzy sets within fuzzy information systems, leading to the development of the theory of fuzzy RSs. Jiang et al. ^[17] introduced a new methodology for utilizing a fuzzy similarity-based RS algorithm in the context of feature weighting and reduction for a case-based reasoning system. The algorithm is utilized in the process of tool selection for die and mould machining. Ding et al. ^[18] conducted a study on three-way group decisions using evidential reasoning in incomplete hesitant fuzzy information systems for liver disease diagnosis. Zhang et al. ^[19] designed an incomplete three-way MADM using adjustable multi-granulation Pythagorean fuzzy probabilistic RSs. They discussed two case studies involving mine ventilator fault diagnosis and air quality evaluations. They also conducted various comparative experiments and sensitivity analyses to demonstrate the effectiveness of their theoretical methodology. Wang ^[20] provided an overview of the properties of fuzzy RSs based on triangular norms. These norms do not necessarily need to be continuous. The purpose of this description is to provide generalization results for fuzzy RS theory from a mathematical perspective. The study conducted by Qi et al. ^[21] focused on the Fermatean fuzzy covering-based RS and its applications in MADM. This study aims to showcase the decision-making processes involved in selecting electric vehicle charging stations in an Indian city using innovative methodologies. The DM results were compared to other conventional techniques employing the Spearman ranking correlation coefficient and Pearson correlation coefficient methods to verify the effectiveness of the novel approaches. The investigation carried out by Theerens et al. ^[22] was centered around specific examples within the broader category of fuzzy quantifier-based fuzzy RSs (FQFRS). The lower and upper approximations in these models are evaluated using binary and unary fuzzy quantifiers, respectively. In addition, they presented a counterexample to support the claim that other FQFRS models are not granularly representable. However, these approaches are still effective in addressing inconsistencies in real-life datasets. Zhou et al. ^[23] introduced the concept of single granulation hesitant Pythagorean fuzzy RSs for the first time. Then, considering the multi-granulation framework, two types of multi-granulation hesitant Pythagorean fuzzy RSs are introduced, known as the optimistic and pessimistic multi-granulation hesitant Pythagorean fuzzy RSs. The relationships between serial hesitant Pythagorean fuzzy relations and hesitant Pythagorean fuzzy approximation operators are established. We provide a real-life instance to illustrate the applicability of the proposed method in MADM. Zhang et al. ^[24] presented an integrated DM framework that utilizes the hesitant fuzzy RS model across two universes and explores various properties of this model. An idea is made for the union, intersection, and composition of hesitant fuzzy approximation spaces, along with an investigation into their properties. In addition, they introduced a novel method for making decisions in uncertain environments by utilizing hesitant fuzzy rough sets across two different universes. Finally, two real-world MADM problems are provided to demonstrate the effectiveness of this approach. The development of an explainable prediction method that combines fuzzy RSs and the TOPSIS approach (developed by Hwang and Yoon ^[25]) was reported by Gaeta et al. ^[26]. The findings possess the potential to aid analysts and decision-makers in acquiring more comprehension of the phenomenon known as information disorder. The results are derived from authentic data and exhibit encouraging possibilities for future research. Hesitancy represents an inherent aspect of the natural world. Determining the superior alternatives that share identical characteristics in routine presents a complex challenge. Expert professionals are finding it challenging to deal with DM because of the ambiguity and hesitation about the outcomes. In addressing the issue of hesitancy, Torra ^[27] introduced the notion of hesitant fuzzy sets (HFS). The hesitant fuzzy sets effectively capture the uncertainty of intricate scenarios and the imprecision of perceptions among individuals. Since their establishment, HFSs have made notable progress in both practical and theoretical aspects. This framework can be applied to resolve a diverse array of DM challenges. A broad range of authors have merged the idea of HFS with other frameworks of fuzzy sets and employed them to address real-world challenges through the application of Dombi aggregation operators (introduced by Dombi in 1982) and the TOPSIS methodology within the context of group DM. Dombi aggregation operators and the TOPSIS approach gained significant recognition as an essential tool for addressing real-world DM complications. A number of researchers have employed the aforementioned concepts across various domains of DM challenges. Xia and Xu ^[28] explored various hesitant fuzzy aggregation operators (AOPs) and discussed their applications. Liu et al. ^[29] performed a study on the Dombi AOPs of the interval-valued HFS, with a specific focus on the Dombi t-norm and t-conorm. Akram et al. ^[30] introduced and explained several averaging and geometric AOPs that utilize the Dombi t-norm and t-conorm. They also discussed the practical applications of these techniques in DM environments. Tehreem et al. ^[31] developed Dombi AOPs in spherical cubic fuzzy information and discussed their applications in MADM. These approaches were presented to demonstrate their validity, practicability, and efficacy. Shi and Ye ^[32] have broadened the idea of Dombi operation to include neutrosophic cubic sets and have effectively applied it to the DM problem. Lu and Ye ^[33] initially established the Dombi AOPs for linguistic cubic variables to assist in the DM problem. Umer et al. ^[34] enhanced the TOPSIS approach by integrating a distance technique that incorporates interval type-2 trapezoidal Pythagorean fuzzy numbers. They thoroughly examined the applications of this approach in addressing MADM problems, diligently considered the viewpoints and insights of decision-makers throughout the evaluation process. A novel approach for determining the ranking order in group DM was proposed by Kacprzak et al. ^[35], which utilizes ordered fuzzy integers and the TOPSIS strategy. Rezaei et al. ^[36] developed an approach to address the issue of sustainable global partner selection by utilizing DM experts who were previously unidentified. Jun et al. ^[37] developed the hybrid TOPSIS methodology based on interval Pythagorean FS (PyFS) and explored its application in MADM. Zhang and Dai ^[38] were the first to develop the TOPSIS approach, which combines decision-theoretic rough fuzzy sets. They demonstrated the effectiveness and reliability of the technique through detailed analysis and evaluation of parameters. In addition, they accomplished simulated experiments to further confirm the effectiveness of the proposed DM approach.

In the aforementioned research initiatives, hybrid models incorporating a PyFS and an RS are rarely accomplished. In addition, the Pawlak RS has been effectively integrated with other uncertainty theories, such as soft set theory, which has enabled the development of several innovative RS models. In order to deal with unclear and reluctant information while making decisions for real-world problems, the concept of Pythagorean hesitant fuzzy rough sets (PyFRSs) is also crucial. The aforesaid literature aroused our interest to put forward a novel notion known as PyHFRSs. The goal of our research is to integrate HFSs with PyFRSs to explore potential applications in tackling MADM challenges in a hesitant fuzzy environment. The main contributions of the manuscript are as follows:

(1) To assemble a list of AOPs based on Dombi t-norm and t-conorm, namely, PyHFR Dombi weighted averaging (PyHFRDWA), PyHFR Dombi ordered weighted averaging (PyHFRDOWA), and PyHFR hybrid weighted averaging (PyHFRHDWA), and investigate their key operating laws. Additionally, describe their related properties.

(2) To introduce and implement the score and accuracy functions employing PyHFRSs.

(3) To provide a DM technique for combining uncertain information employing prescribed aggregation operators.

(4) The initiated operators are employed for a real-world DM challenge involving the selection of wearable health technology devices (WHTDs) for hospitals.

(5) The effectiveness and rationality of the suggested framework were confirmed by sensitivity and comparative analysis with the PyHFR-TOPSIS approach. The obtained results are shown graphically.

1.1.   Structure of the article

The remaining part of this research is outlined as follows: Section 2 summarizes the basic information required for fundamental ideas. In Section 3, we explain the basic operations of the Domi t-norm and t-conorm in detail based on PyHFRS, which will be useful for the subsequent analysis. In Section 4, we introduce the MADM strategy under the PyHRFR information section. Section 5 implements the real-life application of the suggested approach for the selection of WHTDs for hospitals. Sections 6 and 7 present the sensitivity and comparative analyses, respectively. Section 8 concludes the study and presents future recommendations.

2.   Preliminaries

In this section, we will briefly go through the crucial concepts that are essential to having a thorough understanding. These ideas include FS, HFS, intuitionistic FS (IFS), PyHFS, RS, intuitionistic fuzzy RS (IFRS), PyHFRS, and other operational laws that are inescapably interconnected. These key notions will assist and simplify the suggested framework.

Definition 2.1. ^[10] Let $\mathcal{X} = \left\{ \widetilde{\widetilde{{ \varrho }}}_{1}, \widetilde{{ \varrho }}_{2}, \widetilde{ { \varrho }}_{3}, ..., \widetilde{{ \varrho }} _{n}\right\}$ be a nonempty set. By fuzzy set $F$, we mean a structure of the form

where $\mathcal{H}_{F}(\widetilde{{ \varrho }}_{i})\in \left[ 0, 1 \right]$ is known to be membership grade (MG).

Definition 2.2. ^[39] Let $\mathcal{X} = \left\{ \widetilde{{ \varrho }}_{1}, \widetilde{{ \varrho }}_{2}, \widetilde{{ \varrho }} _{3}, ..., \widetilde{{ \varrho }}_{n}\right\}$ be a nonempty set. By HFS $H;$ we mean a structure:

where $\mathcal{H}_{h_{H}}(\widetilde{{ \varrho }}_{i})\in \left[ 0, 1\right]$ is the MG and a set of values, and $\mathcal{H}_{h_{H}}(\widetilde{{ \varrho }}_{i})$ is referred to as the HF element.

Definition 2.3. ^[40] $\ $Let $\mathcal{X} = \left\{ \widetilde{{ \varrho }} _{1}, \widetilde{{ \varrho }}_{2}, \widetilde{{ \varrho } }_{3}, ..., \widetilde{{ \varrho }}_{n}\right\}$ be an nonempty set. An IFS $\digamma$ over $\widetilde{{ \varrho }}_{i}$ is structurally defined as:

and for each $\varrho _{i}\in \mathcal{X}$, the functions $\mathcal{H}_{ \widetilde{F}}:\mathcal{X}\rightarrow \lbrack 0$, $1]$ and $\mathcal{U}_{ \widetilde{F}}:\varrho \rightarrow \lbrack 0, \; 1]$ show the MG and nonmembership grade (NMG), respectively, which must satisfy the property $0\leq \mathcal{H}_{\widetilde{F}}(\varrho _{i})+\mathcal{U}_{\widetilde{F} }(\varrho _{i})\leq 1.$

Definition 2.4. ^[41]$\ $Let $\mathcal{X} = \left\{ \widetilde{{ \varrho }} _{1}, \widetilde{{ \varrho }}_{2}, \widetilde{{ \varrho } }_{3}, ..., \widetilde{{ \varrho }}_{n}\right\}$ be a nonempty universal set. By intuitionistic hesitant FS (IHFS) $E$ over $\mathcal{X}$, we mean a structure as follows:

where $\mathcal{H}_{h_{E}}( \varrho _{i})\in \left[ 0, 1 \right]$ and $\mathcal{U}_{h_{E}}( \varrho _{i})\in \left[ 0, 1\right]$ are sets of some values, which shows the MG and NMG respectively, with the property for all $\eta (\widetilde{{ \varrho }}_{i})\in \mathcal{H}_{h_{E}}(\widetilde{{ \varrho }} _{i})$ and $\nu (\widetilde{{ \varrho }}_{i})\in \mathcal{U} _{h_{E}}(\widetilde{{ \varrho }}_{i})$ such that $\left(\max \left(\eta (\widetilde{{ \varrho }}_{i})\right) \right) +\left(\min \left(\nu (\widetilde{{ \varrho }}_{i})\right) \right) \leq 1$ and $\left(\min \left(\eta (\widetilde{{ \varrho }} _{i})\right) \right) +\left(\max \left(\nu (\widetilde{{ \varrho }}_{i})\right) \right) \leq 1.$

Definition 2.5. ^[9] Let $\mathcal{X} = \left\{ \widetilde{{ \varrho }}_{1}, \widetilde{{ \varrho }}_{2}, \widetilde{{ \varrho }} _{3}, ..., \widetilde{{ \varrho }}_{n}\right\}$ be a nonempty universal set and $\mathcal{Z}$ be any relation on $\mathcal{X}.$ Define a set valued mapping $\mathcal{Z}^{\ast }:\mathcal{X}\rightarrow M(\mathcal{X})$ by $\mathcal{Z}^{\ast }(\xi) = \{a\in \mathcal{X}|( \varrho _{i}, a)\in \mathcal{Z}\},$ for $\varrho _{i}\in \mathcal{X}$, where $\mathcal{Z}^{\ast }( \varrho _{i})$ is called a successor neighborhood of the element $\varrho_{i}$ with respect to relation $\mathcal{Z}.$ The pair $\left(\mathcal{X}, \mathcal{Z} \right)$ is known as a crisp approximation space. Now, for any set $\widetilde{\widetilde{\mathcal{I}}}\subseteq \mathcal{X},$ the lower approximation (LA) and upper approximation (UA) of $\widetilde{\widetilde{ \mathcal{I}}}$ with respect to the space $\left(\mathcal{X}, \mathcal{Z} \right)$ is defined as:

where $\left(\left\downarrow \mathcal{Z}\right. (\widetilde{\mathcal{I}}), \left\uparrow \mathcal{Z}\right. (\widetilde{\mathcal{I}})\right) :M(\mathcal{X})\rightarrow M(\mathcal{X})$ are LA and UA operators and the pair $\left(\left\downarrow \mathcal{Z}\right. (\widetilde{\mathcal{I}}), \left\uparrow \mathcal{Z}\right. (\widetilde{\mathcal{I}})\right)$ is called RS.

Definition 2.6. ^[42] Let $\mathcal{X} = \left\{ \widetilde{{ \varrho }}_{1}, \widetilde{{ \varrho }}_{2}, \widetilde{{ \varrho }} _{3}, ..., \widetilde{{ \varrho }}_{n}\right\}$ be the universal set and $\mathcal{Z}\in IFS(\mathcal{X}\times \mathcal{X})$ be an IF relation. Then,

(1) $\mathcal{Z}$ is reflexive if $\mathcal{H}_{\mathcal{Z}}(\varrho _{i}, \varrho _{i}) = 1$ and $\nu _{\mathcal{Z}}(\varrho _{i}, \varrho _{i}) = 0, \forall \varrho _{i}\in \mathcal{X};$

(2) $\mathcal{Z}$ is symmetric if $\ \forall (\varrho _{i}, £)\in \mathcal{X}\times \mathcal{X}, \; \mathcal{H}_{\mathcal{Z}}(\varrho _{i}, £) = \mathcal{H}_{\mathcal{Z}}(£, \varrho _{i})$, and $\nu _{\mathcal{Z}}(\varrho _{i}, £) = \nu _{\mathcal{Z}}(£, \varrho _{i});$

(3) $\mathcal{Z}$ is transitive if $\forall (\varrho _{i}, \partial)\in \mathcal{X}\times \mathcal{X},$

and

Definition 2.7. ^[43] Let $\mathcal{X} = \left\{ \widetilde{{ \varrho }}_{1}, \widetilde{{ \varrho }}_{2}, \widetilde{{ \varrho }} _{3}, ..., \widetilde{{ \varrho }}_{n}\right\}$ be the universal set. Then, any relation $\mathcal{Z}\in IFS(\mathcal{X}\times \mathcal{X})$ is called an IF relation. The pair $\left(\mathcal{X}\times \mathcal{Z}\right)$ is said to be an IF approximation space. Now for any $\widetilde{\mathcal{I}} \subseteq IFS(\mathcal{X})$, the LA and UA of $\widetilde{\mathcal{I}}$ with respect to IF approximation space $\left(\mathcal{X}, \mathcal{Z} \right)$ are two IFSs and symbolized by $\left\downarrow \mathcal{Z}\right. (\widetilde{\mathcal{I}})$ and $\left\uparrow \mathcal{Z}\right. (\widetilde{ \mathcal{I}})$ and are highlighted below:

and

where

such that

As $\left(\left\downarrow \mathcal{Z}\right. (\widetilde{\mathcal{I}}), \left\uparrow \mathcal{Z}\right. (\widetilde{\mathcal{I}})\right)$ are $IFSs, \; \left\downarrow \mathcal{Z}\right. (\widetilde{\mathcal{I}}), \; \left\uparrow \mathcal{Z}\right. (\widetilde{\mathcal{I}}):IFS(\mathcal{X})\rightarrow IFS(\mathcal{X})$ are LA and UA operators. The pair

is known as an IFRS. For simplicity,

is represented as $\mathcal{Z}(\widetilde{\mathcal{I}}) = ((\downarrow{ \mathcal{H}}, \downarrow{\mathcal{U}}), (\uparrow{\mathcal{H}}, \uparrow{ \mathcal{U}}))$ and is known as an intuitionistic fuzzy rough (IFR) value.

Definition 2.8. Let $\mathcal{X}$ be the universal set and for any subset, $\mathcal{Z}\in PyHFS(\mathcal{X}\times \mathcal{X})$ is said to be a PyHFR relation. The pair $\left(\mathcal{X}, \mathcal{Z}\right)$ is said to be a PyHF approximation space. If for any $\widetilde{\mathcal{I}}\subseteq PyHFS(\mathcal{X})$, then the LA and UA of $\widetilde{\mathcal{I}}$ with respect to PyHF approximation space $\left(\mathcal{X}, \mathcal{Z}\right)$ are two PyHFSs, which are denoted by $\left\downarrow \mathcal{Z}\right. (\widetilde{\mathcal{I}})$ and $\left\uparrow \mathcal{Z}\right. (\widetilde{ \mathcal{I}})$ and defined as:

and

where

such that

and

As $\left(\left\uparrow \mathcal{Z}\right. (\widetilde{\mathcal{I}}), \left\downarrow \mathcal{Z}\right. (\widetilde{\mathcal{I}})\right)$ are $PyHFSs, \; \left\downarrow \mathcal{Z}\right. (\widetilde{\mathcal{I}}), \left\uparrow \mathcal{Z}\right. (\widetilde{\mathcal{I}}):PyHFS(\mathcal{X })\rightarrow PyHFS(\mathcal{X})$ are LA and UA operators. The pair

will be called Pythagorean hesitant fuzzy RSs (PyHFRSs). For simplicity,

is represented as $\mathcal{Z}(\widetilde{\mathcal{I}}) = \left((\downarrow{ \mathcal{H}}, \downarrow{\mathcal{U}}), (\uparrow{\mathcal{H}}, \uparrow{ \mathcal{U}})\right)$ and is known as a PyHFR value.

Definition 2.9. The scoring function employed for the PyHFR value $\mathcal{Z}(\widetilde{ \mathcal{I}}) = (\left\downarrow \mathcal{Z}\right. (\widetilde{\mathcal{I}}), \left\uparrow \mathcal{Z}\right. (\widetilde{\mathcal{I}})) = \left((\downarrow{\mathcal{H}}, \downarrow{\mathcal{U}}), (\uparrow{\mathcal{H}}, \uparrow{\mathcal{U}})\right)$ is given as:

The accuracy function for PyHFRV $\mathcal{Z}(\widetilde{\mathcal{I}}) = (\left\downarrow \mathcal{Z}\right. (\widetilde{\mathcal{I}}), \left\uparrow \mathcal{Z}\right. (\widetilde{\mathcal{I}})) = ((\downarrow{ \mathcal{H}}_{\tau }, {\downarrow{\mathcal{U}}_{\tau }}), (\uparrow{ \mathcal{H}}_{\tau }, \uparrow{\mathcal{U}}_{\tau }))$ is given as:

where $\mathcal{S}$ and $\mathcal{N}$ represent the number of elements in $\mathcal{H}_{\tau }$ and $\mathcal{U}_{\tau }$, respectively.

Definition 2.10. Suppose $\mathcal{Z}(\widetilde{\mathcal{I}}_{1}) = (\left\downarrow \mathcal{Z }\right. (\widetilde{\mathcal{I}}_{1}), \left\uparrow \mathcal{Z}\right. (\widetilde{\mathcal{I}}_{1}))$ and $\mathcal{Z}(\widetilde{\mathcal{I}} _{2}) = (\left\downarrow \mathcal{Z}\right. (\widetilde{\mathcal{I}} _{2}), \left\uparrow \mathcal{Z}\right. (\widetilde{\mathcal{I}}_{2}))$ are two PyHFR values. Then,

(1) if $SR(\mathcal{Z}(\widetilde{\mathcal{I}}_{1})) > SR(\mathcal{Z}(\widetilde{\mathcal{I}}_{2})),$ then $\mathcal{Z}(\widetilde{\mathcal{I}} _{1}) > \mathcal{Z}(\widetilde{\mathcal{I}}_{2}),$

(2) if $SR(\mathcal{Z}(\widetilde{\mathcal{I}}_{1})) < SR(\mathcal{Z}(\widetilde{\mathcal{I}}_{2})),$ then $\mathcal{Z}(\widetilde{\mathcal{I}} _{1}) < \mathcal{Z}(\widetilde{\mathcal{I}}_{2}),$

(3) if $SR(\mathcal{Z}(\widetilde{\mathcal{I}}_{1})) = SR(\mathcal{Z}(\widetilde{\mathcal{I}}_{2})),$ then

(a) if $\mathbf{AC}\mathcal{Z}(\widetilde{\mathcal{I}}_{1}) > \mathbf{AC }\mathcal{Z}(\widetilde{\mathcal{I}}_{2})$ then $\mathcal{Z}(\widetilde{ \mathcal{I}}_{1}) > \mathcal{Z}(\widetilde{\mathcal{I}}_{2}),$

(b) if $\mathbf{AC}\mathcal{Z}(\widetilde{\mathcal{I}}_{1}) < \mathbf{AC}\mathcal{Z}(\widetilde{\mathcal{I}}_{2})$ then $\mathcal{Z}(\widetilde{\mathcal{I}}_{1}) < \mathcal{Z}(\widetilde{\mathcal{I}}_{2}),$

(c) if $\mathbf{AC}\mathcal{Z}(\widetilde{\mathcal{I}}_{1}) = \mathbf{AC }\mathcal{Z}(\widetilde{\mathcal{I}}_{2})$ then $\mathcal{Z}(\widetilde{ \mathcal{I}}_{1}) = \mathcal{Z}(\widetilde{\mathcal{I}}_{2}).$

3.   Dombi t-norm and t-conorm

This section describes in detail the Domi product and dombi sum (see ^[44] for information) and discuss some basic operations based on PyHFRSs, which will be useful for the subsequent analysis. Following are the specific types of triangular norms and co-norms:

Definition 3.1. ^[44] Let $\wp _{1}$and $\wp _{2}$ be considered any two real numbers within the interval [0, 1]. The Dombi t-norm can be expressed as

$\wp _{1}\boxtimes \wp _{2} = \frac{1}{1+\left(\left(\frac{1-\wp _{1}}{\wp _{1}}\right) ^{\zeta }+\left(\frac{1-\wp _{2}}{\wp _{2}}\right) ^{\zeta }\right) ^{\frac{1}{\zeta }}}, \; \zeta > 0.$

The Dombi t-conorm is given by

$\wp _{1}\boxplus \wp _{2} = 1-\frac{1}{1+\left(\left(\frac{1-\wp _{1}}{\wp _{1}}\right) ^{-\zeta }+\left(\frac{1-\wp _{2}}{\wp _{2}}\right) ^{-\zeta }\right) ^{\frac{1}{\zeta }}}, \; \zeta > 0$, respectively.

Definition 3.2. Let $\mathcal{K}_{1}$ = $\left\{ \left(\mathcal{H}_{1s}, \text{ }\mathcal{U} _{1s}\right) :1\leq s\leq \mathcal{\ell }_{\mathcal{K}_{1}}\right\}$ and $\mathcal{K}_{2}$ = $\left\{ \left(\mathcal{H}_{2k}, \text{ }\mathcal{U} _{2k}\right) :1\leq k\leq \mathcal{\ell }_{\mathcal{K}_{2}}\right\}$ be two PyHFRSs and $\zeta > 0,$ and the Dombi operations for PyHFR numbers are outlined below.

(1) $\mathcal{K}_{1}\boxplus \mathcal{K}_{2} = \bigcup\limits_{ \begin{array}{c} \mathcal{H}_{1s}, \text{ }\mathcal{U}_{1s}\in \mathcal{K}_{1} \\ \mathcal{H}_{2k}, \text{ }\mathcal{U}_{2k}\in \mathcal{K}_{2} \end{array} }\left\{ \sqrt{1-\frac{1}{1+\left(\left(\frac{\mathcal{H}_{1s}^{2}}{1- \mathcal{H}_{1s}^{2}}\right) ^{\zeta }+\left(\frac{\mathcal{H}_{2k}^{2}}{1- \mathcal{H}_{2k}^{2}}\right) ^{\zeta }\right) ^{\frac{1}{\zeta }}}}, \sqrt{ \frac{1}{1+\left(\left(\frac{1-\mathcal{U}_{1s}^{2}}{\mathcal{U}_{1s}^{2}} \right) ^{\zeta }+\left(\frac{1-\mathcal{U}_{2k}^{2}}{\mathcal{U}_{2k}^{2}} \right) ^{\zeta }\right) ^{\frac{1}{\zeta }}}}\right\},$

(2) $\mathcal{K}_{1}\boxtimes \mathcal{K}_{2} = \bigcup\limits_{ \begin{array}{c} \mathcal{H}_{1s}, \text{ }\mathcal{U}_{1s}\in \mathcal{K}_{1} \\ \mathcal{H}_{2k}, \text{ }\mathcal{U}_{2k}\in \mathcal{K}_{2} \end{array} }\left\{ \sqrt{\frac{1}{1+\left(\left(\frac{1-\mathcal{H}_{1s}^{2}}{ \mathcal{H}_{1s}^{2}}\right) ^{\zeta }+\left(\frac{1-\mathcal{H}_{2k}^{2}}{ \mathcal{H}_{2k}^{2}}\right) ^{\zeta }\right) ^{\frac{1}{\zeta }}}}, \sqrt{1- \frac{1}{1+\left(\left(\frac{\mathcal{U}_{1s}^{2}}{1-\mathcal{U}_{1s}^{2}} \right) ^{\zeta }+\left(\frac{\mathcal{U}_{2k}^{2}}{1-\mathcal{U}_{2k}^{2}} \right) ^{\zeta }\right) ^{\frac{1}{\zeta }}}}\right\},$

(3) $\lambda \mathcal{K}_{1} = \bigcup\limits_{\mathcal{H}_{1s}, \text{ } \mathcal{U}_{1s}\in \mathcal{K}_{1}}\left\{ \sqrt{1-\frac{1}{1+\left(\lambda \left(\frac{\mathcal{H}_{1s}^{2}}{1-\mathcal{H}_{1s}^{2}}\right) ^{\zeta }\right) ^{\frac{1}{\zeta }}}}, \sqrt{\frac{1}{1+\left(\lambda \left(\frac{1-\mathcal{U}_{1s}^{2}}{\mathcal{U}_{1s}^{2}}\right) ^{\zeta }\right) ^{\frac{1}{\zeta }}}}\right\},$

(4) $\mathcal{K}_{1}^{\lambda }\bigcup\limits_{\mathcal{H}_{1s}, \text{ } \mathcal{U}_{1s}\in \mathcal{K}_{1}}\left\{ \sqrt{\frac{1}{1+\left(\lambda \left(\frac{1-\mathcal{U}_{1s}^{2}}{\mathcal{U}_{1s}^{2}}\right) ^{\zeta }\right) ^{\frac{1}{\zeta }}}}, \sqrt{1-\frac{1}{1+\left(\lambda \left(\frac{\mathcal{H}_{1s}^{2}}{1-\mathcal{H}_{1s}^{2}}\right) ^{\zeta }\right) ^{\frac{1}{\zeta }}}}, \right\}.$

3.1.   Pythagorean hesitant fuzzy rough Dombi weighted arithmetic averaging operator

Let $\beth ^{n}$ = $\left\{ \wp _{\imath } = \langle \left(\downarrow{ \mathcal{H}}_{\imath j}, \text{ }\downarrow{\mathcal{U}}_{\imath j}\right), \left(\uparrow{\mathcal{H}}_{\imath j}, \text{ }\uparrow{\mathcal{U}} _{\imath j}\right) \rangle :1\leq \imath \leq \mathcal{\ell }_{h_{i}}, \text{ }j = 1, 2, 3, ..., n\right\}$ be an n-dimensional of PyHFRSs. A PyHFRDWAA operator is defined by the function PyHFRDWAA: $\beth ^{n} \; \longmapsto \beth$ as follows:

where $w_{\imath }$ is the weight vector of $\wp _{\imath }(\imath = 1, 2, 3, ..., n$), $0\leq w_{\imath }\leq 1$, and $\boxplus _{\imath = 1}^{n}w_{\imath } = 1.$

Theorem 3.3. Let $\wp _{\imath }\in \; \beth ^{n}(\imath = 1, 2, 3, ..., n$). Then,

where $w_{\imath }$ is the weight vector of $\wp _{\imath }(\imath = 1, 2, 3, ..., n$), $0\leq w_{\imath }\leq 1$ and $\boxplus _{\imath = 1}^{n}w_{\imath } = 1.$

Proof. The theorem can be proved using the approach of mathematical induction as follows:

Step 1. When $n = 2$, we get the following findings based on Dombi operations for

The theorem thus holds for n = 2.

Step 2. Suppose the result is true for $n = k$, that is,

Step 3. When $n = k+1,$

So, the results are true for all $n = k+1.$ Hence, the theorem is proved for $n\in Z.$ □

Example 3.4. Let's suppose

for $n = 4$ and $\zeta = 1,$ with weight vector $w = \left(0.15, 0.22, 0.26, 0.37\right).$ We get

$PyHFRDWAA(\wp _{1}, \wp _{2}, \wp _{3}) = \left\{ \begin{array}{c} \left[ (0.1404, 0.1705, 0.2362), (0.1619, 0.1810, 0.2086)\right], \\ \left[ (0.1863, 0.2227, 0.2599), (0.1646, 0.2261, 0.2534)\right] \end{array} \right\}.$

Theorem 3.5. (Idempotency): Let $\wp _{\imath }(\; \imath = 1, 2, 3, ..., n)$ be a number of PyHFRNs. Then,

is a number of PyHFR elements that are equal, i.e., $\wp _{\imath } = \wp$ for all $\imath$, then $PyHFRDWAA(\wp _{1}, \wp _{2}, \wp _{3}, ..., \wp _{n}) = \wp$.

3.2.   PyHFRDOWAA operator

Let

be an n-dimensional of PyHFRSs. A PyHFRDOWAA operator is defined by the function PyHFRDOWAA: $\beth ^{n} \; \longmapsto \beth$ as follows:

where $\wp _{\vartheta (\imath)}$ is the $\imath ^{th}$ largest of $\wp _{\imath }$ and $w_{\imath }$ is the weight vector of $\wp _{\imath }(\imath = 1, 2, 3, ..., n$), such that $0\leq w_{\imath }\leq 1$ and $\boxplus _{\imath = 1}^{n}w_{\imath } = 1.$

Theorem 3.6. Let $\wp _{\imath }\in \; \beth ^{n}(\imath = 1, 2, 3, ..., n$). Then

where $\wp _{\vartheta (\imath)}$ is the $\imath th$ largest of $\wp _{\imath }$ and $w_{\imath }$ is the weight vector of $\wp _{i}(i = 1, 2, 3, ..., n$), such that $0\leq w_{\imath }\leq 1$ and $\boxplus _{\imath = 1}^{n}w_{\imath } = 1.$

Proof. The proof is straightforward and similar to the proof of Theorem 1. □

3.3.   Pythagorean hesitant fuzzy rough Dombi hybrid weighted arithmetic averaging (PyHFRDHWAA) operator

Let $\beth ^{n}$ = $\left\{ \wp _{\imath } = \langle \left(\downarrow{ \mathcal{H}}_{\imath j}, \text{ }\downarrow{\mathcal{U}}_{\imath j}\right), \left(\uparrow{\mathcal{H}}_{\imath j}, \text{ }\uparrow{\mathcal{U}} _{\imath j}\right) \rangle :1\leq \imath \leq \ell _{h_{i}}, \text{ } j = 1, 2, 3, ..., n\right\}$ be an $n$-dimensional of HFRSs and let $w_{\imath }$ be the weight vector of $\wp _{\imath }(\imath = 1, 2, 3, ..., n$), such that $0\leq w_{\imath }\leq 1$ and $\boxplus _{\imath = 1}^{n}w_{\imath } = 1$. A PyHFRDHWAA operator is defined by the function PyHFRDHWAA: $\beth ^{n} \; \longmapsto \beth$ as follows:

Let $\Omega = \left(\eta _{1}, \eta _{2}, ..., \eta _{n}\right) ^{T}$ be the associated weight vector such that $\sum_{\imath = 1}^{n}\eta _{\imath } = 1$ and $0\leq \; \eta _{\imath }\leq 1$.

Theorem 3.7. Let $\wp _{\imath }\in \; \beth ^{n}(\imath = 1, 2, 3, ..., n$). Then,

where $\widehat{\wp }_{\delta (\imath)} = \left(\wp _{\delta (\imath)}\right) ^{n\varpi _{i}} = (\left(\wp _{\imath }\right) ^{n\varpi _{i}}, \left(\wp _{\imath }\right) ^{n\varpi _{i}})$ shows the superior value of permutation from the collection of HFRVs and $n$ represents the balancing coefficient.

Proof. The proof is straightforward and similar to the proof of Theorem 1. □

4.   Multiple attribute group DM approach under PyHRFR information

The MADM is a crucial procedure for selecting an alternative from a set of desirable alternatives based on the opinions of experts regarding attributes. A team of experts thoroughly evaluates each alternative, acquiring various attributes, and stipulates an assessment in the form of PyHFRV for each alternative pertaining to each attribute. The information collected from the decision makers is aggregated using the weights given by the experts. After collecting the appropriate data, it is then compiled to assess the overall value of each alternative, considering the assigned weights for each attribute. The MADM is incredibly beneficial for a wide range of industries. It is widely used in a variety of fields including research areas including business, economics, machine learning, intelligent systems, pattern recognition, image processing, signal assessment, data mining, knowledge discovery, feature selection and reduction, classification, clustering, aiding in DM processes by managing imprecise and inconsistent information, analyzing medical data to assist in diagnosis and treatment planning, engineering, and more. Here, we present an MADM methodology that involves the following crucial steps:

Step 1. Let $A = \{A_{1}, A_{2}, ..., A_{l}\}$, $\mathcal{C} = \{c_{1}, c_{2}, ..., c_{j}\}$ and $\mathcal{D} = \{d_{1}, d_{2}, ..., d_{t}\}$ be the set of alternatives, criteria and decision-makers respectively. Let the wight vector be $\mathcal{W} = (w_{1}, w_{2}, w_{3}..., w_{j}),$ where $w_{s}\in (0, 1]$ and $\boxplus _{s}^{j}w_{s} = 1$. The MADM method comprises the following procedures:

Step 2. The assessment of the alternative $A_{i}$ based on criteria $c_{s}$ by decision-makers $d_{r}\left(r = 1, 2, 3, ..., t\right)$ can be written as $\widetilde{\psi} _{rs}\left(r = 1, 2, 3, ..., t;s = 1, 2, 3, ..., j\right)$. Consequently, the PyHFR-decision matrix D${A_{i}} = [\widetilde{\psi} _{rs}]_{t\times j}$ may be established as follows:

Step 3. Assess the normalized experts matrices as

Step 4. Construct collected PyHFR information using PyHFRDWAA related to $A_{\imath }$ denoted by $\mathcal{L}_{\imath }$, which is defined as follows:

Step 5. To use the aforementioned aggregation information, evaluate the aggregated PyHFR values for each alternative examined in accordance to the given set of attributes/criteria.

Step 6. Compute the score values for $\mathcal{L}_{\imath }(\imath = 1, 2, 3, ..., l).$

Step 7. Order the score value of all $\mathcal{L}_{\imath }(\imath = 1, 2, 3, ..., l)$.

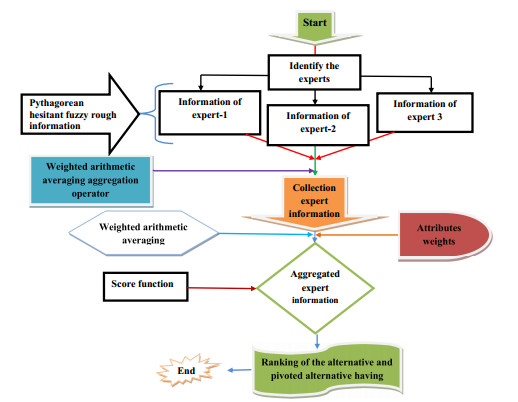
Step 8. Select the option with the highest score value. Figure 1 illustrates the diagrammatic chart of the algorithm for the implied MADM technique.

5.   Numerical application

In this section, we will provide an MADM problem-related wearable medical technology to demonstrate the implementation and adaptability of the aforementioned approach. The market for wearable medical and health-care manufactured products has widened significantly in the years owing to global industrialization. The utilization of wearable technology has increased significantly, having an enormous effect on the health-care industry. Wearable devices, equipped with transmitters and target receptors, are worn on the body or in clothing to detect changes in the human body and offer rapid feedback. This technology assists physicians in understanding the changes happening in the human body and providing timely medicines to patients. The goal of wearable technology in health-care is to transform the industry through providing patients with comprehensive information that can be carried out in order to gain practical insights. Wearable technology is influencing health-care by monitoring electrocardiograms like heart rate, blood pressure, and oxygen levels, as well as recording patient health data like physical activity, nutrition, and sleep patterns. Individuals with chronic illnesses such as diabetes, cardiovascular disease, and neurological issues need regular monitoring of their physiological functioning in order to get appropriate medical treatment. Wearable technology has emerged as a crucial tool in the health-care industry to meet the demands of this requirement. Wearable health technology facilitate patients to accumulate their own health data and transmit it in digital format, minimizing the need for face-to-face appointments. Wearable medical technology could assist hospitals save both resources and time while maintaining convenience to patients. Continuous monitoring of patients is required during their rehabilitation, and the adoption of wearable health monitoring devices has increased the efficiency of this approach. Wearable fitness trackers and other health-tracking technology are beneficial for those who desire to measure their physical activity. This includes not only measuring steps or physical training, but also monitoring the individual's overall mobility and essential indications Individuals' psychological conditions are also assessed employing wearable medical gadgets. These wearable health solutions include sensors that monitor patients' mental health. Wearable device health care provides the benefit of medical education by enabling individuals to effortlessly access critical information, essays, articles, case studies, and other study materials on their smartphone. Wearable medical devices also have benefits for electronic health record systems. Primary care asserts that combine patient-generated fitness or medical data with enormous amounts of information, such as current health data, into electronic medical records, in addition to other biological and genetic data, has significant power and resiliency.

The challenges of incorporating wearable medical technology into health-care systems include the financial strain on medical organizations, whilst not every organization can afford to embrace such devices. Patients may feel uncomfortable when utilizing wearable medical equipment owing to its weight. These technologies are made up of a variety of components and are intended to be attached to the body. Due to data discrepancies, there is insufficient evidence to demonstrate wearable devices' unaltered accuracy. Individuals have data privacy concerns regarding a lack of control over their personal information. Furthermore, during the installation of programs, users are needed to provide authorization to access personal data, exposing them to possible hazards such as forgery and data destruction. Because the integration of patient data via wearable technology is still in its early stages, the area of health wearable technology has hurdles in terms of system compatibility and linkage. Wearable medical devices hold a large quantity of personal information concerning health conditions. It may cause people to get anxious and feel like they are being watched too closely. Furthermore, the medical community struggles to adequately handle the enormous amount of information.

5.1.   The evaluation procedure for selecting an appropriate wearable health technology devices

This section applies the developed model to a case study concerning wearable health technology device selection. Assume an employer has nominated four prospective companies on a worldwide basis with the intention of determining a wearable health technology gadget. A panel of specialists across the world has been invited to investigate and determine the most appropriate gadgets for the organization. Let $\mathcal{D} = \{\mathcal{D}_{1}, \mathcal{D}_{2}, \mathcal{D}_{3}\}$ be a set of three decision-makers. $A = \{A_{1}, A_{2}, A_{3}, A_{4}\}$ symbolizes the set of four devices that were under consideration for selection among them and the set of four index dimensions, in particular: accuracy $(c_{1})$, security $(c_{2})$, intelligence $(c_{3})$, and limitations $(c_{4})$. It should be noted that all of the attributes presented here are of the benefit type. The decision-makers weights vector is $\mathcal{W}$ = $\left[ 0.25, 0.49, 0.56\right] ^{T}$ and the associated attribute weight vector is $\mathcal{W}$ = $\left[ 0.11, 0.25, 0.28, 0.36\right] ^{T}$. To assess the MADM situation by employing the aforementioned scheme for evaluating alternatives, the following procedures are carried out:

Step 1. The information obtained from three experts based on PyHFRVs has been incorporated into Tables 1–3, respectively.

Step 2. All the information provided by the experts are benefit type; there is no requirement for normalization.

Step 3. Table 4 demonstrates the PyHFRDWA and evaluates the accumulated information of three expert analysts. Table 5 shows the score value of the collected experts in formation. Based on score value, the ordered collected experts information is presented in Table 6.

Step 4. Assess the aggregated PyHFR values for each alternative evaluated using the specified set of criteria/attributes utilizing the aforementioned aggregation information. Tables 7 and 8 visualized the aggregated information for PyHFRDWA, PyHFRODWA, respectively. The hybrid collected experts information is shown in Table 9. The score values of hybrid information is presented in Table 10 and the aggregated information for PyHFRHDWA is depicted in Table 11.

Step 5. The score value of the information obtained through PyHFRDWA, PyHFRODWA, and PyHFRHDWA is presented in Table 12 and depicted in Figure 2. Ranking the alternatives based on the score values, we observed that $A_{2}$ is the best alternative.

6.   Sensitivity analysis

It is evident that the PyHFRDWAA includes a parameter $\zeta$, which significantly improves its adaptability and effectiveness in handling fuzzy information. In our example, we use a parameter value of $\zeta$ = 1. We analyze the potential variations in the outcomes achieved with the PyHFRDWAA operator. Table 13 and Figure 3 display the ranking orders determined by the score values obtained through the PyHFRDWAA operator. Vary the value of parameter $\zeta$ from 1 to 200, identify multiple values, and organize them in ascending order based on PyHFR scores. When the value $\zeta$ in the PyHFRDWAA is varied, the optimal alternative is always the same, and the orderings of alternatives ($A_{2} > \; A_{1} > \; A_{4} > \; A_{3}$) are the same for all values of $\zeta$. Using the PyHFRDWAA operator and the score function, we achieved option $A_{2}$ with the highest score value as an optimal alternative and $A_{3}$ with the lowest score values presented in Table 13 for $\zeta = 1, \; 2, \; 5, \; 10, \; 20, \; 50, \; 100, \; 200.$ Therefore, the most appropriate alternative is similar for different values of $\zeta$. Figure 3 depicts a graphical representation of Table 13.

7.   Comparative analysis

The goals of this section are to compare the outcome of the improved TOPSIS scheme with the novel aggregation operators based on PyHFRS. The fundamental concept of the TOPSIS approach states that the better the alternative, the farther it is from the negative ideal solution and the closer it is to the positive ideal solution. As a consequence, researchers have developed several techniques that are capable of completing the process of classifying alternatives in worldwide decision-making problems. These algorithms are devoted to dealing with the ordering of feasible alternatives. We develop a novel TOPSIS methodology based on PyHFRSs that handles the identification and categorization of alternatives. By following these criteria, we explain in detail how the innovative TOPSIS technique works and assess its validity. The feasibility of our technique is then verified, as well as its effectiveness and reliability are shown via comparisons to alternative approaches and a variety of experiments with varying input parameters. In addition, we conduct a simulation experiment to test how our strategy compares to the traditional TOPSIS approach in terms of sorting attribute. The TOPSIS is a framework employed by Hwang and Yoon ^[25] for assessing the advantages and disadvantages of various policy approaches under ideal situations. TOPSIS characterizes the best possible decision as the one that relates closely to the positive ideal solution all of the criteria while simultaneously becoming the farthest away from the negative ideal solution. The method consists of mainly the following aspects:

Step 1. Let $\widetilde{\kappa } = \{\ell _{1}, \ell _{2}, \ell _{3}, ..., \ell _{m}\}$ and $C = \{c_{1}, c_{2}, c_{3}, ..., c_{n}\}$ be the set of alternatives and criteria. The information obtained from the professionals is provided as follows:

where

and

such that

are the PyHFR rough values.

Step 2. First, we assemble information from decision-makers using PyHFR numbers.

Step 3. Second, normalize DM information because the decision matrix may include benefit and cost criteria, which is demonstrated below:

where $\phi$ shows the number of experts.

Step 4. Analyze the normalized information obtained from professionals $\left(N\right) ^{\phi },$ as

Step 5. The score value determines the positive and negative ideal solutions. $\gimel ^{+} = \left(\gimel _{1}^{+}, \gimel _{2}^{+}, \gimel _{3}^{+}, ..., \gimel _{n}^{+}\right)$ and $\daleth ^{-} = \left(\gimel _{1}^{-}, \gimel _{2}^{-}, \gimel _{3}^{-}, ..., \gimel _{n}^{-}\right)$ are the positive ideal solutions (PIS) and negative ideal solutions (NIS). The formula computes PIS $\gimel ^{+}$ is as follows:

In a comparable way, the formula used to determine the NIS $\daleth ^{-}$ is as follows:

Subsequently, calculate the geometric distance between each alternative and the PIS $\gimel ^{+}$using the formula enclosed:

where i = 1, 2, 3, ..., n, and j = 1, 2, 3, ..., m.

By routine calculation, the geometric distance between each alternative and the NIS $\gimel ^{-}$ can be displayed as follows:

where i = 1, 2, 3, ..., n and j = 1, 2, 3, ..., m.

Step 6. Here is the procedure employed for determining the relative closeness indices for each decision-makers alternative:

Step 7. The ranking orders of alternatives may be established, and the most desired option with the shortest distance can be identified.

7.1.   Numerical example

In this section, we demonstrate an MADM problem to show the framework's applicability and versatility. A numerical illustration to choose the best international partner for a multinational company is given. The following is a summary of the key procedures:

Step 1. The decision-makers information is provided in Tables 1 and 3 in the form of PyHFR numbers.

Step 2. The collected information compiled by decision-makers portrayed as PyHFR numbers is displayed in Table 4.

Step 3. There is no need to normalize the information since it is benefit type.

Step 4. The PIS and NIS are determined based on the score value and are displayed in Table 14 as follows:

Step 5. Compute the distance measure of PIS and NIS as follows:

and

Step 6. The calculation of the relative closeness indices for all decision-makers of the alternatives is as follows:

Step 7. The order of alternatives is ranked in descending order as shown in Table 15 and in Figure 4. The minimum distance can be observed to be associated with $A_{2}$. Therefore, option $A_{2}$ is the best choice.

8.   Conclusions

Assessing the performance of wearable health technology devices has exceptional practical value for product optimization and technology enhancement. However, there are numerous distinctions in the technical standards, functions, prices, and service objects of these solutions, all within an uncertain objective environment. Decision-makers often encounter unreliable uncertainty when evaluating alternatives simultaneously. Decision-makers are faced with a daunting task when it pertains to identifying the most optimal wearable health technology devices. To solve these problems, this paper introduced the concept of PyHFRSs, which are robust mathematical tools designed to effectively manage uncertain and imprecise information. The aim is to address the complexity and uncertainty associated with decision information and smart medical solutions. In addition, we introduced the innovative concept of PyHFRWA, PyHFROWA, and PyHFRHA aggregation operators based on PyHFRSs. We provided a comprehensive description of the characteristics and new score and accuracy functions for the proposed operators. Furthermore, the hybrid PyHFR-TOPSIS model for MADM and its stepwise algorithm are demonstrated using the proposed approach. On the other hand, the significance and validity of the evaluation framework are confirmed by numerical examples of the WHTDs evaluation system, and sensitivity and comparative show that the investigated models are more effective and useful than the existing approaches. The study enhances existing aggregation operators and the DM method based on the aforementioned operator, improving the existing fuzzy MADM techniques. The study provides assessment and theoretical support for evaluating and selecting WHTDs in the medical system. This approach can provide a valuable reference for designers of WHTDs in the medical system. It helps to identify areas for product improvement, optimize performance, enhance sustainable development capabilities, expand market influence, and motivate long-term enterprise growth. This method can serve as a valuable resource for hospitals and medical institutions seeking to identify the most effective solutions for their medical systems. By doing so, it has the potential to enhance the quality of medical services and improve the overall patient experience. In addition, this research presents valuable insights for the development and future direction of the national smart medical system, which will ultimately contribute to more effective health-care for humanity.

In the upcoming research, we aim to expand this investigation to include other fuzzy settings and the model can be applied to additional specialized MADM challenges like ^[45,46,47].

Author contributions

Attaullah: Conceptualization, methodology, software, validation, formal analysis, writing-original draft preparation, writing-review and editing, supervision, project administration; Sultan Alyobi: Conceptualization, data curation, writing-original draft preparation, writing-review and editing, supervision, project administration, funding acquisition; Mohammed Alharthi: Conceptualization, software, validation, investigation, resources, visualization; Yasser Alrashedi: Conceptualization, methodology, validation, data curation, project administration. All authors have read and approved the final version of the manuscript for publication.

Acknowledgments

The authors are thankful to the Deanship of Graduate Studies and Scientific Research at University of Bisha for supporting this work through the Fast-Track Research Support Program.

Conflict of interest

The authors declare that they have no conflict of interest.