Solving time fractional partial differential equations with variable coefficients using a spatio-temporal meshless method

1.   Introduction

The time-fractional partial differential equation (TFPDE) is one of the most widely studied fractional partial differential equations in mathematics and physics and has captured continued interests from researchers, due to its widespread applications ^[1]. For example, it is frequently used to model anomalous diffusion in porous media ^[2,3,4,5,6], where heterogeneities cause the diffusion rate to deviate from classical models. Additionally, the TFPDEs are employed to describe the propagation dynamics of light beams ^[7,8] and heat transfer in Maxwell fluids ^[9]. Therefore, it is very significant to study the properties of this kind of equation not only in practice but also in theory. In this paper, we consider the following TFPDEs with variable coefficients ^[10]:

subjected to the initial and boundary conditions:

where $0 < \alpha \leqslant 1$, x is a spatial point, t is the time, ${t_0}$ and ${t_f}$ represent the initial and final time, $\Omega \subset {R^d}$, $d = 1, \; 2$ is a bounded domain with boundary $\Gamma = \partial \Omega$, ${a_i}({\boldsymbol{x}}, t)$, ${b_i}({\boldsymbol{x}}, t)$, $h({\boldsymbol{x}}, t)$, $f({\boldsymbol{x}})$, and $g(t)$ are known functions. $D_t^\alpha u(x, t)$ is the time-fractional derivative, which has several different definitions ^[11,12]. Commonly used fractional derivatives include the Riemann-Liouville, Caputo, and Grunwald-Letnikov derivatives. In this study, we consider the following Caputo definition:

The exact analytical solutions to the above TFPDEs are possible only for a few simple cases, but are virtually impossible for most problems, which greatly limits their applications. On the contrary, this enormously promotes the development of various numerical algorithms ^{[13,14,15,16]}. It is well known that the finite element, finite difference, boundary element, and meshless/meshfree methods are commonly used approaches for solving various integer/fractional order partial differential equations ^{[17,18,19,20]}. Among them, meshless methods have become quite popular in recent years thanks to their ease of implementation and interactive applications. Representative methods in this category include the Galerkin meshless method ^[21,22], the meshless local Petrov-Galerkin method ^[23,24], corrected smoothed particle hydrodynamics ^[25,26], the radial basis function collocation method ^[27,28], the generalized finite difference method ^[29,30,31], the backward substitution method ^[32,33], and localized semi-analytical collocation methods ^{[34,35,36,37]}. In most published works, however, these methods require the discretization of the temporal derivatives by using implicit, explicit, Runge-Kutta or any other approaches ^[38,39], which may be computationally expensive and sometimes mathematically complicated. To address these issues, numerous scholars in recent years have proposed space-time combined meshless methods ^{[40,41,42,43,44]} for solving various partial differential equations numerically.

Inspired by previous work ^[41], this paper makes a first attempt to extend the recently proposed spatio-temporal meshless method (STMM) to the solutions of TFPDEs with variable coefficients. The STMM method first constructs a multiquadric radial basis function (ST-MQ-RBF) in terms of the space-time distance and then directly approximates the solution of Eqs (1.1)–(1.3) by a linear combination of the presented ST-MQ-RBFs at scattered nodes. Compared to the traditional RBF method, the main advantage of the developed approach lies in its complete avoidance of the discretization process for time-fractional-order derivatives, employing the same RBF approximation in both time and space. As a result, the method is simpler, more straightforward, easier to implement, and relatively more accurate.

The outline of the paper is as follows: In Section 2, the STMM for spatial and temporal discretization simultaneously of TFPDEs is proposed, where the numerical approximation for time-fractional derivative is described. Section 3 briefly introduces a multiple-scale technique for solving the ill-conditioned system. In Section 4, numerical examples are studied and discussed. Finally, conclusions and remarks are presented in Section 5.

2.   Spatio-temporal meshless method

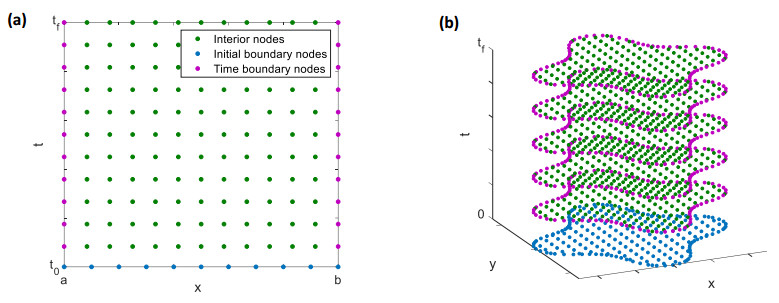
The basic idea of STMM is to introduce a space-time distance into the MQ-RBF and then approximate the solutions of the partial differential equations by using the new ST-MQ-RBFs in the whole space-time domain without the differential approximation of time derivatives. For the above TFPDEs with variable coefficients, $N = {N_i} + {N_0} + {N_b}$ nodes $({x_i}, {t_i})_{i = 1}^N$ should be distributed on the space-time domain ${\Omega ^{st}} = \Omega \times [{t_0}, {t_f}]$ as shown in Figure 1, where ${N_i}, \; {N_0}, \; {N_b}$ represent the numbers of nodes in the domain, on the initial boundary and on the time boundary, respectively. For the ith node, the following MQ-RBF formulation should hold:

where ${\lambda _j}$ are the unknown coefficients, $\phi ({\boldsymbol{x}_i}, {t_i}; \; {\boldsymbol{x}_j}, {t_j})$ are the MQ-RBFs given as follows:

in which $c$ is the shape parameter, ${r_{ij}}$ denotes the space-time distance between the points $({\boldsymbol{x}_i}, {t_i})$ and $({\boldsymbol{x}_j}, {t_j})$, which can be written as

Like the traditional MQ-RBF method, the variables at interior points should satisfy the governing equation, and the variables at boundary points should satisfy initial and boundary conditions. With this regard, we have

The spatial derivatives of the STRBFs in Eq (2.4) can be easily calculated. Here, we concern the calculation of the time-fractional derivative $D_{{t_i}}^\alpha \phi ({\boldsymbol{x}_i}, {t_i}; \; {\boldsymbol{x}_j}, {t_j})$ in Eq (2.4). For $\alpha = 1$, it can be computed by the following expression:

For $0 < \alpha < 1$, from the definition (1.4) of time-fractional derivative, using Gauss numerical integration, we have

where ${\omega _k}$ and ${\xi _k}$ are the nodes and weights of the Gaussian quadrature, ${N_g}$ is the number of Gaussian nodes (in this study, ${N_g}$ is set as 16), and

For $1 < \alpha < 2$,

By combining Eqs (2.4)–(2.6), a resultant linear system in matrix form can be generalized:

where ${\boldsymbol{A}_{N \times N}}$ is the coefficient matrix, $\boldsymbol{\lambda}= {[{\lambda _1}, {\lambda _2}, ..., {\lambda _N}]^T}$ is a vector consisting of the undetermined coefficients; ${\boldsymbol{b}_{N \times 1}}$ is a vector consisting of the right-hand sides in Eqs (2.4)–(2.6). As long as Eq (2.12) is solved efficiently (that is to say, $\boldsymbol{\lambda}$ can be obtained accurately), the unknown variable at an arbitrary point $(\boldsymbol{x}, t)$ in the considered space-time box can be acquired by

3.   A multiple scale technique

For the RBF method, in general, the algebraic equation (2.12) is ill-conditioned. A pre-conditioner is required to reduce the condition number and to yield a regular solution. The multiple scale technique ^{[45,46,47,48,49]} is an effective pre-conditioner tool and thus is applied in this paper. Here, we will give a brief review of this method.

Let $\boldsymbol{A} = [{{A}_1}\; {A_2}\; ...\; {A_N}]$, where $\{ {A_i}\} _{i = 1}^N$ are column vectors of the matrix A. By the multiple scale technique, Eq (2.12) can be reformulated as follows:

where

and

The condition number of the matrix $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\boldsymbol{A}}$ will be greatly reduced due to the reduction of round-off errors. After the system of Eq (3.1) is solved, the solution $\boldsymbol{\lambda} = {({\lambda _1}, {\lambda _2}, ..., {\lambda _n})^T}$ of Eq (2.12) can be recovered from Eq (3.3) as follows:

It should be pointed out that Eq (3.1) is solved using the MATLAB command 'A\B'.

4.   Numerical results and discussions

In this section, two numerical examples including one- and two-dimensional TFPDEs with both regular and irregular geometries are studied by using regular and irregular nodes to illustrate the efficiency and accuracy of the proposed space-time meshless method. To evaluate the accuracy of the proposed STMM, the following L_∞-error, L₂-error and the root-mean-square error (RMSE) are adopted:

where $M$ is the number of test points, ${u_{exa}}$ and ${u_{num}}$ represent the exact and numerical solutions at the jth test point, respectively.

Example 1. Consider the following two one-dimensional TFPDEs with constant and variable coefficients on the domain ${\Omega ^{st}} = [0, 1] \times [0, 1]$:

The exact solution of the above two cases is $u{\text{ }}(x, t) = {x^2} + {t^2}$. The initial and boundary conditions of this problem are

First, we consider the TFPDE with constant coefficients in Case I. Taking ${N_i}$ interior nodes as test points, the numerical accuracy of the proposed STMM for Case I is tested by using different selection strategies of shape parameter c. Table 1 lists the ${L_\infty }$-errors and RMSEs under different values of $\alpha$, and $N = 1840$. For details of the three strategies mentioned in Table 1, we refer to ^[49]. As can be seen, the three techniques of shape parameter optimization are all efficient and accurate, and thus the first approach is adopted in the following calculations. It can also be observed that the accuracy of the algorithm decreases with the increase of $\alpha$. Moreover, the comparison between the numerical errors obtained by the present method with those reported in ^[34] is shown in Table 2, where we set $\delta t = 0.01$, $N = 5151$, ${N_0} = 51$, ${N_t} = 2 \times 100$, ${N_i} = 49 \times 100$ and $\alpha = 0.5$ for the comparison. The results indicate that the proposed scheme is more accurate than that in ^[50]. The number of nodes was kept constant, and Table 3 compares the condition numbers of the coefficient matrix with and without the use of multiscale techniques. It can be seen that the introduction of multiscale techniques significantly reduces the condition number. It is worth noting that the computational results for both cases are essentially the same, so they are not presented here.

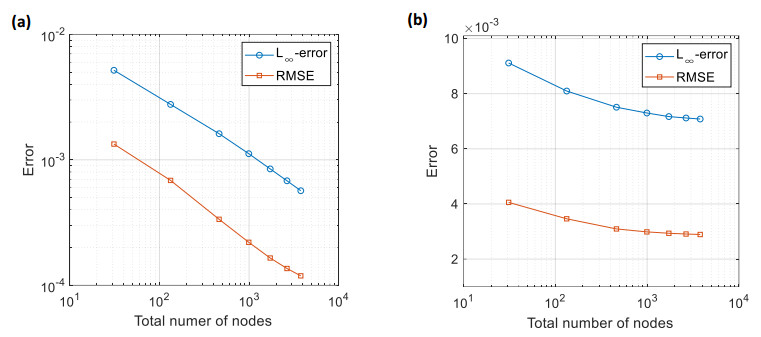
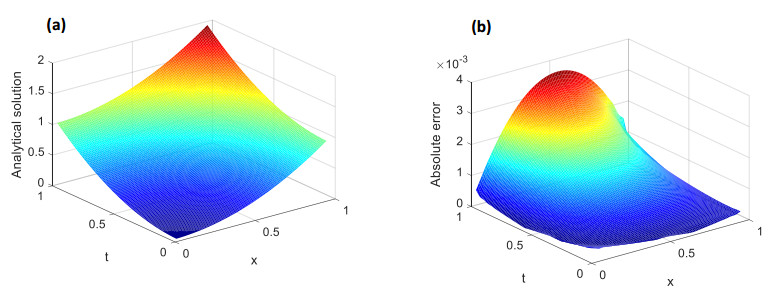
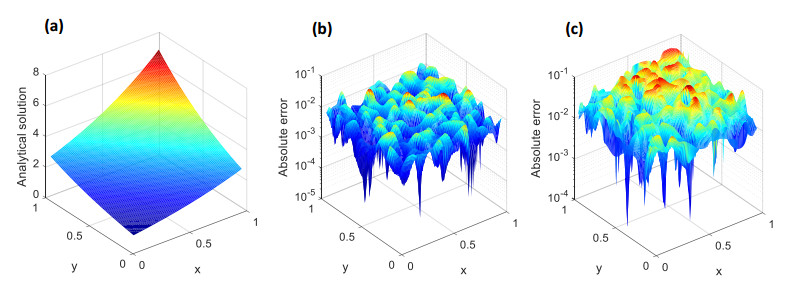
Next, we consider the TFPDE with variable coefficients in Case II. The convergence of the proposed algorithm is investigated when $\alpha = 0.2$ and 0.6, and the absolute error curves are illustrated in Figure 2. The results demonstrate that the STMM has high precision and good convergence. It is also noted that the smaller the $\alpha$, the faster the convergence. As depicted in Figure 3, the graphs of the numerical solution and absolute error with $\alpha = 0.5$ further confirm the validity and accuracy of the present method for solving the TFPDE with variable coefficients.

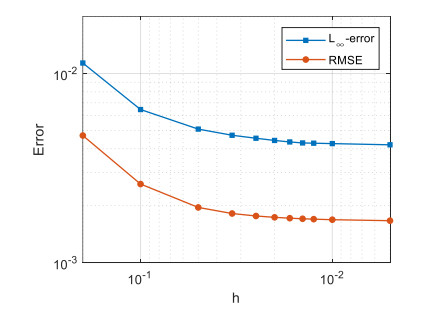
Then, Figure 4 presents the errors with respect to the nodal spacing to show the convergence in space. It can be found that as the nodal spacing decreases, the algorithm demonstrates a clear convergence trend. When the nodal spacing becomes sufficiently small, the calculation accuracy stabilizes.

Finally, we examined the impact of the number of Gaussian points on the accuracy of the algorithm. It can be seen from Table 4 that the algorithm shows a convergence trend as the number of Gauss points increases. Considering that the change in error is minimal, using 16 Gauss points is sufficient to ensure accuracy and save computation time.

Example 2. Consider the following two-dimensional time fractional advection-diffusion equation on $\Omega = [0, \; 1] \times [0, \; 1]$ ^[54]:

with the following initial and boundary conditions:

The exact solution of this problem can be given by

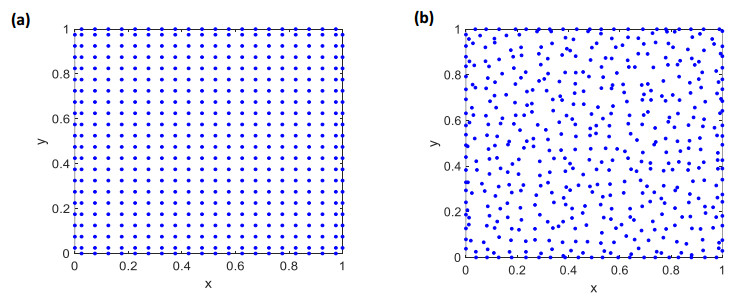
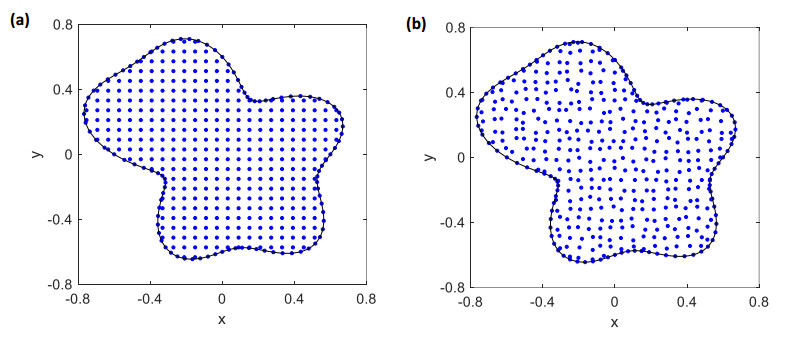
To investigate the influence of the node distribution on the numerical solution, we consider two types of node distribution (regular nodes and irregular nodes) as shown in Figure 5. When $\alpha = 0.5$ and a total of 4560 nodes are used, the analytical solution and absolute errors on the physical domain at $t = 1.0$ with regular and irregular nodal distributions are illustrated in Figure 6. These figures have proven that the newly proposed meshless approach has very good accuracy even using irregular nodal distributions.

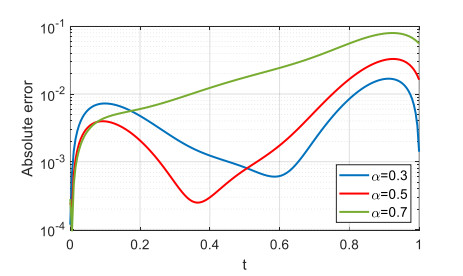
Figure 7 presents the absolute errors at the point (0.5, 0.5, t) for the various fractional orders. Noted that the STMM has high computational accuracy, and the smaller the $\alpha$, the higher the accuracy, which is the same as one-dimensional problems. Furthermore, the convergence of the proposed meshless method is investigated in Table 5. As can be observed, the algorithm converges as the number of nodes increases.

Finally, the proposed methodology is tested on an irregular domain $\Omega$ shown in Figure 8. Using the same exact solution, initial and boundary conditions, we consider the following two-dimensional time fractional PDE with variable coefficients:

where $h(x, y, t) = 0.5\Gamma (3 + \alpha){t^2}{e^{x + y}} - ({x^2} + {y^2} + ({e^x} + {e^y}){t^2}){t^{(2 + \alpha)}}{e^{x + y}}$. The boundary $\partial \Omega$ of the computational domain is defined by the following parametric equation:

where $\rho (\theta) = \frac{{3 + \cos (\theta - \pi /5)\sin (4\theta)}}{{5 + \sin (2\theta)}}$.

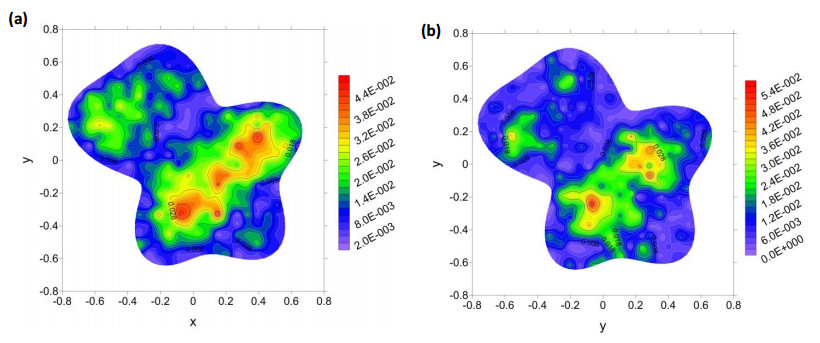
Consider the regular and irregular nodal distributions on the irregular geometry shown in Figure 8. The profiles of absolute errors $t = 1.0$ for these two cases of nodal distribution are depicted in Figure 9, where N = 2646 and $\alpha = 0.5$. It can be seen that the higher accuracy is achieved for different types of node distribution, although the regular nodes are slightly better than irregular nodes.

5.   Conclusions and remarks

A spatio-temporal meshless method is developed for the numerical solution of the TFPDEs with variable coefficients. The developed scheme can directly approximate the solutions of fractional partial differential equations within a space–time scale framework and is very simple mathematically, truly meshless, free of difference approximation, and computationally cost-effective. The numerical experiments further demonstrate the efficiency, precision, and convergence of the proposed STMM for the TFPDEs with variable coefficients.

The non-local nature of fractional derivatives causes the solution's behavior to be influenced by the entire temporal or spatial domain, making numerical solutions inherently challenging. The introduction of variable coefficients further increases the problem's nonlinearity, rendering traditional numerical methods cumbersome and accuracy-limited. The method presented in this paper can efficiently approximate the numerical solution for such problems in a straightforward manner without the need for specialized time discretization techniques, making it applicable to various types of variable coefficient fractional differential equations. It provides a robust tool for solving time fractional PDEs with variable coefficients, thus advancing the field and offering new possibilities for tackling complex real-world problems in engineering and science.

The present scheme can be extended to other fractional partial differential equations, such as the time-space fractional PDEs and complicated high-order and high-dimensional problems. Moreover, the study on local STMM is conducive to the solution of long-time and large-scale dynamic problems. It should be pointed out that the shape parameter in the STMM has a certain influence on the accuracy of the numerical solution, and thus the determination technique of the optimal shape parameter still needs to be discussed in depth. Otherwise, the new ST-RBFs should be studied in order to avert or greatly reduce the influence of shape parameters.

Author contributions

Xiangyun Qiu: Conceptualization, Methodology, Simulation analysis, Writing–original draft; Xingxing Yue: Methodology, Project administration, Supervision. Both authors have read and approved the final version of the manuscript for publication.

Acknowledgements

This work was supported by National Key R & D Program of China (Grant No. 2023YFB2503900).

Conflict of interest

The authors declare no competing financial interests.