Exponential stability of Cohen-Grossberg neural networks with multiple time-varying delays and distributed delays

1.   Introduction

Cohen-Grossberg neural networks, proposed in 1983, have been applied in parallel memory and optimization ^[1,2]. These applications depend on the stability of equilibrium points of Cohen-Grossberg neural networks. In addition, from the perspective of the model structure, the model of Cohen-Grossberg neural networks includes some famous neural networks such as cellular neural networks and Hopfield neural networks as its special cases. So it is important to investigate the stability of Cohen-Grossberg neural networks.

In implementation of neural networks, time delays are unavoidable because of various reasons such as the finite switching speed of amplifiers. Usually, time-varying delays in models of delayed feedback systems serve as a good approximation in many circuits having a small number of cells. Moreover, neural networks usually have a spatial extent due to the presence of a multitude of parallel pathways with a variety of axon sizes and lengths, and hence there is a distribution of propagation delays over a period of time. So time-varying delays and distributed delays should be incorporated in the models of neural networks. In addition, it is worth noting that a time delay in the response of a neuron can influence the stability of a network and deteriorate the dynamical performance creating oscillatory and unstable characteristics ^[3]. Therefore, the stability and its related dynamic analysis have received much attention for various types of delayed neural networks, for example, see ^{[4,5,6,7,8,9,10,11,12,13,14,15,16]} and references therein.

As is well known, the stability condition in the linear matrix inequality forms contains some non-system parameters to be determined and the stability conditions derived by matrix theory, the method of variation of parameters and differential inequality technique completely depend on the system parameters. So the stability condition in the linear matrix inequality forms is usually less conservative. However, as far as our knowledge, perhaps because Cohen-Grossberg neural networks with multiple delays cannot be transformed into the vector-matrix form, there is relatively little research on the exponential stability of such neural networks and the stability condition in the linear matrix inequality forms has not been obtained. Therefore, this paper aims at deriving the sufficient condition in the linear matrix inequality forms for the exponential stability of Cohen-Grossberg neural networks with multiple discrete time-varying delays and multiple distributed time-varying delays.

The innovations of this paper are listed in the following.

1) By using Lyapunov-Krasovskii functional and linear matrix inequality simultaneously, the sufficient conditions in the linear matrix inequality forms are derived to ensure the exponential stability of Cohen-Grossberg neural networks with multiple discrete time-varying delays and multiple distributed time-varying delays.

2) It is confirmed that Lyapunov-Krasovskii functional and linear matrix inequality can be used simultaneously to investigate the neural networks with multiple delays that cannot be transformed into the vector-matrix form.

3) Two examples are provided to show that the sufficient condition established here is better than the existing results derived by matrix theory ^[17], the method of variation of parameters and differential inequality technique ^[18].

2.   Preliminaries

In this paper, we consider the following Cohen-Grossberg neural networks with multiple time-varying delays and distributed delays:

in which $a_{ij}, b_{ij}$ and $d_{ij}$ are some constants, other functions satisfy the following assumption:

$(A_1):$ For $i, j = 1, \cdots, n, c_i(0) = f_i(0) = g_i(0) = h_i(0) = \sigma_{ij}(0, 0) = 0$ and there exist some constants $\underline{c}_i, \underline{d}_i, \overline{d}_i, f^-_i, f^+_i, g^-_i, g^+_i, h^-_i, h^+_i, \tau, \rho$ and $\bar{\tau}$ such that for $t\geq 0$ and every $x, y\in R,$

The initial conditions associated with (2.1) are of the form: $x_i(s) = \xi_i(s), s\in [-\max\{\tau, \rho\}, 0],$ and $\xi = \{(\xi_1(s), \cdots, \xi_1(s))^T: \; -\max\{\tau, \rho\}\leq s\leq 0\}$ is $C([-\max\{\tau, \rho\}, 0]; R^n)$-valued function satisfying

in which $C([-\max\{\tau, \rho\}, 0]; R^n)$ denotes the space of all continuous $R^n$-valued functions defined on $[-\max\{\tau, \rho\}, 0]$, $\|\cdot \|$ denotes the Euclidean norm. It is easy to see that by changing the functions of system (2.1), system (2.1) can convert into the following neural networks studied in ^[17,18]:

3.   Main results

Theorem 3.1. The origin of system (2.1) is globally exponentially stable provided that there exist some positive constants $p_{1}, \cdots, p_{n}, \; u_{i1}, \cdots, u_{in} \; (i = 1, 2, 3)$ such that

in which $\Delta < 0$ denotes that matrix $\Delta$ is symmetric negative definite, $*$ means the symmetric terms of the symmetric matrix $\Delta$,

Proof. It follows from (3.1) that there exists a positive constant $\lambda$ such that $\tilde{\Delta} < 0,$ in which □

Lyapunov-Krasovskii functional $V(t)$ is defined as follows:

in which

Along the trajectory of system (2.1), we obtain

At the same time, we can also obtain

and

in which

So, from (3.3)–(3.8), we have

in which $y(t) = (\tilde{x}^T(t), \tilde{f}^T(x(t)), \tilde{g}^T(x(t)), \tilde{h}^T(x(t)))^T.$

Integrating from $0$ to $t$ for (3.9) and using (3.2), we obtain

which implies the origin of system (2.1) is exponentially stable, in which $\bar{g}_j = \max\{|g^-_j|, |g^+_j|\},$ $\bar{h}_j = \max\{|h^-_j|, |h^+_j|\}, j = 1, \cdots, n.$

For the systems (2.2) and (2.3), we obtain the following results from Theorem 3.1.

Corollary 3.1. The origin of system (2.2) is globally exponentially stable provided that there exist some positive constants $p_1, \cdots, p_n, u_{i1}, \cdots, u_{in} (i = 1, 2)$ such that

in which

the other symbols are the same as Theorem 3.1.

Corollary 3.2. The origin of system (2.3) is globally exponentially stable provided that there exist some positive constants $p_1, \cdots, p_n, u_{11}, \cdots, u_{1n}$ such that

in which

the other symbols are the same as Theorem 3.1.

Remark 3.1. It is obvious that Corollaries 3.1 and 3.2 can be applicable to the networks (2.2) and (2.3) studied in ^[17,18], since these networks are some special cases of system (2.1). Therefore, Corollaries 3.1 and 3.2 can be seen as new stability criteria for the networks (2.2) and (2.3).

Remark 3.2. Based on the method of variation of parameters and differential inequality technique, Theorem 2 in ^[18] shows that the origin of system (2.2) is globally exponentially stable provided that

in which $\xi = \max_{1\leq i\leq n} \{\sup_{x_i\neq 0}\frac{f_i(x_i)}{x_i}\}, \eta = \max_{1\leq i\leq n} \{\sup_{x_i\neq 0}\frac{g_i(x_i)}{x_i}\}, c_0 = \min_{1\leq i\leq n}\{c_i\}, ||A||_2$ denotes the square root of the largest eigenvalue of $A^TA.$ This stability condition completely depends on the parameters of system (2.2) and the stability condition of Corollary 3.1 contains some non-system parameters $p_1, \cdots, p_n, u_{i1}, \cdots, u_{in}(i = 1, 2)$ to be determined. We demonstrate that Corollary 3.1 is applicable to system (2.2) in Example 1 and Theorem 2 in ^[18] is not. So the stability condition of Corollary 3.1 is better.

Remark 3.3. By using matrix theory and inequality analysis, Theorem 2.4 in ^[17] shows that zero solution of system (2.3) is globally exponentially stable provided that $\rho(K) < 1$, in which $\rho(K)$ denotes spectral radius of matrix $K = (k_{ij})_{n\times n}, \; k_{ij} = c_i^{-1}(|a_{ij}|+|b_{ij}|)\alpha_j, \alpha_j$ corresponds to $\max\{|f^-_j|, |f^+_j|\}$ in this paper. Similarly, this stability condition also depends on the parameters of system (2.3) and the stability condition of Corollary 3.2 contains some non-system parameters $p_1, \cdots, p_n, u_{11}, \cdots, u_{1n}$ to be determined. We demonstrate Corollary 3.2 is applicable to system (2.3) in Example 2 and Theorem 2.4 in ^[17] is not. So the stability condition of Corollary 3.2 is better.

4.   Examples

Example 4.1. Consider system (2.2) with the following parameters and functions:

$C = diag\{6, 6, 5, 5\}, f_i(x_i) = tanh(x_i), g_i(x_i) = 0.8 tanh(x_i), \tau_{i}(t) = 0.2sint+0.2, i = 1, 2, 3, 4.$

We calculate that $A_1 = A_2 = B_1 = B_2 = 4I, F_1 = I, G_1 = 0.8I, F_2 = G_2 = 0, \bar{\tau} = 0.2,$ in which $I$ denotes identity matrix. By using MATLAB LMI Control Toolbox, we know when

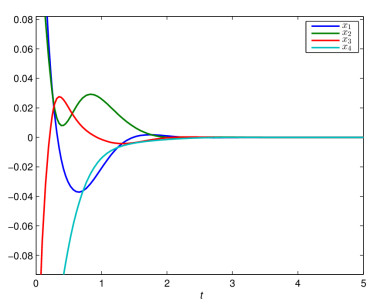
the condition of Corollary 3.1 is satisfied and so Corollary 3.1 is applicable to system (2.2). Figure 1 shows the solution trajectories of system (2.2) with the initial value $(0.3;0.2;-0.2;-0.3)^T$ tend to 0.

On the other hand, we calculate $\xi = 1, \eta = 0.8, ||A||_2 = \sqrt{8}, ||B||_2 = \sqrt{7.4641}, c_0 = \min_{1\leq i\leq 4}\{c_i\} = 5$ and $\alpha = \frac{5.014}{5} > 1$ defined in Remark 3.2. Therefore, Theorem 2 in ^[18] is not applicable to system (2.2) in this example.

Example 4.2. Consider system (2.3) with $C = diag\{5, 5, 5, 5\}, f_i(x_i) = 0.5 tanh(x_i), \tau_{ii}(t) = 0.2sin t+0.2, \tau_{ij}(t) = 0.2cos t+0.2, i\neq j, i, j = 1, 2, 3, 4,$ the matrices $A$ and $B$ are the same as Example 4.1.

We calculate that $A_1 = A_2 = B_1 = B_2 = 4I, F_1 = 0.5I, F_2 = 0, \bar{\tau} = 0.2.$ By using MATLAB LMI Control Toolbox, we know when $P = 76.1324 I, U_1 = 72.4840 I,$ the condition of Corollary 3.2 is satisfied. Figure 2 shows the solution trajectories of system (2.3) with the initial value $(0.3;0.2;-0.2;-0.3)^T$ tend to 0.

On the other hand, we calculate $\alpha_i = 0.5, k_{ij} = 0.2 (i = 1, 2, 3, 4)$ and $\rho(K) = 1$ defined in Remark 3.3. Therefore, Theorem 2.4 in ^[17] is not applicable to system (2.3) in this example.

5.   Conclusions

This paper has investigated the exponential stability of Cohen-Grossberg neural networks with multiple discrete time-varying delays and multiple distributed time-varying delays. Maybe because such networks cannot be converted into the vector-matrix forms, the stability results of the networks are relatively few and the stability conditions in the linear matrix inequality forms have not been established. By using Lyapunov-Krasovskii functional and linear matrix inequality simultaneously, the sufficient conditions in the linear matrix inequality forms of ensuring the exponential stability are derived. It is confirmed that Lyapunov-Krasovskii functional and linear matrix inequality can be used simultaneously to investigate the neural networks with multiple delays that cannot be transformed into the vector-matrix form.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors would like to thank the editor and the reviewers for their detailed comments and valuable suggestions. This work was supported by the National Natural Science Foundation of China (No: 12271416, 11971367, 11826209, 11501499, 61573011 and 11271295), the Natural Science Foundation of Guangdong Province (2018A030313536).

Conflict of interest

The authors declare no conflicts of interest.