Global exponential periodicity of nonlinear neural networks with multiple time-varying delays

1.   Introduction

When we design a nonlinear delayed neural network and apply it to some practical applications including collect computation, associative memory, pattern recognition, learning theory, and optimization ^[1,2,3], we have to consider the existence and stability of the equilibrium point of the delayed neural network. This is because the stable equilibrium point plays an important role in these applications and can avoid some suboptimal responses. Some stability results of various types of nonlinear delayed neural network have been published, see ^{[4,5,6,7,8,9,10,11,12,13,14,15,16]} and the references cited.

The periodic solution is also an important dynamical behavior of the nonlinear delayed neural networks. It is clear that an equilibrium point is a special case of the periodic solution because it can be viewed as a special periodic solution with an arbitrary period. So the analysis of the periodic solution of the nonlinear delayed neural network is more meaningful and complicated. The periodic solution of a class of nonlinear delayed neural networks has been used to learning theory because learning often needs to be repeated ^[17]. The neural network studied in this paper is a class of recurrent neural networks. As known, periodic solution of recurrent neural network can be used to store acoustic characteristics in speech recognition. The reason why the periodic solutions of a recurrent neural network can store the acoustic characteristics is that the periodic solution contains the information for a time series, and the length of the time series usually corresponds to the length of the acoustic characteristics. In practice, a time series of an audio signal is fed as input into the network, if the weights of the network meet our result, then the output is the periodic solution of the time series. We can calculate the average power spectral density (PSD) of the periodic solution and compare it with the PSD of the original audio signal. If the difference between them is small, then the periodic solution can be considered as effectively storing the acoustic characteristics. Some interesting and valuable results of periodic solutions of various types of nonlinear delayed neural networks have been obtained, see ^{[18,19,20,21,22,23,24,25,26,27,28]} and the references cited.

After reading the references cited above, we notice that neural networks with multiple delays $\tau_{ij}(t)$ cannot be converted into the vector-matrix form because of the existence of the multiple delays $\tau_{ij}(t)$. What's more, we notice that although the neural network with multiple delays $\tau_{ij}(t)$ have been actually investigated by Lyapunov-Krasovskii functional method in the literature, to the best of our knowledge, the sufficient conditions in the linear matrix inequality form have not been obtained. That is to say, Lyapunov-Krasovskii functional method and linear matrix inequality method have not been simultaneously used to study the neural network that cannot be converted into the vector-matrix form. Therefore, we naturally wonder whether we can use two methods together to study the neural networks with multiple delays.

The innovations of this paper are listed in the following.

1) By using Lyapunov-Krasovskii functional and linear matrix inequality, we establish two sets of sufficient conditions in the linear matrix inequality form to ensure that two arbitrary solutions of the neural network with multiple delays attracts each other exponentially. This is a key prerequisite to prove the periodic solution of the neural network with multiple delays is existent, unique and globally exponentially stable.

2) The established sufficient conditions can also ensure the exponential stability of the equilibrium point of the neural network with multiple delays.

3) We confirm that Lyapunov-Krasovskii functional and linear matrix inequality can also be applicable to the neural networks which cannot be written in the vector-matrix form. So Lyapunov-Krasovskii functional and linear matrix inequality can be applicable to the neural networks that can or cannot be written in the vector-matrix form.

4) We provide several examples to show that compared with the existing results derived by differential inequality, matrix theory, Laypunov functional and Halanay inequality, the established sufficient conditions are less conservative.

2.   Preliminaries

The nonlinear neural system with multiple time-varying delays studied in this paper can be described as the following mathematical expression

in which $i = 1, \cdots, n, c_i > 0$, the nonlinear activation functions $f_i(\cdot), g_i(\cdot)$ and the multiple time-varying delays $\tau_{ij}(t)$ satisfy that there exist some constants $\alpha^-_i, \alpha^+_i, \beta^-_i, \beta^+_i, \tau$ and $\tilde{\tau}$ such that for all $z_1, z_2\in R (z_1\neq z_2)$, $\alpha^-_i\leq \alpha^+_i, \beta^-_i\leq\beta^+_i$ and $t\geq 0,$

The initial conditions are $x_i(t) = \xi_i(t), t\in [-\tau, 0], i = 1, \cdots, n.$ Let $\xi = \{(\xi_1(t), \cdots, \xi_n(t))^T: \; t\in [-\tau, 0]\}$ be $C([-\tau, 0], R^n)$-valued function with

in which $C([-\tau, 0], R^n)$ denotes the space of all continuous $R^n$-valued functions defined on $[-\tau, 0]$.

It is easy to see that the mathematical expression of system (2.1) cannot be transformed into a vector system. By changing some functions in the mathematical expression, the following systems studied in ^[4,18,19] are some special cases of system (2.1):

3.   Main results

Let $x(t, \xi)$ and $y(t, \psi)$ be the solutions of system (2.1) with arbitrary initial conditions $\xi$ and $\psi$, respectively. For simplicity and convenience, two arbitrary solutions $x(t, \xi)$ and $y(t, \psi)$ denote by $x(t)$ and $y(t)$, respectively. In addition, $\Sigma < 0$ denotes matrix $\Sigma$ is symmetric negative definite, $*$ means the symmetric terms of symmetric matrix $\Sigma$. Define

We first show that two arbitrary solutions $x(t)$ and $y(t)$ of system (2.1) attract each other exponentially.

Theorem 1. Suppose that there exist some positive constants $p_{1}, \cdots, p_{n}, k_{i1}, \cdots, k_{in}$ $(i = 1, 2)$ such that

Then, there exist two positive constants $\lambda$ and $M > 1$ such that

Proof. It follows from $\Sigma < 0$ that there exists a constant $\lambda > 0$ such that

We construct the following Lyapunov-Krasovskii functional

and derive

in which

In addition, it is easy to deduce the following inequalities from (2.2):

and

Let $\gamma(t) = ([x(t)-y(t)]^T, [f(x(t))-f(y(t))]^T, [g(x(t))-g(y(t))]^T)^T, \beta_i = \max\{|\beta^-_i|, |\beta^+_i|\}, i = 1, 2, \cdots, n.$ Then, from (3.2)–(3.6), we deduce

So (3.1) holds and the proof is finished.

Remark 1. Although Theorem 1 gives the sufficient conditions in the linear matrix inequality form, MATLAB executables that solve the matrices $P$, $K_1$, and $K_2$ are difficultly written because the matrix $B_2$ contains all elements of the undetermined matrix $P$. Therefore, it is more expected to obtain some easily verified sufficient conditions.

Theorem 2. Inequality (3.1) holds provided that there exist some positive constants $p_{1}, \cdots, p_{n}, k_{i1}, \cdots, k_{in}$ $(i = 1, 2)$ such that

Proof. It follows from $\Sigma < 0$ that there exists a constant $\lambda > 0$ such that

We construct the following Lyapunov-Krasovskii functional

and derive

The rest proof is similar to that of Theorem 1 and is omitted.

If $p_i = p \; (i = 1, \cdots, n)$ in Theorem 1, then we obtain the following easily verified condition.

Theorem 3. Inequality (3.1) holds provided that there exist some positive constants $p, k_{i1}, \cdots, k_{in} (i = 1, 2)$ such that

It is obvious that the matrices $P$, $K_1$, and $K_2$ in (3.7) and (3.8) can be easily determined by MATLAB LMI Control Toolbox. The focus of this paper is to establish (3.7) or (3.8) to ensure (3.1) holds. Based on (3.1), we can define a Poincar$\acute{e}$ mapping and use the contraction mapping principle to show the periodic solution of system (2.1) is existent, unique and globally exponentially stable. The proof is common and similar to that of ^[19], so it is omitted.

Theorem 4. Let $u_i(t)$ and $\tau_{ij}(t) (i, j = 1, \cdots, n)$ be $\omega$-periodic functions. Then, under the conditions of Theorem 2 (or Theorem 3), there exists a unique and globally exponentially stable $\omega$-periodic solution of system (2.1).

Remark 2. Let $u_i(t) = u_i (i = 1, \cdots, n)$ in (2.1). Then, under the conditions of Theorem 2 (or Theorem 3), there exists a unique and globally exponentially stable equilibrium point of system (2.1).

For system (2.5) and system (2.6), we can easily derive the following result.

Theorem 5. Let $u_i(t)$ and $\tau_{ij}(t) (i, j = 1, \cdots, n)$ be $\omega$-periodic functions. Then, system (2.6) has a unique and globally exponentially stable periodic solution provided that one of the following conditions is true:

(ⅰ) There exist some positive constants $p_{1}, \cdots, p_{n}, k_{i1}, \cdots, k_{in}$ $(i = 1, 2)$ such that

(ⅱ) There exist some positive constants $p, k_{i1}, \cdots, k_{in} (i = 1, 2)$ such that

In particular, system (2.5) has a unique and globally exponentially stable equilibrium point if one of the above conditions is true.

Remark 3. In ^[18], the author has used the theory of fixed point and differential inequality technique to prove there exists exactly one $\omega$-periodic solution of system (2.4) if $\alpha = \frac{\xi||A||_2+\eta ||B||_2 }{c_0} < 1$, where $\xi = \max_{1\leq i\leq n} \{\sup_{x_i\neq 0}\frac{f_i(x_i)}{x_i}\}, \eta = \max_{1\leq i\leq n} \{\sup_{x_i\neq 0}\frac{g_i(x_i)}{x_i}\}, c_0 = \min_{1\leq i\leq n}\{c_i\}, ||A||_2$ denotes the square root of the largest eigenvalue of $A^TA.$ For system (2.4) in Example 1, we demonstrate Theorem 4 is effective and calculate $\alpha = \frac{5.014}{5} > 1$ which implies that the result in ^[18] is not applicable.

Remark 4. In ^[4], the authors have used Brouwer's fixed point theorem, matrix theory and inequality analysis to prove system (2.5) has exactly one equilibrium which is globally exponentially stable if $\rho(K) < 1$, where $\rho(K)$ denotes spectral radius of matrix $K = (k_{ij})_{n\times n},$ $k_{ij} = c_i^{-1}(|a_{ij}|+|b_{ij}|)p_j, p_j = \max\{|\alpha^-_j|, |\alpha^+_j|\}$ in this paper. For system (2.5) in Example 2, we demonstrate Theorem 5 is effective and calculate $\rho(K) = 1$ which implies that the result in ^[4] is not applicable.

Remark 5. In ^[19], the authors have used Laypunov functional and Halanay inequality to prove system (2.6) is globally exponentially periodic provided that $d_i-L_i\sum^n_{j = 1} (|a_{ji}|+|b_{ji}|) > 0$ or $d_i-\sum^n_{j = 1} (|a_{ij}|+|b_{ij}|)L_j > 0, i = 1, \cdots, n,$ where $d_i = c_i$ and $L_j = \max\{|\alpha^-_j|, |\alpha^+_j|\}$ in this paper. For system (2.6) in Example 3, we demonstrate Theorem 5 is effective and calculate $d_i-L_i\sum^4_{j = 1} (|a_{ji}|+|b_{ji}|) = d_i-\sum^4_{j = 1} (|a_{ij}|+|b_{ij}|)L_j = 0, i = 1, \cdots, n,$ which implies that the results in ^[19] are not applicable.

4.   Several examples

Example 1. Consider system (2.4) with the following parameters and functions:

$C = diag\{6, 6, 5, 5\}, f_i(x) = 0.5 tanh(x_i), g_i(x_i) = 0.8 tanh(x_i), u_i = sint,$ $\tau_{i}(t) = 0.2sint+0.2, i = 1, 2, 3, 4.$

We calculate that $B_1 = B_3 = 4I, \tilde{\alpha} = \tilde{\beta} = 0, \bar{\alpha} = I, \bar{\beta} = 0.8I, \tilde{\tau} = 0.2,$ where $I$ denotes identity matrix.

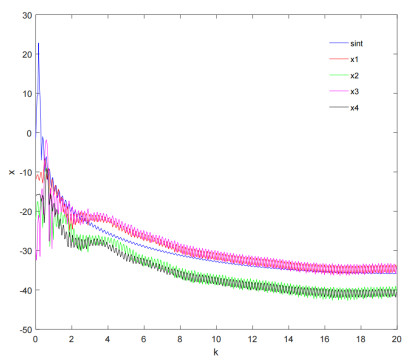
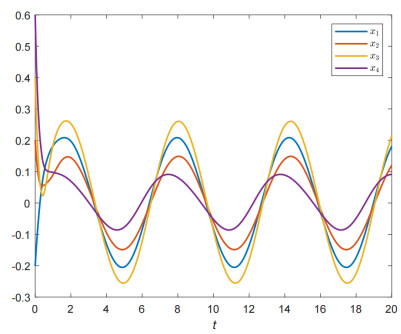
By using MATLAB LMI Control Toolbox, we obtain $P = diag\{ 4.8363, 4.8363, 7.6076, 7.6076 \},$ $K_1 = diag\{ 17.0542, 17.0542, 20.6096, 20.6096 \}, K_2 = 22.1420I$ and $P = 0.1564 I, K_1 = diag\{ 0.4524, 0.4509, 0.4781, 0.4770 \}, K_2 = diag\{ 0.7300, 0.7301, 0.7325, 0.7326 \}$ which satisfy the conditions of Theorem 2 and Theorem 3, respectively. So our theoretical results are effective. Figure 1 shows the solution trajectories of system (2.4) move periodically. Figure 2 shows the average PSD of $x_i(t)$ and $u_i(t) = sint$ are relatively close, which implies the periodic solution $x(t)$ stores effectively the acoustic characteristics of $u(t)$.

On the other hand, we calculate $\xi = 1, \eta = 0.8, ||A||_2 = \sqrt{8}, ||B||_2 = \sqrt{7.4641}, c_0 = \min_{1\leq i\leq 4}\{c_i\} = 5$ and

defined in Remark 3. Therefore, the result proposed in ^[18] is not applicable to system (2.4) in this example.

Example 2. Consider system (2.5) with $C = diag\{5, 5, 5, 5\}, f_i(x_i) = 0.5 tanh(x_i), u_i = 1, \tau_{ii}(t) = 0.2sin t+0.2,$ $\tau_{ij}(t) = 0.2cos t+0.2, i\neq j, i, j = 1, 2, 3, 4,$ the matrices $A$ and $B$ are the same as Example 1.

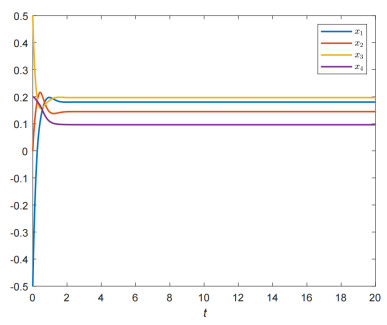
We calculate that $B_1 = B_3 = 4I, \tilde{\alpha} = 0, \bar{\alpha} = 0.5I, \tilde{\tau} = 0.2.$ By using MATLAB LMI Control Toolbox, we obtain $P = diag\{ 6.2027, 6.2027, 7.2511, 7.2511 \}, K_1 = diag\{ 22.3647, 22.3647, 24.8109, 24.8109 \}, K_2 = 25.3107I$ and $P = 2.4441I, K_1 = diag\{ 9.6738, 9.6738, 10.5625, 10.5625 \}, K_2 = 14.5619I$ which satisfy the condition (ⅰ) and the condition (ⅱ) of Theorem 5, respectively. Figure 3 shows the solution trajectories of system (2.5) tend to a point.

On the other hand, we calculate that $p_i = 0.5, i = 1, 2, 3, 4,$ and $\rho(K) = 1$ defined in Remark 4. Therefore, the result proposed in ^[4] is not applicable to system (2.5) in this example.

Example 3. Consider system (2.6) with $C = diag\{4, 4, 4, 4\}, u_i = sin t,$ the matrices $A$ and $B$ are the same as Example 1 and other functions are defined in Example 2.

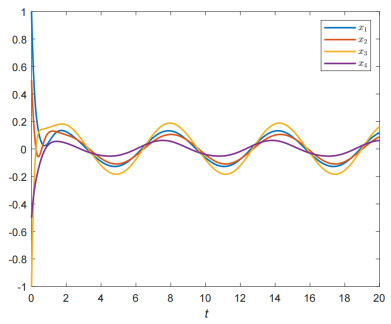
We calculate that $B_1 = B_3 = 4I, \tilde{\alpha} = 0, \bar{\alpha} = 0.5I, \tilde{\tau} = 0.2.$ By using MATLAB LMI Control Toolbox, we obtain $P = diag\{ 7.5477, 7.5477, 9.3961, 9.3961 \}, K_1 = diag\{ 21.5649, 21.5649, 24.6456, 24.6456 \}, K_2 = 24.7554I$ and $P = 0.1679I, K_1 = diag\{ 0.5707, 0.5707, 0.6318, 0.6318 \}, K_2 = 0.9065I$ which satisfy the condition (ⅰ) and the condition (ⅱ) of Theorem 5, respectively. Figure 4 shows the solution trajectories of system (2.6) move periodically.

On the other hand, we calculate that $d_i = 4, L_i = 0.5, d_i-L_i\sum^4_{j = 1} (|a_{ji}|+|b_{ji}|) =$ $d_i-\sum^4_{j = 1} (|a_{ij}|+|b_{ij}|)L_j = 0, i = 1, 2, 3, 4,$ defined in Remark 5. Therefore, the results proposed in ^[19] are not applicable to system (2.6) in this example.

5.   Conclusions

This paper has investigated the global exponential periodicity of nonlinear neural networks with multiple time-varying delays. This type of neural system cannot be transformed into the vector-matrix form because the multiple time-varying delays can not be expressed by the vector form. We note that in many existing references, although the neural networks with multiple delays $\tau_{ij}(t)$ have been actually investigated by Lyapunov-Krasovskii functional method, the linear matrix inequality approach has not been used for this type of neural system that cannot be written in vector-matrix form. So we want to know whether we can use two methods together to study the neural networks with multiple delays. Two sets of sufficient conditions in the linear matrix inequality form are established to ensure two arbitrary solutions of nonlinear neural networks with multiple time-varying delays attract each other exponentially which can lead us to prove the periodic solution of the neural networks with multiple delays is existent, unique and globally exponentially stable by the contraction mapping principle. So the focus of this paper is to establish (3.7) or (3.8) which ensure (3.1) holds. Three examples are given to demonstrate our results are effective. In these examples, we compare our results with the existing results derived by differential inequality, matrix theory, Laypunov functional and Halanay inequality. Three existing results are not applicable to the systems in the three examples, respectively.

Acknowledgments

We would like to thank the editor and the reviewers for their detailed comments and valuable suggestions. This work was supported by the National Natural Science Foundation of China (Nos: 12271416, 11971367, 11826209 and 11271295), the Natural Science Foundation of Guangdong Province (2018A030313536).

Conflict of interest

The authors declare no conflicts of interest.