On study the fractional Caputo-Fabrizio integro differential equation including the fractional q-integral of the Riemann-Liouville type

1.   Introduction

Mathematicians and physicists have become increasingly interested in fractional calculus and quantum calculus (q-calculus), which provide an effective way to describe a wide range of real-world dynamical phenomena encountered in scientific fields and engineering. In addition, they have paid attention to the study of partial differential equations because they are very useful in modelling practical phenomena; for example, for time-fractional stochastic models, see ^[1,2], for the time fractional chemotaxis model, see ^[3], and for the time fractional Rayleigh-Stokes equation, see ^[4]. Researchers find it difficult to obtain direct solutions to most fractional and q-fractional differential equations. As a result, the researchers are interested in studying the existence and uniqueness of solutions to various fractional integro-differential equations. Researchers have obtained numerous results concerning the existence and uniqueness of solutions to a number of fractional integro-differential equations ^[1,6]. Furthermore, many researchers are interested in the existence of solutions to q-fractional integro-differential equations ^[7,8]. Simultaneously, numerous numerical solutions to many types of integro-differential equations have been obtained ^[9,10,11]. The authors presented analytical and numerical solutions to some ordinary integro-differential equations, as well as fractional q integro-differential equations with nonlocal and initial conditions ^[12,13]. We now investigate the nonlocal fractional q integro-differential equations shown below analytically and numerically:

where ${^{CF}I^{\alpha_0}}\phi'(t)$ $, {^{CF}D^{\beta_0}}\phi(t)$ are the Caputo-Fabrizio fractional integral and derivative of order $\alpha_0$ and $\beta_0$ for the unkwon function respectively, $I_q^{\gamma_0}$ is the Riemann Liouville type's fractional q-integral of order $\gamma_0\geqslant0$, $\varrho, \xi$ are constants, and $q, \alpha_0, \beta_0\in (0, 1)$. We use the definitions of the integral and derivative fractional Caputo-Fabrizio to prove the existence, uniqueness, and continuous dependence of the solution. Then, we solve the proposed equation numerically by using two methods: The first is the merging of the cubic b-spline and Simpson's method, and the second is the merging of the finite difference and trapezoidal methods. Both the cubic b-spline and finite difference methods will be applied to the derivative parts of the equation, and both Simpson's method and the trapezoidal method will be applied to the integral part. These methods will transform the proposed equation into a system of algebraic equations. Therefore, we can obtain the solution to the problem by solving this system together.

This paper is structured as follows: In Section 2, we introduce some key definitions and lemmas that will be needed throughout our paper. We give the main results in Section 3. Section 4 contains an overview of the numerical techniques that will be employed in our paper. In Section 5, we discuss the existence of the solution to some examples, and then we will get the numerical solution to them using the cubic-Simpson's method and the finite-trapezoidal method. Finally, we introduce the conclusion section.

2.   Basic concepts

Some key definitions and lemmas related to q-calculus and Fractional calculus will be introduced.

Definition 2.1. ^[14] We can define the Caputo–Fabrizio fractional derivative of order $0 < \mathcal{E} < 1$ of any function $\mathfrak{U}(t) \in C[a, b]$ as follows:

where $\psi$ is a normalization function with the property that $\psi(0) = \psi(1) = 1$.

Later, the above Caputo-Fabrizio fractional derivative is modified by Losada and Nieto ^[11] to become

They demonstrated that $\psi(\mathcal{E}) = \frac{2}{2-\mathcal{E}}$, for any $\mathcal{E} \in (0, 1)$. Hence, we get

Also, they showed that

where ${^{CF}I^{\mathcal{E}} \mathfrak{U}(t)}$ is the fractional integral of order $\mathcal{E}$ for the function $\mathfrak{U}(t).$

Definition 2.2. ^[16] Assume that $\mathfrak{U}(t)$ defined on $[0, 1]$, $q \in (0, 1),$ $\mathcal{E} \geqslant 0$. Then, we can define the fractional q-integral of the Riemann-Liouville type as

where

and satisfy $\Gamma_q(\mathcal{E}+1) = [\mathcal{E}]_q \Gamma_q (\mathcal{E}),$ where $[\mathcal{E}]_q = \frac{1-q^{\mathcal{E}}}{1-q},$

Lemma 2.3. ^[16] Using q-integration by parts, we get the following:

For more details on the properties of q fractional calulus, see ^[18,19].

3.   Main results

Lemma 3.1. Assume that $\nu = (1-q)\rho \sum_{x = 0}^m q^x.$ The solution of (1.1) and (1.2) is obtained as follows:

where,

Proof. Integrating (1.1) first time from $0\rightarrow t$, we obtain

Using (2.1) and (2.2), we get

Put $\phi'(t) = z(t)$ in (3.3), we get

where

using (1.2), then

Therefore,

Now, we obtain (3.1) and (3.2) from (3.4)–(3.6). The proof is completed. □

Theorem 3.2. Let the problem (1.1) and (1.2) satisfy the following conditions:

1) $\mathcal{F}: [0, 1] \times \mathbb{R}^5 \rightarrow \mathbb{R}$, $\mu : [0, 1] \times \mathbb{R} \rightarrow \mathbb{R}$ are measurable and continuous for almost all $t \in [0, 1]$.

2) There exist functions $A_1 (t), A_2(t)\in L_1[0, 1]$ and a positive constants $N_1, N_2 > 0$, such that for any $\phi, z, \zeta, u, \upsilon\in \mathbb{R}$, we have

3)

4)

Then, (3.2) has at least a solution $z(t)\in C[0, 1]$.

Proof. Define the operator $H$ associated with (3.2) by

Let $\vartheta_r = \lbrace z(t) \in \mathbb{R} : \|z\|_C\leq r \rbrace$, where $r = \frac{|\xi|+ \mathfrak{a}_1 + N_1\nu^{-1} |\varrho|+N_1 \mathfrak{a}_2}{1-\bigg(4 N_1+N_1 \frac{\beta_0-(\beta_0-1) \left(e^{\frac{\beta_0}{\beta_0-1}}-1\right)}{\beta_0^2}~~~ +~~~ \frac{N_1 N_2 }{(\gamma_0+1)\Gamma_q(\gamma_0+1)}\bigg)}$.

Thus, for $z(t) \in \vartheta_r$, we get

This proves that $H: \vartheta_r\rightarrow \vartheta_r$ and $\lbrace H z(t) \rbrace$ is uniformly bounded in $\vartheta_r$.

Now, Assume that $0 < t_1, t_2\leq 1$ and $|t_2-t_1| < \delta$; therefore,

As a result, $\lbrace H z(t) \rbrace$ is equi-continuous in $\vartheta_r$.

Assume that $z_k (t)\in \vartheta_r$, $z_k(t) \rightarrow z(t) (k\rightarrow \infty).$ Therefore, the continuity of the two functions $\mathcal{F}$ and $\mu$, implies that $\mathcal{F} (t, \phi_k, z_k, \zeta_k, u_k, \upsilon_k)\rightarrow \mathcal{F} (t, \phi, z, \zeta, u, \upsilon)$ and $\mu (t, z_k)\rightarrow \mu (t, z)$ as $k \rightarrow \infty$. Also,

Using assumptions 1 and Lebesgue dominated convergence theorem ^[20], then

Then, $H z_k(t) \rightarrow H z(t)$ as $k \rightarrow \infty$. As a result, the operator $H$ is continuous in $\vartheta_r$. Therefore, Schauder's fixed point Theorem implies that there exists at least a solution $z(t)\in C[0, 1]$ of (3.2). As a result, Lemma 3.1 implies that (1.1) and (1.2) possess a solution $\phi (t)\in C[0, 1]$.

□

Theorem 3.3. Assume that $\mathcal{F}$ and $\mu$ are measurable and continuous for all $t \in [0, 1]$ and satisfy the following conditions:

(i)

(ii)

Therefore (3.2), has a unique solution.

Proof. Assume that (3.2) has two solutions $z(t), z^*(t)$. Therefore, we have

Hence,

Since $4 N_1+N_1 \frac{\beta_0-(\beta_0-1) \left(e^{\frac{\beta_0}{\beta_0-1}}-1\right)}{\beta_0^2} +\frac{N_1 N_2}{(\gamma_0+1)\Gamma_q(\gamma_0+1)} < 1$, this implies that $z(t) = z^*(t).$ Therefore, the solution of (3.2) is unique. Thus, Lemma $3.1$ implies that the proplem (1.1) and (1.2) possess a unique solution $\phi(t) \in C[0, 1]$. □

3.1.   Continuous dependence on $\varrho$

Definition 3.4. The solution $\phi (t)\in C[0, 1]$ of (1.1) and (1.2) depends continuously on $\varrho$, if

where $\phi^*(t)$ is the solution of

Theorem 3.5. Assume that conditions 1–4 of the Theorem 3.3 are satisfied. Therefore, the solution of (1.1) and (1.2) is continuously dependent on $\varrho.$

Proof. Assume that $z(t)$, $z^*(t)$ are two solutions of (1.1) and (1.2) and (3.7) and (3.8) respectively. Then,

Hence,

Therefore,

Hence,

As a result, the solution of (1.1) and (1.2) is continually dependent on $\varrho$. □

4.   Methodology of numerical technique

The problem (1.1) and (1.2) can be expressed as follows:

Assume that $\mu(t, \phi'(t)) = A_2(t)+ N_2\kappa_3(\phi'(t))$, where $\kappa_1 (\phi'(t)), \kappa_2(\phi(t)), \kappa_3(\phi'(s))$ are nonlinear terms for the unknown function. Then, by using (2.1)–(2.3), Equation (4.1) become:

Now, the interval of integration $[0, t]$ of Eq (4.2) is subdivided into $l$ equally spaced intervals of width $h = (t_i-0)/i, i\geqslant 1$ ^[21]. Taking $\phi'' (t_i) = \phi''_i, \quad \phi'(t_i) = \phi'_i$, $\kappa_1(\phi'(t_i)) = \kappa_1(\phi'_i)$, $\kappa_2(\phi(t_i)) = \kappa_2(\phi_i),$ $\kappa_3(\phi'(s_j)) = \kappa_3(\phi'_j),$ $A_1(t_i) = A_{1, i}, A_2(s_j) = A_{2, j}$, let $k_{i, j} = \frac{1}{\Gamma_q(\gamma_0)}(t_i-qs_j)^{(\gamma_0-1)}$, $K_{i, j} = \frac{1}{1-{\beta_0}}e^\frac{{-\beta_0}(t_i-s_j)}{1-{\beta_0}}$. Therefore, (4.2) can be expressed as follows:

where $B_i = A_{1, i}+N_1\int_{0}^{t_i} k_{i, j} A_{2, j} d_qs$.

4.1.   A summary of the finite-trapezoidal method

$1)$ We use the first and second order central finite difference method to approximate the derivative part of (4.3) as follows:

$2)$ We use the trapezoidal rule to approximate the integral part of (4.3) as follows:

$3)$ Therefore, (4.3) becomes:

4.2.   A summary of the cubic-Simpson's method

We can obtain the numerical solution of (4.3) by using a merge of cubic b-spline with the Simpson's method as follows:

$1)$ The unkown function $\phi(t)$ and its derivatives can be approximated by using cubic b-spline as follows ^[22]:

where $\varOmega_i$ are constants to be determined.

$2)$ We use the Simpson's method ^[23] to approximate the integral part of (4.3).

$3)$ As a result, we can write (4.3) as follows:

5.   Test problems

Now, two numerical examples will be introduced by using the following two methods:

$1)$ Finite-trapezoidal method.

$2)$ cubic-Simpson method.

Problem 1. In (4.2), taking $A_1(t) = t \left(-0.0468103 t^{4/3}-0.0333333 t-0.377778\right)-0.0833333 \cos \left(t^2\right)-0.185185 e^{-1.5 t}-0.166667 \sin (t) \cos (t)$+$2.18519, A_2(t) = t$, $N_1 = \frac{1}{12}, N_2 = \frac{1}{10}, \alpha_0 = 0.4, \beta_0 = 0.6$, $\gamma_0 = \frac{4}{3}, q = 0.5$, $\kappa_1(\phi'(t)) = \sin(\phi'(t)), \kappa_2 (\phi(t)) = \cos(\phi(t))$, $\kappa_3 (\phi'(t)) = \phi'(t).$ Then,

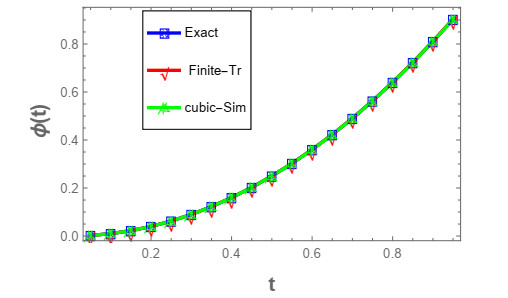
Therefore, the conditions of the Theorem 3.2 are clearly satisfied. As a result, this problem has a unique solution. Now, to solve this problem, we take $l = 20, \rho = 0.2, m = 2, \varrho = 0.0045625, \xi = 0.$ Then, we apply two methods: the first is finite-trapezoidal method and the second is the cubic-Simpson's method. The exact solution of this problem is $\phi(t) = t^2.$

Table 1 and Figure 1 above demonstrate the comparison between the exact solutions and the numerical solutions of the problem using two numerical methods. We can see from the results that both numerical methods are effective. Furthermore, the continuous dependence on $\varrho$ using the cubic-Simpson's method will be studied. Taking $|\varrho-\varrho^*| = 10^{-4}\Rightarrow |\phi(0.2)-\phi^* (0.2)| = 5.71426\times10^{-4}$. Therfore, $\phi(t)$ is continuous dependence on $\varrho$.

Problem 2. In (4.2), taking $A_1(t) = -0.0541126 t^2+\left(0.0415584 t^2-1.19919\right) \cos (t)$+$0.0840336 e^{-0.25 t}+(0.0121212 t+0.121008) \sin (t)+0.0437229, A_2(t) = \sin(t), N_1 = \frac{1}{14}$, $N_2 = \frac{1}{11}, \alpha_0 = 0.6, \beta_0 = 0.2, \gamma_0 = 3$, $q = 0.2, \kappa_1(\phi'(t)) = \phi'(t), \kappa_2 (\phi(t)) = \phi(t)$, $\kappa_3 (\phi'(t)) = \phi'(t).$ Then,

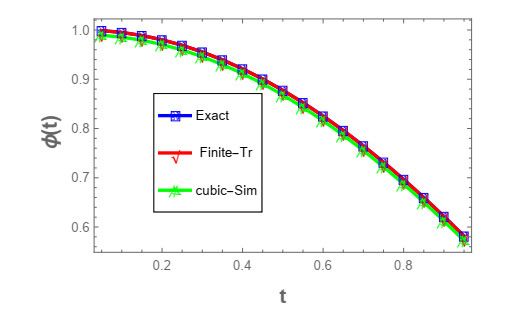
Therefore, the conditions of the Theorem (3.2) are clearly satisfied. As a result, this problem has a unique solution. Now, to solve this problem, we take $l = 20, \rho = 0.5, m = 1, \varrho = 0.430633, \xi = 0$. Then, we apply two methods: the first is finite-trapezoidal method and the second is the cubic-Simpson's method. The exact solution of this problem is $\phi(t) = \cos(t).$

Table 2 and Figure 2 above demonstrate the comparison between the exact solutions and the numerical solutions of the problem using two numerical methods. The results tabulated in the above table demonstrate that the finite difference-trapezoidal method is better than cubic-Simpson method.

6.   Conclusions

We have demonstrated the existence and uniqueness of a solution for a nonlocal fractional q-integro differential equation. We investigated whether or not the answer has a continuous reliance on $\varrho$. This section provides a synopsis of the finite difference, trapezoidal, and cubic Simpson's methods. The numerical solution is applied to two cases, and the results of those solutions are compared with the exact solution. The findings indicated that the approach is not only successful but also straightforward to put into practice.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors are thankful to the Taif University (supporting project number TURSP-2020/160), Taif, Saudi Arabia.

Conflict of interest

The authors declare that they have no competing interests.