High-order numerical algorithm for fractional-order nonlinear diffusion equations with a time delay effect

1.   Introduction

Heroin is highly addictive and an illegal opioid drug and commonly known as hell dust. Usually, it is used in combination with other drugs or with alcohol which results from the risk of overdose. The overdose of heroin can cause a lot of troubles such as coma, shallow and slow breathing and death, etc ^[1]. It is observed that out of 10 heroin addicts, about 9 users used at least one other drug. Typically, people inject heroin, however, sometimes it may be snorted or smoked. Consequences of injecting heroin into a body include the risk of viral infection like HIV, HBV, HCV and bacterial infection of bloodstream and skin, etc. People whose age is between 18 and 25 or addicted to opioid painkiller, are more vulnerable to heroin addiction ^[2]. It is reported that the use of heroin is more than doubled among young adults and it tends to increase. Further, more than 45% of heroin users are addicted to prescription of opioid painkiller.

Heroin addiction develops and propagates in a community like an epidemic disease and almost follows the same pattern. More precisely, people are susceptible to heroin addiction initially, and then they become active users of heroin and finally get recovery through some control measures or by self ceasing the use of heroin. The mathematical study of epidemic diseases has a rich history, and the readers are suggested to see the works of ^[3,4,5,6,7]. From the last two decades, the same modeling approaches have been extended to drug addiction problems for understanding its dynamics ^{[8,9,10,11,12,13]}. Heroin epidemic models comprises of ordinary differential equations and delay differential equations have been investigated and analyzed in ^{[14,15,16,17,18,19,20,21]} and references cited therein.

In the context of partial differential equations (PDEs), mathematicians have developed some novel models called age-structured models to explore several insights into the heroin epidemic. Feng et. al. assumed the age-dependent susceptibility and qualitatively analyzed an age-structured heroin model ^[22]. They studied the existence of steady states and their local and global stabilities. Another paper by Feng et. al. considered treat-age while formulating the model and the authors presented the dynamical aspects of the model ^[12]. Subsequently, the theory was extended by Yang et al. ^[23] and Djilali et al. ^[13] by incorporating different types of incident rates. A recent paper of Wang et al. ^[24] dealt with the multi-group heroin epidemic that includes both treat and susceptibility age. Again the work was restricted only to the dynamical behavior of the concerned model.

To reduce heroin addiction, government officials and health providers should take some agammaessive steps. These control measures include providing educational training to health care providers in prescribing opioid painkillers, expansion of medication-assisted treatments, making informed decisions, behavioral therapy, development and distribution of life-saving drugs, educating vulnerable people about heroin addiction and its consequences, etc ^[2]. It is also suggested to identify those societies who are at most risk to heroin addiction and provide them effective prevention strategies. For active heroin users, it is suggested to treat them with medications or behavioral therapy ^[1]. Also, heroin addiction takes place during the age of 18-25 among young people, thus, it is necessary to make aware vulnerable especially young people about the harm of heroin use. The key aim of modeling epidemics is to identify how to control such outbreaks and to eliminate the same from the community. Since disease epidemics and drugs have the same dynamics; therefore, it is necessary to apply the techniques of control theory to heroin models for controlling heroin addiction.

The age-structured models cited earlier are indeed a great contribution to understanding the heroin epidemic and predicting its future behavior. However, it is worthy to notice that they have given less attention to controlling heroin addiction. Though the authors take into account treatment classes, it doesn't reflect the fact that what type of treatment strategy should be adapted which is more economical. In the current study, the authors aimed to include class-age in susceptible and recovered classes, whereas, heroin users are assumed to depend only on time. Further, to control heroin addiction in a community, we will use two control measures namely; treatment of active heroin users through medications and educating susceptible people about the risk of heroin use.

The rest of the work is organized as follows. Section 1, is about the formulation and existence of the solution to the proposed without control model. The development of the control problem, the existence of optimal control variables, and the characterization of controls are carried out in Section 2. In Section 3, we presented a detailed comparison of both analytical and numerical results. Besides, we simulated both the control and without control problems and showed that the application of control measures could markedly reduce heroin addiction. Finally, concluding remarks are given at the end of the paper.

2.   The model

Like infectious diseases, modeling the heroin epidemic follows the same transmission pattern ^[13,24]. While modeling the heroin epidemic, one must keep in mind some terms such as carriers of heroin use, relapse, time since heroin initiation to habitual use, age of susceptibility and recovery, treatment, and many more factors. It is also suggested to interview heroin addicts and note feedback from professionals in drug abuse-related fields. We assumed that the entire population is composed of individuals susceptible to heroin addiction, heroin users and recovered from drug-life which are respectively denoted by $S(t), \; U(t)$ and $R(t)$. The function $s(t, a)$ denotes the density of susceptible population at any time $t$ and susceptibility-age $a$. Thus the total susceptible population at any time $t$ in terms of density function becomes

In the same way, $r(t, a)$ represent the density of recovered people at time $t$ having recovery-age $a$ and thus $R(t)$ in terms of $r(t, a)$ can be written as

Further, we assumed that the addicts who have treated or they quit the use of heroin by self, again may start the use of heroin. These facts and many others motivate us to formulate the model of the form:

The parameters $\mu, \; \delta, \; \Lambda$ and $\beta(a)$ represent the natural death rate, heroin-induced removal rate, recruitment rate, and the age-specific transmission rate. The term $p$ stand for self-cure (users who cease the use of heroin by self-decision) rate, whereas, $\gamma(a)$ is the age-specific relapse rate. The terms $s_0(a)$ and $r_0(a)$ are non-negative functions of $a$ and it represent the initial age distributions of susceptible and recovered population, respectively. Besides, the parameter used in the model are subject to the following hypothesis:

H1. $\mu, \; p, \; \delta, \; \Lambda > 0$.

H2. $\beta(a), \; \gamma(a)\in L_+^\infty$ with an essential upper bound $\bar{\beta}$ and $\bar{\gamma}$, respectively.

H3. The function $\beta(a)$ as well as $\gamma(a)$ are Lipschitz continuous on $\mathbb{R}_{\geq 0}$, with Lipschitz coefficients $M_\beta$ and $M_\gamma$, respectively.

For the sake of simplicity, let us consider some notations

Equations (2.1a) and (2.1c) can be solved by using the method of characteristics, thus

and

Similarly, by applying direct integration to Eq (2.1b) and considering (2.2) and (2.3), we get solution of system (2.1) of the form

Applying standard fixed point theorem of ^[25] to system (2.4), we can prove that there exist a nonnegative solution of system (2.1) over the interval $[0, \infty)$.

The desired functional space for system (2.1) is of the form

where $L_+^1$ denotes the space of positive and Lebesgue integrable function over $[0, \infty)$. The functions from the space $L_+^1$ are equipped with the norm

Biologically, this norm is equivalent to total population. The initial conditions for system (2.1) can be written as

Existence and uniqueness theorems along with hypothesis of the model suggest that system (2.1) has a unique nonnegative solution using conditions $\mathcal{Z}_0 \in \mathcal{Z}$. Further, a continuous semi-flow $\chi:\mathbb{R}_+\times \mathcal{Z} \rightarrow \mathcal{Z}$ is defined by system (2.1) and solutions have a non-empty omega limit sets because of compact closure ^[26].

3.   Optimal control strategies

Naturally, heroin is highly addictive and can cause a lot of damage if not addressed properly. To overcome its spread, agammaessive steps must be taken by health providers and government officials. It is observed that behavioral therapy and the administration of pharmacological medications are the most effective treatments for heroin addiction. Although, the use of medicines for treatment purpose have some side effects (such as nausea, bone pain, and vomiting, etc) that can be treated with additional supplements. Further, it is noted that the treatment of heroin addicts through medicines has a positive impact and as a result, the rate of crimes and heroin consumption tends to decrease. The present study aims to include two types of measures as control variables; education campaign and pharmacological medications. The former control variable somehow similar to behavioral therapy and will be implemented upon the susceptible population. The educational campaign is widely used in giving-up smoking models as a control variable and it has shown a great effect. The later control will be imposed on heroin addicts. The strategy will be to minimize the susceptible and heroin user population and to maximize the recovered people with the least cost.

From the dynamical perspective, optimal control theory is the most powerful and useful tool than the calculus of variation, particularly in the epidemic problems. Since, heroin addiction is closely related to mathematical epidemiology, therefore, it is proposed to implement the techniques of control theory to minimize the number of susceptible and heroin users. As the problem under discussion lying in infinite-dimensional spaces, thus, we will use the maximum principle type results introduced by Li and Yong ^[27] and suggested by ^[28].

The proposed control problem consist of three state variables $S(t), \; U(t), \; R(t)$ and two control variables $v_1(t), \; v_2(t)$ from the admissible control set

Physical interpretation of the control $v_1(t)$ is educating susceptible population regarding heroin addiction and its consequences, whereas, $v_2(t)$ means to treat active heroin users. Since, $v_1(t)s(t, a)$ denotes the density of susceptible who have been educated. Therefore, the term $v_1(t)s(t, a)$ needs to subtracted from the equation which represent the dynamics of the susceptible population and the same will be added to the equation of recovered people. Likewise, the term $v_2(t)U(t)$ represent the number of heroin addicts who were treated through medicines, thus, it should be subtracted from the equation which describe the dynamics of heroin users. Since, the equation for recovered population is a PDE, therefore, the term $v_2(t)U(t)$ will be included to the boundary condition $r(t, 0)$ which will make it a type of boundary control problem. Further, nature of the problem demands that $v_i(t)\geq 0$ for $i = 1, 2$. The case $v_i(t) = 0$ means implementation of no control measures, whereas, $v_i(t) = 1$ shows that the entire susceptible are educated and the heroin users are treated. Due to wide used of quadratic term for the control variable, our objective functional will also depends quadratically upon the controls. Thus, the objective functional will takes the following form

subject to the model

The terms $B_1, B_2$ are positive constants and it is called balancing factors. The constant $B_1$ and $B_2$ represent the level of acceptance of education campaign and medication by a susceptible and an addict, respectively. The theorem stated and proved below is about the existence of optimal control variables.

Theorem 3.1. There exists a pair of optimal control variables $v_1^\star, v_2^\star\in V_{ad}$ such that, $J(v_1^\star, v_2^\star) = \min_{v_1, v_2\in V_{ad}} J(v_1, v_2)$ subject to the system (3.3).

proof. Clearly, the states and the control variables are nonnegative and bounded. The set $V_{ad}$ of all the controls is convex and closed. Further, the boundedness of the control variables suggests the compactness of the control system that is necessary for the existence of an optimal control. Also in the objective functional, the integrand is a convex function on the control set $V_{ad}$. In addition, there exists two positive real numbers $\eta_1$ and $\eta_2$ and a constant $\xi > 1$ such that

We noticed that our control set and the objective functional fulfill all the hypotheses of Theorem (13.8.1) in ^[29] that guarantee the existence of the optimal system. Thus, there exists an optimal control problem and hence the proof.

In order to obtain the necessary criteria of optimality, we will use the Gateaux derivative rule (also called the weak derivatives). For this purpose, we will introduce other controls $v_i^\epsilon(t) = v_i(t)+ \epsilon h_i(t), \; i = 1, 2$, where $h_i(t)\ne 0$ are variation functions and $0 < \epsilon < 1$. As the state variables are continuously dependent on the control variables, thus, we can write $S(t) = S(v_1(t), v_2(t)), U(t) = U(v_1(t), v_2(t))$ and $R(t) = R(v_1(t), v_2(t))$. By perturbing the controls variables will disturb the state as well and hence state variable will takes the form $S^\epsilon(t) = S(v_1^\epsilon, v_2^\epsilon), U^\epsilon(t) = U(v_1^\epsilon, v_2^\epsilon)$ and $R^\epsilon(t) = R(v_1^\epsilon, v_2^\epsilon)$, where

Accordingly due to $v_1^\epsilon(t), v_2^\epsilon(t)$, system (3.3) becomes

To form the weak derivatives, first we will subtract system (3.3) from (3.4) and will make the difference quotients $\frac{s^\epsilon(t, a)-s(t, a)}{\epsilon}$, $\frac{U^\epsilon(t)-U(t)}{\epsilon}$ and $\frac{r^\epsilon(t, a)-r(t, a)}{\epsilon}$. Next, we will find the sensitivities $\bar{s}(t, a), \; \bar{U}(t)$ and $\bar{r}(t, a)$ which can be obtain by applying $\lim_{\epsilon\rightarrow 0}$ to weak derivatives. The following linearized version of system (3.3) must be satisfied by the sensitivities

Next, we will use the sensitivities to obtain the adjoint system. In the case of ODEs, the adjoint are chosen such that the sensitivity terms drop out. However in PDE models, we need the sensitivity equations for finding the adjoint system. Each equation in the sensitivity PDEs can be written in a simplified form as

with necessary initial and boundary conditions and $\bar{\Psi}_i$'s are the corresponding variables $\bar{s}, \; \bar{U}$ and $\bar{r}$ for $i = 1, 2, 3$ respectively. Here, the linear operators $\mathcal{L}_i$ comes from the linearization of the corresponding state PDE operators. To obtain a characterization of the control variables, it is necessary to derive the adjoint system. The operators in the adjoint system are the adjoint operators of the $\mathcal{L}_i$ acting on $\bar{s}, \; \bar{U}$ and $\bar{r}$ in the sensitivity PDEs. The operators $\mathcal{L}_i$ and the adjoint operator $\mathcal{L}_i^*$ are related by

where $\langle \cdot, \cdot\rangle$ is the $L^2$-inner product. By using the integration by parts in multidimensions, we can throw the derivatives on each state from the operators $\mathcal{L}_i$ onto the derivatives of the adjoint variables $\lambda_i$ in the operators $\mathcal{L}_i^*$. Once we find the adjoint operators, then one can easily obtain the adjoint equations by using

where $x$ stand for the state variables. To do so, first we will consider (3.5a) as

with subsidiary

Here the notation $\langle\langle \cdot, \cdot \rangle\rangle$ is defined as $\langle\langle f_1, f_2\rangle\rangle = \int_0^T\int_0^\infty f_1f_2dadt$. On the other hand, Equation (3.5d) will take the form

with

where $\langle f_1, f_2\rangle = \int_0^Tf_1f_2dt$. In the same way, Equation (3.5c) can be written in the form of

along the condition

For future use, we will compute the weak derivative of the objective functional $J(v_1, v_2)$ as

By rewriting and suitable arrangements, Equations (3.6), (3.8) and (3.10) yields the following adjoint system

with transversality conditions

and boundary conditions

The following theorem will conclude our main discussion regarding the existence of an optimal control problem.

Theorem 3.2. If $v_1^\star, \; v_2^\star$ are in $V_{ad}$ is a pair of optimal control variables which minimizing $J(v_1, v_2)$ and $(S^\star(t), \; U^\star(t), \; R^\star(t))$ and $(\lambda_1(t, a), \; \lambda_2(t), \; \lambda_3(t, a))$ are the corresponding state and adjoint variables, respectively, then

and

proof. With the help of system (3.13), we can write the weak derivative of the objective functional defined in (3.12) as

where

Keeping in mind Eqs (3.6), (3.8) and (3.10), we can write the inequality (3.18) as

for all $v_1(t), \; v_2(t)\in V_{ad}$. As the variation functions $h_1(t), \; h_2(t)\ne 0$ on $V_{ad}$, thus the rest of the integrand must be equal to zero. Hence

and

By considering the lower and upper bounds of the control variables as well as the optimal values of the state variables, we have

and

Formulas developed in relations (3.20) and (3.21) are the required characterization of the optimal controls.

By using these optimal value of the control variables, the desired optimal system can be written as

4.   Numerical simulations

In the previous section, we have presented analytically an optimal control problem keeping in view some predetermined goals. In the present section, we will try to simulate both the optimal control and without control systems and to compare the obtained results. The numerical method to be used will be the finite difference method as the problem containing both ordinary and partial differential equations. This method approximates the derivative by difference quotients and it approximates the solution at each point of the domain. Let the maximum class-age is $A$ and the maximum time is $T$ both of which are finite. The age and time directions are divided into equal space with the same step size $\Delta a = \Delta t$ due to together progression. Thus, all of the points in time and age directions can be computed as $a_k = k\Delta t$ and $t_n = n\Delta t$, respectively. Assume the $M$ and $N$ are the number of points to be incorporated in age time directions so that $A = M\Delta t$ and $T = N\Delta t$. The numerical method computes approximations to the solutions at the mesh points:

Adopting the similar procedure presented in ^[30], system (3.22) will gives the following simulation scheme

Using the same procedure, the schemes for adjoint system (3.13) and system without control (2.1) are developed and then coded in MATLAB along with characterization of control variables defined in (3.20) and (3.21). For simulation purpose, we assumed that $\Delta t = 0.05$, maximum class-age $a = 40$ years and maximum time $T$ for the control strategy is $40$ days. Furthermore, the initial data related to all classes were chosen according to assumption of the model. The values and justification of parameter used in simulation is presented in Table 1. Besides, at initial stage of the control strategy we assumed $v_1(t) = v_2(t) = 0$.

Figures 1 represent the dynamics of all classes with respect to class-age and time. Sub-figure 1a shows the density of susceptible population without control, whereas, Figure 1b shows the same population density with control. Comparison reveal that there are more susceptible to heroin addiction when the control was not implemented. As the control strategy was launched, the control shows his effect and susceptible people tend to decrease. As a result, fewer people will tend to initiate the use of heroin. Figure 1c is self-explanatory and depict that both the controls are effective for reducing the number of heroin addicts in a community. Figures 1d and 1e show the recovered population and again it is clear from the graphs that the recovered population tends to increase as we impose the control strategy.

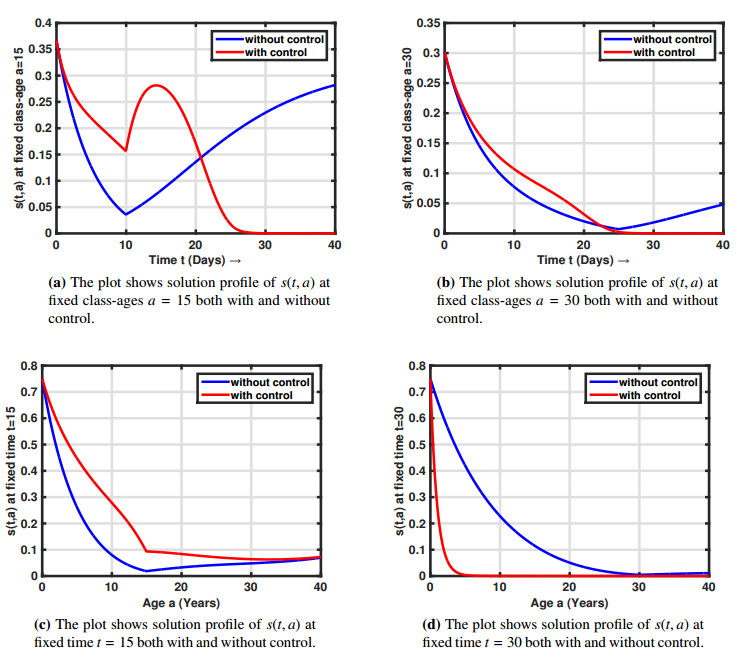
To understand the effectiveness of education control, in Figure 2 we have chosen some sample curves (solution profiles) from the density function of the susceptible population at fixed time and age. Figure 2a represents the solution profile of $s(t, a)$ at fixed age $a = 15$. The figure shows that although education campaign has reverse effect on young people at initial stages but with the passage of time it will work. After 20 days of strategy, the population of young susceptible tends to decline and finally there will be no susceptible whose age of susceptibility is between 15-22. Likewise, Figure 2b represent the solution profile of those susceptible whose age of susceptibility is 30. Again this figure suggest that the education campaign is much more effective in the long run. Similarly, figures 2c and 2d represent solution profiles of $s(t, a)$ at fixed time $t = 15$ and 20, respectively. These figures also indicate the effectiveness of awareness among susceptible. Again, these figures suggest that such type of campaign should be launched for the long run to achieve the desired outcomes.

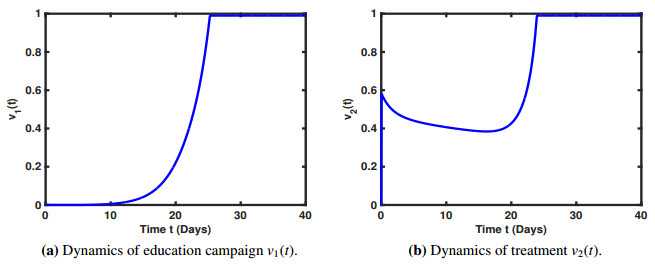
In the same way, we have plotted sample solution curves from $r(t, a)$ at fixed age and time in Figures 3a-3d. These figures shows a much clear effect of both awareness and treatment. Further, it shows that these control measures should be implemented in pairs; the former will control the susceptible people and the later will recover the active heroin users. Finally, Figures 4a and 4b represent the dynamics of the control variables $v_1(t)$ and $v_2(t)$, respectively.

5.   Conclusion

In this manuscript, we have developed an age-structured heroin epidemic model with continuous age-structure in susceptible and recovered classes using previously formulated models on the heroin epidemic. Using two control variables and a suitable objective functional, we investigated a control problem. Using the generalized maximum principle of Pontryagin's type and the Gateaux derivative rule, the authors presented an optimal control problem and characterized the optimal values of the control variables. To compare the theoretical results, we presented some simulation. Simulation of the model suggests that to control the use of heroin in a community, one must impose these two control measures in combination.

Acknowledgments

The authors are grateful to the anonymous reviewers for their valuable comments.

All authors carried out the proof. All authors conceived of the study, and participated in its design and coordination.

Conflict of interest

All authors declare that they have no competing interests.