Applied heat transfer modeling in conventional hybrid (Al2O3-CuO)/C2H6O2 and modified-hybrid nanofluids (Al2O3-CuO-Fe3O4)/C2H6O2 between slippery channel by using least square method (LSM)

Adnan; Khalid Abdulkhaliq M. Alharbi; Waqas Ashraf; Sayed M. Eldin; Mansour F. Yassen; Wasim Jamshed; Adnan; Khalid Abdulkhaliq M. Alharbi; Waqas Ashraf; Sayed M. Eldin; Mansour F. Yassen; Wasim Jamshed

doi:10.3934/math.2023215

AIMS Mathematics

2023, Volume 8, Issue 2: 4321-4341. doi: 10.3934/math.2023215

Previous Article Next Article

Research article Special Issues

Applied heat transfer modeling in conventional hybrid (Al₂O₃-CuO)/C₂H₆O₂ and modified-hybrid nanofluids (Al₂O₃-CuO-Fe₃O₄)/C₂H₆O₂ between slippery channel by using least square method (LSM)

1.
Department of Mathematics, Mohi-ud-Din Islamic University, Nerian Sharif 12080, AJ & K, Pakistan
2.
Mechanical Engineering Department, College of Engineering, Umm Al-Qura University, Makkah, 24382, Saudi Arabia
3.
Department of Applied Mathematics and Statistics (AM & S), Institute of Space Technology (IST), 44000 Islamabad, Pakistan
4.
Center of Research, Faculty of Engineering, Future University in Egypt, New Cairo 11835, Egypt
5.
Department of Mathematics, College of Science and Humanities in Al-Aflaj, Prince Sattam Bin Abdulaziz University, Al-Aflaj 11912, Saudi Arabia
6.
Department of Mathematics, Faculty of Science, Damietta University, New Damietta 34517 Damietta, Egypt
7.
Department of Mathematics, Capital University of Science and Technology, Islamabad, Pakistan

Received: 02 October 2022 Revised: 25 November 2022 Accepted: 28 November 2022 Published: 05 December 2022
MSC : 47H09, 47H10

In this research, a new heat transfer model for ternary nanofluid (Al₂O₃-CuO-Fe₃O₄)/C₂H₆O₂ inside slippery converging/diverging channel is reported with innovative effects of dissipation function. This flow situation described by a coupled set of PDEs which reduced to ODEs via similarity and effective ternary nanofluid properties. Then, LSM is successfully coded for the model and achieved the desired results influenced by $\alpha ,Re,{\gamma }_{1}$ and $Ec$ . It is examined that the fluid movement increases for $Re$ in the physical range of 30–180 and it drops for diverging channel ( $\alpha > 0$ ) when the slippery wall approaches to $\alpha = {60}^{o}$ . The fluid movement is very slow for increasing concentration factor ${\varphi }_{i}$ for $i = \mathrm{1,2},3$ up to 10%. Further, ternary nanofluid temperature boosts rapidly due to inclusion of trinanoparticles thermal conductivity and dissipation factor ( $Ec = \mathrm{0.1,0.2,0.3,0.4,0.6}$ ) also contributes significantly. Moreover, the temperature is maximum about the center of the channel ( $\eta = 0$ ) and slip effects ( ${\gamma }_{1} = \mathrm{0.1,0.2,0.3,0.4,0.5,0.6}$ ) on the channel walls lead to decrement in the temperature $\beta \left(\eta \right)$ .

Keywords:

Citation: Adnan, Khalid Abdulkhaliq M. Alharbi, Waqas Ashraf, Sayed M. Eldin, Mansour F. Yassen, Wasim Jamshed. Applied heat transfer modeling in conventional hybrid (Al2O3-CuO)/C2H6O2 and modified-hybrid nanofluids (Al2O3-CuO-Fe3O4)/C2H6O2 between slippery channel by using least square method (LSM)[J]. AIMS Mathematics, 2023, 8(2): 4321-4341. doi: 10.3934/math.2023215

Related Papers:

[1]	Saleh Mousa Alzahrani . Enhancing thermal performance: A numerical study of MHD double diffusive natural convection in a hybrid nanofluid-filled quadrantal enclosure. AIMS Mathematics, 2024, 9(4): 9267-9286. doi: 10.3934/math.2024451
[2]	Gunisetty Ramasekhar, Shaik Jakeer, Seethi Reddy Reddisekhar Reddy, Shalan Alkarni, Nehad Ali Shah . Biomedical importance of Casson nanofluid flow with silver and Fe₂O₃ nanoparticles delivered into a stenotic artery: Numerical study. AIMS Mathematics, 2024, 9(8): 23142-23157. doi: 10.3934/math.20241125
[3]	C. S. K. Raju, S.V. Siva Rama Raju, S. Mamatha Upadhya, N. Ameer Ahammad, Nehad Ali Shah, Thongchai Botmart . A numerical study of swirling axisymmetric flow characteristics in a cylinder with suspended PEG based magnetite and oxides nanoparticles. AIMS Mathematics, 2023, 8(2): 4575-4595. doi: 10.3934/math.2023226
[4]	Abdul Rauf, Nehad Ali Shah, Aqsa Mushtaq, Thongchai Botmart . Heat transport and magnetohydrodynamic hybrid micropolar ferrofluid flow over a non-linearly stretching sheet. AIMS Mathematics, 2023, 8(1): 164-193. doi: 10.3934/math.2023008
[5]	Gunisetty Ramasekhar, Shalan Alkarni, Nehad Ali Shah . Machine learning approach of Casson hybrid nanofluid flow over a heated stretching surface. AIMS Mathematics, 2024, 9(7): 18746-18762. doi: 10.3934/math.2024912
[6]	Kiran Sajjan, N. Ameer Ahammad, C. S. K. Raju, M. Karuna Prasad, Nehad Ali Shah, Thongchai Botmart . Study of nonlinear thermal convection of ternary nanofluid within Darcy-Brinkman porous structure with time dependent heat source/sink. AIMS Mathematics, 2023, 8(2): 4237-4260. doi: 10.3934/math.2023211
[7]	Vanita Sharma, Satish Kumar . Caliberating length scale parameter and micropolarity on transference of Love-type waves in composite of CoFe₂O₄ and Aluminium-Epoxy laden with Newtonian liquid. AIMS Mathematics, 2020, 5(3): 1820-1842. doi: 10.3934/math.2020122
[8]	M. Hamid, T. Zubair, M. Usman, R. U. Haq . Numerical investigation of fractional-order unsteady natural convective radiating flow of nanofluid in a vertical channel. AIMS Mathematics, 2019, 4(5): 1416-1429. doi: 10.3934/math.2019.5.1416
[9]	Liying Yang, Jinjin Li, Yiliang Li, Qifang Li . Sub-base local reduct in a family of sub-bases. AIMS Mathematics, 2022, 7(7): 13271-13277. doi: 10.3934/math.2022732
[10]	Ziqiang Wang, Jiaojiao Ma, Junying Cao . A higher-order uniform accuracy scheme for nonlinear $ \psi $-Volterra integral equations in two dimension with weakly singular kernel. AIMS Mathematics, 2024, 9(6): 14325-14357. doi: 10.3934/math.2024697

Abstract

Abbreviations: PDEs: Partial differential equations; ODEs: Ordinary differential equations; LSM: Least Square Method

Nomenclature
$\stackrel{ˇ}{u}$	velocity component [m/s]
$\stackrel{ˇ}{p}$	pressure [Pa]
$\stackrel{ˇ}{T}$	temperature [K]
$\stackrel{ˇ}{U}$	velocity at central line [m/s]
${\stackrel{ˇ}{T}}_{w}$	wall temperature [K]
${\widetilde{\rho }}_{mhnf}$	modified density [kgm^-3]
${\widetilde{\rho }}_{hnf}$	hybrid density [kgm^-3]
${\widetilde{\rho }}_{f}$	fluid density [kgm^-3]
${\widetilde{\rho }}_{s}$	nanoparticles density [kgm^-3]
${\widetilde{\mu }}_{mhnf}$	modified dynamic viscosity [Pa-s]
${\widetilde{\mu }}_{hnf}$	hybrid dynamic viscosity [Pa-s]
${\widetilde{\mu }}_{f}$	fluid dynamic viscosity [Pa-s]
${\stackrel{ˇ}{k}}_{mhnf}$	modified thermal conductivity [Wm^-1K^-1]
${\stackrel{ˇ}{k}}_{hnf}$	hybrid thermal conductivity [Wm^-1K^-1]
${\stackrel{ˇ}{k}}_{f}$	fluid thermal conductivity [Wm^-1K^-1]
${\stackrel{ˇ}{k}}_{s}$	nanoparticles thermal conductivity [Wm^-1K^-1]
${\left({\widetilde{c}}_{p}\right)}_{mhnf}$	modified heat capacity [J/K]
${\left({\widetilde{c}}_{p}\right)}_{hnf}$	hybrid heat capacity [J/K]
${\left({\widetilde{c}}_{p}\right)}_{f}$	fluid heat capacity [J/K]
${\left({\widetilde{c}}_{p}\right)}_{s}$	nanoparticles heat capacity [J/K]
$\eta$	dimensionless variable
$F$	dimensionless velocity
$\beta$	dimensionless temperature
$\phi$	nanoparticles concentration
$\alpha$	converging/diverging parameter
${R}_{e}$	Reynolds number
$Pr$	Prandtl number
$Ec$	Eckert number
${\gamma }_{1}$	slip number

1. Introduction

The importance and applications of newtonian fluids (water, ethylene glycol, alcohol and glycerol etc.) cannot be avoided as the viscosity of these fluids remain unchanged under the action of forces and applicable in industries and engineering. As, interaction of oxide nanoparticles (Al₂O₃, CuO and Fe₃O₄) with common fluid in converging/diverging channel is important from the aspects of biomedical engineering which exhibits such flows. Therefore, an enhanced ternary nanofluid ^[1] model in converging/diverging is considered. The development of nanofluids made new insights in the modern world and engineers and researchers became familiar with these fluids. They feel that these fluids are very comfortable to overcome the issues of heat transport and can be used them in the production of various products.

The new type of heat transfer fluids synthesized using hybrid or ternary nanoparticles. Primarily, effective characteristics of these fluids are of much interest which are functions of diameter, temperature, concentration factor and brownian motion etc. Recently, Sahoo ^[2] performed an experiment and introduced a new viscosity model for ternary nanofluid. The experiment executed for (Al₂O₃-SiC-TiO₂)/water with uniform dispersion of each type of nanoparticles within 35–40 ℃ temperature. In 2021, Zayan et al. ^[3] discussed rheological properties of (GO-TiO₂-Ag)/H₂O and (TiO₂-Ag-rGO)/H₂O via experiment. They examined that simple GO based trinanoparticles under temperature variations from 25–50 ℃ exhibit newtonian characteristics. However, at low concentration it behaves like Pseudo Plastic and major contribution of nanoparticles aggregation is suggested to acquire the goal. Numerical treatment of fluid with basic components of trinanoparticles including the nonuniform diffusion and non-Fourier heat flux reported by Algehyne et al. ^[4]. The authors examined that the hybrid nanoliquid has larger tendency to transmit and store energy and it boosts almost 61% to that of mono nanoliquid.

Recently, Dezfulizadeh et al. ^[5] proposed an effective correlation to improve the heat transfer capacity of ternary fluids. They inspired by thermomechanical characteristics of (Cu-SiO₂-MWCNT) and reported the correlations. After the development of variety of effective characteristics of ternary nanoliquids under different circumstances, researchers from applied areas inspired and analyze them from more advanced physical aspects ^[6]. Further, recent advancements in ternary nanofluids for nanomaterials owing to their outstanding thermal and mechanical characteristics described in the Refs. [7,8] and the studies reported therein.

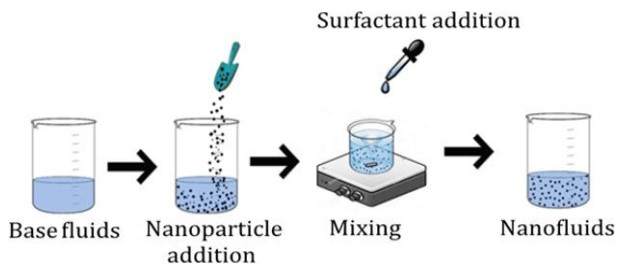
Nanofluids synthesized from uniform composition of nano-additives in the hosting liquid. The dimensions of nanoparticles are usually smaller than 100nm which allow them to dissolve in the base solvent uniformly. The progressive thermal conductivity of nanofluids attracts the attention of industrialist, engineers and scientists for wide applications. These broadly applicable in thermal engineering, heat transport problems, bio-medical engineering ^[9], pollution control and building heating/cooling, heat enhancement ^[10], electronics, paint industries and aerodynamics etc. Interaction of nanoparticles with blood as base liquid became very innovative in the medical sciences, more specifically for detection of cancer cells in human body ^[11,12]. So that, the world entered into a new era with broad and innovative ideas. The composition process of nanofluids is sketched in Figure 1.

Figure 1. Synthesization capturing of nanofluids (first generation heat transfer fluids).

DownLoad: Full-Size Img PowerPoint

After the primary idea of nanofluids, researchers became very curious and invested time to make these fluids effective regarding thermal performance. They thought that inherent characteristics of conventional liquids could be enhanced by adding one more sort of nanoparticles. So, they worked day and night and finally they succeeded and achieve a milestone of Hybrid nanofluids ^[13,14]. These fluids known as second-generation heat transfer fluids with rich thermal conductivity. Recently, researchers reveal that hybrid nanofluids have promising heat transport characteristics due to which these substitute the conventional fluids. These fluids have broad range of applications in the world of nanotechnology, some of them are in solar collectors, solar energy storage devices, cooling parts of electronic devices, manufacturing of various machinery parts, air conditioning, ventilation, heat exchangers and refrigeration etc. The schematic of synthetization of hybrid nanoliquids is demonstrated in Figure 2.

Figure 2. Synthesization capturing of Hybrid nanofluids (Second generation heat transfer fluids).

DownLoad: Full-Size Img PowerPoint

Although, hybrid nanofluids have promising applications in the world of nanotechnology; however, scientists did not stop their efforts to resolve the challenges that could be found in engineering and industrial zone. Therefore, leading scientists of the world gathered at a single platform and revealed that promising heat transport characteristics of hybrid nanofluids could be improved further by adding a third type nanoparticles in the existing hybrid nanofluids. Finally, they introduced the modern world with the concept of Ternary-hybrid nanofluids ^{[15,16,17,18]}. The addition of third type of nanoparticles in the regular hybrid nanofluids boosts thermal conductivity of the resultant mixture that makes them superior heat transport fluids.

In the view of above discussion and literature cited, the following classes exist so far to tackle the heat transport issues of the modern world:

● Conventional fluids with inherent characteristics (poor conductor of heat transport).

● Nanofluids or first-generation heat transfer fluids (better thermal performance than conventional liquids).

● Hybrid nanofluids or second-generation heat transfer fluids (superior thermal performance than conventional and nanofluids).

● Ternary hybrid nanofluids or third-generation heat transfer fluids (recently developed heat transfer fluids with excellent thermal transport characteristics than regular, nanofluids and hybrid nanofluids).

Figure 3 illustrated synthetization process of tri-hybrid nanofluids.

Figure 3. Synthesization capturing of Tri-Hybrid nanofluids (Third generation heat transfer fluids).

DownLoad: Full-Size Img PowerPoint

The rapid growth in the study of heat transport problems provided a new ground to Fluid dynamists to explore the interaction of various flow conditions and physical phenomenon with varying nanomaterials. The production process of industrial products passes through many stages in which the fluid flow through different geometries. In the language of Fluid mechanics, these flow situations modeled through constitutive relations that are latterly used to examine the impacts of physical constraints. For example, magnetic field ^[19] and Joule heating phenomenon could be utilized to purify the industrial production or thermal radiations ^[20] effects, velocity and thermal slip constraints, heat generation/absorption ^[21], activation energy or cross diffusion gradients are such physical constraints that playing imperative role in the modern world.

The detection of different health related diseases is a core issue around the globe and oxide nanoparticles (Al₂O₃, CuO, Fe₃O₄) are widely utilize to cope the problems of implant, wound healing, cancer therapy, antimicrobial activities, drug delivery and in bio-medical sciences ^[22]. Therefore, in the view of above discussed significant aspects of oxide nanoparticles, this study is organized and it will cover the following research gaps:

● Comparative thermal behaviour between [(Al₂O₃-CuO)/C₂H₆O₂]_hnf and ternary hybrid nanofluid [(Al₂O₃-CuO-Fe₃O₄)/C₂H₆O₂]_mhnf.

● The insertion of viscous dissipation in the model strengthens the novelty of the research in the context of thermal enhancement.

● Impacts of fraction factor $\phi$ of (Al₂O₃, CuO, Fe₃O₄) will be examined.

● The quantities of engineering concerns like skin friction coefficient will be examined by fluctuating the physical constraints.

● The models for [(Al₂O₃-CuO)/C₂H₆O₂]_hnf and ternary hybrid nanofluid [(Al₂O₃-CuO-Fe₃O₄)/C₂H₆O₂]_mhnf will be solved by utilizing Least Square Method (LSM).

2. Materials and methods

2.1. Development of the model

In this analysis, considered the steady, incompressible, 2D but unidirectional flow of [(Al₂O₃-CuO)/C₂H₆O₂]_hnf and [(Al₂O₃-CuO-Fe₃O₄)/C₂H₆O₂]_mhnf nanofluids inspired by the novel effects of viscous dissipation and thermal radiation. The fluids flow due a source/sink positioned at the culmination point of the slippery walls in the polar frame. The walls of the channel are separated through separation angle $2\alpha$ and the flow is only along radial direction. Due to unidirectional flow configuration, the fluid accelerates because of only $\stackrel{˘}{u}$ velocity component. Thus, possible velocity vector takes the form ${\boldsymbol{V}} = (\stackrel{˘}{u}, \mathrm{0, 0})$ in which $\stackrel{˘}{u}$ depends on polar coordinates $r$ and $\theta$ . The physical scenario of the flow is pictured in Figure 4. Moreover, in the light of aforesaid conditions, three basic laws are then described the following mathematical expressions ^[23]:

$\frac{1}{r}{\left(r\stackrel{˘}{u}\right)}_{r} = 0$

(1)

${\widetilde{\rho }}_{mhnf}\left[\stackrel{˘}{u}{\stackrel{˘}{u}}_{r}\right]+{\stackrel{˘}{[p}]}_{r}-{\widetilde{\mu }}_{mhnf}\left[{\stackrel{˘}{u}}_{rr}+\frac{1}{r}{\stackrel{˘}{u}}_{r}+\frac{1}{{r}^{2}}{\stackrel{˘}{u}}_{\theta \theta }-\frac{\stackrel{˘}{u}}{{r}^{2}}\right] = 0$

(2)

$-\frac{1}{{r\widetilde{\rho }}_{mhnf}}{\left[\stackrel{˘}{p}\right]}_{\theta }+\frac{2{\widetilde{\mu }}_{mhnf}}{{\widetilde{\rho }}_{mhnf}{r}^{2}}{\left[\stackrel{˘}{u}\right]}_{\theta } = 0$

(3)

$\stackrel{˘}{u}{\left[\stackrel{˘}{T}\right]}_{r}-\frac{{\stackrel{˘}{k}}_{mhnf}}{{\left(\widetilde{\rho }Cp\right)}_{mhnf}}\left[{\stackrel{˘}{T}}_{rr}+\frac{1}{r}{\stackrel{˘}{T}}_{r}+\frac{1}{{r}^{2}}{\stackrel{˘}{T}}_{\theta \theta }\right]-{\widetilde{\mu }}_{\frac{mhnf}{{\left(\widetilde{\rho }Cp\right)}_{mhnf}}}\left[4{\left(\stackrel{˘}{u}\right)}_{r}^{2}+\frac{1}{{r}^{2}}{\left(\stackrel{˘}{u}\right)}_{\theta }^{2}\right] = 0$

(4)

Figure 4. Flow configuration of [Al₂O₃-CuO/C₂H₆O₂]_hnf and [Al₂O₃-CuO-Fe₃O₄/C₂H₆O₂]_mhnf between converging/diverging channel.

DownLoad: Full-Size Img PowerPoint

Here, subscripts $r$ and $\theta$ represent the differentiation w.r.t polar coordinates, $mhnf$ stands for modified hybrid nanofluid, ${\widetilde{\rho }}_{mhnf}$ , ${\widetilde{\mu }}_{mhnf}$ , ${\stackrel{˘}{k}}_{mhnf}$ ${\left(\widetilde{\rho }Cp\right)}_{mhnf}$ are effective density, dynamic viscosity, thermal conductance and heat capacitance of modified hybrid nanofluid. The flow of [(Al₂O₃-CuO)/C₂H₆O₂]_hnf and [(Al₂O₃-CuO-Fe₃O₄)/C₂H₆O₂]_mhnf confined to the following conditions ^[23]:

$\stackrel{˘}{u} = \stackrel{˘}{U},{\stackrel{˘}{u}}_{\theta } = 0,{\stackrel{˘}{T}}_{\theta } = 0 \;{\rm{ at}} \; \theta = 0$

(5)

$\stackrel{˘}{u} = -{\gamma }_{1}{\stackrel{˘}{u}}_{\theta },\stackrel{˘}{T} = {\stackrel{˘}{T}}_{w} \;{\rm{ at}}\; \theta = \alpha$

(6)

Physically, these conditions describe that the fluid particles move with maximum speed at the central line i.e., $\theta = 0$ and temperature is ${\stackrel{˘}{T}}_{\theta }$ . On the other hand, slip condition is implemented at the walls ( $\theta = \alpha$ ) and the temperature of fluid layer adjacent to the wall is same as the wall temperature ${\stackrel{˘}{T}}_{w}$ .

Now, Eq (1) can be transformed in the following version on integrating and also supporting similarity expression as described ^[23]:

$F\left(\eta \right) = \frac{\stackrel{˘}{f}\left(\theta \right)}{{\stackrel{˘}{f}}_{max}},\eta = \theta {\alpha }^{-1},\beta \left(\eta \right) = \frac{\stackrel{˘}{T}}{{\stackrel{˘}{T}}_{w}}$

The following empirical correlations are adopted to update the conventional nanofluid models for hybrid and ternary hybrid nanofluids (THNF) (See Tables 1–3, ^[24,25,26]).

Table 1. Empirical attributes of nanofluids.

Characteristics	Empirical attributes
Dynamic viscosity	$\frac{{\widetilde{\mu }}_{nf}}{{\widetilde{\mu }}_{f}}={\left(1-\phi \right)}^{-25/10}$
Effective density	${\widetilde{\rho }}_{nf}={\widetilde{\rho }}_{f}\left(1-\phi \right)+{\widetilde{\rho }}_{s}\phi$
Heat capacity	${\left(\widetilde{\rho }{C}_{p}\right)}_{nf}={\left(\widetilde{\rho }{C}_{p}\right)}_{f}\left(1-\phi \right)+\phi {\left(\widetilde{\rho }{C}_{p}\right)}_{s}$
Thermal conductivity	$\frac{{\widetilde{k}}_{nf}}{{\widetilde{k}}_{f}}=\frac{\left[{\widetilde{k}}_{s}+{\widetilde{k}}_{f}\left(\widetilde{\chi }-1\right)-\left(\widetilde{\chi }-1\right)\left({\widetilde{k}}_{f}-{\widetilde{k}}_{s}\right)\phi \right]}{[{\widetilde{k}}_{s}+{\widetilde{k}}_{f}\left(\widetilde{\chi }-1\right)+\left({\widetilde{k}}_{f}-{\widetilde{k}}_{s}\right)\phi ]}$ where, $\widetilde{\chi }=\frac{3}{\widetilde{\mathrm{\Phi }}}$ is the shape factor
Electrical conductivity	$\frac{{\widetilde{\sigma }}_{nf}}{{\widetilde{\sigma }}_{f}}=1+\frac{3\left(\frac{{\widetilde{\sigma }}_{s}}{{\widetilde{\sigma }}_{f}}-1\right)\phi }{\left(\frac{{\widetilde{\sigma }}_{s}}{{\widetilde{\sigma }}_{f}}+2\right)-\left(\frac{{\widetilde{\sigma }}_{s}}{{\widetilde{\sigma }}_{f}}-1\right)\phi }$
Thermal expansion	${\left(\rho \beta \right)}_{nf}=\left(1-\phi \right){\left(\rho \beta \right)}_{s}+\phi {\left(\rho \beta \right)}_{f}$

| Show Table

DownLoad: CSV

Table 2. Empirical attributes for hybrid nanofluids ^[27].

Characteristics	Empirical attributes
Dynamic viscosity	$\frac{{\widetilde{\mu }}_{hnf}}{{\widetilde{\mu }}_{f}}={\left(1-{\phi }_{1}\right)}^{-25/10}{\left(1-{\phi }_{2}\right)}^{-25/10}$
Effective density	${\widetilde{\rho }}_{hnf}=\left[\left(1-{\phi }_{2}\right)\left\{\left(1-{\phi }_{1}\right){\widetilde{\rho }}_{f}+{\phi }_{1}{\widetilde{\rho }}_{s1}\right\}\right]+{\phi }_{2}{\widetilde{\rho }}_{s2}$
Heat capacity	${\left(\widetilde{\rho }{C}_{p}\right)}_{hnf}=\left[\left(1-{\phi }_{2}\right)\left\{\left(1-{\phi }_{1}\right){\left(\widetilde{\rho }{C}_{p}\right)}_{f}+{\phi }_{1}{\left(\widetilde{\rho }{C}_{p}\right)}_{s1}\right\}\right]+{\phi }_{2}{\left(\widetilde{\rho }{C}_{p}\right)}_{s2}$
Thermal conductivity	$\frac{{\widetilde{k}}_{hnf}}{{\widetilde{k}}_{nf}}=\frac{\left[{\widetilde{k}}_{s2}+\left(\widetilde{\chi }-1\right){\widetilde{k}}_{nf}-\left(\widetilde{\chi }-1\right){\phi }_{2}\left({\widetilde{k}}_{nf}-{\widetilde{k}}_{s2}\right)\right]}{[{\widetilde{k}}_{s2}+\left(\widetilde{\chi }-1\right){\widetilde{k}}_{nf}+{\phi }_{2}({\widetilde{k}}_{nf}-{\widetilde{k}}_{s2}\left)\right]}$ where $\frac{{\widetilde{k}}_{nf}}{{\widetilde{k}}_{f}}=\frac{\left[{\widetilde{k}}_{s1}+{\widetilde{k}}_{f}\left(\widetilde{\chi }-1\right)-\left(\widetilde{\chi }-1\right)\left({\widetilde{k}}_{f}-{\widetilde{k}}_{s1}\right){\phi }_{1}\right]}{[{\widetilde{k}}_{s1}+{\widetilde{k}}_{f}\left(\widetilde{\chi }-1\right)+\left({\widetilde{k}}_{f}-{\widetilde{k}}_{s1}\right){\phi }_{1}]}$
Electrical conductivity	$\frac{{\widetilde{\sigma }}_{hnf}}{{\widetilde{\sigma }}_{nf}}=\frac{\left[{\widetilde{\sigma }}_{s2}+2{\widetilde{\sigma }}_{nf}-2{\phi }_{2}\left({\widetilde{\sigma }}_{nf-}{\widetilde{\sigma }}_{s2}\right)\right]}{[{\widetilde{\sigma }}_{s2}+2{\widetilde{\sigma }}_{nf}+{\phi }_{2}\left({\widetilde{\sigma }}_{nf-}{\widetilde{\sigma }}_{s2}\right)]}$ where $\frac{{\widetilde{\sigma }}_{nf}}{{\widetilde{\sigma }}_{f}}=\frac{\left[{\widetilde{\sigma }}_{s1}+2{\widetilde{\sigma }}_{f}-2{\phi }_{1}\left({\widetilde{\sigma }}_{f-}{\widetilde{\sigma }}_{s1}\right)\right]}{[{\widetilde{\sigma }}_{s1}+2{\widetilde{\sigma }}_{f}+{\phi }_{1}\left({\widetilde{\sigma }}_{f-}{\widetilde{\sigma }}_{s1}\right)]}$
Thermal expansion	${\left(\widetilde{\rho }\widetilde{\beta }\right)}_{nf}=\left[\left(1-{\phi }_{2}\right)\left\{\left(1-{\phi }_{1}\right){\left(\widetilde{\rho }\widetilde{\beta }\right)}_{f}+{\phi }_{1}{\left(\widetilde{\rho }\widetilde{\beta }\right)}_{s1}\right\}\right]+{\phi }_{2}{\left(\widetilde{\rho }\widetilde{\beta }\right)}_{s2}$

| Show Table

DownLoad: CSV

Table 3. Empirical attributes of ternary hybrid nanofluids.

Characteristics	Empirical attributes
Dynamic viscosity	$\frac{{\widetilde{\mu }}_{mhnf}}{{\widetilde{\mu }}_{f}}={\left(1-{\phi }_{1}\right)}^{-25/10}{\left(1-{\phi }_{2}\right)}^{-25/10}{\left(1-{\phi }_{3}\right)}^{-25/10}$
Effective density	${\widetilde{\rho }}_{mhnf}=\left[\left(1-{\phi }_{3}\right)\left\{\left(1-{\phi }_{2}\right)\left[\left(1-{\phi }_{1}\right){\widetilde{\rho }}_{f}+{\phi }_{1}{\widetilde{\rho }}_{s1}\right]+{\phi }_{2}{\widetilde{\rho }}_{s2}\right\}\right]+{\phi }_{3}{\widetilde{\rho }}_{s3}$
Heat capacity	${\left(\widetilde{\rho }{C}_{p}\right)}_{mhnf}=\left[\left(1-{\phi }_{3}\right)\left\{\left(1-{\phi }_{2}\right)\left[\left(1-{\phi }_{1}\right){\left(\widetilde{\rho }{C}_{p}\right)}_{f}+{\phi }_{1}{\left(\widetilde{\rho }{C}_{p}\right)}_{s1}\right]+{\phi }_{2}{\left(\widetilde{\rho }{C}_{p}\right)}_{s2}\right\}\right]+{\phi }_{3}{\left(\widetilde{\rho }{C}_{p}\right)}_{s3}$
Thermal conductivity	$\frac{{\widetilde{k}}_{mhnf}}{{\widetilde{k}}_{hnf}}=\frac{\left[{\widetilde{k}}_{s3}+\left(\widetilde{\chi }-1\right){\widetilde{k}}_{hnf}-\left(\widetilde{\chi }-1\right){\phi }_{3}\left({\widetilde{k}}_{hnf}-{\widetilde{k}}_{s3}\right)\right]}{[{\widetilde{k}}_{s3}+\left(\widetilde{\chi }-1\right){\widetilde{k}}_{hnf}+{\phi }_{3}({\widetilde{k}}_{hnf}-{\widetilde{k}}_{s3}\left)\right]}$ where $\frac{{\widetilde{k}}_{hnf}}{{\widetilde{k}}_{nf}}=\frac{\left[{\widetilde{k}}_{s2}+\left(\widetilde{\chi }-1\right){\widetilde{k}}_{nf}-\left(\widetilde{\chi }-1\right){\phi }_{2}\left({\widetilde{k}}_{nf}-{\widetilde{k}}_{s2}\right)\right]}{[{\widetilde{k}}_{s2}+\left(\widetilde{\chi }-1\right){\widetilde{k}}_{nf}+{\phi }_{2}({\widetilde{k}}_{nf}-{\widetilde{k}}_{s2}\left)\right]}$ where $\frac{{\widetilde{k}}_{nf}}{{\widetilde{k}}_{f}}=\frac{\left[{\widetilde{k}}_{s1}+\left(\widetilde{\chi }-1\right){\widetilde{k}}_{f}-\left(\widetilde{\chi }-1\right){\phi }_{1}\left({\widetilde{k}}_{f}-{\widetilde{k}}_{s1}\right)\right]}{[{\widetilde{k}}_{s1}+\left(\widetilde{\chi }-1\right){\widetilde{k}}_{f}+{\phi }_{1}({\widetilde{k}}_{f}-{\widetilde{k}}_{s1}\left)\right]}$
Electrical conductivity	$\frac{{\widetilde{\sigma }}_{mhnf}}{{\widetilde{\sigma }hn}_{f}}=\frac{\left[{\widetilde{\sigma }}_{s3}+2{\widetilde{\sigma }}_{hnf}-2{\phi }_{3}\left({\widetilde{\sigma }}_{hnf-}{\widetilde{\sigma }}_{s3}\right)\right]}{[{\widetilde{\sigma }}_{s3}+2{\widetilde{\sigma }}_{hnf}+{\phi }_{3}\left({\widetilde{\sigma }}_{hnf-}{\widetilde{\sigma }}_{s3}\right)]}$ where $\frac{{\widetilde{\sigma }}_{hnf}}{{\widetilde{\sigma }n}_{f}}=\frac{\left[{\widetilde{\sigma }}_{s2}+2{\widetilde{\sigma }}_{nf}-2{\phi }_{2}\left({\widetilde{\sigma }}_{nf-}{\widetilde{\sigma }}_{s2}\right)\right]}{[{\widetilde{\sigma }}_{s2}+2{\widetilde{\sigma }}_{nf}+{\phi }_{2}\left({\widetilde{\sigma }}_{nf-}{\widetilde{\sigma }}_{s2}\right)]}$ where $\frac{{\widetilde{\sigma }}_{nf}}{{\widetilde{\sigma }}_{f}}=\frac{\left[{\widetilde{\sigma }}_{s1}+2{\widetilde{\sigma }}_{f}-2{\phi }_{1}\left({\widetilde{\sigma }}_{f-}{\widetilde{\sigma }}_{s1}\right)\right]}{[{\widetilde{\sigma }}_{s1}+2{\widetilde{\sigma }}_{f}+{\phi }_{1}\left({\widetilde{\sigma }}_{f-}{\widetilde{\sigma }}_{s1}\right)]}$

| Show Table

DownLoad: CSV

Further, shape factor of the nanoparticles is defined in Table 4 for different sort of nanoparticles ^[28].

Table 4. Nanoparticles name, shapes and shape factor values.

Nanoparticle's name	Shape	Shape factor $\widetilde{{\boldsymbol{\chi }}}$
Lamina		16.1576
Platelets		5.7
Hexahedron		3.7221

| Show Table

DownLoad: CSV

Now, after performing necessary cross differentiation of the momentum equations and impinging the similarity equations and empirical correlations, the following updating version of the model is obtained:

${F}_{\eta \eta \eta }+\frac{2\alpha Re\left[\left[\left(1-{\phi }_{3}\right)\left\{\left(1-{\phi }_{2}\right)\left[\left(1-{\phi }_{1}\right)+\frac{{\phi }_{1}{\widetilde{\rho }}_{s1}}{{\widetilde{\rho }}_{f}}\right]+\frac{{\phi }_{2}{\widetilde{\rho }}_{s2}}{{\widetilde{\rho }}_{f}}\right\}\right]+\frac{{\phi }_{3}{\widetilde{\rho }}_{s3}}{{\widetilde{\rho }}_{f}}\right]}{{\left(1-{\phi }_{1}\right)}^{-25/10}{\left(1-{\phi }_{2}\right)}^{-25/10}{\left(1-{\phi }_{3}\right)}^{-25/10}}F{F}_{\eta }+4{\alpha }^{2}{F}_{\eta } = 0$

(7)

$\frac{{\widetilde{k}}_{mhnf}}{{\widetilde{k}}_{f}}{\beta }_{\eta \eta }+\frac{EcPr\left[\left[\left(1-{\phi }_{3}\right)\left\{\left(1-{\phi }_{2}\right)\left[\left(1-{\phi }_{1}\right)+\frac{{\phi }_{1}{\left(\widetilde{\rho }{C}_{p}\right)}_{s1}}{{\left(\widetilde{\rho }{C}_{p}\right)}_{f}}\right]+\frac{{\phi }_{2}{\left(\widetilde{\rho }{C}_{p}\right)}_{s2}}{{\left(\widetilde{\rho }{C}_{p}\right)}_{f}}\right\}\right]+\frac{{\phi }_{3}{\left(\widetilde{\rho }{C}_{p}\right)}_{s3}}{{\left(\widetilde{\rho }{C}_{p}\right)}_{f}}\right]}{{\left(1-{\phi }_{1}\right)}^{\frac{25}{10}}{\left(1-{\phi }_{2}\right)}^{\frac{25}{10}}{\left(1-{\phi }_{3}\right)}^{\frac{25}{10}}}\left(4{\alpha }^{2}{F}^{2}+{F}_{\eta }^{2}\right) = 0$

(8)

$\frac{{\widetilde{k}}_{mhnf}}{{\widetilde{k}}_{f}} = \frac{\left[{\widetilde{k}}_{s3}+\left(\widetilde{\chi }-1\right){\widetilde{k}}_{hnf}-\left(\widetilde{\chi }-1\right){\phi }_{3}\left({\widetilde{k}}_{hnf}-{\widetilde{k}}_{s3}\right)\right]}{[{\widetilde{k}}_{s3}+\left(\widetilde{\chi }-1\right){\widetilde{k}}_{hnf}+{\phi }_{3}({\widetilde{k}}_{hnf}-{\widetilde{k}}_{s3}\left)\right]}\\*\frac{\left[{\widetilde{k}}_{s2}+\left(\widetilde{\chi }-1\right){\widetilde{k}}_{nf}-\left(\widetilde{\chi }-1\right){\phi }_{2}\left({\widetilde{k}}_{nf}-{\widetilde{k}}_{s2}\right)\right]}{\left[{\widetilde{k}}_{s2}+\left(\widetilde{\chi }-1\right){\widetilde{k}}_{nf}+{\phi }_{2}\left({\widetilde{k}}_{nf}-{\widetilde{k}}_{s2}\right)\right]}\\*\frac{\left[{\widetilde{k}}_{s1}+\left(\widetilde{\chi }-1\right){\widetilde{k}}_{f}-\left(\widetilde{\chi }-1\right){\phi }_{1}\left({\widetilde{k}}_{f}-{\widetilde{k}}_{s1}\right)\right]}{[{\widetilde{k}}_{s1}+\left(\widetilde{\chi }-1\right){\widetilde{k}}_{f}+{\phi }_{1}({\widetilde{k}}_{f}-{\widetilde{k}}_{s1}\left)\right]}$

The functions $F$ and $\beta$ depend on $\eta$ . Similarly, the boundary conditions (BCs) transformed in the following version:

$F\left(\eta \right) = 1,{F}^{\text{'}}\left(\eta \right) = 0,{\beta }^{\text{'}}\left(\eta \right) = 0 \;{\rm{ at}} \; \eta = 0 \\ F\left(\eta \right) = -{\gamma }_{1}{F}^{\text{'}}\left(\eta \right),\mathrm{ }\mathrm{\beta }\left(\mathrm{\eta }\right) = 0 \;{\rm{ at}} \; \eta = 1$

The quantity of broad engineering interest (Skin friction coefficient) is modeled in the following way:

${\stackrel{˘}{C}}_{F} = \frac{{\widetilde{\mu }}_{mhnf}}{{{\widetilde{U}}^{2}\widetilde{\rho }}_{mhnf}}{\left[{\widetilde{\tau }}_{r\theta }\right]}_{\eta = 1}$

By adopting the shear stresses and empirical correlations, the following form is attained after performing some mathematical steps:

$R{e}_{r}{\widetilde{C}}_{F} = \frac{{F}^{\text{'}}{\left(\eta \right)}_{\eta = 1}}{\left[{\left(1-{\phi }_{1}\right)}^{\frac{25}{10}}{\left(1-{\phi }_{2}\right)}^{\frac{25}{10}}{\left(1-{\phi }_{3}\right)}^{\frac{25}{10}}\right]*\left[\left[\left(1-{\phi }_{3}\right)\left\{\left(1-{\phi }_{2}\right)\left[\left(1-{\phi }_{1}\right)+\frac{{\phi }_{1}{\widetilde{\rho }}_{s1}}{{\widetilde{\rho }}_{f}}\right]+\frac{{\phi }_{2}{\widetilde{\rho }}_{s2}}{{\widetilde{\rho }}_{f}}\right\}\right]+\frac{{\phi }_{3}{\widetilde{\rho }}_{s3}}{{\widetilde{\rho }}_{f}}\right]}$

(9)

The physical constraints appeared in the above model are Eckert number ( $Ec = \frac{{\widetilde{\mu }}_{f}{\left({C}_{p}\right)}_{f}}{{\widetilde{k}}_{f}}$ ) and velocity slip ( ${\gamma }_{1} = \frac{\gamma }{\alpha }$ ). Moreover, thermophysical values for aforementioned empirical correlations are described in Table 5.

Table 5. Thermophysical values of the guest nanoparticles and the host liquid.

Properties	$\widehat{\rho }(kg/{m}^{3})$	${\widehat{c}}_{p}(J/KgK)$	$\widehat{k}(W/mk)$	$\stackrel{˘}{\sigma }{\left(\mathrm{\Omega }m\right)}^{-1}$
Ethylene glycol (C₂H₆O₂)	1115	2430	0.253	---------
Al₂O₃	$3970$	$765$	$40$	$35\times {10}^{6}$
Cu	8933	385	400	$59.6\times {10}^{6}$
CuO	6500	540	18	$6.9\times {10}^{-2}$
Fe₃O₄	5180	670	9.7	$0.74\times {10}^{6}$

| Show Table

DownLoad: CSV

2.2. Mathematical analysis

The solution of the model described in Eqs (7) and (8) alongside BCs is achieved via Least Square Method (LSM). The LSM works according to the following procedure:

2.2.1. Step 1

In this step, consider the model that going to be solved by LSM. Thus, the following enhanced heat transfer flow model is taken:

(10)

(11)

2.2.2. Step 2

In this step, trial solutions of the model equations defined in the following way:

$\stackrel{ˇ}{F} = {\widetilde{\mathfrak{I}}}_{0}+{\widetilde{\mathfrak{I}}}_{1}\eta +{\widetilde{\mathfrak{I}}}_{2}{\eta }^{2}+{\widetilde{\mathfrak{I}}}_{3}{\eta }^{3}+{\widetilde{\mathfrak{I}}}_{4}{\eta }^{4}+\dots +{\widetilde{\mathfrak{I}}}_{n}{\eta }^{n} = \sum\limits _{l = 0}^{n}{\widetilde{\mathfrak{I}}}_{l}{\eta }^{l}$

$\stackrel{ˇ}{\beta } = {\widetilde{\overline{\mathfrak{I}}}}_{0}+{\widetilde{\overline{\mathfrak{I}}}}_{1}\eta +{\widetilde{\overline{\mathfrak{I}}}}_{2}{\eta }^{2}+{\widetilde{\overline{\mathfrak{I}}}}_{3}{\eta }^{3}+{\widetilde{\overline{\mathfrak{I}}}}_{4}{\eta }^{4}+\dots +{\widetilde{\overline{\mathfrak{I}}}}_{n}{\eta }^{n} = \sum\limits _{l = 0}^{n}{\widetilde{\overline{\mathfrak{I}}}}_{l}{\eta }^{l}$

In these expressions, $\stackrel{ˇ}{F}$ and $\stackrel{ˇ}{\beta }$ depend on the variable $\eta$ . The proposed trial solutions must gratify the BCs of the flow model.

2.2.3. Step 3

By means of trial solutions, residual vectors for the governing flow model [(Al₂O₃-CuO-Fe₃O₄)/C₂H₆O₂]_mhnf in Eqs (10) and (11) described in the following way:

${{\boldsymbol{R}}}_{F} = {\stackrel{ˇ}{F}}_{\eta \eta \eta }+\frac{2\alpha Re\left[\left[\left(1-{\phi }_{3}\right)\left\{\left(1-{\phi }_{2}\right)\left[\left(1-{\phi }_{1}\right)+\frac{{\phi }_{1}{\widetilde{\rho }}_{s1}}{{\widetilde{\rho }}_{f}}\right]+\frac{{\phi }_{2}{\widetilde{\rho }}_{s2}}{{\widetilde{\rho }}_{f}}\right\}\right]+\frac{{\phi }_{3}{\widetilde{\rho }}_{s3}}{{\widetilde{\rho }}_{f}}\right]}{{\left(1-{\phi }_{1}\right)}^{-25/10}{\left(1-{\phi }_{2}\right)}^{-25/10}{\left(1-{\phi }_{3}\right)}^{-25/10}}\stackrel{ˇ}{F}{\stackrel{ˇ}{F}}_{\eta }+4{\alpha }^{2}{\stackrel{ˇ}{F}}_{\eta }\cong 0$

${{\boldsymbol{R}}}_{\beta } = \frac{{\widetilde{k}}_{mhnf}}{{\widetilde{k}}_{f}}{\stackrel{ˇ}{\beta }}_{\eta \eta }+\frac{EcPr\left[\left[\left(1-{\phi }_{3}\right)\left\{\left(1-{\phi }_{2}\right)\left[\left(1-{\phi }_{1}\right)+\frac{{\phi }_{1}{\left(\widetilde{\rho }{C}_{p}\right)}_{s1}}{{\left(\widetilde{\rho }{C}_{p}\right)}_{f}}\right]+\frac{{\phi }_{2}{\left(\widetilde{\rho }{C}_{p}\right)}_{s2}}{{\left(\widetilde{\rho }{C}_{p}\right)}_{f}}\right\}\right]+\frac{{\phi }_{3}{\left(\widetilde{\rho }{C}_{p}\right)}_{s3}}{{\left(\widetilde{\rho }{C}_{p}\right)}_{f}}\right]}{{\left(1-{\phi }_{1}\right)}^{\frac{25}{10}}{\left(1-{\phi }_{2}\right)}^{\frac{25}{10}}{\left(1-{\phi }_{3}\right)}^{\frac{25}{10}}}\left(4{\alpha }^{2}{\stackrel{ˇ}{F}}^{2}+{\stackrel{ˇ}{F}}_{\eta }^{2}\right)\cong 0$

$\frac{{\widetilde{k}}_{mhnf}}{{\widetilde{k}}_{f}} = \frac{\left[{\widetilde{k}}_{s3}+\left(\widetilde{\chi }-1\right){\widetilde{k}}_{hnf}-\left(\widetilde{\chi }-1\right){\phi }_{3}\left({\widetilde{k}}_{hnf}-{\widetilde{k}}_{s3}\right)\right]}{[{\widetilde{k}}_{s3}+\left(\widetilde{\chi }-1\right){\widetilde{k}}_{hnf}+{\phi }_{3}({\widetilde{k}}_{hnf}-{\widetilde{k}}_{s3}\left)\right]}*\frac{\left[{\widetilde{k}}_{s2}+\left(\widetilde{\chi }-1\right){\widetilde{k}}_{nf}-\left(\widetilde{\chi }-1\right){\phi }_{2}\left({\widetilde{k}}_{nf}-{\widetilde{k}}_{s2}\right)\right]}{\left[{\widetilde{k}}_{s2}+\left(\widetilde{\chi }-1\right){\widetilde{k}}_{nf}+{\phi }_{2}\left({\widetilde{k}}_{nf}-{\widetilde{k}}_{s2}\right)\right]}\\*\frac{\left[{\widetilde{k}}_{s1}+\left(\widetilde{\chi }-1\right){\widetilde{k}}_{f}-\left(\widetilde{\chi }-1\right){\phi }_{1}\left({\widetilde{k}}_{f}-{\widetilde{k}}_{s1}\right)\right]}{[{\widetilde{k}}_{s1}+\left(\widetilde{\chi }-1\right){\widetilde{k}}_{f}+{\phi }_{1}({\widetilde{k}}_{f}-{\widetilde{k}}_{s1}\left)\right]}$

2.2.4. Step 4

From hereafter, we need to construct a system of algebraic equations with equal number of unknowns as that of equations. In LSM, the following idea is utilized to construct the desired systems of equations:

$\begin{align*} {{\boldsymbol{E}}}_{F} = \int {{\boldsymbol{R}}}_{F}\left(\eta \right){{\widetilde{\omega }}^{F}}_{l}d\eta = 0,l = \mathrm{0,1},\mathrm{2,3},\dots n \end{align*}$

$\begin{align*}{{\boldsymbol{E}}}_{\beta } = \int {{\boldsymbol{R}}}_{\beta }\left(\eta \right){{\widetilde{\omega }}^{\beta }}_{l}d\eta = 0,l = \mathrm{0,1},\mathrm{2,3},\dots n \end{align*}$

In these constructive relations, ${{\widetilde{\omega }}^{F}}_{l}$ and ${{\widetilde{\omega }}^{\beta }}_{l}$ are the weight functions for $F$ and $\beta$ , respectively. These weight function achieved by implementing the following weight functions formula:

${{\widetilde{\omega }}^{F}}_{l} = \frac{\partial {{\boldsymbol{R}}}_{F}}{\partial {\widetilde{\mathfrak{I}}}_{n}},{{\widetilde{\omega }}^{\beta }}_{l} = \frac{\partial {{\boldsymbol{R}}}_{\beta }}{\partial {\widetilde{\overline{\mathfrak{I}}}}_{n}}$

2.2.5. Step 5

By using the system of algebraic equations in the preceding step, $\widetilde{\mathfrak{I}}\mathfrak{\text{'}}s$ values computed and then plugging all the values in trial solutions, final solution of the original system will be achieved.

3. Results and discussion

3.1. The velocity against physical constraints in converging/diverging channel

The governing physical constraints significantly contribute in the fluid behaviour between convergent/divergent channels. In the particular analysis, these are Re, ${\gamma }_{1}$ (parameter due to slippery walls) and $\alpha$ (convergent/divergent parameter). The significant impacts of aforesaid constraints on the velocity $F\left(\eta \right)$ are furnished in Figures 5 and 6 over the feasible region of the channel. The parallel results are plotted for [(Al₂O₃-CuO)/C₂H₆O₂]_hnf and [(Al₂O₃-CuO-Fe₃O₄)/C₂H₆O₂]_mhnf.

Figure 5.

$F\left(\eta \right)$ against (a) Re vary convergent (b) Re vary divergent (c)

$\alpha$ vary convergent (d)

$\alpha$ vary divergent channel.

DownLoad: Full-Size Img PowerPoint

Figure 6.

$F\left(\eta \right)$ against (a)

${\gamma }_{1}$ convergent (b)

${\gamma }_{1}$ divergent channel.

DownLoad: Full-Size Img PowerPoint

(converging case $\alpha = -{5}^{o}$ ) and (diverging case $\alpha = {5}^{o}$ ) reveal the behaviour of [(Al₂O₃-CuO)/C₂H₆O₂]_hnf and [(Al₂O₃-CuO-Fe₃O₄)/C₂H₆O₂]_mhnf by varying $Re$ in convergent and divergent channel, respectively. From , it is examined that the velocity increases by changing $Re$ from 30–180. For [(Al₂O₃-CuO)/C₂H₆O₂]_hnf velocity increases rapidly than [(Al₂O₃-CuO-Fe₃O₄)/C₂H₆O₂]_mhnf. Physical reason behind this behaviour is the densities of both the nanofluids. The addition of Fe₃O₄ in the hybrid nano-additives (Al₂O₃-CuO) enhances the density of [(Al₂O₃-CuO-Fe₃O₄)/C₂H₆O₂]_mhnf due to which intermolecular forces behave dominantly that resists the fluid motion. The high Re contributed in increase in the velocity $F\left(\eta \right)$ in convergent channel.

Physically, the flow rate rises in converging channel and pressure declines due to which the velocity increases because pressure and velocity are in inverse proportion to each other. elaborates the velocity profile in divergent channel against $Re$ within the range variations from 30–180. Physically, flowing area increases in the direction of flow due to divergent channel, the velocity decreases and pressure rises under these circumstances. Therefore, flow rate declines and backflow visualized near the channel walls.

Similarly, Figure 5c and 5d furnishing the behaviour of [(Al₂O₃-CuO)/C₂H₆O₂]_hnf and [(Al₂O₃-CuO-Fe₃O₄)/C₂H₆O₂]_mhnf against varying $\alpha$ . Physically, area decreases in the direction of flow due to convergent channel due to which flow rate become dominant and pressure drops which allow that the fluid particles move faster. On the other hand, decrement in the fluid movement is observed in due to divergent walls ( $\alpha$ positive) because in this direction, flow rate drops and pressure becomes dominant which push the fluid particles along the walls and backflow phenomena occurred.

The influences of ${\gamma }_{1}$ on the velocity of [(Al₂O₃-CuO)/C₂H₆O₂]_hnf and [(Al₂O₃-CuO-Fe₃O₄)/C₂H₆O₂]_mhnf can be visualized in (converging case $\alpha = -{5}^{0}$ ) and (diverging case $\alpha = {5}^{o}$ ). The upturns in the velocity are examined for both convergent and divergent walls. At the walls, the velocity upturns rapidly because the fluid particles move faster due to imposing slip effects at the walls. The profile is sharp at the central line for diverging channel. Physically, flow rate drops and pressure enhances at the central location of the channel which the particles move at maximum velocity along the middle location of the channel.

3.2. The Temperature against physical constraints in converging/diverging channel

The dissipation effects are very helpful for thermal enhancement in the study of nanofluids. Therefore, (converging case $\alpha = -{5}^{o}$ ) and (diverging case $\alpha = {5}^{o}$ ) designed to support the effects of $Ec$ on the temperature of [(Al₂O₃-CuO)/C₂H₆O₂]_hnf and [(Al₂O₃-CuO-Fe₃O₄)/C₂H₆O₂]_mhnf. From the analysis, it is evident that the temperature upsurges by increasing the effects of viscous dissipation. The internal energy of the fluid particles rises due to stronger dissipation effects. However, it is observed that in [(Al₂O₃-CuO-Fe₃O₄)/C₂H₆O₂]_mhnf has high heat transfer mechanism than [(Al₂O₃-CuO)/C₂H₆O₂]_hnf. Physically, tri-hybrid nanoparticles strengthen thermal conductivity of [(Al₂O₃-CuO-Fe₃O₄)/C₂H₆O₂]_mhnf which allow them to store more heat than binary-hybrid nanomaterial in [(Al₂O₃-CuO)/C₂H₆O₂]_hnf. Further, quite rapid increment in the heat transfer is explored in the case of divergent channel.

Figure 7.

$\beta \left(\eta \right)$ via (a) Ec convergent (b) Ec divergent (c)

$\alpha$ convergent (d)

$\alpha$ convergent.

DownLoad: Full-Size Img PowerPoint

The temperature trends in [(Al₂O₃-CuO)/C₂H₆O₂]_hnf and [(Al₂O₃-CuO-Fe₃O₄)/C₂H₆O₂]_mhnf due to opening or narrowing walls in the direction of flow are plotted in Figure 7c and 7d, respectively. It is investigated that for convergent channel the temperature is maximum than in divergent channel. Physically, in convergent channel flow rate rise due to which the frictional force upsurges between the adjacent layers of the fluid and ultimately the fluid temperature rises.

Figure 8 is the clear description of temperature for [(Al₂O₃-CuO)/C₂H₆O₂]_hnf and [(Al₂O₃-CuO-Fe₃O₄)/C₂H₆O₂]_mhnf for different $Re$ and velocity slip constraints ( ${\gamma }_{1}$ ). From these Figures, it is examined that the temperature drops in convergent channel due to increasing $Re$ and ${\gamma }_{1}$ values. However, upsurges in the temperature are noted in divergent channel for $Re$ . The temperature is maximum at the mean position of the channel. Ternary hybrid nanofluid has maximum thermal storage ability due to ultra-high thermal conductance than hybrid nanofluid.

Figure 8.

$\beta \left(\eta \right)$ via (a) Re convergent (b) Re divergent (c)

${\gamma }_{1}$ convergent (d)

${\gamma }_{1}$ divergent.

DownLoad: Full-Size Img PowerPoint

3.3. Thermophysical attributes against volumetric friction

Comparison of effective properties thermal conductivity, density and viscosity against different nanoparticles concentrations is depicted in –. These results indicate that how effective properties change under various nanoparticles concentration for mono, hybrid and ternary nanofluids. Improved thermal conductivity of ternary nanofluid is very high (due to composite thermal conductivity of trinanoparticles) than hybrid followed by simple nanofluids. This property of ternary nanofluid is better for thermal enhancement and make them effective for industrial applications. Similarly, density and viscosity of ternary nanoliquid is dominant over hybrid and common nanofluids. In hybrid nanofluid, ${\phi }_{2}$ varies wheraes; fixed ${\phi }_{1}, {\phi }_{2}$ with changing concentration ${\phi }_{3}$ taken for ternary nanofluid. Therefore, density, viscosity and thermal conductivity of trinanoparticles jointly contribute in thermal enhancement of ternary fluid.

Figure 9. Thermal conductivity via volumetric fraction.

DownLoad: Full-Size Img PowerPoint

Figure 10. Dynamic viscosity via volumetric fraction.

DownLoad: Full-Size Img PowerPoint

Figure 11. Density via volumetric fraction.

DownLoad: Full-Size Img PowerPoint

Further, these results also helpful to predict the concentration factor of nanoparticles to achieve desired amount of heat. The plotted results directly influenced in the fluid motion and temperature of nanofluids and comprehensively discussed in Sections 4.1 and 4.2, respectively.

3.4. Skin friction coefficient

The trends of shear stresses via $Re$ and ${\gamma }_{1}$ are furnished in for convergent and divergent channel. From keen survey of the results, it is examined that shear stresses declines by strengthen $Re$ and slip effects ( ${\gamma }_{1}$ ). However, maximum decrement is noticed for hybrid nanofluid. The study of walls shear stresses would be beneficial for many industrial and technological purposes.

Figure 12. Skin firction via (a) Re convergent (b) Re divergent (c)

${\gamma }_{1}$ convergent (d)

${\gamma }_{1}$ divergent.

DownLoad: Full-Size Img PowerPoint

3.5. Study and code validation

The code and study validation is performed in this section using LSM. The tabulated results () show that the computed results for $-F\text{'}\text{'}\left(0\right)$ when ${\phi }_{i}$ for $i = \mathrm{1, 2}, 3$ and ${\gamma }_{1}$ set as zero are alingned with previously published work. This gives both the study as well as code validation.

Table 6. Present computation and comparison with previously published work for

$-F\text{'}\text{'}\left(0\right)$ .

Converging walls $\alpha =-{5}^{o}$
$Re$	Current LSM results	Turkyilmazoglu ^[29]	Motsa et al. ^[30]
10	1.78455	1.784547	1.784547
30	1.41369	1.413692	1.413692
50	1.12199	1.121989	1.121989
Diverging walls $\alpha ={5}^{o}$
$Re$	Current LSM results	Turkyilmazoglu ^[29]	Motsa et al. ^[30]
20	2.52719	2.527192	2.527192
60	3.94214	3.942140	3.942140
100	5.86917	5.869165	5.869165

| Show Table

DownLoad: CSV

4. Conclusions

The least square analysis of ternary hybrid nanofluid model formulated for slippery converging/diverging channel is conducted and discussed in depth. The core findings of the study are as follows:

● The ternary nanofluid movement declines for diverging case and increasing $Re$ and back flow observed near the walls.

● The slip effects ( ${\gamma }_{1} = \mathrm{0.1, 0.2, 0.3, 0.4, 0.5, 0.6}$ ) on the channel walls are important to increase the velocity of the fluid inside the channel.

● Ternary nanofluid found to be outstanding heat transfer than common hybrid nanofluids and the role composite thermal conductivity of trinanoparticles is significant for this fact.

● In the presence of dissipation effects ( $Ec = \mathrm{0.1, 0.2, 0.3, 0.4, 0.5, 0.6}$ ) significantly boosts the temperature $\beta \left(\eta \right)$ in converging channel and is maximum for ternary nanofluid.

● The comparison of thermophysical properties shown that when ${\phi }_{i}$ for $i = \mathrm{1, 2}, 3$ increases from $1\%$ to $20\%$ then density, thermal conductivity and heat capacity of ternary nanofluid is dominant over simple nano and hybrid nanofluids and is directly proportional to the $\%$ -volume concentration.

● The validity of study performed for various values of $Re = \mathrm{10, 30, 50}$ for converging case ( $\alpha = -{5}^{o}$ ) and $Re = \mathrm{20, 60,100}$ for diverging case ( $\alpha = {5}^{o}$ ) while keeping other physical parameters fixed and found that the study is aligned with existing science literature.

Acknowledgments

The authors would like to thank the Deanship of Scientific Research at Umm Al-Qura University for supporting this work by Grant Code 22UQU4310392DSR31.

Conflict of interest

There is no financial/competing interest regarding to this work.

References

[1]	S. U. S. Choi, J. A. Eastman, Enhancing thermal conductivity of fluids with nanoparticles, ASME, 1995.
[2]	R. R. Sahoo, Experimental study on the viscosity of hybrid nanofluid and development of a new correlation, Heat Mass Transfer, 56 (2020), 3023–3033. https://doi.org/10.1007/s00231-020-02915-9 doi: 10.1007/s00231-020-02915-9
[3]	M. Zayan, A. K. Rasheed, A. John, M. Khalid, A. F. Ismail, Experimental investigation on rheological properties of water based novel ternary hybrid nanofluids, 2021. https://doi.org/10.26434/chemrxiv.13710241
[4]	E. A. Algehyne, H. F. Alrihieli, M. Bilal, A. Saeed, W. Weera, Numerical approach toward ternary hybrid nanofluid flow using variable diffusion and non-Fourier's concept, ACS Omega, 7 (2022), 29380–29390. https://doi.org/10.1021/acsomega.2c03634 doi: 10.1021/acsomega.2c03634
[5]	A. Dezfulizadeh, A. Aghaei, A. H. Joshaghani, M. M. Najafizadeh, An experimental study on dynamic viscosity and thermal conductivity of water-Cu-SiO₂-MWCNT ternary hybrid nanofluid and the development of practical correlations, Powder Technol., 389 (2021), 215–234. https://doi.org/10.1016/j.powtec.2021.05.029 doi: 10.1016/j.powtec.2021.05.029
[6]	S. Alshahrani, N. A. Ahammad, M. Bilal, M. E. Ghoneim, A. Ali, M. F. Yassen, et al., Numerical simulation of ternary nanofluid flow with multiple slip and thermal jump conditions, Front. Energy Res., 2022, 1–9. https://doi.org/10.3389/fenrg.2022.967307 doi: 10.3389/fenrg.2022.967307
[7]	J. S. Goud, P. Srilatha, R. S. V. Kumar, K. T. Kumar, U. Khan, Z. Raizah, et al., Role of ternary hybrid nanofluid in the thermal distribution of a dovetail fin with the internal generation of heat, Case Stud. Therm. Eng., 35 (2022), 102113. https://doi.org/10.1016/j.csite.2022.102113 doi: 10.1016/j.csite.2022.102113
[8]	I. Zahan, R. Nasrin, S. Khatun, Thermal performance of ternary-hybrid nanofluids through a convergent-divergent nozzle using distilled water-ethylene glycol mixtures, Int. Commun. Heat Mass Transfer, 137 (2022), 106254. https://doi.org/10.1016/j.icheatmasstransfer.2022.106254 doi: 10.1016/j.icheatmasstransfer.2022.106254
[9]	M. Sheikhpour, M. Arabi, A. Kasaeian, A. R. Rabei, Z. Taherian, Role of nanofluids in drug delivery and biomedical technology: methods and applications, Nanotechnol. Sci. Appl., 13 (2020), 47–59. https://doi.org/10.2147/NSA.S260374 doi: 10.2147/NSA.S260374
[10]	A. Ahmadian, M. Bilal, M. A. Khan, M. I. Asjad, Numerical analysis of thermal conductive hybrid nanofluid flow over the surface of a wavy spinning disk, Sci. Rep., 10 (2020), 18776. https://doi.org/10.1038/s41598-020-75905-w doi: 10.1038/s41598-020-75905-w
[11]	C. Jin, K. Wang, A. Oppong-Gyebi, J. Hu, Application of nanotechnology in cancer diagnosis and therapy-a mini-review, Int. J. Med. Sci., 17 (2020), 2964–2973. https://doi.org/10.7150/ijms.49801 doi: 10.7150/ijms.49801
[12]	Y. Zhang, M. Li, X. Gao, Y. Chen, T. Liu, Nanotechnology in cancer diagnosis: progress, challenges and opportunities, J. Hematol. Oncol., 12 (2019), 137. https://doi.org/10.1186/s13045-019-0833-3 doi: 10.1186/s13045-019-0833-3
[13]	A. A. Minea, M. G. Moldoveanu, Overview of hybrid nanofluids development and benefits, J. Eng. Thermophys., 27 (2018), 507–514. https://doi.org/10.1134/S1810232818040124 doi: 10.1134/S1810232818040124
[14]	N. A. C. Sidik, I. M. Adamu, M. M. Jamil, G. H. R. Kefayati, R. Mamat, G. Najafi, Recent progress on hybrid nanofluids in heat transfer applications: a comprehensive review, Int. Commun. Heat Mass Transfer, 78 (2016), 68–79. https://doi.org/10.1016/j.icheatmasstransfer.2016.08.019 doi: 10.1016/j.icheatmasstransfer.2016.08.019
[15]	H. Adun, D. Kavaz, M. Dagbasi, Review of ternary hybrid nanofluid: synthesis, stability, thermophysical properties, heat transfer applications, and environmental effects, J. Clean. Prod., 328 (2021), 129525. https://doi.org/10.1016/j.jclepro.2021.129525 doi: 10.1016/j.jclepro.2021.129525
[16]	H. Adun, M. Mukhtar, M. Adedeji, T. Agwa, K. H. Ibrahim, O. Bamisile, et al., Synthesis and application of ternary nanofluid for photovoltaic-thermal system: comparative analysis of energy and exergy performance with single and hybrid nanofluids, Energies, 14 (2021), 4434. https://doi.org/10.3390/en14154434 doi: 10.3390/en14154434
[17]	N. A. S. Muzaidi, M. A. Fikri, K. N. S. W. S. Wong, A. Z. M. Sofi, R. Mamat, N. M. Adenam, et al., Heat absorption properties of CuO/TiO₂/SiO₂ trihybrid nanofluids and its potential future direction towards solar thermal applications, Arab. J. Chem., 14 (2021), 103059. https://doi.org/10.1016/j.arabjc.2021.103059 doi: 10.1016/j.arabjc.2021.103059
[18]	A. I. Ramadhan, W. H. Azmi, R. Mamat, Experimental investigation of thermo-physical properties of tri-hybrid nanoparticles in water-ethylene glycol mixture, Walailak Journal of Science and Technology, 18 (2021), 9335. https://doi.org/10.48048/wjst.2021.9335 doi: 10.48048/wjst.2021.9335
[19]	G. Li, J. Wang, H. Zheng, G. Xie, B. Sundén, Improvement of cooling performance of hybrid nanofluids in a heated pipe applying annular magnets, J. Therm. Anal. Calorim., 147 (2021), 4731–4749. https://doi.org/10.1007/s10973-021-10848-6 doi: 10.1007/s10973-021-10848-6
[20]	N. A. Zainal, R. Nazar, K. Naganthran, I. Pop, MHD flow and heat transfer of hybrid nanofluid over a permeable moving surface in the presence of thermal radiation, Int. J. Numer. Method. Heat Fluid Flow, 31 (2020), 858–879. https://doi.org/10.1108/HFF-03-2020-0126 doi: 10.1108/HFF-03-2020-0126
[21]	S. Masood, M. Farooq, A. Anjum, Influence of heat generation/absorption and stagnation point on polystyrene–TiO₂/H₂O hybrid nanofluid flow, Sci. Rep., 11 (2021), 22381. https://doi.org/10.1038/s41598-021-01747-9 doi: 10.1038/s41598-021-01747-9
[22]	S. Murthy, P. Effiong, C. C. Fei, Metal oxide nanoparticles in biomedical applications, In: Metal oxide powder technologies, Elsevier, 2020,233–251. https://doi.org/10.1016/B978-0-12-817505-7.00011-7
[23]	N. Ahmed, Adnan, U. Khan, S. T. Mohyud-Din, R. Manzoor, Influence of viscous dissipation on a copper oxide nanofluid in an oblique channel: Implementation of the KKL model, Eur. Phys. J. Plus, 132 (2017), 237. https://doi.org/10.1140/epjp/i2017-11504-y doi: 10.1140/epjp/i2017-11504-y
[24]	A. Shahzad, F. Liaqat, Z. Ellahi, M. Sohail, M. Ayub, M. R. Ali, Thin film flow and heat transfer of Cu‑nanofluids with slip and convective boundary condition over a stretching sheet, Sci. Rep., 12 (2022), 14254. https://doi.org/10.1038/s41598-022-18049-3 doi: 10.1038/s41598-022-18049-3
[25]	N. S. Khashi'ie, N. M. Arifin, M. Sheremet, I. Pop, Shape factor effect of radiative Cu-Al₂O₃/H₂O hybrid nanofluid flow towards an EMHD plate, Case Stud. Therm. Eng., 26 (2021), 101199. https://doi.org/10.1016/j.csite.2021.101199 doi: 10.1016/j.csite.2021.101199
[26]	M. Arif, P. Kimam, W. Kumam, Z. Mostafa, Heat transfer analysis of radiator using different shaped nanoparticles water-based ternary hybrid nanofluid with applications: a fractional model, Case Stud. Therm. Eng., 31 (2022), 101837. https://doi.org/10.1016/j.csite.2022.101837 doi: 10.1016/j.csite.2022.101837
[27]	Adnan, U. Khan, N. Ahmed, S. T. Mohyud-Din, D. Baleanu, K. S. Nisar, et al., Second law analysis of magneto radiative GO-MoS₂/H₂O–(CH₂OH)₂ hybrid nanofluid, Comput. Mater. Con., 68 (2021), 213–228. https://doi.org/10.32604/cmc.2021.014383 doi: 10.32604/cmc.2021.014383
[28]	P. Gumber, M. Yaseen, S. K. Rawat, M. Kumar, Heat transfer in micropolar hybrid nanofluid flow past a vertical plate in the presence of thermal radiation and suction/injection effects, Partial Differential Equations in Applied Mathematics, 5 (2022), 100240. https://doi.org/10.1016/j.padiff.2021.100240 doi: 10.1016/j.padiff.2021.100240
[29]	M. Turkyilmazoglu, Extending the traditional Jeffery-Hamel flow to stretchable convergent/divergent channels, Computers & Fluids, 100 (2014), 196–203. https://doi.org/10.1016/j.compfluid.2014.05.016
[30]	S. S. Motsa, P. Sibanda, G. Marewo, On a new analytical method for flow between two inclined walls, Numer. Algor., 61 (2012), 499–514. https://doi.org/10.1007/s11075-012-9545-2 doi: 10.1007/s11075-012-9545-2

This article has been cited by:

1.	Xianqin Li, A. Abbasi, Kamel Al-Khaled, Hawzhen Fateh M.Ameen, Sami Ullah Khan, M. Ijaz Khan, W. Farooq, Ghulam Rasool, Kamel Guedri, Thermal performance of iron oxide and copper (Fe3O4, Cu) in hybrid nanofluid flow of Casson material with Hall current via complex wavy channel, 2023, 289, 09215107, 116250, 10.1016/j.mseb.2022.116250
2.	Mashael M. AlBaidani, Nidhish Kumar Mishra, Mohammad Mahtab Alam, Sayed M. Eldin, Asla A. AL-Zahrani, Ali Akgul, Numerical analysis of magneto-radiated annular fin natural-convective heat transfer performance using advanced ternary nanofluid considering shape factors with heating source, 2023, 44, 2214157X, 102825, 10.1016/j.csite.2023.102825
3.	José Pereira, Ana Moita, António Moreira, Fewer Dimensions for Higher Thermal Performance: A Review on 2D Nanofluids, 2023, 13, 2076-3417, 4070, 10.3390/app13064070
4.	Basim M. Makhdoum, Zafar Mahmood, Umar Khan, Bandar M. Fadhl, Ilyas Khan, Sayed M. Eldin, Impact of suction with nanoparticles aggregation and joule heating on unsteady MHD stagnation point flow of nanofluids over horizontal cylinder, 2023, 24058440, e15012, 10.1016/j.heliyon.2023.e15012
5.	Zafar Mahmood, Umar Khan, S. Saleem, Khadija Rafique, Sayed M. Eldin, Numerical analysis of ternary hybrid nanofluid flow over a stagnation region of stretching/shrinking curved surface with suction and Lorentz force, 2023, 573, 03048853, 170654, 10.1016/j.jmmm.2023.170654
6.	Bilal Ali, Nidhish Kumar Mishra, Khadija Rafique, Sidra Jubair, Zafar Mahmood, Sayed M. Eldin, Mixed convective flow of hybrid nanofluid over a heated stretching disk with zero-mass flux using the modified Buongiorno model, 2023, 72, 11100168, 83, 10.1016/j.aej.2023.03.078
7.	Muhammad Bilal, Ikram Ullah, Mohammad Mahtab Alam, Syed Irfan Shah, Sayed M. Eldin, Energy transfer in Carreau Yasuda liquid influenced by engine oil with Magnetic dipole using tri-hybrid nanoparticles, 2023, 13, 2045-2322, 10.1038/s41598-023-32052-2
8.	Asla A. AL-Zahrani, Ishtiaque Mahmood, Khaleeq ur Rahman, Mutasem Z. Bani-Fwaz, Elsayed Tag-Eldin, Analytical Study of (Ag–Graphene)/Blood Hybrid Nanofluid Influenced by (Platelets-Cylindrical)nanoparticles and Joule Heating via VIM, 2023, 8, 2470-1343, 19926, 10.1021/acsomega.3c01903
9.	Khalid Abdulkhaliq M. Alharbi, Sayed M. Eldin, Ali Akgul, Investigation of Williamson nanofluid in a convectively heated peristaltic channel and magnetic field via method of moments, 2023, 13, 2158-3226, 10.1063/5.0141498
10.	Khalid Abdulkhaliq M Alharbi, Aneesa Nadeem, Sayed M Eldin, Heat transport mechanism in glycerin-titania nanofluid over a permeable slanted surface by considering nanoparticles aggregation and Cattaneo Christov thermal flux, 2023, 106, 0036-8504, 10.1177/00368504231180032
11.	Nidhish Kumar Mishra, Khaleeq ur Rahman, Sayed M. Eldin, Mutasem Z. Bani-Fwaz, Investigation of blood flow characteristics saturated by graphene/CuO hybrid nanoparticles under quadratic radiation using VIM: study for expanding/contracting channel, 2023, 13, 2045-2322, 10.1038/s41598-023-35695-3
12.	Khaleeq ur Rahman, Sami Ullah Khan, Hijaz Ahmad, Thermal Response of Convective-Radiative Stagnation Point Flow Influenced by Advanced Ternary Nanoparticles (Al2O3–Cu–CuO) and Temperature Slip: Study for Elastic Surface, 2024, 14, 2191-1630, 3286, 10.1007/s12668-024-01456-3
13.	Khalid Abdulkhaliq M. Alharbi, Fateh Ali, Sayed M. Eldin, Influence of chemical reaction and thermal convective condition on the heat and mass transport in boundary layer flow over a magneto-radiated wedge with cross diffusion, 2023, 34, 0129-1831, 10.1142/S0129183123501656
14.	Sumaira Fayyaz, Zafar Mahmood, Sami Ullah Khan, Mohammed A. Tashkandi, Lioua Kolsi, Thermal study of single phase nanofluid model using radiative γAl2O3 nanomaterial under Hall current and momentum slip phenomena, 2024, 0958-305X, 10.1177/0958305X241270239
15.	Nidhish Kumar Mishra, Ishtiaque Mahmood, Waseem Abbas, Mutasem Z. Bani‐Fwaz, Sayed M. Eldin, Numerical heat featuring in Blasius/Sakiadis flow of advanced nanofluid under dissipation and convective heat condition effects, 2024, 104, 0044-2267, 10.1002/zamm.202200622
16.	F. M. Allehiany, Muhammad Bilal, Wafa F. Alfwzan, Aatif Ali, Sayed M. Eldin, Numerical solution for the electrically conducting hybrid nanofluid flow between two parallel rotating surfaces subject to thermal radiation, 2023, 13, 2158-3226, 10.1063/5.0154720
17.	Kamel Smida, Muhammad Umer Sohail, Iskander Tlili, Asma Javed, Numerical thermal study of ternary nanofluid influenced by thermal radiation towards convectively heated sinusoidal cylinder, 2023, 9, 24058440, e20057, 10.1016/j.heliyon.2023.e20057
18.	Chetan Kumar, Vashista Ademane, Vasudeva Madav, Experimental study of convective heat transfer distribution of non-interacting wall and perpendicular air jet impingement cooling on flat surface, 2024, 60, 2214157X, 104532, 10.1016/j.csite.2024.104532
19.	Nidhish Kumar Mishra, Muhammed Umer Sohail, Mutasem Z. Bani-Fwaz, Ahmed M. Hassan, Thermal analysis of radiated (aluminum oxide)/water through a magnet based geometry subject to Cattaneo-Christov and Corcione’s Models, 2023, 49, 2214157X, 103390, 10.1016/j.csite.2023.103390
20.	Nidhish Kumar Mishra, Ghulfam Sarfraz, Mutasem Z. Bani-Fwaz, Sayed M. Eldin, Dynamics of Corcione nanoliquid on a convectively radiated surface using Al2O3 nanoparticles, 2023, 148, 1388-6150, 11303, 10.1007/s10973-023-12448-y
21.	Nidhish Kumar Mishra, Khalid Abdulkhaliq M. Alharbi, Khaleeq ur Rahman, Sayed M. Eldin, Mutasem Z. Bani-Fwaz, Investigation of improved heat transport featuring in dissipative ternary nanofluid over a stretched wavy cylinder under thermal slip, 2023, 48, 2214157X, 103130, 10.1016/j.csite.2023.103130
22.	Hamid Qureshi, Amjad Ali Pasha, Zahoor Shah, Muhammad Asif Zahoor Raja, Salem Algarni, Talal Alqahtani, Kashif Irshad, Waqar Azeem Khan, Application of machine learning for thermal exchange of dissipative ternary nanofluid over a stretchable wavy cylinder with thermal slip, 2024, 60, 2214157X, 104599, 10.1016/j.csite.2024.104599
23.	Walid Aich, Hamad Almujibah, Sherzod Shukhratovich Abdullaev, Mutasem Z. Bani-Fwaz, Ahmed M Hassan, Thermal performance of radiated annular extended surface using advanced nanomaterials influenced by various physical controlling parameters for nucleate boiling case, 2023, 51, 2214157X, 103524, 10.1016/j.csite.2023.103524
24.	Nidhish Kumar Mishra, Waqas Ashraf, Ahmed Mir, Lioua Kolsi, Thermal process computing in nanofluid using dissipation and squeezing constraints, 2024, 104, 0044-2267, 10.1002/zamm.202300195
25.	Aneesa Nadeem, Haitham A Mahmoud, Aatif Ali, Sayed M Eldin, Significance of Koo-Kleinstreuer-Li model for thermal enhancement in nanofluid under magnetic field and thermal radiation factors using LSM, 2023, 15, 1687-8132, 10.1177/16878132231206906
26.	Waseem Abbas, Sayed M. Eldin, Mutasem Z. Bani-Fwaz, Numerical investigation of non-transient comparative heat transport mechanism in ternary nanofluid under various physical constraints, 2023, 8, 2473-6988, 15932, 10.3934/math.2023813
27.	Waqas Ashraf, Analysis of heat transfer performance for ternary nanofluid flow in radiated channel under different physical parameters using GFEM, 2023, 146, 18761070, 104887, 10.1016/j.jtice.2023.104887
28.	Tahir Naseem, Azeem Shahzad, Water-based nanofluid flow and heat transfer in thin film over an unsteady stretching sheet: An entropy analysis, 2023, 1040-7782, 1, 10.1080/10407782.2023.2273453
29.	Khalid Abdulkhaliq M. Alharbi, Mutasem Z. Bani-Fwaz, Sayed M. Eldin, Ali Akgul, Thermal management in annular fin using ternary nanomaterials influenced by magneto-radiative phenomenon and natural convection, 2023, 13, 2045-2322, 10.1038/s41598-023-36418-4
30.	Md Insiat Islam Rabby, Md Wasi Uddin, N.M.S. Hassan, Maglub Al Nur, Rokib Uddin, Sadman Istiaque, Md Mirazul Mahmud Abir, Recent progresses in tri-hybrid nanofluids: A comprehensive review on preparation, stability, thermo-hydraulic properties, and applications, 2024, 408, 01677322, 125257, 10.1016/j.molliq.2024.125257
31.	Bilal Ali, Sidra Jubair, Rheological properties of Darcy–Forchheimer hybrid nanofluid flow with thermal emission and heat source over a curved slippery surface, 2023, 97, 0973-7111, 10.1007/s12043-023-02605-1
32.	Mutasem Z Bani-Fwaz, Adnan , Zafar Mahmood, Muhammad Bilal, Adel A EI-Zahhar, Ilyas Khan, Shafiullah Niazai, Computational investigation of thermal process in radiated nanofluid modulation influenced by nanoparticles (Al2O3) and molecular (H2O) diameters, 2024, 11, 2288-5048, 22, 10.1093/jcde/qwae011
33.	Ghulfam Sarfraz, Sami Ullah Khan, Zafar Mahmood, Yasir Khan, Tadesse Walelign, Significance of Hamilton–Crosser’s model for thermal improvement in transient ternary nanofluid problem from multiple physical aspects, 2024, 0217-9849, 10.1142/S0217984925500903
34.	Aneesa Nadeem, Sami Ullah Khan, Muhammad Bilal, Taoufik Saidani, Wasim Jamshed, Thermal augmentation in Darcy Forchheimer media flow using Extended Tiwari-Das model: Solar radiation aspects, 2025, 18, 16878507, 101298, 10.1016/j.jrras.2025.101298
35.	Hamid Qureshi, Amjad Ali Pasha, Muhammad Asif Zahoor Raja, Zahoor Shah, Salem Algarni, Talal Alqahtani, Waqar Azeem Khan, Moinul Haq, Artificial intelligence analysis of thermal energy for convectively heated ternary nanofluid flow in radiated channel considering viscous dissipations aspects, 2025, 62, 22150986, 101955, 10.1016/j.jestch.2025.101955

Reader Comments

Your name:*

Email:*
© 2023 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Mathematics

1.8 3.4

Metrics

Article views(2320) PDF downloads(121) Cited by(35)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

Figures and Tables

Figures(12) / Tables(6)

AIMS Mathematics

Applied heat transfer modeling in conventional hybrid (Al₂O₃-CuO)/C₂H₆O₂ and modified-hybrid nanofluids (Al₂O₃-CuO-Fe₃O₄)/C₂H₆O₂ between slippery channel by using least square method (LSM)

Related Papers:

Abstract

1. Introduction

2. Materials and methods

2.1. Development of the model

2.2. Mathematical analysis

2.2.1. Step 1

2.2.2. Step 2

2.2.3. Step 3

2.2.4. Step 4

2.2.5. Step 5

3. Results and discussion

3.1. The velocity against physical constraints in converging/diverging channel

3.2. The Temperature against physical constraints in converging/diverging channel

3.3. Thermophysical attributes against volumetric friction

3.4. Skin friction coefficient

3.5. Study and code validation

4. Conclusions

Acknowledgments

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Catalog

AIMS Mathematics

Applied heat transfer modeling in conventional hybrid (Al2O3-CuO)/C2H6O2 and modified-hybrid nanofluids (Al2O3-CuO-Fe3O4)/C2H6O2 between slippery channel by using least square method (LSM)

Related Papers:

Abstract

1. Introduction

2. Materials and methods

2.1. Development of the model

2.2. Mathematical analysis

2.2.1. Step 1

2.2.2. Step 2

2.2.3. Step 3

2.2.4. Step 4

2.2.5. Step 5

3. Results and discussion

3.1. The velocity against physical constraints in converging/diverging channel

3.2. The Temperature against physical constraints in converging/diverging channel

3.3. Thermophysical attributes against volumetric friction

3.4. Skin friction coefficient

3.5. Study and code validation

4. Conclusions

Acknowledgments

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog

Applied heat transfer modeling in conventional hybrid (Al₂O₃-CuO)/C₂H₆O₂ and modified-hybrid nanofluids (Al₂O₃-CuO-Fe₃O₄)/C₂H₆O₂ between slippery channel by using least square method (LSM)