Transition and bifurcation analysis for chemotactic systems with double eigenvalue crossings

1.   Introduction

Chemotaxis is an important biological phenomenon, which is generated by two types of mobilities of the species: one is random walking and the other is the chemically directed movement. Several experiments have demonstrated regular patterns formed by bacterial colonies. For example, experiments on bacteria Escherichia coli and Salmonella typhimurium ^[1,2] demonstrated ringlike or sunflower-like patterns when the bacteria were exposed to certain chemicals in both semi-solid and liquid medium. See also ^[3,4].

Many models were put forward by various authors to explain chemically driven movement and resulting patterns, see among others ^[4] and the references therein. We will focus on a so called Keller-Segel model ^[5] describing the chemotactic behaviors of the slime mold amoebae, which ignores the growth rate of amoeba cells, and is suitable for liquid medium experiments. There is already a vast literature on the mathematical studies for the Keller-Segel model; notable works include studies on blow up mechanisms and global boundedness of solutions ^[6,7,8], attractors ^[9], traveling waves ^[10,11]. There are also ample studies regarding bifurcation and pattern formations of the Keller Segel model. See for example ^{[12,13,14,15]} and related articles ^[16,17], where steady state and Hopf bifurcations are studied. In this article, we will focus on dynamic change of orbits (which are called dynamic transition in ^[18]) of Keller Segel models in a rectangular domain. Apart from single eigenvalue crossing case studies in ^[18], this aspect of dynamics have not yet been looked into to the best of our knowledge.

Recently, a new theoretical framework describing instability processes has been put forward by Ma and Wang ^[18]. Their work focuses on dynamic transitions (detailed orbital connection changes during the instability processes). Notably a new classification system for dynamics during the transitions are given. In sum, there are three types. The continuous type transition indicates a gradual change of states, that is, the bifurcated states (involving steady states, periodic orbits or even complex attractors) change continuously from the basic states when instability set place; the jump type transition shows more rapid and abrupt changes; while the mixed transition is a combination of both. Readers are referred to Chapter 2 of ^[18] for more details regarding this classification system, and various theoretical structures built around it. This theory has been especially useful to explain dynamic details of instability processes in various models, including geophysics, biology and statistical mechanics ^{[18,19,20,21,22]}. We note the main tool of Ma and Wang's framework is finite dimension reduction, hence this theory is not limited to odd multiplicity eigenvalue crossings originally studied by Crandall and Rabinowitz ^[23].

In ^[18], two types of Keller-Segel models are addressed using the dynamic transition theory: the first is a model for rich stimulant chemotactic systems (with rich nutrient supplies). The equations become a two-component system in this case, describing the evolution of the population density of biological individuals and the chemoattractant concentration. It is shown that the chemotactic system always undergoes a continuous or jump type dynamic transition from the homogeneous state to steady state solutions. The type of transition is dictated by the sign of a nondimensional parameter $b$. The second is a more general Keller-Segel model where the stimulant is moderately supplied. In this case, the model is a three-component system describing the evolution of population density of biological individuals, the chemoattractant and the stimulant concentration. This system is shown to undergo a dynamic transition to either steady state patterns or spatiotemporal oscillations. In both cases, the transition can be of either continuous or jump type dictated, respectively, by two nondimensional parameters $b_0$ and $b_1$.

However, only transitions that result from simple eigenvalue crossings are investigated in ^[18]. In this article, we focus on the more involved case where the crossing eigenspace is two dimensional, which typically occurs when certain symmetry exists, for example when the container is square shaped. For simplicity, only a rich stimulant system with balanced diffusion and degradation case is investigated. More general systems can be treated similarly, see Remark 3.2. As the result shows, the chemotactic system can undergo both continuous and jump type dynamic transitions from the homogeneous state depending on parameters $\mu$, $\alpha$ associated with diffusion and growth rate and side length $L_1$ and $L_2$. More complex transition structures are seen (see Theorem 3.1) compared to a single eigenvalue crossing case. For instance, when the transition is continuous, eight steady states are bifurcated from the basic state and the orbit connections between them are displayed (orbital connections were seldom looked into in previous studies). However if the transition is of jump type, either four metastable states are bifurcated or no local bifurcations occur, though in the end, the solutions will both undergo a more drastic change. Numeric evidences are provided to support the theoretical findings and deliver more insights. We note our methods can be easily applied to similar problems, or with different domain shapes, as is pointed in Remark 3.3.

The article is arranged as follows. Section 2 introduces the Keller Segel model with rich stimulant and balanced diffusion-degradation. Section 3 calculates the local center manifold function that is necessary for deriving the transition types, and states the main theorem about dynamic transition, with remarks on different equation setups. Section 4 gives a summary of the major results and provides numeric evidence and approximation solution plots to visualize the results.

2.   Keller-Segel models

The non-dimensional form of the Keller-Segel model is given by (as is formulated in ^[18] Chapter 6.4):

Here, the $\Omega$ is written as

$u_1$ indicates the population density of biological individuals, $u_2$ is the chemoattractant concentration, $u_3$ represents the stimulant or nutrient concentration and $\mu$ and $r$ are the relative diffusion rate of the biological species and the stimulant with respect to the chemoattractant. The parameter $\lambda$ indicates the secretion rate of the chemoattractant from the species, $\alpha$ is the relative growth parameter of the species, $\delta$ and $\delta_0$ are related to the interaction between the species and the stimulant.

2.1.   Rich stimulant system

We know that as nutrient $u_3$ is richly supplied, the Keller-Segel model (2.1) is reduced to a two-component system:

It is easy to see that $u^* = (1, \lambda)$ is a steady state of (2.2). Consider the deviation from $u^*$:

and suppressing the primes, the system (2.2) is then transformed into

The global existence and attractors of the above system have been explored in detail in ^[9]. In this article, we focus on an important case where the diffusion and degradation of the chemoattractant secreted by the bacteria themselves are almost balanced by their production. In this case, the second equation of (2.3) is given by

Hence, the equation can be characterized by

where the operators $\mathcal L_\lambda:H_1 \to H$ and $G: H_1 \times \mathbb R \to \mathbb R$ are defined by

Note, the above equation now becomes a nonlocal evoluionary PDE. Here, the two Hilbert spaces $H$ and $H_1$ are defined by

It is then straightforward to see $\mathcal{L}_\lambda$ is a self-adjoint operator with compact resolvant, and $G$ can be viewed as a polynomial from $H_{1/2}\rightarrow H$, where $H_{1/2} = H^1(\Omega)$ is the interpolation space between $H$ and $H_1$, hence the semi-group methods can be used and we view (2.4) as an dynamical system on $H_{1/2}$ (or $H$, with less smooth trajectory).

2.2.   Eigensystem

First, consider the linearized eigenvalue problem of (2.4):

Let $\rho_k$ and $e_k$ be the eigenvalues and eigenfunctions of $-\Delta$ with the Neumann boundary condition given by

for any $k = (k_1, k_2)\in\mathbb N^2$. Here, $\mathbb N$ is the set of all nonnegative integers. In particular, $e_0 = 1$ and $\rho_0 = 0$.

Obviously, the functions in (2.7) are also eigenvectors of (2.6) and the corresponding eigenvalues $\beta_k$ are

Define a critical parameter by

Let

Then, it follows from (2.8) and (2.9) that

3.   Reduction of dynamics and dynamic transitions

The case where $\mathcal S$ contains only one element is considered in detail in ^[18]. Here, in this work, we consider the case when $\mathcal S$ contains exactly two elements. This case is important as it illustrates the dynamics and bifurcation of chemotaxis when certain symmetry exists, for example if the underlying region is square, double eigenvalue crossing is quite generic.

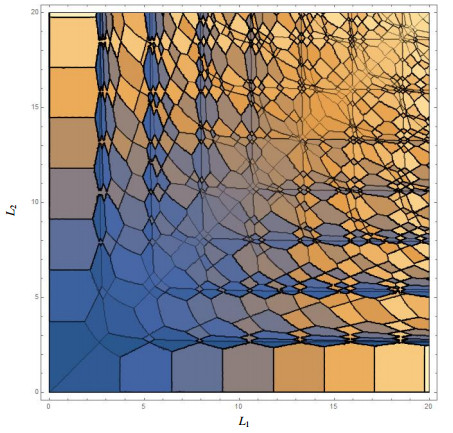
It is straightforward to calculate the critical $\mathcal S$ sets for any particular side length $L_1$ and $L_2$ of the region $\Omega$. Figure 1 is a graph of critical wavenumbers varying $L_1 \text{ and } L_2$, in which boundary lines indicate double eigenvalue crossing. From this graph, it is clear that transitions generated by multiple eigenvalue crossings play increasingly important roles when $L_1$ and $L_2$ are large, where denser boundary lines are seen.

A simple case when $\mathcal S$ contains exactly 2 elements is when $\Omega$ is a small square region with side length $L$

In this case, $\lambda_c$ remains to be the minimum only when $k$ is chosen to be $(0, 1)$ and $(1, 0)$^*.

^*Indeed if we replace $\rho_k$ with $t$, then the RHS of (2.9) will become: $\begin{equation*} \min\limits_t\frac{(t+1)(\mu t+2\alpha)}{t} = \min\limits_t (\mu t+2\alpha t^{-1}+\mu+2\alpha). \end{equation*}$ since the smallest $\rho_k$ is $\rho_{(1, 0)}$ and $\rho_{(0, 1)}$ while the next small one being $\rho_{(1, 1)}$, in order to let the minimum be attained at $\rho_{(1, 0)}$ and $\rho_{(0, 1)}$, the ratio between $\rho_{(1, 0)}$ and $\sqrt{2\mu\alpha}$ must be closer to 1 than that between $\rho_{(1, 1)}$ and $\sqrt{2\mu\alpha}$. Hence the result.

Now denote the eigenfunctions in (2.10) as $\Psi_K$ and we have:

then

3.1.   Reduction analysis

It's known that these eigenfunctions are also an orthogonal basis of $H$. Hence, we have the decomposition:

let $\mathcal{S} = \{K_{01}, K_{02}\}$ and $K_{01} = \{j_{01}, k_{01}\}, K_{02} = \{j_{02}, k_{02}\}$, $j_{01} < j_{02}, k_{01} > k_{02}$. Then, the according to center manifold existence result for parabolic equations, (see for example Chapter 6 of ^[24]), points on center manifold can be rewritten as:

in which $\Phi$ is the center manifold function from the critical two dimensional eigenspace to its orthogonal complement.

Then, (2.4) can be written as: (Using the symmetric property of $\mathcal{L}_\lambda$)

Here, it is evident $\beta_{K_{01}} = \beta_{K_{02}}$ when $\lambda$ is near $\lambda_c$.

It is clear that the linear part of (3.3) is diagonal. Hence, by Thm A.1.1 from Appendix of ^[18],

$P_s$ is the corresponding projection and

we can write $G_2$ as

to make it to be an continuous bilinear operator on $H^1 \times H^1$.

Now, (3.4) can be rearranged as: (note $\mathcal{L}^{-1}$ is invertible in the complement space of the critical eigenspace)

Hence, $\Phi = O(x^2+y^2)$ (in the $H^1$ norm sense). Which yield:

in which default $o$ and $O$ means in $H$ sense.

The general form for $G_2(\Psi_{jk}, \Psi_{j'k'})$ can be calculated:

using easily calculated facts of:

By (2.8), we have the following:

The Eq (3.3) now can be written as:

Eliminate the zero terms (it is not hard to notice all the quadratic terms vanishes), we have the following: (where $c(n_1, n_2) = 9/16$ if none of $n_1, n_2$ is $0$, $c(n_1, n_2) = 3/4$ if only one of $n_1, n_2$ is $0$. $d(n_1, n_2) = 3/4$ if none of $n_1, n_2$ is $0$, $d(n_1, n_2) = 3/2$ if only one of $n_1, n_2$ is $0$.)

The expression for coefficients differs by cases depending on how many indexes of the critical eigenvectors are zero. The calculation is tedious but straightforward and here is a example of one of the coefficients when all $j_{01}, k_{01}, j_{02}, k_{02}$ are nonzero numbers.

which can be simplified as

We will omit the rest terms since all of these coefficients have similar forms.

3.2.   Dynamic transition

To simiplify notation, we rewrite the above reduced equation as follows:

In the following, we will consider a special symmetric case. We assume $L_1 = L_2$, meaning $\Omega$ is a square, and further suppose the critical indexes are $(j_{01}, k_{01})$ and $(k_{01}, j_{01})$ (this is generic when $\Omega$ is a square). Then, we will have $\beta_1 = \beta_2, A = C$ and $B = D$. We notice the square shape set up will bring a certain symmetry to our system, which simplify our analysis below. Indeed, in this situation, symmetry $u_1(x, y)\rightarrow u_1(y, x)$ will bring changes to (3.15) so that $x = y$ and $x = -y$ remain invariant in our system. Hence, the dynamics are determined by (3.17) below.

We first present some results regarding the homogeneous vector field

near $\beta_1 = 0$ in the lemma below. Note, our reduced Eq (3.3) can be written simply as

Hereafter, we let $A = A(0), B = B(0).$ When the critical index is $\{j, 0\}$ with $j\neq 0$, we have $A, B$ with the following formula (the formula for general $\{j, k\}$ involves around 10 to 20 lines of symbolic expression hence is too complicated to be included in this article.)

Lemma 3.1. Suppose $A\neq \pm B$, then for $\beta_1$ sufficiently near $0$, we have the following for the vector field F above:

(1) Point $0$ is nondegenerate for $F$. $F$ has exactly eight straight orbit lines start or end in $0$, which are represented by $x = 0, y = 0, y = x$ and $y = -x$. Each sectorial domain of vector field $F$ separated by these orbit lines must be one of the elliptic, hyperbolic and parabolic regions, and remains the same type for $\beta_1$ sufficiently near $0$. (see ^[18] or Chapter 2.11 Definition 1 of ^[25] for region type definitions.)

(2) For different combinations of signs for $A, A+B$, we have the following Table 1 for the structure of vector field $F$ when $\beta_1$ is near $0$.

Proof. Due the homogeneous nature of vector field $F$, any singular points $(x, y)$ or points on straight orbit lines must satisfy

which is equivalent to $(A-B)xy(x^2-y^2) = 0$, since $A\neq B$, $x = 0$, $y = 0$, $x = y$ and $x = -y$ are four straight orbits for $F$ ($F$ nonzero on these four lines can be derived from $A\neq 0$ and $A+B\neq 0$) and $0$ is consequently nondegenerate for $F$. Then, the remaining statement part 1 of the lemma follow from results regarding nonhyperbolic critical points in $\mathbb{R}^2$, see Chapter 2.11 of ^[25]

The second statement can also be derived by methods similar to Chapter 2 of book ^[18]. To simplify the issue, notice the obvious symmetry of the vector field $F$ around the origin and along the lines of $x = y$ and $x = -y$. Hence, simply determine the type of regions inside two sectors in ${x > 0, -x < y < x}$ is sufficient for our purpose. The types are determined by the sign of $F_2$ for the points $(x, y)$ with $F_1 = 0$. We suppose wlog that $x = 1$, hence correspondingly $-1 < y < 1$ and

then

and the structure inside each sector is determined by the sign of $A-B$. The vector field plot and index is then straightforward by investigating critical points and orbits at infinity using Poincare compactification. □

With this lemma in mind, the dynamic transitions for system (3.3), and the original system (2.4), can be derived in the following theorem, using techniques modified from Section 2.4 of ^[18].

Theorem 3.1. Suppose $\Omega = [0, L]\times[0, L]$ and the PES conditions (2.10) are satisfied for $\mathcal{S} = \{(j_{01}, k_{01}), (k_{01}, j_{01})\}$ with $j_{01}, k_{01}$ being different nonnegative integers and $\lambda_c$ defined by (2.9), then we have the following:

(1) The system (2.4) always undergoes a dynamic transition at $(u_1, \lambda) = (0, \lambda_c)$. Namely, the basis state $u = 0$ is locally (nonlinearly) asymptotically stable for $\lambda < \lambda_c$, and is (nonlinearly) unstable for $\lambda > \lambda_c.$

(2) For the case 1, 3, 4 in Lemma 3.1, the transition is a jump type transition. More specifically, for $\lambda < \lambda_c$, the steady state $0$ of system (2.4) is locally asymptotically stable, and there exists a certain neighborhood $U$ of $O$ in $H$, a $\epsilon > 0$, and a $\delta > 0$, an open and dense set $U_\lambda\subset U$ depending on $\lambda$, such that for any solutions $u_1(t, \phi, \lambda)$ of (2.4), with $\phi\in U_\lambda$ and $\lambda_c < \lambda < \lambda+\epsilon$,

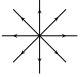
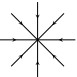
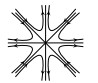
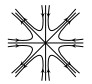
For case 3 and 4, four saddles (or metastable states) are bifurcated from the basic state both when $\lambda > \lambda_c$ and $\lambda < \lambda_c$. For case 3 and 4 the transition structure is shown in figure below:

Case 3: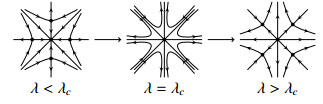

Case 4: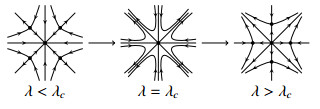

(3) for the case 2 above, the transition is a continuous type transition. More specifically, for $\lambda < \lambda_c$, the steady state $0$ of system (2.4) is locally asymptotically stable, and there exists a certain neighborhood $U$ of $O$ in $H$, a $\epsilon > 0$, an open and dense subset $U_\lambda\subset U$ depending on $\lambda$, such that for solutions $u_1(t, \phi, \lambda)$ of (2.4) with $\phi\in U_\lambda$ and $\lambda_c < \lambda < \lambda+\epsilon$, we have

In fact, there will be eight steady states bifurcated from the basic state when $\lambda > \lambda_c$, four saddles (or metastable states) and four sinks. More specifically, solutions start in $U$ will approach the following four solutions eventually for $\lambda_c < \lambda < \lambda_c+\epsilon$:

and the transition structure is shown in the figure below:

Case 2: (If $A < B$)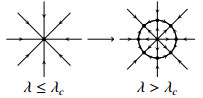

Case 2: (If $A > B$)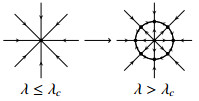

Proof. The first assertion follows from Theorem 5.1.1 & 5.1.3 of Chapter 5 of ^[24], or Theorem 2.1.3 of ^[18]. Let the solution of (3.15) be denoted as $u(t, u_0)$ where $u_0$ is the initial value in a neighbourhood of $0$ in $\mathbb{R}^2$.

Case 1. In this case $A > 0, A+B > 0, A\neq B$ then at $\beta = 0$ there is a neighbourhood $U$ of $0$ containing an open and dense set $\tilde{U}$, where for any $u_0\in\tilde{U}$, we have

thus, by the stability of extended orbits (Theorem 2.1.15 of ^[26]) and the exponential attraction of system orbits by the center manifold, the transition is of jump type. The dynamics for $\lambda < \lambda_c$ is obviously mirrored by case 2 which is discussed below.

Case 2. In this case $A < 0, A+B < 0$. Then $0$ is locally asymptotically stable for system (3.17) at $\beta_1 = 0$, hence by the $S^m$ attractor bifurcation theorem (Theorem 2.2.2 of ^[18]), the steady state $0$ bifurcates to an attractor holomorphic to $S^1$, and the transition type is continuous. Moreover, the system (3.17) is equivalent to the dynamical system without higher order terms in a small neighborhood of the origin. To see this, we first show the eight solutions of the following steady equation persists under higher order perturbations:

where $\beta > 0$ small and $u = \binom{x}{y}$. Now let $u = \sigma\sqrt{\beta}$, we investigate the steady problem with the original equation:

where $\Delta(u, \beta) = o(|u|^3)$ and is of $C^n$ for any $n > 0$ by the smoothness of the center manifold function. It now transforms to

When $\beta\rightarrow 0$,

we then obtain, through the use of implicit function theorem (since we have $\beta^{-\frac{3}{2}}\Delta(\sigma\sqrt{\beta}, \beta)\rightarrow 0$ as $\beta\rightarrow 0$), eight functions $u_i(\beta), i = \{1, 2, \dots, 8\}$ for $0 < \beta\leq \epsilon$, where $\epsilon$ is a fixed number $> 0$ such that $u_i(\beta)$ solves (3.21) and $\beta^{-1/2}u_i\rightarrow \sigma_i$, $\sigma_i$ being the $i$th nonzero solution of $\sigma+F(\sigma, 0) = 0$ hence $u_i(\beta)\rightarrow 0$.

It then remains to show every nonzero solutions that converge to zero must coincide with one of the eight solution curves $u_i$. Suppose $u(\beta)\neq 0$ and $u(\beta)$ satisfies Eq (3.21) and $u(\beta)\rightarrow 0$ when $\beta\rightarrow 0$ then $\sigma = \beta^{-1/2}u$ satisfies (3.22). Hence

$\sigma+F(\sigma, \beta)+o(\sigma^3) = 0$ then shows $\sigma$ is bounded as $\beta\rightarrow 0$, which indicates $\sigma+F(\sigma, 0)\rightarrow 0$, hence $\sigma$ must approach one of $\sigma_i$ (excluding the origin), by uniqueness derived from the implicit function theory, we obtain the persistence of eight steady states of (3.17) under higher order perturbations. The local linear structure of these eight steady states can also be determined by transform (3.17) to

thus, we have four saddles and four sinks, and the sign of $B-A$ determines which is which. Periodic orbits clearly is impossible in this case, hence the bifurcation structure is justified using the Poincare-Bendixson theory in $\mathbb{R}^2$ and Lemma 3.1. The transition is continuous.

Case 3,4. The argument for case 3 and 4 are similar. The proof will be a modification of section 2.4.3 of ^[18]. First, we notice there are four persistent steady states (all are saddles) bifurcated from basic states, the proof is similar to above and is a result of Lemma 3.1. Then, we can infer that apart from the stable manifold of the four orbits, all points will approach a singularity in infinity (using Poincare compactification, and assume higher order perturbation is only local, which clearly does not interfere with our analysis, then the singularities at infinity, four sinks and four sources are stable to perturbations). Then, the phase picture is justified.

Remark 3.1. We note that the persistence of the steady states argument above could be carried over with no issue when the domain is a rectangle, and double eigenvalue crossings take place when $\lambda$ crosses $\lambda_c$ (of course we still need $0$ to be a nondegenerate singular point when $\lambda = \lambda_c$). However, in those cases, the transition structure can lose some of the symmetries outlined in above figures, and elliptic regions (which are filled with homoclinic orbits) might appear, and the transition types are then ambiguous.

Remark 3.2. For the full rich stimulant system (2.2), the eigenvalue analysis has been done in ^[18]. It is shown that the crossing eigenvalues are real and the nonlinear interaction brought about by the center manifold is similar (though more involved) to the above analysis. Moreover the reduced equation still has the form (3.15) while considering double eigenvalue crossing case. Though for the full system (2.1) the transition may include spatial-temporal oscillation, as has already been pointed out in ^[18].

Remark 3.3. It is worth noting here that the Theorem 3.1 can be used on more general domains with double eigenvalue crossings. Disk domains, for example have reduced equations of the same form as in Theorem 3.1 (and this is generic, since the only general single crossings are caused by constant states, which are clearly stable in our model). This can be seen using similar methods dealing with Bessel functions as in ^[22].

4.   Conclusions

In this article, we focus on the dynamic transition of chemotactic systems with double eigenvalue crossings. After performing necessary eigenvalue analysis, we obtain the principles of exchange of stabilities. Thus the system is shown to always exhibit dynamic transition when parameter $\lambda$ increases across a critical threshold. Then, a reduction analysis based on center manifold of the system is done and the bifurcation number $A$ and $B$ is given. It is then shown in Theorem 3.1 that the system (2.4) can undergo both jump and continuous types of transitions depending on the signs of $A$ and $B$. Detailed transition structures are demonstrated.

We note that our analysis leading to Theorem 3.1 can be extended to generic third order systems generated from evolution equations, which constitutes a complement of the second order system treated in Section 2.4 of ^[18]. Third order systems are quite prevalent in reduced parabolic systems, see ^[22,27].

We include several numeric results. In the transition type graph Figure 2, it is clear that all four cases in Lemma 3.1 can occur hence both continuous and jump type transitions are realizable. Note, this implies different jump type transitions (those with metastable states as in case 3 and 4, and those without) can happen.

In Figure 3, we show typical approximate bifurcated states when continuous transition occurs, and the four states in the graph correspond to the four stable bifurcated steady states in orbit plot for case 2 ($A < B$) in Theorem 3.1.

From these results, it is clear the theoretical analysis from the Section 3 is well supported by numeric evidence. Moreover, we list several findings from numerical study which might involve deeper analysis we are yet to explore.

$(1)$ In the transition type graph, it is clear that when $\mu$, or the relative diffusion rate of the biological species $u$ is large enough, the system will always undergoes a continuous transition. This is probably linked to the stabilizing effect brought about by the enhanced mobility of the species.

$(2)$ It is also evident from graph that when $L, \alpha$ is large and $\mu$ is small, the transition types become increasingly unstable with regard to parameter changes. In those parameter regions, the actual transition will resemble transition with multiple ($> 2$) eigenvalue crossings.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The work of H. Pan is supported by National Natural Science Foundation of China (Grant No.12004073), Basic and Applied Basic Research Fund of Guangdong Province of China (Grant No. 2019A1515110711) and Research Fund of Guangdong-Hong Kong-Macao Joint Laboratory for Intelligent Micro-Nano Optoelectronic Technology (No. 2020B1212030010). The work of Y. Mao is supported by the Basic and Applied Basic Research Fund of Guangdong Province of China grant No. 2022A1515110875 and Guangzhou Basic and Applied Basic Research Fund grant No. 2023A04J1329.

Conflict of interest

All authors declare no conflicts of interest in this paper.