Modeling the dynamics of innate and adaptive immune response to Parkinson's disease with immunotherapy

1.   Introduction

Parkinson's disease (PD) is a familiar neurodegenerative disease. The death of dopaminergic neurons that secrete dopamine in the Substantia Nigra pars Compacta (SNc), a brain region, is the primary cause. Also, the autopsies of Parkinson's patients exhibited the presence of Lewy bodies, which are an aggregation of misfolded alpha-synuclein ($\alpha$-syn) protein ^[1,2,3,4,5]. The aggregation of $\alpha$-syn protein within a neuron obstructs the cell's autophagy leading to neuronal death ^[6,7]. As a result, the protein is released into the extracellular surroundings inducing again neuronal loss ^[4,8,9,10]. The pathological $\alpha$-syn acts as a prion-like protein and spreads from cell to cell ^[11,12,13] causing toxic in recipient cells ^[5,7,14,15].

The immune system defends the body from foreign antigens. Microglia are innate immune cells in the central nervous system (CNS) that constantly check the brain's environment ^[16,17] with an immediate non-selective response against viruses ^[18,19]. The activation of microglia leads to the release of anti-inflammatory cytokines to protect and alert neighboring cells ^[20]. Moreover, they act fast to absorb and dispose of misfolded $\alpha$-syn ^[21,22,23] to prevent neurodegeneration. However, activated microglia amid severe inflammation may fail to be regulated, causing damage to healthy neurons ^[20].

Adaptive immune cells are more sophisticated than innate immune cells. It provides more vital protection to the immune system since it develops a memory of antigens when encountered in the future. It is slower than the innate immune cells and takes one to two weeks to confront the antigen. The effector response takes place in two phases: The first phase is antigen recognition, cell preparation, and activation by antigen-specific T and B cells. The second stage is the effector response by activating the T cells and their exit from the lymphatic system to the disease site, alternatively, by releasing antibodies from B cells into the bloodstream. There are two types of T cells: Helper T cells (CD4+), whose function is to recognize antigens and activate the cellular response to remove disease-causing agents and stimulate B cells. The other type is cytotoxic T cells (CD8+), which are responsible for antiviral and antitumor activity ^[18,19]. Lymphatic tissues contain antigen-presenting cells (APCs) whose function is to produce the necessary cytokines for T cells and B cells lymphocyte maintenance ^[18]. They are cells that can break protein into peptides and present them with the major histocompatibility complex (MHC) at the cell surface to interact with the appropriate T cells ^[24]. Mature T cells are activated when the T cell receptor (TCR) recognizes the antigenic peptide complexed with MHC on an APC ^[25].

Microglia cells release pro-inflammatory cytokines when they encounter antigens. The persistent inflammation of the innate immune system causes an increase in the permeability of the blood-brain barrier, whose primary function is to protect the brain environment from any damage. T cells infiltrate the CNS through the blood-brain barrier and release inflammatory cytokines, and neurons eventually die due to the presence of persistent inflammation and a cytotoxic environment. Several studies have confirmed the presence of high levels of T cells in the SNc after death in Parkinson's patients compared to healthy controls ^[18,26].

Immunotherapy is a therapeutic strategy to modulate the immune response to confer neuroprotection in Parkinson's patients by reducing microglia activation, inhibiting pro-inflammatory T cell responses, increasing neuronal support, and removing unfolded protein. There are two types of immunotherapy; the first is active immunization, which offers the patient fragments of the pathogen protein to produce antibodies inside the body to give a long-lasting response due to eliminating the $\alpha$-syn aggregation. The second is passive immunization, where patients are injected with antibodies against the antigen. Active immunization does not require repeated doses; however, passive immunization needs repeated doses ^[15]. An example of active immunization is PD01A, developed by AFFiRiS, which involves delivering a vaccine with a short antigen peptide that mimics a portion of $\alpha$-syn and helps stimulate in vivo antibodies recognize the $\alpha$-syn aggregation and not the monomeric form. Preclinical trials showed decreased $\alpha$-syn scores and improved memory and motor defects. As for passive immunization, PRX002 is the first $\alpha$-syn therapy developed by Prothena. Multiple ascending-dose trials of PRX002 in PD patients have shown a significant reduction of $\alpha$-syn ^[18].

Mathematical models participated in understanding the dynamics of neurodegeneration diseases ^[27,28]. For example, in Alzheimer's disease, Puri and Li ^[29] modeled the interaction between amyloid-$\beta$, neurons, microglia, and astrocytes. They found that activated microglia play a significant role in forming neuropathy. In ^[30], Hao and Friedman used nonlinear partial differential equations to describe the dynamics between neurons, astrocytes, microglia, macrophages, amyloid-$\beta$ aggregation, and hyperphosphorylated tau proteins. They suggested a therapeutic approach to slow the progression of the disease.

For PD models, Kuznetsova and Kuznetsova ^[31] presented a model that explains the aggregation of $\alpha$-syn within a neuron cell. They concluded that deficiency in the degradation mechanisms is the primary cause for $\alpha$-syn accumulation. Moreover, they demonstrated in ^[32], using two models, $\alpha$-syn transmission, active and diffusive, in both healthy and diseased axons. They discovered that $\alpha$-syn aggregation in Lewy bodies appears in diseased axons. In ^[33], Sneppen et al. formed a model describing the connection between $\alpha$-syn aggregation and proteasome activity. They found that $\alpha$-syn aggregation is contained when the ratio between the proteasome and $\alpha$-syn is below a critical level.

The immune system protects the CNS by eliminating any form of toxicity in the brain. The clearance process creates inflammations which result in damaged neurons. The immune system's overactive response may cause neurodegeneration that leads to PD. In ^[34], we discussed the impact of the extracellular $\alpha$-syn on the progression of PD. The model represented the relations between neurons, extracellular $\alpha$-syn, and innate immune response. The model represented the relations between neurons, extracellular $\alpha$-syn, and innate immune response. A reduction in extracellular $\alpha$-syn and a reduction in inflammation induced by activated microglia in the CNS were examined as therapeutic interventions. We found that there is no apparent effect of the latter on delaying neuronal deterioration. Treatments that reduce extracellular $\alpha$-syn, whether alone or in combination with other treatments, preserve neurons and delay Parkinson's disease.

This work investigates the effect of active and passive immunotherapies on delaying the progression of PD. The model includes the immune responses from both the innate and adaptive systems. We model the dynamics between neurons, extracellular $\alpha$-syn, activated microglia, and activated T cells using delay differential equations. Delay differential equations have been used in the literature to model diseases see for example ^[35]. To our knowledge, this is a novel PD model that examines the impact of both active and passive immunotherapies on the dynamics of PD progression. Also, the administering time of the therapies can be explored by using delay differential equations.

The paper is outlined as follows. In Section 2, we formulate the model and present a description of the variables and parameters. The feasible region of the model is demonstrated in Section 3. The stability of the equilibrium points is investigated in Section 4. Finally, Numerical simulations adjacent to parameters analysis are illustrated in Section 5. A brief conclusion is given in Section 6.

2.   Mathematical model

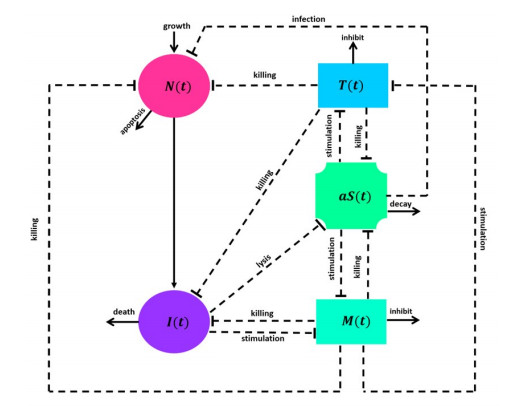
We propose a model describing the dynamics related to the interaction between neurons, extracellular $\alpha$-syn, and innate and adaptive immune cells. The model consists of five compartments: The density of healthy neurons, $N(t)$; the density of infected neurons in the brain, $I(t)$; the density of extracellular $\alpha$-syn, $\alpha S(t)$; the density of the activated microglia, $M(t)$; and the density of the activated T cells, $T(t)$.

We assume that healthy neurons are produced at a rate of $\sigma$ during neurogenesis and die during apoptosis at the rate of $\mu_1$. Extracellular $\alpha$-syn infects healthy neurons at the rate of $\beta$. As a result, healthy neurons move to the infected neuron compartment. $\alpha$-syn accumulates within the infected neurons, causing their death at the rate of $d_1$. During the lysis of the infected neurons, a percentage $e$ of survived $\alpha$-syn wander off into the extracellular. Infected neurons and extracellular $\alpha$-syn in the CNS lead to innate immune response and trigger microglia activation. Consequently, microglia secrete cytokines yielding the death of neurons and extracellular $\alpha$-syn at the rate of $a_1$. The inflammation due to microglia activation increases the permeability of the blood-brain barrier, causing the movement of $\alpha$-syn beyond the CNS. This leads to the response of adaptive immune cells; therefore, T cells are activated. The infiltration of activated T cells propagates inflammation causing the death of neurons and extracellular $\alpha$-syn at the rate of $a_2$. We assume that the activation of microglia and T cells inhibits at the rate of $\mu_{2}$, $\mu_{3}$, respectively.

Inflammation plays a significant role in protecting the CNS; however, at the same time, damage to neurons occurs. The therapeutic approach to PD is to eliminate the excess of $\alpha$-syn from the extracellular space and improve the immune system's tolerance for $\alpha$-syn. Two types of immunotherapies can be delivered to PD patients, active and passive immunization. The active involves immunization with a short antigenic peptide, which imitates $\alpha$-syn. The passive is to deliver anti $\alpha$-syn antibodies to the brain. We embody immunotherapies in the model by assuming that after a time $\tau$, extracellular $\alpha$-syn are eliminated by a percentage of $\epsilon_1$. Accordingly, due to the immunization, the activation of microglia and T cells is inhibited by a percentage of $\epsilon_2$ and $\epsilon_3$, respectively. The model dynamics are depicted in Figure 1.

The model is formulated by the following system of nonlinear delay differential equations where the parameters belong to the interval $(0, 1]$ (see Table 1 for a summary of all the variables and parameters in the model):

The development of the densities in the extracellular $\alpha$-syn, $\tilde{\alpha S}(t, \tau),$ the activated microglia, $\tilde{M}(t, \tau)$ and the activated T cells, $\tilde{T}(t, \tau)$ are described as follows:

Here, we used the same approach as in ^[36] to model the development. Moreover, we express the boundary conditions when $\tau = 0,$ that is, $\tilde{\alpha S}(t, 0)$, $\tilde{M}(t, 0)$ and $\tilde{T}(t, 0)$ in terms of the state variables. By using the method of characteristic coordinates for first order partial differential equations in ^[37], we solve the first order partial differential equations in (2.2). We obtain the following solutions:

Hence, system (2.1) can be rewritten as follows:

3.   Basic analysis

This section demonstrates the well-posedness of model (2.3) by establishing its positivity and boundedness in a feasible region. Also, it explores the model's equilibrium points and their existence criteria and calculates the basic reproduction number using the next-generation method.

Theorem 3.1. If the initial values of model (2.3) are non-negative, $N(0)\geq0$, $I(0)\geq0$, $\alpha S(0)\geq0$, $M(0)\geq0$, and $T(0)\geq0$, then the solutions of the model, $N(t)$, $I(t)$, $\alpha S(t)$, $M(t),$ and $T(t),$ are non-negative for all $t > 0$.

Proof. Let $N(0), \ I(0), \ \alpha S(0), \ M(0)$ and $T(0)$ be non-negative. From system (2.3), we have,

Thus, $N(t)$ and $I(t)$ are non-negative. Similarly,

For $\tau = 0$,

since $\epsilon_{1}\leq 1$. For $\tau > 0$, $\alpha S^{'} \big|_{\alpha S = 0}\geq 0$, since $e^{-(a_{1}+a_{2})\tau} < 1.$ Therefore, $\alpha S$ is non-negative. Applying the same approach, we find,

Hence, the solution $(N(t), I(t), \alpha S(t), M(t), T(t))$ is non-negative for all $t > 0$.

Theorem 3.2. The feasible region of model (2.3),

is positively invariant.

Proof. From the first equation in (2.3), we obtain

Thus,

Integration yields,

Thus, $\lim sup_{t\rightarrow \infty}N(t)\leq \sigma/(a_{1}+a_{2}+\mu_{1})$. Consequently, $I(t)\leq \sigma/(a_{1}+a_{2}+\mu_{1})$, since infected neurons $I$ are a part from the healthy neurons $N$. From the third equation in (2.3), we have

Integration gives,

Therefore, $\lim sup_{t\rightarrow \infty}\alpha S(t)\leq e d_{1}\sigma/[(a_{1}+a_{2}+\mu_{1})(a_1+a_2)]$. Similarly, from the rest of the equations in (2.3), we have

Next, we prove that $\Omega^*$ is a positively invariant set. Let $(N(0), \ I(0), \ \alpha S(0), M(0), \ T(0))$ be in $\Omega^*$, From (2.3), we have

Then

At the boundary,

After simplifying, we get

Hence, the solution $(N(t), I(t), \alpha S(t), M(t), T(t))$ stays in $\Omega^*$. Therefore, $\Omega^*$ is positively invariant.

Equilibrium points of model (2.3) are calculated by equating the right-hand side equations to zero, that is,

At equilibrium, we have

If $\alpha S = 0$, then from (3.3), $I = 0$. Substituting for $\alpha S = I = 0$ in (3.4) and (3.5), we get, $M = T = 0$. Consequently, from (3.1), we obtain, $N^{0} = \sigma/(a_{1}+a_{2}+\mu_{1})$. Hence, the model has a free equilibrium point, $E^{0} = (N^{0}, 0, 0, 0, 0)$, which exists always with no conditions.

Next, we find the basic reproduction number using the free equilibrium point and the next-generation method ^[38]. The infected compartments in model (2.3) are $I$ and $\alpha S$. Let $X = (I, \alpha S)^T$, then Eqs (3.2) and (3.3) can be rewritten as $X' = \mathscr{T}(X)-\mathscr{V}(X)$, where

By evaluating the Jacobian of $\mathscr{T}$ and $\mathscr{V}$ at the free equilibrium point, we have the following matrices $T$ and $V$, respectively:

The inverse of $V$ is

Hence, the next-generation matrix is

The reproduction number is the spectral radius of $K$, that is,

Alternatively,

where $N^{0} = \sigma/(a_{1}+a_{2}+\mu_{1})$.

To find the endemic equilibrium point of the model, that is, $E^{*} = (N^{*}, I^{*}, \alpha S^{*}, M^{*}, T^{*})$, we solve the Eqs (3.1)–(3.5). From Eq (3.1), we obtain

Substituting $N^{*}$ in Eq (3.2), yields

Inserting $I^{*}$ into Eq (3.3), we have

Hence,

Rewriting $\alpha S^{*}$ in terms of $R_{0}$ as

From Eq (3.4), we obtain

Finally, from Eq (3.5), we get

We summarize the results in the following theorem.

Theorem 3.3. Model (2.3) has two equilibrium points:

● Free equilibrium point, $E^{0} = (N^{0}, 0, 0, 0, 0)$ exists always, where $N^{0} = \dfrac{\sigma}{a_{1}+a_{2}+\mu_{1}}$.

● Endemic equilibrium point, $E^* = (N^{*}, I^{*}, \alpha S^{*}, M^{*}, T^{*})$ exists when $R_{0} > 1$, where,

4.   Stability analysis

Using the linearization method for delay differential equations ^[38,39], we examine the local stability of the equilibrium points of model (2.3). For global stability of the free equilibrium point, the theorems of Castillo-Chavez and Song ^[40] are utilized in the same manner as in ^[41].

Theorem 4.1. The free equilibrium point, $E^{0} = (N^0, 0, 0, 0, 0),$ of model (2.3) is locally asymptotically stable if $R_{0} < 0.5(1-\epsilon_{1}e^{-(a_{1}+a_{2})\tau})$.

Proof. First, we prove the stability of $E^0$ for $\tau = 0.$ The Jacobian matrix of model (2.3) evaluated at $E^0$ is:

The characteristic equation, $|\mathrm{J}(E^0)- \lambda \mathrm{I}| = 0$, gives

Thus,

Clearly, $\lambda_{1} = -\mu_{2}$, $\lambda_{2} = -\mu_{3}$ and $\lambda_{3} = -(a_{1}+a_{2}+\mu_{1})$. As for $\lambda_{4, 5}$, they satisfy the equation:

where

All terms of the quadratic equation (4.1) are positive if $R_{0}|_{\tau = 0} < 1$. Hence, the eigenvalues $\lambda_{4, 5}$ are negative. Therefore, for $\tau = 0,$ $E^{0}$ is locally asymptotically stable if $R_{0}|_{\tau = 0} < 1$.

Next, we investigate the stability of $E^0$ for $\tau > 0.$ The Jacobian matrix of model (2.3) evaluated at $E^{0}$ is

where

The characteristic equation for delay differential equations is $|\mathrm{J_{1}}(E^0)+\mathrm{J_{2}}(E^0)e^{-\lambda \tau}- \lambda \mathrm{I}| = 0$. Then

Clearly, $\lambda_{1} = -\mu_{2}$, $\lambda_{2} = -\mu_{3}$ and $\lambda_{3} = a_{1}+a_{2}+\mu_{1}$. For $\lambda_{4, 5}$, they satisfy the equation:

Rewrite (4.3) as:

where

Separate $P(\lambda)$ as:

where

Assume that $\lambda = i w$, where $w\in \mathrm{R}$, Then,

Using Euler's formula, we have

Now,

Let

where $R_{1}, \ R_{2}, \ Q_1$ and $Q_2$ are the real and imaginary parts of $P_{1}$ and $P_{2}$, respectively. Then

Thus,

This equation equals zero if and only if the real and the imaginary parts are zero. Therefore,

By squaring the above two equations, we have

Adding these two equations, we obtain

That is,

Let $u = w^{2}$, then we get

We explore the criteria for Eq (4.5) to have negative roots. If $a^{2}-2b$ and $b^{2}-c^{2}$ are positive, then the roots are negative. Now,

If $R_{0} < 0.5(1-\epsilon_{1}e^{-(a_{1}+a_{2})\tau})$, then $b^{2}-c^{2} > 0.$ Note that $\epsilon_{1}e^{-(a_{1}+a_{2})\tau} < 1$. Thus, The roots of Eq (4.5) are negative if $R_{0} < 0.5(1-\epsilon_{1}e^{-(a_{1}+a_{2})\tau})$. But $w \in \mathrm{R}$, then the eigenvalues $\lambda \neq iw$. Therefore, the eigenvalues do not change their signs to a positive sign when $\tau$ increases and remain negative as they were when $\tau = 0$. Hence, $E^0$ is locally asymptotically stable if $R_{0} < 0.5(1-\epsilon_{1}e^{-(a_{1}+a_{2})\tau}).$

Theorem 4.2. The endemic equilibrium point, $E^{*} = (N^{*}, I^{*}, \alpha S^{*}, M^{*}, T^{*}),$ of model (2.3) is locally asymptotically stable if $R_{0} > \dfrac{2}{(1-\epsilon_{1}e^{-(a_{1}+a_{2})\tau})}$.

Proof. First, we prove the stability of $E^*$ for $\tau = 0.$ The Jacobian matrix of model (2.3) evaluated at $E^*$ is:

The characteristic equation, $|\mathrm{J}(E^*)- \lambda \mathrm{I}| = 0,$ yields

It is easy to see that $\lambda_{1} = -\mu_{2}$ and $\lambda_{2} = -\mu_{3}$. As for $\lambda_{i}$ ($i = 3, 4, 5$), they satisfy the equation:

where,

We can see that $\gamma_2, \ \gamma_1$ and $\gamma_0$ are all positive. Thus, the eigenvalues $\lambda_{3, 4, 5}$ are negative. Hence, for $\tau = 0$, $E^*$ is locally asymptotically stable.

We continue the proof by exploring the stability of $E^*$ for $\tau > 0.$ The Jacobian matrix of model (2.3) evaluated at $E^{*}$ is

where

The characteristic equation is $|\mathrm{J_{1}}(E^*)+\mathrm{J_{2}}(E^*)e^{-\lambda \tau}- \lambda \mathrm{I}| = 0$, we have

We find that $\lambda_{1} = -\mu_{2}$, $\lambda_{2} = -\mu_{3}$ and $\lambda_{i}$ ($i = 3, 4, 5$) satisfy the following equation:

Rewrite (4.8) as

where

Separate $P(\lambda)$ as

where

Assume that $\lambda = i w$, where $w\in \mathrm{R}$. Then,

Using Euler's formula, we get

Now,

Let

Where $R_{1}, \ R_2, Q_1$ and $Q_{2}$ are the real and imaginary parts of $P_{1}$ and $P_{2}$, respectively. Then

Thus,

This equation equals to zero if and only if the real and the imaginary parts are zero. Therefore,

By squaring the above two equations and adding them, we have

That is,

Let $u = w^{2}$, we get

For Eq (4.10) to have negative roots, we must show that $r_{2}^{2}-2 r_{1} > 0, \ r_{1}^{2} -2r_{0} r_{2}-z_{1}^{2} > 0$ and $r_{0}^{2}-z_{0}^{2} > 0.$ First, we start with the coefficient of $u^{2}$,

Thus, $r_{2}^{2}-2 r_{1}$ is positive. Next, we compute $r_{1}^{2}-2r_{0}r_{2}-z_{1}^{2}$,

Thus, the term $r_{1}^{2}-2r_{0}r_{2}-z_{1}^{2}$ is positive if $A$ is positive, where

By using $\beta \alpha S^{*}+a_{1}+a_{2}+\mu_{1} = R_{0}(a_{1}+a_{2}+\mu_{1})$ and $N^{*} = \sigma/R_{0}(a_{1}+a_{2}+\mu_{1})$, we get

Therefore, $A > 0$ if $R_{0} > \dfrac{2(a_{1}+a_{2})}{(1-\epsilon_{1}e^{-(a_{1}+a_{2})\tau})(a_{1}+a_{2}+\mu_{1})}$. Finally,

Thus, $r_{0}^{2}-z_{0}^{2}$ is positive if $R_{0} > \dfrac{2}{(1-\epsilon_{1}e^{-(a_{1}+a_{2})\tau})}.$

Since

then, all coefficient are positive if $R_{0} > \dfrac{2}{(1-\epsilon_{1}e^{-(a_{1}+a_{2})\tau})} = R_0^*.$ Consequently, The roots of Eq (4.10) are negative if $R_{0} > R_0^*$. But $w \in \mathrm{R}$, then the eigenvalues $\lambda \neq iw$. Therefore, the eigenvalues do not change their signs to a positive sign when $\tau$ increases and remain negative as they were when $\tau = 0$. Hence, $E^*$ is locally asymptotically stable if $R_{0} > R_0^*$.

Next, we prove the global stability of the free equilibrium point when $\tau = 0$ by using Castillo-Chavez and Song approach in ^[40]. First, we introduce the following lemma.

Lemma 4.3. Consider a disease model system written in the form:

where $X\in R^m$ denotes the non-disease compartments and $Y\in R^n$ denotes the disease compartments. $U^0 = (X^0, 0)$ denotes the disease free equilibrium of system (4.11). Assuming the conditions (C1) and (C2) below:

${\bf{(C1)}}$ For $\frac{dX}{dt} = F(X, 0), \ X^0$ is globally asymptotically stable,

${\bf{(C2)}}$ $G(X, Y) = AY - \hat G(X, Y)$, with $\hat G(X, Y)\geq 0$ for $(X, Y)\in \Omega$,

where $A = \frac{\partial G}{\partial Y}(X^0, 0)$ has all non-negative off-diagonal elements and $\Omega$ is the region where the model makes biological sense.

If system (4.11) satisfies the above two conditions then the following theorem holds.

Theorem 4.4. The free equilibrium point $E^{0} = (N^{0}, 0, 0, 0, 0)$ of model (2.3) is globally asymptotic stable with respect to $\Omega^*$ if $\mathcal{R}_0 < 1$, $\tau = 0$ and that assumptions (Cl) and (C2) of Lemma 4.3 are satisfied.

Proof. Apply Lemma 4.3 to system (2.3), Consider $X = (N, M, T)^{T}$ and $Y = (I, \alpha S)^{T}$. When $I = \alpha S = 0$, the non-infected subsystem is $X'(t) = F(X, Y),$ which can be rewritten as follows

where $F(X, Y)$ is the right-hand side of the subsystem. Solving the equations, we obtain

where $N(0), \ M(0)$ and $T(0)$ are the initial values. Then $\lim_{t \to \infty}N(t) = \frac{\sigma}{a_{1}+a_{2}+\mu_{1}} = N^{0}$, $\lim_{t \to \infty}M(t) = 0 = M^0$, and $\lim_{t \to \infty}T(t) = 0 = T^0.$ Thus, regardless of the initial values, the non-infected subsystem tends to the free equilibrium point, $X^0 = (N^0, M^0, T^0)$. Hence, the condition (C1) from Lemma 4.3 is satisfied.

Next, we consider the infected subsystem of system (2.3) when $\tau = 0$, that is,

Rewrite the subsystem in (4.12) in matrix form as:

To satisfy the condition (C2), we must express $G(X, Y) = AY - \hat G(X, Y)$ such that $A = \frac{\partial G}{\partial Y}(X^0, 0)$. Now,

Clearly, $A = \frac{\partial G}{\partial Y}(X^0, 0)$ and has non-negative off-diagonal elements. Also, $\tilde{G}(X, Y)\geq 0$ for $(X, Y) \in \Omega^*$ since $N\leq N^0$ in $\Omega^*$. Thus, the condition (C2) in Lemma 4.3 is satisfied. Hence, $E^{0}$ is globally asymptotically stable if $R_{0} < 1$ and $\tau = 0$.

5.   Numerical analysis

The numerical simulations in this section are performed using MATLAB function dde23. First, we illustrate the agreement between the numerical and the qualitative results of model (2.3). Then, sensitivity analysis of the basic reproduction number, $R_0$, is investigated for the model's parameters. Finally, we examine the role of immunotherapies in controlling the progression of PD.

5.1.   Numerical experiments

The qualitative analysis showed that if $R_0 < 1$, the free equilibrium point is stable. If $R_0 > 1$, the endemic equilibrium point exists and is stable. We conduct experiments by solving model (2.3) numerically. The model's parameters are chosen to satisfy the existence and stability conditions. Some parameters are referenced to ^[30], which has similar biological processes and the rest are estimated. Tables 2 and 3 display the parameters values satisfying $R_0 < 1$ and $R_0 > 1$, respectively.

Figure 2 illustrates the time variation of the models' compartments in case $R_0 < 1$ for three different initial histories. We see in the figure that the solution curves tend to the free equilibrium point $E^{0} = (0.0025, 0, 0, 0, 0)$. Similarly, in Figure 3, the solution curves in case $R_0 > 1$ tend to the endemic equilibrium point $E^{*} = (0.0811, 0.0124, 0.0269, 0.1019, 0.0757)$. Hence, the numerical simulations agreed with the qualitative analysis.

5.2.   Sensitivity analysis

The basic reproduction number depends on the models' parameters. Each parameter either increases or decreases the value of $R_0$. We demonstrate the sensitivity of $R_0$ to the parameters in model (2.3) analytically and numerically. Analytically, we evaluate the partial derivative of $R_0$ with respect to one parameter at a time. If the result of the differentiation is positive (negative), then $R_0$ increases (decreases) as the parameter increases. The differentiation of $R_0$ is the following:

From (5.1), we see that the basic reproduction number decreases when the parameters: $\mu_{1}$ and $\epsilon_{1}$ increase. However, it increases when the parameters: $\sigma$, $e$, $\beta$, $\tau$ and $d_{1}$ increase. As for the parameters $a_{1}$ and $a_{2}$, we can not determine the sign of the derivative; however, numerically $R_0$ decreases with increasing $a_{1}$ and $a_{2}$. No change occurs when varying the parameters: $\epsilon_{2}$, $\epsilon_{3}$, $\mu_{2}$ and $\mu_{3}$ since $R_0$ does not depend on them. These results are displayed in Figure 4. In the figure, we numerically graph the dependence of $R_0$ to one parameter at a time. We allow one parameter to vary while fixing the others at a specific value given in Table 3.

Next, we compute the normalized sensitivity index (elasticity) of $R_{0}$ with respect to the models' parameters by using the formula in ^[38]:

where $p$ denotes any parameter. We use the values in Table 3 for the parameters.

Table 4 illustrates the elasticity of $R_{0}$, meaning that a $1\%$ increase in the parameter's value leads to an increase or decrease in the percentage of $R_{0}$. For example, an increase of $1\%$ in $\sigma$, $e$, $\beta$, $d_{1}$ and $\tau$ leads to an increase in $R_{0}$ by $1\%$, $1\%$, $1\%$, $0.2857\%$ and $0.0846\%$, respectively. Whereas, an increase of $1\%$ in $\mu_1, \ a_1, \ a_2,$ and $\epsilon_1$ yield a decrease in $R_0$ by $0.0047, \ 1.0982, \ 1.0982,$ and $0.0423,$ respectively. Also, the table shows that the highest decline in $R_0$ is due to the increase of $a_{1}$ and $a_{2}$. This is expected since these parameters represent the activation of the immune cells to combat the extracellular $\alpha$-syn. The alterations of $R_0$ corresponding to the parameters in Figure 4 are consistent with the sensitivity index in Table 4.

5.3.   Treatment analysis

We incorporated in model (2.3) two immunotherapy approaches for PD, the active and passive immunization. In the active approach, PD patients are vaccinated with a short antigenic peptide imitating $\alpha$-syn to help produce antibodies against extracellular $\alpha$-syn, where the formation of the antibodies needs time. However, in the passive approach, PD patients are vaccinated with antibodies directly. The parameters in the model representing the effect of immunotherapy are $\epsilon_1$, the clearance percentage of extracellular $\alpha$-syn; $\epsilon_2$, the inhibited percentage of activated microglia; and $\epsilon_3$, the inhibited percentage of activated T cells. We assume that these parameters have larger values in passive immunization than in active immunization. This is since the construction of antibodies in active immunization needs time which is not the case in the passive approach. Therefore, we let $\epsilon_1 = 0.6, \ \epsilon_2 = 0.5$, and $\epsilon_3 = 0.5$ in the passive approach. But in the active approach, the parameters take the values: $\epsilon_1 = 0.2, \ \epsilon_2 = 0.15$, and $\epsilon_3 = 0.15$.

First, we examine the effect of active immunization with different administration times. In the model, $\tau$ symbolizes the time delay for the immunization. We assume the time delays are: $10, \ 40,$ and $60$ days. The rest of the parameters in the model are chosen when $R_0 > 1$, the endemic case (see Table 3). Figure 5 illustrates the impact of the active approach with different time delays compared with the no-treatment case ($\epsilon_1 = \epsilon_2 = \epsilon_3 = 0$). Although we see a decline in the size of the compartment $N$ during the beginning period of active immunization, the equilibrium level of $N$ is higher than in the no-treatment case. Moreover, we find that the shorter the time delay for the delivery of active immunization, the highest value of the equilibrium level of $N$. Conversely, the size of the other compartments: $I, \ \alpha S, \ M$, and $T$ elevates at the beginning of active immunization; however, it reaches a lower equilibrium level than in the no-treatment case. Also, the shorter the time delay for administrating active immunization, the lowest value of the equilibrium level of the compartments.

Second, we study the effect of passive immunization with different time delays for vaccine delivery. As previously, we compare the results with the no-treatment case. In Figure 6, we find that the size of compartment $N$ declines but with a higher equilibrium level than in the no-treatment case. However, if the delay of the vaccine is short ($\tau = 10$), no drop is shown in $N$, and neurons are preserved at an equilibrium level. As for the remaining compartments, a rise in their sizes is shown but with a lower equilibrium level than in the no-treatment case. Also, if the vaccine is delivered in a short time delay, $\alpha$-syn declines, and as a result, infected neurons decrease, and the activation of microglia and T cells is inhibited.

Finally, in Figure 7, we compare the two therapeutic approaches with the no-treatment case for two-time delays: $\tau = 10$ and $\tau = 60$. We see that the two immunotherapy approaches impact preserving healthy neurons with different equilibrium levels, which are better than the no-treatment case. However, the best approach is the passive immunization given at an early stage with a short delay. Meanwhile, active immunization with a short delay is far better than passive immunization administered after a long delay. A similar result is shown in the figure for the remaining compartments, where a decrease in their equilibrium levels is the outcome of immunotherapy.

Hence, the analysis shows that passive immunization might be far better than active immunization when both are dispensed with a short delay. However, if passive immunization is delayed for a long time, then active immunization is a good therapy if dispensed with a short delay. This indicates that administering time for immunization is significant in postponing the degeneration of healthy neurons.

We conclude that active and passive immunotherapy affects the progression of PD. If treatment is administered in the early stages of the disease with short time delays, $\alpha$-syn are combated, leading to the inhibition of activated microglia and T cells. Consequently, healthy neurons are maintained. On the contrary, the longer the time offered treatment, the more deteriorated conditions for PD patients.

6.   Conclusions

We built a model to include the innate and adaptive immune responses. The model aimed to investigate the effect of immunotherapy on the progression of Parkinson's disease. Two strategies of immunotherapy were analyzed, the active and passive immunization. The timing of administrating the immunization is crucial. Therefore, the model was formulated using delay differential equations. The qualitative analysis of the model produced two equilibrium points: The free and the endemic equilibrium points. The local stability of the equilibrium points depended on the basic reproduction number, $R_0$. If $R_0$ was less than unity, the free equilibrium point was stable. Conversely, if $R_0$ was greater than unity, the endemic equilibrium point existed and was stable. Numerical experiments were performed with different initial histories to show the agreement with the qualitative results. Moreover, a sensitivity analysis was conducted on $R_0$ to scrutinize the parameters involved in decreasing and increasing the value of $R_0$. We explored the two therapeutic approaches numerically with different time delays. We concluded that active and passive immunotherapy affects the progression of PD. If treatment was administered in the early stages of the disease with short time delays, $\alpha$-syn were combated, leading to the inhibition of activated microglia and T cells. Consequently, healthy neurons were maintained. On the contrary, the longer the time offered treatment, the more deteriorated conditions for PD patients.

For future work, this model can be modified to include in the dynamics two compartments: The resting microglia and the T helper cells. This may describe the dynamics of Parkinson's disease with immunotherapy comprehensively, leading to detailed analysis to reach more meaningful results.

Conflict of interest

The authors declare that there is no conflicts of interest.