Analysis of Covid 19 disease with SIR model and Taylor matrix method

1.   Introduction

The operation of many modern information and measuring systems is associated with the collection and automatic processing of a large amount of measuring data using software and hardware systems equipped with computing machinery. Examples of such systems are a system for transmitting time over long distances using satellites ^[1], a system for comparing remote time scales ^[2], global navigation satellite systems (GNSS) ^[3], software and hardware complexes for determining Earth rotation parameters ^[4], a system of satellite laser rangefinder measurements, radio interferometry with very long baseline radio interferometry, artificial intelligence systems, etc. For example, the data of the system for comparing time scales together with the data collected from GNSS receivers of the International GNSS Service of international network ^[5], is used to solve geodetic and navigation problems ^[6], problems for geometric leveling in gravimetry ^[7] as well as for synchronizing time scales of national laboratories with the Coordinated Universal Time UTC ^[8,9] using GNSS satellites. To increase the accuracy of the final result, it is necessary to detect and remove outliers from measuring data arrays, the source of which is often measuring equipment ^[10], as well as external factors, such as temperature jumps, radio signal re-reflection, atmospheric refraction, etc., when measuring the distance between satellites using laser rangefinders ^[11].

In measurement data processing theory, an outlier is defined sometimes as an observation that is at an abnormal distance from other values in a random sample from a population. In a sense, this definition leaves it up to the analyst (or consensus process) to decide what would be considered abnormal. The uncertainty of this definition is exactly how to isolate anomalous observations from a common data array. An overview of the various approaches together with the classification of outliers is contained in ^[12].

In works ^[13,14] for the first time, the concept of an optimal solution was introduced as a set of measuring data that meets a number of requirements, one of which is to maximize the amount of the set. Data not included in the optimal solution is considered outliers and is removed from post-processing. Articles ^[13,14] shows robust algorithms for finding the optimal solution, in which its approximate value is used for the unknown average appearing in the setting of the problem, which does not always lead to the search for the optimal solution, and, therefore, does not always ensure minimization of the amount of rejected data. Article ^[15] proposes a new formulation of the outlier detection problem, in which an unknown average is considered as an additional parameter to be determined from the condition of minimizing rejected data. The robust algorithm proposed in ^[15] is guaranteed to lead to a solution, if only it exists. An estimate of the complexity of this algorithm, which is proportional to the square of the number of outliers detected, is also provided there. In the case of highly noisy data, when the number of outliers can be comparable to the amount of measured data, the complexity of the algorithm is estimated by a value of the order of N².

The purpose of this article is to develop a fast algorithm for finding the optimal solution with complexity of order NlogN.

2.   Problem setting to find an optimal solution

The results ${y}_{j} = y\left({t}_{j}\right)$ of observations (measurements) of a certain random variable Y(t), formed by measuring devices at moments $\{{t}_{j}{\}}_{j = 1}^{N}$ in time, in many cases can be represented as a one-dimensional time series:

where z is an unknown mean, ${\xi }_{j} = \xi \left({t}_{j}\right)$ is a centered random variable with an unknown distribution. If the measurement data contains a trend that is known a priori or can be approximated by one of the methods (e.g., ^[14,16]), we can come to the series (1) after subtracting the trend from the data.

Most outlier detection methods are based on estimating the standard deviation (SD) of the values of series (1) and comparing it to a predetermined threshold value. An SD estimate is generally performed based on an unbiased variance estimate. However, with a large amount of data, all data can be considered as a general totality, while for z we do not use the estimate as an arithmetic mean; therefore, a biased estimate ${s}_{N} = {\left({N}^{-1}{\sum }_{j = 1}^{N}({y}_{j}-z{)}^{2}\right)}^{1/2}$ can be used when assessing the SD. Both estimations are statistically consistent and can be applied when looking for outliers.

In ^[15], the problem of cleaning the measurement data (1) from outliers with a minimum amount of rejected data was formulated, while an unbiased variance estimate was used for SD. The algorithm proposed there is guaranteed to lead to a solution for the order of $(N + N_\mathrm{out}^2)$ arithmetic operations. Below, we give a modernized version of this algorithm, which allows us to find a solution in the ~$Nlo{g}_{2}N$ of arithmetic operations.

As in ^[15], to search for outliers, we will formulate the problem of finding such a set ${Y}_{L} = \left\{{y}_{{j}_{1}}\text{, ..., }{\mathrm{y}}_{{j}_{L}}\right\}$ of length L, consisting of L numbers of series (1), for which the conditions are met

where ${s}_{{Y}_{L}}$, ${\sigma }_{max}$ are the SD and its associated threshold, respectively; Δ is a parameter defining a threshold for detecting outliers (for example, $\Delta = 3{\sigma }_{max}$); L_min - a specified parameter that limits the length of the desired set from below (for example, L_min = 10); below we consider 1 < L_min < N. Values ${y}_{j}$ that are not included in ${Y}_{L}$ are treated as outliers and removed from further processing.

Often, in the algorithms for finding a solution to the problem (2) – (4), instead of z, an estimate is used in the form of the arithmetic mean of the desired set of numbers ${y}_{{j}_{1}}, ..., {y}_{{j}_{L}}$: $z \approx {L^{ - 1}}\sum\limits_{j \in \left\{ {{j_1}, ..., {j_L}} \right\}} {{y_j}}$. Under the assumption of the stationary and ergodicity of the random process (1), the approximate equality here asymptotically (with L $\to \infty$) goes to the exact one. However, in practice, we always have to deal with a specific series of finite number of measurements. In this case, the true value of z remains unknown and may not coincide with the above estimate, and using it instead of z in the search process may not lead to an optimal solution, but to its approximation, which does not guarantee minimizing the number of detected outliers.

As in ^[15], we will not make any a priori assumptions in this article about either the random process (1) or the nature of the distribution of the random variable ${\xi }_{j}$, as well as apply any estimate for z. We add (see ^[15]) to the conditions (2) – (4) the selection conditions such as below, in which we will consider z as an unknown parameter to be determined along with ${Y_L}$.

Let's introduce a number of designations. With a fixed set ${Y}_{L}$, conditions (2) – (3) are a system of inequalities with respect to z, the solution of which (if it exists) is a bounded subset of the numerical axis that we denote ${Z}_{{Y}_{L}}$. Let us call a set ${Y_L}$, for which $L\ge {L}_{\text{min}}$ and ${Z}_{{Y}_{L}}\ne \varnothing$, a candidate set for solving problems (2) – (6). The SD expressed by equality (2) is a function of z: ${s}_{{Y}_{L}} = {s}_{{Y}_{L}}\left(z\right)$. The minimum of this function on the set $z \in {Z_{{Y_L}}}$ is denoted by ${s_{{Y_L}, \min }}$:

and the value of z, at which this minimum is reached, denote $z_{{Y_L}}^ *$:

Note the following selection conditions (see ^[15]):

1. From all possible candidate sets ${Y_L}$, we will choose the set of the maximum length L (the number of outliers is minimal):

2. Let a maximum of (5) be reached at $L = {\Lambda }$. This means that there is one or more sets ${Y_{\Lambda {\text{, }}{\kern 1pt} 1}}{\text{, }}...{\text{, }}{Y_{\Lambda {\text{, }}{\kern 1pt} n}}$ of length ${\Lambda } \geqslant {L_{{\text{min}}}}$ and their corresponding non-empty sets ${{\text{Z}}_{{Y_{\Lambda {\text{, }}1}}}}{\text{, }}...{\text{, }}{{\text{Z}}_{{Y_{\Lambda {\text{, }}n}}}} \subset$$\mathbb{R}$ such that for each set of ${Y_{{\Lambda, }i}}{\text{, }}i = 1{\text{, }}...{\text{, }}n{\text{, }}$ inequalities (2) – (3) are performed for all $z \in {Z_{{Y_{\Lambda {\text{, }}i}}}}$. From the sets ${Y_{{\Lambda, }i}}$, we will choose the set with the smallest value ${s_{{Y_{{\Lambda, }i}}, \min }}$ (without loss of generality, we assume that such a set is the only one):

A set selected from all candidate sets according to conditions (5) – (6) will just be a solution to the problem (2) to (6). By analogy with ^[13,14,15], let's call it optimal solution.

Definition. For a given sequence of values ${y_j}, {\text{ }}j = 1, \ldots, N,$ a set ${Y_{{\Lambda, \text{opt}}}} = \{ {y_{{j_1}}}{\text{, }}...{\text{, }}{y_{{j_{\Lambda }}}}\}$ satisfying the conditions (2) – (6) is called the optimal solution to the problem (2) – (6). Mean and SD values corresponding to the optimal solution are indicated ${z_{{\text{op}}{\kern 1pt} {\text{t}}}}$ and ${s_{{\text{opt}}}}$:

The values ${y_j}$ of series (1) that are not included in ${Y_{{{\Lambda, \text{opt}}}}}$ are considered outliers.

Thus, the task of cleaning the series (1) from outliers comes down to finding the optimal solution to the problem (2)–(6) and removing numbers from the series (1) that are not part of this solution.

3.   The Structure of the optimal solution

To avoid global enumerating all kinds of sets ${Y_L}$ when searching for the optimal solution, it is necessary to identify such its properties that would make its search quite realistic. Further reasoning relies substantially on the following Statement.

Assertion 1. Let the set ${Y_{{\Lambda, }\; {\text{opt}}}} = \{ {y_{{j_1}}}{\text{, }}...{\text{, }}{y_{{j_\Lambda }}}\}$ be optimal solution for a given sequence of values $\{ {y_j}\}$ and let ${y_{\min }}$ and ${y}_{\text{mах}}$ denote the minimum and maximum numbers of the set $\{ {y_{{j_1}}}{\text{, }}...{\text{, }}{y_{{j_\Lambda }}}\}$:${y_{\min }} = \min \{ {y_{{j_1}}}{\text{, }}...{\text{, }}{y_{{j_{\Lambda }}}}\};$${y}_{\text{mах}} = \text{mах}\left\{{y}_{{j}_{1}}\text{, }\mathrm{...}\text{, }{y}_{{j}_{\text{Λ}}}\right\}.$

Then the interval $({y_{\min }}{\text{, }}{y_{\max }})$ does not contain values ${y_j}$ that are not included in ${Y_{\Lambda, {\text{opt}}}}$.

Proof literally (up to the notation) repeats the proof of the similar Assertion given in ^[15].

Note that the solution to the problem (2) – (6) is not affected by the order of numbers in the series (1). We arrange them in ascending order, so that after renumbering (keeping the previous designations for the numbers of the series (1) and considering them different) inequalities will be fulfilled:

We will arrange all numbers in the optimal solution also in ascending order: ${Y_{{\Lambda, }\; {\text{opt}}}} = \{ {y_{{j_1}}}{\text{, }}...{\text{, }}{y_{{j_\Lambda }}}\}$. By virtue of (9) for indices ${j_1}$, …, ${j_\Lambda }$ holds: ${j_1} < ... < {j_\Lambda }.$ The following statement takes place.

Assertion 2. The ascending set ${j_1}{\text{, }}...{\text{, }}{j_\Lambda }$ of indices in the optimal solution ${Y_{{\Lambda, }\; {\text{opt}}}} = \{ {y_{{j_1}}}{\text{, }}...{\text{, }}{y_{{j_\Lambda }}}\}$ contains all consecutive integers from ${j_1}$ to ${j_\Lambda }$.

Proof directly follows from Assertion 1 (cf. ^[15]).

Thus, the optimal solution is some segment of unknown length Λ of ordered ascending series (1). This allows us, instead of a global enumeration of all possible sets (with a total of ${2^N}$), to look for a solution to the problem (2)–(6) among the sets $\{ {y_k}{\text{, }}...{\text{, }}{y_{k + L - 1}}\}$ consisting of segments of the ordered series (1), varying only two parameters k and L, subject to the conditions ${L_{{\text{min}}}} \leqslant L \leqslant N$ and 1≤k≤N–L+1. The total number of such sets is equal to 0, 5(N–L_min+1) (N–L_min+2).

4.   Auxiliary formulas for implementing the search algorithm

The sets, among which an optimal solution is sought, are uniquely determined by two parameters k and L, where k is the index of the smallest of the numbers in the set and L is the length of the set. Consider one such set corresponding to the pair (k; L), and let us introduce the following notation for it: $Y(k; L) = \{ {y_k}{\text{, }}...{\text{, }}{y_{k + L - 1}}\}$.

Denote by $z\left({k{\text{; }}L} \right)$ the arithmetic mean of the numbers of the set $Y(k; L)$, and by $s\left({k{\text{; }}L} \right)$ the corresponding SD, so that:

It is easy to see that the SD value defined in (2) at $z = z(k{\text{; }}L)$ coincides with $s(k{\text{; }}L)$. Let's transform the expression (2) for SD. Taking into account (10) and (11), we get for SD squared:

In this section, we will give without inference the conditions under which the set $Y(k; L)$ is a candidate for the solutions of the system (2) – (6), i.e. for this set there is a solution in z of the system of inequalities (2) – (3). The derivation of these conditions differs in insignificant details from the similar derivation given in ^[15]. Let's enter the designations:

A necessary condition for the existence of a solution to the system (2) - (3) for a fixed set $Y(k; L)$ is fulfillment of inequalities:

and

Let inequalities (14) and (15) be fulfilled.

One of the four mutually exclusive Cases is possible, which we will give here without explanation (see details in ^[15]).

Case 1. $z\left({k; L} \right) < {z_L}$; ${\left[{{z_L}- z\left({k; L} \right)} \right]^2} \leqslant {\text{σ }}_{\max}^2 - {s^2}\left({k; L} \right)$.

The set $Y(k; L)$ is a candidate for solving to the problem (2) – (6), at this ${s_{Y(k; L), \min }} = {s_{Y(k; L)}}({z^ * })$, ${z^ * } = {z_L}$, where ${s_{Y(k; L)}}(z)$ is calculated by formula (12).

Case 2. ${z_L} \leqslant z\left({k; L} \right) \leqslant {z_R}$.

The set $Y(k; L)$ is a candidate for solving to the problem (2) - (6), at this ${s_{Y(k; L), \min }} = s\left({k{\text{; }}L} \right)$, ${z^ * } = z\left({k{\text{; }}L} \right)$.

Case 3. ${z_R} < z\left({k; L} \right)$ and ${\left[{{z_R}- z\left({k; L} \right)} \right]^2} \leqslant {\text{σ }}_{\max}^2 - {s^2}\left({k; L} \right)$.

The set $Y(k; L)$ is a candidate for solving to the problem (2) – (6), at this ${s_{Y(k; L), \min }} = {s_{Y(k; L)}}({z^ * })$, ${z^ * } = {z_R}$.

Case 4. None of Cases 1–3 is implemented.

The set $Y(k; L)$ is not a candidate for solving to the problem (2) – (6).

Thus, if inequalities (14) and (15) are fulfilled and one of the Cases 1–3 is implemented, then the set $Y(k; L) = \{ {y_k}{\text{, }}...{\text{, }}{y_{k + L - 1}}\}$ is a candidate for solving to the problem (2) – (6), and for it, according to the formulas given for these Cases, both the value ${s_{Y(k; L), \min }}$ of minimum of SD as well as the point z* at which this minimum is reached are determined. In other cases (one of the inequalities (14), (15) is not performed or Case 4 is implemented) the set $Y(k; L)$ is not a candidate for solving to the problem (2) – (6).

To examine the conditions (14), (15), as well as the inequalities specified for Cases 1–3, in order to minimize the number of arithmetic operations, we use recurrent relations similar to the relations in ^[15], which allow us to find z(k; L) and s²(k; L) via z(k; L+1) and s²(k; L + 1) for seven arithmetic operations:

The values ${a_L}$, ${b_L}$, ${c_L}$ in (16), (17) may be calculated in advance as elements of one-dimensional arrays. Similarly, it is possible to calculate the values z (k + 1; L) and s²(k+1; L) if z (k; L) and s²(k; L) are known:

In this case, nine arithmetic operations are required, since the value of the expression ${a}_{L}({y}_{k+L}-{y}_{k})$ is enough to calculate once.

To find a solution to the problem (2) – (6), an algorithm can be used that is practically no different from the algorithm described in ^[15], and is a sequence of steps, on each of which candidate sets are sought among all possible sets of a certain length, starting with the maximum possible length N, and ending with a length at which a candidate will be found.

As mentioned above, the number of arithmetic operations required to find the optimal solution using this algorithm is estimated by the magnitude of the order $(N + N_\text{out}^2)$. The next two Sections describe a fast algorithm for finding a solution to the problem (2) – (6) with complexity of the order $N\; \log{_2}N$. The use of this algorithm becomes preferable compared to the algorithm given in ^[15], in the case where the number of outliers in the data is comparable or exceeds the magnitude of the order ${(N\; \log{_2}N)^{0.5}}$.

5.   Mathematical prerequisites for development of fast algorithm

In this section, we make the necessary preparations to build a fast algorithm for finding outliers. Recall that in this and the following Sections we are dealing with a sequence $\{{y}_{j}{\}}_{j = 1}^{N}$ in ascending order. The following statement is the key when building a fast algorithm.

Assertion 3. For an arbitrary set $Y(k; L + 1) = \{ {y_k}, {y_{k + 1}}, ..., {y_{k + L}}\}$ and any value of z, the inequality is true:

Proof. One of two cases is possible:

a. $2z \leqslant {y_{k + L}} + {y_k}$, $\Rightarrow z - {y_k} \leqslant {y_{k + L}} - z$,

b. $2z > {y_{k + L}} + {y_k}$, $\Rightarrow z - {y_k} > {y_{k + L}} - z$.

Suppose, for example, that case a) occurs. Let's show that in this case the inequality will be fulfilled

Indeed, let us show first that:

Inequalities

and the inequalities corresponding to the case (a) imply:

From these inequalities follows (23). Now we will prove (22). This inequality in expanded form is written as follows:

From here, we get inequality

which is valid because of (23). Hence, the inequality (22) from which the last inequality was derived by equivalent transformations is also true.

Similarly, in the case (b), the inequality $s_{Y(k ; L+1)}^2(z) \geq s_{Y(k+1 ; L)}^2(z)$ is proved, which together with (27) proves Assertion 3.

For a given L, consider N–L+1 ordered sets of length L: $Y(1;L), \; \; Y(2;L), \ldots, Y(N - L + 1;L)$. For each value z, we have N–L+1 corresponding values $s_{Y(1;L)}^2(z)$, $s_{Y(2;L)}^2(z)$, …, $s_{Y(N?L + 1;L)}^2(z)$. We will designate a minimum of them:

The following statement takes place.

Assertion 4. For any z, the sequence $s_{L, \min}^2(z)$ decreases monotonically as L decreases from N to ${L_{{\text{min}}}}$:

Proof. Let's show that for all L = ${L_{{\text{min}}}}$, …, N–1, the inequality $s_{L + 1, \min}^2(z) \geqslant s_{L, \min}^2(z)$ holds. Let k be one of the numbers 1, ..., N–L and $z\in \mathbb{R}$. Consider a set $Y(k; L + 1) = \{ {y_k}, {y_{k + 1}}, ..., {y_{k + L}}\}$ of length L+1. We have:

The first inequality here is true by virtue of Assertion 3, the last one – follows from the definition of $s_{L, \min}^2(z)$ given in (27). Thus, for any k = 1, …, N–L:

Therefore, the inequality will also be fulfilled

which proves Assertion 4.

Assertion 4 implies

Corollary 1. If for some ${L_{\text{0}}}$ and any z the inequality

is fulfilled, then no set $Y(k; L) = \{ {y_k}, {y_{k + 1}}, ..., {y_{k + L - 1}}\}$ of length L ≥ ${L_{\text{0}}}$ can be a solution to problem (2) – (6).

Proof. Let $Y(k; L) = \{ {y_k}, {y_{k + 1}}, ..., {y_{k + L - 1}}\}$ be an arbitrary set of length L ≥ L₀. From Assertion 4, in view of monotonicity of $s_{L, \min}^2(z)$ in L (see (28)), inequalities $s_{L, \min}^2(z) \geqslant s_{{L_0}, \min}^2(z) > \sigma _{\max}^2$ follow for all L≥L₀ and any z. Since inequality $s_{Y(k; L)}^2(z) \geqslant s_{L, \min}^2(z)$ holds for a set $Y(k; L)$ with any z, it follows from previous inequalities that $s_{Y(k; L)}^2(z) > \sigma _{\max}^2$. Thus, the condition (2) for the set $Y(k; L)$ is not met with any z. Therefore, this set cannot be a solution to the problem (2) – (6).

In particular, we come to the next important result. If, for example, an inequality $s_{{L_{\min}}, \min}^2(z) > \sigma _{\max}^2$ takes place for any $z\in \mathbb{R}$, then the problem (2) – (6) has no solution.

In the algorithm described in ^[15], ~${N^2}$ arithmetic operations are required to make sure that there is no solution, since the complexity of this algorithm is estimated by the value of order $N + N_\text{Out}^2$, and if solution does not exist, it should be put here ${N_\text{Out}} = N - {L_{\min }}\;$. Taking into account Assertion 4 and Corollary 1, the solution search procedure can be started by checking the fulfillment of the conditions:

This, as shown below (see Proof of Assertion 7), will require the order of N arithmetic operations. If none of the above inequalities are fulfilled with any z, then the search for a solution must stop, since solution not exists. As a result, only ~ N arithmetic operations are required to ensure that there is no solution to the problem (2) – (6).

6.   Fast outliers search algorithm

This Section describes the main result formulated below (see Assertion 7). Consider a number of supporting statements.

Assertion 5. If at some $z = {z_0}$ a set $Y(k; L + 1) = \{ {y_k}\, ,..., {y_{k + L}}\}$ of length L+1 satisfies conditions (2) and (3). Then at least one of the two sets $\{ {y_k}\, ,..., {y_{k + L - 1}}\}$ or $\{ {y_{k + 1}}\, ,..., {y_{k + L}}\}$ of length L also satisfies (2) and (3) with $z = {z_0}$.

Proof. Indeed, let a set $Y(k; L + 1) = \{ {y_k}\, ,..., {y_{k + L}}\}$ satisfies the conditions of Assertion 5 for $z = {z_0}$. This means that the following inequalities hold

and

Assertion 3 and inequality (30) imply

From this it follows that

This means that at least one of the sets $\{ {y_k}\, ,..., {y_{k + L - 1}}\}$ or $\{ {y_{k + 1}}\, ,..., {y_{k + L}}\}$ of length L satisfies condition (2) with $z = {z_0}$. Condition (3) is also satisfied for each of these two sets, since each of the numbers included in them satisfies the inequality $|{y_j} - {z_0}| \leqslant \Delta$, as follows from (31).

From Assertion 5 we have

Corollary 2. Let the conditions (2) – (3) be met for a set $Y(k; {L_0}) = \{ {y_k}\, ,..., {y_{k + {L_0} - 1}}\}$ of length ${L_0} \geqslant {L_{\min }}$, at some value $z = {z_0}$. Then:

(ⅰ) for any $L = {L_{\min }}, ..., {L_0} - 1$ there exists also a set of length L for which the conditions (2) – (3) are satisfied at $z = {z_0}$;

(ⅱ) the optimal solution ${Y_{\Lambda, \; opt}}$ exists and its length $\Lambda \geqslant {L_0}$.

Proof. Applying Assertion 5 to the set $Y(k; {L_0})$, we get that for at least one of the sets $Y(k; {L_0} - 1)$ or $Y(k + 1;{L_0} - 1)$ of length ${L_0} - 1$, the conditions (2) – (3) with $z = {z_0}$ are also met. Reapplying Assertion 5 to one of these sets, we get that there is a set of length ${L_0} - 2$ for which the conditions (2) – (3) with $z = {z_0}$ are met, etc. Repiting of these reasoning the required number of times proves the validity of statement (ⅰ).

Let us prove (ⅱ). Conditions expressed by Eqs. (5) – (6) are conditions according to which an optimal solution is chosen from all candidate sets, i.e. sets for which inequalities (2) – (3) have solutions for z. From the assumption of Corollary 2, it follows that there is at least one candidate set for solving the problem (2) – (6): this set is $Y(k; {L_0})$. Therefore, the optimal solution ${Y_{\Lambda, \; opt}}$ exists and its length satisfies inequality $\Lambda \geqslant {L_0}$ according to (5).

Corollary 3. If no set of length ${L_0}$ meets the conditions (2) – (3) for any value of z, then:

(ⅰ) no set $Y(k; {L}_{1}) = \{{y}_{k}, ..., {y}_{k+{L}_{1}-1}\}$ of lengths ${L}_{1} > {L}_{0}$ satisfies conditions (2) to (3) for any value of z;

(ⅱ) for an optimal solution ${Y_{\Lambda, \; opt}}$, if it exists, must be fulfilled $\Lambda < {L_0}$.

Proof. Let us prove (ⅰ). Suppose the opposite. Let the Corollary 3 assumptions be fulfilled, but there exists a set $Y(k; {L_1})$ of lengths ${L_1} > {L_0}$ such that conditions (2) – (3) are met for some value of z. Then, according to Corollary 2, for each $L = {L_{\min }}, ..., {L_0}, ..., {L_1}$, including $L = {L_0}$, there is a set of length L, for which conditions (2) – (3) will also be met for $z = {z}_{0}$, which contradicts the assumption made.

The statement (ⅱ) is obvious since the optimal solution is a Λ-length set for which the conditions (2) – (3) are met at some value of z, hence according to (ⅰ), $\Lambda < {L_0}$.

From Corollaries 2 and 3 follows

Assertion 6. The values of L, denoting the lengths of sets for which the solution to the system of inequalities (2) – (3) in z exists, are arranged sequentially on the numerical axis without gaps from ${L_{\min }}$ to some maximum value Λ≤N. Moreover, for any $L > \Lambda$ the system (2) – (3) has no solutions for any z.

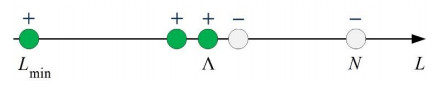
Figure 1 shows a numerical axis in which L values from the interval ${L_{\min }}, ..., N$ are marked with a circle of either green or white. A green circle with the sign "+" on top means that for a given value of L there is a set of length L for which the system of inequalities (2) – (3) with respect to z has a solution. White circle with the sign "–" means that for any of the sets of the corresponding length, the system of inequalities (2) – (3) has no solutions in z.

Our purpose is to prove the following Statement.

Assertion 7. For any (unordered) time series (1), a solution to problem (2) – (6) can be found in no more than ~ Nlog₂N arithmetic operations.

Proof. As is known, ordering the numbers of series (1) requires the ~Nlog₂N arithmetic operations (see, for example, ^[17]). Therefore, to prove the formulated Statement, we consider, as above, that the numbers of series (1) are in ascending order. Let us show that the entire further search will also require ~Nlog₂N arithmetic operations.

We will look for the maximum value of the L = Λ length of sets for which the solution to problem (2) – (6) exists by dividing the ranges of possible L values in half, starting from the range $[{L_{{\text{min}}}}, N]$. To do this, we will consider a sequence of steps, starting from Step 1, in each of which the range of possible values of L decreases by about 2 times. The meaning of the proposed algorithm is to check the existence of solutions not for all values L from the ranges under consideration, but only for their end values.

Step 0. Denote $[N_{Left}^{(0)}, N_{Right}^{(0)}]$– the segment of the numerical axis, where $N_{Left}^{(0)}$ = ${L_{{\text{min}}}}$, $N_{Right}^{(0)}$ = N. At this step, we check: 1) Whether there is a solution of the maximum possible length N, and if not, we check: 2) Whether there is a solution to the problem (2) – (6) at all. Possible cases are presented schematically in Figure 2.

1) The set of maximum length N is all the numbers of the series (1): $\{ {y_1}, ..., {y_N}\}$. We check whether there is a solution to the system (2) – (3) for this set (i.e., whether the conditions (14), (15) are met and one of Cases 1–3 is implemented). If yes, this set is the solution to the problem (2) – (6), since all other requirements (4) – (6) have been met, and the further search is stopped. (This case is shown in Figure 2 a): The value L = N corresponds to the green circle, all other values L < N also correspond to the green circles (see Corollary 2). The values ${z_{{\text{opt}}}}$ and ${{\text{σ }}_{{\text{opt}}}}$ are calculated by formulas corresponding to one of Cases 1–3.) Otherwise

2) We check whether there is a solution to the problem (2) – (6) at all. To do this, consider $N - {L_{\min }} + 1$ sets of minimum length ${L_{{\text{min}}}}$ in the following order:

If, in sequence (33), there is a set for which the system (2) – (3) has a solution (see Figure 2 c)), then this means (see Corollary 2) that the optimal solution to the problem (2) – (6) exists and its length Λ ≥${L_{\min }}$. To find the Λ we go to Step 1 (see below). If no solution to the system (2) – (3) exists for any of the sets of length ${L_{{\text{min}}}}$, then the algorithm terminated. Based on Corollary 3, we conclude that the solution to the problem (2) – (6) does not exist at any L ≥ ${L}_{\text{min}}$ (see Figure 2 b): the value of L = ${L_{{\text{min}}}}$ is marked with a white circle, all other values of L > ${L_{{\text{min}}}}$ also correspond to white circles).

To calculate the values of z(k; L) and s² (k; L) involved in the checks of the fulfillment of conditions (14), (15), as well as for the verification of the fulfillment of Cases 1–3, recurrent formulas (16) – (20) are used in accordance with the diagram shown in Figure 3, which shows only z(k; L).

Let's estimate the number of arithmetic operations in this step. To calculate the values of z(1; N), s²(1; N) by formulas (10), (11) 4N arithmetic operations are required. Transitions in the ↓ direction to calculate the z(1; N–1) and s²(1; N–1), …, z(1; Lmin) and s²(1; Lmin) are performed according to formulas (16) - (18), and in the → direction to calculate values of z(2; Lmin) and s²(2; Lmin), …, z(N–Lmin+1; Lmin) and s²(N–Lmin+1; Lmin) – according to the formulas (19) – (20). Seven arithmetic operations are required for each transition in the ↓ direction and nine in the → direction.

In addition, no more than ten operations are required for each transition in the → direction to check whether conditions of Cases 1, 3 are met. The total number of arithmetic actions in this Step does not exceed the value $4N + 10 + 26\; (N - {L_{\min }}) \leqslant 30N$.

Step 1: Step 1 is the same as Step k described below with k = 1.

…

Step k: At the k-th step, where (k ≥ 1), we consider the segment $[N_{Left}^{(k-1)}, N_{Right}^{(k-1)}]$, at this for $L = N_{Left}^{(k - 1)}$ the solution of the system (2) – (3) exists, but for $L = N_{Right}^{(k - 1)}$- not exists (see Fig. 4).

If $N_{Right}^{(k - 1)} - N_{Left}^{(k - 1)} > 1$, we divide the segment $[N_{Left}^{(k-1)}, N_{Right}^{(k-1)}]$ in half, as a result of which we get two segments: left $[N_{Left}^{(k-1)}, N_{Mid}^{(k-1)}]$ and right $[N_{Mid}^{(k-1)}, N_{Right}^{(k-1)}]$, where $N_{Mid}^{(k - 1)}$ = $N_{Left}^{(k - 1)}$+$\left[{\left({N_{Right}^{(k - 1)} - N_{Left}^{(k - 1)}} \right)/2} \right]$, [·] – denotes the integer part of the number. Next, we check for the existence of solutions to the system (2) – (3) the sets of length L = $N_{Mid}^{(k - 1)}$:

The following two cases are possible, shown schematically in Figure 5.

Case (a). Solution to the system (2) – (3) exists for at least one of the sets (34) (see Figure 5 a): the circle corresponding to the set length $N_{Mid}^{(k - 1)}$ is marked in green). According to Corollary 2 (ⅱ), further search is carried out for values $L \geqslant N_{Mid}^{(k - 1)}$. We set $N_{Left}^{(k)}$ = $N_{Mid}^{(k - 1)}$, $N_{Right}^{(k)}$ = $N_{Right}^{(k - 1)}$ and proceed to Step (k + 1).

Case (b). Solution to the system (2) – (3) does not exist for any of the sets of length L = $N_{Mid}^{(k - 1)}$ (see Figure 5 b): the circle corresponding to the set length of $N_{Mid}^{(k - 1)}$ is marked in white). According to Corollary 3 (ⅱ), further search is carried out for values $L < {N}_{Mid}^{(k-1)}$. We set ${N}_{Left}^{\left(k\right)}$ = $N_{Left}^{(k - 1)}$, $N_{Right}^{(k)}$ = $N_{Mid}^{(k - 1)}$ and proceed to Step (k + 1).

The estimate of the number of operations required to check the sets (34) is similar to the estimate performed in Step 0. In this case, the transitions in the ↓ direction are not taken into account, since the values $z(1, {N}_{Mid}^{(k-1)})$ and ${s}^{2}(1, {N}_{Mid}^{(k-1)})$ are already calculated in Step 0. Given only the transitions in the direction → we get an upper estimate for the number of arithmetic operations in this Step: $24\left(N-{N}_{Mid}^{\left(k-1\right)}\right)+8\le 24N$.

If ${N}_{Right}^{(k-1)}-{N}_{Left}^{(k-1)} = 1$, the maximum length Λ of the set for which solution to the system (2) – (3) exists is equal to $\Lambda = {N}_{Left}^{(k-1)}$. In this case, we come to the final stage of the algorithm: finding all candidate sets of length Λ and choosing the optimal solution from them. To do this, we check each of the sets of length Λ in the sequence:

If there are more than one candidate set, we renumber them in any order: $Y({k_1};\Lambda){\text{, }}...{\text{, }}Y({k_n}; \Lambda)$. Further, for each set, depending on which of Cases 1–3 is implemented, we will determine the points $z_1^ * {\text{, }}...{\text{, }}z_n^ *$ and associated values ${s}_{Y({k}_{1};\Lambda), min}^{2{}_{Y({k}_{n}; \Lambda), min}^{2}}$ of the minima of the squares of the SD using the formulas corresponding to this Case. To provide the condition (6) of the problem, we will choose a set $Y({k_m}; \Lambda)$ for which the values $s_{Y\left(k_1 ; \Lambda\right), \min }^2, \ldots, s_{Y\left(k_n ; \Lambda\right), \min }^2$ is minimal as the optimal solution; the search stops there, at this ${z}_{\text{opt}} = {z}_{m}^{*};$ ${\sigma }_{\text{opt}} = {s}_{Y({k}_{m}; \Lambda), min}$

The number of arithmetic operations required to check the sets (35) does not exceed the 24N value (see above). In addition, in this Step of the algorithm, it is additionally necessary to calculate values $s_{Y({k_1};\Lambda), \min }^2{\text{, }}...{\text{, }}s_{Y({k_n}; \Lambda), \min }^2$. The largest number of calculations will be if the number n of these values​ coincides with the number (N–Λ+1) of the tested sets of length Λ and for each set either Case 1 or Case 3 is implemented. Then, according to formula (12), three arithmetic operations are required to calculate each of said values. Therefore, in total, no more than 3 (N–Λ+1) arithmetic operations are required. Thus, the final estimate for the number of arithmetic operations for the final Step of the algorithm does not exceed 27N. The search process continues until the length of the segment $[N_{Left}^{(k)}, N_{Right}^{(k)}]$ is 1 in one of the algorithm Steps. The number of steps will not exceed log₂N. Indeed, we have:

Applying this inequality recursively k times, we get:

From the inequality (36) it can be seen that if $k = {\log _2}N$ the length of the segment $[N_{Left}^{(k)}, N_{Right}^{(k)}]$ is less than 2, therefore, the algorithm will end in no more than $k = {\log _2}N$ steps.

Since the number of arithmetic operations required at each Step of the algorithm is of order N, the entire search process will require of order Nlog₂N arithmetic operations.

Assertion 7 is proved.

7.   Testing of the proposed algorithm on the Geodetic Satellite "AJISAI" (EGS) Laser ranging data

To check the effectiveness of the proposed Fast algorithm, it was tested on real data obtained by Dr. Igor Yu. Ignatenko when he measured the pseudo-range to the geodetic satellite "AJISAI" (EGS) in 2019 using a laser rangefinder. The measurement results are shown in Figure 6. The time propagation t of the laser beam to and from the satellite in ms is plotted on the vertical axis; the time from the beginning of the day in s is plotted on the horizontal axis.

After finding the polynomial trend through the minimizing set method developed by the author of this article and described in ^[14], and subtracting it from the measurement data, a time series in the format (1) with N = 48282 was obtained, see Figure 7. For the obtained time series of time deviations, an optimal solution was found.

The Table presents the comparative results of the search for the optimal solution obtained using two algorithms proposed earlier by the author in ^[14] and ^[15], as well as the fast algorithm described in this article. Seven variants of the optimal solution search procedure corresponding to different values ${\sigma _{\max}}$ and Δ were carried out. The values of N_out – the number of outliers detected and ${t_{calc}}$ – the calculation time in ms, were obtained in each variant for each of the algorithms.

As one can see from the Table, the optimal solution obtained by the method described in ^[14], in which the unknown average was approximated by the arithmetic mean of the desired numbers, always gives a slightly higher value for the number of outliers detected than the other two of the methods under consideration. As the magnitude of the thresholds ${\sigma _{\max}}$ and Δ decreases, the solutions obtained by the three methods become indistinguishable, with the found N_out values becoming almost the same.

Time cost analysis for each of the algorithms shows an increase in the efficiency of the fast search algorithm proposed in this article. For example, in the seventh calculation, the time cost of finding a solution using the fast algorithm described in the previous Section is almost 180 times less than the time of finding a solution using the algorithm from ^[14], and almost 150 times less than that of using the algorithm described in ^[15].

8.   Conclusions

The developed algorithm is guaranteed to find the optimal solution for time series of noisy data obtained from various types of measuring devices. A characteristic feature of the proposed algorithm is that its implementation is not based on any a priori assumptions about the distribution of random numbers (measurement results) representing the sample, as well as regarding a random process realized. The result of the solution search is not affected by the binding of data to the time axis, or by the length of time intervals between successive measurements. The robust algorithm proposed to find the optimal solution completely eliminates the possibility of unjustified rejection of any part of the data, ensuring the outliers-free solution, if only it exists, with the maximum possible amount of data used in further processing. Unlike previously proposed algorithms for finding the optimal solution, the proposed algorithm requires the order of NlogN arithmetic operations, regardless of the number of outliers detected. The use of this algorithm becomes more preferable than previously proposed ones in the case where the data is highly noisy and the number of outliers contained in it exceeds the order of magnitude ${(N\; \log{_2}N)^{0.5}}$. The algorithm can be effectively applied in information and measuring systems of various types, in control systems, in systems with artificial intelligence, in solving scientific, applied, managerial and other problems in various fields of human activity.

Acknowledgements

The author thanks his colleague Dr. Igor Yu. Ignatenko for providing the results of measurements of satellite pseudo-ranges using laser rangefinders and cooperation.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest.

The author declares no conflict of interest.