Regularity of extended conjugate graphs of finite groups

1.   Introduction

It is evidenced in the literature that one can use conjugacy classes to investigate structures of finite groups, see ^{[1,2,3,4,5,6,8,11,12,14]}, to name a few. In fact, the number of distinct conjugacy classes of a finite group is an important numerical property; it is indeed the number of non-equivalent irreducible representations of that group over the complex numbers. Among other things, the class equation,

where $g_1, g_2, \dots, g_n$ are representatives of the distinct conjugacy classes of $G$ not contained in the center $Z(G)$, is a fundamental tool in studying structures of finite groups and has several applications in mathematics. In ^[1], the authors use the equivalence relation on a finite group $G$ defined by $x\sim y$ if and only if $|{K(x)}| = |{K(y)}|$ for all $x, y\in G$ to study the structure of $G$, where $K(g)$ denotes the conjugacy class of $g$. The set of sizes of equivalence classes with respect to this relation is called the same-size conjugate set of $G$, denoted by $U(G)$. In this article, we focus on the study of finite groups $G$ with $|{U(G)}| = 2$ from a graph-theoretic point of view.

In ^[10], the authors introduce the notion of a conjugate graph associated to a finite non-abelian group. If $G$ is a finite non-abelian group, the conjugate graph of $G$, denoted by $\Gamma_G^c$, is defined as an undirected graph with vertex set $G\setminus Z(G)$ such that two distinct vertices joined by an edge if they are conjugate. They show that several properties of finite groups can be studied via their conjugate graphs. In fact, they prove that if $G$ is a finite group such that $\Gamma_G^c\cong \Gamma_S^c$, then $S\cong G$, where $S$ is a finite non-abelian simple group that satisfies Thompson's conjecture. It turns out that several algebraic properties of finite groups can be expressed via their conjugate graphs with isolated vertices of their centers. Therefore, we extend this definition in a natural way by introducing the notion of an extended conjugate graph. In this work, we show that several properties of finite groups are reflected in their extended conjugate graphs and vice versa. We also show that there is a nice relation between a graph-theoretic property, namely regularity, and an algebraic property, namely nilpotency. We then find out some sufficient conditions and necessary conditions for the non-central part of an extended conjugate graph to be regular. A few concrete examples that illustrate our results are given as well.

2.   Preliminaries

In this section, we collect preliminary results in group theory and graph theory for reference. For basic knowledge of abstract algebra and graph theory, we refer the reader to ^[9] and ^[17], respectively. The list of symbols used throughout this article is given at the end of the article.

Recall that the center of a group $G$ is defined by $Z(G) = \{z\in G\colon zg = gz \text{ for all } g\in G\}$. The centralizer of an element $g\in G$ is defined by $C_{G} (g) = \{x \in G \colon xgx^{-1} = g\}$. For all $a, b\in G$, define $a\mathfrak{c} b$ if and only if $b = hah^{-1}\ \text{for some} \ h\in G$. Then $\mathfrak{c}$ is an equivalence relation on $G$. The equivalence class of $g\in G$ is called the conjugacy class of $g$, which is given by $K(g) = \{xgx^{-1} \colon x \in G \}$.

Theorem 2.1. Let $G_1, G_2, \ldots, G_n$ be groups. For any element $(g_1, g_2, \ldots, g_n)\in \prod\limits_{{i = 1}}^{{n}}G_i$,

Proof. This is a standard result in abstract algebra.

Given a finite group $G$, define $R(G)$ to be the probability that a pair of elements, chosen at random in $G$, will commute with each other (cf. p. 200, ^[15]), that is,

The number $R(G)$ will be referred to as the probability of commutativity in $G$.

Theorem 2.2. (Theorem 1, ^[15])If $G$ is a finite group with $n$ conjugacy classes, then

Let $G$ be a finite group. Let $n_1, n_2, \ldots, n_r$, where $n_1 > n_2 > \cdots > n_r = 1$, be all the numbers each of which is the size of the conjugacy class of some element of $G$. The vector $(n_1, n_2, \ldots, n_r)$ is called the conjugate type vector of $G$. A group $G$ with the conjugate type vector $(n_1, n_2, \ldots, n_r)$ is called a group of conjugate type $(n_1, n_2, \ldots, n_r)$, see p. 17 of ^[14].

Theorem 2.3. (Theorem 1, ^[14])Any group of conjugate type $(n_1, 1)$ is nilpotent.

Recall that an undirected simple graph is regular if every its vertex has the same degree. A graph isomorphism is a bijection between the vertex sets of two graphs that preserves adjacency. A graph isomorphism from a graph $\Gamma$ to itself is called a graph automorphism. A graph $\Gamma$ is vertex-transitive if for each pair of two vertices $u$ and $v$ in $\Gamma$, there exists a graph automorphism $\phi$ of $\Gamma$ such that $\phi(u) = v$.

Theorem 2.4. (p. 221, ^[7])Every complete graph is vertex-transitive.

Theorem 2.5. (Proposition 3.1, ^[16])A graph is vertex-transitive if and only if its components are all vertex-transitive and are pairwise isomorphic.

3.   Main results

In this section, we introduce the definition of an extended conjugate graph associated to a finite group and investigate properties of finite groups via their extended conjugate graphs. In Section 3.1, we indicate that several properties of finite groups are reflected in their extended conjugate graphs and vice versa. In particular, we show that the probability of commutativity in a finite group can be expressed in terms of its extended conjugate graph and give a graph-theoretic proof of the well-known class equation for finite groups. In Section 3.2, we show that there is a remarkable connection between a graph-theoretic property, namely regularity, and an algebraic property, namely nilpotency. We then find out some sufficient conditions and necessary conditions for the non-central part of an extended conjugate graph to be regular. In Section 3.3, we explore extended conjugate graphs associated to groups of order $pq$, $p^3$, and $p^4$, where $p$ and $q$ are distinct primes. We show that a non-abelian group of order $p^3$ always has a regular conjugate graph and that a non-abelian group of order $p^4$ may have a regular or non-regular conjugate graph. We also find their clique and domination numbers.

3.1.   Algebraic properties of finite groups via extended conjugate graphs

Let $G$ be a finite non-abelian group. In ^[10], the authors define the conjugate graph of $G$, denoted by $\Gamma_G^c$, to be an undirected graph with the vertex set $G\setminus Z(G)$ such that two distinct vertices joined by an edge if they are conjugate. It turns out that several algebraic properties of finite groups can be expressed via their conjugate graphs that add isolated vertices of their centers. Therefore, we extend this definition as follows.

Definition 3.1. (Extended conjugate graphs) Let $G$ be a finite group. The extended conjugate graph of $G$, denoted by $\Gamma^e_G$, is defined as an undirected graph with the vertex set $G$ and the edge set $E = \{{\{u, v\}\colon u, v\in G, u\ne v, v = gug^{-1}\ \text{for some}\ g\in G}\}$.

By definition, it is clear that if $G$ is a finite non-abelian group, then the extended conjugate graph of $G$ is the union of the conjugate graph of $G$ and the isolated vertices corresponding to the elements of $Z(G)$. In other words, the conjugate graph of $G$ is simply the subgraph of $\Gamma_G^e$ induced by $G\setminus Z(G)$, that is, $\Gamma_G^c = \Gamma_G^e[G\setminus Z(G)]$. As is well known, $z\in Z(G)$ if and only if $K(z) = \{{z}\}$. Hence, a finite group $G$ is abelian if and only if its extended conjugate graph is the empty graph with $|{Z(G)}|$ vertices. Therefore, it seems reasonable to study the extended conjugate graph of a finite non-abelian group.

Proposition 3.2. Let $G$ and $H$ be finite groups. If $G$ and $H$ are isomorphic as groups, then $\Gamma_G^e$ and $\Gamma_H^e$ are isomorphic as graphs.

Proof. It is not difficult to check that if $\varphi\colon G\to H$ is a group isomorphism, then $\varphi$ is a graph isomorphism from $\Gamma_G^e$ to $\Gamma_H^e$ as well.

Proposition 3.2 indicates that construction of an extended conjugate graph is an invariant of groups: groups that are isomorphic have extended conjugate graphs that are isomorphic. We remark that the converse to Proposition 3.2 is not true; a counterexample will be exhibited in Section 3.3.2.

Let $G$ be a finite group. As usual, the extended conjugate graph of $G$ induces an equivalence relation $\mathfrak{p}$ on $G$: $u\; \mathfrak{p}\; v$ if and only if either $u = v$ or there is a path from $u$ to $v$ in $\Gamma^e_G$. Therefore, $\Xi$ is a component of $\Gamma_G^e$ if and only if there is an equivalence class $C$ determined by $\mathfrak{p}$ such that $\Xi$ is the subgraph of $\Gamma^e_G$ induced by $C$, that is, $\Xi = \Gamma^e_G[C]$. Note that $u\; \mathfrak{p}\; v$ if and only if $u$ and $v$ are in the same component of $\Gamma^e_G$.

Lemma 3.3. Let $G$ be a finite group. For all $u, v \in G$, $u$ and $v$ are conjugate if and only if $u\; \mathfrak{p}\; v$.

Proof. The direct implication is clear. To prove the reverse implication, suppose that $u\ne v$ and that there is a path from $u$ to $v$, say $u = u_0, u_1, \dots, u_n = v$. By definition, there are elements $g_1, g_2, \ldots, g_n\in G$ such that $u_1 = g_1 u_0 g_1^{-1}$, $u_2 = g_2 u_1 g_2^{-1}, \ldots,$ and $u_n = g_n u_{n-1} g_n^{-1}$. Hence, $v = (g_n g_{n-1} \cdots g_1) u (g_n g_{n-1} \cdots g_1)^{-1}$.

Lemma 3.4. Let $G$ be a finite group. Then $\Xi$ is a component of $\Gamma^e_G$ if and only if $\Xi = \Gamma^e_G[C]$ for some conjugacy class $C$ of $G$.

Proof. The lemma follows from Lemma 3.3.

In view of Lemma 3.4, there is a strong relationship between the components of the extended conjugate graph and the conjugacy classes of a finite group. In particular, we have the following theorem.

Theorem 3.5. Let $G$ be a finite group. Then the number of components of the extended conjugate graph of $G$ equals the number of conjugacy classes of $G$.

Proof. The theorem follows from Lemma 3.4.

Corollary 3.6. If $G$ is a finite group, then the number of components of the extended conjugate graph of $G$ equals $\dfrac{1}{|{G}|} \sum\limits_{{g\in G}}^{{}}|{C_G(g)}|$.

Proof. It is a standard result in abstract algebra that the number of conjugacy classes of $G$ is $\dfrac{1}{|{G}|} \sum\limits_{{g\in G}}^{{}}|{C_G(g)}|$.

Recall that $R(G)$ is the probability that a pair of elements of a finite group $G$, chosen at random in $G$, will commute with each other. One nice result shows that $R(G)\leq \frac{5}{8}$ for all finite non-abelian groups $G$ and equality holds if and only if $|{G/Z(G)}| = 4$; see, for instance, Theorem 2 of ^[15]. As a consequence of Theorem 3.5, we obtain a formula that relates a numerical property of finite groups to a graph-theoretic property of their extended conjugate graphs.

Theorem 3.7. If $G$ is a finite group, then

Proof. The theorem follows from Theorems 2.2 and 3.5.

As an immediate consequence of Theorem 3.7, we obtain an upper bound for the number of components of the extended conjugate graph of a finite group $G$ in terms of the order of $G$.

Corollary 3.8. Let $G$ be a finite non-abelian group. Then the number of components of $\Gamma_G^e$ is less than or equal to $\frac{5}{8}|{G}|$ and equality holds if and only if $|{G/Z(G)}| = 4$.

Proof. The corollary follows from Theorem 2 of ^[15] and Theorem 3.7.

The next theorem gives an upper bound for the number of components of the extended conjugate graph of a finite group $G$ in terms of the least prime that divides the order of $G$.

Theorem 3.9. Let $G$ be a finite non-abelian group. If $p$ is the least prime dividing $|{G}|$, then the number of components of $\Gamma_G^e$ is less than or equal to $\dfrac{p^2+p-1}{p^3}|{G}|$. Furthermore, equality holds if and only if $|{G/Z(G)}| = p^2$.

Proof. By Theorem 3 of ^[15], $R(G)\leq \dfrac{p^2+p-1}{p^3}$. By Theorem 3.7, the number of components of $\Gamma_G^e$ is $R(G)|{G}|$. Hence, the number of components of $\Gamma_G^e$ is less than or equal to $\dfrac{p^2+p-1}{p^3}|{G}|$. By Theorem 3 of ^[15], $R(G) = \dfrac{p^2+p-1}{p^3}$ if and only if $|{G/Z(G)}| = p^2$, which completes the proof.

Recall a useful formula in the theory of finite groups: if $G$ is a finite group, then $|{G}| = |{K(g)}||{C_G(g)}|$ for all $g\in G$; see, for instance, Proposition 6 in p. 123 of ^[9]. We express this result via the notion of an extended conjugate graph, as shown in the following proposition.

Proposition 3.10. Let $G$ be a finite group and let $g\in G$. If $\Xi$ is a component of $\Gamma^e_G$ containing vertex $g$, then $V(\Xi) = K(g)$ and $|V(\Xi)| = [G\colon C_G(g)]$.

Proof. By Lemma 3.4, $\Xi = \Gamma_G^e[C]$, where $C$ is a conjugacy class of $G$. Since $g\in V(\Xi)$, we have $g\in C$ and so $C = K(g)$. Hence, $V(\Xi) = C = K(g)$. As mentioned above, $|V(\Xi)| = |K(g)| = \dfrac{|G|}{|C_G(g)|} = [G\colon C_G(g)]$.

It is remarkable that Proposition 3.10 can be utilized to give a graph-theoretic proof of the class equation as follows. Let $G$ be a finite group and consider the extended conjugate graph of $G$. Suppose that $\Theta_1, \Theta_2, \dots, \Theta_m, \Xi_1, \Xi_2, \dots, \Xi_n$ are the distinct components of $\Gamma_G^e$, where $\Theta_i$ has one vertex and $\Xi_j$ has at least two vertices for all $i = 1, 2, \dots, m, j = 1, 2, \dots, n$. Thus, $m = |Z(G)|$. Let $g_j$ be a vertex in $\Xi_j$ for all $j = 1, 2, \dots, n$. Then, by counting the number of vertices of $\Gamma_G^e$,

We clarify the structure of extended conjugate graphs in the following proposition. In fact, the extended conjugate graph of any finite group is a union of complete graphs.

Proposition 3.11. Let $G$ be a finite group. If $\Xi$ is a component of $\Gamma_G^e$, then $\Xi$ is a complete graph.

Proof. Let $a, b\in V(\Xi)$ with $a\ne b$. By Lemma 3.4, $\Xi = \Gamma^e_G[C]$ for some conjugacy class $C$ of $G$. Hence, $a$ and $b$ are conjugate and so there is an edge between $a$ and $b$.

Recall that a subset $C$ of vertices of a graph $\Gamma$ is called a clique if the induced subgraph $\Gamma[C]$ is a complete graph. The maximum cardinality of a clique is called the clique number of $\Gamma$, denoted by $\omega(\Gamma)$. In light of Proposition 3.11, if $g$ and $h$ are not in the same conjugacy class of a finite group $G$, then any subset of $G$ that contains both $g$ and $h$ is never a clique. In fact, $C$ is a clique if and only if $C \subseteq K(g)$ for some $g\in G$. Therefore, by Propositions 3.10 and 3.11, if $G$ is a finite group, then the clique number of the extended conjugate graph of $G$ is given by

The next proposition gives an upper bound for the clique number of the extended conjugate graph of a finite group $G$ in terms of the order of the quotient group $G/Z(G)$.

Proposition 3.12. For any finite group $G$, the clique number of the extended conjugate graph of $G$ is less than or equal to the order of $G/Z(G)$, that is, $\omega(\Gamma_G^e)\leq |{G/Z(G)}|$.

Proof. Let $g\in G$. Since $Z(G)\subseteq C_G(g)$, it follows that $|{Z(G)}|\leq |{C_G(g)}|$. Thus,

Since $g$ is arbitrary, $\omega(\Gamma_G^e)\leq |{G/Z(G)}|$, as required.

Recall that a dominating set for a graph $\Gamma$ is a subset $D$ of $V(\Gamma)$ such that every vertex not in $D$ is adjacent to at least one vertex in $D$. The domination number, denoted by $\gamma(G)$, is defined as the minimum cardinality of a dominating set of $\Gamma$. By Proposition 3.11, every component of an extended conjugate graph is a complete graph. Hence, we obtain the following proposition immediately.

Proposition 3.13. For any finite group $G$, the domination number of the extended conjugate graph of $G$ equals the number of the components of the extended conjugate graph of $G$.

We close this section with the relationship that relates the domination numbers of a finite group $G$, its normal subgroup $N$, and its quotient group $G/N$.

Theorem 3.14. Let $G$ be a finite group and let $N$ be a normal subgroup of $G$. Then

Proof. As proved in ^[11], $k(G)\leq k(G/N)k(N)$. Hence, $\gamma(\Gamma_G^e)\leq \gamma(\Gamma_{G/N}^e)\gamma(\Gamma_N^e)$ because $k(H) = \gamma(\Gamma_H^e)$ for any finite group $H$ by Theorem 3.5 and Proposition 3.13.

3.2.   Regularity of the non-central part of extended conjugate graphs

Observe that if $G$ is a finite non-abelian group, then there are at least two conjugacy classes of $G$ such that one is the singleton $\{{e}\}$ and the other has at least two elements. This implies that the whole extended conjugate graph of $G$ is never regular. Moreover, it is never vertex-transitive by Theorem 2.5. Therefore, it makes sense to restrict attention to regularity and vertex-transitivity of the induced subgraph of $\Gamma_G^e$ by $G\setminus Z(G)$. Throughout the remainder of this article, by the non-central part of the extended conjugate graph of $G$ we mean the induced subgraph $\Gamma_G^e[G\setminus Z(G)]$, which coincides with the conjugate graph of $G$. In this section, we focus on sufficient conditions and necessary conditions for the non-central part of an extended conjugate graph to regular.

Theorem 3.15. Let $G$ be a finite non-abelian group. Then the following statements are equivalent:

(i) the non-central part of the extended conjugate graph of $G$ is a union of $K_m$'s;

(ii) the non-central part of the extended conjugate graph of $G$ is regular;

(iii) the non-central part of the extended conjugate graph of $G$ is vertex-transitive.

Proof. That (i) implies (ii) is trivial. Suppose that the non-central part of $\Gamma_G^e$ is regular. Let $\Xi_1$ and $\Xi_2$ be two components of the non-central part of $\Gamma_G^e$. Pick $u\in V(\Xi_1)$ and $v\in V(\Xi_2)$. By Proposition 3.11, $\Xi_1$ and $\Xi_2$ are complete graphs. Hence, $\deg{u} = |{V(\Xi_1)}|-1$ and $\deg{v} = |{V(\Xi_2)}|-1$. By assumption, $\deg{u} = \deg{v}$ and so $|{V(\Xi_1)}| = |{V(\Xi_2)}|$. By Theorems 2.4 and 2.5, the non-central part of $\Gamma_G^e$ is vertex-transitive. This proves that (ii) implies (iii). Suppose that the non-central part of $\Gamma_G^e$ is vertex-transitive and assume that it is the union of $K_{m_1}, K_{m_2}, \ldots, K_{m_r}$. By Theorem 2.5, $K_{m_i}$ and $K_{m_j}$ must be isomorphic for all $i, j$ and so $m_i = |{V(K_{m_i})}| = |{V(K_{m_j})}| = m_j$ for all $i, j$. This proves that (iii) implies (i).

In ^[14], Itô investigates the structure of finite groups of conjugate type $(n_1, 1)$ from an algebraic point of view. By definition, if $G$ is a finite group of conjugate type $(n_1, 1)$, then $G$ is non-abelian and every conjugacy class not in the center of $G$ has the same size $n_1$. Hence, the non-central part of the extended conjugate graph of $G$ is regular. This allows us to formulate a graph-theoretic version of Itô's result as follows.

Theorem 3.16. Let $G$ be a finite non-abelian group. If the non-central part of the extended conjugate graph of $G$ is regular, then $G$ is nilpotent.

Proof. By Theorem 3.15, the non-central part of $\Gamma_G^e$ is a union of $K_m$'s. This implies that all conjugacy classes not contained in $Z(G)$ have the same size $m$ and so $G$ is of conjugate type $(m, 1)$. By Itô's result (see Theorem 2.3), $G$ is nilpotent.

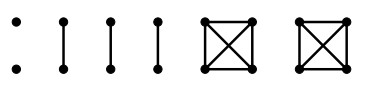
We remark that the converse to Theorem 3.16 is not true. The dihedral group $D_{16}$ is nilpotent since it is a $2$-group. However, the non-central part of the extended conjugate graph of $D_{16}$ is not regular. In fact, it consists precisely of three copies of $K_2$ and two copies of $K_4$, see Figure 1. As a consequence of Theorem 3.16, we obtain a simple condition to confirm the non-regularity of the non-central part of an extended conjugate graph.

Theorem 3.17. If $G$ is a non-trivial finite group having a trivial center, then the non-central part of the extended conjugate graph of $G$ is not regular.

Proof. Suppose that $G\ne\{{e}\}$ and that $Z(G) = \{{e}\}$. Then the upper central series of $G$ never reaches $G$ and so $G$ is not nilpotent. By Theorem 3.16, the non-central part of $\Gamma_G^e$ is not regular.

As an application of Theorem 3.17, the non-central part of the extended conjugate graph of the following group is not regular:

$(1)$ the symmetric group $S_n$ for all $n\geq 3$;

$(2)$ the dihedral group $D_{2n}$ for all odd integers $n\geq 3$;

$(3)$ any non-abelian finite simple group;

$(4)$ any Frobenius group,

because its center is trivial. In particular, we have the following theorem, which states that the regularity of the non-central part of an extended conjugate graph can be used to test non-simplicity of finite non-abelian groups.

Theorem 3.18. Let $G$ be a finite non-abelian group. If the non-central part of the extended conjugate graph of $G$ is regular, then $G$ is not simple.

Proof. We prove the contrapositive. Suppose that $G$ is simple. Then $G\ne\{{e}\}$. Since $G$ is not abelian, $Z(G)\ne G$. By definition, $Z(G) = \{{e}\}$ because $Z(G)\unlhd G$. By Theorem 3.17, the non-central part of $\Gamma_G^e$ is not regular.

Lemma 3.19. Let $G_1, G_2, \ldots, G_n$ be finite groups such that at least one of them is non-abelian and set $J = \left\{ {{{{j}}\colon{{1\leq j\leq n, G_j \; is\; non-abelian}}}} \right\}$. If the non-central part of the extended conjugate graph of $\prod\limits_{{i = 1}}^{{n}}G_i$ is regular, then $|{J}| = 1$ and the non-central part of the extended conjugate graph of $G_j$ with $j\in J$ is regular.

Proof. Note that $\prod\limits_{{i = 1}}^{{n}}G_i$ is not abelian because $J\ne\emptyset$. Denote by $e_k$ the identity of $G_k$ for all $k = 1, 2, \ldots, n$.

We first prove that $|{J}| = 1$. Assume to the contrary that $|{J}| \geq 2$. Thus, we can pick $i, j\in J$ with $i\ne j$ so that $G_i$ and $G_j$ are non-abelian. Let $g\in G_i\setminus Z(G_i)$ and let $h\in G_j\setminus Z(G_j)$. Set

Since $Z\left(\prod\limits_{{i = 1}}^{{n}}G_i\right) = \prod\limits_{{i = 1}}^{{n}}Z(G_i)$, $x$ and $xy$ do not lie in $Z\left(\prod\limits_{{i = 1}}^{{n}}G_i\right)$. Using Theorem 2.1, we obtain that $|{K(x)}| = |{K(g)}|$ and $|{K(xy)}| = |{K(g)}||{K(h)}|$. Since $|{K(h)}| > 1$, it follows that $|{K(x)}| \ne |{K(xy)}|$, contrary to the assumption. This implies $|{J}| = 1$.

Fix $j\in J$ and let $g, h\in G_j\setminus Z(G_j)$. Note that $(e_1, \ldots, e_{j-1}, g, e_{j+1}, \ldots, e_n)$ and $(e_1, \ldots, e_{j-1}, h, e_{j+1}, \ldots, e_n)$ do not lie in $Z\left(\prod\limits_{{i = 1}}^{{n}}G_i\right)$. By Theorem 2.1,

and

By assumption, $|{K((e_1, \ldots, e_{j-1}, g, e_{j+1}, \ldots, e_n)) }| = |{K((e_1, \ldots, e_{j-1}, h, e_{j+1}, \ldots, e_n))}|$, which implies that $|{K(g)}| = |{K(h)}|$. This shows that any two components of the non-central part of $\Gamma_{G_j}^e$ have the same number of vertices, which completes the proof.

We remark that the converse to Lemma 3.19 is in general not true. It is trivially true when $n = 1$. However, there is a counterexample when $n\geq 2$. In fact, consider the direct product $D_8\times D_8$. Using the presentation $D_8 = \langle{r, s\colon r^4 = s^2 = e, rs = sr^{-1}}\rangle$, we obtain that the conjugacy classes of $D_8$ are

Therefore, the component of $\Gamma_{D_8\times D_8}^e$ containing $(e, r)$ has two vertices, whereas the component of $\Gamma_{D_8\times D_8}^e$ containing $(r, s)$ has four vertices, see Figure 2.

We are now in a position to give a sufficient and necessary condition for the non-central part of an extended conjugate graph to be regular.

Theorem 3.20. Let $G$ be a finite non-abelian group. Then the non-central part of the extended conjugate graph of $G$ is regular if and only if $G\cong P\times A$, where $P$ is a finite $p$-group such that the non-central part of its extended conjugate graph is regular and $A$ is a finite abelian group.

Proof. Suppose that the non-central part of $\Gamma_G^e$ is regular. By Theorem 3.16, $G$ is nilpotent. As a standard result in the theory of finite groups, $G\cong P_1\times P_2\times \cdots\times P_n$, where $P_1, P_2, \ldots, P_n$ are the Sylow subgroups of $G$ corresponding to each prime dividing $|{G}|$. By Proposition 3.2, $\Gamma_G^e\cong \Gamma_{P_1\times P_2\times \cdots\times P_n}^e$. Since

for all $\sigma\in S_n$, we can rearrange the factors $P_i$'s so that $P_1, P_2, \ldots, P_r$ are non-abelian and $P_{r+1}, P_{r+2}, \ldots, P_n$ are abelian. Since $G$ is non-abelian, $P_1, P_2, \ldots, P_r$ exist. In the case when $P_{r+1}, P_{r+2}, \ldots, P_n$ do not exist, we define $A = \{{e}\}$; otherwise, we define $A = P_{r+1}\times P_{r+2}\times \cdots \times P_n$. A similar argument as in the proof of Lemma 3.19 shows that $r = 1$. Define $P = P_1$. Since $P$ is a Sylow subgroup of $G$, it is indeed a finite $p$-group. By Lemma 3.19, the non-central part of $\Gamma_P^e$ is regular. The converse can be proved by using Theorem 2.1.

We remark that the group $P$ mentioned in Theorem 3.20 is of conjugate type $(p^k, 1)$ for some prime $p$ and for some $k\in \mathbb{N}$. In fact, for each $x\in P\setminus Z(P)$, $|{K(x)}| > 1$ and $|{K(x)}|$ divides $|{P}|$. Hence, $|{K(x)}| = p^k$, where $p$ is a unique prime factor of $|{P}|$ and $k\in \mathbb{N}$. Next, define two classes of finite non-abelian groups:

and

Theorem 3.16 asserts that $\mathcal{S}$ is (properly) contained in the class of finite nilpotent groups. Theorem 3.20 asserts that $\mathcal{S}$ will be completely determined once $\mathcal{T}$ is completely determined. In other words, the study of finite non-abelian groups whose conjugate graphs are regular reduces to the case of finite $p$-groups. This will be partially done in Section 3.3 in the case of $p^3$ and $p^4$.

For any finite group $G$, let $\pi(G)$ be the set of prime divisors of $|{G}|$. Define a set $\rho(G)\subseteq \pi(G)$ by the condition that $p\in\rho(G)$ if and only if a Sylow $p$-subgroup of $G$ is non-abelian. In view of Lemma 3.19 and Theorem 3.20, we obtain the following theorem.

Theorem 3.21. Let $G$ be a finite nilpotent group that is non-abelian. Then the non-central part of the extended conjugate graph of $G$ is regular if and only if $|{\rho(G)}| = 1$ and the non-central part of the extended conjugate graph of a Sylow subgroup of $G$ corresponding to a unique prime in $\rho(G)$ is regular.

Corollary 3.22. If $G$ is a finite nilpotent group with $|{\rho(G)}|\geq 2$, then the non-central part of the extended conjugate graph of $G$ is not regular.

It is easy to see that any direct product of non-abelian groups of prime power order satisfies the condition of Corollary 3.22. In ^[18], the authors show that two specific non-abelian groups of order $16$ and $81$ have regular conjugate graphs. We generalize this result to a general case, as shown in the following theorem.

Theorem 3.23. Let $G$ be a finite non-abelian group. If $|G/Z(G)| = p^2$, where $p$ is a prime, then the non-central part of the extended conjugate graph of $G$ is the union of $n$ copies of $K_p$, where $n = \dfrac{|G|-|Z(G)|}{p}$.

Proof. Let $g\in G\setminus Z(G)$. Then $|K(g)|\geq 2$. Note that $Z(G)\leqslant C_G (g)\leqslant G$, which implies $p^2 = [G\colon Z(G)] = [G\colon C_G (g)][C_G (g) \colon Z(G)] = |K(g)|[C_G (g) \colon Z(G)]$. Thus, $|K(g)|$ divides $p^2$ and so $|K(g)| = p$ or $|K(g)| = p^2$. If $|K(g)| = p^2$, we would have $[C_G (g) \colon Z(G)] = 1$ and would have $Z(G) = C_G (g)$, which would imply $g\in Z(G)$, a contradition. Hence, $|K(g)| = p$. Therefore, the component containing $g$, which is a complete graph by Proposition 3.11, has $p$ vertices. Since the non-central part of $\Gamma_G^e$ has $|G|-|Z(G)|$ vertices, the number of copies of $K_p$ equals $\dfrac{|G|-|Z(G)|}{p}$.

Corollary 3.24. Let $G$ be a finite non-abelian group. If $|G/Z(G)| = p^2$, where $p$ is a prime, then the non-central part of the extended conjugate graph of $G$ is regular.

The converse to Corollary 3.24 is not true; a counterexample is the inner holomorph of the dihedral group $D_8$, denoted by $\mathrm{IHol}(D_8)$. The conjugacy classes of $\mathrm{IHol}(D_8)$ is computed in the Appendix. In fact, $|{Z(\mathrm{IHol}(D_8)}|) = 2$ and the non-central part of the extended conjugate graph of $\mathrm{IHol}(D_8)$ is the union of $15$ copies of $K_2$, see Figure 3. However, $|{\mathrm{IHol}(D_8)/Z(\mathrm{IHol}(D_8))}| = 16$ is not the square of a prime. As an application of Theorem 3.23, we obtain a formula for determining the clique number as well as the domination number of a finite non-abelian group $G$ such that $G/Z(G)$ has a prime squared order.

Corollary 3.25. Let $G$ be a finite non-abelian group. If $|G/Z(G)| = p^2$, where $p$ is a prime, then $\omega(\Gamma_G^e) = p$.

Proof. Note that $|{K(g)}| = 1$ for all $g\in Z(G)$. By Theorem 3.23, $|{K(g)}| = p$ for all $g\in G\setminus Z(G)$. Hence, $\omega(\Gamma_G^e) = p$ by Eq (3.2).

Corollary 3.26. Let $G$ be a finite non-abelian group. If $|G/Z(G)| = p^2$, where $p$ is a prime, then $\gamma(\Gamma_G^e) = \dfrac{(p-1)|{Z(G)}| + |{G}|}{p}$.

Proof. By Theorem 3.23, the number of components of $\Gamma_G^e$ equals $|{Z(G)}| + \dfrac{|{G}|-|{Z(G)}|}{p}$. Then the corollary follows from Proposition 3.13.

3.3.   Extended conjugate graphs of finite groups of particular order

In light of Theorem 3.20, it suffices to study regularity of the extended conjugate graph of a finite $p$-group. Therefore, in this section, we examine the extended conjugate graph of a group of order $pq$, $p^3$ and $p^4$, where $p$ and $q$ are distinct primes. We emphasize that groups of order $p$ and $p^2$ are always abelian for any prime $p$.

Suppose that $G$ is a non-abelian group of order $pq$, where $p$ and $q$ are primes. We remark that $p$ and $q$ are necessarily distinct since any group of prime squared order is abelian. Furthermore, $p\mid (q-1)$ since if $p\nmid (q-1)$, then $G\cong \mathbb{Z}_{pq}$ (cf. p. 143 of ^[9]) and so $G$ is abelian. Note that, as mentioned in p. 179 of ^[9], if $p$ and $q$ are distinct primes such that $p\mid (q-1)$, then there is a unique non-abelian group of order $pq$, up to isomorphism.

Proposition 3.27. If $G$ is a non-abelian group of order $pq$, where $p$ and $q$ are distinct primes, then the non-central part of the extended conjugate graph of $G$ is not regular.

Proof. By Lagrange's theorem, $|{Z(G)}| \in \{{1, p, q, pq}\}$. Since $G$ is not abelian, it follows that $|{Z(G)}| \ne pq$. If $|{Z(G)}|\in\{{p, q}\}$, then $|{G/Z(G)}|$ would be a prime and $G/Z(G)$ would be a cyclic group, which would imply that $G$ is abelian, a contradiction. Hence, $|{Z(G)}| = 1$. By Theorem 3.17, the non-central part of $\Gamma_G^e$ is not regular.

3.3.1.   Non-abelian groups of order $p^3$

In this section, we prove that an arbitrary non-abelian group of order $p^3$, where $p$ is a prime, always has a regular conjugate graph. This enables us to compute the clique and domination numbers of the extended conjugate graph associated to a non-abelian group of order $p^3$ explicitly.

Theorem 3.28. Let $p$ be a prime. The non-central part of the extended conjugate graph of any non-abelian group of order $p^3$ is the union of $p^2-1$ copies of $K_p$ and hence is a regular graph.

Proof. Let $G$ be a non-abelian group of order $p^3$. By Lagrange's theorem, $|{Z(G)}|\in\{{1, p, p^2, p^3}\}$. A similar argument as in the proof of Proposition 3.27 shows that $|{Z(G)}|\not\in\{{p^2, p^3}\}$. Since $G$ is a non-trivial finite $p$-group, $Z(G)\ne\{{e}\}$ and so $|{Z(G)}|\ne 1$. This forces $|{Z(G)}| = p$. Hence, $|{G/Z(G)}| = p^2$. By Theorem 3.23, the non-central part of $\Gamma_G^e$ is the union of $n$ copies of $K_p$, where $n = \dfrac{|G|-|Z(G)|}{p} = p^2 -1$.

Corollary 3.29. Let $p$ be a prime. If $G$ is a direct product of a non-abelian group of order $p^3$ and a finite abelian group, then the non-central part of the extended conjugate graph of $G$ is regular.

Proof. The corollary follows from Theorems 3.20 and 3.28.

It is not difficult to check that any nilpotent non-abelian group of order $p^3q$ or $p^3q^2$, where $p$ and $q$ are distinct primes, satisfies the condition of Corollary 3.29.

Corollary 3.30. If $G$ is a non-abelian group of order $p^3$, where $p$ is a prime, then $\omega(\Gamma_G^e) = p$.

Theorem 3.31. If $G$ is a non-abelian group of order $p^3$, where $p$ is a prime, then $\gamma(\Gamma_G^e) = p^2 + p -1$ and $R(G) = \dfrac{p^2 + p -1}{p^3}$.

Proof. As in the proof of Theorem 3.28, $|{Z(G)}| = p$ and $|{G/Z(G)}| = p^2$. It then follows by Corollary 3.26 that $\gamma(\Gamma_G^e) = \dfrac{(p-1)|{Z(G)}| + |{G}|}{p} = p^2 + p -1$. That $R(G) = \dfrac{p^2 + p -1}{p^3}$ follows from Theorem 3.7 and Proposition 3.13.

3.3.2.   Non-abelian groups of order $p^4$

In this section, we show that the non-central part of the extended conjugate graph associated to a non-abelian group of order $p^4$, where $p$ is a prime, may be regular or non-regular. Furthermore, in the case when it is regular, it must be a union of complete graphs $K_p$.

Theorem 3.32. Let $p$ be a prime. If $G$ is a non-abelian group of order $p^4$, then either

$(1)$ the non-central part of the extended conjugate graph of $G$ is not regular or

$(2)$ the non-central part of the extended conjugate graph of $G$ is a union of $K_p$'s.

Proof. Suppose that $|{G}| = p^4$. If the non-central part of $\Gamma_G^e$ is not regular, then we are done. Therefore, we may assume that the non-central part of $\Gamma_G^e$ is regular. By Lagrange's theorem, $|{Z(G)}|$ lies in $\{{1, p, p^2, p^3, p^4}\}$. A similar argument as in the proof of Theorem 3.28 shows that $|{Z(G)}|\not\in\{{1, p^3, p^4}\}$. Thus, $|{Z(G)}|$ is $p$ or $p^2$. In the case when $|{Z(G)}| = p^2$, we obtain that $|{G/Z(G)}| = p^2$ and so the non-central part of $\Gamma_G^e$ is a union of $K_p$'s by Theorem 3.23. Next, suppose that $|{Z(G)}| = p$. Hence, there are $p^4 - p$ non-central elements of $G$. By hypothesis, these elements contribute to conjugacy classes of the same size. Note that if $g\in G\setminus Z(G)$, then $|{K(g)}| > 1$ and $|{K(g)}|$ divides $|{G}|$. Hence, $|{K(g)}| \in\{{p, p^2, p^3, p^4}\}$. However, $p^2, p^3,$ and $p^4$ do not divide $p^4 - p$. Hence, $|{K(g)}| = p$. This shows that each component of the non-central part of $\Gamma_G^e$ is $K_p$.

Corollary 3.33. For any prime $p$, there is no non-abelian group of order $p^4$ such that the non-central part of its extended conjugate graph is a union of $K_m$'s, where $m\in\{{p^2, p^3, p^4}\}$.

Proof. Suppose that $G$ is a non-abelian group of order $p^4$. If the non-central part of $\Gamma_G^e$ is not regular, then we are done. In the case when the non-central part of $\Gamma_G^e$ is regular, it must be a union of $K_p$'s by Theorem 3.32.

The next proposition gives a sufficient and necessary condition for the non-central part of the extended conjugate graph associated to a group of order $p^4$, where $p$ is a prime, to be regular.

Proposition 3.34. Let $G$ be a non-abelian group of order $p^4$, where $p$ is a prime. Then the non-central part of the extended conjugate graph of $G$ is regular if and only if the clique number of the extended conjugate graph of $G$ is $p$.

Proof. Suppose that the non-central part of $\Gamma_G^e$ is regular. By Theorem 3.32, it must be a union of $K_p$'s. Hence, $\omega(\Gamma_G^e) = p$. To prove the converse, suppose that $\omega(\Gamma_G^e) = p$. Let $g\in G\setminus Z(G)$. Note that $|{K(g)}|\ne 1$ and that $|{K(g)}|$ divides $p^4$. By assumption, $|{K(g)}|\leq p$. Hence, $|{K(g)}| = p$ and so the non-central part of $\Gamma_G^e$ is a union of $K_p$'s.

We are now in a position to prove the main result of this section, which describes some aspects of the extended conjugate graph associated to a non-abelian group of order $p^4$, where $p$ is a prime.

Theorem 3.35. Let $G$ be a non-abelian group of order $p^4$, where $p$ is a prime. Then the following statements hold:

$(1)$ if $|{Z(G)}| = p^2$, then $\omega(\Gamma_G^e) = p$, $\gamma(\Gamma_G^e) = p^3 + p^2 -p$, and $R(G) = \dfrac{p^2+p-1}{p^3}$;

$(2)$ if $|{Z(G)}| = p$ and if the non-central part of the extended conjugate graph of $G$ is regular, then $\omega(\Gamma_G^e) = p$, $\gamma(\Gamma_G^e) = p^3 + p -1$, and $R(G) = \dfrac{p^3 + p -1}{p^4}$;

$(3)$ if $|{Z(G)}| = p$ and if the non-central part of the extended conjugate graph of $G$ is not regular, then $\omega(\Gamma_G^e) = p^2$, $p-1 < \gamma(\Gamma_G^e) < p^3 + p -1$, and $\dfrac{p-1}{p^4} < R(G) < \dfrac{p^3 + p -1}{p^4}$.

Proof. To prove Part (1), suppose that $|{Z(G)}| = p^2$. Then $|{G/Z(G)}| = p^2$ and so the non-central part of $\Gamma_G^e$ is regular. By Proposition 3.34, $\omega(\Gamma_G^e) = p$. By Corollary 3.26, $\gamma(\Gamma_G^e) = p^3 + p^2 -p$. By Theorem 3.7, $R(G) = \dfrac{\gamma(\Gamma_G^e)}{|{G}|} = \dfrac{p^2+p-1}{p^3}$.

To prove Part (2), suppose that $|{Z(G)}| = p$ and that the non-central part of $\Gamma_G^e$ is regular. By Proposition 3.34, $\omega(\Gamma_G^e) = p$. As in the proof of Theorem 3.32, the non-central part of $\Gamma_G^e$ is a union of $K_p$'s. Hence, $\gamma(\Gamma_G^e) = |{Z(G)}| + \dfrac{|{G}|-|{Z(G)}|}{p} = p^3 + p - 1$ and so $R(G) = \dfrac{p^3 + p - 1}{p^4}$.

To prove Part (3), suppose that $|{Z(G)}| = p$ and that the non-central part of $\Gamma_G^e$ is not regular. By Proposition 3.12, $\omega(\Gamma_G^e) \leq |{G/Z(G)}| = p^3$. Next, we show that no component of $\Gamma_G^e$ is $K_{p^3}$. Assume to the contrary that $|{K(g)}| = p^3$ for some $g\in G$. Note that $g\not\in Z(G)$. As in the proof of Theorem 3.23, $p^3 = |{K(g)}|[C_G(g)\colon Z(G)]$, which implies $Z(G) = C_G(g)$, a contradiction. Moreover, by assumption, not all components of $\Gamma_G^e$ are $K_p$. Hence, at least one component of $\Gamma_G^e$ is $K_{p^2}$ and so $\omega(\Gamma_G^e) = p^2$.

Note that $\gamma(\Gamma_G^e) > |{Z(G)}| > p-1$ because $G$ is non-abelian. As in the proof of Theorem 3.32, $|{K(g)}|\in\{{p, p^2, p^3}\}$ for all $g\in G\setminus Z(G)$. Assume by contradiction that $\gamma(\Gamma_G^e) \geq p^3 + p -1$. Hence, the non-central part of $\Gamma_G^e$ has at least $p^3 -1$ components. As mentioned above, every component of the non-central part of $\Gamma_G^e$ has at least $p$ vertices. By assumption, there is at least one component of the non-central part of $\Gamma_G^e$ having $m$ vertices with $m\in\{{p^2, p^3}\}$. Hence, the non-central part of $\Gamma_G^e$ has at least $(p^3 -2)p + m$ vertices. This leads to a contradiction since

Thus, $\gamma(\Gamma_G^e) < p^3 + p -1$. This also implies that $\dfrac{p-1}{p^4} < R(G) < \dfrac{p^3 + p -1}{p^4}$.

We remark that the first and third cases of Theorem 3.35 occur; a few concrete examples are listed in Table 1. Presentations of concrete groups mentioned in this article are listed in Table 2.

As noted before, the converse to Proposition 3.2 is not true. The extended conjugate graphs $\Gamma_{D_8\times \mathbb{Z}_2}^e$ and $\Gamma_{Q_8\times \mathbb{Z}_2}^e$ are isomorphic (see Figure 4) but the groups $D_8\times \mathbb{Z}_2$ and $Q_8\times \mathbb{Z}_2$ are not isomorphic since $D_8\not\cong Q_8$ (cf. ^[13]).

4.   Conclusions

In this work, we define the extended conjugate graph of a finite group $G$ and study several properties of extended conjugate graphs that are related to the algebraic structure of their corresponding groups. As an application of these results, we give a graph-theoretic proof of the class equation. We also obtain a few conditions for the non-central part of an extended conjugate graph to be a regular graph. Finally, we study extended conjugate graphs of groups of order $pq, p^3$, and $p^4$, where $p$ and $q$ are distinct primes, in detail.

Acknowledgments

The work of T. Suksumran was supported by the Research Group in Mathematics and Applied Mathematics, Chiang Mai University under Grant no. R000029618. The authors would like to thank the referees for their careful reading of the manuscript and their invaluable comments that improve the final version of the manuscript.

Conflict of interest

The authors declare no conflict of interest.

Appendix

The inner holomorph of the dihedral group $D_8$ is a group of order $32$, which can be recognized as a group of matrices over $\mathbb{Z}_2$:

together with the usual matrix multiplication. The conjugacy classes of $\mathrm{IHol}(D_8)$ are as follows:

List of symbols

$|S|$        cardinality of $S$

$Z(G)$        center of $G$

$C_G(g)$        centralizer of $g$ in $G$

$\omega(\Gamma)$        clique number of $\Gamma$

$K_m$        complete graph with $m$ vertices

$K(g)$        conjugacy class of $g$

$\Gamma_G^c$        conjugate graph of $G$

$(n_1, n_2, \ldots, n_r)$    conjugate type vector, conjugate type of a group

$\mathrm{Dic}_4$        dicyclic group of degree $4$

$D_{2n}$        dihedral group of order $2n$

$\prod\limits_{{i = 1}}^{{n}}G_i$        direct product group $G_1\times G_2\times\cdots\times G_n$

$\gamma(\Gamma)$        domination number of $\Gamma$

$\Gamma_G^e$        extended conjugate graph of $G$

$Q_{16}$        generalized quaternion group of order $16$

$\mathbb{Z}_n$        group of integers modulo $n$

$[G\colon H]$        index of $H$ in $G$

$\Gamma[S]$        induced subgraph of $\Gamma$ by $S$

$\mathrm{IHol}(D_8)$        inner holomorph of the dihedral group $D_8$

$k(G)$        number of conjugacy classes of $G$

$R(G)$        probability of commutativity in $G$

$QD_{16}$        quasidihedral group of order $16$

$Q_8$        quaternion group of order $8$

$U(G)$        same-size conjugate set of $G$

$SD_{16}$        semidihedral group of order $16$

$\pi(G)$        set of prime divisors of $|G|$

$\rho(G)$        set of primes $p$ such that a Sylow $p$-subgroup of $G$ is non-abelian

$S_n$        symmetric group of degree $n$

$\mathrm{deg}\, {v}$        vertex degree of $v$

$V(\Gamma)$        vertex set of $\Gamma$