Fractional order modeling and analysis of dynamics of stem cell differentiation in complex network

1.   Introduction

Fractals are fragmented shapes at all scales with self-similarity properties theirs fractal dimension exceeds their topological dimension ^[1,2,3,4]. Fractals appear in chaotic dynamical systems such as the attractors ^[5]. The global attractors of porous media equations, and their fractal dimension which is finite under some conditions, were suggested in ^[6,7,8,9]. The distance of pre-fractal and fractal sets were derived in terms of some the preselected parameters ^[10].

Non-standard analysis can be used to build the curvilinear coordinate along the fractal curves (i.e. Cesàro and Koch curves) ^[11,12]. The theory of scale relativity suggests the quantum mechanics formalism as the mechanics for fractal space-time ^[13]. Analysis on fractals was studied by using probability theory, measure theory, harmonic analysis, and fractional spaces ^{[14,15,16,17,18,19]}.

Using fractional calculus, electromagnetic fields were provided for fractal charges as generalized distributions and applied to different branches of physics with fractal structures ^[20,21,22]. Non-local fractional derivatives do not have any geometrical and physical meaning so far ^[23,24]. Existence, controllability, and synchronization of the fractional differential equations were investigated ^{[4,25,26,27,28,29]}.

Local fractional derivatives are needed in many physical problems. The effort of defining local fractional calculus leads to new a measure on fractals ^[30,31].

In view of this new measure, the $C^{\mu}$-Calculus was formulated for totally disconnected fractal sets and non-differentiable fractal curves ^{[32,33,34,35]}. During the last decade, several researchers have explored in this area and applied it in different branches of science and engineering ^[36,37]. Fractal differential equations (FDEs) were solved and analogous existence and uniqueness theorems were suggested and proved ^[38,39,40]. The stability of the impulsive and Lyapunov functions in the sense of Riemann-Liouville like fractional difference equations were studied in ^{[41,42,43,44]}.

Motivated by the works mentioned above, we give analogues of asymptotic behaviors of the solutions of FDEs. The stability and asymptotic behavior of differential equations have an important role in various applications in science and engineering. The Lyapunov's second method was applied to show uniform boundedness and convergence to zero of all solutions of second-order non-linear differential equation ^[45,46]. The reader is advised to see the references cited in ^[47,48].

Our aim in this work is to give sufficient conditions for the solutions of FDEs to be uniformly bounded and for the solutions with fractal derivatives to go to zero as $t\rightarrow\infty$.

The outline of the manuscript is as follows:

In Section 2 we give basic tools and definition we need in the paper. In Section 3 we define fractal Lyapunov stability and function. Section 4 gives asymptotic behaviors and conditions for the solutions of FDEs. We present the conclusion of the paper in Section 5.

2.   Preliminaries

In this section, fractal calculus is summarized which is called generalized Riemann calculus ^{[32,33,34,35]}. Fractal calculus expands standard calculus to involve functions with totally disconnected fractal sets and non-differentiable curves such as Koch and Cesàro curves. Fractal calculus was applied for the function with Cantor-like sets with zero Lebesgue measures and non-integer Hausdorff dimensions ^[35,49].

2.1.   The middle-$\mu$ Cantor set

The Cantor-like sets contain totally disconnected sets such as thin fractal, fat fractal, Smith-Volterra-Cantor, k-adic-type, and rescaling Cantor sets ^[49]. The middle-$\mu$ Cantor set is obtained by following process ^[49]:

First, delete an open interval of length $0 < \mu < 1$ from the middle of the $I = [0, 1]$.

Second, remove two disjoint open intervals of length $\mu$ from the middle of the remaining closed intervals of the first step.

$\vdots.$

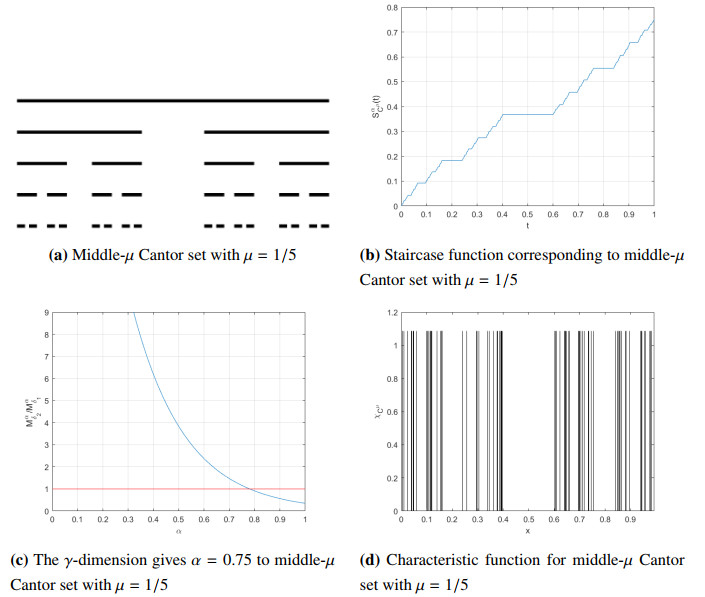
In $m^{th}$ stage, omit $2^{m-1}$ disjoint open intervals of length $\mu$ from the middle of the remaining closed intervals (See Figure 1a).

Finally, we have middle-$\mu$ Cantor set as follows:

The Lebesgue measure of $C^{\mu}$ set is given by

The Hausdorff dimension of middle-$\mu$ Cantor set using Hausdorff measure is given by

where $H$ indicates Hausdorff measure ^[14,15,49].

2.2.   Local fractal calculus

The flag function of $C^{\mu}$ is defined by ^[32,33],

where $J = [c_{1}, c_{2}]$. Let $Q_{[c_{1}, c_{2}]} = \{c_{1} = t_0, t_1, t_2, \dots, t_m = c_{2}\}$ be a subdivision of $J$. Then, $\mathbb{L}^{\alpha}[C^{\mu}, Q]$ is defined in ^[32,33,35] by

where $0 < \alpha\leq 1$.

The mass function of $C^{\mu}$ is defined in ^[32,33,35] by

here, infimum is taking over all subdivisions $Q$ of $[c_{1}, c_{2}]$ satisfying $|Q|: = \max_{1\leq i\leq m}(t_{i}-t_{i-1})\leq\delta$.

The integral staircase function of $C^{\mu}$ is defined in ^[32,33,35] by

where $t_{0}$ is an arbitrary and fixed real number (See Figure 1b).

The $\gamma$-dimension of $C^{\mu}\cap[c_{1}, c_{2}]$ is

Figure 1c presents approximate $\mathcal{M}^{\alpha}_{\delta_{2}}/\mathcal{M}^{\alpha}_{\delta_{1}}$, where $\delta_{2} < \delta_{1}$. This gives us $\gamma$-dimension since that value converging to the finite number as $\delta\rightarrow 0$. This result can also be concluded by choosing different various pairs of $(\delta_{1}, \delta_{2})$.

The characteristic function $\chi_{C^{\mu}}(\alpha, t):\Re\rightarrow \Re$ is defined by

In Figure 1d we have plotted the characteristic function for the middle-$\mu$ choosing $\mu = 1/5$.

The $C^{\alpha}$-limit of a function $h:\Re \rightarrow \Re$ as $z\rightarrow t$ is defined in ^[32,33,35] by

If $l$ exists, then we can write

The $C^{\mu}$-continuity of a function $h$ at $t\in C^{\mu}$ is defined in ^[32,33] by

The $C^{\mu}$-Differentiation of a function $h$ at $t\in C^{\mu}$ is defined in ^[32,33,35] by

if limit exists.

The $C^{\mu}$-integral of $h$ on $[c_{1}, c_{2}]$ is denoted by $\int_{c_{1}}^{c_{2}}h(t) d_{C^{\mu}}^{\alpha}t$ and is approximately given in ^[32,33,35] by

We refer the reader for more meticulous definitions to see in ^[32,33,35]. In Figure 1 we have sketched the middle-$\mu$ Cantor, the staircase function, the characteristic function, and graph of $\mathcal{M}^{\alpha}_{\delta_{2}}/\mathcal{M}^{\alpha}_{\delta_{1}}$ versus to $\alpha$.

3.   Fractal Lyapunov stability

In this section, we generalize the Lyapunov stability definition for the functions with fractal support.

Let us consider the following fractal differential equation with an initial condition

where $g(h(t)):\Re \rightarrow\Re$, $C^{\mu} = K$ and $g$ has an equilibrium point $h_{e}$, then $g(h_{e}) = 0$.

1) The equilibrium point $h_{e}$ is called fractal Lyapunov stabile if we have

2) The stable equilibrium point $h_{e}$ is said fractal asymptotically stable if

3) The equilibrium point $h_{e}$ is called fractal exponentially stable if

where $t\geq 0, \; \kappa, \lambda\in \Re,$ and $\; \kappa > 0, \; \lambda > 0$.

Fractal Lyapunov function of Eq. (3.1) is a function $L:\Re \rightarrow\Re^{+}, \; R^{+} = [0, +\infty)$ which is $C^{\mu}$-continuous. Also, its $\alpha$-order derivative is $C^{\mu}$-continuous. Thus the fractal derivative of $L$ with respect to Eq. (3.1) is written as $L^{*}$ and if it has following condition

then, the zero solution of Eq. (3.1) is fractal asymptotically stable.

Example 1. Consider the following fractal differential equation

where $0 < \alpha\leq 1$. The general the solution of Eq. (3.3) is

A fractal Lyapunov function for studying the stability of Eq. (3.3) is

Then, we have

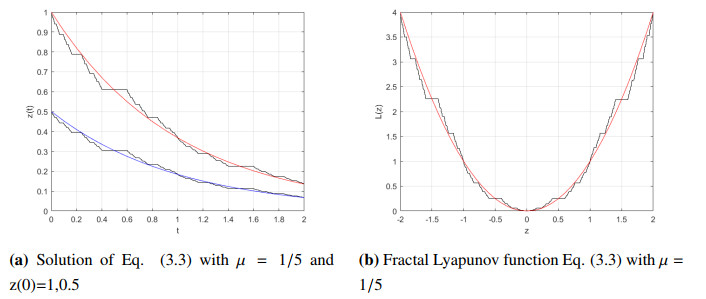
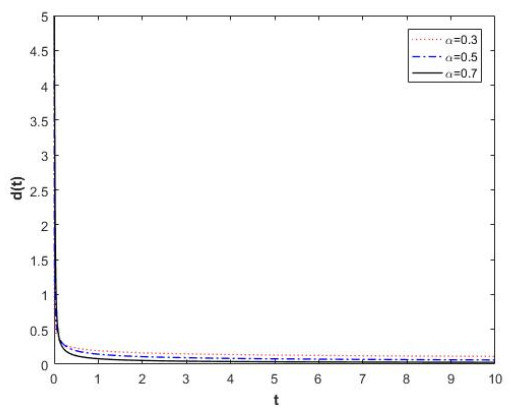
Thus, the zero solution of Eq. (3.3) is fractal asymptotically stable (See Figure 2a).

In Figure 2 we have plotted the solution of Eq. (3.3) in 2a and corresponding Fractal Lyapunov function in 2b.

Remark. In Figure 2, the red curves indicate the orbit of the solutions of Eq. (3.3) and Lyapunov function in the case of $\alpha = 1$.

4.   Qualitative behaviors of solutions of FDEs

In this section, we present the generalized conditions for the uniform boundedness and convergence of the solutions of the second $\alpha$-order of non-linear fractal differential equations. On the other hand, we modify and adopt the ordinary calculus conditions in fractal calculus ^[46]. The main results are obtained using the generalized Lyapunov function with the fractal sets support ^{[32,33,35,45,46]}.

Let us consider the following second $\alpha$-order fractal differential equation

where $t\in C^{\mu}, \; y\in \Re, 0 < \alpha\leq 1$. Through this paper, it is assumed that $u, \; v \in C^{\alpha}(C^{\mu})$, $f\in C^{\alpha}(\Re^2, \Re)$, and $q\in C^{\alpha}(C^{\mu}\times\Re^2, \Re)$. By these $C^{\alpha}$-continuity assumptions the existence of the solutions of Eq. (4.1) is guaranteed. We also assume that the functions $f, \; h,$ and $\; q$ satisfy the fractal Lipshitz condition in the unknown function $y$ and its fractal derivative $D_{K, t}^{\alpha}y$. Hence, the uniqueness of solutions of Eq. (4.1) is guaranteed ^[39,40]. By rewritten Eq. (4.1) in the form of the fractal system of differential equations and setting $S_{K}^{\alpha}(t) = t'$, we obtain

where $u(t'), \; v(t'), \; f(y, D_{K, t}^{\alpha}y), \; h(y), \; z(t') = D_{K, t}^{\alpha}y$ and $q(t', y, z)$ are $C^{\mu}$-continuous functions at every point $t\in C^{\mu}$ and they have well behavior such that the fractal uniqueness theorem holds for the fractal system (4.2). Meanwhile, $u(t')$, $v(t')$ are $C^{\mu}$-differentiable on $C^{\mu}$ ^[39].

A. Assumptions

(C1) There are positive constants $u_{0}, \; v_{0}, \; E, \; Q$, such that

where we consider $S_{K}^{\alpha}(t) < t^{\alpha}$ ^[32,33,35].

(C2) $\lambda_{1}(>0), \; \lambda_{2}(>0) \in \Re$ and $\epsilon_{0}, \; \epsilon_{1}, \; \epsilon_{2}$ are small positive numbers such that

(C3) $h(0) = 0, \; h(y)\; \text{sgn}(y) > 0, \; (y\neq0)$, such that

and

(C4)

where $\zeta_{0}(t') = D_{K, t}^{\alpha}v_{+}, \; D_{K, t} ^{\alpha}v_{+} = \max(D_{K, t}^{\alpha}v_{+}, 0)$.

Theorem 1. If assumptions (C1) – (C4) hold, then the zero solution of Eq. (4.1) when $q(S_{K}^{\alpha}(t), y, z) = 0$ is fractal stable.

Proof: For proving this theorem we consider the following fractal Lyapunov function

which is positive definite. By calculating fractal time derivative of (4.3) along the fractal system (4.2), we obtain

We know that $v(t')$ is an increasing function. Hence $D_{K, t}^{\alpha}v(t')\geq0$. Then, we have

In fact, it is obvious that $L_{2}(t', 0, 0) = 0$ and

where $\bar{\lambda} = \min (\lambda_{2}, \frac{1}{2Q^{\alpha}})$. Then the proof is complete.

B. Assumption

(C5) There are positive constants $0\leq\sigma\leq 1, \; 0\leq\Delta\leq 1$, such that

are $C^{\mu}$-Continuous functions and

where $\sigma' = \sigma^{\alpha}$.

(C6)

(C7)

Theorem 2. Let $q(S_{K}^{\alpha}(t), y, z)\neq0$ and assume $(C1)-(C5)$ hold. Then the solutions of Eq. (4.1) are fractal uniformly bounded and fractal convergent, namely

To prove this theorem, we define a fractal Lyapunov function for Eq. (4.1) by

where $k$ is positive constant.

Before giving the proof of the above theorem, we present two lemmas, Lemma 1 and Lemma 2, which are needed in the proof of the theorem.

Lemma 1. If assumptions (C1) and (C3) hold, then

Proof: In view of assumptions (C1) and (C3) we can derive

where $E_{1} = \min(v_{0}, 1/2)$.

In the same manner, by assumptions (C1) and (C3), we can obtain

where $E_{2} = \max(Q, 1)$.

Lemma 2. If assumptions (C1) – (C4) are valid, then

where $E_{3}, E_{4}\in\Re$.

Proof: Fractal differentiating of the fractal Lyapunov function (4.5) along with fractal system (4.2), we get

By using the assumptions of the Theorem 2, we obtain

where

Here, in view of (C5), the term $|q(t', y, z)||z|$ can be written as

Hence, we have

Set $\Delta = E_{3}$. Then

Using the following inequality

taking into account (4.6) and (4.7) we obtain

To complete the proof of the theorem, we consider the fractal Lyapunov function $L_{0}$ defined by

where

and

with $\bar{y} = (y, z)\in \Re^2$ and $t\in C^{\mu}$, and $\psi_{1}, \psi_{2}$ are $C^{\mu}$-continuous and increasing functions such that $\psi_{1}(||\bar{y}||)\rightarrow\infty$ while $||\bar{y}||\rightarrow\infty$.

Fractal differentiating fractal Lyapunov function (4.8) and considering the fractal system (4.2) and assumptions of Theorem 2, we have

If we choose $k\geq\frac{1}{32}$, then it follows that there exists a positive $E_{5}$ such that

By considering (4.9) and (4.10) it follows that all solutions of Eq. (4.2) are fractal uniformly bounded.

Consider the fractal system of differential equations

where $M, N$ are $C^{\mu}\subset \Re^{+}$-continuous and vector functions, and $C^{\mu}\times Q\subset \Re^2$ is an open set. Moreover, it is clear that

where $N_{1}(t', \bar{y}), N_{2}(\bar{y})$ are $C^{\mu}$-continuous and non-negative functions.

Lemma 3. Let $L: C^{\mu}\times Q$ be a function $C^{\mu}$-continuous and $C^{\mu}$-differentiable such that

where $B(||\bar{y}||)$ is a positive definite in the closed set $\Psi\in Q$ and $M(t', \bar{y})$ satisfies the following.

(1) $M(t', \bar{y})$ tends to $K(\bar{y})$ for $\bar{y}\in \Psi$ as $t\rightarrow \infty$, $K(\bar{y})$ is a $C^{\alpha}$-continuous on $\Psi$.

(2)

such that if

we have

(3) $N_{2}(\bar{y})$ is positive definite on closed $\Psi$ of $Q$.

Then every bounded solution of Eq. (4.11) approaches to the fractal system

which is contained in $\Psi$ as $t\rightarrow \infty.$

Proof. Now, we consider (4.2). It follows that

and

Then

We can also write

and

The functions $M(t', \bar{y})$ and $N(t', \bar{y})$ satisfy the conditions of Lemma 3. Set $\psi_{1}(||\bar{y}||) = E_{5}^{\alpha}z^2$, then

where the function $||\bar{y}||$ is positive definite on $\Psi = \{(y, z)|y\in \Re, z = 0\}$. We get

by using (C4) condition of Theorem 1. If we suppose

then all the conditions of Lemma 3 are satisfied. It is straight forward to see that $N_{2}(\bar{y})$ is positive definite function. Since the solutions of fractal system (4.2) are bounded, therefore by using Lemma 3 we have

which is semi-invariant set of the fractal system contained in $\Psi$ as $t\rightarrow \infty$. In view of (4.13), we have following

Fractal system Eq. (4.14) has solution

In order to remain in $\Psi$, the solutions must be

which implies $k = 0, h(c_{1}) = 0$, so that $c_{1} = c_{2} = 0$. Then $\bar{y} = \bar{0}$ is the solution of $D_{K, t}^{\alpha} \bar{y} = \mathfrak{K}(\bar{y})$ remaining in $\Psi$. Consequently, we arrive at

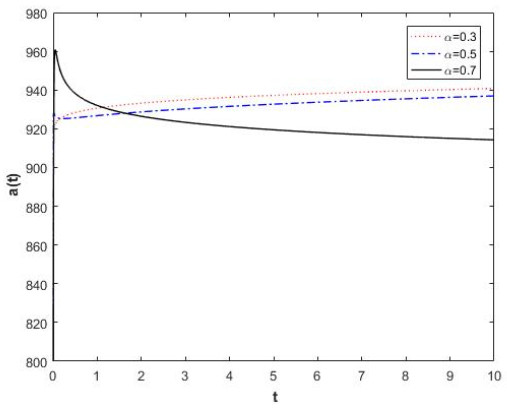
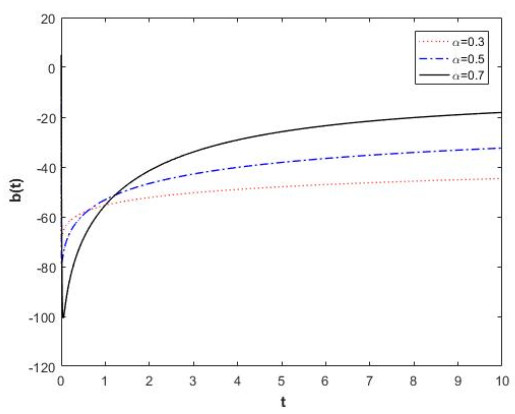
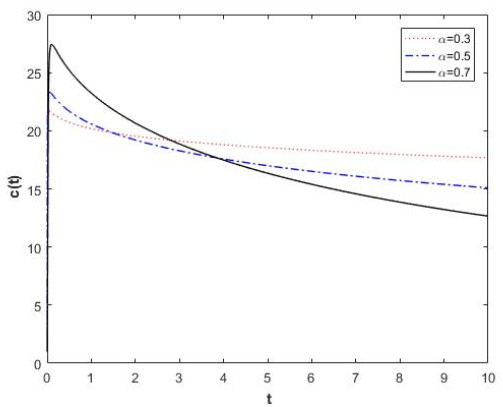
Example 2. Consider the fractal differential equation

This is equivalent to the fractal system

where

and, if we suppose

Consider the fractal function

which is a strong fractal Lyapunov function. Fractal differentiating of $L_{1}(y, z)$ and Eq.(4.17) we get

Using the assumption theorem we obtain

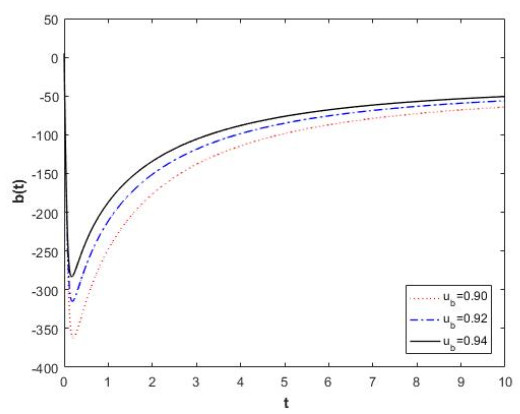
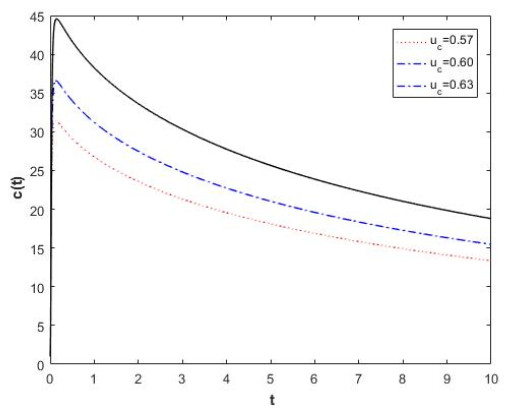
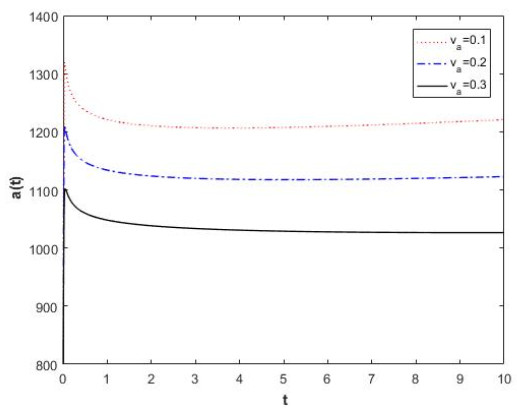
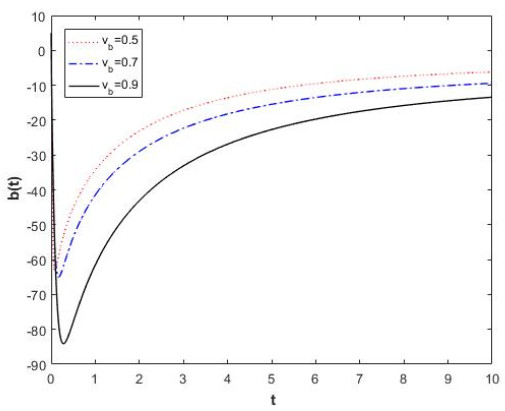
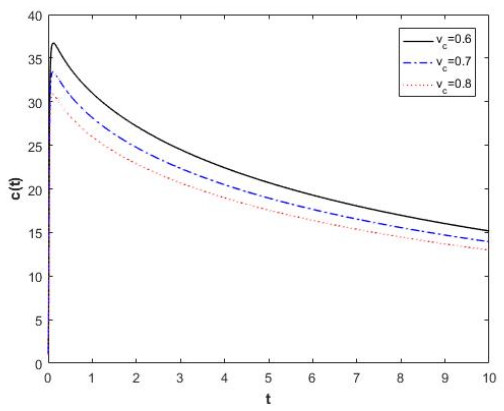
which shows that the solutions of Eq. (4.15) are fractal uniformly bounded and fractal ultimately bounded.

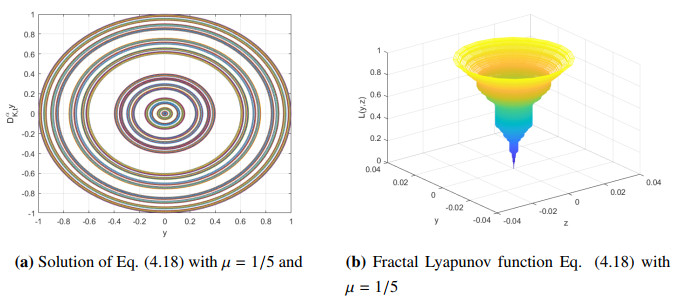
Example 3. Consider harmonic oscillator on the fractal time as follows:

where $\mathfrak{C}_{K}$ is constant. The equivalent fractal system is

The fractal Lyapunov function correspond to Eq. (4.18) is

where $L(0, 0) = 0$ and $L(y, z) > 0$ for $(y, z)\in \Re^{2}\backslash(0, 0)$.

Then, it is obtain that

Hence, the zero solution $(0, 0)$ is a fractal stable point. In Figure 3, we have sketched solutions of Eq. (4.18) and Eq. (4.20).

Remark: We noted that for the physical model of Examples 1, 2 and 3 the parameter $t$ can be considered as the fractal time ^[50].

5.   Conclusion

In this paper, we have suggested conditions for the fractal stability, uniformly boundedness and the asymptotic behaviors of solutions of second $\alpha$-order fractal differential equations. The analogous theorems of stability, uniformly boundedness and asymptotic behavior from standard calculus have been given and adopted in fractal calculus. The generalized conditions include solutions and functions which are non-differentiable in sense of ordinary calculus.

Acknowledgements

This research was completed with the support of the Scientific and Technological Research Council of Turkey (TÜBİTAK) (2221-Fellowships for Visiting Scientists and Scientists on Sabbatical Leave – 2221-2018/3 period) when Alireza Khalili Golmankhaneh was a visiting scholar at Van Yuzuncu Yil University, Van, Turkey.

The authors of this paper would like to express their sincere appreciation to the dear anonymous editor and referee for their valuable comments and suggestions which have led to an improvement in the presentation of the paper.

Conflict of interest

The authors declare that there is no conflict of interest.