Analysis of fractal fractional Lorenz type and financial chaotic systems with exponential decay kernels

1.   Introduction

Fractional-order (FO) derivatives have been studied since the 17th-century. Since its inception, they have evolved mainly as a purely theoretical branch of mathematics. In recent decades, however, FO differential systems are frequently implemented to model physical processes, which occur in engineering ^[1], biomathematics ^[2], mathematical physics ^[3], and many more ^[4,5,6]. When only initial inputs are used to predict future behaviors of the spread, models with standard differentiation might be employed to depict the dynamic systems of an infectious illness. Standard differentiation and related integral operators, on the other hand, are inadequate when the condition is unexpected, as is frequently the case owing to difficulties connected with real-world issues. Non-local operators, in general, are better suited to such scenarios since they can preserve non-localities as well as certain memory influences, which means that they rely on whether there is a power law, fading memory, or overlap influence. Furthermore, there are certainly more sophisticated phenomena that a power law, fading memory, and crossover characteristics cannot reproduce. Atangana developed new nonclassical operators in 2017 by combining fractional and fractal operators ^[7]. Fractal-fractional operators (FFOs), which were recently proposed, may be more appropriate mathematical tools for dealing with such patterns. FFOs have been widely used in the investigation of different mathematical models. We briefly discuss some applications of the FFOs in different fields of science. The FFOs have been applied to study the transmission and dynamics of infectious disease models. For instance, Xuan et al. investigated the complex evolution of cancer model usin Caputo FFO ^[8]. The dynamics of an HIV disease model has been investigated by applying FFOs in the Atangana-Baleanu sense ^[9]. Using an FFO, Akgül et al. analyzed the behaviour and evolution of a cervical cancer model ^[10]. Moreover, FFOs are also used for the analysis of models in engineering, physics and finance ^[11,12].

In recent years, chaos complex structures have become a popular research topic. Almost all academics from a wide range of subjects have been pulled to analyze chaotic environments. The development of the famous Lorenz attractor led to the development of chaos theory, which has grown over the last few decades as a result of a thorough investigation. FFOs generalize classical and fractional operators. Therefore, due to their complex nature, FFOs have been used to study the more complex dynamics of chaotic systems with various dimensions. For instance, Ahmad et al. analyzed the hidden complex attractors of a chaotic system by using the Caputo FFO ^[13]. A new chaotic system with integrated circuit has been modeled by using FFOs to study the hidden attractors ^[14]. Qureshi et al. developed a strange chaotic attractor by applying FFOs ^[15]. Using FFOs, Abro et al. analyzed meminductor and memcapacitor systems ^[16]. A 4-D hyper-chaotic system has been investigated by applying a FFO with a power law kernel ^[17]. There are some other chaotic systems that have been investigated by using FFOs ^[18,19]. Inspired by the above literature, we chose to study a Lorenz system with cubic nonlinearity and financial system with quadratic nonlinearity by using FFO with exponential decay kernel. Some basic concepts are given below.

Definition 1.1. ^[7] Let $\mathcal{X} : [a, \infty) \rightarrow \Re$, be a continuous and fractal differentiable function on an open interval $(a, b)$ with fractional order $\beta$, then, a $\gamma$ order fractal-fractional derivative of the function $\mathcal{X}$ in the Caputo sense with an exponential decay-type kernel is given by

where $0 < \gamma, \beta\leq n\in\mathbb{N},$ $\mathit{M}(0) = \mathit{M}(1) = 1$ and the scalar $a\in[-\infty, 0],$ for $t\geq0.$

It is useful to note that $a\leq0.$ However, it is only for $a = 0$ that we have a classical operator with fading memory. Otherwise, we would want to look into more generic formula. In this case, we suppose that $a < 0$ and $t > 0;$ therefore, the integral

belongs to $(a, 0).$

Definition 1.2. ^[7] It is possible to get a fractal fractional integral of the function $\mathcal{X}\left(t\right)$ of the exponential decaying type by taking the assumption that $\mathcal{X}\left(t\right)$ is continuous on $(a, b)$ and applying $\gamma$ as a fractal fractional integral order of the function.

2.   Construction of a numerical scheme

A power-law kernel fractal fractional differential operator takes the role of the time derivative in the general Cauchy problem formulation.

Let us begin with a Cauchy problem for a generic FFO differential equation:

We have

Thus, we get

At $t = t_{n}$, we can write

At $t = t_{n+1},$

Which leads to

Using the second order Lagrange interpolation to approximate $\mathcal{X}(t, f(t))$ within $[t_{n-1}, t_{n}]$ gives

Substituting for the polynomial approximation, we get

$\begin{alignedat}{1}f(t_{n+1}) & = f(t_{n})+\frac{\gamma\beta}{\mathit{M}(\gamma)}\sum_{p = 0}^{n}\int_{t_{n}}^{t_{n+1}}{}^{\gamma-1}\left[\frac{t-t_{p-1}}{h}\mathcal{X}(t_{p}, f(t_{p}))-\frac{t-t_{p}}{h}\mathcal{X}(t_{p-1}, f(t_{p-1}))\right]dt\\ & +\frac{\beta(1-\gamma)t_{n}^{\beta-1}}{\mathit{M}(\gamma)}\mathcal{X}(t_{n}, f(t_{n})), \end{alignedat}$ $\begin{alignedat}{1}f(t_{n+1}) & = f(t_{n})+\frac{\gamma\beta}{\mathit{M}(\gamma)}\sum_{p = 0}^{n}\int_{t_{n}}^{t_{n+1}}t^{\gamma-1}\frac{t-t_{p-1}}{h}\mathcal{X}(t_{p}, f(t_{p}))dt\\ & -\frac{\gamma\beta}{\mathit{M}(\gamma)}\sum_{p = 0}^{n}\int_{t_{n}}^{t_{n+1}}t^{\gamma-1}\frac{t-t_{p}}{h}\mathcal{X}(t_{p-1}, f(t_{p-1}))dt+\frac{\beta(1-\gamma)t_{n}^{\beta-1}}{\mathit{M}(\gamma)}\mathcal{X}(t_{n}, f(t_{n})), \end{alignedat}$ $\begin{alignedat}{1}f(t_{n+1}) & = f(t_{n})+\frac{\gamma\beta}{\mathit{M}(\gamma)}\sum_{p = 0}^{n}\frac{\mathcal{X}(t_{p}, f(t_{p}))}{h}\int_{t_{n}}^{t_{n+1}}t^{\gamma-1}\left(t-t_{p-1}\right)dt\\ & -\frac{\gamma\beta}{\mathit{M}(\gamma)}\sum_{p = 0}^{n}\frac{\mathcal{X}(t_{p-1}, f(t_{p-1}))}{h}\int_{t_{n}}^{t_{n+1}}t^{\gamma-1}\left(t-t_{p}\right)dt+\frac{\beta(1-\gamma)t_{n}^{\beta-1}}{\mathit{M}(\gamma)}\mathcal{X}(t_{n}, f(t_{n})). \end{alignedat}$

Evaluating these integrals gives

Let

$\begin{alignedat}{1}I_{1} & = \int_{t_{n}}^{t_{n+1}}t^{\gamma-1}\left(t-t_{p-1}\right)dtt = \int_{t_{n}}^{t_{n+1}}t^{\gamma-1}tdt-\int_{t_{n}}^{t_{n+1}}t^{\gamma-1}t_{p-1}dt, \\ & = \int_{t_{n}}^{t_{n+1}}t^{\gamma}dt-\int_{t_{n}}^{t_{n+1}}t^{\gamma-1}t_{p-1}dt = \frac{1}{\gamma+1}\left(t_{n+1}^{\gamma+1}-t_{n}^{\gamma+1}\right)-\frac{t_{p-1}}{\gamma+1}\left(t_{n+1}^{\gamma+1}-t_{n}^{\gamma+1}\right) \end{alignedat}$

and

$\begin{alignedat}{1}I_{2} & = \int_{t_{n}}^{t_{n+1}}t^{\gamma-1}\left(t-t_{p}\right)dtt = \int_{t_{n}}^{t_{n+1}}t^{\gamma-1}tdt-\int_{t_{n}}^{t_{n+1}}t^{\gamma-1}t_{p}dt, \\ & = \int_{t_{n}}^{t_{n+1}}t^{\gamma}dt-\int_{t_{n}}^{t_{n+1}}t^{\gamma-1}t_{p}dt = \frac{1}{\gamma+1}\left(t_{n+1}^{\gamma+1}-t_{n}^{\gamma+1}\right)-\frac{t_{p}}{\gamma+1}\left(t_{n+1}^{\gamma+1}-t_{n}^{\gamma+1}\right), \end{alignedat}$

which then implies that the Caputo-Fabrizo (CF) numerical scheme be given by

3.   Application of the FFO to the Lorenz chaotic system

We present a chaotic system in fractional fractal calculus in this section. A chaotic system with eight polynomial terms was recently published ^[20]; its butterfly-shaped chaotic attractors were examined by using a full theoretical discussion and numerical simulations. The following nonlinear integer-order differential equations with a cubic term and three quadratic nonlinearities describe the system mentioned above with numerous and complicated chaotic dynamics:

The fractal fractional system is given by

where $0 < \gamma, \beta\leq1$ are fractional orders, and $X(0) = X_{0}, Y(0) = Y_{0}$ and $Z(0) = Z_{0}$ are the initial conditions.

3.1.   Stability of the equilibrium points

In this part, we discuss the FO system's stability by using the Matignon criterion. It is a famous criterion used in fractional calculus. Stability analysis is one of the fundamental points in chaotic and hyperchaotic systems. In general, all equilibrium points when the system is chaotic fail to be stable.

One equilibrium point: $E_{p} = \left(0, 0, 0\right)$ can be found after the resolutions. Determining the Jacobian matrix is the next step:

When $c = 3, d = 14,$ and $e = 4$ the system (3.2) has five steady states

At the equilibrium point $E_{1} = \left(0, 0, 0\right)$, the Jacobian matrix (3.3) is given by

which has the following eigenvalues

We notice that the first eigenvalue satisfies $\left|arg(\lambda_{1})\right| = \pi\geq\frac{\alpha\pi}{2}$. The second eigenvalue satisfies that $\left|arg(\lambda_{2})\right|\leq\frac{\alpha\pi}{2}$ for all values of $\alpha$. Therefore the equilibrium point $E_{1} = \left(0, 0, 0\right)$ is an unstable point. The equilibrium point $E_{2} = \left(-2.5905, -0.7670, 0.5095\right)$ is analogous in this regard; the Jacobian matrix is

which has the following eigenvalues

Here, $\lambda_{2}$ satisfies $\left|arg(\lambda_{2})\right| = \pi\geq\frac{\alpha\pi}{2}$ for all values of $\alpha$, and $\lambda_{3}$ satisfies $\left|arg(\lambda_{3})\right|\leq\frac{\alpha\pi}{3}$. Therefore the equilibrium point $E_{2} = \left(-2.5905, -0.7670, 0.5095\right)$ is an unstable saddle point. Similarly, we can easily establish that $E_{3}, E_{4},$ and $E_{5}$ are saddle points as well. Thus, the new chaotic system (3.2) has five unstable steady states.

3.2.   Numerical simulations

We use the numerical scheme of (2.5) to show the findings of the fractal fractional system (3.2) in this section.

Using the numerical approach provided, we get

3.3.   Simulation results

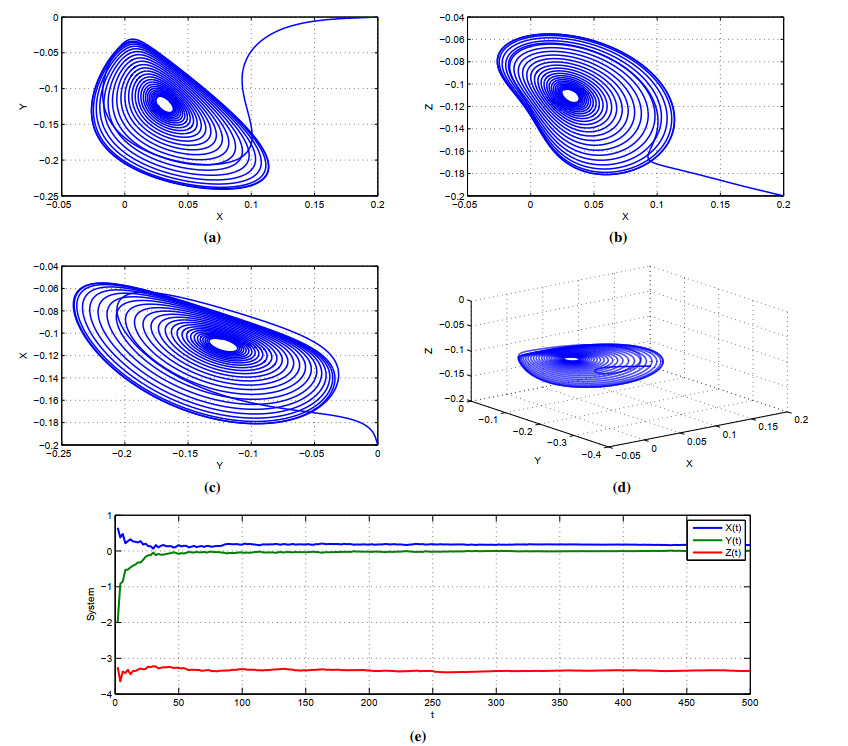
This subsection gives some numerical findings that demonstrate the effects of FFO on the dynamical system (3.2), particularly from the perspective of the complex characteristics. We also apply the suggested numerical scheme to get the desired simulations. For the simulations, we also take into consideration that $c = 3, d = 14, c = 3.9$ and $\left(X_{0}, Y_{0}, Z _{0}\right) = \left(0.2, 0.4, 0.2\right)$. Figure 1(a)–(c) show the approximate solutions in the fractal fractional sense. These graphs provide chaotic structures for $\gamma = 1.0, 0.90, 0.80$ and $\beta = 1$; the simulation included the state variables' time-domain responses as well as the 2-D and 3-D phase portraits. These simulations shows that the equilibrium points are unstable. The observed findings are consistent with the theoretical results, which indicates that $\gamma = 1.0, 0.90, 0.80$ has a great effect on the chaotic behavior of the system (3.6). Furthermore, the above-mentioned figures show that the suggested numerical technique is successful in portraying the chaos dynamics. Figure 1(e) shows the Lyapnavou spectra for the proposed system. Figure 2 shows the chaotic maps of the considered system for $\gamma = 1.0, 0.90, 0.80$ and $\beta = 0.9$. In all subfigures, we can see that the fractal dimension greatly influences the shape of the chaotic maps of the proposed system. For Figure 3, we fixed the fractional order $\gamma = 0.8$ and set the fractal dimension $\beta = 1.0, 0.9, 0.8$. From these figures, we conclude that the FFO provides a new form of dynamics of the proposed Lorenz system.

4.   Financial system

The research in ^[21] revealed a dynamic financial model made up of three first-order differential equations. The interest rate $\mathcal{X}$, the investment demand $\mathcal{Y}$, and the price index $\mathcal{Z}$ are the three state variables described by the model. The elements that primarily drive the changes in $\mathcal{X}$ are (1) the investment market contradiction and savings, and (2) the structural adjustment from goods pricing. The rate of change of $\mathcal{Y}$ is proportional to the rate of investment as well as proportional to the cost of investment and the interest rate through inversion. On the one hand, the contradiction between supply and demand in the commercial market controls $\mathcal{Z}$ changes. The amounts of commercial supply and demand have been assumed to be constant in this case. The price of a commodity is inversely related to the volume of the commercial supply and demand. Real interest rates, on the other hand, may be used to reflect changes in inflation rates, as the inflation rate is equal to the nominal interest rate minus the real interest rate. Because the original model has nine different parameters that can be changed, it must be even more simplified. By selecting the appropriate coordinate system and assigning a dimension to every single state variable, we can get the following more simplified model with only three key parameters:

where $c\geq0$ represents the amount saved, $d\geq0$ represents the cost per investment, and $e\geq0$ represents the demand elasticity of commercial marketplaces. All three constants i.e., $c, d$, and $e,$ are nonnegative and self-evident.

4.1.   Fractal fractional financial system

For the commensurate fractal-fractional-order model, we presented the generalization of the system (4.1), which takes the following form:

where $c\geq0$ represents the amount saved, $d\geq0$ represents the cost per investment, and $e\geq0$ represents the demand elasticity of commercial marketplaces. All three constants i.e., $c, d$, and $e,$ are nonnegative.

4.2.   Stability of the equilibrium points

(1) If $c\geq9$, the system (4.2) has one fixed point:

(2) If $c < 9$, system (4.2) has three fixed points:

We use Lyapunov's first indirect approach to explore the stability of equilibrium points, which yields the following result.

Stability of $p_{1}$

At the equilibrium point $p_{1}$, the Jacobian matrix of system (4.2) is

The characteristic polynomial of the above matrix is as follows:

Its eigenvalues are $\lambda_{1} = -0.881, \lambda_{2} = -\frac{1}{10}\; and\; \lambda_{3} = 7.180.$ We see that the value of $\lambda_{3}$ is positive; then $\left|arg(\lambda_{3})\right| = 0 < \frac{\gamma\pi}{2}\forall\gamma\in\left(0, 1\right)$, so $p_{1}$ is unstable for all $\gamma\in\left(0, 1\right)$.

Stability of $p_{2, 3}$

At the equilibrium point $p_{2, 3}$, the Jacobian matrix of system (4.2) is

The aforementioned matrix has the following characteristic polynomial:

and its eigenvalues are $\lambda_{1} = 0.238, 1.375i$, and $\lambda_{3} = -0.8366;$ we have that

The critical value of $\gamma$ is

(1) $p_{2, 3}$ are locally asymptotically stable if $\gamma < 0.8436.$

(2) If $\gamma > 0.8436,$ then $p_{2, 3}$ is unstable.

4.3.   Numerical simulations

We use the numerical technique described by (2.5) to show the findings of the fractional fractal system (3.2) in this section.

Using the numerical approach provided, we get

4.4.   Simulation results

This subsection provides numerical findings that demonstrate the suggested operator effectiveness. As previously stated, an enhanced Lagrange interpolation approach has been developed for numerical simulations. We have applied $\gamma = 1, 0.9, 0.8$ and $\beta = 0.9$ for Figure 4. The initial conditions were set as 0.4, 0.2 and 0.2 respectively. Figure 4(a)–(c) show the 2-D and 3-D chaotic maps of the proposed financial system. Figure 4(d) shows the Lyapunov exponent of the provided finance model. Figure 5 shows the chaotic structures of the suggested finance system for $\beta = 1, 0.8, 0.75$ and $\gamma = 0.7$. From these figures, the effects of the applied FFO on the chaotic behavior can be clearly observed.

5.   Conclusions

In this study, we have investigated a fractal fractional chaotic Lorenz system with cubic nonlinearities and a fractal fractional chaotic financial system with quadratic nonlinearities by using the CF fractal fractional derivative. The stability of the equilibrium points was investigated by using the fractional Routh-Hurwitz criterion. The chaotic model was then implemented by using an efficient Lagrange interpolation approach, and its complicated behaviors were discussed. The simulation results are shown in Figures 1–6, which demonstrate that the suggested operator has great a impact on the chaotic behavior of the suggested systems.

Conflict of interest

The authors have no competing interests.