Hankel determinants of a Sturmian sequence

1.   Introduction

Let ${\bf{s}} = (s_j)_{j\ge 0}$ be an integer sequence. For all $m\geq 0$, $n\geq 1$, the $(m, n)$-order Hankel matrix of ${\bf{s}}$ is

The $(m, n)$-order Hankel determinant of ${\bf{s}}$ is $H_{m, n} = \det M_{m, n}$.

Hankel determinants of automatic sequences have been widely studied, due to its application to the study of irrationality exponent of real numbers; see for example ^{[1,3,5,6,7,9,15]} and references therein. In 2016, Han ^[10] introduced the Hankel continued fraction which is a powerful tool for evaluating Hankel determinants. By using the Hankel continued fractions, Bugeaud, Han Wen and Yao ^[4] characterized the irrationality exponents of values of certain degree two Mahler functions at rational points. Recently, Guo, Han and Wu ^[8] fully characterized apwenian sequences, that is $\pm 1$ sequences whose Hankel determinants $H_{0, n}$ satisfying $H_{0, n}/2^{n-1}\equiv 1\pmod 2$ for all $n\geq 1$.

However, the Hankel determinants of other low complexity sequences, such as Sturmian sequences, are rarely known. Kamae, Tamura and Wen ^[11] explicitly evaluated the Hankel determinants of the Fibonacci word. Tamura ^[13] extended this result to infinite words generated by the substitutions $a\to a^kb, b\to a$ ($k\ge 1$). In this paper, we study the Hankel determinants of the sequence generated by the substitution

Denote by ${\bf{s}} = (s_{n})_{n\ge 0} = \lim_{n\to\infty}\tau^{n}(1)$ the fixed point of $\tau$. Since $\tau^{n+1}(1) = \tau^n(\tau(1)) = \tau^n(1)\tau^n(0)\tau^n(1)$, the word $\tau^n(1)$ is a prefix of ${\bf{s}}$. The first values of ${\bf{s}}$ can be obtained by finding $\tau^n(1)$. For example,

and

It follows from [14,Proposition 2.1] that ${\bf{s}}$ is a Sturmian sequence. See also the sequence A104521 in ^[12].

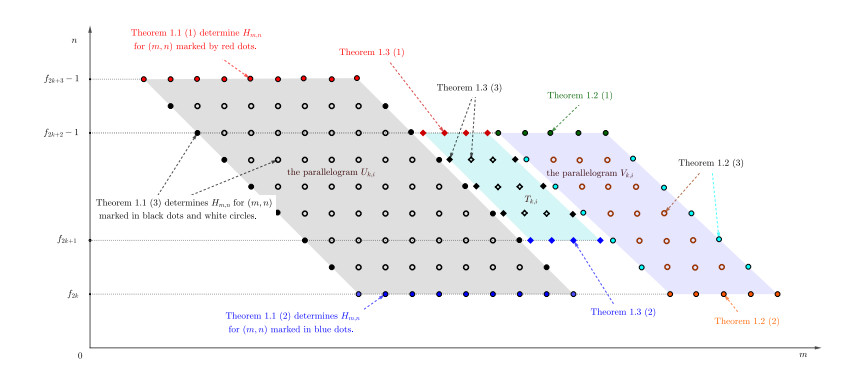
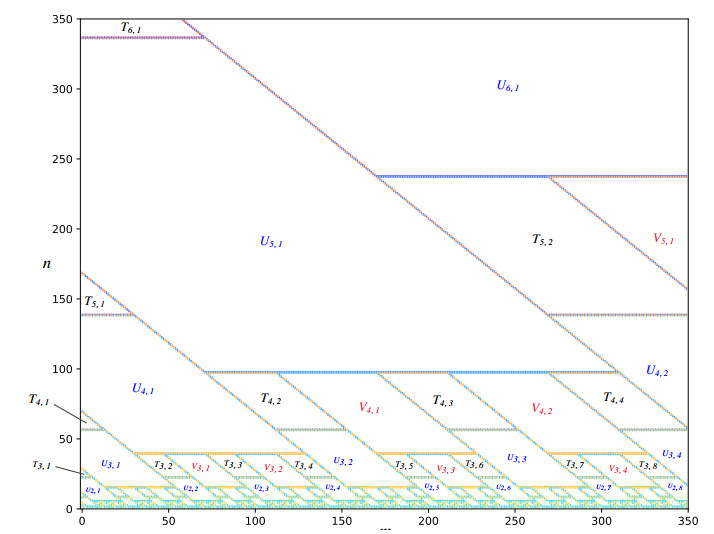
We give the explicit values of Hankel determinants $H_{m, n}$ for the sequence ${\bf{s}}$ for all $m\ge 0$ and $n\ge 1$. In Figure 1, we use the color at the point $(m, n)$ to indicate the value of $H_{m, n}$. For example, if $H_{m, n}\neq H_{m', n'}$, then points $(m, n)$ and $(m', n')$ will be marked by different colors. In particular, if $H_{m, n} = 0$, then the point $(m, n)$ is marked by white. Then we can see the distribution of first values of $H_{m, n}$ from Figure 1 and the collection of all the points $(m, n)$ with $H_{m, n} = 0$ are the union of disjoint parallelograms. These parallelograms (together with their boundaries) are divided into parallelograms of three types, labelled by $U_{k, i}$, $V_{k, i}$ and $T_{k, i}$ where $k\geq 0$ and $i\geq 1$ (for detailed definitions, see Section 3).

For all $k\geq 0$ and $i\geq 1$, Theorem 1.1 (resp. Theorem 1.2, Theorem 1.3) gives the exact value of $H_{m, n}$ for all $(m, n)\in U_{k, i}$ (resp. $V_{k, i}$, $T_{k, i}$); see Figure 2. Since for $k\geq 0$ and $i\geq 1$, the parallelograms $U_{k, i}$, $V_{k, i}$ and $T_{k, i}$ are disjoint and they tile the lattices in the first quadrant; see Proposition 3.1 in Section 3. Combing this nice property and Theorem 1.1, 1.2 and 1.3, we obtain the values of $H_{m, n}$ for all $m\geq 0$ and $n\geq 1$.

To state our results, we need four (technically defined) integer sequences $(f_n)_{n\geq 0}$, $(\alpha_i)_{i\ge 1}$, $(\beta_i)_{i\ge 1}$ and $(\gamma_i)_{i\ge 1}$; see Section 3 for their definitions. These four sequences are used to locate the corners of parallelograms $U_{k, i}$, $V_{k, i}$ and $T_{k, i}$. Our main results are the following.

Theorem 1.1. Let $k\ge 0$ and $U_k = \cup_{i\ge 1}U_{k, i}$. For all $(m, n)\in U_{k}$,

1. when $n = f_{2k+3}-1$, $H_{m, n} = (-1)^{k+1}(-1)^{\frac{f_{2k+5}}{2}-\Phi_{k+1}(m+n)} \cdot\frac{f_{2k+1}}{2}$;

2. when $n = f_{2k}$, $H_{m, n} = (-1)^{k+1}(-1)^{\frac{f_{2k+2}-1}{2}}\cdot \frac{f_{2k+1}}{2}$;

3. when $f_{2k} < n < f_{2k+3}-1$, if $m+n = \alpha_i-f_{2k+2}+1$ or $\alpha_i$ for some $i\ge 1$, then

otherwise $H_{m, n} = 0$.

Theorem 1.2. Let $k\ge 0$ and $V_{k} = \cup_{i\ge 1}V_{k, i}$. For all $(m, n)\in V_{k}$,

1. when $n = f_{2k+2}-1$, $H_{m, n} = (-1)^{\frac{f_{2k+2}+f_{2k+1}-3}{2}}\cdot \frac{f_{2k+1}}{2}$;

2. when $n = f_{2k}$, $H_{m, n} = (-1)^{k+1}(-1)^{\frac{f_{2k+2}-1}{2}}\cdot \frac{f_{2k+1}}{2}$;

3. when $f_{2k} < n < f_{2k+2}-1$, if $m+n = \beta_i+1$ or $\beta_i+f_{2k+1}$ for some $i\ge 1$, then

otherwise $H_{m, n} = 0$.

Theorem 1.3. Let $k\ge 0$ and $T_{k} = \cup_{i\ge 1}T_{k, i}$. For all $(m, n)\in T_{k}$,

1. when $n = f_{2k+2}-1$, $H_{m, n} = (-1)^{\frac{f_{2k}-1}{2}}\cdot f_{2k}$;

2. when $n = f_{2k+1}$, $H_{m, n} = (-1)^{\Phi_k(m+n)-\frac{f_{2k+1}}{2}-1}\cdot f_{2k}$;

3. when $f_{2k} < n < f_{2k+2}-1$, if $m+n = \gamma_i-f_{2k}+1$ or $\gamma_i$ for some $i\ge 1$, then

otherwise $H_{m, n} = 0$.

Sketch of proofs of main results

The computational result indicates that the collection of points $(m, n)$ such that the Hankel determinant $H_{m, n} = 0$ is covered by disjoint parallelograms of three different types, denoted by $U_{*, *}, V_{*, *}$ and $T_{*, *}$; see Figure 1. This inspires us to calculate the Hankel determinant $H_{m, n}$ in each parallelogram (according to the location of $(m, n)$). Then connect the values of Hankel determinants in different parallelograms.

Step 1 Locate the parallelograms.

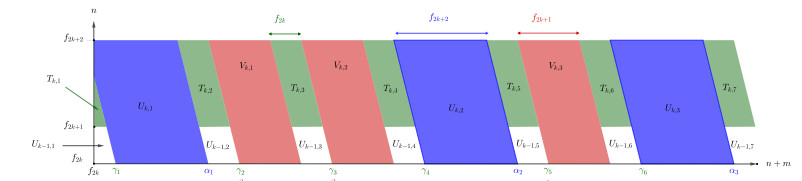
We first find that the second coordinates of the corners of those parallelograms can be expressed in terms of an integer sequence $(f_n)_{n\geq 0}$ (see Figure 2 for example). Then we see that the first coordinates of corners of three types of parallelograms are determined by three integer sequences $(\alpha_i)_{i\ge 1}$, $(\beta_i)_{i\ge 1}$ and $(\gamma_i)_{i\ge 1}$ introduced in Section 3. Then we characterize the parallelograms (observed in Figure 1) by (3.1). Proposition 3.1 showed that parallelograms defined by (3.1) tile the first quadrant.

Step 2 Calculate $H_{m, n}$ for $(m, n)$ inside the parallelograms $U_{k, *}$, $V_{k, *}$ and $T_{k, *}$.

Lemma 4.1 show that $H_{m, n} = 0$ for all $(m, n)$ which are not on the boundary of those parallelograms. Now the white part in Figure 1 is clear.

Step 3 Reduction on the boundary of $U_{k, *}$, $V_{k, *}$ and $T_{k, *}$.

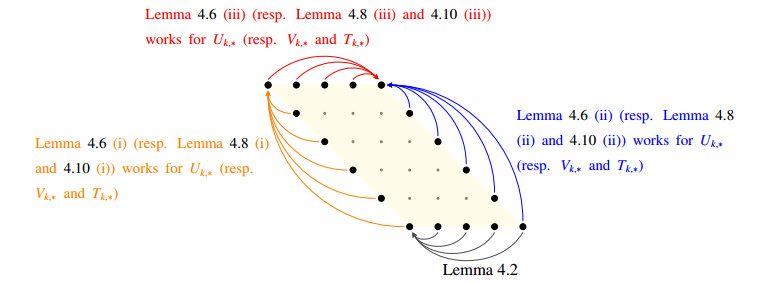
● By Lemma 4.2 and Lemma 4.6 (resp. Lemma 4.8, Lemma 4.10), calculating $H_{m, n}$ for all $(m, n)$ on the boundary of $U_{k, *}$ (resp. $V_{k, *}$, $T_{k, *}$) is reduced to calculate the determinant $H_{m, n}$ for only one point $(m, n)$ on its boundary. See Figure 3.

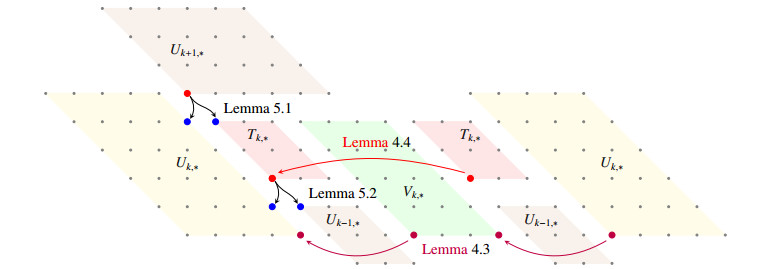
● Lemma 4.3 connects the values of $H_{m, n}$ for $(m, n)$ on the lower edge of $U_{k, *}$ and $V_{k, *}$. Lemma 4.4 builds similar connections for the values of $H_{m, n}$ for $(m, n)$ on the lower edge of $T_{k, i}$ and $T_{k, i+1}$. See Figure 4.

Therefore, to obtain the values of $H_{m, n}$ for all $(m, n)$ on the boundary of all $U_{k, *}$ and $V_{k, *}$, we only need to calculate $H_{m, n}$ for one point $(m, n)$ on the boundary of $U_{k, 1}$.

Step 4 Reduction on $k$. Lemma 5.1 enable us to calculate $H_{m, n}$ for $(m, n)$ on the boundary of $U_{k+1, *}$ by using the values of $H_{m, n}$ on the boundary of $U_{k, *}$ and $T_{k, *}$. Lemma 5.2 enable us to calculate $H_{m, n}$ for $(m, n)$ on the boundary of $T_{k, *}$ by using the values of $H_{m, n}$ on the boundary of $U_{k, *}$ and $U_{k-1, *}$. See Figure 4.

Step 5 According to step 3 and step 4, to obtain the value of $H_{m, n}$ for all $(m, n)$, we only need to calculate $H_{m, n}$ for $(m, n)$ on the boundary of $U_{k, 1}$, $V_{k, 1}$ and $T_{k, 2}$ for all $k$. These have been done by Theorem 5.3, Corollary 5.4 and Corollary 5.5.

The paper is organized as follows. In Section 2, we introduce the $f$-representation of positive integers and give a criterion (Proposition 2.4) to determine $s_n$ according the $f$-representation of $n$. This criterion leads us to the key ingredient (Theorem 2.5) in calculating the Hankel determinants. Then we introduce the truncated $f$-representation which is essential in describing the parallelograms. In Section 3, we show that the parallelograms $U_{k, i}$, $V_{k, i}$ and $T_{k, i}$ tile all the integer points in the first quadrant. In Section 4, we first show that the Hankel determinants vanish when $(m, n)$ is inside a parallelogram of those three types. Next we show the relations of Hankel determinants $H_{m, n}$ on the boundary of a parallelogram $U_{k, i}$ (or $V_{k, i}$, $T_{k, i}$) for a given $k$ and $i$. Finally, for any $k\ge 0$, we describe the relation of values of Hankel determinants for parallelograms $U_{k, i}$ for all $i\ge 1$. In Section 5, we give the expressions for Hankel determinants on the boundary of $U_{k, i}$ (or $V_{k, i}$, $T_{k, i}$) for all $k\ge 0$. In the last section, we formulate and prove our main results.

2.   Some properties of the sequence s

In this section, we first introduce the $f$-representation of positive integers according to the sequence $(f_n)_{n\ge 0}$. By understanding the occurrences of $0$s in the sequence ${\bf{s}}$, we prove a key result (Proposition 2.4) which can determine $s_n$ according to the $f$-representation of $n$. Then we give the essential result (Theorem 2.5). In subsection 2.3, we introduce the truncated $f$-representation which is useful in determining the parallelograms. In section 2.4, we investigate to some sub-sequences of $(f_{n})_{n\ge 0}$ which are need in evaluating the coefficients of the Hankel determinants. Then we characterize two sub-sequences of ${\bf{s}}$ which helps us understand $H_{m, n}$.

2.1.   The occurrence of 0's in ${\bf{s}}$.

We introduce an auxiliary sequence $(f_n)_{n\ge 0}$ to determine the positions of $0$'s. For all $n\geq 0$, we define

Then $f_0 = 1$, $f_1 = 2$, and for all $n\ge 0$,

The first values are

Remark 2.1. The sequence $(f_n)_{n\geq 0}$ can be expressed in terms of Pell numbers $(p_n)_{n\geq 0}$ defined by the recurrence $p_0 = 1$, $p_1 = 2$ and $p_{n+2} = 2p_{n+1}+p_n$ for all $n\geq 0$. See the sequence A000129 in ^[12]. Indeed, $p_n$ (resp. $p_{n-1}$) is the number of 1's (resp. 0's) in $\tau^n(1)$. It is easy to verify that $f_{2n} = p_{n+1}-p_{n}$ and $f_{2n+1} = 2p_n$.

Since $(f_n)_{n\ge 0}$ is an increasing non-negative integer sequence, it is a numeration system in the following sense.

Lemma 2.2 (Theorem 3.1.1 ^[2]). Let $u_0 < u_1 < u_2 < \dots$ be an increasing sequence of integers with $u_0 = 1$. Every non-negative integer $N$ has exactly one representation of the form $\sum_{0\leq i\leq r}a_iu_i$ where $a_r\neq 0$, and for $i\ge 0$, the digits $a_i$ are non-negative integers satisfying the inequality

Proposition 2.3. Every integer $n\ge 0$ can be uniquely expressed as $n = \sum_{0\leq i\leq r}a_if_i$ with $a_i\in\{0, 1\}$, $a_r\neq 0$, and

Proof. Suppose $a_i\in\{0, 1\}$. By Lemma 2.2, we only need to show that $a_0f_0+a_1f_1+\dots+a_tf_t < f_{t+1}$ for all $t$ if and only if the condition (2.2) holds.

The 'only if' part. Suppose there is an index $i$ such that $a_ia_{i+1} = 1$. Then

which is a contradiction for $t = i+1$. Suppose there is an even index $i$ such that $a_ia_{i+2} = 1$. Then

which is a contradiction for $t = i+2$.

The 'if' part. Suppose the condition (2.2) holds. When $t$ is odd, the maximum possible value of $a_0f_0+a_1f_1+\dots+a_tf_t$ occurs when $a_ta_{t-1}\dots a_0 = 1010\dots10$, and this maximum value $f_1+f_3+\dots + f_{t-2}+f_{t} = f_{t+1}-1$. When $t$ is even, the maximum possible value of $a_0f_0+a_1f_1+\dots+a_tf_t$ occurs when $a_ta_{t-1}\dots a_0 = 1001010\dots10$. In this case, the maximum value is $f_1+f_3+\dots +f_{t-5} + f_{t-3} + f_{t} = f_{t+1}-1$.

Definition ($f$-representation). Let $n\ge 0$ be an integer. We call the representation $n = \sum_{0\leq i\leq r}a_if_i$ in Proposition 2.3 the $f$-representation of $n$. We also write $n = \sum_{i = 0}^{+\infty}a_if_i$ where $a_i = 0$ for all $i > r$. In the case that we need to emphasize that $a_i$ depends on $n$, we write $a_i = a_i(n)$ as a function of $n$.

Proposition 2.4. For any integer $n\geq 0$ with the $f$-representation $\sum_{i = 0}^{r}a_i(n)f_i$, we have $s_n = 0$ if and only if $a_0(n) = 1$.

Proof. One can verify directly that the result holds for all $n < f_4 = 7$. Assume that the result holds for $n < f_{2k}$ where $k\geq 2$. We only need to prove it for all $f_{2k}\leq n < f_{2k+2}$.

Suppose $f_{2k}\le n < f_{2k+1}$. One has $a_{2k}(n) = 1$ and hence $a_0(n-f_{2k}) = a_0(n)$. Note that $f_{2k} = |\tau^{k}(1)|$ and

We see that $s_n$ is the $(n+1)$-th letter of $\tau^{k+1}(1)$ and it is also the $(n+1-f_{2k})$-th letter of $\tau^{k}(0) = \tau^{k-1}(1)$. Consequently, $s_{n} = s_{n-f_{2k}}$. Since

by the inductive assumption, we have $s_{n-f_{2k}} = 0$ if and only if $a_0(n-f_{2k}) = 1$. Therefore, $s_n = 0$ if and only if $a_0(n) = 1$.

Suppose $f_{2k+1}\le n < f_{2k+2}$. In this case $a_{2k+1}(n) = 1$ and $a_0(n-f_{2k+1}) = a_0(n)$. Since $|\tau^{k}(10)| = f_{2k+1}$, it follows from (2.3) that $s_n = s_{n-f_{2k+1}}$. Note that

By the inductive assumption, $s_{n-f_{2k+1}} = 0$ if and only if $a_{0}(n-f_{2k+1}) = 1$ which implies the result also holds for all $f_{2k+1}\le n < f_{2k+2}$.

2.2.   Comparing digits in the sequence ${\bf{s}}$ with a fixed gap

We introduce the truncated $f$-representations (of positive integers) which are useful in telling two digits with a fixed gap in ${\bf{s}}$ are equal or not.

Definition. (Truncated $f$-representation) Let $n\geq 0$ be an integer with the $f$-representation $\sum_{i = 0}^{+\infty}a_i(n)f_i$. For all integers $k\ge 0$, the truncated $f$-representation of $n$ is

The next lemma gives a criterion that when two digits (with a fixed gap) in ${\bf{s}}$ are equal by using their positions.

Theorem 2.5. Let $n\geq 0$ be an integer with the $f$-representation $\sum_{i = 0}^{+\infty}a_i(n)f_i$. Then

$(i)$ for all $k\ge 0$, $s_{n+f_{2k}}\neq s_n$ if and only if $\Phi_{k}(n)\in\{\frac{f_{2k+1}}{2}, \frac{f_{2k+1}}{2}-1\}$;

$(ii)$ for all $k\ge 1$, $s_{n+f_{2k+1}}\neq s_n$ if and only if $\Phi_{k}(n)\in\{\frac{f_{2k+3}}{2}, \frac{f_{2k+3}}{2}-1, \frac{f_{2k+3}}{2}+f_{2k}, \frac{f_{2k+3}}{2}+f_{2k}-1\}$.

Proof. (ⅰ) We prove by induction on $k$. When $k = 0$, by Proposition 2.3, there are only four possible values for $a_0(n)a_1(n)a_2(n)$. By Eq (2.1), we have

Then we see that $a_0(n)\neq a_0(n+f_0)$ if and only if $\Phi_{0}(n) = 0$ or $1$. The result holds for $k = 0$.

When $k = 1$, note that $\Phi_{1}(n)\leq \sum_{i = 0}^{4}f_i < f_5 = 10$. We see

Then we have $a_0(n)\neq a_0(n+f_2)$ if and only if $\Phi_{1}(n) = 1$ or $2$, that is $\frac{f_3}{2}-1$ or $\frac{f_3}{2}$. The result also holds for $k = 1$.

Now assume that the result holds for all $0\leq k < \ell$ with $\ell\ge 2$. We prove it for $k = \ell$. Let $w = a_{2\ell-2}(n)a_{2\ell-1}(n)\dots a_{2\ell +2}(n)$ and $v = a_{2\ell-2}(n+f_{2\ell})a_{2\ell-1}(n+f_{2\ell})\dots a_{2\ell +1}(n+f_{2\ell})$. According to Proposition 2.3, $w$ can take only 10 different values.

While $w\neq 01000$, one can determine $v$ directly using Eq (2.1); thus in these cases, $a_{i}(n+f_{2\ell}) = a_i(n)$ for all $0\leq i\leq 2\ell -3$; see Table 1. For instance, when $w = 10010$,

Hence one can see that $a_0(n+f_{2\ell}) = a_0(n)$.

When $w = 01000$, set $n' = \sum_{i = 0}^{2\ell-2}a_i(n)f_i$. Then $a_0(n) = a_0(n')$ and

Noticing that $n' + f_{2\ell -4} < f_{2\ell -2}$, we have $a_i(n+f_{2\ell}) = a_i(n'+f_{2\ell-4})$ for all $0\leq i\leq 2\ell -2$. In particular, $a_0(n+f_{2\ell}) = a_0(n'+f_{2\ell-4})$. By Proposition 2.4 and the inductive assumption,

By Eq (2.1), we have

Then we obtain that

It follows from Proposition 2.4 that the result holds for $k = \ell$.

(ⅱ) For any $k\ge 1$, let $u = a_{2k}(n)a_{2k+1}(n)a_{2k+2}(n)$. It follows from Proposition 2.4 that $u\in\{100,010,001\}$. The proof is divided into the following three cases.

● When $u = 001$, we also have $a_{2k+3}(n) = a_{2k+4}(n) = 0$. So

Let $n' = \sum_{i = 0}^{2k-1}a_i(n)f_i$. Then $a_0(n) = a_0(n')$. Since $n' < f_{2k}$ and $n'+f_{2k-2} < f_{2k+1}$, we have $a_i(n'+f_{2k-2}) = a_i(n+f_{2k+1})$ for all $0\leq i\leq 2k$. Thus

where in the last step we use Theorem 2.5(ⅰ). By Eq (2.1) and Eq (2.4),

So when $u = 001$, $a_0(n+f_{2k+1})\neq a_0(n)$ if and only if

● Suppose $u = 010$. Applying Eq (2.1) twice, we obtain that

Then

Let $n' = \sum_{i = 0}^{2k-1}a_i(n)f_i$. Using Theorem 2.5(ⅰ), the same argument as in the case $u = 001$ leads us to the fact that

● When $u = 100$, we have $a_{2k-2}(n) = a_{2k-1}(n) = 0$. Then

which implies that $a_0(n+f_{2k+1}) = a_0(n)$.

2.3.   Integers with the same truncated $f$-representation

To apply Theorem 2.5, we need to investigate the integers of the same truncated $f$-representations. The following two lemmas (Lemma 2.6 and Lemma 2.8) serve for this purpose.

For all $k\ge 0$, denote

Let $E_k = E'_k\cup E''_k = (x^{(k)}_j)_{j\ge 1}$ where $x^{(k)}_1 < x^{(k)}_2 < x^{(k)}_3 < \dots$. The first values of $E_k$ are

Lemma 2.6. Let $k\ge 0$ and $x\in E'_k$ with $x = x^{(k)}_j$ for some $j\ge 2$. Then $x-f_{2k+2} = x^{(k)}_{j-1}\in E_k$.

Proof. Let $x\in E''_{k}$ with $x = x_{j}^{(k)}$ for some $j\ge 2$. Note that $\frac{f_{2k+3}}{2}+f_{2k} = f_{2k+2}+\frac{f_{2k-1}}{2}$. By Proposition 2.3, have $a_{2k+3}(x) = a_{2k+4}(x) = 0$. When $0 < b < f_{2k}-\frac{f_{2k-1}}{2}$, we see

which implies that $x+b\notin E_k$. When $f_{2k}-\frac{f_{2k-1}}{2}\leq b < f_{2k+2}$,

So $x+b\notin E_k$. Since $\Phi_{k}(x+f_{2k+2}) = \frac{f_{2k+3}}{2}$, we have $x+f_{2k+2} = x_{j+1}^{(k)}\in E'_k$.

Let $x\in E'_{k}$ with $x = x_{j}^{(k)}$ for some $j\ge 1$. According to Proposition 2.3, $a_{2k+3}(x)a_{2k+4}(x) = 00$, $10$ or $01$, which can be divided into two sub-cases.

● $a_{2k+3}(x)a_{2k+4}(x) = 00$. For $0 < b\leq f_{2k}$, we see $\Phi_{k}(x+b) = \Phi_{k}(x)+b = \frac{f_{2k+3}}{2}+b$. Thus $x+f_{2k} = x_{j+1}^{(k)}\in E''_k$.

● $a_{2k+3}(x)a_{2k+4}(x) = 01$ or $10$. For $0 < b < f_{2k}$, we see

Thus $x+b\notin E_k$. For $f_{2k}\leq b < f_{2k+2}$, we have

which yields that $x+b\notin E_k$. Noting that $\Phi_k(x+f_{2k+2}) = \Phi_k(x) = \frac{f_{2k+3}}{2}$, we obtain that $x+f_{2k+2} = x_{j+1}^{(k)}\in E'_k$.

From the above argument, we see that if $x = x_{j}^{(k)}\in E'_k$ for some $j\ge 2$, then either $x-f_{2k+2} = x_{j-1}^{(k)}\in E''_k$ or $x-f_{2k+2} = x_{j-1}^{(k)}\in E'_k$ with $a_{2k+3}(x-f_{2k+2})a_{2k+4}(x-f_{2k+2})\neq 00$. The result holds.

Remark 2.7. From the proof of Lemma 2.6, we see the gaps between two adjacent elements in $E_k$ are $f_{2k}$ and $f_{2k+2}$. That is $x_{j+1}^{(k)}-x_{j}^{(k)} = f_{2k}$ or $f_{2k+2}$ for all $j\ge 1$. Moreover, the gaps between two adjacent elements in $E'_k$ are $f_{2k+2}$ and $f_{2k+3}$.

For all $k\ge 0$, let

where $y^{(k)}_1 < y^{(k)}_2 < y^{(k)}_3 < \dots$. Write $F''_k = F_k-F'_k$. The first values of $F_k$ are

Lemma 2.8. For any $y\in F_k$ with $y = y^{(k)}_j$ for some $j\ge 1$, we have

Proof. We prove the result by giving the construction of $F_k$. It clear that $y_1^{(k)} = \frac{f_{2k+1}}{2}$. Now suppose $y = y_{j}^{(k)}\in F_k$ where $j\ge 1$. According to Proposition 2.3, we see $a_{2k+3}(y)a_{2k+4}(y) = 00$, $01$ or $01$.

● $a_{2k+3}(y)a_{2k+4}(y) = 00$, i.e., $y\in F'_{k}$. Note that $\frac{f_{2k+1}}{2} = f_{2k-1}+\frac{f_{2k-3}}{2}$. For $0 < b < f_{2k+3}-\frac{f_{2k+1}}{2}$, we have $\Phi_k(y+b) = \frac{f_{2k+1}}{2}+b$, so $y+b\notin F_k$. For $f_{2k+3}-\frac{f_{2k+1}}{2}\leq b < f_{2k+3}$,

so $y+b\notin F_{k}$. Since $\Phi_{k}(y+f_{2k+3}) = \Phi_{k}(y)$, we obtain that $y+f_{2k+3} = y_{j+1}^{(k)}\in F_{k}-F_{k}'$.

● $a_{2k+3}(y)a_{2k+4}(y) = 10$ or $01$. For $0 < b < f_{2k+2}-\frac{f_{2k+1}}{2}$, we have $\Phi_k(y+b) = \frac{f_{2k+1}}{2}+b$, so $y+b\notin F_k$. For $f_{2k+2}-\frac{f_{2k+1}}{2}\leq b < f_{2k+2}$, since

we also have $y+b\notin F_{k}$. It follows from $\Phi_k(y+f_{2k+2}) = \Phi_{k}(y)$ that $y+f_{2k+2} = y_{j+1}^{(k)}\in F_k$.

The result follows from the above two sub-cases.

Remark 2.9. From the proof of Lemma 2.8, we see the gaps between two adjacent elements in $F_k$ are $f_{2k+2}$ and $f_{2k+3}$. That is $y_{j+1}^{(k)}-y_{j}^{(k)} = f_{2k+2}$ or $f_{2k+3}$ for all $j\ge 1$. Moreover, the gaps between two adjacent elements in $F''_k$ are $f_{2k+2}$ and $f_{2k+4}$.

2.4.   Two subsequences of ${\bf{s}}$

The subsequences $(s_{\frac{f_{2k+1}}{2}})_{k\ge 0}$ and $(s_{\frac{f_{2k+1}}{2}-1})_{k\ge 0}$ can be determined according to the parity of $k$; see Lemma 2.11. We start with an auxiliary lemma which concerns the parity of $\frac{f_{2k+1}}{2}$.

Lemma 2.10. For all $k\ge 0$,

$(i)$ $f_{2k}\equiv\begin{cases} 1, & \mathit{\text{if}}\; k\equiv 0 \; \mathit{\text{or}}\; 3 \pmod 4, \\ 3, & \mathit{\text{if}}\; k\equiv 1 \; \mathit{\text{or}}\; 2 \pmod 4, \end{cases}\pmod 4$,

$(ii)$ $f_{2k+1}\equiv \begin{cases} 2, & \mathit{\text{if}}\;k\;\mathit{\text{is even}}, \\ 0, & \mathit{\text{if}}\;k\;\mathit{\text{is odd}}, \\ \end{cases}\pmod 4$.

Proof. (ⅰ) Note that $f_0 = 1$ and $f_{2} = 3$. Since $f_{2n}$ is odd for all $n\ge 0$, using Eq. (2.1) twice, we have for all $k\ge 2$,

The result follows by induction on $k$.

(ⅱ) The initial value is $f_1 = 2$. Using Eq. (2.1) and the previous result (ⅰ), we have for all $k\ge 1$,

which is the desired result.

In the calculation of $H_{m, n}$, we need to know $s_n$ explicitly for some $n$. The next lemma determines the values of two sub-sequences ${\bf{s}}$.

Lemma 2.11. For all $k\ge 0$,

Proof. By Eq (2.1), we obtain that for all $k\ge 0$,

When $k$ is odd,

When $k\ge 2$ is even,

It follows from (2.6) and (2.7) that for all $k\geq 0$,

and

Then by Proposition 2.4, the result follows.

3.   Partition of the lattice

According to the values of the Hankel determinants of ${\bf{s}}$, we tile the integer lattice using the following parallelograms. Given a $k\ge 0$, write the elements in $E'_{k+1}$, $F''_{k}$ and $E'_k$ in ascending order as follows:

Moreover, let $\beta_i = \beta'_{i}+f_{2k}$ for all $i\ge 1$. We define three different types of parallelograms: for $i\ge 1$,

see Figure 1. Let $U_k = \cup_{i\ge 1}U_{k, i}$, $V_{k} = \cup_{i\ge 1}V_{k, i}$ and $T_{k} = \cup_{i\ge 1}T_{k, i}$.

Proposition 3.1. The parallelograms $\{U_{k, i}\}$, $\{V_{k, i}\}$, and $\{T_{k, i}\}$ introduce a partition of pairs of positive integers. Namely, $\mathbb{N}\times\mathbb{N}_{\ge 1} = \bigsqcup_{k\geq 0} (U_{k}\sqcup V_{k}\sqcup T_{k})$ where $\sqcup$ denotes the disjoint union.

Proof. Let $m\ge 0$ and $n\ge 1$ be two integers. Since $(f_k)_{k\ge 0}$ and $(\gamma_{k})_{k\ge 1}$ are two increasing unbounded non-negative integer sequences, there exist $k\ge 0$ and $\ell\ge 1$ such that $f_{2k}\le n < f_{2k+2}$ and $\gamma_{\ell-1} < n+m\leq \gamma_{\ell}$ where $\gamma_0: = 0$. The result clearly holds when $\ell = 1$. Now we assume that $\ell\ge 2$. From the proof of Lemma 2.6 we see that $\gamma_{\ell}-\gamma_{\ell-1} = f_{2k+2}$ or $f_{2k+3}$ for all $\ell\ge 2$. When $\gamma_{\ell}-f_{2k} < n+m\leq \gamma_{\ell}$, we have

see also Figure 5. When $\gamma_{\ell-1} < n+m\leq \gamma_{\ell}-f_{2k}$, we have the following two cases:

Case 1: $\gamma_{\ell}-\gamma_{\ell-1} = f_{2k+2}$. In this case, we shall verify that $(m, n)\in V_k$. To do this, we only need to show that $\gamma_{\ell-1}-f_{2k}\in F''_{k}$. Since $\gamma_{\ell-1}\in E'_{k}$, we have $\Phi_{k}(\gamma_{\ell-1}) = \frac{f_{2k+3}}{2}$ and $\Phi_{k}(\gamma_{\ell-1}-f_{2k}) = \frac{f_{2k+3}}{2}-f_{2k} = \frac{f_{2k+1}}{2}$. So $(\gamma_{\ell-1}-f_{2k})\in F_{k}$. Suppose on the contrary that $(\gamma_{\ell-1}-f_{2k})\in F'_{k}$. Then $\Phi_{k+1}(\gamma_{\ell-1}-f_{2k}) = \frac{f_{2k+1}}{2}$ and $\Phi_{k+1}(\gamma_{\ell-1}) = \frac{f_{2k+3}}{2}$. This implies $\Phi_{k}(\gamma_{\ell-1}+f_{2k+2}) = \frac{f_{2k+1}}{2}$ and $(\gamma_{\ell-1}+f_{2k+2})\notin E'_k$. Note that in this case $\gamma_{\ell} = \gamma_{\ell-1}+f_{2k+2}$. We conclude that $\gamma_{\ell}\notin E'_{k}$ which is a contradiction. Hence, $(\gamma_{\ell-1}-f_{2k})\in F''_{k}$. The result follows.

Case 2: $\gamma_{\ell}-\gamma_{\ell-1} = f_{2k+3}$. We assert that, in this case, $\gamma_{\ell-1}-f_{2k}\in F'_{k}$. Since $\gamma_{\ell-1}\in E'_{k}$, we have $\Phi_{k}(\gamma_{\ell-1}) = \frac{f_{2k+3}}{2}$. Consequently, $\Phi_{k}(\gamma_{\ell-1}-f_{2k}) = \frac{f_{2k+1}}{2}$ and $(\gamma_{\ell-1}-f_{2k})\in F_{k}$. Suppose $(\gamma_{\ell-1}-f_{2k})\in F''_{k}$. Then $\Phi_{k}(\gamma_{\ell-1}) = \frac{f_{2k+3}}{2}$ and $\Phi_{k+1}(\gamma_{\ell-1})\neq \frac{f_{2k+3}}{2}$. It follows that $\Phi_{k}(\gamma_{\ell-1}+f_{2k+3}) = \frac{f_{2k+3}}{2}+f_{2k}$. Since $\gamma_{\ell-1}+f_{2k+3} = \gamma_{\ell}$, we obtain that $\gamma_{\ell}\notin E'_{k}$ which is a contradiction. Now we have $\gamma_{\ell-1}-f_{2k}\in F'_{k}$. This yields that $\Phi_{k+1}(\gamma_{\ell-1}) = \frac{f_{2k+3}}{2}$. Observing that $\Phi_{k+1}(\gamma_{\ell}-f_{2k}) = \Phi_{k+1}(\gamma_{\ell-1}+f_{2k+2}) = \frac{f_{2k+5}}{2}$, we see $\gamma_{\ell}-f_{2k}\in E'_{k+1}$. So $(m, n)\in U_k$.

4.   Relations of Hankel determinants

In this section, we use the Theorem 2.5 to show the determinant value inside $U_k$, $V_k$, $T_k$ is 0. For some integer $k\ge 0$, we prove the relationship between the determinant value of the boundary of $U_k$, $V_k$, $T_k$. We assert that as long as we know one value of $U_k$($V_k$ or $T_k$), we can know all its values.

4.1.   Inside the parallelograms

The Hankel determinant $H_{m, n}$ vanishes if $(m, n)$ is not on the boundary of any parallelogram $U_{k, i}$, $V_{k, i}$ or $T_{k, i}$.

Lemma 4.1. Let $m\ge 1$ and $n\ge 0$ be two integer.

$(i)$ If $(m, n)$ is inside $V_{k, i}$ for some $k\ge 0$ and $i\ge 1$, i.e.,

then $H_{m, n} = 0$.

$(ii)$ If $(m, n)$ is inside $T_{k, i}$ for some $k\ge 0$ and $i\ge 1$, i.e.,

then $H_{m, n} = 0$.

$(iii)$ If $(m, n)$ is inside $U_{k, i}$ for some $k\ge 0$ and $i\ge 1$, i.e.,

then $H_{m, n} = 0$.

Proof. Let $A_{m+i}$ be the $i$-th row of $H_{m, n}$. Then

(ⅰ) When $m\leq \beta'_i+1$, recall that $\beta'_i = \beta_i-f_{2k}\in F''_{k}$. Since $n\leq f_{2k+2}-2$, by Lemma 2.8, we have $\Phi_{k}(\beta'_k + j)\neq \frac{f_{2k+1}}{2}$ or $\frac{f_{2k+1}}{2}-1$ for all $1\leq j\leq n$. Then it follows from Theorem 2.5(ⅰ) that

which gives $H_{m, n} = 0$. When $m > \beta'_i+1$, note that $n+m\leq \beta'_k + f_{2k+2}-1$. By Lemma 2.8, we have $\Phi_{k}(m + j)\neq \frac{f_{2k+1}}{2}$ or $\frac{f_{2k+1}}{2}-1$ for all $1\leq j\leq n$. Then it follows from Theorem 2.5(ⅰ) that

So $H_{m, n} = 0$.

(ⅱ) Recall that $\gamma_i\in E'_k$ and by Lemma 2.6, $\gamma_i$ and $\gamma_i-f_{2k+2}$ are adjacent elements in $E_k$. Let

Combining Lemma 2.6 and Theorem 2.5(ⅱ), we have $A_{m+r} = A_{m+r+f_{2k+1}}$ which means $H_{m, n} = 0$.

(ⅲ) Recall that $\alpha_i\in E'_{k+1}$ and by Lemma 2.6, $\alpha_i$ and $\alpha_i-f_{2k+4}$ are adjacent elements in $E_{k+1}$. When $m\le \alpha_i - f_{2k+4} + 1$, note that $\alpha_i-f_{2k+4}+n < \alpha_i - f_{2k+2} - 1$. By Theorem 2.5(ⅱ), we have

Thus $H_{m, n} = 0$. When $m > \alpha_i - f_{2k+4} + 1$, since $n+m-1\leq \alpha_i-2$, by Theorem 2.5(ⅱ), we obtain that

which also implies $H_{m, n} = 0$.

4.2.   Determinants on the horizontal edges of the parallelograms

We first deal with the Hankel determinants $H_{m, n}$ on the horizontal edges with $n = f_{2k}$ and $f_{2k+1}$ where $k\ge 0$.

Lemma 4.2. Let $k\ge 0$ and $i\ge 1$.

$(i)$ $\textrm{(Bottom edge of $ V_{k, i} $)}$ $H_{\beta'_i+r, \, f_{2k}} = H_{\beta'_i+1, \, f_{2k}}$ for all $1\leq r\leq f_{2k+1}$.

$(ii)$ $\textrm{(Bottom edge of $ U_{k, i} $)}$ $H_{\alpha_i-f_{2k+3}+r, \, f_{2k}} = H_{\alpha_i-f_{2k}, \, f_{2k}}$ for all $1\leq r\leq f_{2k+2}$.

$(iii)$ $\textrm{(Bottom edge of $ T_{k, i} $)}$ $H_{\gamma_{i}-f_{2k+2}+r, \, f_{2k+1}} = (-1)^{r+1}H_{\gamma_{i}-f_{2k+1}, \, f_{2k+1}}$ for all $1\leq r \leq f_{2k}$ with $\gamma_{i}-f_{2k+2}+r\ge 0$.

Proof. (ⅰ) Let $A_j = (s_{\beta'_i+j}, \, s_{\beta'_i+j+1}, \, \dots, \, s_{\beta'_i+j+f_{2k}-1})$. Then for $1\leq j < f_{2k+1}$,

Recall that $\beta'_i\in F''_k$. By Lemma 2.8, since $j+f_{2k}-1\leq f_{2k+2}-2$, we see $\Phi_k(\beta'_i+\ell)\neq \frac{f_{2k+1}}{2}$ or $\frac{f_{2k+1}}{2}-1$ for all $1\leq \ell \leq f_{2k+2}-2$. Applying Theorem 2.5(ⅰ), we have

Therefore, for $1\leq j < f_{2k+1}$,

where the last equality follows from Lemma 2.10(ⅰ).

(ⅱ) Recall that $\alpha_i\in E'_{k+1}$ and $\Phi_{k+1}(\alpha_i) = \frac{f_{2k+5}}{2}$. Let $y = \alpha_i-f_{2k+3}$. Then $\Phi_{k+1}(y) = \frac{f_{2k+1}}{2}$ and $y\in F'_k$. Let $B_j = (s_{y+j}, \, s_{y+j+1}, \, \dots, \, s_{y+j+f_{2k}-1})$. Then for $1\leq j < f_{2k+2}$,

Since $j+f_{2k}-1\leq f_{2k+3}-2$, by Lemma 2.8 and Theorem 2.5(ⅰ),

Therefore, for $1\leq j < f_{2k+2}$,

where the last equality follows from Lemma 2.10(ⅰ).

(ⅲ) Recall that $\gamma_i\in E'_{k}$. By Lemma 2.6, $g: = \gamma_i-f_{2k+2}\in E_{k}$. Write

For $1\leq r < f_{2k}$,

By Theorem 2.5, $A_{g+r} = A_{g+r+f_{2k+1}}$. Then using Lemma 2.10, for all $1\leq r < f_{2k}$,

and $H_{g+r, \, f_{2k+1}} = (-1)^{f_{2k}-r}H_{g+r+f_{2k}, \, f_{2k+1}} = (-1)^{1+r}H_{g+r+f_{2k}, \, f_{2k+1}}.$

In fact, for all $i\ge 1$, the Hankel determinants on the bottom of $U_{k, i}$ and $V_{k, i}$ take the same value which depends only on $k$. The following lemma helps us to connect the determinants on the bottom of $U_{k, *}$ and $V_{k, *}$.

Lemma 4.3. Let $k\ge 0$ and $i\ge 1$. If $\gamma_{i+1}-\gamma_i = f_{2k+3}$, then $H_{\gamma_i+f_{2k}+1, \, f_{2k}} = H_{\gamma_{i+1}-f_{2k}+1, \, f_{2k}}$. If $\gamma_{i+1}-\gamma_i = f_{2k+2}$, then $H_{\gamma_i+1, \, f_{2k}} = H_{\gamma_{i+1}-f_{2k}+1, \, f_{2k}}$.

Proof. Suppose $\gamma_{i+1}-\gamma_i = f_{2k+3}$. Then $\Phi_{k}(\gamma_{i}+f_{2k}) = \frac{f_{2k+3}}{2}+f_{2k}$. Since $3f_{2k} = f_{2k+2}+f_{2k-1} < f_{2k+3}$, by Theorem 2.5(ⅱ), we have

Therefore

When $\gamma_{i+1}-\gamma_i = f_{2k+2}$, we have $\Phi_{k}(\gamma_i) = \frac{f_{2k+3}}{2}$. By Theorem 2.5(ⅱ),

So $H_{\gamma_i+1, \, f_{2k}} = H_{\gamma_{i+1}-f_{2k}+1, \, f_{2k}}$.

Next we give the connection between $T_{k, i}$ and $T_{k, i+1}$.

Lemma 4.4. For all $i\ge 1$, $H_{\gamma_i-f_{2k+1}, \, f_{2k+1}} = H_{\gamma_{i+1}-f_{2k+1}, \, f_{2k+1}}$.

Proof. If $\gamma_{i+1}-\gamma_i = f_{2k+3}$, then $\Phi_{k+1}(\gamma_i) = \frac{f_{2k+3}}{2}$ and $\Phi_{k+1}(\gamma_i+f_{2k+1}) < \frac{f_{2k+5}}{2}$. By Theorem 2.5(ⅱ), we have

Consequently, $H_{\gamma_i-f_{2k+1}, \, f_{2k+1}} = H_{\gamma_{i+1}-f_{2k+1}, \, f_{2k+1}}$.

If $\gamma_{i+1}-\gamma_i = f_{2k+2}$, then $\Phi_{k+1}(\gamma_i) = \frac{f_{2k+3}}{2}+f_{2k+3}$ or $\frac{f_{2k+3}}{2}+f_{2k+4}$. By Theorem 2.5(ⅰ), we have

Consequently, $H_{\gamma_i-f_{2k+1}, \, f_{2k+1}} = H_{\gamma_{i+1}-f_{2k+1}, \, f_{2k+1}}$.

According to Lemma 4.3 and Lemma 4.4, the values of the determinants on the bottom edges of $U_{k, i}$ and $V_{k, i}$ only depends on $k$. We improve Lemma 4.2 to the following proposition.

Proposition 4.5. Let $k\ge 0$. For all $i\ge 1$,

$(i)$ $\textrm{(Bottom edges of $ U_{k, i} $ and $ V_{k, i} $)}$ for all $1\leq r\leq f_{2k+1}$ and $1\leq r'\leq f_{2k+2}$,

$(ii)$ $\textrm{(Bottom edge of $ T_{k, i} $)}$ $H_{\gamma_{i}-f_{2k+2}+r, \, f_{2k+1}} = (-1)^{r+1}H_{\gamma_{1}-f_{2k+1}, \, f_{2k+1}}$ for all $1\leq r \leq f_{2k}$ with $\gamma_{i}-f_{2k+2}+r\ge 0$.

Proof. Since $\alpha_i-f_{2k+2}\in E'_k$ and $\beta'_i+f_{2k}\in E'_k$, Lemma 4.3 shows that the values of two determinants on the bottom edge of two adjacent parallelograms in $\{U_{k, j}\}_{j\ge 1}\cup\{V_{k, j}\}_{j\ge 1}$ are the same. Then Lemma 4.2 implies the result (ⅰ). The result (ⅱ) follows from Lemma 4.2(ⅲ) and Lemma 4.4.

4.3.   On the boundary of $U_{k, i}$

Lemma 4.6. Let $k\ge 0$ and $i\ge 1$. For all $0\leq r\leq f_{2k+2}-1$ with $\alpha_i-f_{2k+4}+2+r\ge 0$,

$(i)$ $\textrm{(Right edge of $ U_{k, i} $)}$ $H_{\alpha_i-f_{2k+3}+1+r, f_{2k+3}-1-r} = (-1)^{rk}(-1)^{\frac{r(r-1)}{2}}H_{\alpha_i-f_{2k+3}+1, f_{2k+3}-1}$,

$(ii)$ $\textrm{(Left edge of $ U_{k, i} $)}$ $H_{\alpha_i-f_{2k+4}+2+r, f_{2k+3}-1-r} = (-1)^{rk}(-1)^{\frac{r(r-1)}{2}}H_{\alpha_i-f_{2k+3}+1, f_{2k+3}-1}$,

$(iii)$ $\textrm{(Upper edge of $ U_{k, i} $)}$ $H_{\alpha_i-f_{2k+4}+2+r, f_{2k+3}-1} = (-1)^r H_{\alpha_i-f_{2k+3}+1, f_{2k+3}-1}$.

Proof. Write $y = \alpha_i-f_{2k+3}$. Recall that $\alpha_i\in E'_{k+1}$. So $\Phi_{k+1}(y) = \frac{f_{2k+1}}{2}$ and $y\in F'_{k}$.

(ⅰ) For $0\le r < f_{2k+2}$, let $A_{y+r+j}$ be the $j$-th column of $M_{y+1+r, \, f_{2k+3}-1-r}$. Applying Lemma 2.8 and Theorem 2.5(ⅰ), we see $s_{y+r+\ell} = s_{y+r+\ell+f_{2k}}$ for $1\le \ell \le f_{2k+3}-r-2$ and $s_{y+f_{2k+3}-1}\neq s_{y+f_{2k+3}-1+f_{2k}}$. Then Proposition 2.4 and Lemma 2.11 yields $s_{y+f_{2k+3}-1}-s_{y+f_{2k+3}-1+f_{2k}} = (-1)^{k}$. Therefore,

and

where in the last equality we apply Lemma 2.10 and ${\bf{0}}_{i, j}$ denotes the $i\times j$ zero matrix. It follows from Eq (4.1) that

(ⅱ) Let $B_{y-f_{2k+2}+1+r+j}$ be the $j$-th row of $M_{y-f_{2k+2}+2+r, f_{2k+3}-1-r}$. Combining Lemma 2.8, Theorem 2.5(ⅰ), Proposition 2.4 and Lemma 2.11, a similar argument as above yields

Applying Eq (4.2), we have

(ⅲ) Let $C_j$ be the $j$-th column of $M_{y-f_{2k+2}+2+r, f_{2k+3}-1}$. Then

where $C'_{p} = C_{f_{2k+3}-1-r+p}-C_{f_{2k+3}-1-r+p-f_{2k}}$ for $1\le p \le r$. According to Lemma 2.8, Theorem 2.5(ⅰ), we have $s_{y+\ell} = s_{y+\ell+f_{2k}}$ for all $1\leq \ell \leq f_{2k+3}-2$ and $f_{2k+3}+1\leq \ell \leq f_{2k+3}+r-2$. By Proposition 2.4 and Lemma 2.11, we obtain that $s_{y+f_{2k+3}-1+f_{2k}}-s_{y+f_{2k+3}-1} = (-1)^{k+1}$ and $s_{y+f_{2k+3}+f_{2k}}-s_{y+f_{2k+3}} = (-1)^{k}$. Thus

where $X$ is the $r\times r$ matrix

Expanding by the last $r$ columns, we have

Remark 4.7. From Proposition 4.5(ⅰ) and Lemma 4.6, Hankel determinants on the boundary of $U_{k, i}$ can be determined by $H_{\alpha_1-f_{2k+3}+1, f_{2k+3}-1} = H_{\frac{f_{2k+1}}{2}+1, f_{2k+3}-1}$ (the upper right corner of $U_{k, 1}$).

4.4.   On the boundary of $V_{k, i}$

Lemma 4.8. Let $k\ge 0$ and $i\ge 1$. For all $0\leq r\leq f_{2k+1}-1$,

$(i)$ $\textrm{(Left edge of $ V_{k, i} $)}$ $H_{\beta'_i-f_{2k+1}+2+r, f_{2k+2}-1-r} = (-1)^{rk}(-1)^{\frac{r(r+1)}{2}}H_{\beta'_i-f_{2k+1}+2, f_{2k+2}-1}$,

$(ii)$ $\textrm{(Right edge of $ V_{k, i} $)}$ $H_{\beta'_i+1+r, f_{2k+2}-1-r} = (-1)^{rk}(-1)^{\frac{r(r+1)}{2}}H_{\beta'_i+1, f_{2k+2}-1}$,

$(iii)$ $\textrm{(Upper edge of $ V_{k, i} $)}$ $H_{\beta'_i-f_{2k+1}+2+r, f_{2k+2}-1} = H_{\beta'_i+1, f_{2k+2}-1}$.

Proof. (ⅰ) Denote by $A_{\beta'_i-f_{2k+1}+1+r+j}$ the $j$-th row of $M_{\beta'_i-f_{2k+1}+2+r, f_{2k+2}-1-r}$. Then

From Lemma 2.8, Theorem 2.5 and Lemma 2.11, we have

For $0\leq r\leq f_{2k+1}-1$,

Thus

(ⅱ) Let $B_{\beta'_i+r+j}$ be the $j$-th column of $M_{\beta'_i+1+r, f_{2k+2}-1-r}$.

Recall that $\beta'_i\in F''_k$. By Lemma 2.8, $\beta'_i$ and $\beta'_i+f_{2k+2}$ are adjacent elements in $F_k$. It follows from Theorem 2.5(ⅰ) and Lemma 2.11 that

Hence $H_{\beta'_i+1+r, f_{2k+2}-1-r} = (-1)^{r(k+1)}(-1)^{\frac{r(r-1)}{2}}H_{\beta'_i+1, f_{2k+2}-1}$.

(ⅲ) Let $C_{\beta'_i-f_{2k+1}+1+r+j}$ be the $j$-th column of $M_{\beta'_i-f_{2k+1}+2+r, f_{2k+2}-1}$. Then

where $C'_{p} = C_{\beta'_i+f_{2k}+p}-C_{\beta'_i+p}$ for $1\leq p \leq r$. By Lemma 2.8 and Theorem 2.5(ⅰ), we have $s_{\beta'_i+\ell} = s_{\beta'_i+\ell+f_{2k}}$ for $1\leq \ell \leq f_{2k+2}-2$ and $f_{2k+2}+1\leq \ell \leq r+f_{2k+2}-1$. Moreover, by Proposition 2.4 and Lemma 2.11, we have $s_{\beta'_i+f_{2k}+f_{2k+2}-1}-s_{\beta'_i+f_{2k+2}-1} = (-1)^{k+1}$ and $s_{\beta'_i+f_{2k}+f_{2k+2}}-s_{\beta'_i+f_{2k+2}} = (-1)^{k}$. Thus

where $X$ is the $r\times r$ matrix

Now expanding $H_{\beta'_i-f_{2k+1}+2+r, f_{2k+2}-1}$ by its last $r$ columns, we obtain that for $0\leq r \leq f_{2k+1}-1$,

Remark 4.9. From Proposition 4.5(ⅰ) and Lemma 4.8, Hankel determinants on the boundary of $V_{k, i}$ can be determined by $H_{\frac{f_{2k+1}}{2}+f_{2k+3}+1, f_{2k}}$ (the lower left corner of $V_{k, 1}$).

4.5.   On the boundary of $T_{k, i}$

Lemma 4.10. Let $k\ge 0$ and $i\ge 1$.

$(i)$ $\textrm{(Left edge of $ T_{k, i} $)}$ For all $0\le r\le f_{2k}-1$ with $\gamma_i-f_{2k+3}+2+r\ge 0$,

$(ii)$ $\textrm{(Right edge of $ T_{k, i} $)}$ For all $0\le r\le f_{2k}-1$ with $\gamma_i-f_{2k+2}+1+r\ge 0$,

$(iii)$ $\textrm{(Upper edge of $ T_{k, i} $)}$ For all $0\le r\le f_{2k}-1$ with $\gamma_i-f_{2k+3}+2+r\ge 0$,

Proof. To shorten the notation, write $x = \gamma_i-f_{2k+3}+2$ and $x' = \gamma_i-f_{2k+2}+1$.

(ⅰ) Let $\max\{0, -x\}\leq \ell \leq f_{2k}-1$ and let $A_{j}$ be the $j$th row of $H_{x+\ell, f_{2k+2}-1-\ell}$. By Theorem 2.5(ⅱ) and Lemma 2.11, we see

Then for $\max\{0, -x\}\leq \ell\leq f_{2k}-1$,

Applying the above equality $r$ times, one has

(ⅱ) Let $\max\{0, -x'\}\leq \ell \leq f_{2k}-1$ and let $B_j$ be the $j$th column of $H_{x'+\ell, f_{2k+2}-1-\ell}$. By Theorem 2.5(ⅱ) and Lemma 2.11, we see

Therefore, for $\max\{0, -x'\}\leq \ell \leq f_{2k}-1$,

Applying the above equality $r$ times, one has

(ⅲ) Let $\max\{0, -x\}\leq r \leq f_{2k}-1$ and let $C_j$ be the $j$th column of $M_{x+r, f_{2k+2}-1}$. Then

where $C'_p = C_{f_{2k+2}-r-1+p}-C_{f_{2k}-r-1+p}$ for $1\le p \le r$. Note that

By Lemma 2.6 and Theorem 2.5(ⅱ), for $1\leq q\leq f_{2k+2}-2$ and $f_{2k+2}+1\leq q \leq f_{2k+2}+r-2$,

Moreover, by Lemma 2.11, $s_{\gamma_i+f_{2k+1}-1}-s_{\gamma_i-1} = (-1)^{k}$ and $s_{\gamma_i+f_{2k+1}}-s_{\gamma_i} = (-1)^{k+1}$. Then

where $X$ is the $r\times r$ matrix

Therefore,

Remark 4.11. From Proposition 4.5(ⅱ) and Lemma 4.10, Hankel determinants on the boundary of $T_{k, i}$ can be determined by $H_{\frac{f_{2k+3}}{2}+f_{2k}+1, f_{2k+1}}$(the lower left corner of $T_{k, 2}$).

5.   Evaluating the Hankel determinants

In section 4, we show that for any $k\ge 0$, to know all the determinants on the boundary of $U_{k, i}$ (resp. $V_{k, i}$, $T_{k, i}$) for all $i$, it is enough to know the value of one determinant on the boundary $U_{k, i}$ (resp. $V_{k, i}$ or $T_{k, i}$) for some $i$. In this section, for certain $i$, we shall give the expression of a determinant on the boundary $U_{k, i}$ (resp. $V_{k, i}$ or $T_{k, i}$) for all $k$.

The next result allows us to determine the determinant on the lower left corner of $U_{k, i}$ by using the determinants on the boundary of $U_{k-1, *}$ and $T_{k-1, *}$.

Lemma 5.1. $\textrm{(Lower left corner of $ U_{k, i} $)}$ For all $k\ge 1$ and $i\ge 1$,

Proof. Let $y = \alpha_i-f_{2k+3}$ and let $A_j$ be the $j$th column of $H_{y+1, f_{2k}}$. Then

Recall that $\alpha_i\in E'_{k+1}$. Then $\Phi_{k+1}(y) = \frac{f_{2k+1}}{2}$ and $\Phi_{k-1}(y+f_{2k}) = \frac{f_{2k-1}}{2}$. This implies $y\in F'_k$ and $y+f_{2k}\in F_{k-1}$. By Lemma 2.8 and Theorem 2.5(ⅰ), the fact $y+f_{2k}\in F_{k-1}$ yields that $s_{y+\ell} = s_{y+f_{2k-2}+\ell}$ for $1\leq \ell \leq f_{2k}-2$. By Lemma 2.11, $s_{y+f_{2k}-1}-s_{y+f_{2k}+f_{2k-2}-1} = (-1)^{k+1}$ and $s_{y+f_{2k}}-s_{y+f_{2k}+f_{2k-2}} = (-1)^{k}$. So

where

Since $y+f_{2k}\in F'_{k}$, by Lemma 2.8 and Theorem 2.5(ⅰ), we see

and $X = (-1)^{f_{2k}-2}H_{y+1, f_{2k}-1}$. Then the result follows from Eq (5.1) and Lemma 2.10.

Now we show how to obtain the determinant on the lower left corner of $T_{k, i}$ by using determinants on the boundary of $U_{k, i-1}$ and $U_{k-1, i+1}$.

Lemma 5.2. $\textrm{(Lower left corner of $ T_{k, i}) $}$ For all $k\ge 1$ and $i\ge 2$,

Proof. Let $y = \gamma_i-f_{2k+2}$ and let $A_j$ be the $j$th column of $H_{y+1, f_{2k+1}}$. Then

Recall that $\gamma_i\in E'_{k}$. By Lemma 2.6, $y\in E_k$ and $\Phi_{k}(y+f_{2k+1}) = \frac{f_{2k+1}}{2}$. This implies $y+f_{2k+1}\in F_{k}$. By Lemma 2.8 and Theorem 2.5(ⅰ), the fact $y+f_{2k+1}\in F_{k}$ yields that $s_{y+\ell} = s_{y+f_{2k}+\ell}$ for $1\leq \ell \leq f_{2k+1}-2$. By Lemma 2.11, $s_{y+f_{2k+1}-1}-s_{y+f_{2k+1}+f_{2k}-1} = (-1)^{k}$ and $s_{y+f_{2k+1}}-s_{y+f_{2k+1}+f_{2k}} = (-1)^{k+1}$. So

where

Since $y\in E_{k}$, by Lemma 2.6 and Theorem 2.5(ⅱ), we see

and $X = (-1)^{f_{2k+1}-2}H_{y+1, f_{2k+1}-1}$. Then the result follows from Eq (5.2) and Lemma 2.10.

Now We are able to give the exact value of the Hanker determinant on the upper right corner of $U_{k, i}$, and hence we know all the determinants on the boundary of $U_{k, i}$.

Theorem 5.3. $\textrm{(Upper right corner of $ U_{k, 1} $)}$ Let $k\ge 1$. Then

Proof. We can check directly that the result holds for $k = 1, 2$. Now suppose $k\ge 3$. Let $h_{k} = H_{\frac{f_{2k+1}}{2}+1, \, f_{2k+3}-1}$. Then

Applying Lemma 4.6(ⅰ) for $k-1$^* and $r = f_{2k-2}$,

^*We need to mention that $\alpha_i$'s depend also on $k$. For example, $\alpha_1^{(k-1)} = \frac{f_{2k+3}}{2}$ and $\alpha_1^{(k)} = \frac{f_{2k+5}}{2}$.

Applying Lemma 4.10(ⅰ) for $k-1$ and $r = f_{2k-2}$,

Combing previous equations, we have

The initial values are $h_1 = 2$, $h_2 = -5$. The result follows from the recurrence relation of $h_k$ and its initial values.

Corollary 5.4. $\textrm{(Lower left corner of $ V_{k, 1} $)}$ For all $k\ge 1$,

Proof. By Proposition 4.5,

Corollary 5.5. $\textrm{(Lower left corner of $ T_{k, 2} $)}$ For all $k\ge 1$, $H_{\frac{f_{2k+3}}{2}+f_{2k}+1, f_{2k+1}} = f_{2k}$.

Proof. From Lemma 5.2, we have

Note that $H_{\frac{f_{2k+3}}{2}+f_{2k}+2, f_{2k+1}-1}$ is on the upper left corner of $U_{k-1, 2}$. By Lemma 4.6(ⅲ),

According to Proposition 4.5 and Lemma 4.6, the determinants on the upper left corner of $U_{k-1, 1}$ and $U_{k-1, 1}$ are equal. Namely, $H_{\frac{f_{2k-1}}{2}+f_{2k+3}+1, f_{2k+1}-1} = H_{\frac{f_{2k-1}}{2}+1, f_{2k+1}-1}$. Therefore,

It follows from Lemma 4.6(ⅰ) and Lemma 2.10 that

Using Eq (5.3), Eq (5.4) and Eq (5.5), we have

6.   Proof of Theorem 1.1, 1.2 and 1.3

Proof of Theorem 1.1. Suppose $(m, n)\in U_{k, i}$ for some $i$. Then $\alpha_{i}-f_{2k+2} < n+m\leq \alpha_i$ and $m = \alpha_i-f_{2k+2}+1-n+r$ where $0\leq r < f_{2k+2}$.

Case 1: $n = f_{2k+3}-1$. Applying Lemma 4.6(ⅰ), Proposition 4.5 and then Lemma 4.6(ⅰ) again, we have

where the last equality follows from Theorem 5.3. Since $r = \alpha_i-m-n = \frac{f_{2k+5}}{2}-\Phi_{k+1}(m+n)$, by Lemma 4.6(ⅲ),

where the last equality follows from Eq (6.1).

Case 2: $n = f_{2k}$. By Proposition 4.5, we have

where $\ell = f_{2k+3}-1-f_{2k}$ is even by Lemma 2.10.

Case 3: $f_{2k} < n < f_{2k+3}-1$. If $m+n = \alpha_i$ (or $\alpha_i-f_{2k+2}+1$), then applying Lemma 4.6(ⅰ) (or Lemma 4.6(ⅱ)) and then Eq (6.1), we have

where $\ell = f_{2k+3}-1-n$. If $\alpha_i-f_{2k+2}+1 < m+n < \alpha_i$, then Lemma 4.1 yields $H_{m, n} = 0$.

Proof of Theorem 1.2. Suppose $(m, n)\in V_{k, i}$ for some $i$. Then $\beta_i < n+m\leq \beta_i+f_{2k+1}$.

Case 1: $n = f_{2k+2}-1$. By Lemma 4.8(ⅲ) & (ⅰ), we have

According to Proposition 4.5(ⅰ) and Corollary 5.4,

The result follows from Eq (6.2) and Eq (6.3).

Case 2: $n = f_{2k}$. By Proposition 4.5, $H_{m, n} = H_{\alpha_1-f_{2k}, \, f_{2k}}$. Then the result follows from Theorem 1.1(ⅱ).

Case 3: $f_{2k} < n < f_{2k+2}-1$. If $m+n = \beta_i+1$ (or $\beta_i+f_{2k+1}$), then by Lemma 4.8(ⅰ) (or Lemma 4.8(ⅱ)), we have

If $\beta_i+1 < m+n < \beta_i+f_{2k+1}$, then Lemma 4.1 shows $H_{m, n} = 0$.

Proof of Theorem 1.3. Suppose $(m, n)\in T_{k, i}$ for some $i$. Then $\gamma_i-f_{2k} < n+m\leq \gamma_i$.

Case 1: $n = f_{2k+2}-1$. By Lemma 4.10(ⅲ) & (ⅰ),

where the last equality follows from Lemma 2.10(ⅰ). Using Proposition 4.5(ⅱ) and Corollary 5.5,

The result follows from Eq (6.4) and Eq (6.5).

Case 2: $n = f_{2k+1}$. Write $m = \gamma_i-f_{2k+2}+r$ with $1\leq r\leq f_{2k}$. By Proposition 4.5(ⅱ) and Corollary 5.5,

Note that $\gamma_i = m+n+f_{2k}-r$ and $1\leq r\leq f_{2k}$. Consequently,

which gives $r = \Phi_{k}(m+n)-\frac{f_{2k+1}}{2}$. Then the result follows.

Case 3: $f_{2k} < n < f_{2k+2}-1$. If $m+n = \gamma_i-f_{2k}+1$ (or $\gamma_i$), then by Lemma 4.10(ⅰ) (or Lemma 4.10(ⅱ)),

If $\gamma_i-f_{2k}+1 < m+n < \gamma_i$, then Lemma 4.1 yields $H_{m, n} = 0$.

7.   Conclusions

In this paper, we study the Hankel determinants $H_{m, n}$ of the Sturmian sequence ${\bf{s}} = \tau^{\infty}(1)$. In Theorem 1.1, 1.2 and 1.3, we give the closed form of the Hankel determinants $H_{m, n}$ for all $m\ge 0$ and $n\ge 1$. To extend the results to other Sturmian sequences, the difficulty is to locate the parallelograms that are composed by $(m, n)$'s such that $H_{m, n} = 0$. This will need further effort.

Acknowledgments

We thank the referees for their valuable comments and suggestions. This work was supported by Guangzhou Science and Technology program (202102020294), Guangdong Basic and Applied Basic Research Foundation (2021A1515010056) and the Fundamental Research Funds for the Central Universities from SCUT (2020ZYGXZR041).

Conflict of interest

The authors declare that they have no conflict of interest.