1.
Introduction
Development an effective techniques for solving models involving fractional derivatives and temporal delays has recently attracted a lot of attention, which is encouraging. Flexible representation and the capability to accurately describe various phenomena are the main reasons why they are preferred over integer-order models. Fractional derivatives, unlike regular ones, are non-local in nature and could be used to describe memory effects, while time delays indicate the history of a previous state. It appears that the addition of the delay term in fractional differential equations is paving the way for new possibilities and opening new vistas in many scientific fields. This kind of fractional differential equation is effectively applied in many fields, including bioengineering, control theory, population dynamics, economics, electrochemistry, physics, and many more [1,2,3,4,5,6,7]. As the systems become increasingly sophisticated and linked, time delays are incorporated to account that changes in one variable may affect other variables with certain lags. For example, in biological models, delays explain incubation time or the time required for a plant to reach maturity. In control theory, time delays are considered in feedback control systems to account for delayed feedback. Economic models use delays to match transportation and information transfer more closely. The literature has paid considerable attention to fractional partial differential equations involving delays. Liu in [8] combined the Crank-Nicolson approach and the Legendre spectral technique to provide a fully discrete methodology for the nonlinear delayed diffusion-reaction equations. An effective approximation approach for nonlinear delayed fractional order diffusion equations was developed and evaluated by Pimenov and Hendy in [9]. In [10], a numerical approach was described for solving a certain form of a delayed fractional model with distributed order in time. The authors in that work used the Crank–Nicholson method to obtain the numerical solution. For solving the nonlinear form of fractional diffusion equations with temporal delay, Li et al. [11] suggested a linearized compact scheme. The spatial discretization in the mentioned work was accomplished with the help of the compact finite difference approach, while the temporal discretization was made by utilizing an L1 formula to the time fractional derivative and an extrapolation for the nonlinear component. For the solution of time-delayed nonlinear fractional diffusion equations, Mohebbi [12] developed a numerical method that is guaranteed to be stable under any conditions. The temporal direction was discretized using a finite difference method, while the spatial component via Chebyshev spectral collocation method. By developing a novel form of fractional Grönwall inequality in a discrete style, Hendy and Macías-Díaz [13] were capable of proving the stability and convergence of numerical solutions to the nonlinear time-fractional diffusion equations with multi-time delays.
On the other hand, substantial effort has been expended in the scientific literature to develop efficient formulas for approximating the time fractional derivatives in the Caputo sense. The L1 formula is considered one of the most extensive methods used for the solution of fractional differential equations that include Caputo derivatives [14,15,16,17,18,19,20]. In the case of a non-uniform mesh, the L1 approximation provides a decent approximation when the mesh is refined close to the point tn+1 [21]. Even though the non-uniform mesh performs better than the uniform one, the second-order approximation will not be generated at all mesh nodes. In order to get a close approximation to the Caputo fractional derivative of order β (0<β<1), Gao et al.[22] constructed a novel formulation called the L1−2 formula with 3−β convergence order in temporal direction at time tk(k≥2). This formula is produced by approximating the integrated function with three points using a piecewise quadratic interpolation approximation and it is properly defined as a modification of the L1 formula with some correction terms added. In [23,24], the Caputo time-fractional derivative is discretized by applying a numerical formula with 3−β order, known as, the L2 formula. This formula is generated with the use of piecewise quadratic interpolating polynomials. Through the development of a discrete energy analysis approach, a comprehensive theoretical examination of the stability and convergence of this method is performed for every β∈(0,1). Alikhanov [25] devised a new difference scheme called the L2−1σ formula based on a high-order approximation for the Caputo fractional derivatives with 3−β convergence order in temporal direction at time t=tk+σ with σ=1−β2. It was shown in [26,27,28] that the L2−1σ formula may be extended and used to solve the multi-term, distributed, variable-order time-fractional diffusion equations. On the basis of this formula, a number of recent studies have investigated and developed high-order techniques for time fractional models in the Caputo sense. An implicit technique for solving fractional diffusion equations with time delay is shown in [29], which combines the Alikhanov formula for time approximation with the central difference method for spatial discretization. A second-order numerical approach was suggested by Nandal and Pandey in [30] for solving a nonlinear fourth-order delayed distributed fractional subdiffusion problem. They estimated the time-fractional derivative with the Alikhanov formula as well as the spatial dimensions with the compact difference operator. For the fractional order nonlinear Ginzburg-Landau equation, Zaky et al. [31] numerically developed a useful technique by discretizing time direction using the Alikhanov formula and space direction with the methodology of spectral Legendre-Galerkin. Following up on the L2−1σ formula, a slew of new works have appeared (see, for example, [32,33,34,35,36]). Without loss of generality, in this work, we numerically propose a high-order algorithm for solving the following time-delayed nonlinear fractional order reaction-diffusion equations:
initialized and constrained by the conditions
In this case, time and space domains are represented by I=[0,T]⊂R and Ω=[a,b]⊂R, respectively. Additionally, β∈(0,1) represents the temporal order of fractional time in which the time-fractional derivative is interpreted according to Caputo, whereas α∈(1,2) represents the fractional order of space. The Riemann-Liouville fractional derivatives on its both sides for n−1<α<n, are provided by [37]
where Γ(x) symbolizes the usual function of gamma. This allows us to give a definition for the Riesz space of fractional derivatives, which is [38]
The Caputo derivative ∂βΘ∂tβ is defined as
Our primary objectives of current work are to develop and investigate an effective numerical algorithm for a nonlinear time-delayed fractional order reaction-diffusion (1.1). A combination scheme is proposed that mixes the Alikhanov L2−1σ difference formula with Galerkin spectral Legendre scheme. More specifically, the spatial discretization is handled by utilizing Legendre–Galerkin spectral approach, whereas the fractional derivative in the temporal direction is discretized through the L2−1σ formula. Additionally, a suitable version of discrete fractional Grönwall inequalities is utilized in order to assert the unconditional stability and convergence of the proposed technique. The structure of this study is as follows. In the subsequent section, we shall describe and characterize the key features of fractional derivative spaces, Sobolev spaces, as well as Jacobi polynomials. On a uniform mesh, we detail in section 3 the way to construct the fully discrete L2−1σ Galerkin spectral scheme for the problems (1.1) and (1.2). Section 4 recalls several technical lemmas from the literature before proving that the suggested methodology is unconditionally stable and convergent. Finally, Section 5 includes a numerical test that validates the obtained scheme's convergence analysis.
2.
Basic concepts
Here, we briefly review some fundamental concepts in fractional derivative spaces as well as the essential elements of their properties, see [39] for further details. Then, Jacobi polynomials' primary features are mentioned. Assume that (⋅,⋅)0,Ω refer the standard inner product related to L2(Ω) space with the usual L2 norm and the maximum norm ‖⋅‖∞. Define the space C∞0(Ω) consists of all smooth functions that have compact support in Ω. Consider that Hr(Ω) and Hr0(Ω) are the standard Sobolev spaces, and their associated norms and seminorms, respectively, are ‖⋅‖r and |⋅|r. To further clarify, we characterize the approximation space W0N as:
where in PN(Ω) stands for the set of all polynomials defined on the domain Ω that have a degree no greater than N. The interpolation operator of type Legendre-Gauss-Lobatto depicted by the symbol IN:C(ˉΩ)→WN, can be defined as follows
Definition 1. The semi-norm and norm related to the space of left fractional derivatives are specified for a given ε>0, respectively, as follows:
also, JεL and JεL,0 are defined to be the closures of C∞(Ω) and C∞0(Ω), respectively, in relation to ‖⋅‖JεL(Ω).
Definition 2. The semi-norm and norm related to the space of right fractional derivatives are specified for a given ε>0, respectively, as follows:
also, JεR and JεR,0 are defined to be the closures of C∞(Ω) and C∞0(Ω), respectively, in relation to ‖⋅‖JεR(Ω).
Definition 3. The semi-norm and norm related to the space of symmetric fractional derivatives are specified for a given ε>0, respectively, as follows:
also, Jεs and Jεs,0 are defined to be the closures of C∞(Ω) and C∞0(Ω), respectively, in relation to ‖⋅‖Jεs(Ω).
Definition 4. Assuming that ε>0, then the fractional Sobolev space Hε(Ω) is defined as follows:
with respect to following semi-norm and norm
wherein F(ˆΘ) stands for the Fourier transform of function ˆΘ, denoting the zero extension of function Θ beyond the spatial domain Ω. Also, we define Hε(Ω) and Hε0(Ω) as the closures of C∞(Ω) and C∞0(Ω), respectively, with consideration to ‖⋅‖Hε(Ω).
Remark 2.1. If ε≠n−12, n∈N, then according to the above definitions, fractional derivative spaces JεL, JεR, Jεs and Hε are identical, with equivalent semi-norms and norms.
The adjoint property, which we will revisit below, will play a crucial part in the study that follows.
Lemma 2.1. For a given ε>0, such that 1<ε<2, then for any two functions Θ∈Hε0(Ω) and υ∈Hε/20(Ω), the following relation is satisfied
A brief overview of the basics of Jacobi polynomials follows. We recommend reading [40,41] for more information on orthogonal polynomials, and [42,43,44,45,46,47,48,49] for applications of spectral methods to these type of polynomials. For p,q>−1 and x∈(−1,1), the hypergeometric functions make it possible to write the Jacobian polynomials as follows:
where (⋅)i signifies the symbol of Pochhammer. Assuming that N is a positive integer, then the following three-term recurrence relations hold for {γp,qi(x)}Ni=0, as they hold for all classical orthogonal polynomials
Where the coefficients of recursion are provided by
The existence of orthogonality in the set of Jacobi polynomials is due to a weight function, which is represented by ωp,q(x)=(1−x)p(1+x)q, more precisely,
where δi,j represents the function of the Kronecker delta, and
In specifically, the Legendre polynomial is a subclass of the Jacobi polynomial, which it can be stated as:
3.
The numerical scheme
Here, in this section, we will focus on developing a high-order numerical approximation for the problems (1.1) and (1.2) based on combining Alikhanov L2−1σ difference formula and the spectral method of Legendre-Galerkin in order to discretize the temporal and space–fractional derivatives, respectively. We begin with temporal discretization following that, we detail the suggested scheme's spatial discretization.
3.1. Temporal discretization
We choose a time step given by τ=sNs, where Ns is a positive integer, in order to uniformly divide the temporal domain I. This defines a class of uniform partitions denote by tk=kτ, for each −Ns≤k≤M, where M=⌈Tτ⌉. Denote tk+σ=(k+σ)τ=σtk+1+(1−σ)tk, for k=0,1,…,M. Take Θk+σ=Θk+σ(⋅)=Θ(⋅, tk+σ). For the Caputo derivative (1.5), we recall the Alikhanov L2−1σ difference formula [25].
Definition 5. The following coefficients are defined for any value of the parameter σ=1−β2, 0<β<1,
and
Consequently, the L2−1σ difference formula which applied in this investigation can be formulated in light of the lemma below.
Lemma 3.1. Under the premise that Θ(t)∈C3[0,tk+1], 0≤k≤M−1, the high order L2−1σ difference formula reads as follows:
where δtΘl=Θl+1−Θl. For the sake of theoretical clarity, we rewrite (3.16) in an equivalent form as:
where D(0,β,σ)1=−D(0,β,σ)0=σ1−β, for k=0, and for k≥1,
Definition 6. For the temporal Caputo fractional derivative, the L2−1σ approximation formula at node tk+σ,k∈Z[0,M−1] is defined as:
By means of Taylor's theorem, it is observed that the following lemma is valid.
Lemma 3.2. For a given function Θ(t)∈C2[0,T], the following identities hold
Following that, at each specified time tk+σ, we shall present a semi-discretized version of the system (1.1). To that end, the uniform L2−1σ formula (3.19) is used to estimate the time-fractional component, and Taylor's approximations are used to discretize the nonlinear source term. Thus, the resulting discrete-time system is as follows:
We also take into account initial-boundary approximations as the following form
According to Lemmas (3.1) and (3.2), this semi-scheme is technically accurate to the second order. Later in this context, a comprehensive study of the convergence rate for the full-discrete scheme will be provided. Next, we introduce the following two parameters:
Then, this permits the recasting of the semi-scheme (3.20) into the equivalent form given below
3.2. Spatial discretization
We first present the space function below to give suitable base functions that precisely meet the boundary requirements specified in spectral techniques for space fractional order equations in order to linearize the space-fractional components [50,51]:
where ψn symbolizes the base functions, which are represented by the Legendre polynomial as:
where x=12((b−a)ˆx+a+b)∈[a,b]. Therefore, the fully discrete L2−1σ Galerkin spectral scheme for (3.22) can be expressed as follows: find Θk+1∈W0N, k≥0 such that satisfying the following system:
where π1,0N is a suitable projection operator in this case. Following this, we could further generalize the approximation as:
where ˆΘk+1i are an undetermined expansion coefficients. The uniform full discrete scheme for the problems (1.1) and (1.2) can be expressed as a linear system in a matrix form using (3.26), lemma 2.1 and allowing υ=ψk, for each 0≤k≤N−2 as follows:
where
The elements of the stiffness matrix S and the mass matrix ˜M can be easily handled using the next two lemmas.
Lemma 3.3. [50,51] The following relation can be used to manipulate the components that make up the stiffness matrix S, namely,
the formula where the coefficients aji may be determined reads
and {ϖ−α2,−α2r,x−α2,−α2r}Ni=0 are Jacobi-Gauss collection points and their corresponding weights related to the weight function ω−α2,−α2.
Lemma 3.4. [50,51] The nonzero components of the symmetric mass matrix ˉM are given by
4.
Theoretical analysis
This section aims to verify how effectively the numerical solution of the suggested approach for the problems (1.1) and (1.2). We start in the first part with a review of certain technical lemmas that will be important later on. In the second subsection, we conduct stability and convergence studies of the suggested method. We assume that the Lipschitz condition below holds for the function F, which is necessary for the theoretical analysis, i.e,
where L is a positive constant.
4.1. Technical Lemmas
Here, we recall some lemmas that will be used in our investigation. To avoid tying these definitions to specific values for N, n, and τ, we will refer to C and CΘ in the following as arbitrary positive constants that can shift depending on the circumstances. Additionally, we accept on the convention Z[a,b]=Z∩[a,b], where Z is the set of all positive integers. For the rest of this discussion, we'll be using the following notation
The orthogonal projection operator, denoted by πα2,0N:Hα20(Ω)→W0N, will have the following property:
We provide the following semi-norm and norm to facilitate theoretical analysis.
The three lemmas below are all mentioned in [50].
Lemma 4.1. Suppose that α and s are two real integers such that α≠1/2, 0<α<1, α<s. Then, for every function Θ∈Hα20(Ω)∩Hs(Ω), the approximation that follows valid
where C is a positive constant C independent of N.
Lemma 4.2. We assume that Θ∈Hα20(Ω) and that Ω=(a,b). Then, there are two positive, independent constants C1<1 and C2 with respect to Θ, such that the following remains true
Lemma 4.3. The inverse inequality that follows holds true for every given set of values for Θ∈PN(Ω)
where C is a constant that is positive and independent of Θ and N.
The properties of the interpolation operator IN are summarized in the following lemma and remark.
Lemma 4.4. [41] Assume that Θ∈Hs(Ω), then for s≥1 and 0≤l≤1, the following relation is valid
where C>0 is a constant independent of N.
Remark 4.1. The smoothness of the solution to a fractional differential equation does not imply the smoothness of the source term. Consequently, the solution Θ has a different regularity order s than the regularity order r for the source term G, which means that
where C>0 is a constant independent of N, Θ and g.
Lemma 4.5. [52] All absolutely continuous functions Θ(t) on [0,T] satisfy the following inequality
Lemma 4.6. [25] The following inequality holds for any Θ(t) identified on the interval Ω and β∈(0,1). If Θk+σ=σΘk+1+(1−σ)Θk, then
It's worth noting that a significant amount of consideration has been paid to developing fractional Grönwall inequalities in their continuous form in recent years. However, their discrete form has received less attention, and a few recent studies [11,53,54,55] have attempted to close the gap. In what follows, we present a developed discrete version of Grönwall inequality that agrees with the L2−1σ difference schemes and plays an important part in demonstrating the stability and convergence of our suggested approach.
Lemma 4.7. [13,28] Assume that {Qi}∞i=−Ns and {ζn}∞n=0 are both non-negative sequences. Suppose that μi,i∈Z[1,6] are independent positive constants with respect to τ, such that the sequences satisfying
In that case, there is a positive constant τ≤τ∗=β√1/(2Γ(2−β)μ1), which causes
where Eβ(z) represent the Mittag-Leffler function and
4.2. Stability analysis
The variational formulation of the proposed scheme can be obtained by means of (3.17), (3.20) side by side to Lemma 3.2. More specifically, we need to find {ΘkN}Mk=1∈PN, such that satisfying the following:
with initial conditions
Due to the linear iterative nature of the method, a solution to an algebraic equation system is all that is required at each iteration. The suggested scheme's well-posedness, meaning it is uniquely solvable and continues to rely on its initial boundary conditions which is sufficient to hold the Lax-Milgram lemma's assumptions [56]. In particular, it can be seen from Eq (4.38) that the bilinear shape A(⋅,⋅) is continuous as well as coercive related to Hα/20×Hα/20. We further presume that {˜ΘkN}Mk=1 is the solution of the following variational form
with initial conditions
Now, we are ready to offer the stability theorem in the context of the subsequent discussion.
Theorem 4.1. The suggested method (4.38) in this sense, is said to be unconditionally stable, which means it holds the following for τ>0,
where C is a generic positive constant independent of N and τ.
Proof. Subtracting (4.39) from (4.38) and by taking ΘkN−˜ΘkN:=ηkN, then the error equation holds
Applying the Lipschitz condition (4.31) and using Hölder inequality side by side to Young inequality, we derive the following for the first term of the right-hand side
Using the Hölder inequality, the Young inequality, as well as the interpolation operator property, we obtain the second term as
Hence, (4.40) becomes
Taking υN=ηk+σN and using lemma 4.6 and (4.34), we deduce that
following the omission of the second term in the left hand side, we have
A direct application of the Grönwall inequality (see Lemma 4.7), we find that for ϵ>0, there exists a positive independent constant τ∗=β√1/(2Γ(2−β) 4ϵ(σ+1)2(1+Cϵ2L2)), such that when τ<τ∗, the following is hold
with
Therefore, the proposed method is guaranteed to be unconditionally stable.
4.3. Convergence
Here, we present the proof of the convergence theorem for the suggested scheme (4.38) using discrete error estimates.
Theorem 4.2. Let {Θk}Mk=−Ns and {ΘkN}Mk=−Ns, be the exact and the approximate solutions of problem (1.1) and the proposed method (4.38), respectively. Assume that Θ∈C2([0,T];L2(Ω))∩C1([0,T];Hs(Ω)). Then for an arbitrary constant C independent of N and τ, the following statement is valid
where r is the source term's regularity order.
Proof. Take Θk−ΘkN=ξkN=(Θk−πα2,0NΘk)+(πα2,0NΘk−ΘkN)Δ=˜ξkN+ˆξkN. In addition, (1.1) has the following weak formulation:
By subtracting (4.38) from (4.42), and using the notion of orthogonal projection, then the error equation satisfies
where
To proceed, we make an estimate of the terms ρ(k,σ)1, ρ(k,σ)2, ρ(k,σ)3 and ρ(k,σ)4 on the right-hand side. Regarding the first term ρ(k,σ)1, we have
Invoking Taylor expansion holds
In addition, we use Hölder's and Young's inequalities to
By plugging into the Lipschitz condition (4.31) and using Hölder inequality side by side to Young inequality, we deduce that
In addition, considering the Lemmas 4.1 and 4.2, it can be shown that
then (4.46) becomes
Substituting (4.45) and (4.47) into (4.44), we obtain that
Hölder's inequality, Young's inequality, and Lemma 4.4 allow us to deduce the following for the second term ρ(k,σ)2 as follows:
For the third term ρ(k,σ)3, it holds
combining 3.1 with Hölder inequality and Young inequality yields
furthermore, by means of Lemma 4.1, we have
Thus (4.50) becomes
By the aid of Remark 4.1, we obtain the following for the fourth term ρ(k,σ)4
Substituting (4.48), (4.49), (4.51) and (4.52) into (4.43), we can infer that
where
Taking υN=ˆξk+σN in (4.53) and applying Lemma 4.6, we can conclude that
hence, after omitting the second term on the left side of the above equation, we get
with R=2˜R. By means of Lemma 4.7 we find that for ϵ>0, there is some positive independent constant τ∗=β√1/(2Γ(2−β) 4ϵ(σ+1)2(3+Cϵ2L2)), when τ<τ∗, we have
with
Consequently, the scheme converges regardless of circumstances. The triangle inequality and (4.36) were then combined to complete the (4.41) proof.
5.
Numerical experiments
As such, we perform a test example to further characterize the suggested system's temporal and spatial convergence orders. We also show how the dynamics of the solution to systems of fractional diffusion equations with delay are affected by fractional orders in the temporal and spatial directions. In order to investigate both temporal and spatial convergence orders independently, we will determine the orders of convergence in both using the L2−Error norms, which are described as follows:
where M1≠M2.
Example 1. Consider the following nonlinear delayed diffusion problem
such that problem (5.55) admits an exact solution t2Γ(3)x2(1−x)2 with respect to a given function G(x,t).
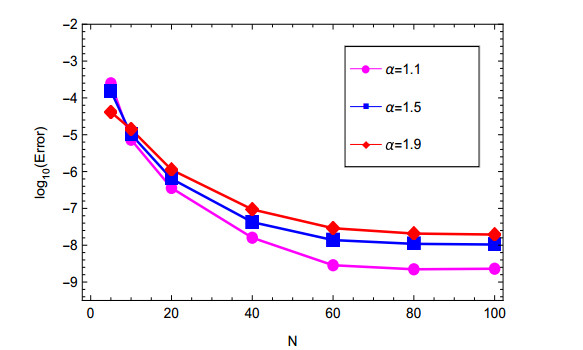
As shown in Table 1, a comparison between the L2-errors and their accompanying convergence orders for different values of α and β with N=100 for both L1 and L2−1σ schemes are listed. It is shown that 2−β temporal accuracy has been reached for the L2-errors in the case of L1 scheme, (see our previous work [48]), while a high order of second temporal accuracy has been reached for the L2-errors in case L2−1σ scheme which accords with the temporal order of convergence provided by Theorem 4.2. Orders of spatial convergence are shown for various values of α values at τ=1/500 in Figure 1. In addition, when the L2 errors diminish exponentially, spatial-spectral accuracy increases for a smooth solution. The convergence findings coincide completely with the theoretical ones. At each level of convergence, we see full concordance between theoretical and experimental results.
6.
Conclusions and remarks
In this study, we introduced an effective spectral Galerkin approach to handle the nonlinear fractional order reaction-diffusion equations with a fixed delay. This approach is accomplished by constructing a numerical algorithm that integrates the efficacy of L2−1σ type approximation side by side to the effectiveness of the Galerkin spectral Legendre technique. In other words, on a uniform mesh, we used the L2−1σ difference formula and the Legendre-Galerkin spectral technique for time and space discretizations, respectively. According to the literature overview, the majority of earlier research provided error estimates only in a limited (local) time period or when the numerical solution declines in time. However, we presented a theoretical analysis to obtain the optimal error estimates for the suggested scheme with no constraints compared to earlier studies, using the developed L2−1σ fractional Grönwall type inequality in a discrete version. In the case of smooth solutions, the suggested scheme's convergence analysis was established, and it was demonstrated that the scheme under consideration is effective with second-order precision in time and spectral accuracy in space. In the situation of a non-smooth solution in time, a high-order graded L2−1σ scheme can be dealt with using a non-uniform Alikhanov scheme [55,57] to preserve the second order. Additionally, a more generic investigation for problem (1.1) is possible by replacing the fixed delay with a distributed one. These preparations are meant to serve as a road map for future study. Finally, a numerical test is offered to demonstrate the effectiveness of the proposed scheme and show that is consistent with theoretical results.
Acknowledgment
The authors are grateful to the handling editor and the anonymous referees for their constructive feedback and helpful suggestions, which highly improved the paper. V.G. Pimenov wishes to acknowledge the support of the RSF grant, project 22-21-00075.
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: