Mathematical modelling of OAS2 activation by dsRNA and effects of dsRNA lengths

1.   Introduction

Host detection of viral pathogens by the innate immune response is an effective first line of defence against infection. In eukaryotic cells, the innate immune system relies heavily on protein recognition of evolutionarily conserved viral double-stranded RNA (dsRNA) to stimulate interferon production that prepares neighbouring cells for attack ^[1]. The interferon response then up-regulates the transcription of additional antiviral proteins to amplify the response. A key family of interferon-stimulated antiviral enzymes are the 2'-5'-oligoadenylate synthetases (OAS). OAS enzymes specifically bind viral dsRNA and through a complex cascade attenuate viral replication. An understanding of how these enzymes discriminate viral from host dsRNA remains a key unresolved question.

OAS enzymes require viral dsRNA as a cofactor to polymerise ATP into chains of unusual 2'-5' linked oligoadenylates (2-5A) ^[2]. These chains bind to and activate RNase L, which degrades cellular and viral RNA thereby restricting viral propagation ^[3]. In humans, three genes (OAS1/2/3) each produce enzymes with one, two and three repeats of a 346 amino acid core OAS unit ^[4]. Each version has different dsRNA affinity, builds different 2-5A chain lengths, and responds to different viral infections. Interaction between multiple OAS enzymes (oligomerisation) appears to be central to these differences, presumably to respond to different viral dsRNA lengths. OAS1, comprising a single domain, forms monomer, dimers and tetramers, and will bind dsRNA of any length longer than 17 base pairs (bp) ^[5]. OAS2 can form a dimer and requires a minimum of 35 bp ^[6]. OAS3 is not known to oligomerize and requires at least 50 bp dsRNA for activation ^[7]. While high-resolution structures of OAS enzymes show that dsRNA is responsible for dramatic reorganisation of the enzyme active site, little is known regarding the impact of dsRNA binding on oligomerisation or the detailed catalytic mechanism.

OAS enzymes are differentially expressed in specific cell types, and their presence in different sub-cellular fractions such as mitochondria, nuclear, and rough/smooth microsomal fractions suggest that these proteins may have distinct functional roles. OAS1, 2, and 3 differ significantly in their response to common members of the Flaviviridae family of human viral pathogens including Yellow fever, Dengue fever, Japanese encephalitis, Tick-borne encephalitis and West Nile virus. Preliminary data from ^[6] suggests that OAS1 and OAS2 may have distinct substrate specificity in terms of dsRNA length, which may explain their divergent roles in antiviral processes.

The OAS enzymatic mechanism is complex as it involves dsRNA cofactors of variable length and structure, an ATP substrate that is polymerised into chains of variable length, and non-covalent OAS self-association. As a result of this complexity, the detailed biochemical process is not completely defined. In this work, we focus on OAS2 activation by dsRNA. Based on in vitro experimental data published in ^[6], the process appears to depend on concentrations and lengths of dsRNA; however, limitations of the experimental data that can only be accurately recorded at the endpoint of enzymatic activity prevents complete definition of the process. Hence, mathematical modelling is used to investigate possible OAS2 activation mechanisms and the effects of dsRNA lengths. Plausible biochemical scenarios are translated to mathematical models and their responses are compared to in vitro experimental data to test different hypotheses. In total, three kinetic models are derived. After calibration of models to data, a model selection method is used to determine the model that best represents the data. Furthermore, analysing parameter estimates allows us to propose a mechanism accounting for the role of dsRNA length in OAS2 activation.

2.   Experimental data

OAS2 enzymes require dsRNA as a cofactor for enzymatic activity. In the presence of substrate ATP, OAS2 binds to dsRNA and the enzyme polymerises ATP into chains of 2-5A leaving pyrophosphate (PPi) as a byproduct ^[2]. In vitro experimental data considered in this work are concentrations of PPi recorded at six time points (including the initial time, $t_0 = 0$ min). The byproduct concentration is measured at $t_1 = 5$ min, $t_2 = 10$ min, $t_3 = 15$ min, $t_4 = 20$ min and $t_5 = 30$ min for one concentration $c_O = 0.3\mu$g/mL of OAS2, and five concentrations of dsRNA are considered with seven different lengths ^[6]. The five dsRNA concentrations $c_j$ are $c_1 = 0.5\mu$g/mL, $c_2 = 1\mu$g/mL, $c_3 = 2\mu$g/mL, $c_4 = 4\mu$g/mL and $c_5 = 8\mu$g/mL. The seven lengths $L_k$ considered for dsRNA are $L_1 = 40$bp, $L_2 = 50$bp, $L_3 = 60$bp, $L_4 = 70$bp, $L_5 = 80$bp, $L_6 = 90$bp and $L_7 = 120$bp. The ATP concentration used in the experiments is $1$mg/mL$\gg c_O$. Experimental data used in this work have been published in ^[6]; for details on in vitro experiments yielding them refer to ^[6].

3.   Modelling

In the in vitro experiments considered ^[6], the substrate, which is ATP, is in abundance. Hence, the contribution of substrate to enzyme kinetics is not of interest in this work; no equation describes ATP concentration in models. The OAS2 enzyme consists of two OAS domains ^[8]. As shown in Koul et al. ^[6], a minimal length of 35bp for dsRNA is required to activate OAS2, and both OAS2 domains must be bound simultaneously by dsRNA to lead to product formation. Furthermore, the binding and unbinding of enzymes and cofactors are reversible reactions; neither enzyme nor cofactor are consumed during these reactions nor the formation of product and byproduct. Finally, as previously mentioned, the experimental data only monitors the concentration over time of the byproduct (PPi) for a given enzyme concentration and different cofactor concentrations and lengths. In the experimental data, the formation of byproduct is sensitive to both cofactor concentrations and lengths.

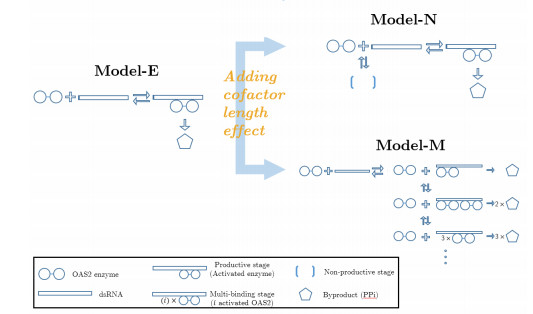
Based on these observations and available in vitro experimental data three mathematical models are developed to investigate the activation of OAS2 by dsRNA and the role of the dsRNA length on the activation (Figure 1).

3.1.   Model-E

The first model considers an enzymatic kinetics describing only the kinetics of the enzyme $E$ and cofactor $R$ as the substrate is in abundance. The activated enzyme or productive stage $D$, which is formed by the OAS2 and the cofactor bound to the two domains of OAS2, is not consumed in the formation of byproduct $P$. Assumptions of Model-E are as follows (Figure 1)

and the model equations are

where $k_1$ is the rate of association of an OAS2 and dsRNA, it describes the rate of production of the compound $D$ or activated enzyme. To reduce the model complexity, binding of the two domains of OAS2 to the same dsRNA is not explicitly described and is approximated as an one-step binding. The rate $k_{1m}$ is the dissociation rate of the enzyme and cofactor. Note that in Model-E once a dsRNA molecule is bound with an OAS2, it cannot accommodate another OAS2 enzyme. The parameter $k_p$ is the rate of formation of the byproduct by the activated enzyme. Parameters are listed in Table 1. Model-E is considered with non-negative initial conditions $E(0) = c_O$, $R(0) = c_R$, $D(0) = 0$ and $P(0) = 0$, where the positive constants $c_O$ and $c_R$ are the initial concentrations of OAS2 and dsRNA, respectively.

3.2.   Model-N

A way to represent the impact of the dsRNA length on OAS2 activation is to consider that some interactions are not complete ^[9] as the two domains of OAS2 have to bind to dsRNA to produce an active OAS2. Hence, the formation of compounds in which both domains are not properly attached to cofactor is hypothesised. These compounds are called non-productive compounds, their specific forms are not described. Based on this assumption, the non-productive binding stage $N$ that cannot result in the formation of the product and byproduct is added to Model-E. After a non-productive binding, OAS2 can detach from dsRNA and attach to dsRNA again. The assumptions for Model-N are as follows (Figure 1)

yielding the model equations

where the additional parameters $k$ and $k_m$ are the association and dissociation rates of the non-productive compound $N$, respectively (Table 1). Model-N is considered with the initial conditions $E(0) = c_O$, $R(0) = c_R$, $D(0) = N(0) = 0$ and $P(0) = 0$.

3.3.   Model-M

Another possible effect of cofactor length on OAS2 activation is the occurrence of multi-binding of OAS2 on a same dsRNA. dsRNA is not consumed nor changed by the OAS2 activation; OAS2 interacts with dsRNA, facilitates product formation, and then detaches from dsRNA. In the in vitro experiments considered, the longer the dsRNA used, the more product formation observed at a given OAS2 concentration ^[6]. Hence, another reasonable scenario is that longer dsRNA able to accommodate more than one OAS2 (presumably $>$ 70 bp) can be bound with more than one OAS2 simultaneously, leading to an increased product formation. Hence, the multi-binding assumption that allows up to $n$ OAS2 bound to one dsRNA simultaneously, is summarised as follows (Figure 1):

where $n = \left\lfloor{\frac{L}{2R_O}}\right\rfloor$, with $L$ the length of dsRNA and $R_O$ the radius of an OAS2 enzyme. The compound $D_i$ represents $i$ activated OAS2 attached to the same dsRNA with $i\in \{1, \cdots, n\}$. As shown in ^[6], the activity of OAS1, which is the monomeric equivalent of the catalytic domain of OAS2, does not depend on cofactor length. Therefore, the rate of formation of byproduct per activated enzyme is assumed to be constant and does not depend on the number of OAS2 bound to the same dsRNA. The compound $D_i$ produces $i$ byproducts at rate $k_p$.

The kinetics of OAS2 in presence of dsRNA of length $L$ is then described by the following system of $n+3$ equations:

where the additional parameters $k_{i}$ with $i > 1$ are the rates of subsequent association of one OAS2 to a dsRNA already associated with $i-1$ OAS2. The rates $k_{im}$ with $i > 1$ are the dissociation rates of one OAS2 from a dsRNA bound with $i$ OAS2. The initial conditions for Model-M are $E(0) = c_O$, $R(0) = c_R$, $D_i(0) = 0$ with $i\in\{1, \cdots, n\}$ and $P(0) = 0$. Note that when dsRNA used in experiments have a length $L$ smaller or equal to $70 \rm{bp}$, then Model-M is considered with $n = 1$ which is equivalent to Model-E.

4.   Experimental data versus models

Before calibrating models to data, their behaviour is characterised. Mathematical analysis of models is carried out and presented in ^[10]; all models are well-posed. Furthermore, reduced models obtained by decoupling the $P$ equation from systems (3.1), (3.2) or (3.3) are shown to have an unique stable positive steady state (results not shown; see ^[10]).

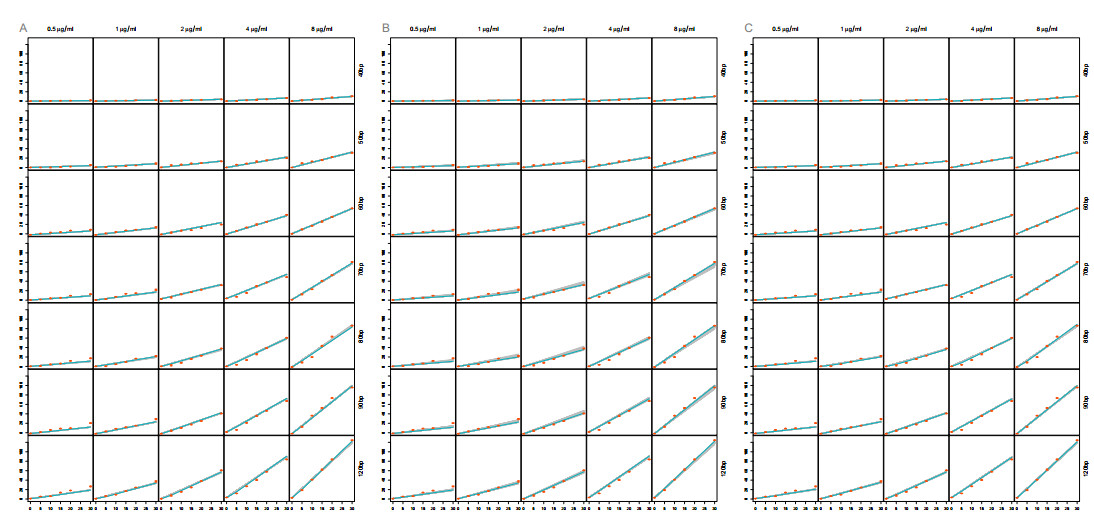
To calibrate models, numerical solutions of $P$ in systems (3.1), (3.2) or (3.3) are compared to in vitro experimental data, published in ^[6], that track the concentration of PPi over time for different concentrations of dsRNA $c_j$ ($= c_R$) of a given length $L_k$ ($= L$). The experimental data are shown in Figures 2 or 5 as red errors bars.

Once each model is calibrated to experimental data, the best model amongst the three models considered is selected based on the data, goodness of the fit and model parsimony using the corrected Akaike Information Criterion (AICc) ^[11,12].

4.1.   Model calibration

Experimental data (in red in Figures 2 or 5) show that the formation of byproduct increases with the concentration and length of the cofactor. Although the aim of the work is to find a mechanism that can explain the formation of byproduct for all lengths and concentrations of dsRNA simultaneously, we wanted first to verify if models can accommodate changes in concentrations for a given length and if the effect of dsRNA length on the production of $P$ can be identified through the variation of the parameter estimate values obtained when models are calibrated to each length independently. Thus, two strategies are used to estimate free parameter values listed in Table 1. First, model responses are fitted to experimental data obtained with the five concentrations of dsRNA for a given length at the five time points. The second strategy considers all five concentrations for seven lengths of dsRNA at the five time points.

In the first strategy, for the length $L_k$ with $k\in \{1, \cdots, 7\}$, the cost function to be minimised is:

where $\pmb{p}$ is the free parameter vector, $P_{c_j, L_k}(\pmb{p}, t_i)$ is the predicted concentration of PPi (solution for $P$ of a given model) at time $t_i$ for the concentration of dsRNA $c_R = c_j$ of length $L = L_k$. The experimental concentrations of PPi are $D_{t_i, c_j, L_k}$ at time $t_i$ for the concentration of dsRNA $c_R = c_j$ of length $L = L_k$. The parameters $m_j( = 5)$ and $m_i( = 5)$ are the numbers of dsRNA concentrations and time points considered in the study, respectively. In this first calibration strategy, parameters are estimated on $25$ observation points by minimising (4.1).

In the second strategy, parameters are estimated over $175$ observation points and the cost function is then:

where $m_k( = 7)$ is the number of dsRNA length considered in the study.

To find the estimates $\pmb{\hat{p}}$ for free parameter values for both strategies, the optimisation problem $RSS(\pmb{\hat{p}}) = { \min\limits_{\pmb{p}}RSS(\pmb{p})}$ is numerically solved using the genetic algorithm developed in the R package GA ^[13,14]. To obtain confidence intervals for estimates $\pmb{\hat{p}}$, the genetic algorithm is run several times and let converge to obtain several plausible points in the multidimensional parameter space. The likelihood of a particular estimate $\pmb{\hat{p}}$ is a measure of how well the data supports that particular value of parameters. Maximising the likelihood is equivalent to minimising the negative of the log-likelihood function. Assuming independent and normally distributed additive measurement errors, the negative log-likelihood of the estimates $\pmb{\hat{p}}$ for a given model can be roughly approximated by $RSS_{L_k}(\pmb{\hat{p}})$ for the first or $RSS(\pmb{\hat{p}})$ for the second calibration strategy ^[15]. Hence, the likelihood of different estimates obtained with the heuristic approach is assessed using RSS values.

4.2.   Model selection

For each calibration strategy (one length or all lengths), the AICc of model $i\in \{ \rm{Model-E}, \rm{Model-N}, \rm{Model-M}\}$ is computed as follows:

where $K_i$ is the number of estimated parameters (number of free parameters in mathematical model $i$ + 1), $M$ is the number of observations. For the one length strategy, $M$ is equal to 25 whereas, for the all lengths strategy, $M$ is 175. The constant $RSS^i(\pmb{\hat{p}_{Best}})$ is the smallest value of the errors obtained in multiple runs of the genetic algorithm in calibrating model $i$ for a given strategy. For each calibration strategy, the best model is the one with the smallest AICc.

To help the interpretation of results, the Akaike weights are then computed ^[15,16]. The Akaike weight $w_i$ of model $i$ is

where $\Delta_i = AICc_i - { \min_i{AICc_i}}$ and $Q( = 3)$ is the number of models considered in the study. The Akaike weights can be interpreted as the probability of the models to be the most likely given the experimental data and set of models considered. A model can be considered as the single best model if its weight $w_i$ satisfies $w_i > 0.95$.

5.   Results

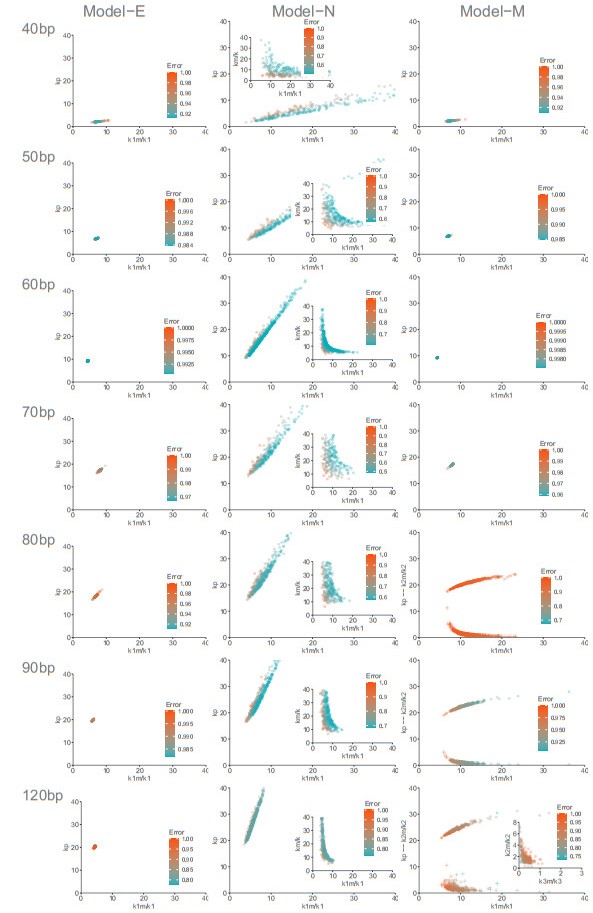
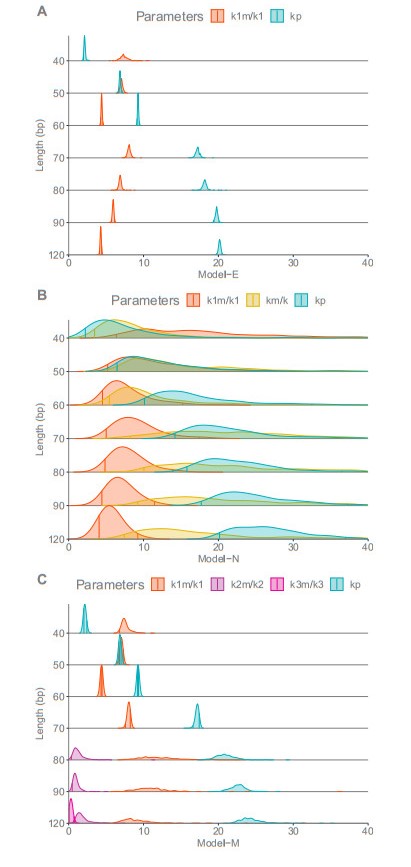
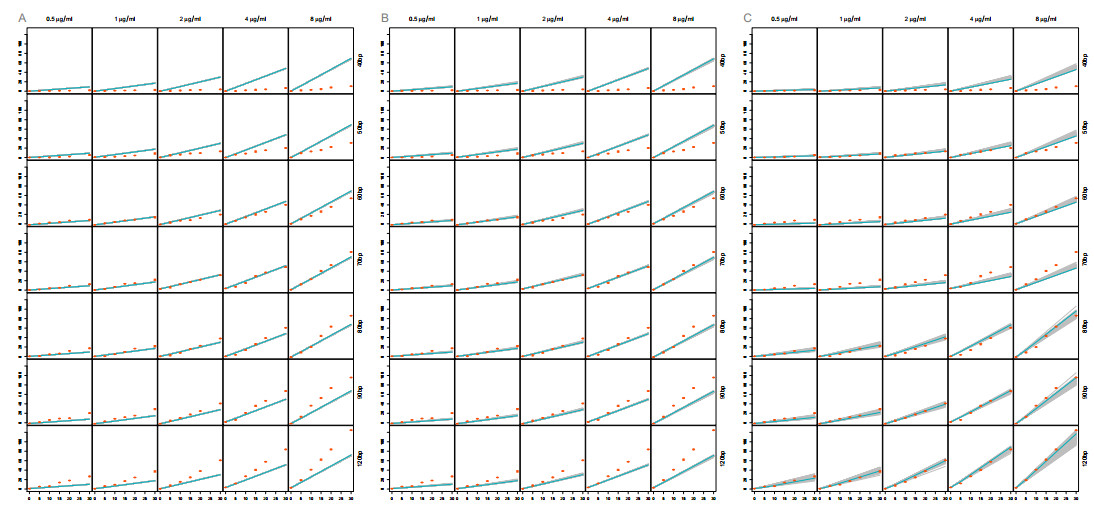
Fitting results obtained with the first and second strategy are shown in Figures 2 and 5, respectively. Parameter estimates, which are obtained with the first strategy, are shown in multidimensional parameter spaces with information related to their likelihood in Figure 3 and distributions and confidence intervals (95$\%$ of values obtained by calibrating models) of parameter values are shown in Figure 4. Details on parameter estimates obtained with the second calibration strategy are given in Figure 6. Results of model selection for both strategies are given in Table 2.

5.1.   First calibration strategy

When each length of dsRNA is considered independently, all models well represent the formation of PPi over time for all concentrations of dsRNA of a given length (Figure 2). Models accommodate changes in the cofactor concentration.

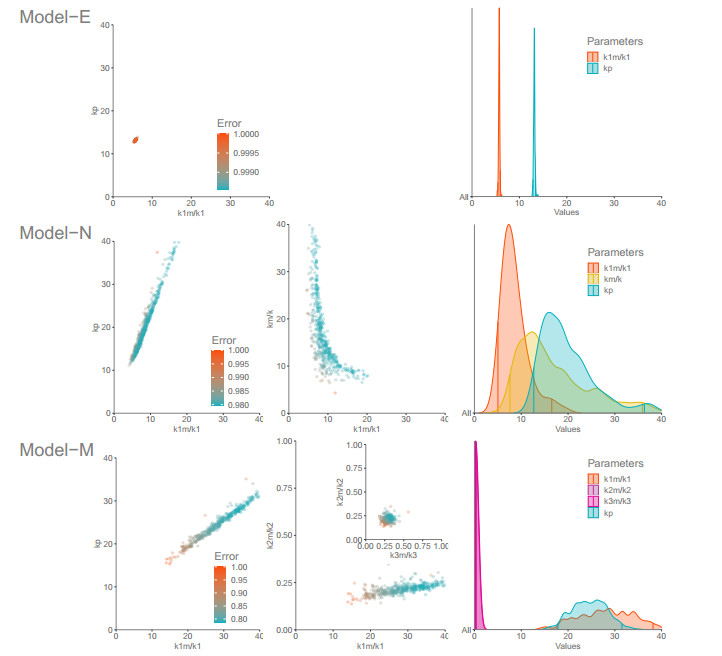
For the three models, values of the rate of production of PPi, $k_p$, are getting larger as the dsRNA length increases (Figures 3 and 4). When only one OAS2 is allowed on a single dsRNA molecule, there exists a linear relationship between the dissociation constant of enzyme and dsRNA $k_{1m}/k_1$ and the rate $k_{p}$ (Figure 3). Interestingly, for the shortest length 40bp, values for $k_{1m}/k_1$ are larger than $k_p$ values whereas this trend is reversed for lengths longer than 60bp. For short dsRNA, the binding of enzyme and cofactor is the limiting mechanism whereas for the longer dsRNA the limiting factor is the formation of product.

Model-E appears to be the most identifiable. Intervals of parameter estimates obtained for Model-E are quite narrow and fitting errors do not vary much (Figures 3 and 4A). The genetic algorithm always converges to similar parameter values with similar errors when calibrating Model-E for individual length data.

On the contrary, intervals for parameter estimates obtained for Model-N are more disperse and errors span over wider ranges (Figures 3 and Figure 4B). For Model-N, similar parameter value distributions (Figure 4B) with more clustered estimates in parameter spaces (Figure 3) are obtained as the length gets larger than 70bp. Interestingly, for long lengths (more than 80bp), the formation of non-productive compounds is mostly found less favourable than the formation of productive compounds ($k_{m}/k > k_{1m}/k_1$) (Figure 3). For long lengths (more than 80bp), unproductive states are short-lived in comparison to productive states.

For Model-M, when dsRNA are long enough to allow the binding of multiple OAS2 to the same dsRNA (from 80 to 120bp), we can observe that the dissociation constants $k_{im}/k_{i}$ for the subsequent bindings of OAS2 are smaller than those of prior ones, $k_{1m}/k_{1} > k_{2m}/k_{2} > k_{3m}/k_{3}$ (Figures 3 and 4C). This result indicates that subsequent bindings are more favourable than the prior ones, which suggests a cooperative dynamics for OAS2 activation.

Keeping in mind that for lengths smaller or equal to 70bp Model-M and Model-E are equivalent, Model-E is found to be the best model using AICc when dsRNA are shorter than or equal to 70bp (Table 2). For 80 and 90bp long dsRNA, the confidence set of models is Model-E and Model-M. Finally, for the 120bp length, the simplest model Model-E is selected as the unique best model. However, note that if only the goodness of fit ($RSS(\pmb{\hat{p}_{Best}}) = RSS_{L_k}(\pmb{\hat{p}_{Best}})$ in Table 2) is used as a criterion the most complex model Model-M is the best model for dsRNA longer than 70bp, whereas the three models are indistinguishable for dsRNA shorter or equal to 70bp.

5.2.   Second calibration strategy

When all dsRNA lengths are considered simultaneously, Model-E and Model-N well represent the experimentally observed formation of PPi over time for all concentrations of dsRNA of intermediate lengths 60-80bp, whereas they fail to accurately represent byproduct formation for shorter and longer lengths (Figure 5A-B). As with the first calibration strategy, estimates for shared dissociation constants and $k_p$ are found to be of the same order of magnitude for Model-E and Model-N (Figure 6). Despite the additional experimental data considered with the second calibration strategy, Model-N still appears to be highly non-identifiable.

On the other hand, Model-M gives a good representation of all dsRNA concentrations regardless of dsRNA length (Figure 5C). Despite requiring the largest number of parameters, Model-M is also selected as the unique best model when compared to all data (Table 2). Furthermore, note that the use of additional data in the second strategy improves the identifiability of Model-M: when considering all experimental data, narrower confidence intervals for estimates are obtained and estimate values are more clustered in multidimensional parameter spaces (Figure 6).

Finally, for the best model, Model-M, all estimates found for $k_{1m}/k_1$ and $k_p$ are linked by the same linear relationship with mostly $k_p < k_{1m}/k_1$. Furthermore, there exists the same linear relationship between all estimates found for $k_{1m}/k_1$ and $k_{2m}/k_2$ ensuring $k_{1m}/k_1 > k_{2m}/k_2$ (Figure 6). Estimates for dissociation constants of the activation by the same dsRNA of a second ($k_{2m}/k_2$) and a third ($k_{3m}/k_3$) OAS2 have similar values. The dissociation constant of the first enzyme ($k_{1m}/k_1$) is more than ten times larger than the second ($k_{2m}/k_2$) and third ($k_{3m}/k_3$). The second and third enzymes have higher affinity (which is the inverse of the dissociation constant) than the first enzyme. This suggests that subsequent bindings of OAS2 are facilitated by the first binding and that there is cooperative binding of OAS2 to a single dsRNA molecule.

6.   Conclusions

In this work, using mathematical modelling we investigate the effect of dsRNA length on the activation of OAS2; dsRNA serve as cofactors to enable the enzymatic activity of OAS2. Based on experimental data, our working hypothesis is that the activity of OAS2 increases as its cofactor length increases. Three models are designed: a simple enzymatic activity (Model-E), enzymatic activity with reversible inhibition (Model-N) and activation of multiple OAS2 by a single dsRNA (Model-M). In Model-E, the cofactor length is not explicitly accounted for, whereas Model-N considers the possibility of the formation of a reversible unproductive RNA-protein interaction that results from the binding of only one domain of OAS2 to dsRNA due to its length. Model-M more explicitly incorporates the cofactor length by allowing a single dsRNA of sufficient length (more than 70bp) to bind to and activate multiple OAS2 enzymes. Moreover, two strategies are adopted to calibrate models. First, dsRNA lengths data are considered independently that yields an implicit length-dependency of the model parameters and gives us another tool to characterise the effect of the cofactor length on the different parts of the kinetics. In the second calibration strategy, all dsRNA concentrations and lengths data are considered simultaneously as the aim of our study is to propose a scenario that accommodates changes in both cofactor concentrations and lengths.

The power/strength of our study lies on the consideration of multiple models tested against experimental data with various strategies and then compared via model selection; see also ^[17,18]. When considering kinetics for a single dsRNA length, the simplest enzymatic model Model-E is selected as the best model; however, when considering the kinetics for all dsRNA lengths simultaneously, the multiple binding model Model-M is the best model. Interestingly, a closer look at the estimates of parameters found for Model-M suggests that the multiple binding of OAS2 to the same dsRNA follows a cooperative regime (affinity of the activation of subsequent OAS2 enzymes is much higher than this of the first activation). Model-N, with transient inhibition, is never found to best explain the data even though it gives a good representation when lengths are considered independently. Note that a more complex version of Model-N with transitions from the non-productive compound $N$ to productive compound $D$ was also considered. As it provided similar results than Model-N but was even more penalized by the extra parameters, we did not present it in the work. However, the consideration of the formation of unproductive stages and its poor performance allow us to conclude that this scenario is not a mechanism that drives OAS2 activation by dsRNA.

Hence, based on our analysis, we can propose a mechanism for OAS2 activation that accounts for the impact of the length of its cofactor: multiple OAS2 can bind to the same dsRNA, when its length permits, and subsequent bindings are facilitated which underlies an enzyme with a cofactor cooperativity. This hypothesis now has to be experimentally verified, but this seems to be in preliminary agreement with the recent observation emphasising stable self-association of OAS2 as central to its mechanism ^[8].

Here, only three models are presented but more models have been developed in the base for this paper ^[10]. To the best of our knowledge, these mathematical models are the first models developed for the activation of OAS2 by dsRNA. Finally, other modelling approaches can be considered to account for the effect of cofactor length on the enzyme activation such as the use of length-dependent binding rate for enzymes to cofactors ^[19,20].

Acknowledgments

The work was originally part of DL's MSc thesis at The University of Manitoba. SMK and SP are supported in part by NSERC Discovery Grants and a Faculty of Science Collaborative Grant (University of Manitoba).

Conflict of interest

All authors declare no conflicts of interest in this paper.