Approximate mixed type quadratic-cubic functional equation

1.   Introduction

In this paper, we consider the minimization problem of

subject to the $\mathbb{R}^n$-valued integral-type state equation with $\alpha \in (0, 1)$,

and the terminal state constraint

In (1.1)–(1.3), $x(\cdot) \in \mathbb{R}^n$ is the state with the initial state $x_0 \in \mathbb{R}^n$, and $u(\cdot) \in U$ is the control with $U$ being the control space (see Section 2). Hence, we consider the following terminal state-constrained optimal control problem:

where $\mathcal{U}^p[0, T]$ is the set of admissible controls of (1.2). The problem aforementioned is referred to as (P) throughout this paper, and the precise problem statement of (P) is provided in Section 2. Note that the optimal control problems with and without state constraints capture various practical aspects of systems in science, biology, engineering, and economics ^{[2,4,5,6,29,41,43]}.

The state equation in (1.2) is known as a class of Volterra integral equations. The main feature of Volterra integral equations is the effect of memories, which does not appear in ordinary (state) differential equations. In fact, Volterra integral equations of various kinds have been playing an important role in modeling and analyzing of practical physical, biological, engineering, and other phenomena that are governed by memory effects ^{[7,17,19,32,34]}. We note that one major distinction between (1.2) and other classical Volterra integral equations is that (1.2) has a kernel $\frac{f(t, s, x, u)}{(t-s)^{1-\alpha}}$, which becomes singular at $s = t$. In fact, $\alpha \in (0, 1)$ in the singular kernel $\frac{f(t, s, x, u)}{(t-s)^{1-\alpha}}$ of (1.2) determines the amount of the singularity, in which the large singular behavior occurs with small $\alpha \in (0, 1)$. Hence, the singular kernel in (1.2) can be applied to various areas of science, engineering, finance and economics, in which certain extraordinary phenomena have to be described. For example, the model of fluid dynamics may have some singular phenomena, leading to the deformation of the corresponding dynamic equation ^[17,33,36].

The study of optimal control problems for various kinds of Volterra integral equations via the maximum principle have been studied extensively in the literature; see ^{[3,12,13,18,20,22,23,30,35,39,40]} and the references therein. Specifically, the first study on optimal control for Volterra integral equations (using the maximum principle) can be traced back to ^[40]. Several different formulations (with and without state constraints and/or delay) of optimal control for Volterra integral equations and their generalizations are reported in ^{[3,7,12,18,20,30,35,39]}. Some recent progress in different directions including stochastic frameworks can be found in ^{[13,22,23,26,27,42]}. We note that the above-mentioned existing works (with the exception of the stochastic case in ^[26,27,42]) considered the situation with nonsingular kernels only in Volterra integral equations, which corresponds to the case of $f(t, s, x, u) = (t-s)^{1-\alpha} g(t, s, x, u)$ in (1.2). Hence, the problem settings in the earlier works can be viewed as a special case of (P).

Recently, (P) without the terminal state constraint in (1.3) was studied in ^[34]. Due to the presence of the singular kernel, the technical analysis including the maximum principle (without the terminal state constraint) in ^[34] should be different from that of the existing works mentioned above. In particular, the proof for the well-posedness and estimates of Volterra integral equations in [34, Theorem 3.1] requires a new type of Gronwall's inequality. Furthermore, the maximum principle without the terminal state constraint in [34, Theorem 4.3] needs a different duality and variational analysis via spike perturbation. More recently, the linear-quadratic optimal control problem (without the state constraint) for linear Volterra integral equations with singular kernels was studied in ^[28].

We note that the state equation in (1.2) is strongly related to classical state differential equations and (Caputo) fractional order differential equations. In particular, let $\mathcal{D}_{\alpha} ^C [x(\cdot)]$ be the Caputo fractional derivative operator of order $\alpha \in (0, 1)$ [32, Chapter 2.4]. Subsequently, by [32, Theorem 3.24 and Corollary 3.23], (1.2) becomes ($\Gamma(\cdot)$ denotes the gamma function)

In addition, when $f(t, s, x, u) = (t-s)^{1-\alpha} g(s, x, u)$, (1.2) is specialized to

As (1.4) and (1.5) are special cases of our state equation in (1.2), the state equation in (1.2) is able to describe various types of differential equations including fractional and ordinary differential equations. We also mention that there are several different results on optimal control for fractional differential equations; see ^{[1,8,14,25,31]} and the references therein.

The aim of this paper is to obtain the Pontryagin maximum principle for (P). As noted above, since ^[34] did not consider the state-constrained control problem, (P) can be viewed as a generalization of ^[34] to the terminal state-constrained control problem. The main theoretical significances and technical difficulties are the proof of the maximum principle in Theorem 3.1, which is presented in Section 5. In particular, due to (i) the inherent complex nature of the Volterra integral equation with singular kernels, (ii) the presence of the terminal state constraint, and (iii) the generalized standing assumptions of $f$, our maximum principle and its detailed proof must be different from those provided in the existing literature (e.g., ^{[12,18,22,23,30,34,35,39]}). Note also that as our state equation in (1.2) includes the case of Caputo fractional differential equation in (1.4), the maximum principle in Theorem 3.1 also covers [8, Theorem 3.12]. However, as the variational analysis of this paper and that of ^[8] are different, the proof techniques including the characterization of the adjoint equation must be different. Indeed, the maximum principle of this paper is new in the optimal control problem context and its proof requires a different technique, compared with the existing literature.

The detailed statements of the main results of this paper are provided as follows:

● Regarding (ii), as mentioned above, the proof in Section 5 must be different from that of the unconstrained control problem in [34, Theorem 4.3]. Specifically, in contrast to [34, Theorem 4.3], due to the terminal state constraint in (1.3), we have to employ the Ekeland variational principle and the spike variation technique, together with the intrinsic properties of the distance function and the generalized Gronwall's inequality, to establish the duality analysis for Volterra-type forward variational and backward adjoint equations with singular kernels (see Lemma 5.2, Lemma 5.3 and Section 5.6). Note that this analysis leads to the desired necessary condition for optimality. Such a generalized proof of the maximum principle including the duality and variational analysis was not needed in [34, Theorem 4.3], as it did not consider the terminal state constraint in the corresponding optimal control problem. Note also that without the terminal state constraint, our maximum principle in Theorem 3.1 is reduced to the unconstrained case in [34, Theorem 4.3] (see Remark 3.1).

● As for (i), since our Volterra integral equation in (1.2) covers both singular and nonsingular kernels, the proof for the maximum principle in Section 5 should be different from that of the classical state-constrained maximum principle with the nonsingular kernel only (when $f(t, s, x, u) = (t-s)^{1-\alpha} g(t, s, x, u)$ in (1.2)) studied in the existing literature (e.g., [12, Theorem 1], [22, Theorem 3.1] and ^{[18,23,30,35,39]}). In particular, due to the presence of the singular kernel in (1.2), we need a different proof for duality and variational analysis (see Lemma 3, Lemma 5.3 and Section 5.6). In addition, unlike the existing literature (e.g., [12, Theorem 1] and [22, Theorem 3.1]), our adjoint equation is obtained by the backward Volterra integral equation with the singular kernel, as a consequence of the new duality analysis with the singular kernel in Section 5.6 (see Theorem 3.1 and Remark 3.2).

● Concerning (iii), we mention that unlike the existing works for classical optimal control of Volterra integral equations with nonsingular kernels (e.g., [12,(4) and (5)], [22, page 3437 and (A3)], and ^[18,23,39]), our paper assumes neither the differentiability of (singular or nonsingular) kernels in $(t, s, u)$ (time and control variables) nor the essentially boundedness of a class of admissible controls (see Remark 3.2). Hence, the detailed proof of the maximum principle provided in this paper must be different from those given in the existing literature.

As mentioned above, the main motivation of studying (P) is to provide the general maximum principle for terminal state-constrained optimal control problems of various classes of differential and integral type equations. Specifically, as mentioned above, (1.2) covers Volterra integral equations with singular and nonsingular kernels (see Remark 3.2), ordinary differential equations (see (1.5)), and Caputo-type fractional differential equations (see (1.4)). Hence, the terminal state-constrained optimal control problems for such kind of (differential and integral) state equations can be solved via the maximum principle of this paper (see Theorem 3.1). As stated above, the maximum principle for (P) has not been presented in the existing literature.

We mention that Volterra integral equations and terminal state-constrained optimal control problems can be applied to various practical applications in science, engineering, economics, and mathematical finance; see ^{[2,4,5,6,7,17,19,29,32,34,41,43]} and the references therein. In particular, Volterra integral equations can be used to study the so-called tautochrone problem in mechanical applications, the heat transfer problem in diffusion models, the shock wave problem, the renewal equation in the theory of industrial engineering, the investment problem in economics, and the problem of American option pricing ^{[7,17,19,32,34]}. The interacting biological population model can be described by Volterra integral equations ^[7]. Furthermore, as mentioned above, in a practical point of views, the singular kernel in (1.2) can be applied to those Volterra integral equations to study their singular and/or peculiar behavior. Hence, we can use the modeling framework of (1.2) for any differential and Volterra integral equations to capture the memory and/or singular effects, which can be observed in real world (e.g., the deformation of fluid dynamics due to singular phenomena ^[17,33,36], and the dependency of the current stock price on past investment strategies over a period of time ^[7,17]). We also note that the (terminal) state-constrained optimal control problems can be formulated for these examples (e.g., the Volterra-type renewal integral equation in industrial applications, the Volterra-type heat transfer integral equation in diffusion models, and the Volterra-type investment integral equation in economics). In fact, there are huge potential applications of optimal control problems, and their various different practical examples in science, engineering, biology, economics, and mathematical finance, including the optimal control for partial differential equations (PDEs), can be found in ^{[2,4,5,6,29,41,43]} and the references therein.

In view of the preceding discussion, we believe that the maximum principle of this paper broadens both the theoretical generality and the applicability of the domain of optimal control problems.

The rest of this paper is organized as follows. The problem statement of (P) is given in Section 2. The statement of the maximum principle for (P) is provided in Section 3. We study an example of (P) in Section 4. The proof of the maximum principle is given in Section 5. Finally, we conclude this paper in Section 6.

2.   Problem formulation

Let $\mathbb{R}^n$ be an $n$-dimensional Euclidean space, where $\langle x, y \rangle : = x^\top y$ is the inner product and $|x| : = \langle x, x \rangle^{1/2}$ is the norm for $x, y \in \mathbb{R}^n$. For $A \in \mathbb{R}^{m \times n}$, $A^\top$ denotes the transpose of $A$. Let $[0, T]$ be a time interval such that $T < \infty$. Let $\mathbb{1}_{S}(\cdot)$ be the indicator function of any set $S$. In this paper, $C \geq 0$ denotes a generic constant, whose value is different from line to line. For any differentiable function $f:\mathbb{R}^n \rightarrow \mathbb{R}^l$, let $f_x : \mathbb{R}^n \rightarrow \mathbb{R}^{l \times n}$ be the partial derivative of $f$ with respect to $x \in \mathbb{R}^n$. $f_x = \begin{bmatrix} f_{1, x}^\top & \cdots & f_{l, x}^\top \end{bmatrix}^\top$ with $f_{j, x} \in \mathbb{R}^{1 \times n}$, and when $l = 1$, $f_x \in \mathbb{R}^{1 \times n}$. For $f : \mathbb{R}^n \times \mathbb{R}^l \rightarrow \mathbb{R}^l$, $f_{x} : \mathbb{R}^n \times \mathbb{R}^l \rightarrow \mathbb{R}^{l \times n}$ for $x \in \mathbb{R}^n$, and $f_y: \mathbb{R}^n \times \mathbb{R}^l \rightarrow \mathbb{R}^{l \times l}$ for $y \in \mathbb{R}^l$. For $1 \leq p < \infty$, define

● $L^p([0, T];\mathbb{R}^n)$: The space of functions $\psi:[0, T] \rightarrow \mathbb{R}^n$ such that $\psi$ is measurable and satisfies $\|\psi(\cdot)\|_{L^p([0, T];\mathbb{R}^n)} : = (\int _0^T |\psi(t)|^p \text{d} t)^{1/p} < \infty$;

● $C([0, T];\mathbb{R}^n)$: The space of functions $\psi:[0, T] \rightarrow \mathbb{R}^n$ such that $\psi$ is continuous and satisfies $\|\psi(\cdot)\|_{\infty} : = \sup_{t \in [0, T]} |\psi(t)| < \infty$.

Next, we state the precise problem statement of (P) provided in Section 1. In (1.2), $\alpha \in (0, 1)$ is the parameter of the singularity, $x(\cdot) \in \mathbb{R}^n$ is the state with the initial state $x_0 \in \mathbb{R}^n$, and $u(\cdot) \in U$ is the control with $U$ being the control space. In (1.2), $\frac{f(t, s, x, u)}{(t-s)^{1-\alpha}}$ denotes the singular kernel (with the singularity appearing at $s = t$), with $f:[0, T] \times [0, T] \times \mathbb{R}^n \times U \rightarrow \mathbb{R}^n$ being a generator. Note that $\alpha \in (0, 1)$ determines the level of singularity of (1.2); see Figure 1. In (1.2), $f$ is dependent on two time parameters, $t$ and $s$. While $t$ is the outer time variable to determine the current time, $s$ is the inner time variable describing the path or memory of (1.2) from $0$ to $t$. In (1.1), $l:[0, T] \times \mathbb{R}^n \times U \rightarrow \mathbb{R}$ is the running cost, while $h: \mathbb{R}^n \times \mathbb{R}^n \rightarrow \mathbb{R}$ is the terminal cost.

Assumption 1. (i) $(U, \rho)$ is a separable metric space. $f$ and $f_x$ are continuous on $[0, T] \times [0, T]$ and Lipschitz continuous in $(x, u) \in \mathbb{R}^n \times U$ with the Lipschitz constant $K \geq 0$. $|f(t, s, 0, u)| \leq K$ for $(t, s, u) \in [0, T] \times [0, T] \times U$.

(ii) $l$ and $l_x$ are continuous on $[0, T]$ and Lipschitz continuous in $(x, u) \in \mathbb{R}^n \times U$ with the Lipschitz constant $K \geq 0$. $|l(t, 0, u)| \leq K$ for $(t, u) \in [0, T] \times U$. $h$, $h_{x_0}$, and $h_x$ are Lipschitz continuous in both variables with the Lipschitz constant $K \geq 0$.

(iii) $F$ is a nonempty closed convex subset of $\mathbb{R}^{2n}$.

For $p > \frac{1}{\alpha}$ and $u_0 \in U$, we define the space of admissible controls for (1.2) as

Note that $p > \frac{1}{\alpha}$ is needed for the well-posedness of (1.2), which is stated in the following lemma [34, Theorem 3.1 and Proposition 3.3]:

Lemma 2.1. Let (i) of Assumption 1 hold and $p > \frac{1}{\alpha}$. For any $(x_0, u(\cdot)) \in \mathbb{R}^n \times \mathcal{U}^p[0, T]$, (1.2) admits a unique solution in $C([0, T];\mathbb{R}^n)$, and there is a constant $C \geq 0$ such that $\|x (\cdot) \|_{L^p([0, T];\mathbb{R}^n)} \leq C (1 + |x_0| + \|\rho(u(\cdot), u_0) \|_{L^p([0, T];\mathbb{R}_+)})$.

Under Assumption 1, the main objective of this paper is to solve (P) via the Pontryagin maximum principle. Note that Assumption 1 is crucial for the well-posedness of the state equation in (1.2) by Lemma 2.1 as well as the maximum principle of (P). Assumptions similar to Assumption 1 have been used in various optimal control problems and their maximum principles; see ^{[9,12,13,15,16,20,22,23,27,33,34,37,39,40,43]} and the references therein. Note also that we do not need the differentiability of $f$ in $(t, s, u)$, which was assumed in the existing literature (e.g., [12,(4) and (5)], [22, page 3437 and (A3)], and ^[18,23,39]); see Remark 3.2.

3.   Statement of the maximum principle

We provide the statement of the maximum principles for (P). The proof is given in Section 5.

Theorem 3.1. Let Assumption 1 hold. Suppose that $(\overline{u}(\cdot), \overline{x}(\cdot)) \in \mathcal{U}^p[0, T] \times C([0, T];\mathbb{R}^n)$ is the optimal pair for (P), where $\overline{x}(\cdot) \in C([0, T];\mathbb{R}^n)$ is the corresponding optimal state trajectory of (1.2). Then there exists a pair $(\lambda, \xi)$, where $\lambda \in \mathbb{R}$ and $\xi = (\xi_1, \xi_2) \in \mathbb{R}^{2n}$, such that the following conditions hold:

● Nontriviality condition: $(\lambda, \xi) \neq 0$, where $\lambda \geq 0$ and $\xi \in N_F (\overline{x}_0, \overline{x}(T))$ with $N_F(x)$ being the normal cone to the convex set $F$ defined in (5.1);

● Adjoint equation: $p(\cdot) \in L^p([0, T];\mathbb{R}^n)$ is the unique solution to the following backward Volterra integral equation with the singular kernel:

● Transversality conditions:

● Hamiltonian-like maximum condition:

Remark 3.1. Without the terminal state constraint in (1.3), Theorem 3.1 holds with $\lambda = 1$ and $\xi = 0$. This is equivalent to [34, Theorem 4.3].

Remark 3.2. By taking $f(t, s, x, u) = (t-s)^{1-\alpha} g(t, s, x, u)$ in Theorem 3.1, we obtain the maximum principle for the optimal control problems of classical Volterra integral equations with nonsingular kernels. Note that Theorem 3.1 is more general than the existing maximum principles for Volterra integral equations with nonsingular kernels (e.g., [12, Theorem 1], [22, Theorem 3.1] and ^{[18,23,30,35,39]}), where Theorem 3.1 assumes neither the differentiability of the corresponding kernel with respect to time and control variables nor the essential boundedness of a class of admissible controls (e.g., [12,(4) and (5)], [22, page 3437 and (A3)]). In addition, unlike the existing literature, the adjoint equation in Theorem 3.1 must be obtained in integral form, as a consequence of the new duality analysis with singular kernels in Section 5.6.

4.   Example: time-varying linear-quadratic control problem

The motivation of this section is to demonstrate the applicability of Theorem 3.1 to the state-constrained linear-quadratic problem for Volterra integral equations with singular kernels. We consider the minimization of the objective functional of $J(x_0, u(\cdot)) = \int_0^T [ x(s) + \frac{1}{2} u(s)^2 ] \text{d} s$ subject to the $\mathbb{R}$-valued Volterra integral equation with the singular kernel:

For Case I, the terminal state constraint is given by $(x_0, x(T)) \in F = \{x_0 = 10, \; x(T) = 10 \} \subset \mathbb{R}^2$. Here, we may assume that $U$ is an appropriate sufficiently large compact set satisfying Assumption 1. Note that this example is closely related to the (terminal) state-constrained linear-quadratic control problem, which can be applied to study the singular aspects of various applications in science, engineering, and economics.

Let $T = 3$. By Theorem 3.1, the adjoint equation is $p(t) = -\lambda$. From the first transversality condition in (i), we have $\xi \in \mathbb{R}^2$. Then by the second transversality condition in (ii), $\int_0^3 p(t) \text{d} t = -3\lambda = \xi_1 + \xi_2$. Hence, we can choose $\lambda = 1$ and $\xi_1 = \xi_2 = -1.5$. By the Hamiltonian-like maximum condition and the first-order optimality condition, the (candidate) optimal solution of Case I is as follows:

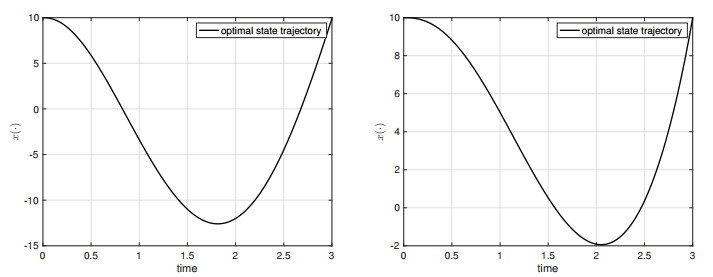
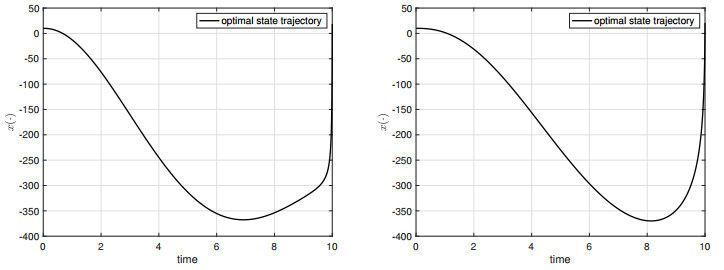
We apply (4.2) to get the optimal state trajectory of (4.1). For Case I, the optimal state trajectory of (4.1) controlled by (4.2) when $\alpha = 0.1$ and $\alpha = 0.5$ is shown in Figure 2. Similar1y, when $T = 10$, the optimal state trajectory is depicted in Figure 3.

We now consider Case II, where the (terminal) state constraint is generalized by

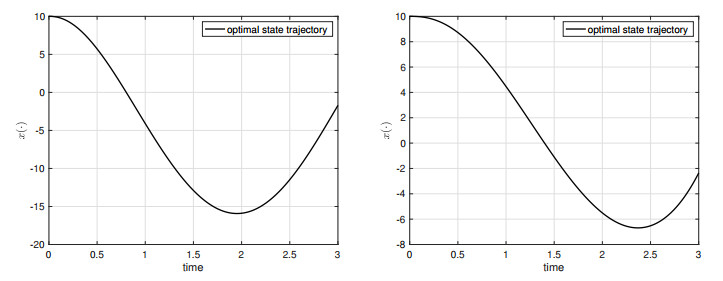
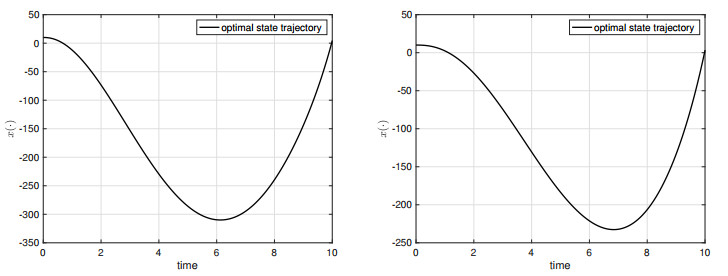
Similar to Case I, the adjoint equation is given by $p(t) = -\lambda$. The first transversality condition in (i) implies that $\xi_1 \in \mathbb{R}$ and $\xi_2 = 0$. From the second transversality condition in (ii), it follows that $\int_0^3 p(t) \text{d} t = -3 \lambda = \xi_1$. Hence, we can choose $\lambda = 1$, $\xi_1 = -3$, and $\xi_2 = 0$. Then analogous to (4.2), the (candidate) optimal solution of Case II is given by $\overline{u}(t) = \int_t^3 \frac{- t^2 }{(r-t)^{1-\alpha}} \text{d} r$, a.e. $t \in [0, 3]$. Figure 4 depicts the optimal state trajectory (with $\alpha = 0.1$ and $\alpha = 0.5$) when $T = 3$, and Figure 5 shows the case when $T = 10$. Note that the numerical results of this section are obtained by the finite-difference method to approximate the solutions of (4.1) and (4.2).

Remark 4.1. The purpose of the examples in this section is to show an analytic method for applying Theorem 3.1. In the future research problem, a shooting-like method has to be developed to solve (P) numerically, which can be applied to several different complex situations of (P). This requires extending the classical approach (e.g., ^[11,16]) to the case of Volterra integral equations with singular kernels.

5.   Proof of Theorem 3.1

This section provides the proof of Theorem 3.1.

5.1.   Preliminaries on distance function

Recall that $F$ is a nonempty closed convex subsets of $\mathbb{R}^{2n}$. Let $d_{F} : \mathbb{R}^{2n} \rightarrow \mathbb{R}_{+}$ be the standard Euclidean distance function to $F$ defined by $d_{F}(x) : = \inf_{y \in F} |x-y|$ for $x \in \mathbb{R}^{2n}$. Note that $d_{F}(x) = 0$ when $x \in F$. Then it follows from the projection theorem [38, Theorem 2.10] that there exists a unique $P_{F}(x) \in F$ with $P_{F}(x) : \mathbb{R}^{2n} \rightarrow F \subset \mathbb{R}^{2n}$, the projection of $x \in \mathbb{R}^{2n}$ onto $F$, such that $d_{F}(x) = \inf_{y \in F} |x-y| = |x - P_{F}(x)|$. By [38, Lemma 2.11], $P_{F}(x) \in F$ is the corresponding projection if and only if $\langle x - P_{F}(x), y- P_{F}(x) \rangle \leq 0$ for all $y \in F$, which leads to the characterization of $P_{F}(x)$. In view of [38, Definition 2.37], we have $x - P_{F}(x) \in N_{F}(P_{F}(x))$ for $x \in \mathbb{R}^{2n}$, where $N_{F}(x)$ is the normal cone to the convex set $F$ at a point $x \in F$ defined by

Based on the distance function $d_F$, (1.3) can be written by $d_F (\overline{x}_0, \overline{x}(T)) = 0 \; \Leftrightarrow\; (\overline{x}_0, \overline{x}(T)) \in F$.

Lemma 5.1. [24, page 167] and [21, Proposition 2.5.4] The function $d_F(x)^2$ is Fréchet differentiable on $\mathbb{R}^{2n}$ with the Fréchet differentiation of $d_F(x)^2$ at $x \in \mathbb{R}^{2n}$ given by $D d_F(x)^2(h) = 2 \langle x-P_F(x), h \rangle$ for $h \in \mathbb{R}^{2n}$.

5.2.   Ekeland variational principle

Recall that the pair $(\overline{x}(\cdot), \overline{u}(\cdot)) \in C([0, T];\mathbb{R}^n) \times \mathcal{U}^p[0, T]$ is the optimal pair of (P). Note that the pair $(\overline{x}_0, \overline{x}(T))$ holds the terminal state constraint in (1.3). The optimal cost of (P) under $(\overline{x}(\cdot), \overline{u}(\cdot))$ can be written by $J(\overline{x}_0, \overline{u}(\cdot))$.

Recall the distance function $d_F$ in Section 5.1. For $\epsilon > 0$, we define the penalized objective functional as follows:

We can easily observe that $J_{\epsilon}(\overline{x}_0, \overline{u}(\cdot)) = \epsilon > 0$, i.e., $(\overline{x}_0, \overline{u}(\cdot)) \in \mathbb{R}^n \times \mathcal{U}^p[0, T]$ is the $\epsilon$-optimal solution of (5.2). We define the Ekeland metric $\widehat{d}:(\mathbb{R}^n \times \mathcal{U}^p[0, T]) \times (\mathbb{R}^n \times \mathcal{U}^p[0, T]) \rightarrow \mathbb{R}_{+}$:

where

Note that $(\mathbb{R}^n \times \mathcal{U}^p[0, T], \widehat{d})$ is a complete metric space, and $J_{\epsilon}(x_0, u)$ in (5.2) is continuous on $(\mathbb{R}^n \times \mathcal{U}^p[0, T], \widehat{d})$ [33, Proposition 3.10 and Corollary 4.2,Chapter 4].

In view of (5.2)–(5.4), we have

By the Ekeland variational principle [33, Corollary 2.2,Chapter 4], there exists a pair $(x_0^\epsilon, u^\epsilon) \in \mathbb{R}^n \times \mathcal{U}^p[0, T]$ such that

and for any $(x_0, u(\cdot)) \in \mathbb{R}^n \times \mathcal{U}^p[0, T]$,

We write $(x^\epsilon(\cdot), u^\epsilon(\cdot)) \in C([0, T];\mathbb{R}^n) \times \mathcal{U}^p[0, T]$, where $x^{\epsilon}(\cdot)$ is the state trajectory of (1.2) under $(x_0^\epsilon, u^\epsilon(\cdot)) \in \mathbb{R}^n \times \mathcal{U}^p[0, T]$.

5.3.   Spike variation

The next step is to derive the necessary condition for $(x_0^\epsilon, u^\epsilon(\cdot)) \in \mathbb{R}^n \times \mathcal{U}^p[0, T]$. To this end, we employ the spike variation technique, as $U$ does not have any algebraic structure. Hence, standard (convex) variations cannot be used.

For $\delta \in (0, 1)$, we define $\mathcal{E}_{\delta} : = \{ E \in [0, T]\; |\; |E| = \delta T\}$, where $|E|$ denotes the Lebesgue measure of $E$. For $E_{\delta} \in \mathcal{E}_{\delta}$, we introduce the spike variation associated with $u^\epsilon$:

where $u(\cdot) \in \mathcal{U}^p[0, T]$. Clearly, $u^{\epsilon, \delta}(\cdot) \in \mathcal{U}^p[0, T]$. By definition of $\overline{d}$ in (5.4),

We also consider the variation of the initial state given by $x_0^{\epsilon} + \delta a$, where $a \in \mathbb{R}^n$. Let $x^{\epsilon, \delta}(\cdot) \in C([0, T];\mathbb{R}^n)$ be the state trajectory of (1.2) under $(x_0^\epsilon + \delta a, u^{\epsilon, \delta}(\cdot)) \in \mathbb{R}^n \times \mathcal{U}^p[0, T]$. By (5.7) and (5.8), it follows that

5.4.   Variational analysis I and II

We now study variational analysis of (5.9).

Lemma 5.2. The following result holds:

where $Z^\epsilon$ is the solution to the first variational equation related to the optimal pair $(x_0^\epsilon, u^{\epsilon}(\cdot)) \in \mathbb{R}^n \times \mathcal{U}^p[0, T]$ given by

with

Proof. For $\delta \in (0, 1)$, let $Z^{\epsilon, \delta}(t) : = \frac{x^{\epsilon, \delta}(t) - x^{\epsilon}(t)}{\delta}$, a.e. $t \in [0, T]$, where based on the Taylor expansion, $Z^{\epsilon, \delta}$ can be written as (note that $f_{x}^{\epsilon, \delta}(t, s) : = \int_0^1 f_x(t, s, x^{\epsilon}(s) + r (x^{\epsilon, \delta}(s) - x^{\epsilon}(s)), u^{\epsilon, \delta}(s)) \text{d} r$)

Then we complete the proof by showing that $\lim_{\delta \downarrow 0} \sup_{t \in [0, T]} |Z^{\epsilon, \delta}(t) - Z^{\epsilon}(t)| = 0$.

By Assumption 1, we have $|\widehat{f}(t, s)| \leq 4 K + 4 K|x^\epsilon(s)| + 4 K\rho(u^\epsilon(s), u(s)) = : \widetilde{\psi}(s)$ and $|f_x^{\epsilon, \delta}(t, s)| \leq K$. Based on Assumption 1, we can show that

where $b(t) = |\delta a | + \int_0^t \mathbb{1}_{E_{\delta}}(s) \frac{\widetilde{\psi}(s)} {(t-s)^{1-\alpha}} \text{d} s$. By [34, Lemma 2.3], it follows that

We apply the Gronwall's inequality in [34, Lemma 2.4] to get

From Lemma 2.1, $Z^{\epsilon}$ is a well-defined linear Volterra integral equation. Then with $\hat{b}(t) : = |a| + \int_0^t \frac{\widetilde{\psi}(s)}{(t-s)^{1-\alpha}} \text{d} s$ and using a similar approach, we can show that

We obtain

Notice that by Assumption 1, together with (5.11) and (5.12), it follows that as $\delta \downarrow 0$,

For convenience, let

and

By (5.14), $\lim_{\delta \downarrow 0} \sup_{t \in [0, T]} b^{(1, 1)}(t) = 0$. In addition, by invoking [34, Lemma 5.3.2], it follows that $\sup_{t \in [0, T]} b^{(1, 2)}(t) \leq \delta.$. Then from (5.13), we have

By applying [34, Lemma 2.4], it follows that

Hence, we have

This completes the proof. □

Based on the Taylor expansion,

where

and

Let us define

By Lemma 2.1, $\widehat{Z}^{\epsilon}$ is a well-defined Volterra integral equation. It then follows that

Notice that $\lim_{\delta \downarrow 0} \sup_{t \in [0, T]} |Z^{\epsilon, \delta}(t) - Z^{\epsilon}(t)| = 0$ by Lemma 5.2. By [33, Corollary 3.9,Chapter 4], it follows that $\sup_{t \in [0, T]} | \int_0^t (\frac{1}{\delta} \mathbb{1}_{E_{\delta}}(s) - 1) \widehat{l}(s) \text{d} s | \leq \delta$. Hence, similar to Lemma 5.2, we have

From (5.9), we have

Let

For $\xi^{\epsilon} \in \mathbb{R}^{2n}$ ($\xi_1^{\epsilon} \in \mathbb{R}^n$ and $\xi_2^{\epsilon} \in \mathbb{R}^n$), let

Then from (5.15), (5.17), and (5.18), as $\delta \downarrow 0$, (5.16) becomes

where by (5.2), (5.17), and (5.18) (see also the discussion in Section 5.1),

Lemma 5.3. For any $(a, u(\cdot)) \in \mathbb{R}^n \times \mathcal{U}^p[0, T]$, the following results hold:

(i) $\lim_{\epsilon \downarrow 0} \{ |x_0^\epsilon - \overline{x}_0 | + \overline{d}(u^\epsilon(\cdot), \overline{u}(\cdot)) \} = 0$;

(ii) $\sup_{t \in [0, T]} | Z^{\epsilon}(t) - Z(t) | = o(1), \; | \widehat{Z}^{\epsilon}(T) - \widehat{Z}(T) | = o(1)$, where

with $\widetilde{f}(t, s) : = f(t, s, \overline{x}(s), u(s)) - f(t, s, \overline{x}(s), \overline{u}(s))$, $\widetilde{l}(s) : = l(s, \overline{x}(s), u(s)) - l(s, \overline{x}(s), \overline{u}(s))$, $\overline{h}_{x_0} : = h_{x_0} (\overline{x}_0, \overline{x}(T))$, and $\overline{h}_{x} : = h_x (\overline{x}_0, \overline{x}(T))$.

Proof. Part (i) is due to (5.6). The proof of (ii) is similar to Lemma 5.2. □

We consider the limit of $\epsilon \downarrow 0$. Instead of taking the limit with respect to $\epsilon \downarrow 0$, let $\{\epsilon_k\}$ be the sequence of $\epsilon$ such that $\epsilon_k \geq 0$ and $\epsilon_k \downarrow 0$ as $k \rightarrow \infty$. We replace $\epsilon$ with $\epsilon_k$. Then by (5.20), the sequences $(\{\lambda^{\epsilon_k} \}, \{\xi^{\epsilon_k} \})$ are bounded for $k \geq 0$. From the standard compactness argument, we may extract a subsequence of $\{\epsilon_k\}$, still denoted by $\{\epsilon_k\}$, such that

By (5.17) and the property of the limiting normal cones [41, page 43],

From (5.21) and (5.20), together with Lemma 5.3, as $k \rightarrow \infty$, it follows that

Therefore, as $k \rightarrow \infty$, (5.19) becomes for any $(a, u) \in \mathbb{R}^n \times \mathcal{U}^p[0, T]$,

5.5.   Proof of Theorem 3.1: nontriviality condition

When $\lambda > 0$, the nontriviality condition in Theorem 3.1 holds. When $\lambda = 0$, from (5.20)–(5.22), we must have $\xi \in N_F (\overline{x}_0, \overline{x}(T))$ and $|\xi^{\epsilon_k}| \rightarrow |\xi| = 1$. Hence, we have $(\lambda, \xi) \neq 0$, i.e., they cannot be zero simultaneously. This proves the nontriviality condition in Theorem 3.1.

5.6.   Proof of Theorem 3.1: adjoint equation and duality analysis

Then by using the variational equations in Lemma 5.3, (5.23) becomes

With the adjoint equation $p(\cdot) \in L^p([0, T];\mathbb{R}^n)$ in Theorem 3.1, (5.24) becomes

In (5.25), the standard Fubini's formula and Lemma 5.3 lead to

Moreover, by definition of $N_F$ in (5.1), it follows that for any $y = (y_1, y_2) \in F$,

Hence, (5.25) becomes for any $(a, u) \in \mathbb{R}^n \times \mathcal{U}^p[0, T]$ and $y = (y_1, y_2) \in F$,

We use (5.26) to prove the transversality conditions and the Hamiltonian-like maximum condition.

5.7.   Proof of Theorem 3.1: transversality conditions

In (5.26), when $u = \overline{u}$, for any $y = (y_1, y_2) \in F$, we have

When $(y_1, y_2) = (\overline{x}_0, \overline{x}(T))$, the above inequality holds for any $a, -a \in \mathbb{R}^n$, which implies

Under (5.27), the above inequality becomes $0 \leq \langle \xi_1, \overline{x}_0 - y_1 \rangle + \langle \xi_2, \overline{x}(T) - y_2 \rangle$ for any $y = (y_1, y_2) \in F$. This, together with (5.27), proves the transversality conditions in Theorem 3.1. In addition, as $p (\cdot) \in L^p([0, T];\mathbb{R}^n)$, the nontriviality condition implies the nontriviality of the adjoint equation in Theorem 3.1.

5.8.   Proof of Theorem 3.1: Hamiltonian-like maximum condition

We prove the Hamiltonian-like maximum condition in Theorem 3.1. Define

When $(y_1, y_2) = (\overline{x}_0, \overline{x}(T))$ and $a = 0$ in (5.26), by the Fubini's formula, (5.26) can be written as

As $U$ is separable, there exists a countable dense set $U_0 = \{u_i, \; i \geq 1\} \subset U$. Moreover, there exists a measurable set $S_i \subset [0, T]$ such that $|S_i| = T$ and any $t \in S_i$ is the Lebesgue point of $\Lambda(t, \overline{x}(t), u(t))$, i.e., it holds that $\lim_{\tau \downarrow 0} \frac{1}{2\tau} \int_{t-\tau}^{t+\tau} \Lambda(s, \overline{x}(s), u(s)) \text{d} s = \Lambda(t, \overline{x}(t), u(t))$ [10, Theorem 5.6.2]. We fix $u_i \in U_0$. For any $t \in S_i$, define

Then (5.28) becomes

This is implies that

Since $\cap_{i \geq 1} S_i = [0, T]$ by the fact that $U_0$ is countable, $\Lambda$ is continuous in $u \in U$, and $U$ is separable, (5.29) implies the Hamiltonian-like maximum condition in Theorem 3.1. This completes the proof.

6.   Conclusions

In this paper, we have studied the Pontryagin maximum principle for the optimal control problem of Volterra integral equations with singular kernels. The main technical difference in the proof compared with the existing literature is the variational and duality analysis. In fact, the variational analysis in our paper needs to handle the singular kernel, and the duality analysis requires to characterize the integral-type adjoint equation with the singular kernel to get the desired Hamiltonian-like maximization condition.

There are several important potential future research problems. One {direction} is to study (P) with additional generalized state constraints including the running state constraint. Another {direction} is to study the numerical aspects of solving (P) such as the shooting method and the Lagrangian collocation approach. Finally, one can extend (P) to the infinite-dimensional problem, which can be applied to studying optimal control of integral-type partial differential equations and integral-type systems with delays and singular kernels.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This research was supported in part by the Korea Institute of Energy Technology Evaluation and Planning (KETEP) and the Ministry of Trade, Industry & Energy (MOTIE) of the Republic of Korea (RS-2023-00235742), in part by the National Research Foundation of Korea (NRF) Grant funded by the Ministry of Science and ICT, South Korea (NRF-2021R1A2C2094350) and in part by Institute of Information & communications Technology Planning & Evaluation (IITP) grant funded by the Korea government (MSIT) (No. 2020-0-01373, Artificial Intelligence Graduate School Program (Hanyang University)).

Conflict of interest

The author declares no conflict of interest in this paper.