Global dynamic analysis of periodic solution for discrete-time inertial neural networks with delays

1.   Introduction

Inertial neural networks (INNs) was firstly introduced by Wheeler and Schieve ^[1] in 1997. After that, lots of results for INNs have been gained. Jian and Duan ^[2] considered the finite-time synchronization for fuzzy neutral-type inertial neural networks with time-varying coefficients and proportional delays. Some novel delay-independent criteria about finite-time synchronization were obtained by using finite-time stability theory and combining with inequality techniques and some analysis methods. Long etc. ^[3] investigated finite-time stabilization of state-based switched chaotic inertial neural networks with distributed delays by the theory of finite-time control and non-smooth analysis. In ^[4], the global exponential stabilization (GES) of inertial memristive neural networks with discrete and distributed time-varying delays was studied. Using the generalized Halanay inequality, matrix measure and matrix-norm inequality, the authors ^[5] investigated the global dissipativity for INNs with delays and parameter uncertainties. For more research contents about INNs, see e.g. ^[6,7,8,9,10] and related references.

Recent years, periodic solution problems of INNs have been studied by some authors. Aouiti etc. ^[11] studied the exponential stability of piecewise pseudo almost periodic solutions for neutral-type inertial neural networks with mixed delays and impulses by using inequality techniques and Lyapunov method. Huang and Zhang ^[12] considered a class of non-autonomous inertial neural networks with proportional delays and time-varying coefficients by combining Lyapunov function method with differential inequality approach. For more results of periodic solutions of neural network systems, see e. g. ^{[13,14,15,16,17,18,19,20]}.

Classic INNs with multiple time-varying delays which can be described by

where $t\geq0, \; i = 1, \cdots, n$, $x_i(t)$ denotes the state of $ith$ neuron at time $t$, $a_i(t) > 0$ is the damping coefficient, $b_i(t) > 0$ denotes the strength of different neuron at time $t$, $c_{ij}(t)$ and $d_{ij}(t)$ are the neuron connection weights at time $t$, $f_j(\cdot)$ is the activation function which is a continuous function, $\tau_j(t)$ is a delay function, $I_i(t)$ is an external input of $ith$ neuron at time $t$. For system (1.1) and its generalization, there exist lots of results, see e.g. ^[21,22]

To our best knowledge, there are few results reported on the research of discrete-time INNs with multiple time-varying delays. Motivated by the above work, in this paper, we study the periodic solutions problem for a discrete-time inertial neural networks with multiple time-varying delays as follows:

which initial conditions are given by

where $\tau$ is defined by (1.4), $n\in\mathbb{Z}_0^+ = \{n\in \mathbb{Z}:n\geq0\}, \; i = 1, 2, \cdots, m, \; a_i(n) > 0$ is a $N-$periodic function, $\tau_{j}(n)$ is non-negative $N-$periodic function, $b_i(n), c_{ij}(n), d_{ij}(n)$ and $I_i(n)$ are $N-$periodic functions. Let

$N$ is a positive integer. For a periodic function $f(n)$ on $\mathbb{Z}_0^+$, let

Denote

The highlights of this paper are threefold:

(1) The discrete-time delayed INNs as shown in system (1.2) is established, which is different from the existing continuous INNs, see e.g. ^[1,2,7,8].

(2) For discrete-time INNs, Lyapunov-Krasovskii functional is no longer applicable for studying stability problems. In this paper, we develop innovative mathematical analysis for the stability of discrete-time INNs.

(3) Discretization is needed in the implementation of continuous-time neural networks. Hence, the research of discrete-time INNs has important theoretical and practical values.

The following sections are organized as follows: In Section 2, sufficient conditions are established for existence and uniqueness of periodic solution to system (1.2). The exponential stability is given in Sections 3. In Section 4, an numerical example is given to show the feasibility of our results. Finally, some conclusions and discussions are given about this paper.

2.   Existence and uniqueness of periodic solution

In this section, we need the following assumptions.

(H$_1$) There exists non-negative constant $p_j$ such that

(H$_2$) There exist non-negative constants $q_j$ and $e_j$ such that

(H$_3$) There exists constants $L_j\geq0$ such that

Lemma 2.1 ^[23] Assume that $\mathcal{X}$ and $\mathcal{Y}$ are two Banach spaces, and $L:D(L)\subset \mathcal{X}\rightarrow \mathcal{Y},$ is a Fredholm operator with index zero. Furthermore, $\Omega\subset \mathcal{X}$ is an open bounded set and $N:\bar{\Omega}\rightarrow \mathcal{Y}$ is $L$-compact on $\bar{\Omega}$. if all the following conditions hold:

$(1) \; Lx\neq\lambda Nx, \forall x\in\partial\Omega\cap D(L), \forall \lambda\in(0, 1),$

$(2) \; Nx\notin ImL, \forall x\in\partial\Omega\cap KerL,$

$(3) \; deg\{JQN, \Omega\cap KerL, 0\}\neq 0$,

where $J:ImQ\rightarrow KerL$ is an isomorphism. Then equation $Lx = Nx$ has a solution on $\bar{\Omega}\cap D(L).$ Let

where $\xi_i > 0$ is a constant. Then system (1.2) is changed into the following system:

Theorem 2.1 Suppose that assumption (H$_1$) holds. Then system (1.2) has at least one $N-$periodic solution, provide that the following conditions hold:

where $i = 1, 2, \cdots, m, \; M$ and $\widetilde{m}$ are defined by (2.15) and (2.16).

Proof Let

Let

equipped with the norm

Then $l_N$ is a Banach space. Let

Obviously, $l_N^0$ and $l_N^c$ are both closed linear subspaces of $l_N$, and $l_N = l_N^0\oplus l_N^c, \; \mathrm{dim}l_N^c = 2m.$ Define a linear operator

and

Let $N: l_N\rightarrow l_N$ with

and

Then, $KerL = l_N^c$ and $ImL = l_N^0.$ Hence, $L$ is a Fredholm mapping of index zero. Define continuous projectors $P, \; Q$ by

and

Let

then

Since $\mbox{Im}L\subset l_N$ and $D(L)\cap \mbox{Ker}P\subset l_N,$ then $K_p$ is an embedding operator and is a completely operator in $\mbox{Im}L$. Let $\Omega\subset l_N$. In view of the definitions of $Q$ and $N$, we know that $QN(\bar{\Omega})$ is bounded on $\bar{\Omega}$. Hence nonlinear operator $N$ is $L$-compact on $\overline{\Omega}$. Let

where $L$ and $N$ are defined by (2.3)-(2.6). $\forall x\in\Omega_1$, it follows that

By (2.7), we have

and

Using $\xi_i < 1$, we gain

i.e.,

By (2.8), we have

and

Using $1-(a_i^+-\xi_i) > 0$ and assumption (H$_1$), we have

From $a_i^–-\xi_i > 0$ and (2.10), we have

From $(a_i^–-\xi_i)\xi_i-[(a_i(n)-\xi_i)\xi_i-b_i(n)]^+ > 0$, (2.9) and (2.11), we gain

By (2.9) and (2.12), we get

Hence, $\Omega_1$ is a bounded set and condition (1) of Lemma 2.1 holds. In view of (2.12) and (2.13), let

Let $\Omega_2 = \{w\in l_N: ||w|| < M+1\}$. We claim that

Assume that (2.14) does not hold. In fact, $\forall w\in\partial\Omega_2\cap KerL,$ then $w\in\mathbb{R}^{2m}$ is a constant vector, and there exists at least one $i\in\{1, 2, \cdots, m\}$ such that

or

Case 1: If (2.15) holds, let $y_{i} = M+1, \; x_i = \pm\widetilde{m}$, then by (2.5),

i.e.,

which is contract to $\xi_i\widetilde{m}\neq \pm(M+1)$. If $y_{i} = -(M+1), \; x_i = \pm \widetilde{m}$, we also obtain the similar contraction.

Case 2: If (2.16) holds, let $y_{i} = \widetilde{m}, \; x_i = \pm(M+1)$, then by (2.5),

i.e.,

which is contract to $\xi_i(M+1)\neq\pm\widetilde{m}$. If $y_{i} = -\widetilde{m}, \; x_i = \pm (M+1)$, we also obtain the similar contraction. Hence, condition (2) of Lemma 2.1 holds. We will show that condition (3) of Lemma 2.1 holds. Take the homotopy

We claim $H(w, \mu)\neq{\bf0}$ for all $w\in\partial\Omega_2\cap KerL.$ If this is not true, then

and

By (2.17), we have

Thus,

In view of (2.18) and (2.19), we have

and

which is a contradiction. And then by the degree theory,

Applying Lemma 2.1, we reach the conclusion.

Theorem 2.2 Suppose that assumption (H$_2$) holds. Then system (1.2) has at least one $N-$periodic solution, provide that the following conditions hold:\\

where $\check{\xi} = \min_{i = 1, 2, \cdots, m}\xi_i$,

where $M$ is defined by (2.25), $\widetilde{m} < M$ is a positive constant.

Proof We only prove that $\Omega_1$ is bounded, other proofs are similar to the proofs of Theorem 2.1. In fact, $\forall w\in\Omega_1,$ by $1-(a_i^+-\xi_i) > 0$, by assumption (H$_2$) we have

From (2.20) and $a_i^–\xi_i-\frac{[(a_i(n)-\xi_i)\xi_i-b_i(n)]^+}{\xi_i} > 0$, we get

and

Using $\xi_i < 1$, similar to the proof of Theorem 2.1, we have

From $\rho_1-\frac{m\rho_2}{\check{\xi}} > 0,$ (2.21) and (2.22), we have

Hence, there exists $C_i > 0$ such that

In view of (2.22) and (2.23), we get

In view of (2.23) and (2.24), let

Due to the assumption (H$_3$), the term $f_j(x_j), \; j = 1, 2, \cdots, m$ in system (1.2) satisfies Lipschiz condition on $\mathbb{R}$. Thus, by basic results of functional differential equation, we have the following theorems for the unique existence of periodic solution to system (1.2).

Theorem 2.3 Suppose all the conditions of Theorem 2.1 and assumption (H$_3$) hold. Then system (1.2) has unique $N-$periodic solution.

Theorem 2.4 Suppose all the conditions of Theorem 2.2 and assumption (H$_3$) hold. Then system (1.2) has unique $N-$periodic solution.

3.   Exponential stability of periodic solution

Since system (1.2) is equivalent to system (2.2) under the transformation (2.1), then we will consider the exponential stability problems of system (2.2).

Definition 3.1 If $w^*(n) = (x^*_1(n), \cdots, x^*_m(n), y^*_1(n), \cdots, y^*_m(n))^\top$ is a periodic solution of system (2.2) and $w(n) = (x_1(n), \cdots, x_m(n), y_1(n), \cdots, y_m(n))^\top$ is any solution of system (2.2) satisfying

then $w^*(n)$ is globally asymptotic stable, where $L > 0$ is a constant, $\phi$ is initial condition of $w(n)$, $\phi^*$ is initial condition of $w^*(n)$.

Theorem 3.1 Under conditions of Theorem 2.3, system (2.2) has unique $T-$periodic solution $w^*(n) = (x^*_1(n), \cdots, x^*_n(n), y^*_1(n), \cdots, y^*_n(n))^\top$ which is exponential stable, provided that

Proof By (2.2), we have

and

For $i = 1, 2, \cdots, m,$ define function:

In view of condition (3.1), we get $F_i(1) > 0$. Hence, there exists a constant $\alpha_0 > 1$ such that

By (3.2), we have

By (3.3), we have

Define

where $\alpha_0$ is defined by (3.4). By (3.5), we have

By (3.6), we have

Assume that $K = \max_{s\in[-\tau, 0]_\mathbb{Z}}|\phi_i(s)-\phi_i^*(s)|, \; i = 1, 2, \cdots, 2m.$ Then we claim that

Otherwise, there exist integer $i_0\in\{1, 2, \cdots, m\}$ and $n_0\in\mathbb{Z}_0^+$ such that

and

If (3.10) and (3.11) hold, by (3.7) we have

thus, $\alpha_0 > \frac{1}{2}$ which is contradict to $\alpha_0 > 1$. On the other hand, if (3.10) and (3.11) hold, by (3.8) and (3.4) we have

which is a contradiction. Hence, (3.9) holds, i.e.,

and

Hence, periodic solution of system (2.2) is exponentially stable, i.e., periodic solution of system (1.2) is exponentially stable.

4.   Numerical example

This section presents an example that demonstrates the validity of our theoretical results as follows:

where

Obviously, $p_1 = 0.2$ and assumption (H$_2$) holds. Furthermore, $L_1 = 0.2$ and assumption (H$_3$) holds. By simple calculating, we have

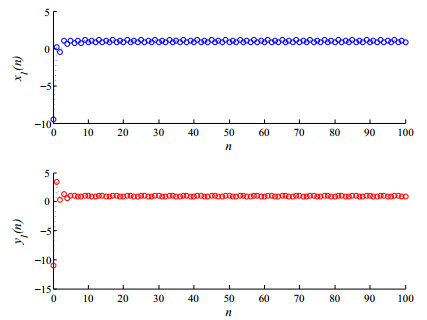
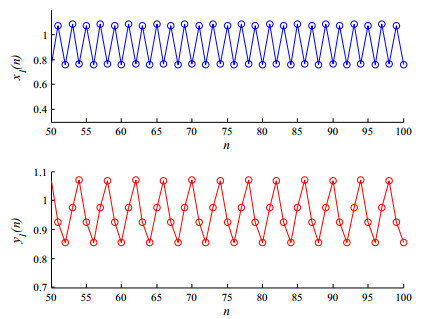
Thus, all assumptions of Theorem 3.1 hold and system (4.1) exists unique periodic solution which is globally exponentially stable. The corresponding numerical simulations are presented in Figures 1 and 2 with random initial conditions. Figure 1 shows that system (4.1) exists at least one periodic solution. Figure 2 shows that system (4.1) exist stable periodic solutions.

Remark 4.1 For all we know, the periodic solution problems of discrete-time INNs with delays are studied in the present paper for the first time. Using Mawhin's continuation theorem and some innovative mathematical analysis techniques, we get some brand new results on the existence, uniqueness and exponential stability of periodic solution of discrete-time INNs. We can confirm the truth of the proposed methods, for example, in ^[8,9,10,11] cannot be generalized to the problems studied in this article. There are a large number of periodic phenomena in nature and society. One of the important trends in the investigations of inertial neural networks is related to the periodic solutions of these systems. Hence, studying periodic solution problems of system (1.2) has important theoretical and practical values.

Remark 4.2 In this paper, we obtain stability results of INNs which can be extended to INNs with distributed delays, see ^[24]. In the future work, we will study global stability problem of INNs with distributed delays.

5.   Conclusions and discussions

In this paper we study the problems of periodic solutions for discrete-time inertial neural networks with multiple delays. First, by applying Mawhin's continuous theorem to the system, we get a set of sufficient conditions for guaranteeing the existence and uniqueness of periodic solutions to the considered system. Then, on the basis of existence and uniqueness, we obtain globally exponential stability of periodic solutions. The efficacy of the obtained results has been demonstrated by an numerical example. It is important to note that the practical implementation of INNs is typically encountered with certain type of uncertainties such as interval parameters. Extending the results of this paper to discrete-time INNs with interval uncertainties proves to be an interesting problem. In addition, it is also interesting and challenging to extend the approach presented in this paper to discrete-time neural network-based problems with mixed delays such as state estimation and approximation, fault isolation and diagnosis, or filter/observer design. These issues require further investigations in the future works.

Acknowledgments

The authors would like to express the sincere appreciation to the reviewers for their helpful comments in improving the presentation and quality of the paper.

Conflict of interest

The authors confirm that they have no conflict of interest in this paper.