Caputo-Fabrizio fractional differential equations with instantaneous impulses

Abbreviations: WSNs: Wireless sensor networks; SACC: Security aware congestion control; AHP: Analytical Hierarchy Process; SNs: Sensor nodes; CM: Cluster member; CH: Cluster head; DPI: Data packet irregularity; CBN: Communication behaviour of node; RER: Remaining energy ratio; DRR: Data repetition rate; BS: Base station; MCDM: Multi criteria decision making; TSTH: Trust score threshold; RS: Recommendation score; PDR: Packet delivery ratio; ML node: Malicious node; NP: Node potential; NLL: Node load level; TBR: Traffic burst rate; CC: Congestion control; MNs: Member nodes; ID: Identity; RE: Residual energy; DoS: Denial of service attack; QoS: Quality of service

1.   Introduction

Wireless sensor networks (WSNs) have been around for a long time. They were first developed in the 1990s and they are now being used in many different industries such as healthcare, environment, agriculture, and many more. These networks are usually composed of sensors, actuators, and computational devices that communicate with one another through wireless communication links ^[1]. In WSNs, a large number of battery-powered sensor nodes (SNs) are deployed randomly around an area to sense, collect, and transmit data to the base station (BS) ^[2]. It is essential to emphasize that wireless sensor networks are designed and deployed for mission-critical tasks. Sensor nodes transmit sensitive information in applications such as battlefield monitoring, diagnostics, gas monitoring, and so on. As a result, it is important to receive data as intended by the sender. The primary reasons for this technology's extensive use are rapid and easy installation of network equipment without interrupting the environment, as well as little human participation, i.e. enabling automation ^[3]. However, these SNs have limitations in terms of battery, memory, transmission range, computational power, and other resources. As a result, the acquired data is transmitted with little processing to the SNs within its range. The communication between the nodes generates a lot of traffic and causes congestion.

Many factors and reasons might lead to congestion in WSNs, such as resource constraints, transmitting more data than the node can receive, etc. In this paper, one more case has been considered in which malicious nodes might intentionally reject data packets to increase retransmissions or send a lot of redundant packets, resulting in congestion-like conditions. Black hole, grey hole, DoS, on-off attacks are such attacks that can be a major source of congestion occurrence ^[4,5]. As a result, relying solely on congestion control techniques is not sufficient to ensure fair service delivery. Also, neglecting this issue would not be the best course of action since congestion leads to other network calamities as well ^[6,7]. It is, therefore, essential to initially prevent this adversity by identifying malicious nodes from the network. Existing congestion control solutions in the literature ^{[8,9,10,11,12,13]} take the mistaken assumption that all nodes are genuine and behave appropriately. This led us to design a security attack-resistant proactive congestion control algorithm that would not only evaluate the natural way of congestion occurrence but would also consider the scenario where hostile nodes purposefully try to block packets from reaching their destination. In our proposed technique firstly, we have tried to remove malicious nodes causing congestion using a trust-based scheme. We have followed a clustering procedure because it offers several advantages for large-scale sensor networks. By using the clustering approach, sensor networks can reduce their energy consumption needs and routing table overhead. Moreover, cluster head nodes also act as relay nodes so choosing an energy-efficient and least congested node will lead to a congestion-free path for packet transmission to the sink node.

However, implementation of the clustering method succeeds only when there is absolute cooperation between the nodes at intra and inter-cluster level ^[14]. Whenever a malicious or selfish node is elected as a cluster head, with the intention to create congestion, performance is adversely affected. If CH is unable to function due to the heavy communication load, it is no longer operational, and all nodes belonging to the cluster lose their communication abilities. The increasing number of illegitimate CHs becomes a bottleneck for the entire WSN, leading to shorter network lifetimes. WSNs appear to rely heavily on CHs. This calls for an effective cluster head selection process. According to research, cluster heads chosen based on a single criterion do not have high energy efficiency. As a result, an ideal cluster head is one that is selected based on a variety of characteristics. The Multi-Criteria Decision Making (MCDM) approach comes up with the optimum solution by evaluating multiple conflicting criteria ^[15]. There are many interlocking factors involved in congestion occurrence that affect packet transmission efficiency, i.e. Buffer space, traffic burst rate, residual energy of CHs, etc ^[16]. These factors can be coordinated in order to ensure optimal power utilization by reducing power consumption and balancing load among the nodes and CHs. So to deal with all the factors effectively there is a need to establish multi-criteria, decision-making scheme which will be able to give a relative importance to each and every factor responsible for congestion. For instance, an important factor to protect a node from being overloaded is to ensure that the node has enough energy and buffer to cope with this. Therefore, to elect a cluster head, this study examines some crucial network parameters such as remaining energy ratio, node load factor, the potential value of the nodes, traffic burst rate using popular MCDM approach such as Analytical Hierarchy Process technique ^[17] so that a secure, least congested node having sufficient energy for transmission will be selected as cluster head. A collaborative effort has been undertaken in this study to alleviate congestion and security challenges utilizing the lightweight energy-efficient trust-based method in clustered WSN. In this way, our technique addresses congestion, security and energy efficiency altogether. The proposed approach beats existing related solutions in terms of energy efficiency, and security and simulation results validate it.

1.1.   Congestion control in WSNs

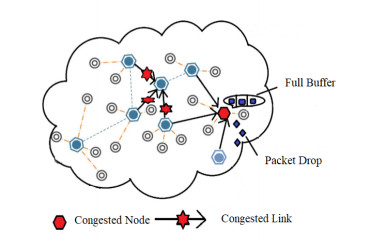
Congestion happens whenever packets move between the nodes at varying rates. Both the links and the nodes can experience congestion in WSNs ^[7]. Congestion occurs on a node when the high rate of incoming packet arrival causes the buffer to fill to capacity ^[14]. During network congestion, a limited buffer capacity on the nodes could result in some packets getting lost. As a result, energy is squandered and the network performance is decreased ^[13]. When there is fast data packet transmission across a radio link, data packets can collapse, resulting in link-level congestion. In other words, it can also be understood as when there are more demands for resources than their availability, the network is said to be congested, which reduces performance and increases delay. Wireless sensor networks are highly susceptible to the congestion problem, which is a very serious issue for these resource-constrained networks because congestion degrades energy utilization and performance due to excessive packet loss and retransmissions. When networks run out of power, routing holes may appear, which will impede the ability of the network to accomplish its goal. As a result, this issue needs to be addressed carefully. So researchers have come up with a variety of ways to address congestion in WSNs. Figure 1 illustrates both types of congestion. Mathematically we can express the congestion scenario by the following condition

There are two ways to deal with congestion either proactive or reactive. Proactive method works in the direction of escaping from the occurrence of congestion whereas the reactive method tells how the network should react when congestion has already occurred in order to reduce its consequences.

In essence, the congestion control protocol should properly identify congestion, alert the corresponding sensor nodes, and then implement an appropriate mitigation strategy. The most common approach in this regard is traffic or resource control. Some researchers have also tried to combine both techniques altogether in their technique and proposed a hybrid version. Other contemporary researchers have discovered a variety of techniques that can be applied for solving congestion such as congestion control using queue-assisted schemes, optimization approach and multi-criteria decision-making approach (MCDM). Unfortunately, this area for congestion control has not yet been explored to a great extent. So to bridge this research gap this paper focuses on congestion control using the AHP method which is a popular MCDM-based technique.

1.2.   Contribution of the paper

The contribution of this paper is summarized in following points.

● Trust-based model has been applied for calculating node potential value. This value aids in distinguishing between authentic and malicious nodes, allowing the communication mechanism to eliminate the malicious nodes. Remaining Energy Ratio (RER), Data Repetition Rate (DRR), Data Packet Irregularity(DPI) and, Communication Behaviour of Node (CBN) have been used as trust metrics. Therefore, the proposed technique can address a range of internal threats such as black-hole attacks, gray-hole attacks, DoS attacks, and on-off attacks ^[5] which are the leading cause of congestion.

● Nodes have been divided into small groups called clusters, with one most potential node serving as the cluster head in order to save energy and improve network longevity. For cluster head selection AHP method has been used. This cluster head is responsible for collecting data from its cluster members and establishing communication with the other cluster heads. The cluster head is responsible for preserving intra-cluster routing information and forwarding both control and data packets in addition to serving as the local coordinator.

● Decision criteria selected for electing cluster heads which also act as relay nodes are the remaining energy ratio, the node load factor, traffic burst rate, and node potential value.

The remainder of the paper is arranged as follows. Section 2 describes the trust-based technique and AHP method in more detail. In section 3 of the paper, we have compiled existing trust-based congestion control and congestion-aware routing techniques for WSN, we have also observed their merits and shortcomings. Section 4 explains our proposed technique in an illustrative manner. In section 5, we have shown the performance evaluation of our technique through simulation. In section 6 we have mentioned limitations and future scope of our work. Finally, section 7 concludes the work.

2.   Background

2.1.   Trust-based model for WSN

Trust is elicited mostly through human psychology, it is defined as a "belief or faith in the honesty, goodness, talent, reliability, or safety of a person, organization, or item" ^[18]. In general, trust is a relationship between a trustor (a person who trusts) and a trustee (a person who is trusted) ^[19]. As we trust or distrust any individual, organization or machine based on our past experiences with them in positive or negative ways, similarly, sensor nodes in a WSN can be either trustworthy or untrustworthy based on how they act in terms of packet transmission ^[20]. An ideal trust based system will help to determine which network nodes are trustworthy and which are untrustworthy ^[21]. By removing the untrustworthy nodes from the network, the trustworthy nodes can work together to deliver reliable network services ^[22]. There are three broad categories of node trust models: centralised, distributed, and hybrid. It is the responsibility of BS, to compute the trust scores of all SNs in centralized trust models ^[23]. One of the major problems with a centralised solution is the single point of failure ^[24]. SNs in distributed trust models compute and maintain trust vectors for the entire network. This strategy has the disadvantage that it requires a lot of computing power and memory. Hybrid trust was developed as a response to the limitations of both centralized and distributed trust computation methods. Clusters of sensor nodes are built in hybrid trust models, and a distributed method is employed inside the cluster as well as a centralized approach with the clusters ^[25,26].

External incursions are protected using cryptographic techniques like authentication, encryption, and watermarking, but these approaches are incapable of detecting malicious behaviour within infiltrated nodes ^[27]. When SNs misbehave due to attacks like black hole, wormhole, sinkhole, grey hole, Sybil, and on-off attacks, trust assessment methods are the only way to protect the WSN by preventing them from transmitting data ^[28]. Cryptographic approaches need more processing, a longer convergence time, and more storage space than safe algorithms based on trust ^[29]. As a result, trust-based security solutions outperform cryptographic algorithms. Trust evaluation methodologies are primarily used to improve the predictability, security, and collaboration of SNs, and they play a vital role in decision-making ^[30,31]. Moreover, these approaches are simple to put into practice in real applications. The benefits of trust-based security and decision making systems outlined above encourage us to create revolutionary trust-based security-aware congestion control framework.

2.2.   Analytical Hierarchy Process (AHP)

In engineering and science, multi-criteria decision-making is an approach for solving complex decision problems with multiple attributes, also known as MCDM. This method compares and ranks multiple decisions based on their respective levels of desirable attributes. A variety of MCDM approaches are available. The Analytic hierarchy process (AHP) ^[17] method invented by TL-Saaty in the 20th century, is used in this paper due to its ability to make the best decision out of several alternatives. The AHP method uses math and psychology to weigh different possibilities and choose the best one. AHP is a method for making decisions based on organizing multiple criteria into a hierarchy, assessing each criterion's relative importance, comparing alternatives based on each criterion, and determining which alternative is the best. In the AHP, complex problems are broken down into smaller problems, called decision factors, and weighted based on their relative importance to the given goal. AHP synthesizes their importance to the given goal and comes up with the ideal solution. The application of the AHP is used across a wide range of fields such as computer programming, information investigation, and fuzzy set theory. The AHP method involves three steps: 1. Setting up the hierarchy 2. Estimating the local weights of each influencing factor 3. Compiling the results for obtaining the global weights.

2.2.1.   Setting up the hierarchy

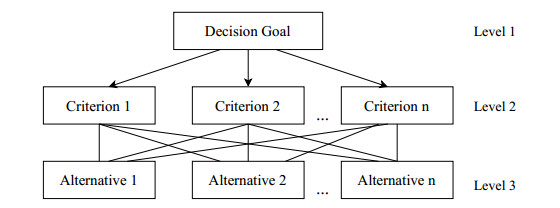
The hierarchy structure of AHP is composed of various levels. The top-level encompasses the goal (objective) of a decision problem, the second level includes various factors affecting that decision, and the bottom level shows different feasible alternative solutions. As shown in Figure 2, highest level is representing the objective of the decision problem and the next level is a number of criteria affecting the goal it can take value from 1 to n. The last level shows the candidate solutions that have an optimal solution as well.

2.2.2.   Estimation of the local weights of each influencing factor

Within the AHP process, the second step entails calculating the local weights of influencing factors. This weight indicates both the weight of each decision factor towards the goal, as well as the weight of each candidate towards each factor. Local weight is calculated for each influencing factor in three steps: pairwise comparison, weight vector calculation, and consistency check.

● Pairwise comparison

Comparing the decision factors under the top-most goal yields a pair-wise comparison matrix. A decision-making matrix shows the ijth entry as the ratio of the preference of the ith option to the jth option. Quantitative values are divided by their respective values. When values are qualitative, they are converted into quantitative values by using Table 1 which ranks the deciding factors on a scale of 1 to 9. These values indicate the intensity of preference among them. The preference value of 1 means 'equal importance' and a preference value of 9 means 'extreme importance'. For example, there is a pair-wise comparison matrix called Matrix-M, which compares four decision parameters, P1, P2, P3, and P4. The Decision Factor P1 is compared to the Decision Factor P2, and a value of a is assigned i.e P1 has a times more weight than P2.

● Calculating a weight factor

The eigen value equation for the nxn comparison matrix M is written as MW = $\lambda$maxW. where W is a non zero vector called Eigen vector, and $\lambda$max is a scalar Eigen value. After standardizing, the Eigen vector W is called local weights of each decision factor(j), which can be represented as $W^{T}_{j}$ = $\{W1, W2... Wn\}$.

● Consistency check

After calculating the local weight of each decision factor and alternative, the consistency ratio (CR) of the comparison matrix is calculated. As given in Eq 2.1, Consistency Ratio of comparison matrix is the ratio of Consistency Index (CI) to Random Index (RI).

where n is rank of Matrix A and RI is a Random Index value as given in Table 2. If CR $\leq$ 0.1 then the estimated comparison matrix is accepted. It demonstrates that the error probability percentage is less than 10% and that the computed weights are precise and acceptable. otherwise new matrix must be constructed until CR $\leq$ 0.1.

2.2.3.   Synthesizing the results for global weights

Numerical weights are calculated for each decision alternative in the final step of the process. The global weight of each alternative is computed by multiplying the local weight and the weight of its corresponding parents. The final weight of the matrix is calculated using the following equation.

The final weight of each alternative is calculated using the following equation.

where $W_{ni}$ is the final weight value of node i, $W_{ni/j}$ is the weight value of $i^th$ node with respective decision factor j, and $W_{j}$ is the weight value of decision factor j. Toward the end of the process, each of the alternative options is assigned numerical priority. Most desired values are obtained from the computed numerical values.

3.   Related work

From the extensive literature review, we observed that among the major concerns in WSNs are energy efficiency, congestion-free packet transmission, and security. Researchers have discovered a variety of solutions to address the congestion problem in WSNs but there is hardly any congestion control approach that has focused on the above-mentioned issues conjointly. Some experts have created specific congestion management algorithms while others have attempted to make routing techniques congestion aware in order to avoid bottleneck scenarios ^{[32,33,34,35]}. We have listed out some of the significant relevant congestion control techniques from the literature that have been designed over the last decade in Table 3. This table gives insight about some State-of-The-Art congestion control algorithms, whether they have considered the major research issues such as security and clustering or not in their problem-solving approach. Some significant relevant existing techniques have been elaborated below-SS Babu et al. ^[36] introduced a new geometric mean-based trust management system that evaluates direct trust from QoS features (trust metrics) and indirect trust from neighbor node recommendations, allowing trustworthy nodes to participate exclusively in routing. They have simulated their algorithm for a network with 36 sensor nodes only and they have not used clustering moreover, they have not mentioned which type of security attacks can be tackled by their approach.

A. Chakraborty et al. ^[37] have presented a trust integrated congestion aware routing technique. Firstly, they have tried to remove malicious nodes from the network that aggravate congestion by sending fake messages. The source node selects the node with the highest trust value as the next transmitting node and this process continues till the packet reaches the destination. The disadvantage of this method lies in the energy efficiency because they have not applied a clustering approach for packet transmission, nodes are directly sending packets to the base station in a hop-by-hop fashion.

J. Duan et al. have proposed trust aware secure routing framework (TSRF) ^[38] for WSNs which is able to resist a variety of internal attacks in the network. The semirings theory was also utilized to develop an optimized routing algorithm that considered the combination of trust metrics and other quality of service metrics.

A Beta and Link Quality Indicator (LQI) based Trust Model (BLTM) for WSNs has been presented ^[39]. A direct trust is calculated by considering communication trust, energy trust, and data trust. Afterwards, the weight of communication trust, energy trust, and data trust is discussed. In addition, an LQI analysis is proposed for maintaining the accuracy and stability of trust values when nodes are connected by poor-quality links. LQI analysis helps in avoiding link level congestion.

M. Gholipour et al. ^[40] have proposed a congestion control technique with the help of MADM approach. They have applied the TOPSIS method for ranking the weights of sensor nodes in order to select the best next relay node for packet delivery. They have used buffer occupancy ratio, congestion degree, and cumulative queue length to make routing decisions. But the limitation of their work is that they have escaped the security aspect.

Sumathi, K. and Pandiaraja, P. ^[41] have presented a new idea of dynamic alternate buffer switching technique (BETCC) in which when congestion arises then they switch the primary buffer which going to be filled completely with secondary spare buffer. They have also incorporated the trust-based model for identifying intentional causes of congestion. the major shortcoming of this approach is that secondary buffer is an overhead for resource constraint environment and they have analyzed their protocol in hierarchical topology only so how the network will perform in case of random deployment is unknown.

The DI-RED (2020) ^[42] approach uses a cache state with a dual threshold in the router buffer to control congestion in Wireless Sensor Networks (WSNs). Aside from that, congestion is managed by the channel transmission condition, which is monitored by the queuing variation tendency and the transmission rate. They have also not considered the case of malicious nodes that intentionally tries to create congestion scenario.

A. Beheshtias and A. Ghaffari et al. (2019) ^[43] have proposed a trust-aware routing protocol for WSNs. The suggested system uses fuzzy logic to determine the routes' trust values. The shortest route from the source to the destination was then chosen while taking trust and security into account. The suggested method measures the trust model using fuzzy logic and applies the multidimensional scaling-map (MDS-MAP) optimal routing methodology.

Khan T. et al. have proposed a well-organized trust estimation-based routing scheme (ETERS) ^[24] that is based on a multi-trust approach to mitigate various internal attacks that threaten clustered wireless sensor networks, including badmouthing, Sybil, selective forging, on-off, black hole, and gray-hole attacks. An equal load balance on all CHs can be achieved by electing a robust CH after a certain period. During the evaluation of communication trust, ETERS also accounts for irregular attenuation factors to model the impact of external factors, such as natural calamities (earthquakes), etc.

A new discrete congestion management approach for WSNs ^[44] (2021) is proposed in this work by controlling incoming and outgoing packets at a specific node. Next, a discrete-time sliding mode congestion controller (DSMC) based on the exponential-reaching-law is devised, which effectively changes bottleneck nodes' queue length to the desired value.

A. Ghaffari et al. ^[45] have proposed a new algorithm which utilizes optimized blackhole algorithm for cluster head selection and applied an ant colony algorithm for determining a route between source cluster head to sink node. They claim that the combination of the black hole algorithm and ant colony optimization give better results in terms of energy consumption and network lifetime.

Yan J. and Qi B. have proposed a congestion-aware routing algorithm (CARA) ^[33] for WSNs. The technique takes into account both the geographical relationship and the traffic load and proposes four route assessment parameters: forward rate, node load factor, cache remaining rate, and forward average cache remaining rate. Routing decisions are made using the multi-parameter fusion approach. As a consequence, the CARA algorithm realizes the sensor network node's and the surrounding area's congestion perception and optimizes network transmission performance.

It is clear from the preceding trust-based approaches that various important attempts have been made to address security-conscious routing techniques. However, only a small percentage of them evaluated the congestion situation while assessing their trustworthiness. To bridge this gap, we have suggested a unique trust-based congestion control strategy for clustered WSNs that combines efforts to overcome congestion and security issues.

4.   Proposed methodology

Three of the most important concerns in WSNs are energy efficiency, congestion-free packet transmissions, and security. We have integrated these major research issues to ensure that our technique provides reliable packet delivery.

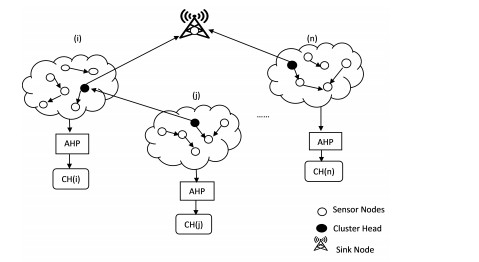
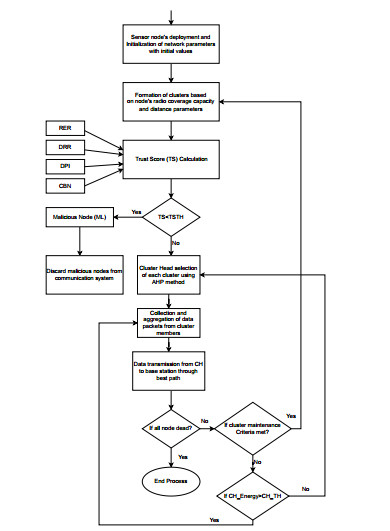
Our algorithm works in two phases: In first phase trust-based scheme has been applied in order to distinguish genuine and malicious nodes. Then this adversarial nodes are blocked to take part in communication system. And second phase begins with the selection of the most promising node as the cluster head using the AHP method. We have shown the network scenario of our proposed work in Figure 3. Detailed description of phase 1 and phase 2 of our algorithm can be seen in the following subsection.

4.1.   Phase 1—identification of malicious nodes

In order to prevent the deliberate attempt of selfish nodes to create congestion, we have implemented trust based scheme which calculates the node potential value (trust score) of each sensor nodes based on their packet transmitting-receiving behavior and energy consumption rate. This node potential value takes the numerical continuous value from 0 to 1. A node with a value less than the threshold value signifies that it is not the best candidate for transmission, a node with a trust score tending towards value 1 suggests that it could be a good candidate for transmission so we have also taken it for consideration as a decision factor for electing a cluster head. The trust score threshold value (TSTH) has been prefixed. The higher the value of TSTH, the more secure the network. The trust score of trusted nodes is greater than TSTH, whereas the trust score of malicious nodes is less than TSTH, so they are eliminated.

4.1.1.   Trust score calculation

In order to evaluate trust between nodes, we set up the wireless scenario with 100 nodes and set a trust value of 0.5 i.e we have assumed all the nodes are genuine initially. A modified version of the LEACH protocol ^[46] is used for transmission. In WSNs, the sensor's authentication depends not only on the historical data of the node itself, but also on the adjacent nodes with spatio-temporal correlation. Therefore, the behavior of nodes can be analyzed, and a quantitative evaluation model can be established through the history of interaction between nodes. Specifically, the sensor nodes in adjacent areas monitor each other and calculate their trust, which can effectively identify malicious nodes to resist network attacks. In our trust calculation, we have taken into consideration the remaining energy ratio, incoming data packets irregularity, data repetition rate and communication behavior of nodes because these parameters can reflect the effects of a security attack, and thus can be used to identify malicious nodes. The formula for calculating these trust metrics are given as follows:

● Remaining energy ratio (RER) The residual energy is the energy that remains after a series of transmission activities have taken place. Under normal operation, the rate of energy consumption in a network with all genuine nodes is always constant. Nodes that carry out DoS attacks, on the other hand, use more energy than their regular counterparts. For this reason, we have considered remaining energy ratio (RER) as one of the parameters for detecting malicious nodes. Using the following equation, we calculated RER:

The RER value will behave abnormally when malicious nodes carry out attacks such as flooding and denial of service.

● Data repetition rate (DRR) Data repetition rate can reflect abnormal behaviour of the node due to its pattern of sending the same packets repeatedly.

where SDP(t) is the number of transmitted data packets at time t, and RDP(t) is the number of the repeated samples.

● Data packet irregularity (DPI) There is a possibility that if there are too many samples during the monitoring cycle, it might be a denial of service attack. In contrast, if the number is too small, there is a high probability of selfish behaviour. So this abnormal behaviour can easily be tracked by analysing data packet irregularity (DPI). DPI has been calculated by the following equation:

where $\Delta Sdp(t)$ denotes the expected value for the number of data samples.

● Communication behaviour of node (CBN) Packet delivery ratio (PDR) is very useful parameter to analyse the packet transmitting and receiving behaviour of a node. This measure is highly important for analysing the network's communication mechanism. This parameter aids in the detection of malicious nodes as well. The value of PDR tends to 1, if all of the packets are successfully transmitted out of the entire number of packets sent. If the node does not transmit any amount of packets successfully, the PDR is zero. The uncooperative interactions between nodes will rapidly increase if a malicious node uses the selective forwarding attack. In this way we can easily detect blackhole, and greyhole attack, etc.

Packet delivery ratio $PDR_{i}^{j}(t1, t2)$ at interval t1 and t2 is computed using following equation.

${Trans_{pkt}}_{i}^{j}(t1, t2)$ = Total number of packets delivered successfully from node i to node j at time t1 and t2.

${Rec_{pkt}}_{i}^{j}(t1, t2)$ = Total number of packets received from node i to node j at time t1 and t2. CBN is the statistical expectation of packet transmission behaviour of a node. Expected behaviour of the node or PDR can be calculated using beta distribution function. So we have computed communication behaviour of node i to j at time interval (t1, t2) $CBN_{i}^{j}(t1, t2)$ as follows

where $C int _{i}^{j}$, $N int _{i}^{j}$ denotes the number of cooperation and non-cooperation between node i and j. Number of successfully received packets out of total transmitted packets has been considered as cooperation and the number of dropped packets out of transmitted packets has been considered as non-cooperation. Furthermore, The original Beta-based trust evaluation model, on the other hand, does not include the influence of external variables on interactions of nodes, such as packet loss due to network congestion. This work improves the original model by including an external attenuation factor $\alpha$ to overcome this problem. $\alpha$ is the ratio of non-cooperation caused by a malicious node to total non-cooperative interactions. The effect of external influences on the credibility score evaluation can be reduced by attenuation of non-cooperation observed by nodes i to j. The accuracy of trust evaluation has improved compared to the initial model.

If all the above-described parameters are taken together, direct trust can be calculated either by using simple additive weighting (SAW) or the weighted product method.

where variable k symbolizes number of trust metrics (TM) used. And $w_{i}$ refers to the weights associated with each trust metric. In this paper we have used SAW method. Therefore, direct trust has been calculated by applying Eq 4.10 as follows.

Where $w_{\alpha}$, $w_{\beta}$, $w_{\gamma}$ and $w_{\delta}$ are the weights of RER, PSI, DRR and CBN respectively and sum of all the weights is 1. For trust score calculation we are not limiting ourselves to observe only direct interactions among nodes. We have also incorporated the recommendation trust. And combination of both the trust score yields the overall trust score which is the final trust score that has been considered in malicious node isolation process and as one of the decision parameters in AHP process for cluster head selection. Recommendation trust has been calculated by averaging the assessment of trust score given by nodes for a particular node that share common neighbours. Following equation is used for recommendation score calculation.

Here $Rec_{Score}(n_{b}/n_{i})$ represents recommended trust value for node $n_{b}$ by neighbor nodes $n_{i}$ where N represents the total number of recommendations made to the node $n_{b}$. Combining the direct trust and recommendation trust, we get the overall trust which can be expressed as:

4.2.   Phase 2—cluster head selection process

After the segregation of malicious nodes, phase 2 begins with the election of a cluster head using AHP method. In the beginning, each node transmits information about its local conditions, such as how much residual energy, buffer space it has and how far it is from the base station to the sink node and based on this information base station performs necessary computations and saves it in separate records. It is essential to figure out WSN's operation and the necessary information exchange in order to execute the proposed algorithm. In the setup phase, a certain number of clusters must be confirmed and set in advance.

(1) The query request message (Q-REQ) is broadcasted by the BS to every cluster. This message is a short message that intends to seek the current status of sensor nodes.

(2) Every node responds to Q-REQ with their current status (Q-Reply), including its basic information, such as node's ID, node's energy, node's distance to the sink, etc.

(3) BS follows the information it receives and incorporates the collected Q-Reply messages into the centralized selection of appropriate CH of each cluster using the AHP algorithm.

(4) Now BS broadcasts a notification message (NTF). In this message, a list of CH's IDs and its cluster number is provided.

(5) A particular node i is notified to become CH for the current round once it locates its ID in the list. And the remaining nodes whose ID is not there in the list also get to know that they are member nodes. Decision factors for selecting cluster head has been explained in the following subsection.

4.2.1.   Decision factors for selecting cluster head

The number of optimal clusters is calculated based on the relationship between nodes and their associated attributes. It continues with a density of nodes. And once the nodes begin to die, clusters are combined into a larger cluster, and the process continues. The optimal number of CHs are computed by using the following equation

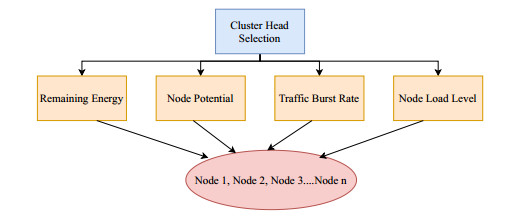
where M*M—the deployment region, n—the number of nodes, and dtoBS is distance between the CH and the BS. The decision parameters used as input to the AHP decision-making method are depicted in Figure 4. Following are the short description of decision factors that has been considered for selecting cluster head of each cluster using AHP method.

● Remaining energy (RE) The cluster heads have more responsibility than any other member nodes in the network. So a node should be chosen as a cluster head only when it has sufficient energy, or the nodes will be withdrawn from the base station due to its premature death. Residual energy is calculated by subtracting the total energy consumed by the node to perform transmission, reception, data aggregation and overhearing from initial energy ^[47]. This term has already been explained through Eqs 4.1–4.3.

● Node potential (NP) Node potential is basically the overall trust score of a node which is calculated by Eq 4.12. This parameter has been considered here for the security aspect as it reflects the service proving capability along with the active participation nature.

● Node load level (NLL) The load level of a node can be calculated using the buffer space. Buffer occupancy parameter allows us to determine how much buffer space is available and how much of it is already occupied. In other words, it can be seen as a parameter which tells to which extent node is ready to receive upcoming packets. In this way, this parameter can also help us to identify the congestion status of a particular node. We have utilized min-max normalization formula for calculating the node load level. With min-max normalization, the values of load level are transformed into [0; 1], which indicates the traffic information of the node. Using this field, packets will be directed to idle or underloaded areas. The following formula is used for the computation of node load level.

$\epsilon$ is a very small value lies between (0, 1).

We have assumed that all nodes are having initial buffer of 50 packets. We have taken two threshold value queuemin and queuemax which represents high load state and low load state respectively of a particular node, which lies within the range of buffer size. If the value of NLL comes out to be 1 or it tends to be 1 it indicates that node has enough buffer to accommodate the incoming packets if this value reaches near about 0 it tells that there is no space left for packets as buffer is already full So this type of node is not a good candidate for further packet transmission.

● Traffic burst rate (TBR) The parameter node load level makes sure that packets will be routed via non-congested locations. However, sometimes there is a burst of traffic that can cause congestion. When a burst happens at node $n_{i}$ that has enough buffer space, still $n_{i}$ is obviously not a good choice to be the next relay node since many packets will reach $n_{i}$'s queue at the same time. As a result, buffer occupancy is not the only appropriate criterion for identifying the next relay node. To address this issue, a new statistic called 'traffic burst rate' is established. It specifies the changing tendency of the traffic at a particular node over time. Value of this metric is calculated by using the following equation:

In the above equation, numerator is depicting the time interval between the arrivals of two adjacent data packets in the MAC layer, while the average processing time of data packets in the node is denoted by $T_{processing}$. If its value is greater than 1 means, the arrival rate of data packets is larger than the forwarding rate. In other words, congestion in this node is possible in the near future. As a result, this node is unfit to be the next relay node.

Based on the four decision factors outlined above, the remaining energy, node load factor, traffic burst rate, and the trust score of the nodes, the cluster head is selected. Using these parameters as inputs, the AHP process calculates weight values for each node in the cluster. A CH is then determined by selecting the node with the highest weight value.

4.2.2.   AHP method for cluster head selection

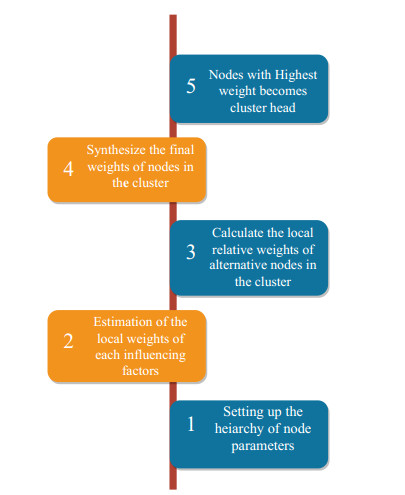
There are five modules involved for the cluster head selection process as shown in Figure 5. The first module defines the key parameters required to select the cluster head and structure the hierarchy. The second module calculates the local weight values based on the hierarchy established in the first module. The third module uses the local weight values obtained from the second module to calculate the nodes' final weight value. The last module selects the best cluster head in the cluster based on the highest weight value. The following section describes in detail the working of five modules involved in the proposed solution.

● Establishing the hierarchy of decision parameters

The first step in the proposed cluster head election consists of structuring the problem as a hierarchy. The proposed AHP hierarchy model is given in Figure 4. From Figure 4 it can be seen that an optimal CH selection is a goal at the top level. Subsequent levels consider key decision parameters including remaining energy, node load factor, and traffic burst rate, and the bottom level contains n alternatives in the cluster.

● Calculating local weight vector of decision parameters A second step involves assigning relative weights to key decision parameters, namely RE, NP, NLL, and TBR, towards the goal. A pair-wise comparison of the four key decision parameters will yield the evaluation $matrix_{M}$. These parameters are compared by using a scale of 1–9 as shown in Table 1. The initial local weights of the criteria and alternatives that are supposed to assign manually representing personal judgements must be carefully assigned. From the literature, we observed that the authors who have applied AHP technique for decision making, some of them have prepared questionnaires regarding criteria and alternatives and based on answers received from the experts, they derived the initial local weights whereas many of them have not disclosed their method of assigning weights. In our proposed technique we have assigned these values on the basis of an extensive literature survey ^{[9,24,26,36,37,40,48,49,50,51]}. It has been discovered from existing relevant works that for congestion control purpose Node Load Nevel (NLL) plays very important role that's why it has been given the highest weight-age. Traffic Burst Rate (TBR) is another major factor for maintaining congestion, so it has been given second top priority. Most of the researchers have considered Remaining Energy (RE) as a decision parameter for cluster head selection so, we have also considered this parameter as a decision factor. Node Potential (NP) is also a crucial parameter for a security point of view as most of the security attacks create congestion-like scenario so only genuine node should be selected as cluster head. Here in our proposed technique we have assigned more weights to NLL, TBR and RE than NP as we have applied trust-based mechanism in first phase in order to eliminate malicious nodes from the network. Here is the $Matrix_{DF}$:

Using the eigen vector WT = [0.467, 0.277, 0.159, 0.095] of this matrix M, we can derive the local weights of key decision parameters. The parameters RE, NP, NLL and TBR have local weights 0.46, 0.27, 0.15 and 0.095 respectively. The values obtained can be seen from following Table 4.

Equation 2.3 computes the maximum eigen value $\lambda$max, which equals 4.0261. Following this, CR = 0.0097 is calculated using Eq 2.1. The CR obtained for $Matrix_{DF}$ is meets the condition CR $\leq$ 0.1, this relationship tells that at most 10% inconsistency is allowed. If the consistency ratio is greater than 10%, we need to revise the subjective judgment. Our matrix yields 0.97% inconsistency so $Matrix_{DF}$ passes the consistency check.

● Obtaining the relative local weight values of alternative nodes in cluster

The next step is to calculate the local relative weights of the nodes in the cluster in accordance with each decision factor. A pair-wise comparison matrix must also be constructed between nodes in the cluster to calculate relative local weights if the values would have been qualitative but, in our case the deciding factors are quantitative in nature so normalization method has been used to get the local weights of nodes in the cluster. For an instance, we have illustrated below the values of the decision factors of a cluster of an individual round.

Here, parameter followed by $\downarrow$, $\uparrow$ is indicating that desired cluster head is supposed to have least value and high value of that parameter respectively.

After the normalization process, the obtained local weights of alternatives corresponding the criteria, is shown as follows

● Synthesize the overall weight value of nodes in the cluster

In the fourth step, each cluster node is given its overall weight value. These values are derived from Eqs 2.4 and 2.5. The node with the highest weight value is elected as CH. Global weights are obtained by multiplying matrix $MATRIX_{Alt^{3}}$ with the local weight vector of decision factors [0.467, 0.277, 0.15, 0.095].

According to the results obtained from matrix multiplication, node N1 of the cluster has the highest global weight, so it will be the cluster head for this round.

In this way, AHP method helps to select CH of each cluster. Unlike existing clustering techniques, in our proposed method CH is not rotated in every round of simulation. The threshold value determines whether CH should be changed. Cluster head reselection procedure is invoked when CH's energy falls below the threshold value. By doing this we can control frequent head rotations in every round. Along with cluster head rotation cluster maintenance is also necessary by considering the dynamic changing topology. The Cluster maintenance procedure is executed under the following conditions:

– Cluster size becomes equal or less than the half of the original cluster size

– The CH leaves the cluster

– The CH of two adjacent clusters move closer proximity to each other such that they are at 1- Hop distance.

4.3.   Algorithm of proposed security aware congestion control technique using AHP method (SACC-AHP)

The proposed technique considers a WSN that is made up of a sink node $\mathcal{S}_{n}$ and multiple sensor nodes $\lbrace$ ${n_{1}, n_{2}, n_{3}...n_{k} }$ $\rbrace$ distributed randomly in a certain area. There is a limited spectrum of radio coverage across all sensor nodes, and their initial energy, hardware configuration, and interface all share the same limitations. The sensor nodes are also assumed to be compromisable if there are no security mechanisms protecting them. Initially, all nodes were assigned a trust value of 0.5, indicating that they were genuine. Following node deployment, base station collects all the local information (node's position, energy, distance, etc.) of sensor nodes and based on the received information it applies clustering approach and nodes are partitioned into distinct clusters $\lbrace$ $\mathcal{C}_{1}, \mathcal{C}_{2}, \mathcal{C}_{3}...\mathcal{C}_{n}$ $\rbrace$ it also calculates their node potential value (trust score) which is a deciding factor between malicious and genuine nodes. If the trust score comes out to be less than the threshold value(TSTH), those nodes are considered malicious and discarded. In each cluster one relay node has to be selected for inter-cluster communication known as cluster head $\lbrace$ $\mathcal{CH}_{1}, \mathcal{CH}_{2}, \mathcal{CH}_{3}...\mathcal{CH}_{n}$ $\rbrace$ and the remaining nodes become its members. To select one most suitable node among nodes in a cluster, the AHP method has been applied. Each cluster member will send packets to the respective cluster head, which will aggregate and send them to the base station via the best possible route based on the depth of the node field.

This parameter tells how far is the cluster head from the sink. And the depth is computed by counting the number of hops from the source node to the sink. The packet is directed to take the shortest route possible to its destination via the depth field. This process continues until all the nodes deplete their energy. And when the size of the cluster gets very small owing to the depletion of energy in member nodes or because of mobility, or any of the cluster maintenance criteria satisfied as explained above, cluster reformation begins. When CH's energy falls below the threshold value, the cluster head selection procedure is invoked. In this way proposed SACC-AHP technique saves energy and reduces the overhead by avoiding CH rotation in every round of simulation. Figure 6 clearly depicts the flow of our proposed technique in pictorial form. Step by step procedure of SACC-AHP technique has been outlined in algorithm 1. Notations that have been used in network modeling are shown below.

Sink Node - $\lbrace$ $\mathcal{S}_{n}$ $\rbrace$

Sensor Nodes - $\lbrace$ ${n_{1}, n_{2}, n_{3}........n_{k} }$ $\rbrace$

Clusters - $\lbrace$ $\mathcal{C}_{1}, \mathcal{C}_{2}, \mathcal{C}_{3}.....\mathcal{C}_{n}$ $\rbrace$

Cluster Heads - $\lbrace$ $\mathcal{CH}_{1}, \mathcal{CH}_{2}, \mathcal{CH}_{3}.....\mathcal{CH}_{n}$ $\rbrace$

Cluster Members - $\lbrace$$\langle$ $\mathcal{C}^{i}_{1},$ $\mathcal{C}^{i}_{2}, .....$ $\mathcal{C}^{i}_{j}$ $\rangle$, $\mathcal{C}^{j}_{1},$ $\mathcal{C}^{j}_{2}, .....$ $\mathcal{C}^{j}_{l}$ $\rangle$, ....... $\langle$$\mathcal{C}^{l}_{1},$ $\mathcal{C}^{l}_{2}, .....$ $\mathcal{C}^{l}_{m}$ $\rangle$ $\rbrace$

4.3.1.   Complexity of the algorithm

Any network-based algorithm's computational complexity is directly proportional to the number of nodes used in the network. The proposed algorithm works in two phases firstly it computes trust score of N sensor nodes using four trust metrics that perform some arithmetic operations to yield that value which incurs 4*(N) = $\mathcal{O}$(N) operations. And the second phase begins with the selection of cluster head using the AHP method of each cluster. Let us consider the cluster size M = N/2. According to ^[52] time complexity of the AHP method is $\mathcal{O}$$\lbrace$min($l^{2}$m, $m^{2}$l)$\rbrace$ where l is criteria and m is alternatives. In our case, four criteria have been taken which is constant and alternatives are nodes of a particular cluster i.e size of the cluster. So, the cluster head selection process takes $\mathcal{O}$(M) operations which implies the algorithm grows linearly with respect to M(Cluster Size) in this step. Thus total computational complexity of the proposed algorithm includes the summation of the calculations required from each step. i.e. $\mathcal{O}$(N) + $\mathcal{O}$(M). The term "space complexity" describes an algorithm's memory requirements. The type of data containers utilized in the code has a significant impact on memory overhead. Since a decision matrix of size l^*m has been employed, thus the space complexity of the proposed algorithm is is $\mathcal{O}$(M).

5.   Performance evaluation

This section shows the performance evaluation of our proposed technique against existing relevant techniques like LEACH ^[46], TCEER ^[37], TASRP ^[48], CARA ^[33] and SACC, etc. using simulation. SACC is a special case of the proposed method, where the AHP method has not been applied for cluster head selection. In the LEACH protocol, a clustering approach is used for communication in WSNs for the first time, and the cluster head is selected by a randomized approach. Comparative analysis has been performed using it. In each security aspect has been neglected. So, the impact of introducing security features in our proposed technique will be clearly visible with this comparison. TCEER technique has been considered as well for comparison because in TCEER trust model has been used a for malicious node isolation and secure transmission but they have not used clustering approach in this way compared with this algorithm will give insight about energy consumption analysis. Similarly, TASRP, the algorithm has been considered for performance evaluation of our technique because in this approach security and clustering approach has been implemented but they have avoided the congestion scenario. CARA is a congestion aware routing protocol designed for WSNs using multi-criteria, decision-making method. Because this technique is so pertinent to our strategy, it has been employed for performance evaluation. And we have also compared our proposed technique with a variant of our technique i.e SACC in which a trust model for security and clustering approach has been implemented but for cluster head selection instead of applying the MADM approach we have used the weighted sum method so this comparison will clearly show the importance of MADM approach for better decision making. This section firstly shows the list of assumptions that have been made while performing the simulation and the simulator configuration used in the study followed by the analysis of obtained simulation results.

5.1.   List of assumptions

In this section, we present several assumptions and the construction of the network model to explain and support the protocol proposed, this is due to the constraints such as limited power supply, computation capability, and buffer storage in WSNs.

● All the nodes have unique ID and location.

● Sensor nodes are battery operated so they are energy constraint.

● Propagation channel is symmetric.

● With the exception of sink nodes, sensor nodes are both source and intermediate nodes.

● All nodes are equally susceptible to attack.

● There are no resource limitations at the base station.

● Base station is far away from sensor node and it is stationary.

● All nodes that are fewer than r metres away from the base station interact with it directly (r refers to the radio radius of nodes).

● CHs maintain record of Cluster member's Ids, location, and current residual energy. CHs are the most significant SN inside a cluster. The CHs sends the consolidated data to the BS.

5.2.   Network configuration

Simulation has been performed using MATLAB software version 2020a. For simulation purpose, a network with 200 $\times$ 200 $mt.^2$ has been setup in which 100 nodes having mobility feature have been deployed randomly. Experiments were conducted at mobility speeds ranging from 5 m/s to 20 m/s. And all the necessary parameters and their value used for simulation are shown in Table 5. We performed a simulation of around 2000 rounds. The results can be seen in the figure also. Performance evaluation of our proposed method has been done by comparing it with LEACH ^[46], TCEER ^[37], TASRP ^[48], CARA ^[33] and SACC that is a variation of the proposed method in which cluster head has been selected without applying the AHP technique. These algorithms have been compared in terms of energy efficiency, network lifetime, throughput and packet delivery rate, etc.

5.3.   Result analysis

A thorough examination of the performance of our suggested approach was conducted, taking into account the most essential network factors such as energy consumption, network lifetime, throughput, and so on.

5.3.1.   Energy consumption analysis

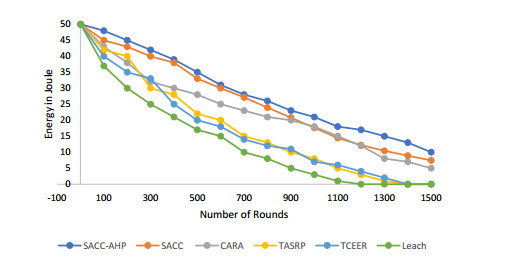
For performance evaluation of our technique firstly, energy consumption analysis has been performed to see how the energy of sensor nodes are being consumed in performing the whole task. Sensor nodes consume energy in the communication process including transmitting and receiving. It also incur negligible amount of energy when it remains idle. It can be seen in the graph shown in Figure 7 that our proposed techniques offer high energy efficiency compared to LEACH ^[46], TCEER ^[37], TASRP ^[48], CARA ^[33] and SACC because it discovers and isolates the spiteful nodes from the system at a very early stage using a lightweight trust model so that they no longer can waste the precious energy of nodes and then cluster head which is one of the trusted nodes has been selected using the MADM approach and this node has the responsibility to transmit packets to the base station. So most eligible node in terms of energy, buffer load and security are being selected for transmission every time.

5.3.2.   Network lifetime analysis

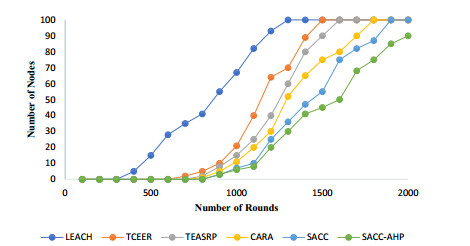
Network lifetime of WSN can be defined as a time when all sensor nodes run out of energy and the network goes down. The results of this analysis has been shown in Figure 8. It has already been seen that our proposed method consumes less energy than existing techniques so technically it will have a better network lifetime than others.

5.3.3.   Throughput analysis

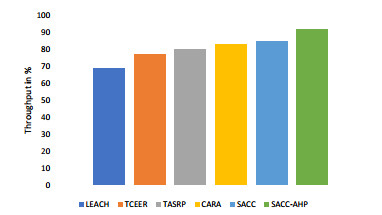
In the context of WSN, throughput is measured as the amount of data packets moved successfully from the source to the sink. Figure 9 shows the throughput analysis of the SACC-AHP technique. It can be observed that SACC-AHP maintains the throughput percent even in the presence of malicious nodes as it accurately identifies and removes them from the communication system so they do not get the enough chance to affect the throughput and other network metrics adversely. The proposed work justifies this by stating that the cluster head selects the relay node based on hop count, residual energy, congestion status, and trust score. Packet delivery analysis has also been done and results have been shown in Table 6. TCEER and TASRP, CARA and LEACH protocol have less throughput and PDR than our technique this might be because security aware congestion control in clustered WSN scenarios has not been considered.

5.3.4.   Malicious node identification analysis

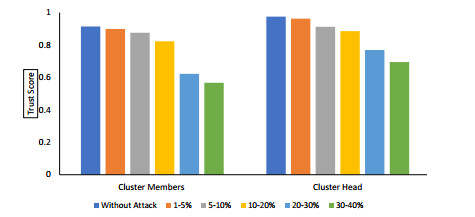
As shown in Table 7, our proposed technique is highly accurate at identifying malicious nodes as compared to TCEER and TASRP algorithms. In this experiment, we intentionally increased the number of malicious nodes in the network to determine how many would be identified. A majority of the malicious nodes were detected, despite the generation of up to 40 percent of malicious nodes.

5.3.5.   Impact of malicious nodes on trust score

We have shown effect of attacks (black-hole, grey-hole, DoS attack, etc.) on the trust score of cluster head and member nodes in Figure 10. In order to explore the impact of selfish nodes on the trust score of all the nodes, we purposely inserted up to 40% malicious SNs into a WSN of 100 nodes. It is evident from the graph that the average trust score for all nodes is between 0.9 and 1 in the absence of any attacks, and that trust score sharply declines as the proportion of malicious nodes increases. The reason behind this decreasing rate is due to the behavior of malicious nodes and its negative impact on its neighbor nodes which get reflected by their trust score.

6.   Limitations and future work

The process of manually assigning relative weights in the AHP method is a limitation. We intend to rectify this limitation in our future work by applying fuzzy logic or predictive modeling approach for determining the weights of decision parameters so that there would not be any type of bias. Our goal is also to extract and also optimize certain factors that prompt congestion thereby affecting the lifespan of the WSN. We will also try to enhance the security aspect by trying to resolve more malicious attacks on the nodes. And we would also try to incorporate the management of link level congestion into future congestion control methods.

7.   Conclusions

It is important to note that some security threats have a direct impact on network congestion, which results in processing and communication overhead, as well as spikes in energy consumption, which limits the lifespan of networks. Malicious nodes exacerbate congestion by delivering fraudulent messages or dropping valuable data packets. As a result, relying only on congestion control techniques is insufficient to assure reliable transmission. In this paper, a unique approach has been implemented for congestion control in clustered WSN. Our proposed SACC-AHP algorithm combines a lightweight dynamic trust based model with a multi-criteria, decision-making method. SACC-AHP technique first identifies malicious nodes blocks them for transmission and then elects cluster head based on multi-criteria, decision-making method. Cluster heads act as relay nodes, which are responsible for data transmission to the sink node. In this way, only the most active, least congested and reliable node gets a chance to deliver data packets to the destination node. According to the simulation results, the suggested SACC-AHP approach improves performance by consuming less energy and enhancing security and packet delivery. We intend to create distributed intrusion detection systems for WSNs in the future, which can both increase the reliability of trust assessment and boost WSN security.

Conflict of interest

The authors declare there is no conflict of interest.