Qualitative analysis of fractional relaxation equation and coupled system with Ψ-Caputo fractional derivative in Banach spaces

1.   Introduction

The use of bivariate distributions is essential in a wide variety of fields since they are used to represent and analyze the relationship between random variables (RVs). A substantial quantity of research is involved in developing bivariate distributions. Morgenstern ^[31] introduced a straightforward technique for creating a two-variable set of distributions by utilizing marginal values. Farlie ^[14] introduced a broader version of Morgenstern's approach, referred to as the FGM family of distributions. Several researchers have devised and investigated numerous bivariate distributions. For example, a new bivariate Fréchet distribution based on FGM and Ali-Mikhail-Haq copulas was proposed by Almetwally and Muhammed ^[4]. Furthermore, based on the FGM copula, Almetwally et al. ^[5] introduced a bivariate Weibull distribution and obtained some properties of it. Using generalized OSs, Nagy et al. ^[32] examined the statistical properties of the q-Weibull distribution in univariate and bivariate situations. Recently, Fayomi et al. ^[15] derived several structural statistical properties for a novel family of bivariate continuous Lomax generators.

Sklar ^[39] proposed a joint distribution function (JDF) of given two RVs $W_1$ and $W_2$ by using a copula $C(u, v),$ and the two marginals DFs $\textsf{F}_{W_1}(w_1) = P(W_1\leq w_1)$ and $\textsf{F}_{W_2}(w_2) = P(W_2\leq w_2)$ as

When the JDF is absolutely continuous, we get

where $\textsf{f}_{W_1, W_2}(w_1, w_2)$ is the joint probability density function (JPDF) of $\textsf{F}_{W_1, W_2}(w_1, w_2)$ and $c(u, v)$ is the PDF of the copula $C(u, v)$ (for more details about copula and the Sklar theorem, see Barakat et al. ^[9], Iordanov and Chervenov ^[22], Joe ^[24], and Nelsen ^[33].

One of the most widespread and beneficial copula is the FGM copula $C(u, v) = uv[1+\delta(1-u)(1-v)], \; 0\leq u, v\leq1, \; -1\leq\delta\leq 1, \;$ (cf. Nelsen, ^[33], Eq 3.2.10). The corresponding bivariate DF is the FGM model

where $\bar{\textsf{F}}_{W_i}(w_i)$ is the survival function (or the reliability function $\bar{\textsf{F}}_{W_i}(w_i) = P(W_i > w_i)$) of ${\textsf{F}}_{W_i}(w_i), \; i = 1, 2.$ The PDF of the distribution (1.3) is given by

Thanks to the simple shape of the FGM copula, this copula provides numerous benefits when modeling bivariate distributions. The FGM copula has its versatility in representing a broad spectrum of dependence structures. Finance, actuarial science, and bioinformatics are a few fields where the FGM copula is used (cf. Teugels, ^[41]). Furthermore, the FGM copula enables the creation of bivariate distributions that encompass a diverse set of marginals, including both continuous and discrete marginals, cf. Nelsen ^[33]. In addition, the FGM copula has a straightforward structure, making it computationally efficient and straightforward to implement in practical applications, cf. Joe ^[24]. The FGM distribution is a flexible and valuable family in applications as long as the correlation between the variables is not too high. Schucany et al. ^[37] showed that the correlation coefficient, $\rho,$ between the two marginal DFs $\textsf{F}_{W_1}(w_1)$ and $\textsf{F}_{W_2}(w_2)$ satisfies $-\frac{1}{3}\leq\rho \leq\frac{1}{3},$ whenever these margins are continuous distributions with bounded nonzero variances. Additionally, for uniform margins, $\rho$ reaches its maximum, $\frac{1}{3}.$

In statistics, a parsimonious model fits the data well by utilizing a small number of independent variables, as well as a small number of unknown parameters. Models that are parsimony aim towards simplicity. This idea is consistent with Occam's razor, which states that if there are two possible explanations for a given situation, the simplest one is typically correct. The parsimony principle, when used in statistical models, seeks to explain data with the fewest number of parameters while yet offering essential advantages.

Alkhazaalh and Al-Zoubi ^[6] proposed a new continuous distribution using the Epanechnikov kernel function and the EX distribution. Therefore, this distribution was named the Epanechnikov-exponential distribution and is denoted as the EP-EX distribution. The DF and PDF of the EP-EX distribution are respectively given by

and

where $\varphi$ is the scale parameter. The EP-EX distribution is considered a parsimonious model with no shape parameter like the EX distribution. Furthermore, the EX and EP-EX distributions have an analytically straightforward shape. Alkhazaalh and Al-Zoubi ^[6] demonstrated that the EP-EX distribution (1.5) is more adaptable and powerful than the EX distribution through an application to an actual data set. However, theoretically, each of the two distributions can describe groups of various kinds of data sets, meaning that neither is superior to the other because the kurtosis, 7.7734, and skewness, 1.7945, of the EP-EX distribution are smaller than the kurtosis, 9, and skewness, 2, of the EX distribution, respectively. This makes the two distributions complementary to each other rather than competitors. However, the EP-EX distribution has a non-constant hazard function, unlike the EX distribution, which gives the EP-EX distribution an advantage in processing the reliability data. Alkhazaalh and Al-Zoubi ^[6] showed that the mean, variance, and moment generating function (MGF) of EP-EX distribution are given, respectively, by

Two parsimonious and complementary bivariate DFs that may describe different kinds of bivariate data sets are obtained using the FGM copula and the EX and EP-EX marginals. Each of these models has a single shape parameter, $\delta.\,$ We concentrate on the second model with the EP-EX marginals here because the first model with the EX marginals has been well-examined in the literature (e.g., see EX-FGM as a special case of Weibull-FGM bivariate DF introduced by Almetwally et al. ^[5]). We examine this model from several statistical angles and information theory.

The paper is organized in the following manner. Sections 2 and 3 provide a detailed description of the distributional characteristics of the EP-EX-FGM model. Furthermore, Section 4 explores the reliability measures, such as the hazard function, reversed hazard (RH) function, and positive quadrant dependence feature. Moreover, recent information measures such as bivariate extropy, bivariate weighted extropy, and bivariate cumulative residual extropy (bivariate CREX) are evaluated. Section 5 employs the maximum likelihood (ML) and Bayesian techniques to estimate the parameters of the model. Furthermore, the model's parameter is calculated using confidence intervals based on asymptotic methods. In Section 6, Monte Carlo simulations were employed to approximate the ML and Bayesian estimators. The evaluation of bivariate real-world data sets in Section 7 produced outstanding outcomes. Section 8 serves as the conclusion of the paper.

2.   The Epanechnikov-exponential FGM distribution

Let $W_1\sim \text{EP-EX}(\varphi_1)$ and $W_2\sim \text{EP-EX}(\varphi_2).$ Thus, according to (1.1), the JDF of bivariate EP-EX based on FGM copula, denoted by EP-EX-FGM$(\varphi_1;\varphi_2),$ is given by

Moreover, according to (1.2), the corresponding JPDF of the JDF (2.1) is given by

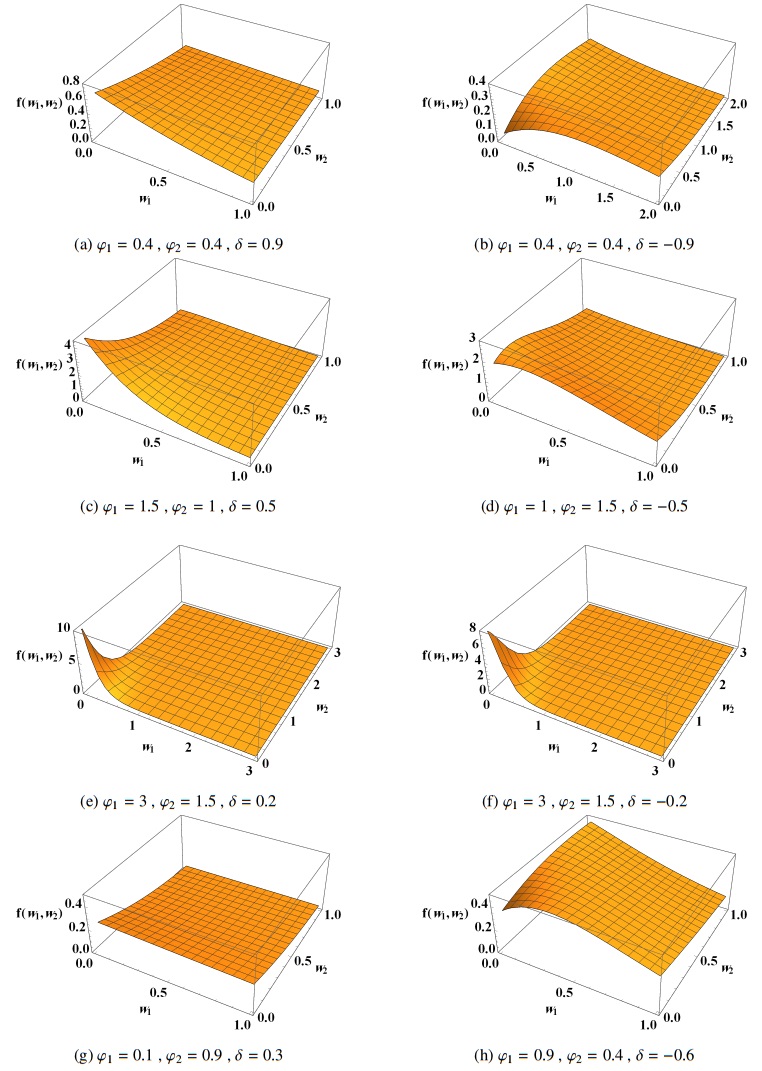
The 3D Figure 1 illustrates the JPDF for specific parameter values. The graphs depicted in Figure 1 illustrate the remarkable wealth and versatility of this family since it is capable of handling several forms of data.

3.   Properties of EP-EX-FGM

3.1.   Moments

It is easy to show that the $(s_1, s_2)$th, $s_1, s_2 = 1, 2, ...,$ product moments of the EP-EX-FGM$(\varphi_1;$ $\varphi_2)$ are given by

Thus, by using (3.1) at $s_1 = s_2 = 1,$ we get

Therefore, the coefficient of correlation between $W_1$ and $W_2$ is

We notice that $\rho_{_{W_1, W_2}} = 0$ when $\delta = 0,$ which implies that $W_1$ and $W_2$ are independent. The maximum and minimum values of $\rho_{_{W_1, W_2}}$ from EP-EX-FGM$(\varphi_1;$ $\varphi_2)$ are 0.261 and $-0.261,$ respectively.

By using (2.2), the MGF of $W_1$ and $W_2$ is given by

3.2.   Conditional distribution and concomitants of OSs

After simple algebra, the conditional PDF and DF of $W_2$ given $W_1 = w_1$ are respectively given by

and

Consequently, for the EP-EX-FGM$(\varphi_1;$ $\varphi_2),$ the regression curve for $W_2$ given $W_1 = w_1$ is

Thus, the conditional expectation is non-linear with respect to $w_1.$

The concomitants are a vital tool when selection and prediction problems are involved. The idea of concomitants of OSs was first proposed by David ^[12]. Many studies have been published on the concomitants of the OS model. Researchers such as Abd Elgawad et al. ^[2], Barakat et al. ^[8,10], and Scaria and Nair ^[36] have studied this issue.

Let $(W_{1i}, W_{2i}), i = 1, 2, ..., n,$ be a random sample from a continuous bivariate DF $F_{W_1, W_2}(w_1, w_2).$ If we denote $W_{1r:n}$ as the $r$th OS of the $W_1$ sample values, then the $W_2$ values associated with $W_{1r:n}$ are called the concomitants of the $r$th OS and are denoted by $W_{2[r:n]}, r = 1, 2, ..., n.$ The PDF of the concomitant of the $r$th OS is given by

where $\textsf{f}_{1r, n}(w_1)$ is the PDF of the $r$th OS of $W_{1i}, i = 1, 2, ..., n.$ Thus, the PDF of $W_{2[r:n]}$ is given by

Also, the MGF of $W_{2[r:n]}$ is given by

The $\ell$th moment of $W_{2[r:n]}$ is given by

3.3.   Mean residual life (MRL)

The MRL is the average life of a unit after it has survived for a specific amount of time $t.$ The MRL function is like the PDF or the characteristic function for a distribution with a finite mean, the MRL completely determines the distribution via an inversion formula (cf. Guess and Proschan, ^[17]). The MRL is not only used for parametric modeling, but also for nonparametric modeling. Actuaries apply MRL to set rates and benefits for life insurance. In the biomedical setting, researchers analyze survivorship studies by MRL. Shanbag and Kotz ^[38] introduced the concept of the MRL for vector-valued RVs as

where

and

The expressions for $m_1(w_1, w_2)$ and $m_2(w_1, w_2)$ in EP-EX-FGM$(\varphi_1;$ $\varphi_2)$ are obtained as

and

where $D_j = \left(2\left(\frac{1}{2}(e^{-3\varphi_jw_j}-3e^{-2\varphi_jw_j})+1\right)-1\right)$, $j = 1, 2.$ Substituting (3.3) and (3.4) in (3.2) yields EP-EX-FGM's MRL.

3.4.   Vitality function

The vitality function is a helpful tool for modeling lifetime data. It was thoroughly explored by Kupka and Loo ^[28] in relation to their research on the aging process. This idea was applied by Kotz and Shanbhag ^[27] to produce multiple lifetime distribution characterizations. The vitality function offers a more direct assessment of the failure pattern since it is expressed in terms of an increased average lifespan, whereas the hazard rate represents the chance of sudden death within a lifespan. The vitality function linked to a non-negative RV $W$ is defined as $m(w) = E (W|W > w).$ The bivariate vitality function of a random vector $(W_1, W_2)$ is defined on a positive domain as a binomial vector as

where

and

For more details, see Sankaran and Nair ^[35]. Also, $V_i(w_1, w_2)$ is related to $m_i(w_1, w_2)$ by

Here, $V_1(w_1, w_2)$ computes the expected lifetime of the first component as the sum of current age $w_1$ and the average lifetime remaining for it, assuming the second component has survived past age $w_2.$ $V_2(w_1, w_2)$ has a similar interpretation. Using (3.3) and (3.4) in (3.6), we obtain $V_1(w_1, w_2)$ and $V_2(w_1, w_2)$ of EP-EX-FGM as

and

From (3.7) and (3.8), the vitality function of EP-EX-FGM can be obtained using (3.5).

4.   Reliability and information measures

In this section, we derive reliability measures such as hazard function, RH function, MRL, vitality function, positive quadrant dependence feature, bivariate extropy, bivariate weighted extropy, and bivariate CREX in the context of EP-EX-FGM$(\varphi_1;$ $\varphi_2)$. Sreelakshmi ^[40] introduced the relationship between copula and reliability function, which is defined as follows:

The reliability function $R(w_1, w_2) = P(W_1 > w_1, W_2 > w_2)$ for the EP-EX-FGM$(\varphi_1;$ $\varphi_2)$ is

4.1.   Hazard function

The bivariate hazard function at a point $(w_1, w_2)$ is defined, according to Basu ^[11], by $H(w_1, w_2) = \frac{\textsf{f}_{W_1, W_2}(w_1, w_2)}{R(w_1, w_2)}.$ Thus, we get

One of the key constraints of Basu ^[11] is that $H(w_1, w_2),$ as defined by (4.1), is not a vector quantity, as defined by $R^{2}\rightarrow R.$ The bivariate hazard function was created in vector form by Johnson et al. ^[25] and Sreelakshmi ^[40] to get around this restriction.

where $R$ denotes the bivariate reliability function for the FGM copula. For the FGM copula, Vaidyanathan ^[42] studied the elements in vector (4.2). For the EP-EX-FGM copula, we can, after simple algebra, get the following relations:

and

The vector hazard function of EP-EX-FGM$(\varphi_1;$ $\varphi_2)$ is obtained by substituting (4.3) and (4.4) in (4.2). Figure 2 depicts 3D plots of the joint hazard function (JHF) of an EP-EX-FGM for various parameter values.

4.2.   Reversed hazard function

The RH function at a point $(w_1, w_2)$ is defined as $RH(w_1, w_2) = \frac{\textsf{f}_{W_1, W_2}(w_1, w_2)}{\textsf{F}_{W_1, W_2}(w_1, w_2)}.$ Thus, we get

4.3.   Positive quadrant dependence

Our goal in this section is to examine the positive quadrant dependence property, denoted by PQD, (negative quadrant dependence, denoted by NQD) of the RVs $W_1$ and $W_2$ associated with the EP-EX-FGM. As a type of RV dependence, PQD was introduced by Lehmann ^[30]. This kind of dependence describes the joint behavior of two RVs when they are both large (or small). More specifically, two RVs are PQD if there is at least as much chance that they are both tiny at the same time as there would be if they were independent. The following theorem reveals these properties for the EP-EX-FGM$(\varphi_1;$ $\varphi_2).$

Theorem 4.1. The EP-EX-FGM$(\varphi_1;$ $\varphi_2)$ is PQD (NQD) for positive (negative) values of $\delta.$

Proof. Consider

where

For all values of $w_1$ and $w_2,$ $\phi(w_1, w_2)$ is always non-negative because the DF and reliability function take values ranging from zero to one. On the other hand, we have for positive values of $\delta,$ $\delta\phi(w_1, w_2)\geq0$ $\forall w_1, w_2,$ that the EP-EX-FGM is PQD. Likewise, for negative values of $\delta,$ $\delta\phi(w_1, w_2)\leq0$ $\forall w_1, w_2,$ the EP-EX-FGM is NQD. Thus, EP-EX-FGM has both PQD and NQD. □

4.4.   Bivariate extropy, bivariate weighted extropy, and bivariate CREX

Lad et al. ^[29] introduced the concept of extropy as dual to entropy, facilitating the comparison of uncertainties of two RVs. If the extropy of $W_1$ is less than that of another variable $W_2,$ then $W_1$ is said to have more uncertainty than $W_2.$ Due to the difficulty of deriving the entropy for model (1.6), our focus in this subsection will be on the extropy. Extropy has several applications, such as scoring the forecasting distributions using the total scoring rule, comparing the uncertainties of two RVs, etc. Recently, the literature has numerous research works on this measure, e.g. Abd Elgawad et al. ^[1], Husseiny and Syam ^[20], and Husseiny et al. ^[21].

It is possible to introduce a bivariate version of extropy based on the FGM family in the following theorem.

Theorem 4.2. Consider two non-negative continuous RVs $W_{1}$ and $W_{2}$ with JPDF $\textsf{f}_{W_1, W_2}(w_1, w_2)$. Then, the bivariate version of extropy based on FGM is given by

where

Proof. By using (1.4), we get

Since each bivariate integral in the above formula is separable into the product of its univariate integrals, and by incorporating (4.6) in the above integrations, the required result directly follows. This completes the proof. □

Corolary 4.1. Let $W_1\sim \mathit{{EP}}(\varphi_1)$ and $W_2\sim \mathit{{EP}}(\varphi_2).$ Using (4.6), and after simple algebra, we get $J(W_i) = -\frac{33 \varphi_i}{80}, \;$ $\Psi_{w_i}(1) = \frac{643 \varphi_i}{2240},$ and $\Psi_{w_i}(2) = \frac{725 \varphi_i}{4928}, \; i = 1, 2.$ Thus, by using Theorem 4.2, the bivariate extropy based on EP-EX-FGM is

In a spirit similar to that of the bivariate version of extropy, we can also introduce bivariate weighted extropy based on FGM family in the following theorem.

Theorem 4.3. Let $W_{1}$ and $W_{2}$ be non-negative continuous RVs with JPDF $\textsf{f}_{W_1, W_2}(w_1, w_2).$ Then, the bivariate weighted extropy based on FGM is given by

where

Proof. We obtain the results by applying Theorem 4.2's proving techniques. □

Corolary 4.2. Let $W_1\sim \mathit{{EP}}(\varphi_1)$ and $W_2\sim \mathit{{EP}}(\varphi_2).$ Using (4.8), and after simple algebra, we get $J^{w}(W_i) = -\frac{53}{400}, \;$ $\Psi_{W_i}^{w}(1) = \frac{836497}{5644800},$ and $\Psi_{W_i}^{w}(2) = \frac{33010783}{341510400}, \; i = 1, 2.$ Thus, by using Theorem 4.3, the bivariate weighted extropy based on EP-EX-FGM is

Proposition 4.1. Let $W_{1}$ and $W_{2}$ follow an FGM family.

● If $W_{2} = aW_{1}+b,$ then $J(W_{2}) = \frac{1}{a}J(W_{1}).$

● If $\delta = 0$, then $J(W_{1}, W_{2}) = J(W_{1})J(W_{2})$.

It is worth noting that, as was shown by Balakrishnan et al. ^[7], there exist distributions with the same extropy, but different weighted extropy. Moreover, there exist distributions with the same weighted extropy, but different extropy.

Replacing the PDF in the extropy function with the survival function, Jahanshahi et al. ^[23] proposed a new measure of uncertainty of a non-negative continuous RV called cumulative residual extropy (CREX). Jahanshahi et al. ^[23] showed that if two RVs $W_1$ and $W_2$ are lifetimes of two systems $A$ and $B,$ and if the CREX of $W_1$ is less than the CREX of $W_2,$ then system $A$ has less uncertainty than system $B.$ We can define the bivariate CREX based on FGM family in the following theorem.

Theorem 4.4. Let $W_{1}$ and $W_{1}$ be non-negative continuous RVs with JDF $\textsf{F}_{W_1, W_2}(w_1, w_2).$ Then, the bivariate CREX based on FGM is given by

where

Proof. By using (1.3), we get

Since each bivariate integral in the formula above can be divided into the product of its univariate integrals, the required result can be obtained immediately by incorporating (4.10) in the integrations above. The proof is now complete. □

Corolary 4.3. Let $W_1\sim \mathit{{EP}}(\varphi_1)$ and $W_2\sim \mathit{{EP}}(\varphi_2).$ Using (4.10), and after simple algebra, we get $J^{c}(W_i) = -\frac{73}{480 \varphi_i}, \;$ $\Psi_{W_i}^{c}(1) = \frac{1957}{20160 \varphi_i},$ and $\Psi_{W_i}^{c}(2) = \frac{20987}{443520 \varphi_i}, \; i = 1, 2.$ Thus, by using Theorem 4.4, the bivariate CREX based on EP-EX-FGM is

Figure 3 displays the values of bivariate extropy, weighted extropy, and CREX in EP-EX-FGM. In 3D representation (a, b), we find that the value of $J(W_{1}, W_{2})$ increases as the values of $\varphi_1$ and $\varphi_2$ increase. Also, there is symmetry for the $J^{w}(W_{1}, W_{2})$ values in the 2D plot (c) according to $\delta$ values.

5.   Methods of estimation

In this section, we discuss two estimation methods for estimating the unknown parameters of the EP-EX-FGM distribution: ML and Bayesian estimations. Moreover, we construct asymptotic confidence intervals by using the Fisher information matrix (FIM) for the model's parameters.

5.1.   The ML estimation

The ML technique is a widely used and significant statistical technique. By using the ML technique, one can obtain estimates of parameters that have favorable statistical properties, such as consistency, asymptotic unbiasedness, efficiency, and normality asymptotically. It is necessary to calculate the parameter estimates that maximize the probability of the sample data to obtain the parameter estimates with the ML method. The log-likelihood function $\ln L$ is obtained by using the PDF given in (2.2).

We obtain the following normal equations by partially differentiating $\ln L$ with respect to the vector of parameters $\tau = (\varphi_1, \varphi_2, \delta)$ and equating them to zero. The following are those derivatives:

and

where $\; l, j = 1, 2,$ and $l\neq j.$

Because the likelihood equations for $\varphi_1, \varphi_2,$ and $\delta$ are nonlinear and challenging to solve analytically, numerical methods like the Newton-Raphson method can be employed to find the ML estimates of the distribution parameters $\varphi_1, \varphi_2,$ and $\delta.$

5.2.   Asymptotic confidence intervals

Based on the asymptotic normality of the ML estimates, the FIM is frequently used to create asymptotic confidence intervals for the unknown parameters in $\tau$ (for more details about other uses of FIM, see Barakat et al., ^[8]). Under specific assumptions of regularity, the ML estimates denoted as $\widehat{\tau}$ are distributed according to the normal distribution. As the sample size $n$ tends to infinity, the distribution of the estimator $\widehat\tau = (\widehat{\varphi_1}, \widehat{\varphi_2}, \widehat{\delta})$ approaches a normal distribution with mean $\tau$ and covariance matrix equal to the inverse of the FIM, denoted as ${\mathit{\boldsymbol{I}}}^{-1}(\tau).$ The FIM consists of the negative expected values of the second-order derivatives of $\ln L,$ as expressed by

The entries of the matrix in (5.1) are given by

where $l, j = 1, 2, \; l\neq j.$ According to Jia et al. ^[26], in cases where it is challenging to obtain the anticipated values directly, an alternative approach is to estimate them by calculating the negative second-order derivatives of the natural logarithm of the likelihood function, evaluated at the ML estimates. Hence, we approximate the expected values by the negatives of the second-order derivatives evaluated at the ML estimates $\widehat{\tau }.$ Thus, the estimated value of the FIM is ${\mathit{\boldsymbol{I}}}(\widehat{\tau }).$ Moreover, $100(1- \theta)$ asymptotic confidence intervals for the parameter $\tau$ can be constructed as follows:

where $J_{q_lq_l}, \; q_l = \widehat\varphi_l, \widehat\delta,$ is the element in ${\mathit{\boldsymbol{I}}}^{-1}(\widehat\tau),$ corresponding to the element $I{q_lq_l}$ in the estimated matrix ${\mathit{\boldsymbol{I}}}(\widehat\tau)$, and $Z_{\frac{\theta}{2}}$ is the percentile of the standard normal distribution with right tail probability $\frac{\theta}{2}.$

5.3.   Bayesian estimation

The Bayesian estimation technique is a powerful tool for estimating unknown parameters based on observable data. Using Bayes, theorem, a concept in probability theory, new information can be gathered to update the probability of a hypothesis. Because this approach takes prior knowledge into account when estimating, it provides some advantages over the traditional ML approach. Moreover, it is capable of assessing the degree of uncertainty surrounding each parameter. We must select an acceptable prior PDF and hyper-parameter values that reflect our belief regarding the data. While employing a Bayesian technique, the data analyst needs to be more explicit about all modeling assumptions. Choosing a suitable prior distribution usually involves taking into consideration the distribution's basic form (shape and domain) as well as its key characteristics (variance and mean). For the parameters $\varphi_l,$ $l = 1, 2$, we select gamma-independent priors, specifically

while the copula parameter $\delta$ has uniform prior distribution defined on $(-1, 1).$ The prior JPDF is given by

The likelihood method's estimate and variance-covariance matrix can be used to determine how to elicit the independent joint prior's hyper-parameters. The gamma prior's mean and variance can be used to represent the derived hyper-parameters. For more information, see Gupta and Kundu ^[18], Dey et al. ^[13], and Hamdy and Almetwally ^[19]. The parameters $\varphi_l$, $l = 1, 2,$ of EP-EX-FGM should be well-known and positive. The likelihood function is given by

The corresponding posterior density is given as follows:

The marginal posterior distributions $\Pi(\varphi_l|\delta, w_1, w_2),$ and $\Pi(\delta|\varphi_l, w_1, w_2)$ of the parameter $\varphi_l, \; l = 1, 2,$ may be found by integrating out the nuisance parameters from the posterior distribution $\Pi(\tau|w_1, w_2)$ as follows:

and

where $l = 1, 2.$ We use the well-known squared error loss function, which yields the posterior means as the Bayes estimates of $\tau,$ say $(\hat{\varphi_l}, \hat{\delta}),$ which are given by $\hat{\varphi_l} = \int_0^\infty \varphi_l\Pi(\varphi_l|w_1, w_2) d\varphi_l$ and $\hat{\delta} = \int_{-1}^1\delta\Pi(\delta|w_1, w_2) d\delta.$ Notice that the preceding integrals cannot be obtained explicitly. Because of this, we use the Monte Carlo method to find an approximate value of these integrals, see Tables 1–4.

6.   Simulation

The performance of ML and Bayesian estimates are contrasted numerically in this section. For the parameters of the EP-EX-FGM model, the performance of the various techniques and the analytically deduced results may be evaluated exactly. The Mathcad package was used, and 1000 samples from an EP-EX-FGM model had been gathered. The values of the parameters can be defined as follows:

● In Table 1: $\varphi_1 = 0.6$, $\varphi_2 = 3.$

● In Table 2: $\varphi_1 = 2$, $\varphi_2 = 0.3.$

● In Table 3: $\varphi_1 = 0.5$, $\varphi_2 = 0.7.$

● In Table 4: $\varphi_1 = 2$, $\varphi_2 = 4.$

The sample-sizes $n$ are 20, 50,100, and 150. The simulation results of bias and mean squared error (MSE) on 5000 iterations of Monte Carlo simulation are shown in Tables 1–4. The following conclusions can be drawn from Tables 1–4:

● The ML and Bayesian estimates of unknown parameters are fairly good in terms of bias and MSE.

● With an increase in sample size, the MSEs decrease and the estimated values of the parameters approach the nominal values of the parameters.

● For $\delta = -0.4$, both ML and Bayesian estimate values are smaller than the case of $\delta = 0.5$.

Moreover, Figure 4 shows the comparison between ML and Bayesian estimations for both $\varphi_1$ and $\varphi_2$ at specific values of the parameters. This figure shows that the two techniques give close values.

7.   Real data applications

In this section, we use the EP-EX-FGM model to examine two bivariate real data sets. The benefits of EP-EX-FGM over alternative bivariate models will be thoroughly discussed in the first one, which focuses on computer science. Additionally, several arguments supporting the fit of the estimated theoretical model to the empirical data will be presented. We talk briefly about the second application, which relates to medical applications.

7.1.   Computer science data set

Based on Oliveira et al. ^[34], data was gathered and analyzed. The data set contains $n = 50$ simulated rudimentary computer systems with processors ($W_{1}$) and memory ($W_{2}$). An operating computer will be able to operate when both parts are working properly (the processors and memory). Assume the system is nearing the end of its lifecycle. The degeneration advances rapidly in a short period. In the case of the first component, a deadly shock can destroy either it or the second component at random, due to the system's greater vulnerability to shocks (see, Ahmad et al. ^[3]). The independence presumption is not accurate because both components can be killed by a deadly shock at the same time, so we discuss this issue using the FGM copula. We fit the EP-EX distribution to the processor lifetime and memory lifetime separately. The ML estimates of the scale and shape parameters are $\hat{\varphi _1} = 0.345952$, $\hat{\varphi _2} = 0.362599$, and $\hat{\delta} = 0.452819$. To analyze the maximum values of the estimators by profile likelihood, Figures 5 and 6 were constructed based on $W_{1}$ and $W_{2}.$ Also, Figures 7–12 illustrate statistical visualizations, including a scatter plot, empirical CDF, Q-Q plot, a density plot, paired smooth histogram, and a paired violin plot. Table 5 clearly shows that, in terms of data fit, the EP-EX-FGM model performs better than the bivariate generalized EX-FGM distribution (GEX-FGM), the bivariate exponential FGM distribution (EX-FGM), and the bivariate Weibull FGM distribution (W-FGM). Furthermore, by using the Python programming language, our data set, and the Kolmogorov-Smirnov (KS) test, the EP-EX-FGM model demonstrates an outstanding match with a p-value of 0.832 and a test statistic of 0.085.

7.2.   Medical science data set

We now use the EP-EX-FGM family to fit a second real data set that Grover et al. ^[16] covered. We conducted our investigation using two data sets. Retrospective data on 132 individuals diagnosed with type 2 diabetes according to ADA guidelines is included in the first dataset, which originates from Dr. Lal's Path Lab, a respected NABL-certified path lab. To collect up-to-date pathology reports for these patients, researchers conducted a house-to-house survey that began when they were diagnosed with diabetes and ended in November 2007. The duration of diabetes, fasting blood glucose, diastolic blood pressure, systolic blood pressure, low-density lipoprotein, and serum creatinine levels were all documented for each patient, starting from childhood and continuing into adulthood. The mean serum creatinine level (SrCr) and the mean duration of diabetes are represented by the RVs $W_1$ and $W_2,$ respectively.

This study only looks at kidney problems caused by type 2 diabetes, therefore it automatically ignores the effects on the eyes, heart, and other organs. Additionally, we have removed cases where renal problems occurred before diabetes. Participants in our research with individuals with the same duration of diabetes experience variable degrees of kidney function. A patient's renal health is evaluated using SrCr because its fast rise in value is a critical sign for DN risk prediction. So, the data were split into two groups based on SrCr values: DN (SrCr 1.4 mg/dL) and NDN (Non-Diabetic Nephropathy; SrCr 1.4 mg/dL). At the end of the trial, 60 (or 45.45%) of the 132 individuals had DN, and 72 (or 54.55% of the total) had NDN. The ML estimates of the scale and shape parameters are $\hat{\varphi _1} = 0.423, \; \hat{\varphi _2} = 0.0433,$ and $\hat{\delta} = 0.98$. Moreover, we estimate AIC = 202.373 and BIC = 205.206.

8.   Conclusions

This study introduces a new bivariate EP-EX-FGM model: an improved version of the bivariate distribution based on the FGM copula. In the area of bivariate modeling, the proposed distribution represents a substantial and original contribution. This study introduces a new statistical model called EP-EX-FGM, which is a bivariate EP-EX distribution based on the FGM copula. Within the analysis of bivariate data, this work is both important and innovative in the field of bivariate modeling. The correlation coefficient between $W_1$ and $W_2$ for the suggested distribution EP-EX-FGM ranges from a maximum value of $0.261$ to a minimum value of $-0.261.$ In addition, we have explored dependability measures such as the hazard function, the MRL function, and the vitality function. Moreover, it has been demonstrated that the proposed model satisfies the PQD(NQD) characteristic, depending on the sign of the shape. The parameter estimators were generated using ML and Bayesian approaches, and the overall outcome indicates that Bayesian estimation outperforms its counterpart. Furthermore, a Monte Carlo simulation study was conducted to assess the performance of the estimators. Asymptotic confidence intervals for the likelihood estimation were produced for the parameters in this model. Finally, the significance and adaptability of the EP-EX-FGM were investigated through the analysis of real data sets.

Author contributions

H. M. Barakat: Conceptualization, formal analysis, writing original draft, software, investigation, methodology, supervision; M. A. Alawady: Conceptualization, formal analysis, writing original draft, software, investigation, methodology, supervision; I. A. Husseiny: Conceptualization, writing original draft, formal analysis, software, investigation, methodology, supervision; M. Nagy: Validation, resources, writing – review & editing, data curation, methodology; A. H. Mansi: Writing – review & editing, investigation; M. O. Mohamed: Conceptualization, formal analysis, writing original draft, software, investigation, methodology, supervision; All authors have read and agreed to the published version of the manuscript.

Acknowledgments

The authors are grateful to the editor and anonymous referees for their insightful comments and suggestions, which helped to improve the paper's presentation. This research was conducted under a project titled "Researchers Supporting Project", funded by King Saud University, Riyadh, Saudi Arabia under grant number (RSPD2024R969).

Funding

This research was conducted under a project titled "Researchers Supporting Project", funded by King Saud University, Riyadh, Saudi Arabia under grant number (RSPD2024R969).

Conflict of interest

The authors declare no conflicts of interest.