On the 2-metric resolvability of graphs

1.   Introduction and Preliminaries

For a connected and simple graph $G = (V(G), E(G))$, $d(s, w)$ represents the length of the shortest path between two vertices $s, w \in V(G)$. Let an ordered set of vertices $\Re = \{v_1, v_2, \ldots, v_l\} \subset V(G)$ and $s\in V(G)$, then $r(s|\Re) = \big(d(s, v_1), d(s, v_2), \ldots, d(s, v_l)\big)$ denotes the representation of vertex $s$ with respect to $\Re$. The set $\Re$ is called a resolving set or metric generator if for each pair of vertices $s, w \in V(G)$, the representations $r(s|\Re)$ and $r(w|\Re)$ uniquely identify $s$ and $w$ i.e., $r(s|\Re)\neq r(w|\Re)$ ^[1,2]. A resolving set or metric generator of least number of entries is called a basis for $G$ and its count is known as the metric dimension of $G$, represented by $\dim(G)$. Consider the set of distinctive vertices of $s, w \in V(G)$ is $D(s, w) = \{v\in V(G): d(s, v)\neq d(w, v)\}$ and the set of non-trivial distinctive vertices $s, w$ is $D^*(s, w) = D(s, w)-\{s, w\}$. Now, the two vertices $s, w$ are twins if and only if $D^*(s, w) = \phi$. The degree $d_v$ of the vertex $v\in V(G)$ is defined as the number of edges attached to $v$ ^[3,4,5,6,7]. The following lemma is used in proving the result later in this article.

Lemma 1.1. ^[8] Let $\dim(G) = 2$ and $\{v_1, v_2\}$ be a resolving set of $G$, then $\max\{d_{v_1}, d_{v_2}\}\leq 3$.

In 1953, the idea of metric dimension associated to a general metric space was introduced (see ^[9]). Later, Slater defined the notion of resolving set for the connected graph $G$, in 1975 (see ^[10] and ^[11]). It was also discussed independently by Harary et al. in 1976 (see ^[12]). The resolving sets were basically defined to locate any intruder in a network but later many applications in robotics, chemistry and biology were presented in ^[13]. However, the weakness in the original concept of metric dimension was the possible uniqueness of the vertex identifying the vertices of the graph. This led to the more general concept of $k$-metric dimension (denoted by $\dim_k(G)$), introduced by A. Estrado-Moreno et al., in 2014 (see^[14]), where there are $k$ vertices identifying the vertices of the graph. This notion corresponds to the classical version of metric dimension, for $k = 1$.

The notion of $k-$resolving set is defined as follows: Let $\Re = \{v_1, v_2, \ldots, v_l\}$ be an order set of vertices in a graph $G$ and $AD((s, w)|\Re) = (|d_G(s, v_1)-d_G(w, v_1)|, \ldots, |d_G(s, v_l)-d_G(w, v_l)|)$ be the absolute difference representation of $s, w\in V(G)$ with respect to $\Re$. The set $\Re$ is called a $k-$resolving set for $G$, if for any distinct vertices $s, w \in V(G)$, the representation of vertices $r(s|\Re)$ and $r(w|\Re)$ differs in at least $k$ positions. In other words, $\Re$ is called a $k-$resolving set for $G$, if $AD((s, w)|\Re)$ has at least $k$ non zero entries. A $k-$resolving set of minimum cardinality in $G$ is known as $k-$metric basis and its cardinality is the $k-$metric dimension of $G$, denoted by $\dim_k(G)$.

Since, it was studied in ^[15] that computing the $k-$metric dimension of a graph $G$ is NP-hard. Also, obtaining the $k-$resolving set of a graph $G$ for each value of $k$ is a remote possibility. This leads to the definition: If $\eta$ is the largest integer for which $G$ has a $\eta-$resolving set, then we say that $G$ is a $\eta$ metric dimensional graph. In other words, the difference in representation $r(s|\Re)- r(w|\Re) = (a_1, a_2, \ldots, a_l)$ has $a_i\neq 0$ for at least $\eta$ position. Such a graph $G$ is called $\eta$-metric dimensional graph. Thus, for any $k\in \{1, \ldots, \eta\}$, $\dim_k(G)$ can be computed in a $\eta-$metric dimensional graph (see ^[16]).

A. Estrado-Moreno et al. gave a necessary and sufficient condition for the existence of $k$-metric basis and presented some important results on the $\dim_k(G)$ in ^[17]. The $k-$metric dimension of general metric spaces is also studied in ^[18]. The closed formulae and tight bounds for the $k-$metric dimension of corona product of graphs and lexicographic product of graphs were computed in articles ^[19] and ^[20] respectively. The $k$-metric dimension of grid graphs is computed in ^[16]. Furthermore, this concept was extended to the more general case of non-necessarily connected graphs in ^[21]. The case $k = 1$ and the equally interesting case $k = 2$ has gathered the most attention, lately.

The $2-$metric dimension has also been discussed under the name of the fault-tolerant metric dimension, first introduced by Slater in ^[22]. Later, Hernando et.al. in ^[23] gave the relation between the metric and the $2-$metric dimension, i.e., $\dim_2(G) \leq \dim(G)(1+2.5^{\dim(G)-1})$. The $2-$metric dimension of some families of generalized Peterson graphs $P(n, t)$ are discussed in ^[24]. For more details on $2-$metric dimension, we refer to the articles ^{[25,26,27,28,29,30,31]} and ^[32].

The bounds and formulae for dealing with the $k-$metric dimension as studied in ^[20] can be helpful in dealing with the $2-$metric dimension of graphs. Here, we include some of the important results on the $2-$metric dimension of the connected graphs with order $n\geq2$.

Theorem 1.2. ^[14] If $G$ is a $\eta-$metric dimensional graph and let $k_1, k_2$ be two integers. If $1\leq k_1 < k_2 \leq \eta,$ then $\dim_{k_1}(G) < \dim_{k_2}(G).$

Theorem 1.3. ^[14] If $G\neq P_n$, then for each $k\in \{1, ..., \eta\}$, $\dim_{k}(G)\geq k+1.$

Theorem 1.4. ^[17] $G\cong P_n$ if and only if $\dim_{2}(G) = 2$.

Theorem 1.5. ^[17] Every vertex of $G$ is twin if and only if $\dim_{2}(G) = n$.

In this paper, we computed the $2-$metric dimension of some families of graphs. In Section $2$, we disproved the conjecture given in ^[1] by computing the exact value of $\dim_{2}(C_n(1, 2))$. In Section $3$, the $2-$metric dimension of the family, generalized prism graph, $P_m\times C_n$ is computed. Finally, in Section $4$, we improved the result of the metric dimension of the family, {Möbius} ladder graph, $M_n$ given in ^[2] by computing the exact value of $\dim_{2}(M_n)$.

2.   The $2-$metric dimension of family of the circulant graph $C_n(1, 2)$

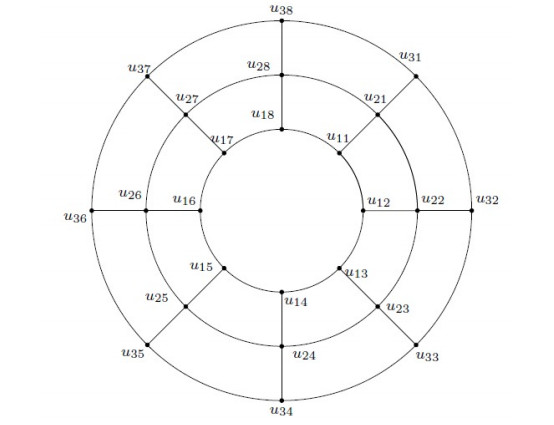
The circulant graph $C_n(1, 2)$ is formed by cyclically arranging the vertices $\{v_1, v_2, \ldots, v_n\}$ in such a way that, for $(1\leq k \leq n)$, each vertex $v_k$ is adjacent to the $2$ vertices that immediately follow $v_k$ and $2$ vertices that immediately precede $v_k$, i.e., join $v_k$ to $v_{k+1}, v_{k+2}$ and to $v_{k-1}, v_{k-2}$. The graph $C_8(1, 2)$ is shown in Figure 1.

The following lemma will be helpful in computing the $2-$metric dimension of family of the circulant graph $C_n(1, 2)$.

Lemma 2.1. ^{[33, 34]} For $n\geq 5$, the circulant graph $C_n(1, 2)$;

It is conjectured in ^[1], the $\dim_2(C_n(1, 2))$ as:

Conjecture 1. ^[1] $\dim_2(C_n(1, 2)) = 7$, for $n \geq 7$.

In ^[30], J. B. Liu et al. disproved the conjecture in case of even $n$. The result is given below:

Theorem 2.2. ^[30] $\dim_2(C_n(1, 2)) = 4$, for $n \geq 8$ and $n \equiv 0 \mathit{\text{mod}} 2$.

Here, we have computed the exact value of the $2-$metric dimension for the graph $C_n(1, 2)$, for all $n\geq 5$.

Theorem 2.3. The $2-$metric dimension of $C_n(1, 2)$, for $n \geq 5$ is

Proof. To prove this theorem, we consider the following cases:

Case $1$: (When $n$ is even)

Here, we have the following subcases:

Case $1$a: (When $n = 6$)

It can be easily verified that $\Re = \{v_1, v_2, v_3, v_4, v_5, v_{6}\}$ is a $2-$resolving set for $C_6(1, 2)$. This implies that $\dim_2(C_6(1, 2))\leq6.$ Therefore, by using Lemma 1.2 and Theorem 1.2, we have $\dim(C_6(1, 2)) = 3 < \dim_2(C_6(1, 2))\leq6.$ The only thing that remains to show is $\dim_2(C_6(1, 2))\neq4$ or $5$. Here, it is sufficient to show that any set of cardinality $5$ cannot be the $2-$resolving set for $C_6(1, 2)$. We have this only possibility:If $\Re = \{v_1, v_2, v_3, v_4, v_5\}$, then $AD((v_3, v_6)|\Re) = (0, 0, 2, 0, 0).$

Case $1$b: (When $n$ is even and $n\geq 8$)

The result follows that $\dim_2(C_n(1, 2)) = 4$, by Theorem 2.2.

Case $2$: (When $n$ is odd)

Here, we have the following subcases:

Case $2$a: (When $n = 5$)

It can be easily verified that $\Re = \{v_1, v_2, v_3, v_4, v_5\}$ is $2-$resolving set for $C_5(1, 2)$. This implies that $\dim_2(C_5(1, 2))\leq5.$ Therefore, by using Lemma 1.2 and Theorem 1.2, we have $\dim_2(C_5(1, 2)) = 5$.

Case $2$b: (When $n\equiv 1 \ \text{ mod }4$ and $n\geq 9$)

Take $\Re = \{v_1, v_2, v_{3}, v_{\frac{n+3}{2}}, v_{\frac{n+5}{2}}\}$, then the representation of the vertices $v_i$ are:

For even $i$:

and for odd $i$:

Since it can be easily seen that for all $s, w \in V(C_n(1, 2))$, the $AD((s, w)|\Re)$ has non-zero entries in at least two positions, implying that $\dim_2(C_n(1, 2))\leq5.$ Therefore, by Lemma 1.2 and Theorem 1.2, we have $\dim_2(C_n(1, 2)) = 5$.

Case $2$c : (When $n\equiv3 \ \text{ mod } 4$ and $n\geq 7$)

Take $\Re = \{v_1, v_2, v_3, v_4\}$, then the representations of the vertices $v_i$ are:

For even $i$:

and for odd $i$:

Since it can be easily seen that for all $s, w \in V(C_n(1, 2))$, the $AD((s, w)|\Re)$ has non-zero entries in at least two positions, implying that $\dim_2(C_n(1, 2))\leq4.$ Therefore, by Lemma 1.2 and Theorem 1.2, we have $\dim_2(C_n(1, 2)) = 4$. This concludes the proof.

3.   The $2-$metric dimension of family of the generalized prism graph $P_m \times C_n$

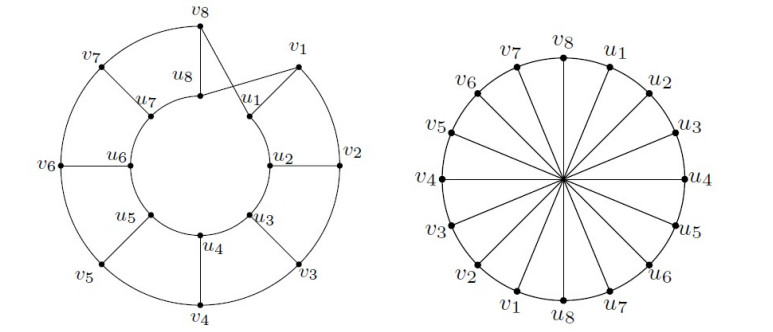
The generalized prism graph $P_m\times C_n$ has vertex set $V(P_m\times C_n) = \{u_{ij}|1\leq i\leq m\wedge1\leq j\leq n\}$ and edge set $E(P_m\times C_n) = \{u_{ij}u_{i(j+1)}, u_{ij}u_{(i+1)j}|1\leq i\leq m\wedge1\leq j\leq n\},$ where subscripts $i$ and $j$ are to be read as modulo $m$ and $n$ respectively (see Figure 2).

The following lemmas will be helpful in proving next theorem.

Lemma 3.1. Let $\dim_2(G) = 3$ and $\{v_1, v_2, v_3\}$ be a $2-$resolving set of $G$, then $\max\{d_{v_1}, d_{v_2}, d_{v_3}\}\leq 3$.

Proof. In view of Theorem 1.4 $G$ cannot be a path graph, therefore, the proof is obvious by using Lemma 1.1 and Theorem 1.2.

Lemma 3.2. ^[34] For $n \geq 3$, the metric dimension of the generalized prism graph $P_m\times C_n$ is

In the theorem given below, we have computed the $2-$metric dimension of $P_m\times C_n$.

Theorem 3.3. The $2-$metric dimension of $P_m\times C_n$, for $n \geq 3$ is

Proof. To prove this theorem, we consider the following cases:

Case $1$: (When $n$ is even)

Take $\Re = \{u_{11}, u_{12}, u_{1(\frac{n+2}{2})}, u_{1(\frac{n+4}{2})}\}$, then the representation of the vertices $u_{ij}$ is:

Since it can be easily seen that for all $s, w \in V(P_m\times C_n)$, the $AD((s, w)|\Re)$ have non-zero entries in at least two positions, implying that $\dim_2(P_m\times C_n)\leq4.$ Therefore, by Lemma 3.2 and Theorem 1.2, we have $\dim_2(P_m\times C_n) = 4$.

Case $2$: (When $n$ is odd)

Here, we have the following subcases:

Case $2$a: (When $n = 3$)

It can be easily verified that $\Re = \{u_{11}, u_{12}, u_{13}\}$ is $2-$resolving set for $P_m\times C_3$. This implies that $\dim_2(P_m\times C_3)\leq3.$ Therefore, by using Lemma 3.2 and Theorem 1.2, we have $\dim_2(P_m\times C_3) = 3$.

Case $2$b: (When $n$ is odd and $n\geq 5$)

Take $\Re = \{u_{11}, u_{12}, u_{1(\frac{n+1}{2})}, u_{1(\frac{n+2}{2})}\}$, then the representation of the vertices $u_{ij}$ is:

Since it can be easily seen that for all $s, w \in V(P_m\times C_n)$, the $AD((s, w)|\Re)$ has non-zero entries in at least two positions, implying that $\dim_2(P_m\times C_n)\leq4.$ Therefore, by Lemma 3.2 and Theorem 1.2, we have $\dim(P_m\times C_n) = 2 < \dim_2(P_m\times C_n)\leq4$. The only thing that remains to show that any set of cardinality $3$ cannot be the $2-$resolving set. In view of Lemma 3.1, we have the following cases:

$a)$ If $\Re = \{u_{11}, u_{1s}, u_{1t}\}, \text{with} \ \ 1 < s < t\leq \frac{n+1}{2}$, then $AD((u_{11}, u_{22})|\Re) = (2, 0, 0).$

$b)$ If $\Re = \{u_{11}, u_{1s}, u_{1t}\}, \text{with} \ \ 1 < s\leq \frac{n-1}{2} < t\leq n$, then

$c)$ If $\Re = \{u_{11}, u_{ns}, u_{nt}\}, \text{with}\ \ 1\leq s < t\leq \frac{n-1}{2}$, then

$d)$ If $\Re = \{u_{11}, u_{ns}, u_{nt}\}, \text{with} \ \ 1\leq s\leq \frac{n+3}{2} < t\leq n$, then

Hence, in all above cases, there is no $2-$resolving set for $P_m\times C_n$ of cardinality $3$. This completes the proof.

4.   The $2-$metric dimension of family of the Möbius ladder graph $M_n$

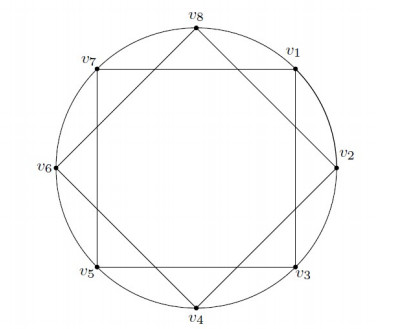
The family of the Möbius ladder graphs are the graphs with an even number of vertices. They are formed by adding edges connecting opposite pair of vertices in the cycle. It has exactly $\frac{n}{2}$ $4$-cycles which joined together in such a way to form a topological Möbius strip. It can also be viewed as prism with two crossed edges. The two different views of the graph $M_{16}$ is shown in the Figure 3.

Lemma 4.1. ^[2] The metric dimension of $M_n$, for $n\geq 8$ is

In the following theorem, we have computed the $2-$metric dimension of $M_n$.

Theorem 4.2. The $2-$metric dimension of $M_n$, for $n\geq 3$ is $4$.

Proof. To prove this theorem, take $\Re = \{u_1, u_2, v_1, v_2\}$. Representation of the vertices $u_i$ and $v_i$ with respect to $\Re$ are

Since it can be easily seen that for all $s, w \in V(M_n)$, the $AD((s, w)|\Re)$ has non-zero entries in at least two positions, implying that $\dim_2(M_n)\leq4.$ Therefore, by Lemma 4.1 and Theorem 1.2, we have $\dim_2(M_n) = 4$.

Since, the metric dimension of the graph is always strictly less than the $2-$metric dimension of the graph, the following result is obviously stated.

Theorem 4.3. The metric dimension of Möbius ladder graph is $3$, for every $n$.

5.   Conclusion

In this paper, the $2-$metric dimension of the families circulant graph $C_n(1, 2)$, the generalized prism graph $P_m\times C_n$ and Möbius ladder graph $M_n$ are computed, which were found to be constant. Here, we end with the following open problem.

Open Problem Find the $2-$metric dimension of the family of the generalized Petersen multigraphs $P(2n, n)$ for $n\geq2$.

Acknowledgment

The research was supported by the National Natural Science Foundation of China (Grant Nos. 11971142, 11871202, 61673169, 11701176, 11626101, 11601485).

Conflict of interest

The authors declare that no competing interests exist.