Some novel fixed point theorems in partially ordered metric spaces

1.   Introduction

In past decades, the progress of fixed point theory in metric spaces is highly active branch of research in nonlinear analysis. Current evolution in fixed point theory is bucked up by its utility in proving existence of solution of differential and integral equations (refer to ^{[1,2,3,4,5,6]}).

One of the most famous problem in nonlinear analysis is the Banach fixed point theorem ^[7], this introduced a number of interesting ideas for other researchers to study on contractions, some of them are ^[8,9,10]. One of the famous extension of the Banach's result was given by Dass and Gupta ^[11], where they generalized the Banach contraction as rational expression.

Theorem 1.1. ^[11] Let $(E, d)$ be a metric space and $J$ be a self-maps of $E$ such that

for all $f, g \in E$, $h, m > 0$ with $h + m < 1$, and for some $f_{0} \in E$, the sequence of iterates ${ J^{i} (f_0)}$ has a sub-sequence ${ J^{i_{k}} (f_{0})}$ with $z = \lim { J^{i_{k}} (f_{0})}$.

Then $J$ has a unique fixed point $z \in E$.

On the line of previous results, Pachpatte ^[12], Cìri$\mathop {\rm{c}}\limits^{、}$ ^[13] and Fisher ^[14] proposed a problem with rational contraction and derived some results. Jungck ^[15] articulated idea of commuting maps in mid 70's. The intent of this introduction was to present commuting mappings as a tool to extend, unify and generalize many widely known results of literature. He generalized the most famous Banach's result for two self maps. This foundation by Jungck ^[15] gave a new source of distinguished thoughts to researchers to think, observe and discuss the various fixed point problems with new approach. In early 80's, Sessa ^[16] leaded this approach and defined the concept of weak commutativity in metric spaces. Further in mid 80's, Jungck ^[17] generalized this idea and led the foundation of weakly compatible mappings and compatible mappings. Result of Jungck ^[17] was further unified by Gupta and Mani ^[18] through rational expression.

Now a days, trends are rapidly increasing to weaken the contraction. Partially ordered metric space plays an important role to fulfill the requirement of weaker contraction. The roll of partially ordered space significantly increased in last 20 years because of its important features. In most of the previously derived results continuity of mappings plays a crucial role in obtaining fixed point. To derive a fixed point problem in such spaces, continuity condition of map(s) is no longer required; however, results can be derived by assuming that map should be non-decreasing or weakly increasing or may be any other assumptions. Sufficient work already had been done in partially ordered metric spaces. Some of the related results on this emerging theory, we refer to ^{[19,20,21,22]}. Ran and Reurings ^[23] were the first who unified the existence of fixed points in partially ordered metric spaces. Nieto and Lopez ^[24] further refined and extended above results with the help of non-decreasing functions and then proved some fixed point results in such spaces. These studies further gave other aspects of weak contractions to researchers, in particular, problems related to partially ordered metric spaces. Some of widely known results of this theory can be found in (^[25,26,27]).

Definition 1.1. ^[24] Suppose $E$ is a non-empty set and $\preceq$ is a partially ordered relation on set $E$. Then a map $J: E \rightarrow E$ is said to be non-decreasing if for each $f, g \in E, \; f \leq g$ implies $J(f) \leq J(g)$.

In 2010, Altun et al. ^[28] contributed in this field by defining notion of weakly increasing mappings. In addition, by using implicit relations, they derived some results (both for weakly increasing and non-decreasing operators) in a partially ordered metric space. This foundation of Altun et al. ^[28] is of considerable interest for others related to these areas. Some more results on this theory are referred to ^[29,30,31] and the references there in.

Definition 1.2. ^[28] Suppose $E$ is a non-empty set, $\preceq$ is a partially ordered relation on set $E$ and let $J, K: E \rightarrow E$. If for each $f \in E$, $J f \preceq K J f$ and $K f \preceq J K f$, then the map $J$ and $K$ are weakly increasing.

Example 1.1. ^[28] Let $E = [0, 1]$ be endowed with usual ordering. Let $J, K : E \to E$ defined by

Then clearly $J$ and $K$ are weakly increasing mappings, but not non-decreasing.

Example 1.2. ^[28] Let $E = [1, \infty)$ be endowed with usual ordering. Let $J, K: E \to E$ defined by

Then $J$ and $K$ are weakly increasing mappings.

Remark 1.1. Clearly, weakly increasing mappings doesn't implies that it is non-decreasing.

2.   Main results

This section will be devoted to prove some fixed point results for non-continuous self-maps without using the compatibility and commutative property for new type of contraction (2.1). Before stating main theorem, lets recall a definition, that will be quite useful in proving our main result.

Definition 2.1. ^[10] A function $\pi :[0, \infty) \rightarrow [0, \infty)$ is known as altering distance function if the following properties are satisfied:

(i) $\pi$ is continuous and non-decreasing,

(ii) $\pi (t) = 0$ if and only if $t = 0.$

Theorem 2.1. Let $(E, d)$ be a partially ordered metric space and let $J, K: E \rightarrow E$ be weakly increasing mappings. Suppose that for every comparable pair $(f, g) \in E$, we have

where $\pi$ is an altering distance function and $\theta :[0, \infty) \rightarrow [0, \infty)$ is a continuous function such that

Then $J$ and $K$ have a common fixed point.

Proof. Set initial approximation $f_{0} \in E$ as an any arbitrary point. Define $J f_{0} = f_{1}$ and $K f_{1} = f_{2}$. In general, construct sequences $\left\{ f_{i}\right\}, \left\{ g_{i}\right\} \in E$ such that

Since $J$ and $K$ are weakly increasing function

Continuing this process, we obtain

Assume that

Since $f_{2 i}$ and $f_{2 i +1}$ are comparable, we can use (2.1) and (2.2) to write

This is a contradiction. Thus our assertion in (2.4) is false. Therefore, $g_{2 i} = g_{2 i +1}$ for some $i \in N$, let us say $i = k$. That is, for some $i = k$, we have $g_{2k} = g_{2k+1}$ and $l = f_{2k+1}$, this implies by referring (2.3) that $K l = l$. Further, we assert that for any $l \in E$ such that $K l = l$ implies that $J l = l$. To get this, set $f = g = l$ in (2.1), we obtain

But (2.2) and the continuity of $\pi$ and $\theta$ imply that $\theta(0) = 0$ since $\pi(0) = 0$, we thus obtain $J l = l.$ Therefore, we get $J l = K l = l$. This proves that common fixed point of $J$ and $K$ is $l$.

Remark 2.1. It should be noted from (2.1) that if $p$ is a fixed point of $K$, then $J l = p$ for all $l$ comparable with $p$.

Assumptions we have made in Theorem 2.1 are not sufficient to prove the uniqueness of the fixed point. Let us define a sufficient condition to overcome this problem:

Theorem 2.2. Let $(E, d)$ be a partially ordered metric space and let $J, K: E \rightarrow E$ be weakly increasing mappings. Suppose that for every comparable pair $(f, g) \in E$ the following condition is satisfying:

where $\pi$ is an altering distance function and $\theta :[0, \infty) \rightarrow [0, \infty)$ is a continuous function such that

Also, for each $f, g \in E$ there exists $z \in E$ which is comparable to $f$ and $g$.

Then both maps $J$ and $K$ preserve a unique common fixed point.

Proof. Existence of common fixed point follows from Theorem 2.1. Lets prove the uniqueness of common fixed point. Suppose on contrary that $l \neq p$ are two common fixed points of $J$ and $K$ such that $J l = K l = l$ and $J p = K p = p$. Now we will discuss two different cases.

Case 1. If $l$ is comparable to $p$, then $J l = l$ is comparable to $p = K p$. Also from above Remark 2.1, $J l = p$.

Hence, from (2.1)

Therefore $d(l, p) = 0$, this is a contradiction to our assumption, thus $l = p$.

Case 2. Secondly, suppose that $l$ is not comparable to $p$. Then there exists $q \in X$ such that $q$ is comparable to $l$ and also comparable to $p$. This implies that $K q = q$ is comparable to $l = K l$ and also comparable to $J p = p$. Therefore, from (2.1)

Thus $d(p, K q) = 0$, i.e., $K q = p$. Analogously, we can show that $d(l, K q) = 0$, i.e., $K q = l$.

Since the function $K$ is well defined, we have $l = p$. This finishes the proof of Theorem 2.2.

3.   Examples and remark

In this section, we give some examples in support of our findings and one remark which signifies the importance of our result.

Example 3.1. Let $E = (0, 1]$ and metric $d$ is usual metric. We define partial order $\preceq$ in $E$ as $f \preceq g$ if and only if $g \leq f$ for all $f, g \in E$. Define selfmaps $J, K: E \rightarrow E$ such that

Clearly, the maps $J$ and $K$ are weakly increasing.

Define an altering distance function $\pi :[0, \infty) \rightarrow [0, \infty)$ and a function $\theta :[0, \infty) \rightarrow [0, \infty)$ by

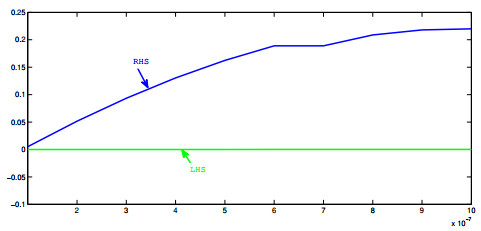
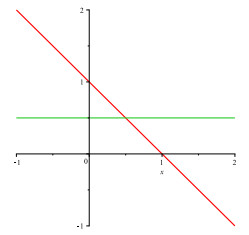
It is clear that $\theta$ is a continuous function and satisfying the condition $0 < \theta(s) < \pi(s).$ Thus all the assumptions made in Theorem 2.1 are satisfied (see Figure 1). Also $1 \in E$ is the only one common fixed point of $J$ and $K$ (see Figure 2).

Example 3.2. Let $E = \Big\{0, 0.5, 1 \Big\}$ and metric $d$ is usual metric. We define partial order $\preceq$ in $E$ as $f \preceq g$ if and only if $g \leq f$ for all $f, g \in E$. Define selfmaps $J, K: E \rightarrow E$ such that

Also, we assume that function $\pi$ and $\theta$ is defined as:

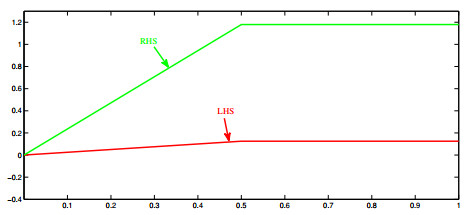
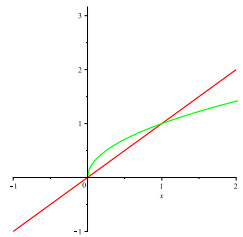
Clearly, maps $J$ and $K$ are weakly increasing. Also, for all $s \in E$, $0 < \theta(s) < \pi(s)$. Thus all the assumptions made in Theorem 2.1 are satisfied (see Figure 3). Also $0.5 \in E$ is the only one common fixed point of $J$ and $K$ (see Figure 4).

Remark 3.1. Suppose, if we take $K = J$, in (2.1), we get

Then here we are leaving this problem for future research, to get fixed point without completeness of space and without continuity of map $J$.

4.   Conclusion

We conclude this note by mentioning that the contraction in Theorem 2.1 is specially constructed for two self maps to get common fixed point. Moreover, on adding condition (2.5) in the hypothesis of Theorem 2.1, we get uniqueness of fixed point. Example 3.1 and Example 3.2 notify that the results proved in Theorem 2.1, 2.2 are much weaker from other existing results.

Acknowledgements

The authors wish to thank the editors and referees for their valuable guidance and support in improving the quality of this paper. No funding is available to publish this manuscript.

Conflict of interest

The authors declare that there is no conflict of interest.