Orientable vertex imprimitive complete maps

1.   Introduction

If a graph can be embedded in a surface, then naturally there will be a problem: How many non-isomorphic ways can it be done? One of the main aims of topological graph theory is to enumerate all the symmetrical embeddings of a given class of graphs in closed surfaces, see ^[1,2,3]. As one of a series of papers toward solving the problem of counting the number vertex transitive embeddings of complete graphs, we restrict our attention here to the orientable vertex imprimitive embeddings of complete graphs.

Let $\mathcal{M} = (V, E, F)$ be an orientable map with vertex set $V$, edge set $E$, and face set $F$, that is, $\mathcal{M}$ is a 2-cell embedding of the finite underlying graph $\Gamma = (V, E)$ in an orientable surface. For convenience, a map $\mathcal{M}$ is called a complete map if its underlying graph is a complete graph.

An automorphism of a map $\mathcal{M}$ is a permutation of $V\cup E\cup F$, which preserves $V$, $E$, $F$, and their incidence relations, so it is exactly an automorphism of the underlying graph which preserves the supporting surface. All automorphisms of $\mathcal{M}$ form the automorphism group $\text{Aut}(\mathcal{M})$ under composition.

A map $\mathcal{M}$ is said to be $G$-vertex-imprimitive (or a vertex-imprimitive embedding of its underlying graph) if $G = \text{Aut}(\mathcal{M})$ acts imprimitively (but transitively) on the vertex set $V$. Furthermore, if $G$ also preserves the orientation of the supporting surface, then $\mathcal{M}$ is called orientable vertex-imprimitive. Here, a permutation group $G$ acting transitively on a set $\Omega$ is imprimitive, which means that $G$ preserves a nontrivial partition of $\Omega$.

Recent development concerning the theory of maps was closely related to the theory of map colorings, with the topic of highly 'symmetrical' maps always at the center of interest, and recent investigation began with Biggs ^[4,5]. In the past fifty years, plenty of results about 'symmetrical' maps have been obtained, see ^[2,6,7] and the references therein. In particular, see ^[2,3,5] for arc transitive complete maps, see ^[8,9,10] for vertex transitive complete maps, and see ^[11,12] for edge transitive complete maps. Very recently, some special families of edge-transitive embeddings of complete bipartite graphs are classified in ^{[13,14,15,16,17,18]}. Additionally, the Cayley map of the quaternion group $Q_8$ constructed in [19, Figure 7] is a complete 4-partite map with arcs colored $i$, $j$, $k$; the map constructed has the property that removing the arcs colored $i$ creates an imprimitive map whose automorphism group action preserves the partition of the edges into those colored $j$ and those colored $k$. For more information about the embeddings of complete graphs, see ^[20,21,22].

The purpose of this paper is to enumerate the number of orientable vertex imprimitive maps with underlying graphs being complete graphs. Recall that $\phi(n)$ is the Euler phi-function, i.e. the number of positive integers which is less than and co-prime to $n$, where $n$ is a positive integer. The main result of this paper is now stated as follows.

Theorem 1.1. Let $\mathcal{M}$ be an orientable, vertex imprimitive, complete map with automorphism group $G = \mathit{\text{Aut}}(\mathcal{M})$, and let $G_\alpha$ be the stabilizer of a vertex $\alpha$ of $\mathcal{M}$. Then $\mathcal{M}$ is a Cayley map of ${\mathbb Z}^d_p$ for some integer $d\geq2$ and odd prime $p$. In addition, the group $G\cong{\mathbb Z}^d_p{:}G_\alpha$ is a Frobenius group whenever $G_\alpha$ is a cyclic group. Furthermore, if $G_\alpha\cong{\mathbb Z}_{p-1}$ acting on the neighborhood of $\alpha$ has $\lambda$ orbits with $\lambda(p-1) = p^d-1$ and $\lambda\geq4$ is a prime, then the number of non-isomorphic orientable vertex imprimitive complete maps equals

where $|\mathcal{A}_\lambda| = (\lambda-1)!(p-1)^{\lambda-1}\phi(p-1)$ and $|\mathcal{A}_1| = \phi(p^d-1).$

As a by-product of the Theorem 1.1, we can deduce the following conclusions when $\lambda$ is a composite integer.

Corollary 1.2. Let $p_1$ and $p_2$ be two different primes.

(i) If $\lambda = p_1p_2$, then the number of non-isomorphic orientable vertex imprimitive complete maps equals $\frac{|\mathcal{A}_{p_1p_2}|-|\mathcal{A}_{p_1}|-|\mathcal{A}_{p_2}|+|\mathcal{A}_1|}{|{{\sf SL}}(d, p)|}.$

(ii) If $\lambda = p_1^2p_2$, then the number of non-isomorphic orientable vertex imprimitive complete maps equals $\frac{|\mathcal{A}_{p_1^2p_2}|-|\mathcal{A}_{p_1p_2}|-|\mathcal{A}_{p_1^2}|+|\mathcal{A}_{p_1}|}{|{{\sf SL}}(d, p)|}.$

This paper is organized as follows. After this introductory section, some preliminary results are given in Section 2, then the enumeration of different and non-isomorphic orientable vertex imprimitive complete maps is given in Sections 3 and 4, respectively. Finally, we give the complete proof of Theorem 1.1 in Section 5.

2.   Preliminaries

In this section, we need some notations for convenience and give some results that will be used in the following discussion.

Let $p$ be an odd prime and let $d\geq2$ be an integer. The elementary abelian $p$-group of order $p^d$ will be denoted by $\text{Z}^d_p$. We use $o(a)$ and $\langle a\rangle$ to denote the order of $a$ and the group generated by $a$, respectively. We use $\text{Z}_{p-1}$ and $\text{D}_{2p}$ to denote the cyclic group of order $p-1$ and the dihedral group of order $2p$, respectively. The general linear group and the special linear group of the field ${\mathbb F}_{p^d}$ are denoted by $\text{GL}(d, p)$ and $\text{SL}(d, p)$, respectively. The centralizer and the normalizer of $\text{Z}_{p-1}$ in $\text{GL}(d, p)$ are denoted by $C_{{{\sf GL}}(d, p)}(\text{Z}_{p-1})$ and $N_{{{\sf GL}}(d, p)}(\text{Z}_{p-1})$, respectively. Let $H$ and $K$ be two groups. Then we use $H{:}K$ to denote a semi-direct product of $H$ by $K$, in which $H$ is a normal subgroup. We use $\text{Z}(H)$, $\text{Aut}(H)$, and $\text{Inn}(H)$ to denote the center, the automorphism group, and the inner automorphism group of $H$, respectively.

Let $F = {\mathbb F}_{p^d}$ be the field of order $p^d$. Let $F^+ = {\mathbb F}^+_{p^d}$ and $F^\times = {\mathbb F}^\times_{p^d}$ be the additive group and the multiplicative group of $F$, respectively. It follows that

Let $\textbf{0}$ be the identity of the $F^+$. Let $F^{\#}$ be the set of all nonidentity elements of $F^+$, namely, $F^{\#} = F^+\setminus\{\textbf{0}\}$. Then the complete graph ${{\sf K}}_{p^d}$ may be represented as a Cayley graph

A Cayley map $\mathcal{M}$ is an embedding of a Cayley graph $\Sigma = \text{Cay}(H, S)$ into a surface, such that $\text{Aut}(\mathcal{M})$ contains a subgroup $N$ acting regularly on the vertices and $\mathcal{M}$ is called a Cayley map of $N$ (or a Cayley embedding of $\Sigma$ with respect to $N$). Moreover, Cayley maps form a very interesting family of vertex-transitive maps ^[6,9].

For a vertex $v$, a cyclic permutation of the neighbour set ${{\it \Gamma}}(v)$ of $v$ is called a rotation at $v$ and denoted by $R_v$. A rotation system $R({{\it \Gamma}})$ of a graph ${{\it \Gamma}}$ is the set of rotations at all vertices, that is, $R({{\it \Gamma}}) = \{R_v\}_{v\in V}$. Hence, each rotation system $R({{\it \Gamma}})$ defines an orientable embedding of ${{\it \Gamma}}$, refer to [23, pp.104–108].

Noting that the vertex rotations $R_v$ can be regarded as permutations not only of the set ${{\it \Gamma}}(v)$ but also of the generating set $S$, the Cayley maps have another equivalent definition ^[24]. A map with an underlying graph being Cayley graph $\Sigma = \text{Cay}(H, S)$ is a Cayley map if the induced local cyclic permutations of $S$ are all the same. Moreover, each cyclic permutation $\rho$ of $F^{\#}$ gives rise to a unique orientable Cayley embedding of $\text{K}_{p^d}$ with the underlying graph $\Gamma = \text{Cay}(F^+, F^{\#})$. Thus, if two cyclic permutations $\rho_1$ and $\rho_2$ of $F^{\#}$ are different, then the orientable vertex imprimitive complete maps generated by them are also considered to be different.

3.   Enumeration of different embeddings

In this section, we determine enumeration of different vertex imprimitive embeddings of a complete graph. Now, we begin by citing the well-known conclusion about vertex transitive maps.

Lemma 3.1. ([8, Lemma 2.2]) Let $\mathcal{M}$ be a vertex-transitive map and let $G = \mathit{\text{Aut}}(\mathcal{M})$. Then the stabilizer $G_\alpha\cong {\mathbb Z}_k$ or ${{\sf D}}_{2k}$ for a vertex $\alpha$, and each orbit of $G_\alpha$ acting on the neighborhood of $\alpha$ has length $k$.

Next, from [8, Theorem 1.1] and [23, Lemma 5.4.1], we can directly obtain the following lemma.

Lemma 3.2. Let $\mathcal{M}$ be an orientable vertex imprimitive complete map. Let $G = \mathit{\text{Aut}}(\mathcal{M})$. Then $\mathcal{M}$ is a Cayley map of ${\mathbb Z}^d_p$, $G\cong{\mathbb Z}^d_p{:}{\mathbb Z}_k$ is a Frobenius group, and $G_\alpha\cong{\mathbb Z}_k$ such that $(k, p) = 1$.

Assume that $G_\alpha: = \langle a\rangle$ with $o(a)\geq2$. Then $G\cong F^+{:}\langle a\rangle$ is a Frobenius group by Lemma 3.2. It follows that $\langle a\rangle$ is half-transitive on $F^+$, and $|\langle a\rangle| = k$ is a divisor of $|F^+|-1 = p^d-1$. Specially, if $|\langle a\rangle| = p-1$, thus, $G_\alpha$ acting on $\Gamma(\alpha)$ has $\lambda$ orbits with $\lambda = (p^d-1)/(p-1)\geq4$, then we get the lemma as follows.

Lemma 3.3. If $G\cong F^+{:}{\mathbb Z}_{p-1}$, then there are exactly $(\lambda-1)!(p-1)^{\lambda-1}\phi(p-1)$ different orientable vertex imprimitive complete maps.

Proof. Taking $\alpha = \textbf{0}$ for convenience with $\textbf{0}$ the identity element of $F^+$. It follows that $G_\textbf{0}$ partitions the neighborhood $\Gamma(\textbf{0})$ of $\textbf{0}$ into $\lambda$ orbits with $\lambda\geq4$, and the length of each orbit is $p-1$ in view of Lemma 3.1. Since $F^{\#}$ is the set of all nonidentity elements of $F^+$, then $|F^{\#}| = p^d-1$, and, further, we have

where $\Delta_i$ is an orbit of $G_\textbf{0}$ acting on $\Gamma(\textbf{0})$, and $|\Delta_i| = p-1$ with $1\leq i\leq \lambda$.

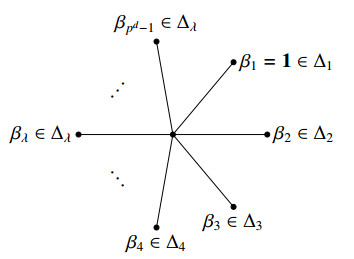
Note that the vertex $\textbf{0}$ and the neighbors can be lied on a disc such that $\textbf{0}$ is in the center and the neighbors of $\textbf{0}$ are around $\textbf{0}$. Without loss of generality, we may assume that the $p^d-1$ neighbors of $\textbf{0}$ (i.e. all the elements of $F^{\#}$) are in clockwise order around $\textbf{0}$ and denoted by $\beta_1, \beta_2, \cdots, \beta_{p^d-1}$, then

is a cyclic permutation of $F^{\#}$. Further, we can obtain that the number of the cyclic permutations of $F^{\#}$ equals the number of arrangements of $\beta_i$, and it follows that to determine the number of the orientable vertex imprimitive complete maps, we only need to determine the different choices of $\beta_i$ with $1\leq i\leq p^d-1$.

Set $\beta_1 = \textbf{1}$ and $\beta_1\in\Delta_1$ for convenience, where $\textbf{1}$ is the identity element of $F^\times$. If $\beta_2\in\Delta_1$, then $\textbf{1}^{a^l} = \beta_2$ for some $a^l$, where $0 < l\leq p-2$. It follows that $a^l: \beta_2\mapsto\beta_3\mapsto\beta_4\mapsto\cdots\mapsto\textbf{1}$. Thus, $(l, p-1) = 1$ and $G_\textbf{0} = \langle a^l\rangle$ acting on $\Gamma(\textbf{0})$ has only one orbit, which is a contradiction, so $\beta_2\not\in\Delta_1$ and $\beta_2\in\Delta_i$ with $2\leq i\leq \lambda$. Without loss of generality, set $\beta_2\in\Delta_2$ for convenience, then $\beta_2$ has $(\lambda-1)(p-1)$ different choices.

If $\beta_3\in\Delta_2$, then $\beta_2^{a^j} = \beta_3$ for some $a^j$, where $0 < j\leq p-2$. Furthermore, there is $a^j: \beta_2\mapsto\beta_3\mapsto\beta_4\mapsto\cdots\mapsto\textbf{1}$. It follows that $(j, p-1) = 1$, $\beta_1\in\Delta_2$ and $G_\textbf{0}$ acting on $\Gamma(\textbf{0})$ has only one orbit, which is a contradiction. Thus, $\beta_3\not\in\Delta_2$.

If $\beta_3\in\Delta_1$, then $\textbf{1}^{a^{j'}} = \beta_3$ for some $a^{j'}$, where $0 < j'\leq p-2$. It follows that there are $a^{j'}: \textbf{1}\mapsto\beta_3\mapsto\beta_5\mapsto\cdots\mapsto\textbf{1}$ and $a^{j'}: \beta_2\mapsto\beta_4\mapsto\beta_6\mapsto\cdots\mapsto\beta_2$. Thus, $G_\textbf{0} = \langle a^{j'}\rangle$ acting on $\Gamma(\textbf{0})$ has two orbits, which is a contradiction. It follows that $\beta_3\not\in\Delta_1$ and $\beta_3\in\Delta_i$ with $3\leq i\leq \lambda$. Without loss of generality, set $\beta_3\in\Delta_3$ for convenience, so $\beta_3$ has $(\lambda-2)(p-1)$ different choices.

If $\beta_4\in\Delta_3$, then $\beta_3^{a^t} = \beta_4$ for some $a^t$, where $0 < t\leq p-2$. Moreover, there has $a^t: \beta_3\mapsto\beta_4\mapsto\beta_5\mapsto\cdots\mapsto\textbf{1}$. Thus, $(t, p-1) = 1$, $\textbf{1}\in\Delta_3$ and $G_\textbf{0} = \langle a^t\rangle$ acting on $\Gamma(\textbf{0})$ has only one orbit, which is a contradiction. so $\beta_4\not\in\Delta_3$.

If $\beta_4\in\Delta_2$, then $\beta_2^{a^{t'}} = \beta_4$ for some $a^{t'}$, where $0 < t'\leq p-2$. It follows that there are $a^{t'}: \beta_2\mapsto\beta_4\mapsto\beta_6\mapsto\cdots\mapsto\beta_2$, and $a^{t'}: \beta_3\mapsto\beta_5\mapsto\beta_7\mapsto\cdots\mapsto\textbf{1}$. Thus, $G_\textbf{0} = \langle a^{t'}\rangle$ acting on $\Gamma(\textbf{0})$ has two orbits, which is a contradiction, so $\beta_4\not\in\Delta_2$.

If $\beta_4\in\Delta_1$, then $\textbf{1}^{a^{t''}} = \beta_4$ for some $a^{t''}$, where $0 < t''\leq p-2$. Further, there are $a^{t''}: \textbf{1}\mapsto\beta_4\mapsto\beta_7\mapsto\cdots\mapsto\textbf{1}$, $a^{t''}: \beta_2\mapsto\beta_5\mapsto\beta_8\mapsto\cdots\mapsto\beta_2$, and $a^{t''}: \beta_3\mapsto\beta_6\mapsto\beta_9\mapsto\cdots\mapsto\beta_3$. Thus, $G_\textbf{0} = \langle a^{t''}\rangle$ acting on $\Gamma(\textbf{0})$ has three orbits, which is a contradiction, so $\beta_4\not\in\Delta_1$ and $\beta_4\in\Delta_i$ with $4\leq i\leq \lambda$. Without loss of generality, set $\beta_4\in\Delta_4$ for convenience, and we deduce that $\beta_4$ has $(\lambda-3)(p-1)$ different choices.

If $\beta_5\in\Delta_4$, then $\beta_4^{a^k} = \beta_5$ for some $a^k$, where $0 < k\leq p-2$. It follows that there is $a^k: \beta_4\mapsto\beta_5\mapsto\beta_6\mapsto\cdots\mapsto\textbf{1}$. Thus, $(k, p-1) = 1$, $\textbf{1}\in\Delta_4$, and $G_\textbf{0} = \langle a^k\rangle$ acting on $\Gamma(\textbf{0})$ has only one orbit, which is a contradiction, so $\beta_5\not\in\Delta_4$.

If $\beta_5\in\Delta_3$, then $\beta_3^{a^{k'}} = \beta_5$ for some $a^{k'}$, where $0 < k'\leq p-2$. Correspondingly, there are $a^{k'}: \beta_2\mapsto\beta_4\mapsto\beta_6\mapsto\cdots\mapsto\beta_2$ and $a^{t'}: \textbf{1}\mapsto\beta_3\mapsto\beta_5\mapsto\cdots\mapsto\textbf{1}$. Thus, $G_\textbf{0} = \langle a^{k'}\rangle$ acting on $\Gamma(\textbf{0})$ has two orbits, which is a contradiction, so $\beta_5\not\in\Delta_3$.

If $\beta_5\in\Delta_2$, then $\beta_2^{a^{k''}} = \beta_5$ for some $a^{k''}$, where $0 < k''\leq p-2$. Further, there are $a^{k''}: \textbf{1}\mapsto\beta_4\mapsto\beta_7\mapsto\cdots\mapsto\textbf{1}$, $a^{k''}: \beta_2\mapsto\beta_5\mapsto\beta_8\mapsto\cdots\mapsto\beta_2$ and $a^{k''}: \beta_3\mapsto\beta_6\mapsto\beta_9\mapsto\cdots\mapsto\beta_3$. Thus, $G_\textbf{0} = \langle a^{k''}\rangle$ acting on $\Gamma(\textbf{0})$ has three orbits, which is a contradiction, so $\beta_5\not\in\Delta_2$.

If $\beta_5\in\Delta_1$, then $\textbf{1}^{a^{m}} = \beta_5$ for some $a^m$, where $0 < m\leq p-2$. It follows that there are $a^{m}: \textbf{1}\mapsto\beta_5\mapsto\beta_9\mapsto\cdots\mapsto\textbf{1}$, $a^{m}: \beta_2\mapsto\beta_6\mapsto\beta_{10}\mapsto\cdots\mapsto\beta_2$, $a^{m}: \beta_3\mapsto\beta_7\mapsto\beta_{11}\mapsto\cdots\mapsto\beta_3$, and $a^{m}: \beta_4\mapsto\beta_8\mapsto\beta_{12}\mapsto\cdots\mapsto\beta_4$. Thus, $G_\textbf{0} = \langle a^{m}\rangle = \langle a\rangle$ acting on $\Gamma(\textbf{0})$ has four orbits, namely, $\lambda = 4$. Since the number of generators of $G_\textbf{0}$ is $\phi(p-1)$, we obtain that $a^{m}$ has $\phi(p-1)$ different choices. Noting that $G_\textbf{0}$ is cyclic, besides $\textbf{1}$, $\beta_2$, $\beta_3$, and $\beta_4$, the remaining vertices of $\Delta_1$, $\Delta_2$, $\Delta_3$, and $\Delta_4$ can be obtained by $\textbf{1}$, $\beta_2$, $\beta_3$, and $\beta_4$ through the conjugate action of $a$, $a^2$, $a^3$, $\cdots$, $a^{p-2}$, respectively. So

is a cyclic permutation of $F^{\#}$. It follows that the number of $\rho$ is determined by the choices of $\textbf{1}$, $\beta_2$, $\beta_3$, $\beta_4$, and $a$. Further, the number of $\rho|_{\lambda = 4}$ equals

Let the corresponding maps generated by $\rho|_{\lambda = 4}$ be

Thus, the number of different orientable vertex imprimitive complete maps equals $3!(p-1)^3\phi(p-1)$ if $\lambda = 4$.

Next, suppose that $\lambda\geq6$ as $\lambda\neq5$. According to the above derivation, we can obtain that $\beta_5\not\in\Delta_i$ with $1\leq i\leq 4$, and $\beta_5\in\Delta_j$ with $5\leq j\leq \lambda$. Without loss of generality, set $\beta_5\in\Delta_5$ for convenience, and further, $\beta_5$ has $(\lambda-4)(p-1)$ different choices. Similarly, $\beta_6\in\Delta_i$ with $6\leq i\leq \lambda$. It follows that $\lambda = 6$ and $\beta_6$ has $(\lambda-5)(p-1)$ different choices. Note that $a$ has $\phi(p-1)$ different choices, then

is a cyclic permutation of $F^{\#}$. Thus, the number of $\rho|_{\lambda = 6}$ equals

Let the corresponding maps generated by $\rho|_{\lambda = 6}$ be

Thus the number of different orientable vertex imprimitive complete maps equals $5!(p-1)^5\phi(p-1)$ if $\lambda = 6$.

In fact, $\lambda$ can be generalized. If $G_\alpha = \langle a\rangle$ acting on $\Gamma(\alpha)$ has $\lambda$ orbits, then $\beta_i\in\Delta_i$ such that $\beta_1 = \textbf{1}$ and $1\leq i\leq \lambda$, and

is a cyclic permutation of $F^{\#}$ (see Figure 1). Since $\beta_i$ has $(\lambda-i+1)(p-1)$ different choices with $2\leq i\leq \lambda$, and $a$ has $\phi(p-1)$ different choices, it follows that the number of $\rho|_{\lambda}$ equals

Let the corresponding maps generated by $\rho|_{\lambda}$ be

Hence if $G_\alpha\cong {\mathbb Z}_{p-1}$, then there are exactly $(\lambda-1)!(p-1)^{\lambda-1}\phi(p-1)$ different orientable vertex imprimitive complete maps.

Remark. The proof of Lemma 3.3 provides a general construction for orientable vertex imprimitive embeddings of complete graphs.

Recall that a Cayley map ${\text{CayM}}(G, S)$ is called balanced if $s$ and $-s$ are placed on the antipodal points for all elements $s\in S$, see ^[7]. Let $\eta$ be the unique involution of $\text{GL}(1, p^d)$. Since the map $\mathcal{M}_\lambda$ is a Cayley map of the group $F^+$ by Lemma 3.2, then

is an automorphism of $\mathcal{M}_\lambda$.

Lemma 3.4. A map $\mathcal{M}_\lambda$ is balanced if and only if $\beta_i^{-1} = \beta_{i+\frac{p^d-1}{2}}$ with $1\leq i\leq \lambda$.

Proof. Assume that $\mathcal{M}_\lambda$ is balanced, then the vertex $\beta_i^{-1}$ is placed at the antipodal position of the vertex $\beta_i$ with $p$ as an odd prime and $1\leq i\leq \lambda$. Thus, $\beta_i^{-1} = \beta_{i+\frac{p^d-1}{2}}$.

Conversely, assume that $\beta_i^{-1} = \beta_{i+\frac{p^d-1}{2}}$, then for any $1\leq l\leq p-2$, we can obtain that

reading the subscripts modulo $(p^d-1)$. So, $\beta_j^{-1} = \beta_{\frac{p^d-1}{2}+j}$ is at the antipodal position of $\beta_j$ for all $j$ with $1\leq j\leq{p^d-1\over2}$, and, therefore, $\mathcal{M}_\lambda$ is balanced.

4.   Enumeration of non-isomorphic embeddings

We notice that many different orientable vertex imprimitive complete maps may be isomorphic. To determine the number of non-isomorphic complete maps, we prepare the following lemmas, and we first give the well-known Clifford's theorem.

Lemma 4.1. ([25, Theorem 5.9]) Let $V$ be an irreducible $FH$-module and let $N$ be a normal subgroup of $H$. Then the following statements are true:

(i) $V$ is a completely reducible $FN$-module, and

where $W_i(i = 1, 2, ..., r)$ are all non-isomorphic irreducible $FN$-submodules of $V$.

(ii) $H$ permutes $\{W^n_1, W^n_2, \cdots, W^n_r\}$ transitively.

(iii) If $K$ is the stabilizer of $H$ on $W^n_1$, then $H$ is irreducible on $W^n_1$.

According to Lemma 4.1, we can get the next following lemma which will determine the normalizer of ${\mathbb Z}_{p-1}$ in $\text{GL}(d, p)$.

Lemma 4.2. Let $G\cong {\mathbb Z}_p^d{:}{\mathbb Z}_{p-1}$. Then $N_{{{\sf GL}}(d, p)}({\mathbb Z}_{p-1})\cong \mathit{\text{GL}}(d, p)$ and $\mathit{\text{Aut}}(G)\cong{\mathbb Z}_p^d{:}\mathit{\text{GL}}(d, p)$.

Proof. Let $V = {\mathbb Z}_p^d$, namely, consider ${\mathbb Z}_p^d$ as a $d$-dimensional linear space over field $F_p$. By [26, Theorem 7.3 of Chapter 2], we can obtain that $\text{GL}(d, p)$ has a cyclic subgroup ${\mathbb Z}_{p^d-1}$. Since ${\mathbb Z}_{p-1}$ is a normal subgroup of ${\mathbb Z}_{p^d-1}$, and ${\mathbb Z}_{p-1}$ acting on ${\mathbb Z}_p^d$ is reducible, equivalently, $p-1$ is not a primitive divisor of $p^d$, then due to Lemma 4.1, we have

where $dim(V_i) = \frac{d}{2}$ and $V_i$ is a faithful irreducible $F_p{\mathbb Z}_{p-1}$-module with $i = 1, 2$. By [27, 27.14(3)], it follows that $C_{\text{GL}(d, p)}({\mathbb Z}_{p-1}) = \text{GL}(d, p)$. Since

it is easy to see that $N_{{{\sf GL}}(d, p)}({\mathbb Z}_{p-1})\cong \text{GL}(d, p)$. Furthermore, by [28, Lemma 4.5], we have

Two maps $\mathcal{M}_1$ and $\mathcal{M}_2$ are isomorphic if there is a one-to-one correspondence from the vertices of $\mathcal{M}_1$ to the vertices of $\mathcal{M}_2$ that maps flags to flags, and it is denoted by $\mathcal{M}_1\cong\mathcal{M}_2$. It follows that $\text{Aut}\mathcal{M}_1\cong\text{Aut}\mathcal{M}_2$ if $\mathcal{M}_1\cong\mathcal{M}_2$. A complete map is a complete Cayley map if its automorphism group is regular on the vertices. Moreover, the complete Cayley maps of non-isomorphic groups are not isomorphic, and we have the following lemma.

Lemma 4.3. $\mathcal{M}^\sigma_\lambda\cong\mathcal{M}_\lambda$ for each $\sigma\in \mathit{\text{Aut}}(G)$. On the contrary, $\sigma\in \mathit{\text{Aut}}(G)$ if $\mathcal{M}^\sigma_\lambda\cong\mathcal{M}_\lambda$.

Proof. Since $G = \text{Aut}(\mathcal{M}_\lambda)\cong {\mathbb Z}_p^d{:}{\mathbb Z}_{p-1}$, then $G_\alpha\cong{\mathbb Z}_{p-1}$ is a cyclic group for any $\alpha\in V$. Suppose that $\sigma$ fixes $\alpha$ for each $\sigma\in\text{Aut}(G)\cong{\mathbb Z}_p^d{:}\text{GL}(d, p)$. Note that ${\mathbb Z}_p^d$ is a regular and normal subgroup of $\text{Aut}(G)$, then for any $1\neq x\in {\mathbb Z}_p^d$, we have $\alpha^x = \alpha x$ or $x^{-1}\alpha$ if $x$ is the right or left multiplication, respectively. Thus, $\alpha^x\neq\alpha$, namely, $x$ does not fix $\alpha$. Hence, $\sigma\in \text{GL}(d, p)$. It follows that ${\mathbb Z}_{p-1}^\sigma\cong{\mathbb Z}_{p-1}$ since ${\mathbb Z}_{p-1}\lhd \text{GL}(d, p)$. Note that for each $\tau\in\text{Aut}(G)$,

such that $\tau = x\sigma$, where $x\in {\mathbb Z}_p^d$ and $\sigma\in \text{GL}(d, p)$. Moreover, we can obtain $\mathcal{M}^\sigma_\lambda\cong\mathcal{M}_\lambda$ for each $\sigma\in \text{Aut(G)}$ by arbitrariness of $x$.

On the contrary, if $\mathcal{M}^\sigma_\lambda\cong\mathcal{M}_\lambda$, then $\text{Aut}(\mathcal{M}^\sigma_\lambda)\cong\text{Aut}(\mathcal{M}_\lambda) = G$. It follows that for each $\sigma\in\text{Aut}(\mathcal{M}_\lambda)$,

Since $G$ is a Frobenius group, it is easy to see that the center $\text{Z}(G) = 1$, then $G\cong G/\text{Z}(G)\cong \text{Inn}(G)\lhd \text{Aut}(G)$. Hence, $\sigma\in \text{Aut}(G)$.

Now, we determine the number of non-isomorphic orientable vertex imprimitive complete maps if $G_\alpha\cong{\mathbb Z}_{p-1}$.

Let

Then $\mathcal{A}_\lambda$ is a finite nonempty set and $|\mathcal{A}_\lambda| = (\lambda-1)!(p-1)^{\lambda-1}\phi(p-1)$. Let $X = \text{Aut}(G)$. Thus, by Lemma 4.2, we have

Note that ${\mathbb Z}_p^d\lhd X$ and ${\mathbb Z}_p^d$ acts on $V$ regularly, and, thus, by [29, Exercise 1.4.1], we have $X_\alpha\cong\text{GL}(d, p)$, $G\lhd X$, and $G_\alpha\lhd X_\alpha$. Further, by [26, Theorem 7.3 of Chapter 2], we can obtain that $\text{GL}(d, p)$ has a cyclic subgroup ${\mathbb Z}_{p^d-1}$ and, for convenience, $\langle z\rangle: = {\mathbb Z}_{p^d-1}$.

Lemma 4.4. If $G\cong F^+{:}{\mathbb Z}_{p-1}$ and $\lambda$ is a prime, then there are $\frac{(\lambda-1)!(p-1)^{\lambda-1}\phi(p-1)-\phi(p^d-1)}{|{{\sf SL}}(d, p)|}$ non-isomorphic orientable vertex imprimitive complete maps.

Proof. Since $o(a) = p-1 = \frac{p^d-1}{\lambda}$, it follows that $z^\lambda = a$. Let

be a cyclic permutation of $F^{\#}$ such that $\beta_i = \textbf{1}^{z^i}$ and $2\leq i < \lambda$.

Thus, we have

That is, $z^i$ can be identified with the permutation

Thus, $G_\alpha = \langle z^i\rangle$ and $a = z^\lambda\in\langle z^i\rangle$. Further, $i|\lambda$, which is a contradiction, as $\lambda$ is a prime.

Let $(\textbf{1}, \beta_2, \beta_3, \cdots, \beta_\lambda, \textbf{1}^a, \beta_2^a, \beta_3^a, \cdots, \beta_\lambda^a, \cdots, \textbf{1}^{a^{p-2}}, \beta_2^{a^{p-2}}, \beta_3^{a^{p-2}}, \cdots, \beta_\lambda^{a^{p-2}})$ be a cyclic permutation of $F^{\#}$ such that $\beta_2 = \textbf{1}^z$, and it gives rise to a unique orientable complete map $\mathcal{M}_1$. We have

namely, $z$ can be identified with the permutation

It follows that $\text{Aut}(\mathcal{M}_1) = F^+{:}\langle z\rangle = G.\lambda > G$ and $\mathcal{M}_1$ is arc transitive. Thus, $\mathcal{M}_1\in\mathcal{A}_1$, $\mathcal{A}_1\subset\mathcal{A}_\lambda$ and

So, $X\setminus G$ contains no element, which is an automorphism of $\mathcal{M}'_\lambda$ for $\mathcal{M}'_\lambda\in\mathcal{A}_\lambda\setminus\mathcal{A}_1$. Since $G\lhd X$ and

then we have that $X/G$ acting on $\mathcal{A}_\lambda\setminus\mathcal{A}_1$ is semi-regular.

Let $X$ act on $\mathcal{A}_\lambda\setminus\mathcal{A}_1$. It follows that $(\mathcal{M}'_\lambda)^X$ is an orbit of this action, and the length of this orbit equals

Thus, by Lemma 4.3, there are

non-isomorphic orientable vertex imprimitive complete maps.

Below, we give an example to show existence of the orientable vertex imprimitive complete maps.

Example 4.5. Let $\mathcal{M}$ be a Cayley map of ${\mathbb Z}^3_3$ with $p = 3$ and $d = 3$. Then $G\cong{\mathbb Z}_3^3{:}{\mathbb Z}_2$ is a Frobenius group and $G_\alpha\cong{\mathbb Z}_2$ acting on ${\mathbb Z}_3^3$ is half-transitive. Since $2$ is not a primitive divisor of $3^3-1$, it follows that $\mathcal{M}$ is an orientable vertex imprimitive embedding of $\text{K}_{27}$, and $G_\alpha$ acting on $\Gamma(\alpha)$ has $\lambda = 13$ orbits. Furthermore, by Lemma 4.4, we can obtain that there are $\frac{|\mathcal{A}_{13}|-|\mathcal{A}_1|}{|\text{SL}(3, 3)|}$ non-isomorphic such maps.

Next, we can obtain the following results by the proof of Lemma 4.4.

Corollary 4.6. If $\lambda = p_1p_2$ with $p_i$ different primes and $i = 1, 2$, then the number of non-isomorphic orientable vertex imprimitive complete maps equals

Corollary 4.7. If $\lambda = p_1^2p_2$ with $p_i$ different primes and $i = 1, 2$, then the number of non-isomorphic orientable vertex imprimitive complete maps equals

It is an open problem to generalize the above corollaries for the general case in which $\lambda = p_1^{l_1}p_2^{l_2}\cdots p_t^{l_t}$, where $p_i(1\leq i\leq t)$ are pairwise different primes and $l_i\geq1$ are arbitrary positive integers.

5.   Proof of the main results

In this section, we complete the proof of Theorem 1.1 in view of the above series of results.

Proof of Theorem 1.1. Let $\mathcal{M} = (V, E, F)$ be an orientable vertex imprimitive complete map. Let $G = \text{Aut}(\mathcal{M})$. By Lemma 3.2, we have that $\mathcal{M}$ is a Cayley map of ${\mathbb Z}_p^d$ and $G\cong{\mathbb Z}^d_p{:}G_\alpha$ is a Frobenius group, where $G_\alpha$ is a cyclic group for each $\alpha\in V$, $p$ is an odd prime, and $d\geq2$. Further, if $G_\alpha\cong{\mathbb Z}_{p-1}$ acting on the neighborhood of $\alpha$ has $\lambda$ orbits with $\lambda(p-1) = p^d-1$ and $\lambda\geq4$ is a prime, then by Lemma 3.3 and Lemma 4.4, there are exactly

non-isomorphic orientable vertex imprimitive complete maps.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The work on this paper was in part done when the author visited South University of Science and Technology. The author is very thankful for Professor Cai Heng Li. Also, the author would like to thank the anonymous reviewers for their valuable comments and suggestions. This work was supported by the NSFC(11861076), the Natural Science Foundation of Henan Province(232300420357).

Conflict of interest

The author declare there is no conflict of interest.