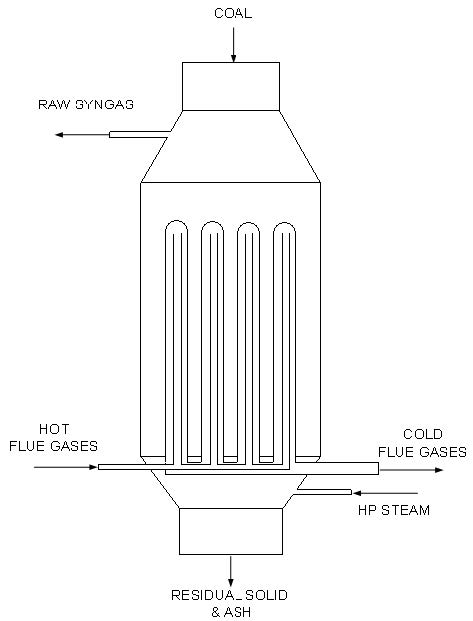
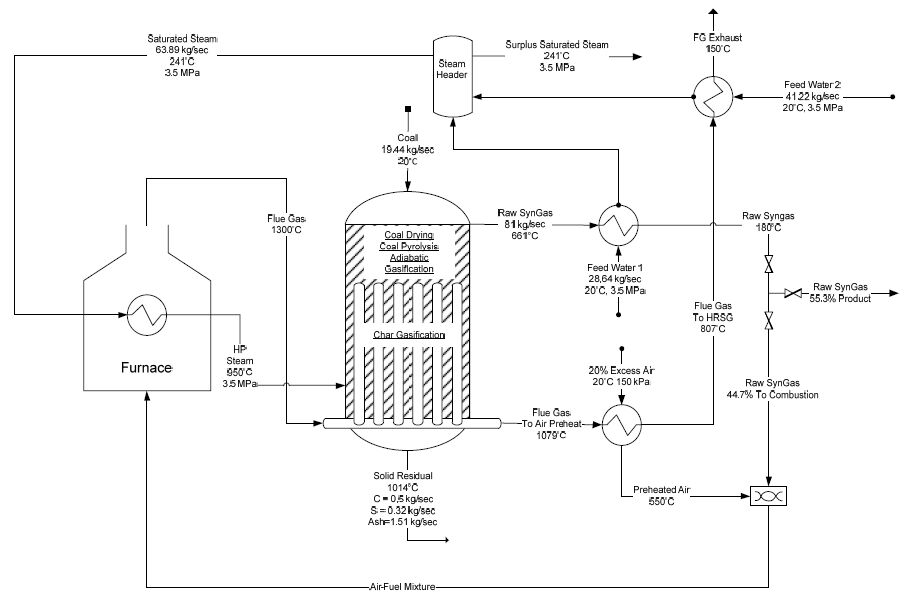
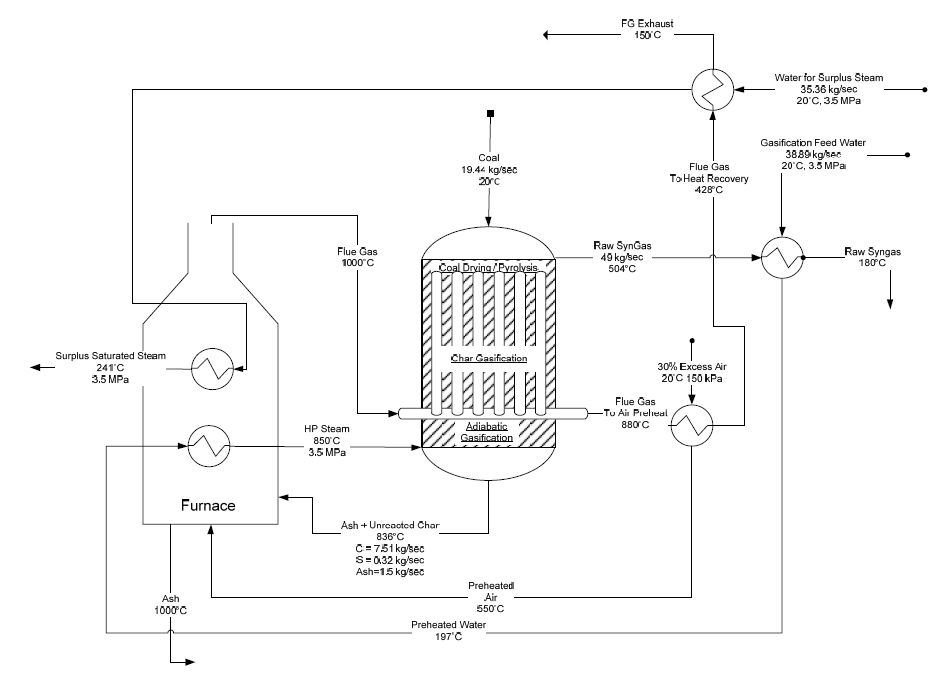
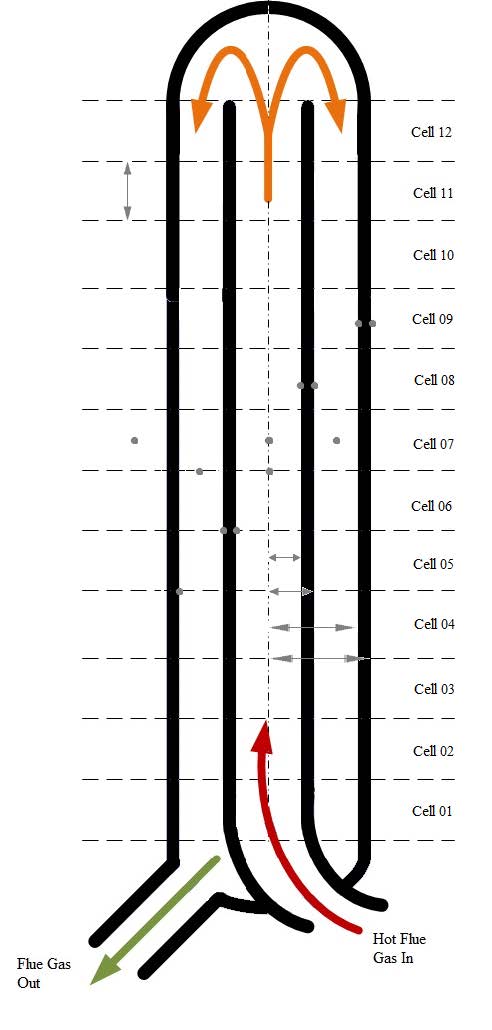
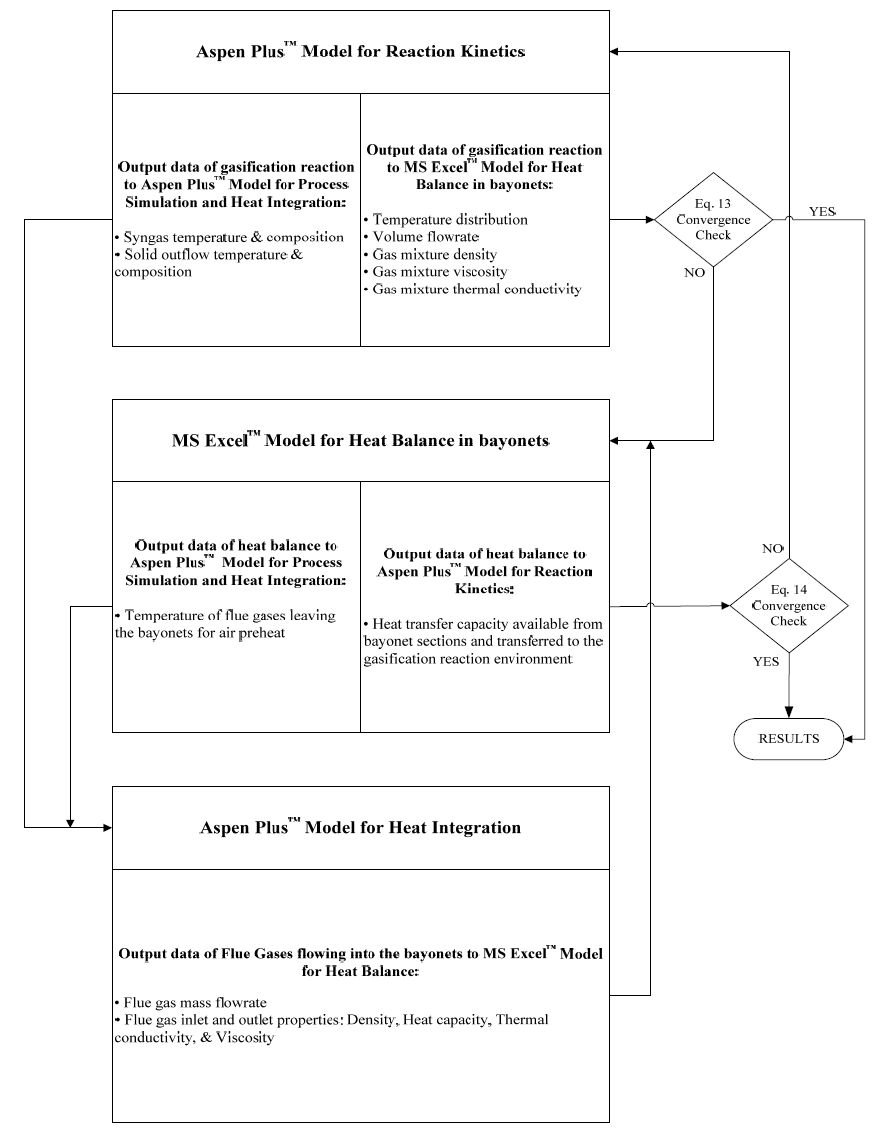
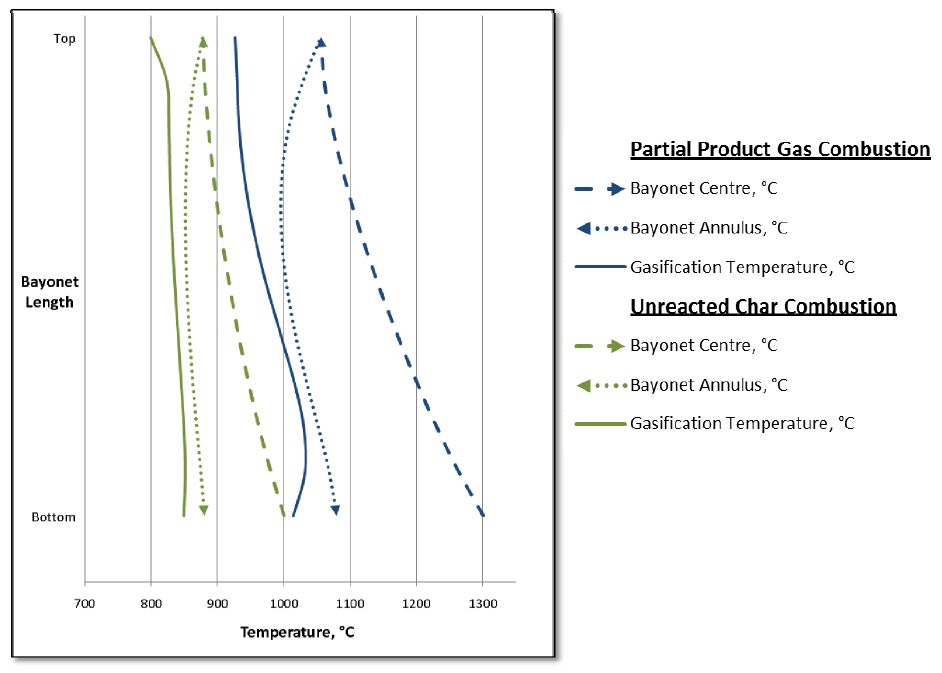
In this work, the development and simulation of a new coal gasification process with indirect heat supply is performed. In this way, the need of pure oxygen production as in a conventional gasification process is avoided. The feasibility and energetic self-sufficiency of the proposed processes are addressed. To avoid the need of Air Separation Unit, the heat required by gasification reactions is supplied by the combustion flue gases, and transferred to the reacting mixture through a bayonet heat exchanger installed inside the gasifier. Two alternatives for the flue gas generation have been investigated and compared. The proposed processes are modeled using chemical kinetics validated on experimental gasification data by means of a standard process simulator (Aspen PlusTM), integrated with a spreadsheet for the modeling of a special type of heat exchanger. Simulation results are presented and discussed for proposed integrated process schemes. It is shown that they do not need external energy supply and ensure overall efficiencies comparable to conventional processes while producing syngas with lower content of carbon dioxide.
1.
Introduction
Consider the following singularly perturbed Fredholm integro-differential equation (SPFIDE) in the interval $ \bar{I} = [0, T] $:
where $ 0 < \varepsilon \ll 1 $ is a perturbation parameter, $ A $ is a given constant and $ \lambda $ is a real parameter. We assume that $ f\left (t, u \right)\in C^1\left(\bar{I}\times R\right) $, $ K\left (t, s, u \right)\in C^1\left(\bar{I}\times\bar{I}\times R\right) $ and there exist constants $ \alpha $, $ \beta $ such that $ 0 < \alpha\le\left | \partial f/\partial u \right | $, $ \left | \partial K/\partial u \right |\leq \beta $. Under these assumptions, the problem (1.1) has a unique solution (see [1]).
It is well known that the SPFIDEs arise widely in scientific fields such as mathematical biology [2], material mechanics [3], hydrodynamic [4] and so on.These problems depend on such a small positive parameter $ \varepsilon $ that the solution varies rapidly when $ \varepsilon \rightarrow 0 $. Due to the presence of this perturbation parameter $ \varepsilon $, classical numerical methods on a uniform mesh fail to give accurate results. Therefore, it is necessary to develop suitable numerical methods that are $ \varepsilon $-uniformly convergent for solving these problems.
Over the past few years, there has been a growing interest in the numerical methods for Volterra integro-differential equations (see, e.g., [5,6,7,8,9,10]) and Fredholm integro-differential equations (see, e.g., [11,12]). When the differential term of these integro-differential equations contains a small positive perturbation parameter $ \varepsilon $, these problems are called singularly perturbed integro-differential equations. Recently, some robust numerical methods are proposed to solve singularly perturbed Volterra integro-differential equations[13,14,15,16]. Meanwhile, the authors in [17,18] developed fitted finite difference schemes on a uniform mesh for second-order SPFIDEs and gave some convergence results based on the prior information of the exact solution. Durmaz, et.al., [19] proposed a second-order uniformly convergent finite difference scheme on a Shishkin mesh for a singularly perturbed Fredholm integro-differential equation with the reduced second type Fredholm equation. In [20], the authors presented a fitted finite difference approach on a Shishkin mesh for a first-order singularly perturbed Fredholm integro-differential initial value problem with integral condition. Kumar et al. [21] proposed a non-standard finite difference scheme with Haar wavelet basis functions for a singularly perturbed partial integro-differential equation. Recently, Cakir et al., [22] solved first-order nonlinear SPFIDEs on a Sinshkin mesh with first-order convergence rate.
From the literatures we have mentioned above, the existing numerical methods of SPFIDEs given in [19,20,21] are layer-adapted mesh approaches, which require a priori information about the location and width of the boundary layer. Thus, adaptive grid methods by equidistributing monitor functions are widely used to solve some singularly perturbed problems, see [25,26,27,28,29] for example. The advantages of these adaptive grid methods is to cluster automatically the grid points within the boundary layer. To the best of our knowledge, there is no report about this adaptive grid method for problem (1.1). Therefore, the aim of this paper is to solve problem (1.1) numerically by a finite difference scheme on an adaptive grid obtained by equidistributing a positive monitor function. The discrete scheme is constructed by using the backward Euler formula and right rectangle formula to approximate derivative term and nonlinear integral term, respectively. It is proved under some additional conditions that the proposed adaptive grid method is first-order uniformly convergent, with respect to $ \varepsilon $.
The rest of this paper is as follows. In Section 2, preliminary results of the exact solution are laid out. A discretization scheme is established in Section 3, in which a prior error analysis and a posterior error estimate are carried out successively. Numerical results obtained by the adaptive gird algorithm are given in Section 4 to support the theoretical analyses. The paper ends with a summary of the main conclusions in Section 5.
Notation Throughout this paper, $ C $ which is not necessarily the same at each occurrence, indicates a positive constant independent of the mesh division parameter $ N $ or the singular perturbation parameter $ \varepsilon $. To simplify the notation, we set $ v_{k} = v\left (t_{k} \right) $ for any function $ v(t) $. In our estimates, the maximum norm of a continuous function $ v(t) $ with the domain $ [0, T] $ is defined as $ \left \| v\left (t \right) \right \|_{\infty} = \mathrm{ess} \underset{t\in \left [0, T \right]}{\sup} \left | v\left (t \right) \right | $ as well as the maximum norm of a discrete vector $ \mathit{\boldsymbol{x}} = \left \{ x_i \right \}_{i = 0}^{N} $ with $ N+1 $ elements is defined as $ \left \| \mathit{\boldsymbol{x}} \right \|_{\infty} = \underset{i = 0, 1, 2, \cdots, N}{\max }\left | x_{i} \right | $.
2.
Preliminary results
In this section, we list the bounds for the exact solution $ u\left(t\right) $ and its first-order derivative.
Lemma 2.1. [22, Lemma 1] Assume the constant $ \lambda $ satisfies
Then we have
where
Corollary 2.1. For any two functions $ v\left(t\right) $ and $ w\left(t\right) $ satisfying
and
where $ \tilde{F}(t) $ is a bounded piece-wise continuous function, we have
Proof. The proof is similar to [15, Corollary 2.1].
3.
Discretization and error analysis
3.1. Discrete scheme
Let $ \bar{\Omega } _{N}: = \left\{0 = t_{0} < t_{1} < \dots < t_{N} = T \right\} $ be an arbitrary non-uniform mesh and $ h_{i} = t_{i}-t_{i-1} $ be the local mesh size for $ i = 1, 2, \cdots, N $. For a given mesh function $ \left \{ v_{i} \right \} _{i = 0}^{N} $, define the backward finite difference operator as follows:
Then to construct the discretization scheme for problem (1.1), we integrate Eq (1.1) over $ \left(t_{i-1}, t_i \right) $ and use the right rectangle rule to approximate the integral part, which yield,
where
and
Neglecting the truncation error $ R_i $ in Eq (3.2), we obtain the discretization scheme of problem (1.1)
where $ u_i^N $ is the approximation of $ u(t) $ at point $ t = t_i $.
3.2. A prior error analysis
Let $ e_i^N: = u_i^N-u_i $, $ i = 0, 1, \cdots, N $, be the absolute error at $ t_i $ of the numerical solution. Then we can obtain the following error equations
where $ R_i $ is the local truncation error defined in Eq (3.3) at $ t_i $.
Lemma 3.1. For $ i = 1, 2, \cdots, N $, the truncation error $ R_i $ defined in Eq (3.3) satisfies
Proof. At first, based on the conditions $ f\left(t, u\right)\in C^1(\bar{I}\times R) $ and $ 0 < \alpha\le\left | \partial f/\partial u \right | $, we obtain
Then, since $ K\left(t, s, u\right)\in C^1\left(\bar{I}\times\bar{I}\times R\right) $ and $ \left | \partial K /\partial u \right | \le \beta $, we have
and
Finally, the desired result of this lemma can be followed by Eqs (3.7), (3.8) and (3.9).
Lemma 3.2. Under the assumption
we have
where $ \mathit{\boldsymbol{e}}^N = \left \{ e_i^N \right \} _{i = 0}^{N} $, $ \mathit{\boldsymbol{R}} = \left \{ R_i \right \} _{i = 0}^{N} $ and $ G_{ij} = \frac{\partial }{\partial u}K\left(t_i, s_j, u_j+\zeta e_j^N\right), \ 0 < \zeta < 1 $.
Proof. Applying the mean value theorem to Eq (3.5), we get
where
According to maximum principle for the operator $ \varepsilon D^-e_i^N+a_ie_i^N $, we have
which immediately leads to the desired result with the assumption (3.10).
Based on the above Lemmas 3.1–3.2, we get the following convergence results.
Theorem 3.1. Let $ u(t) $ be the solution of problem (1.1) and $ u_i^N $ be the solution of discrete scheme (3.4). Then
Corollary 3.1. Under the conditions of Theorem 3.1, there exists an adaptive grid $ \left \{ t_i \right \} _{i = 0}^{N} $ such that
Proof. Based on the mesh equidistribution principle presented in [29], the mesh $ \left \{ t_i \right \}_{i = 0}^{N} $ given by our adaptive grid algorithm satisfies
where $ M(t) $ is called the monitor function, which can be chosen as
Therefore, it follows from Lemma 2.1 that
3.3. A posteriori error analysis
In this section, we shall derive an a posteriori error estimation for the numerical solution $ \left \{ u_i^N \right \} _{i = 0}^{N} $. Recall that $ \tilde{u}^N\left(t\right) $ is a piece-wise linear interpolation function through knots $ \left(t_i, u_i^N\right), \ i = 0, 1, \cdots, N $. Then, for any $ t\in J_i: = \left [t_{i-1}, t_i \right] $, we obtain
Theorem 3.2. Let $ u(t) $ be the exact solution of problem (1.1), $ \left \{ u_i^N \right \} _{i = 0}^{N} $ be the discrete solution of problem (3.4) and $ \tilde{u}^N(t) $ be its piece-wise linear interpolation function defined in Eq (3.21). Then we have
Proof. For any $ t\in\left (t_{i-1}, t_i \right] $, it follows from Eq (1.1) and Eq (3.4) that
where
With the assumptions of functions $ f\left(t, u\right) $, $ K\left(t, s, u\right) $ and the definition of $ \tilde{u}^N\left(t\right) $, we have
and
where $ 0 < \xi_1 < 1 $, $ 0 < \xi_2 < 1 $, and $ 0 < \xi_3 < 1 $. The result can be derived from Eqs (3.23), (3.26), (3.27) and Corollary 2.1.
From Corollary 3.1, it is easy to conclude that there exists a mesh $ \left \{ t_i \right \}_{i = 0}^{N} $ and a monitor function $ M\left(t\right) $ given in Eq (3.19) such that the inequality (3.17) holds true. However, $ {u}'\left(t\right) $ is not available. Therefore, based on the a posterior error estimation (3.22), we choose the discrete analogue of $ M\left(t\right) $ as
Therefore, the idea is to adaptively design a mesh in which the values of monitor function $ tilde{M}_i $ are the same on each mesh interval. This is equivalent to find $ \left \{ \left(t_i, u_i^N\right) \right \}_{i = 0}^{N} $, such that
Furthermore, to obtain this equidistributed mesh $ \left\{t_i\right\}_{i = 0}^N $ and the corresponding numerical solution $ u_i^N $, we give the following iteration algorithm:
4.
Numerical experiments and discussion
In Section 4.1, We first present the iterative scheme. Then numerical experiments are given in Section 4.2 to validate the theoretical result of this paper. All experiments were performed on a Windows 10 (64 bit) PC-Intel(R) Core(TM) i5-4200H CPU 2.80 GHz, 8 GB of RAM using MATLAB R2021a.
4.1. Iterative scheme
In order to avoid solving the nonlinear equations (3.4), we apply the quasilinearization technique that performs a first-order Taylor expansion on the last iteration values and obtain
where
4.2. Numerical examples
For all the numerical experiments below, we choose $ \mu^* = 1.1 $, which is defined in Step 4 in Algorithm 1.
Example 4.1. We consider a SPFIDE in the form [22]
Since the analytic solution of this problem is not available, we use the following formulas to calculate the errors and the corresponding convergence rates:
where $ \hat{\mathit{\boldsymbol{u}}}^{2N} $ is the numerical solution obtained on the fine mesh $ \bar{\Omega } _{2N} = \bar{\Omega } _{N}\bigcup \left\{\frac{t_{i}+t_{i+1}}{2}\right\}_{i = 0}^{N-1} $. The maximum errors and $ \varepsilon $-uniform rates of the convergence are respectively defined as
In the numerical experiments, we apply the presented adaptive grid algorithm to solve this problem. The resulting errors $ e_{\varepsilon }^N $ and the orders of the convergence $ p_{\varepsilon }^N $, for particular values of $ \varepsilon $ and $ N $ are listed in Table 1. In addition, to compare the performance of the presented adaptive mesh with the Shishkin mesh [22] and the Bakhvalov mesh [23], some numerical results are given in Table 2.
According to the results in Table 1, for fixed $ N $, the error increases with a diminishing speed and the convergence rate goes away from 1 as $ \varepsilon $ decreases, while for fixed $ \varepsilon $, the error deceases to half as $ N $ doubles and the convergence rate is getting closer to 1. According to the results in Table 2, our adaptive mesh demonstrates both less error and more accurate first-order convergence rate than Shishkin mesh. In general, the performance of our adaptive grid algorithm is better when $ \mu^* $ which is used to distribute the grid uniformly is closer to 1. However, the enhance becomes very limited after certain threshold and it can not work out successfully when $ \mu^* $ is so close to 1 due to the enormous amount of calculations. Here the limitation of the adaptive mesh lies.
The behaviors of the numerical solution are presented in Figures 1, 2. Obviously, it can be seen that in these two figures the solution of the test problem decreases successively near to 0 at first and increases progressively close to 1 then and has a boundary layer at $ t = 0 $. Figure 3 shows the $ \varepsilon $-uniform convergence of the method with different $ \varepsilon $. To be more physical, the first-order uniform convergence stands for our method in spite of violent changes of the numerical solution in the bound layer at $ t = 0 $. From Figure 3, no matter how close $ \varepsilon $ tends to zero, the maximum point-wise errors are bounded by $ O\left(N^{-1}\right) $ which validates our theoretical analyses. For $ \varepsilon = 2^{-8} $, Figure 4 displays how a mesh with $ N = 64 $ evolves through successive iterations of the algorithm by using monitor function (3.28).
Example 4.2. We consider a first-order nonlinear singularly perturbed mixed type integro-differential equation in [24] in the form:
where
It is testified that it satisfies the assumption (3.10). The analytic solution of this problem is $ u\left(t\right) = e^{-t/\varepsilon} $. We use the following formulas to calculate the errors and the corresponding convergence rates:
The maximum errors and $ \varepsilon $-uniform convergence rates are defined in Eq (4.6).
The resulting errors $ e_{\varepsilon }^N $ and the orders of the convergence $ p_{\varepsilon }^N $, for particular values of $ \varepsilon $ and $ N $ are listed in Table 3. In addition, to compare the performance of the presented adaptive mesh with the Shishkin mesh [22] and the Bakhvalov mesh [23], some numerical results are given in Table 4.
The behaviors of the numerical solution are presented in Figures 5, 6. Obviously, it can be seen that in these two figures the solution of the test problem gradually decreases to zero with a decreasing velocity rate as well as has a boundary layer at $ t = 0 $. Figure 7 shows the $ \varepsilon $-uniform convergence of the method with different $ \varepsilon $. From Figure 7, no matter how close $ \varepsilon $ tends to zero, the maximum point-wise errors are bounded by $ O\left(N^{-1}\right) $ which validates our theoretical analyses. For $ \varepsilon = 2^{-8} $, Figure 8 displays how a mesh with $ N = 64 $ evolves through successive iterations of the algorithm by using monitor function (3.28).
The unique but significant difference between these two examples can be found in Table 4. At the situation $ \varepsilon = 2^{-8} $, adaptive mesh demonstrates better than Bakhvalov mesh. This is because the construction of the Bakhvalov mesh is based on prior information of the exact solution. Therefore the effect of this method is tightly relevant to the form of equation. The existing Bakhvalov mesh may display wonderful at suitable equations but poor when it is adverse. However, the adaptive mesh based on posterior error estimate requires none of prior information of the exact solution and displays steadily at various equations.
5.
Concluding remarks
This paper considers a nonlinear singularly perturbed Fredholm integro-differential equation for a first-order initial value problem. A first-order $ \varepsilon $-uniformly convergent numerical method for solving this problem is presented, which comprises an adaptive grid based on the posterior error estimate and the mesh equidistribution principle. The difference scheme including the weights and the remainders is established using the backward Euler formula for the derivative term, together with the composite right rectangle quadrature rule for the integral term. A theoretical analysis based on prior error bound is conducted to prove the first-order convergence of the proposed method. Two examples show that our adaptive mesh demonstrates better than Shishkin mesh and performs as well as Bakhvalov mesh. In the future, we will try to extend the proposed adaptive grid method for solving other related integro-differential equations which can be found in [5,6,31].
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad: