LSTM-SAC reinforcement learning based resilient energy trading for networked microgrid system

1.   Introduction

Renewable Energy (RE) is vital to building a resilient and secure future energy system. The penetration of distributed energy resources (DER) into the entire power system facilitates the liberalization of electricity markets, the availability of standby capacity for peak demand, the enhancement in reliability and power quality, the augmentation of the local electricity network, the support to the existing grid, the combined generation of electricity and heat, the efficient use of low-priced fuel, etc. ^[1]. Now, one question that arises is, "What should be the business and technology platforms that can manage the variability of a generation of DER, diversity, and complexity in the transfer of electricity to end-users?" ^[2]. New technologies, which are also to be developed, should have capabilities to interface the augmented power system infrastructure with power market stakeholders. System operators and other entities who deal with electricity markets should possess the controllability and visibility of different DERs; moreover, there should be requisite interfacing between these system components to achieve optimized monitoring and control operations ^[3]. New acceptable business models need to be created along with an expansion in power system elements due to trading entities as per the repercussion of the enhancement in investment in DER, wholesale electricity market, demand response programs, energy storages, and plug-in-electric vehicles (PEVs) technologies. Consumers are gaining a prime importance in whole power system developments due to the following objectives: a) to estimate and predict the proportion of customer participation in demand reduction; b) to identify the localized demand response and its impact on a utilities' distribution system; c) to include the demand response and distributed energy resources into the utilities' action plan; and d) to identify the effect of the reduction of load on the utilities' procurement plan ^[4,5].

There must be some ways to utilize demand reduction by consumers during peak and non-peak hours. The possibilities are to be examined such that a DER and a combination of DER at the local level not affecting that does not affect the power grid can have the generation capacity to cater to the consumers' demand, at most, during peak hours, and to identify whether the production capacity of DER is surplus during peak hours and non-peak hours ^[6]. It is a challenging task to sum up the surplus power generation of different DERs that posses the stochastic generation capacity. It is not clear whether and by which ways it is possible to utilize the aggregated power available from dispersedly interconnected DER and demand reduction of numerous heterogeneous loads and then postpone new power system infrastructure developments with an uprise of the power demand. The aggregated power from DERs should be available for sale in electricity markets with many bids/offers ^[7].

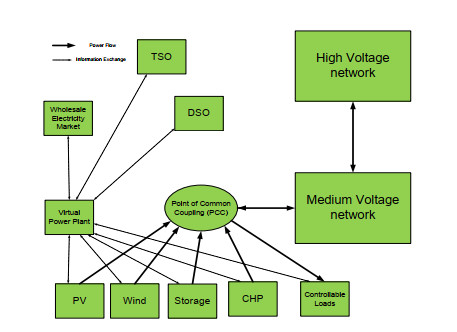
In the cyber-physical system of microgrids, distributed control schemes are found to be better in solving economic dispatch problems compared to central control schemes because distributed control schemes are robust, easily scalable, and possess a lower cost of implementation. Though distributed control schemes show advantages over central control schemes, these are prone to cyber-attacks. Therefore, to mitigate the effects of cyber-attacks, an attack-robust distributed economic dispatch strategy is designed. In a transactive energy framework, microgrid (MG) aims to schedule an optimal hourly strategy in the day-ahead market to maximize profits. Next, MGs try to minimize the imbalance of cost in the real-time market. The installation of a microgrid provides a lucrative solution to dependency on the supply of power from the main grid and obtains economic benefits from locally generated power ^[8]. The basic architecture of the microgrid is shown in Figure 1.

Attack-resilient intelligent power management has been developed such that the efficient operation of an emergency power system in the presence of a cyber-attack can be ensured. An adaptive neuro-fuzzy inference system (ANFIS) based methodology can validate the integrity of critical data about an energy management system and is capable of detecting the occurrence of cyber-attacks ^[9]. The various energy management systems (EMS) available in the literature have pros and cons based on the minimum operating cost, customer privacy, flexibility, computation power reduction, reliability, and resiliency. In islanded mode, a microgrid operates independently; hence, there is a possibility that the microgrid may become less tolerant to faults and its resiliency gets affected.

A mechanism has to be developed to improve the resiliency of the independent microgrid ^[10]. By promoting the dispersion of power resources, the resiliency of the microgrid can be improved ^[11]. The feasibility of the resilient operation is to be analyzed with three actions unit commitments, energy storage schedules, load curtailment, and adjustable load schedules. The resiliency-oriented optimal scheduling model for the microgrid was developed in ^[12]. A mechanism must be developed to ensure the economically optimal operation, a robustness against uncertainties present in the system, and a fast-islanding operation with minimum consumer inconvenience. The mathematical modeling of optimal scheduling that considers resiliency for microgrids is not widely available. To build a resilient and environment-friendly microgrid that emphasizes customers, an intelligent and distributed autonomous framework was developed ^[13]. In this model, the occurrence of major outages due to natural disasters such as floods, tsunamis, earthquakes, heavy rains, etc. was considered. The severity and occurrence of these events may increase in the future ^[14]. In the grid-connected mode, a proactive operation model was implemented while considering a scheduling horizon of 24 hours. This proactive scheme works on initial warnings created well before the occurrence of major outages. The resilient-oriented operation scheme for microgrids considers the major outages. A cyber-physical system of the multi-energy system is prone to Denial of Service (DoS) attacks; consequently, the implementation of distributed energy management algorithms is affected ^[15]. In the load-shedding algorithm, the possibility of maximum load curtailment has to be identified. In the ramp-down algorithm, the maximum possible generation and the remaining amount of surplus power at different time instants has to be identified.

The approach of reinforcement learning (RL) is goal-directed while learning from the given environment. In reinforcement learning, the agents are software programs. First, these agents discern the environment and make decisions accordingly for an action. The actions of the agents must be optimal and superior. The environment of an RL space should be either deterministic, observable, discrete, or continuous, and either single or multi-agent. The variables of the RL algorithm known as hyperparameters are set for the model. These are different from the parameters of the model. The hyperparameters are epsilon, alpha, and gamma, where epsilon is a greedy factor, alpha is the learning rate, and gamma is the discount factor ^[16,17]. RL-based energy management has been implemented in the creation of an energy management system for an electrified powertrain ^[18]. The design of a resilient multi-energy microgrid system faces the challenges of stochastic uncertainties of renewable generation, the development of model-free control schemes under undesirable conditions, and the achievement of robust and efficient operations ^[19]. A multi-agent deep RL algorithm has been designed for the resilience-driven routing and scheduling operations of the mobile energy storage system ^[20]. The resilience quantification and planning of the power distribution grid were analyzed with a zigzag topological approach ^[21].

In order to achieve several goals, such as lowering operating expenses and guaranteeing power supply dependability, a deep reinforcement learning-based energy scheduling approach is suggested ^[22]. To enhance the control performance of energy management system (EMS), SAC is applied to the EMS of an electric vehicle (EV) equipped with a hybrid energy storage system (HESS) ^[23]. The deep reinforcement learning algorithm is used to identify and calibrate problematic parameters using PMU measurements ^[24]. By maintaining the variance of the state-action returns within a tolerable range, a deep off-policy actor-critic variation is proposed to learn a continuous return distribution ^[25]. In order to maximize their financial benefits and enhance system reliability, a study suggests a residential demand response strategic bidding approach for load aggregators with deep reinforcement learning ^[26]. To harness energy flexibility, a major commercial building's cooling setpoint has been controlled using deep reinforcement learning based on Soft Actor Critic ^[27]

1.1.   Resilient energy trading

The components and stakeholders of a cyber-physical system of microgrids are shown in Figure 1. In a networked microgrid, a resilient energy trading system is crucial to ensure the energy security and price stability, especially as the world faces increasing climate risks and the transition to more sustainable energy sources. A networked microgrid consists of multiple interconnected microgrids that can operate either autonomously or in coordination with a main power grid. This structure enhances the resilience, flexibility, and efficiency in energy management. Peer-to-peer energy trading in networked microgrids enables prosumers (producers + consumers) to trade excess energy directly with consumers. When resilience is incorporated, the trading mechanism ensures the fault tolerance, cybersecurity, and adaptability against disruptions (e.g., cyberattacks, extreme weather, or grid failures), as seen in Figure 2.

In energy trading, resilience is key to ensuring the continued flow of electricity, even in the face of disruptions such as supply shocks, demand volatility, technological changes, or environmental challenges. To build resilience in energy trading, the following strategies must be adopted:

● Sourcing energy from a variety of regions and suppliers to reduce the dependence on any one source;

● Using AI and machine learning to predict market trends and quickly respond to disruptions;

● Modernizing grids and storage solutions to effectively handle fluctuations in the supply and demand; and

● Creating policies that encourage market transparency and provide support during crises.

1.2.   Causes impacting resilient energy trading

Resilient energy trading ensures stable, secure, and adaptive transactions, even under uncertain conditions. However, several factors can impact its efficiency and robustness. These causes can be categorized into technical, economic, cyber, environmental, and regulatory factors. Resilient energy trading is influenced by multiple factors, including technical, economic, cyber, and environmental challenges, as shown in Table 1.

A. Impact on Trading due to Transmission line faults (Short Circuits, Overloads)

● Power flow disruptions affect the energy prices and trading stability.

● Some buses become isolated, thus causing supply shortages.

● Increased congestion in unaffected transmission lines.

B. Impact on Trading due to Generator Failure (Bus Outage, Frequency Instability)

● Sudden loss of generation capacity causes price spikes.

● Microgrid-dependent areas face severe power shortages.

● Market participants hoard energy, thus leading to unfair pricing.

1.3.   Long short-term memory and soft actor-critic algorithms

The Long Short-Term Memory (LSTM) network is part of the deep recurrent neural network (RNN) class with backpropagation and does not use gradients. Various memory gates are added in the LSTM network, which possess the blocks that are comprised of gates to manage the block's state and output ^[28,29]. The text classification tasks have been solved using optimal LSTM topologies. The soft actor-critic (SAC) algorithm, including maximum entropy with LSTM, has been considered for the energy management of multi-energy systems ^[30]. The workload prediction model was designed considering the LSTM model ^[31]. In time series forecasting, the LSTM model was used in ^[32]. The spiking neural P (SNP) based LSTM model was created to process sequential data ^[33]. The stock market values were predicted using the LSTM model ^[34]. A method was suggested to predict the parts with the highest frequency with the Random Forest (RF), while LSTM predicted the remaining parts ^[35]. A multi-scale FCN (MFCN) and LSTM network were considered for learning spatial and temporal features ^[36]. In the error detection of electroencephalography (EEG), a bidirectional LSTM neural network was implemented. The electrocardiogram signals were partitioned into normal and abnormal using LSTM ^[37]. The multi-series classification has been performed with a full convolution network- LSTM ^[38]. The levelized cost of electricity (LCOE) and payback period approach was used to assess the solar-powered microgrid's economic viability ^[39]. A technique for transferring tokens between networked microgrids with interoperable blockchains has been created. A technique for token transfers between networked microgrid interoperable blockchains has been devised for safe and private smart power contracts between electricity suppliers and customers ^[40]. Under grid-to-vehicle and vehicle-to-grid systems, the electric vehicle network hub enables blockchain-based safe and robust energy trading ^[41].

1.4.   Research gap

Resilient energy trading ensures the secure, adaptive, and efficient energy exchange in decentralized networks. However, several research gaps hinder its full potential. The major points in the research gap are highlighted below:

● Existing optimization models fail to adapt to dynamic price fluctuations, grid failures, and adversarial conditions;

● Current energy trading frameworks struggle with data privacy, non-independent and identically distributed (IID) data distribution, and communication failures;

● Vulnerabilities to DDoS attacks, data poisoning, and blockchain smart contract exploits threaten the resilience of energy trading;

● Current models do not address climate-induced disruptions (e.g., wildfires, hurricanes) that affect the energy trading resilience;

● There is a lack of holistic models that integrate renewable energy, microgrids, and energy storage; and

● Limited research has been done on the design of quantification techniques for real-time energy resilience.

Addressing these research gaps requires integrating RL, federated learning, blockchain security, and real-world validation. Advancing resilient energy trading frameworks will enhance the stability, security, and efficiency in decentralized energy markets.

1.5.   Contributions

In this paper, LSTM-soft actor-critic (SAC) RL-based resilient energy management is suggested for a networked microgrid system. In the networked microgrid system, the peer-to-peer resilient energy trading mechanism is adaptive and robust to undesirable scenarios such as the occurrence of faults in transmission lines, the failure of generators, and the failure of supply from the main grid. The LSTM-SAC reinforcement learning is proposed to train the networked MG system to make it resilient and adaptive. The state observations comprise the expected values of the electrical load demand, power generations by the distributed generators, and the state of charge (SoC) and state of health (SoH) of energy storage devices and electric vehicles. The action part contains either buying or selling rates for surplus and deficit power, charging and discharging rates of energy storage devices, and electric vehicles. The LSTM-SAC RL finds the actions for optimal Q values that maximize the reward for different scenarios of undesirable events in a microgrid.

The proposed LSTM-SAC for Resilient Energy Trading is comprised of the following major features, particularly in dynamic and uncertain energy markets:

● Unlike standard SAC, integrating LSTM enables the model to learn from past energy trading patterns, grid conditions, and demand fluctuations;

● SAC-LSTM recognizes trends and adjusts strategies based on historical sequences, thus improving decision-making in volatile energy markets;

● Multiple microgrids use SAC-LSTM, and they dynamically learn optimal trading strategies while ensuring resilience against failures; and

● By considering past failures and recovery mechanisms, SAC-LSTM enhances the resilience of energy trading strategies.

The major contributions of this paper are highlighted below:

● This paper formulates the resilient energy trading process by incorporating DC-OPF that considers line outages (topology change) and generator failures;

● The proposed LSTM-SAC network does not use the gradient descent technique to estimate Q-values, while the policy is maximized and avoids overestimates and underestimates of Q-values;

● The networked microgrid is trained with the proposed LSTM-SAC algorithm that formulates the reward function comprised of microgrid losses and profits, which are determined based on the surplus and deficit power and the time of occurrence of fault; and

● A Markov Decision Process (MDP) is used to develop the RL-based resilient energy trade problem.

1.6.   Paper organization

This paper is organized as follows: Section 1 covers the introduction; Section 2 includes the basic concepts of RL; Section 3 focuses on the resilient energy trading problem formulation; Section 4 discusses RL-based secure and resilient energy trading; Section 5 covers the proposed LSTM-SAC RL scheme for resilient energy trading systems; Section 6 includes a simulation and results; and Section 7 concludes the paper.

2.   Reinforcement learning: An introduction

The approach of RL is goal-directed while learning from the given environment. In RL, the agents are software programs. First, these agents discern the environment and make decisions accordingly for an action. The actions of the agents must be optimal and best. The environment of the RL space should be deterministic, observable, discrete or continuous, and single or multi-agent. There are four main parts of RL such as a policy, a reward signal, a value function, and/or a model function ^[42,43].

a. Policy: A policy is the learning process and behavior of the agent in the environment. A policy defines the action to be taken out of discerned states from the environment. The policy is the core part of the RL and maybe a simple function or a look-up table.

b. Reward: The reward is the goal of the RL problem. At each discrete time step, an agent receives a reward, which is a number from the environment. The objective of the agent is to maximize its reward. The reward the agents receive depends on the good or bad events. The reward of any number to the agent depends on the stochastic functions of the environment and the agent's actions.

c. Value function: A value function indicates the good things that will occur in the long run. The value function depends on an agent who expects to collect the reward in future actions. The environment directly gives a reward to the agents with an estimation of values on the actions during their entire lifetime.

RL is based on mathematical principles from MDPs, probability, optimization, and dynamic programming. An MDP is defined by a tuple ($S, A, P, R, \gamma$),

where $S$ is the set of state, $A$ is the set of actions, $P\left({s}^{'}\right|s, a)$ is the transition probability from state $s$ to ${s}^{'}$ given action, $r(s, a)$ is the reward function, and $\gamma$ is the discount factor (0 $\le \gamma \le 1)$ .

The state value function is shown below:

It represents the expected cumulative reward when starting from state $s$ and following the policy.

The action –value function is shown below:

It represents the expected cumulative reward starting from state $s$ , taking action $a$ , and then following the policy $\pi$ . The Bellman equation expresses the recursive relationship of the value function:

The Bellman Equation for the Q-Function is as follows:

For the optimal policy ${\pi }^{*}$ , the value function satisfies the following:

The optimal Q-function satisfies the Bellman optimality equation:

Using the Q-function, the policy is improved using the following:

This interprets the action that maximizes the expected reward. The temporal difference learning updates the value function as follows:

where α is the learning rate. Q-learning is an off-policy learning method with the following update rule:

where $\max_{{a}^{'}}\;Q({s}^{'}, {a}^{'})$ represents the best possible future value.

3.   Resilient energy trading system: Problem formulation

An adaptive neuro-fuzzy inference system is developed to make the attack-resilient energy management of a microgrid. In a multi-energy system, the optimal operation of each energy hub and optimal energy trading path are considered during DoS attacks ^[9]. A load shedding of a non-critical load is implemented in a microgrid that is islanded after a disaster in a networked microgrid system ^[10]. In the islanded mode, a microgrid gets disconnected from the main grid and, consequently, becomes less tolerant to faults; then, the resiliency of the microgrid is affected ^[11,12]. The system must be smart enough to anticipate such as electricity price changes and unknown fluctuations. However, some events are rare and extreme, which deeply affects the system. Resiliency is described as the capability of the system to adapt itself during the occurrence of these rare and extreme events and be robust enough to these events ^[13]. A resiliency-oriented microgrid optimal scheduling model has been developed. The operating model employed a normal and resilient operation. The capability of the microgrid has to be identified to supply loads during main grid supply interruptions. The networked microgrid system must be robust and adaptive to operational uncertainties of loads and non-dispatchable generation. The worst-case scenarios with prevailing uncertainties are to be considered to make the system robust and resilient ^[14,15].

Considering the uncertainty of the DG, the total generation cost of MG k is given below:

where ${N}_{g}$ is the total number of distributed generating units in the network microgrid system, T is the total number of time intervals, ${\mathbb{E}(P}_{g, i}^{k}\left(t\right)) = {\bar{P}}_{g, i}^{k}\left(t\right)+\Delta {P}_{g, i}^{k}(t)$ is the expected value of power generation, and ${\bar{P}}_{g, i}^{k}\left(t\right)$ is the forecasted value of power generation by DG i.

$\Delta {P}_{g, i}^{k} < \mathrm{m}\mathrm{a}\mathrm{x}(\Delta {P}_{g, i}^{k, })$ represents an uncertainty part of DG i and is limited by a maximum value in the worst-case scenario.

The operating limits (superscript $k$ is dropped for simplicity) are as follows:

where ${L}_{t}$ is the total demand. The state of charge of the energy storage system is as follows:

where ${P}_{bt}^{c}$ and ${P}_{bt}^{d}$ are the charging and discharging power of energy storage devices, respectively, with constraints ${P}_{min}^{c}\le {P}_{bt}^{c}\left(t\right)\le {P}_{max}^{c}$ and ${P}_{min}^{c}\le {P}_{bt}^{c}\left(t\right)\le {P}_{max}^{c}$ .

The state of charge of an electric vehicle is shown below:

where ${P}_{ev}^{c}$ and ${P}_{ev}^{d}$ are the charging and discharging power of electric vehicles, respectively, with the constraints ${P}_{min}^{c}\le {P}_{ev}^{c}\left(t\right)\le {P}_{max}^{c}$ and ${P}_{min}^{d}\le {P}_{ev}^{d}\left(t\right)\le {P}_{max}^{d}$ .

3.1.   Operative schedule of energy storage devices and electric vehicles

It is required to completely charge the battery after different operations in a day so that a fully charged battery will be available for the next day's operations. To obtain a fully charged battery, a set of intervals is reserved for charging, as shown below:

where ${N}_{c}^{f}$ is the cardinality of set ${\varOmega }_{c}^{r}$ and can be found as follows:

3.2.   Operation and maintenance cost

The operation and maintenance cost in a microgrid is formulated as follows:

3.3.   Surplus and deficit power

At a particular time instant $t$ , the surplus or deficit power in MG is described as follows, while the uncertainty of the system is considered. At time instant $t$ , let ${\Delta \mathrm{P}}^{\mathrm{k}}$ be the surplus or deficit power in MG $\mathrm{k}$ ; then,

where ${\alpha }_{bt, j}$ and ${\alpha }_{ev, l}$ are the binary parameters defined for energy storage system $\mathrm{j}$ and electric vehicle $l$ . These parameters are 1 for charging and -1 for the discharging mode. ${\mathbb{E}(P}_{agg}^{k}\left(t\right))$ is the expected aggregated load demand and $\mathbb{E}\left({P}_{g, i}^{k}\left(t\right)\right)$ is the expected power generation by DG $i$ at time $t$ in MG, and ${\mathrm{N}}_{\mathrm{g}}$ is the number of distributed generators in the microgrid.

The objective is to minimize the overall cost of the microgrid. For each node in the microgrid, the overall cost includes the following components:

a. The cost of power purchased from the utility grid or prosumers, and

b. The cost of the power generated by the distributed generator.

The operational and maintenance costs include the cost of the battery wear due to charging and discharging. If the microgrid is in surplus power, then it can sell energy to the distribution network operator (DNO), other MG, prosumers, and utility grid and generate revenues and follows:

where ${MG}_{cost}^{k} = {TC}^{k}\left(t\right)+{C}_{OM}\left(t\right)$ , ${MG}_{prof}\left(t\right)$ is the profit, ${MG}_{loss}\left(t\right)$ is the loss of the microgrid, and ${C}_{res}$ is resilient energy trading.

3.4.   Resilient optimal power flow: An overview

The security of the electrical distribution network is an important criterion. The network must be capable to withstand any sudden loss of a part of the network. One of the goals of the work is to design a resilient energy management system. Resilient energy management develops a mechanism to withstand the different sorts of faults such as line faults, distributed grid faults, power outages, and communication network faults.

A. Transmission line fault

During the occurrence of faults, the power could not flow through the faulty transmission line. In this energy management system, this power flow is described as follows:

The power flow has been set equal to zero through the faulty line. The ${t}_{L}^{0}$ is the occurrence time of the fault, and ${t}_{L}^{f}$ is the final time of the fault duration. If the information of the fault duration is not known, then a future time instant constraint must be imposed. Consequently, the power has to be transferred through the other transmission lines to avoid overloading the other transmission lines. If the fault occurs in the radial transmission, then it is cumbersome to deliver power to the disconnected MG.

B. Distribution Grid Fault

During a distribution grid fault, the MG is unable to draw power from the utility grid until recovery. This is described as a constraint:

where ${t}_{g}^{i}$ is the initial time of grid fault, and ${t}_{g}^{f}$ is the final fault time. In all cases of a fault occurrence, the constraints related to the faults are included in the optimization problem.

C. Communication network fault

A communication network fault may occur if the communication link is physically disconnected or if the link may fail due to a cyber attack. The sort of fault can be described in the adjacency matrix, $B$ , as if the communication link between node/agent fails; then,

where ${b}_{i, j}\in B$ represents the communication link between two nodes $i$ and $j$ in the networked microgrid system. Due to the occurrence of faults, the performance of the energy management algorithm diminishes and convergence problems may occur.

3.5.   DC optimal power flow (DC-OPF) for resilient energy management

Resilient Energy Management (REM) ensures stable and efficient power distribution under uncertainties such as cyberattacks, equipment failures, or natural disasters. DC Optimal Power Flow (DC-OPF) plays a key role in optimizing the power dispatch while enhancing the system resilience. DC-OPF is a linear approximation of the AC power flow problem and is widely used in power system operations for economic dispatch and congestion management. In the presence of faults, the topology of the network may change due to line outages, bus faults, or generator failures, thus requiring modifications in the standard DC-OPF formulation.

The classical DC-OPF problem aims to minimize the generation cost while satisfying a power balance and transmission constraints. In the presence of faults (e.g., line tripping, generator failure, or bus outage), the network topology and constraints change of DC-OPF is written below.

The standard DC-OPF objective is to minimize the total power generation cost as follows:

where the quadratic cost function for generator $i$ is as follows:

Subject to constraints

a. Generator limits

b. Transmission Line Flow Limits

c. Line outages (Topology Change)

If a line $\left(i, j\right)$ is outaged due to a fault, it is removed from the system, thereby modifying the admittance matrix and power flow equations as follows:

where $\mathcal{F}$ is the set of faulted lines, ${\theta }_{i}$ and ${\theta }_{j}$ are the voltage phase angles at buses $i$ and $j$ , respectively, ${x}_{ij}$ is the reactance of the transmission line between buses $i$ and $j$ . The reactance matrix $X$ and the incidence matrix B are updated to reflect the removal of the affected lines.

To ensure robustness,

d. If a generator at bus $i$ fails, then

where ${\mathcal{G}}_{faulted}$ represents the set of failed generators. The system needs dispatching of the remaining generators to maintain a power balance as follows:

where $\mathcal{С}$ is the possible contingencies, and ${P}_{{d}_{j}}$ is the power demand at the bus.

The line power flow has to be calculated using the following DC power flow equation:

where ${P}_{L}^{t}\in {\mathcal{R}}^{{N}_{L}}$ is the vector obtained by stacking the power flows in each line at time $t$ . $b\in {\mathcal{R}}^{{N}_{L}\times {N}_{L}}$ is a diagonal matrix in which each element $b(i, j)$ is the susceptance of line $i$ . $B\in {\mathcal{R}}^{{N}_{B}\times {N}_{B}}$ is the admittance matrix, and ${P}_{g}\in {\mathcal{R}}^{{N}_{B}}$ is the vector obtained by stacking all the bus power injections. The elements of the adjacency matrix of the microgrid ${A}_{b}^{L}\in {\mathcal{R}}^{{N}_{L}\times {N}_{L}}$ are ${A}_{b}^{L}\left(i, j\right)\in \left\{\mathrm{0, 1}-1\right\}$ if line $i$ and bus are not connected, line $i$ starts at bus $j$ , or line $i$ ends at the bus, respectively.

3.6.   Resilient energy trading in networked microgrids

The microgrid seeks to minimize the cost of buying energy and maximize the revenue from selling energy. The Resilient energy trading is formulated while considering the DC-OPF in the presence of faults as follows:

subject to (26),

where ${C}_{s}^{t}$ , ${C}_{b}^{t}$ are the selling and buying market prices, respectively, ${C}_{st}^{t}$ is the price to store the energy, ${C}_{p}^{t}$ is the peer-to-peer trading price, ${P}_{s}^{t}$ and ${P}_{b}^{t}$ are the power sold and bought to the main grid, respectively, and ${\lambda }_{1}, {\lambda }_{2}, {\lambda }_{3}, {\lambda }_{4}$ are the weighting factors.

3.7.   Particle Swarm Optimization

PSO optimizes DC-OPF by iteratively updating a population of candidate solutions (particles) based on their velocity and position updates as follows:

1. Initialize the particles (each particle represents a possible set of generator outputs ${P}_{gi}$ )

2. Evaluate the fitness function (generation cost)

3. Update the particle velocity and position

where $w$ is the inertia weight, ${c}_{1}$ and ${c}_{2}$ are acceleration coefficients, ${r}_{1}$ and ${r}_{2}$ are random numbers in [0, 1], ${p}_{best, i}$ is the personal best position of particle $i$ , and ${g}_{best}$ is the global best position among all the particles. Repeat until the convergence criteria is met.

4.   Reinforcement learning for resilient energy trading system

The RL-based resilient energy trading problem is formulated as an MDP:

$S$ is the state space representing the energy market, demand, price, and grid conditions.

$A$ is the action space for trading decisions (buy/sell/store energy).

$\mathcal{P}$ is the state transition probability.

$r$ is the reward function modeling profits, resilience, and stability.

$\gamma$ is the discount factor balancing short-term vs. long-term rewards.

${N}_{rel} =$ Network reliability

${\boldsymbol{Ol}}_{\boldsymbol{total}} =$ Operating loss in resilient energy trading

${R}_{t}$ is grid resilience index that measures how well the energy trading system maintains functionality and restores operations after a fault. The Grid Resilience index in energy trading quantifies the power grid's ability to maintain the stability, efficiency, and reliability while enabling seamless energy transactions under normal and stressed conditions. It ensures that the energy market remains functional despite disruptions such as cyberattacks, equipment failures, demand surges, or renewable intermittency. Before any fault or disruption occurs, the grid operates under normal trading conditions with optimal pricing, demand-supply balance, and stable grid parameters. Once a disruption (fault, cyberattack, or market instability) occurs, post-fault resilience determines the system's ability to either maintain or restore trading operations with a minimal impact.

It is expressed as follows:

where:

${E}_{post\; fault}:$ Total energy traded before the fault

${E}_{pre\; fault}$ : Total energy traded after the fault

If ${R}_{t} = 100\%$ , then the system is fully resilient (no impact of faults). If ${R}_{t}$ $< 100\%$ , then there is degradation in trading due to faults.

Pre-Fault Energy Trading is affected by the following factors:

● Availability of power from conventional and renewable sources,

● Diversity of generation sources (coal, nuclear, solar, wind, hydropower),

● Real-time energy consumption patterns of industries, households, and businesses,

● Demand-response mechanisms to prevent extreme price hikes, and

● Consistent pricing to ensure fair transactions and minimal volatility.

The post fault energy trading is affected by the following factors:

● Amount of energy that can be quickly restored after a fault,

● Availability of backup power sources such as microgrids or battery storage,

● Sudden price spikes or fluctuations due to power shortages,

● Impact on energy buyers and sellers, and

● How quickly the grid can isolate faults and reroute power.

4.1.   Network reliability in resilient energy trading

It refers to the ability of the energy trading systems to maintain stable, secure, and continuous operations despite faults, cyber threats, market fluctuations, and physical grid failures. Several factors influence the network reliability, which are categorized based on technical, economic, and security aspects. Network reliability in energy trading is defined as the probability that all critical components (power grid, trading platform, cybersecurity, and market operations) function properly. The network reliability index is defined as follows:

where ${P}_{g}$ = Probability that the power grid is operational,

${P}_{trad}$ = Probability that the energy trading platform is functioning,

${P}_{cyb} =$ Probability that the cybersecurity system is intact, and

${P}_{mar} =$ Probability that the energy market remains stable.

The state transition probability is defined below.

4.2.   Operating loss in resilient energy trading

The operating loss in resilient energy trading refers to the financial and energy losses that occur due to system failures, cyber threats, market disruptions, and grid instabilities. These losses are categorized into direct financial losses, energy loss, opportunity cost, and recovery expenses. The total operating loss in a resilient energy trading system is expressed as follows:

where:

${\boldsymbol{O}\boldsymbol{l}}_{\boldsymbol{e}\boldsymbol{n}\boldsymbol{e}\boldsymbol{r}\boldsymbol{g}\boldsymbol{y}} =$ Loss due to untraded energy

${\boldsymbol{O}\boldsymbol{l}}_{\boldsymbol{m}\boldsymbol{a}\boldsymbol{r}\boldsymbol{k}\boldsymbol{e}\boldsymbol{t}} =$ Loss due to market price fluctuations

${\boldsymbol{O}\boldsymbol{l}}_{\boldsymbol{c}\boldsymbol{y}\boldsymbol{b}\boldsymbol{e}\boldsymbol{r}} =$ Loss from cyberattacks or data breaches

${\boldsymbol{O}\boldsymbol{l}}_{\boldsymbol{r}\boldsymbol{e}\boldsymbol{v}} =$ Cost of restoring operations after failure

where $A$ is the transition rate matrix and is defined as follows:

where ${\lambda }_{i} =$ failure rate at state $i$ , and ${\mu }_{i} =$ Recovery rate due to self-healing.

Let us consider the nodes in the microgrid defined as an agent. At some discrete-time interval t, the variables considered are load demand, distributed generation, SoC and SoH, and profit. Under extreme and normal conditions, the system state for an MG is described as follows:

where $i = \mathrm{1, 2}, 3\dots., {N}_{dg}$ , $j = \mathrm{1, 2}, 3\dots., {N}_{bt}$ , $l = \mathrm{1, 2}, 3\dots., {N}_{ev}$ , and ${s}_{k}\in S$ and $S = \{{s}_{1}, {s}_{2}\dots \dots., {s}_{n}\}$ .

$S$ represents the set of all feasible system states in the system of MG. ${s}_{k}$ stands for a feasible state, and n is the number of all feasible system states. All feasible system states concerns all possible values of the electricity demand, distributed power generation, and SOC/SOH of the battery. Next, the action of MG is defined on the following decision variables:

where ${a}_{k}\left(k\right)\in U$ , $U = \{{a}_{1}$ , ${a}_{2}$ , ……., ${a}_{n}\}$ , $U$ is the set of all feasible actions of corresponding states, and ${N}_{bt}$ and ${N}_{ev}$ are the numbers of the energy storage devices and electric vehicles, respectively.

4.3.   The reward function for resilient energy trading

The reward function is formulated for resilient energy trading (44). At time $t$ , the reward function is comprised of three components: the profit or loss of MG, the surplus or deficit power, and the duration of the occurrence of a fault,

where $\left(\Delta {P}^{k}\right) = \Delta {P}^{k}/(1+\mathrm{l}\mathrm{n}(|\Delta {P}^{k}|)$ ${T}_{fault} = |{t}_{fault}^{f}-{t}_{fault}^{i}|$ , ${T}_{fault}$ is the duration of the fault, ${t}_{fault}^{i}$ is the time of occurrence of fault, and ${t}_{fault}^{f}$ is the time of the end of the fault. ${\beta }_{p}$ is 1 if MG is in profit, else 0 similarly, ${\beta }_{l} = 1$ if MG is in loss, else it is zero, and ${\varphi }_{fault}$ is 1 if fault occurs else it is 0.

The reward function is defined based on either the surplus or deficit power. The first component is related to the profit of the microgrid, and the second component is related to the loss incurred in the microgrid. The third component is related to the surplus or deficit power. The $\beta$ and $\omega$ are the weighting factors to scale the components. There is an objective to choose $Q$ values that generate greater values of reward.

5.   Proposed LSTM SAC reinforcement learning strategy

At a time index, the LSTM cell is comprised of three types of gates, such as Forget ${f}_{t}$ , an Input gate with an input ${i}_{t}$ and an update ${g}_{t}$ , and an output ${o}_{t}$ . The LSTM focuses on time-series forecasting. Let, $\{{x}_{t-1}, {x}_{t-2}, \dots.., {x}_{t-n}\}$ denote the input sequence. The suitable weight matrices are considered for corresponding inputs of the network activation functions. The internal memory cell state ${C}_{t-1}$ defines elements of the internal state vector that need to be maintained, updated, or crashed through interaction with outputs of the previous time step ${h}_{t-1}$ and the inputs of the current time step ${x}_{t}$ . The sigmoid activation function is used in the forget gate. The sigmoidal function (or Relu function) and hyperbolic tangent functions are used for the input and the update of the Input gate. The output gate decides what to forget from the previous state ${h}_{t-1}$ and updates cell state ${c}_{t}$ , and which value will pass the output gate. ${f}_{t}$ , ${i}_{t}$ , ${g}_{t},$ and ${o}_{t}$ are defined as follows:

The cell memory is recursively updated by interactions with the previous time step value and with the values of ${f}_{t}$ and ${g}_{t}$ gates. The process continues to repeat for the next time step.

In the proposed scheme, the Q-function and policy are simultaneously learned. It considers off-policy data and the Bellman equation to learn the Q-function that is used in computing the policy. The optimal action is chosen by taking argmax over the Q-values of all actions. Thus, the actor is the policy network that directly outputs the action. For exploration promotion, some Gaussian noise is included in the action that is determined by the policy. The actor output is fed to the Q network to calculate the Q-value. The target networks are created for both the critics and actors. The target networks are updated based on the main networks. The actor (policy network) loss is the sum of the Q-values of the states. The critic network is used to compute the Q-values. The action network computes the action that is passed to the critic network. Using the reward function (44), the error propagates back to update the LSTM CRITIC and LSTM ACTOR networks, as shown in Figure 3.

5.1.   Soft Actor-Critic (SAC) with LSTM for resilient energy trading

SAC is a model-free, off-policy RL algorithm that optimizes both reward maximization and entropy regularization for better exploration. Integrating LSTM into SAC improves its ability to handle sequential dependencies in energy trading, thus making it more resilient to uncertainties in decentralized markets.

Energy trading in decentralized markets is highly dynamic due to the following:

● Fluctuations in the energy demand and supply;

● Uncertain energy prices; and

● Cyber threats and adversarial conditions.

The proposed SAC-LSTM algorithm has the following features:

Temporal awareness: LSTM captures past energy trading patterns.

Exploration-exploitation balance: SAC's entropy regularization ensures robust decision-making.

Resilience: SAC can adapt to adversarial trading conditions and market fluctuations

5.2.   SAC with LSTM policy and Q-Functions

The policy network outputs a stochastic action distribution using LSTM embeddings:

where ${h}_{t} = LSTM({s}_{t}, {h}_{t-1})$ represents the hidden state, and ${\mu }_{\theta }\left({h}_{t}\right)$ and ${\sigma }_{\theta }\left({h}_{t}\right)$ are the mean and variance of the active distribution, respectively. The objective function includes entropy regularization,

where $H\left({\pi }_{\theta }\right) = -\sum {\pi }_{\theta }\mathrm{log}{\pi }_{\theta }$ is the entropy that controls exploration (automatically tuned in SAC).

Critic (Q-Value) Network with LSTM

The Q-function is learned using two critics to reduce overestimation bias.

The target Q-function follows soft Bellman updates,

where the target value is as follows:

Automatic Temperature (α\alphaα) Adjustment

SAC dynamically adjusts the entropy weight $\alpha$ :

where ${H}_{0}$ is the target entropy.

Steps of Proposed LSTM- SAC algorithm for resilient energy trading

1. Input: Consider States in the environment

2. Output: Action taken in the environment

3. Set ${\beta }_{p}$ , ${\beta }_{l}$ , $\omega$ , ${\varphi }_{fault}$ and ${Q}_{th}$

4. Initialize the replay buffer D

5. Set two different target network parameters as follows:

     ${\varPhi }_{targ, 1}\leftarrow {\varPhi }_{1}$ and ${\varPhi }_{targ, 2}\leftarrow {\varPhi }_{2}$ and

6. For episode 1, 2, 3, ……N do

Initialize states of peer-to-peer resilient energy trading parameters of microgrid for different scenarios,

7. For time slot $t = \mathrm{1, 2}, 3\dots \dots \dots.., T, do$

Evaluate reward $r\left(t\right)$ where

8. For different $\left(s, a\right)$ pair

  Derive the optimal control action ${a}^{*} = arg\; \max_{a}\;{Q}^{*}(s, a)$

  Execute the control action in the environment

9. Update the state ${S}^{'}$ , store the transition in replay buffer D

10. Building LSTM network for the actor and critic for the optimal ${Q}^{*}\left(s, a\right)$

11. Check for overestimates ${Q}^{*}\left(s, a\right)\le {Q}_{th}$

  Model = sequential();

  Model.add (LSTM (neurons), activation = RELU, return_sequences = True)

  Model.compile (Loss = RMSE, optimizer = ADAM);

12. While epoch = 1, 2, ….. DO

        Train model;

        Validate model;

        Return model

     End

  Evaluate future state optimal target Q-function ${Q}^{*}({s}^{'}, {a}^{'})$

  $t\leftarrow t+1$

  End

6.   Results and discussions

A networked microgrid comprised of 04 IEEE 14 bus system is considered with different capacities of distributed generations, energy storage devices, and electric vehicles. The stochastic values of the generation capacity of distributed generators and electricity demand are considered. In an MG, 10 distributed generators (DGs), 04 energy storage devices, and 02 electric vehicles are available in the system. The minimum and maximum power generation by the distributed generators are in the range of 45 MW and 3500 MW.

It is assumed that the MG is facilitated to also get power from the main grid. The simulation work was performed using the GAMS software and MATLAB. The adjacency matrix varies during normal conditions and the occurrence of extreme events. During different scenarios, state-action pairs are generated and $Q(s, a)$ values are approximated using the LSTM network for SAC RL. In the environment, the optimal ${Q}^{*}(s, a)$ value and ${a}^{*}$ , which maximize the reward, are obtained.

At a time instant with an aggregated load demand, the generations by different distributed generators are obtained under normal conditions. The optimal power generations of different DGs have been obtained using (26) to (33) and (36) to (37); then, the surplus or deficit power changes were calculated during normal and extreme conditions. The charging schedules of Electric vehicles and energy storage devices were obtained using (17). Due to the occurrence of extreme events, there may be several scenarios on networked microgrids. Out of various scenarios, only one scenario was considered for resilient peer-to-peer energy trading, which is shown in Table 2. Let extreme events occurs at time $t = 10 \;hours$ , and the system is recovered at $t = 20 \;hours$ so the duration of the fault is ${T}_{fault} = 10\; hours.$

Accordingly, the profit or loss of the MG is evaluated in Equation (22). The MG is trained for different scenarios using a LSTM-SAC RL algorithm. The optimal Q values (9) are obtained and the corresponding optimal action (45) and reward (46) are evaluated. The optimal action ${a}^{*}$ is obtained with optimal ${Q}^{*}$ values, while rewards at different time intervals are generated and maximized. To avoid a gradient descent, the LSTM neural network is implemented to generate an optimal ${Q}^{*}$ while the reward is maximized. For different scenarios, such as the occurrence of a fault on a transmission line, the failure of distributed generators, or the failure of supply from the main grid, the networked microgrid system is trained for optimal actions while the reward is maximized. In a scenario, in MG1, the distributed generators 9 and 10 fail, and in MG2, the distributed generators 5 and 6 fail. As shown in Table 2, during the scenario of extreme conditions, the optimal power generation (36)-(37) using the PSO algorithm by microgrid 1 and microgrid 2 are obtained, and are shown in Figures 4 and 5, respectively. The state of charge of the energy storage devices and electric vehicles are computed and shown in Figures 6 and 7, respectively. For microgrid 1 and microgrid 2, during this scenario, the surplus and deficit powers are evaluated at different time intervals, which is shown in Figure 8. The rewards of microgrids 1 and 2 are calculated and shown in Figure 9 during time intervals of extreme conditions. For scenario 1, the grid resilient factor was calculated to 90% (39).

In the learning process, the rewards were obtained for microgrid 1 and microgrid 2, and the time intervals were identified while the rewards were negative. The negative rewards show that the microgrid has a loss during the occurrence of extreme events for peer-to-peer energy trading.

The LSTM network comprises hidden units: 200, training options: adam, MaxEpochs: 250, and Error: Root mean square error (RMSE). The convergence in the LSTM network is shown in Figure 10. Stochastic scheduling has been implemented in peer-to-peer energy trading while energy storages are incorporated to improve resiliency.

7.   Conclusions

In this paper, a multi-LSTM-SAC RL for the resilient energy management of microgrids was proposed for secure and resilient peer-to-peer energy trading. This proposed mechanism was tested in a networked microgrid system comprised of an IEEE 14 bus with energy storage devices and electric vehicles. The MG was trained with LSTM-SAC RL for different scenarios, such as the failure of generation by one or more than one generator or the occurrence of a fault in the transmission line. During the extreme conditions, secure and resilient peer-to-peer energy trading was designed. At different time intervals of extreme events, the optimal power generation, the surplus or deficit power, the state of charge of energy storage devices, and the electric vehicle power were evaluated. The convergence in the proposed learning scheme is obtained and optimal actions were obtained for different extreme events. This learning scheme did not use gradient descent; otherwise, the LSTM algorithm was used to estimate the Q values. Furthermore, this learning scheme avoids overestimating the Q values for resilient energy management. The convergence in the learning mechanism was obtained and loss was minimized. The proposed LSTM-SAC resilient peer-to-peer energy trading creates a platform to maximize profit under extreme conditions.

Author contributions

Desh Deepak Sharma: Conceptualization, methodology, investigation, Ramesh C. Bansal: Validation, visualization; All authors: Writing ‒ original draft, writing ‒ review and editing. All authors approved the final manuscript.

Use of AI tools declaration

The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work is supported by research project granted by Council of Science and Technology, Uttar Pradesh, India (project id 3246), and Department of Higher Education, U.P. (Project Id :78/2024/1015).

Conflict of interest

The authors declare that there are no conflicts of interest in this paper.