1.
Introduction
A microgrid (MG) is a concept that facilitated the integration of the distributed generators (DGs) and the other essential energy storage (ESS) systems into a power distribution network to provide an independent capability to operate under the existing load setup. The idea of a MG is considered a viable remedy and solution for reducing the unpredictable generation and demand energy swings that very often occur in the distribution network [1]. MGs are designed to accomodate any application of local demand generation. There is no commonly acknowledged standard minimum or maximum size of MG. The use of MGs is one of the potential options for more intelligent and efficient energy operations [2]. This study further investigates the enhanced MG operation by providing a better control strategy. The MG's structure can be segregated into either classic type or hybrid type. Classic type MGs are formed from conventional micro sources like DGs and a static switch with a traditional network structure [3]. The DG units, distributed storage units, and loads are grouped to form the MG which can be connected to the utility grid as well as operated autonomously and independently. However, in classic MGs there is an inadequacy, as with the traditional network structure when it comes to accommodating high levels of DG penetration and the requirement for the integration of DG sources into the energy market. Reduced dynamic performance in primary level controllers [4], the substantial communication networks required for secondary and next level controllers and the hierarchical structure that cores a centralized controller are additional issues with the traditional MG concept. The usage of the MG has been widespread due to various advantages like high quality and reliability of the power system, no need for transmission lines, improved efficiency, lower costs, and environmental friendliness as compared to others. Therefore, the MG power system is now anticipated to be used to establish a smart power system for remote places. The high cost of energy generation, high operational costs and environmental concerns are common issues in classical MG operation.
The aforementioned issue could have a viable solution in the form of an MG utilizing a hybrid microgrid (HMG). HMGs mostly combine traditional and renewable energy sources. The literature [5] refers to these MGs as HMGs since they integrate many technologies like fossil fuel, DGs, hydropower, solar power, wind power, battery, electric vehicles (EVs), gas, etc. HMGs often rely on the various local renewable energy sources (RESs) that are supplemented by conventional energy sources as backup systems [6]. There is a need for better coordinated control strategies particularly for HMG systems in the case of rural and industrial electrification. An HMG design uses a bidirectional power controller in place of the traditional static transfer switch to reach the power quality needs of the various MG components and the various types of loads. Many electrical and energetic challenges can be solved by HMGs [7]. The electrification of rural regions is now mostly dependent on HMG systems. These MGs include storage technologies in addition to certain RESs, such as photovoltaics (PVs), wind, biomass, or a combination of these sources. The hybrid electric production created from the RES can therefore be delivered as AC, DC or both. There are various benefits by using these HMG systems to generate electric power, including clean energy, supply reliability, decreased system congestion and a new investment area. In a hybrid system, wind and solar energy are often mixed and serve to complement one another. They are easily accessible anywhere around the globe and have substantial environmental advantages [8]. Additional investments in the development of solar and wind energy have been encouraged and promoted in recent years due to the simplicity of installation, cheap maintenance costs, livelihood for the conservation of traditional energy supplies, and favorable laws on renewable sources. Due to the aforementioned reasons, HMG building is taking place in a variety of locations, including military bases, a small community, a commercial zone, academic institutions, and industrial parks [9]. Due to their substantial emissions of greenhouse gases and the presence of sensitive loads, industrial sites are of interest. For industrial-scale and household-scale customers, different HMG models exist [10]. A major reason to design and build an HMG in industrial parks is the significance of the sensitive loads. Industrial microgrids (IMGs) are systems for distributing low-voltage electricity, and they are made up of ESSs, industrial controllable loads and RESs like wind generators (WGs) and PVs [11]. These technologies can decrease the output of conventional fossil fuels as well as long-distance power transmission losses, which reduces environmental pollution and the energy crisis [12]. An IMG is a collection of Distributed energy resources (DERs) that houses an industrial process such as a manufacturing, refining, transformation, desalination or renewable energy generating process such as fuel cell (FC), PV and wind sources [13]. Further research is necessary to develop a hybrid industrial-based MG to handle the inherent issues and challenges to optimal performance.
However, there is a great deal of worry over the adaptability, stability and dependability of IMGs because of the fluctuations and uncertainties in energy output and consumption. The power imported and exported from and to the main grid, the ESS and the controlled loads must all be adjusted in IMGs to arrange power flows to achieve certain goals [13]. If the DERs are not properly sized and there is neither an effective protection system nor an optimization and reliability program that gives the system the required robustness, industrial plants with their large step changes in loads and sensitive loads could experience outages due to a lack of power supply. However, for a variety of reasons, it is difficult to identify an efficient energy management system for IMGs. First of all, the production process in IMGs is often made up of many connected and succeeding industrial loads that must always work together and cannot be handled separately. This makes it challenging to manage both energy and resources at the same time. Second, industrial load profiles rely on shift patterns that are often made up of multiple peaks during the day. With relatively little base load during the night, household demand is at its highest in the mornings and evenings. The appropriateness of generator machinery and the measurements of its capability depend on the pattern of peak and base loads. Last but not least, there are differences in the importance of the supply security. Naturally, the industry needs a constant supply to prevent inadequate output brought on by power outages [14]. Third, the processes and demand patterns of the various industrial loads found in IMGs differ greatly. The complexity of the model rises as a result of the need to generalize a universal model over the whole production process to include the physical features of various loads. Fourth, as the operation of industrial engineering is a real-time activity, IMG energy control must adhere to stringent real-time standards. Inconsistent energy supply and demand can lead to serious technical and financial problems [15]. Therefore, a wider range of energy generating equipment and a wider range of installation capabilities may be added to the HMG model since power and heat consumption are substantially advanced in an industrial environment.
To address these aforementioned issues, we propose the novel modeling of a hybrid industrial microgrid (HIMG). The goal of this study is to determine, from the available resources at a particular site, the perfect combination of RESs (wind, solar, EV and FC) and component sizing that can meet the industrial demand reliably and consistently, as well as to assess whether or not such a hybrid option is a cost-effective solution [16]. As discussed earlier the demerits of conventional energy sources can be managed by adding an RES or vice versa. EVs, PVs, wind turbines (WTs), FCs, DGs and batteries make up the HIMG. As options for power generation that provide pollution-free green energy, micro-sources including the EV, WT, PV and FC, are emerging [17]. Like other renewable energies, EVs are among the modern, promising components of renewable communities that display enticing qualities while being incorporated into the power grid. The impact of EVs as controlled loads on the frequency management of power networks has been extensively researched, as seen in [18]. Due to the charging and discharging of their batteries, EVs might increase the complexity of the frequency regulation of the entire system, even though their use would result in an upgrading of the power grid toward the HIMG [19]. The inertia of RESs is low, and the network stability associated with such units is also poor. As a consequence, environmental pollution and HIMG stability are seen as the key issues [20]. Frequency stability for HIMGs is one of the many inherent issues that needs further attention because it is being taken into account in this work.
Therefore, HIMGs require a strong control strategy because the sources are irregular, stochastic, and variable. Several types of controllers can be used to suppress these issues such as PI [21], PID [22], FOPID [23], SMC [24], MPC [25], fuzzy [26], adaptive controllers [27] and so on. This study's major goal was to choose the best design, control method and economic evaluation for HIMG systems. SMC, on the other hand, is one of the best methods for nonlinear systems with uncertainties and outside perturbations. Power converters are among its most devoted users because of their durability and a natural fit for switching type devices. The dynamic stability and dependability of the HIMG system may be jeopardized by high-frequency vibrations caused by the chattering phenomenon associated with SMC. To mitigate this issue fractional calculus has been applied to SMC to design a fractional sliding mode controller (FSMC) controller [28]. The FSMC has strong performance against changes in gain, reduces chattering and efficiently handles parameter fluctuation and disturbances [29]. To verify the suggested controller, simulation research has been done. The suggested controller was built with EVs in mind. Results from simulations show that under different operating situations, the EV control approach may deliver effective frequency regulation performance [30]. Due to its manually selected settings, FSMC is generally not intelligent. Therefore, this issue may be resolved by using an appropriate optimization technique like an iterative teaching-learning-based optimizer (ITLBO) [31]. This research provides a frequency regulation strategy for an HIMG to control the frequency by using ITLBO optimized fractional sliding mode controller (AFSMC). The major contributions of this study are briefly outlined as follows:
 Analysis of the modeling of the hybrid industrial microgrid made up of various energy sources (DG, WT, PV, EVs, FC and battery) has been studied in detail in this work.
Analysis of the modeling of the hybrid industrial microgrid made up of various energy sources (DG, WT, PV, EVs, FC and battery) has been studied in detail in this work.
 To ensure that the system states converge to the source in a finite amount of time, a nonlinear sliding surface was designed and fractional energy terms were fused into the sliding surface for frequency stabilization and to enhance the damping of oscillations due to a low inertia industrial MG.
To ensure that the system states converge to the source in a finite amount of time, a nonlinear sliding surface was designed and fractional energy terms were fused into the sliding surface for frequency stabilization and to enhance the damping of oscillations due to a low inertia industrial MG.
 The impact of the state of the charge (SoC) of the battery and EVs is investigated for frequency control in the test system considered. The vehicle-to-grid (V2G) impact on frequency control along with the other sources present in the system was analyzed in this study.
The impact of the state of the charge (SoC) of the battery and EVs is investigated for frequency control in the test system considered. The vehicle-to-grid (V2G) impact on frequency control along with the other sources present in the system was analyzed in this study.
 FSMC controllers are not parameter-independent like other linear and nonlinear controllers. So, in this study, a unique tuning approach based on the ITLBO is provided. By establishing the controller gain settings appropriately, an attempt has been made to improve the overall performance. The suggested ITLBO control approach is also flexible and simple to determine the best FSMC controller settings.
FSMC controllers are not parameter-independent like other linear and nonlinear controllers. So, in this study, a unique tuning approach based on the ITLBO is provided. By establishing the controller gain settings appropriately, an attempt has been made to improve the overall performance. The suggested ITLBO control approach is also flexible and simple to determine the best FSMC controller settings.
 This optimal FSMC moderate the system's frequency discrepancies to maintain the frequency stable while differentiating and evaluating the system's behaviour.
This optimal FSMC moderate the system's frequency discrepancies to maintain the frequency stable while differentiating and evaluating the system's behaviour.
The remaining sections of the manuscript are structured as follows. The scheme, modeling, and state-space formulation of the HIMG and its associated resources including EVs for the simulation are explained in Section 2. Section 3 discusses the different control strategies simulated with the proposed approach. Section 4 presents the suggested evolutionary-based tuning approach for optimally setting the FSMC gain parameters. Section 5 shows the simulation results in the time domain for several test cases as well as their corresponding technical analysis. Section 6 outlines the conclusions of all of the work done.
2.
Modeling of HIMG
This section outlines the HIMG model and operation, as well as the associated control strategy and test system utilized in the simulation. Figure 1 shows the schematic diagram of an HIMG. To investigate the dynamic frequency responses of the system, a microgrid that consists of a DG, WG, FC, battery, PV system, an EV aggregator and loads was modeled in this study. Depending on the current internal supply-demand situation, the interlinking converters' function is to facilitate bidirectional energy transmission between the sub-grids AC and DC bus. Due to the different ways that AC and DC components operate, an HIMG is difficult to set up and maintain, which causes voltage and frequency problems. A bidirectional interlinking converter connects the microgrid's AC and DC components. The AC side of the microgrid is linked to a synchronous generator, AC loads, a solar energy system, a wind energy source, and a fuel cell, and the DC side is connected to an electric car charging station and ESS [32].
An AC/DC microgrid is a system that combines an AC subsystem with a DC subsystem. Both AC and DC power can be received and supplied by the AC/DC power. The authors applied a grid-connected DC-AC solar PV panel, an EV and a FC as shown in Figure 1. The AC/DC interconverter connects the AC bus and a DC bus in a way that maintains continuous energy production. The DC bus, the battery, and the EV are all connected by DC/DC converters [33]. The configuration of the HIMG system includes the previously mentioned energy sources of the DG, WT, PV, FC, EV, and battery as shown in Figure 2. The total power delivered to the load Pt is calculated as follows:
where Pdg, Pwt, Ppv, Pev, Pfc and Pbt are the power of the DG, WT, PV, EV, FC, and battery sources respectively. Therefore, the total deviated power delivered to the load ΔPt is:
where ΔPdg, ΔPwt, ΔPpv, ΔPev, ΔPfc and ΔPbt denote the deviated power of DG, WT, PV, EV, FC, and battery sources respectively. The capacity of power systems to keep a stable frequency within a predetermined range as a result of an imbalance between generation and load is known as frequency stability [34]. Therefore, the frequency response of the HIMG can be described as
where M is the inertia constant and D is the damping coefficient of the microgrid system. Pd stands for the change in load demand power. To keep the system frequency at the nominal value, a DG must be able to regulate its generation according to the short-term gaps between generation and load demand. Figure 2 depicts the HIMG's mathematical model.
2.1. Modeling the DG
A DG is used to produce electricity by driving a synchronous generator with a diesel engine governor. Due to the erratic nature of the WT and PV systems' power outputs, the DG is regarded as the most dependable choice for delivering uninterrupted and superior power to the key loads in an HIMG. The mathematical representation of a DG with a regulator and a turbine is shown in Figure 2. The engine runs at a fixed pace because of its time regulator system, and the frequency of the AC signal is 50 Hz. The 15 MW capacity primary power generator is anticipated. It can modify voltage and frequency while enhancing system dependability. The diesel generator's (Pdg) rated power is shown as [8]
Fc stands for fuel consumption, Pdgo for output power and A and B for constants that reflect the fuel consumption's linear curve. An approximate model is considered for the DG in this study.
2.2. Modeling PVs
The covered area of the panels and the quantity of irradiance generated were used to calculate how much electricity a solar farm might produce. The quantity of light shining on a solar cell directly affects the output current. Irradiance (1 kW/m2) and temperature (25֯C) are the input variables used to calculate the current, power and voltage as output factors. PV energy is becoming more and more popular across all RESs because of its low cost and lack of machine-driven components. The single diode model, whose equivalent circuit is shown in Figure 3, is the most widely used model used for a PV array. It consists of a current source (II) parallel to a single diode, a parallel resistor (R2), indicating a leakage current (IP), and a series resistor (R1) as inner resistance to the current flow [23].
The PV's nonlinear V-I characteristic equation can be written as follows:
where II is the input current, IP is the parallel current, ID is the diode saturation current, I0 is the current flowing across PV cells, IS is the saturation current of the diode, ξ is the diode ideality factor, Vt is the thermal voltage, I0 is the current flowing through the diode and V0 is the voltage flowing across PV. An inverter is used to convert the DC power of the PV system into AC power on the microgrid side when a PV farm output is linked to the MG [28]. The first-order lag approximate model to the nonlinear dynamics is considered in this study.
2.3. Modeling the WT
In the majority of MGs, the WT is regarded as a key renewable energy system. The mechanical power output of a WT system is highly variable because of the sporadic nature of wind speed; it is given in (10).
where ρ is the air density (in kg/m3), As is the area swept (in m2), K is the power coefficient and Vw is the wind speed (in m/s). The essential RESs provided by PV and wind energy systems generate a precarious and sporadic means of output power. Therefore, these adverse effects on the industrial consumer of non-ESSs have been properly sized and installed according to the technical requirements. The first-order lag approximate model to the nonlinear dynamics of the WT is considered in this study [8].
2.4. Modeling the FC
The ESSs incorporate a fuel cell to counteract the potential failures brought on by the intermittent nature of the WT and PV systems. In Figure 2, an inverter and an interconnection device that operate in synchrony with the HIMG follow the FC block. It uses hydrogen as an input to produce energy. The FC functions as a backup generator and a production controller for electricity. According to the requirement, fuel cells can deliver electricity at peak times. The approximate first-order lag model of the fuel cell's nonlinear dynamics is considered in this study as follows [22].
2.5. Modeling the EV
To reduce frequency issues in the HIMG, the EVs can also take part in frequency stabilization via the EV aggregator. Through the use of V2G technology, the EV batteries may be used in the frequency stability analysis. In V2G and grid-to-vehicle systems, the charging/discharging state of EVs may be regulated to control the power flow [35]. A large-scale battery system may be created by using an EV's battery. The total charged or drained power of the EVs in the controlled state can be simply estimated by using the EV battery. The AFSMC output signal (Uev) in Figure 2 represents the model input. Pev represents the overall power output of the EVs' charging and discharging systems. Eag is the result of the total energy model and represents the total energy of all of the controlled EVs. The suggested control structure shown in Figure 2 may be used by EVs after charging to give a frequency signal only when the condition as mentioned in (9) is true:
where Emxag and Emnagcontrol stands for the maximum and minimum energy capacities, respectively. The computation of (9) through (10) to arrive at the aforementioned energy capacity limitations is dependent on the control strategy. The total number of EVs that can be controlled (Ncon) and exchanging power with the HIMG can be calculated as:
where Nconin, NconI and NconO stand for the initial number of controllable EVs, the number of EVs moving from the charging state to the controllable state and the number of EVs transitioning from the charging state to the driving state, respectively. Appendix I contains the corresponding values used for these expressions. Readers interested in learning more about total energy management may refer to [36‒38]. The average SoC (SoCavg) of the controllable EV can be represented as:
2.6. Modeling the battery
Solar PV and wind energy systems have brought many technical difficulties, including power quality, dependability, safety, grid operation, and economics [8]. Due to the climatic variables that have a significant influence on power generation, solar PV and wind energies are quite unpredictable, therefore, DGs cannot always give adequate assistance to the power system. An essential component of standalone microgrid systems is the battery. This provides a substantial contribution to maintaining system stability by quickly supplying power to the system. By exchanging power with the MG, the battery energy storage functions as a local active power source to stabilize the frequency deviation response. The battery's capacity is (in kWh) as follows:
where Pl stands for the total energy load that is transferred to the renewable energy system, K for battery autonomy, D for depth of discharge (percent) to prevent driving the battery's storage to its minimum state, and ηi and ηb for inverter and battery efficiency (percent), respectively, to take energy transfer losses into account. As a standard, the lower and upper limits of the SoC were considered as 80% and 90%, respectively. In the case of EVs, and within this range, the EVs are allowed to participate in the V2G scheme of operation. In the case of local batteries integrated into the system, the limits were set according to the standard as 20% and 90%, respectively.
2.7. Modelingthe state space
To describe the dynamics of the test system HIMG, the state-space modeling is provided in (18)–(27). These 10 state equations with 10 state variables make up the state-space model [25].
The state dynamics of the system considered are rewritten in the following equations:
where Dα stands for a fractional integral term of α order (0 < α < 1) and the following terms are introduced: A, B, C, D, U and E represent the state matrix, system matrix, input matrix, direct transition matrix, and input, respectively, and can be represented as
3.
Proposed controller design
HIMG control may be calculated by first looking at the control of each of its EVs. This HIMG was equipped with a controller to manage the combined power of the DG, FC, and EVs. Here, the outcomes of the fractional order controller have been utilized. Additionally, a nonlinear SMC controller is suggested to enhance the dynamic performance while bringing about strong stability.
3.1. Theory of fractional calculus
The definition of the primary operator rDtα(.) in fractional calculus is given in (29), where r, t and α are the operation's limits and order, respectively. Although α Ɛ R, α may alternatively be a complex number [39].
The Grunwald-Letnikov definition (30), the Riemann-Liouville definition (31) and the Caputo definition (32) are the three definitions that are frequently used for the fractional differintegral for n - 1 < α < n.
Attribute 1 ([40]): For every fixed value, ξ Ɛ R then rDtα.ξ = 0.swz
Attribute 2 ([40]): For α Ɛ (0, 1) and w(t) Ɛ Cm [0, T], then
Lemma 1 ([40]): Let ψ(t) Ɛ Cm [0, T], and α Ɛ (0, 1) then,
Proof: Due to (33), one obtains
Further, |ψ(t)|ˈ = sign(ψ(t)) * ψ(t)ˈ; as a result, one finds (26) as
Theorem 1 ([41]): Assume that given an α Ɛ (0, 1), the Lipschitz-satisfying fractional-order system rDtα.y(t) = g (y, t) has an equilibrium point similar to y = 0. Consider that class-K functions α1, α2, and α3 fulfill the Lyapunov function V (t, y(t)).
where p Ɛ (0, 1), rDtα is the system's equilibrium point. Then, y(t) is asymptotically stable.
Theorem 2 ([30]): Assuming the subsequent fractional system is
let ˄: (0, ꝏ) [0, X] → Rn present as
The fractional order system (39) may therefore be expressed as
where u(w) = (2sin(απ)/ π). w1-2α, α Ɛ (0, 1)
3.2. FSMC controller design
The suggested FSMC has a sliding surface for integration. The additional degree of freedom offered by fractional operators might enhance the controller's performance as compared to a regular SMC. Fractional calculus offers additional design options for control system architecture since it enhances the variety of differential and integer degrees of freedom as compared to classical calculus. In this work, a fractional order integral type controller has been employed, and it is shown in Figure 4.
kp and ki are controller gains, α = 1 is the integral component's order and e is the system error. A fractional integral sliding surface is created in this case and given below as [29]
where K, a vector of positive constants and 1 < p < 2 are present. According to the sliding mode control theory, the system should meet the following conditions when it is in the sliding mode:
By using the attribute 1, Dα.S(t) = 0. Hence,
The aforementioned equation may be simplified as follows:
The state trajectories of this sliding mode dynamic, which is stable, reduce to the equilibrium X = 0, according to the frequency distributed model theorem. As per Theorem 2, fractional sliding dynamics (36) can be demonstrated by the following equation:
3.3. Stability analysis
The benefits of using a positive Lyapunov function of the form V1=12∫∞0a(w)Λ2(w,t)dw include [42]:
The fractional-order sliding dynamics (45) are thus asymptotically stable according to Theorem 1. Now, a reliable controller is created to validate the presence of sliding action.
Theorem 3. Take into account the linear system of fractional order (18). The system's state trajectories will eventually reach its equilibrium point if it is subject to control law in this case.
Proof. Taking the Lyapunov Function given in (49) gives
Using Lemma 1 and applying Dα of V2(t) the equation becomes
S can be replaced from (42) in (50) as
Applying the DαX from the dynamical model (28) and the fractional integral sliding surface (42), using the AFSMC controller (45) becomes:
Using Lemma 1:
Case 1: If s > 0, then sign (s) = 1and 0 < tan h(s) = Ɛ < 1; then,
Case 2: If s < 0, then sign(s) = -1 and -1 < tan h(s) = ξ < 0; hence,
As a result, Theorem 1 states that the state trajectories of the fractional order system (18)–(27) will asymptotically converge to S = 0, and that, if both kp and ki are chosen to be positive, the lemma is satisfied.
4.
Teaching-learning-based optimization algorithm
An effective meta-heuristic algorithm that can assist in resolving the system's intricate activities is required for the HIMG design. Numerous real-time engineering problems can be resolved by using the population-based optimization method known as the ITLBO algorithm. Incredibly, ITLBO performs better than other meta-heuristic algorithms. The teacher and a group of students who represented the set of solutions were included in the initial population of the ITLBO algorithm. There are three stages to how the ITLBO operates: Teacher (choosing the teacher), Learner Phase 1 (Best Classmates) and Learner Phase 2. While the instructor imparts information to each student during the teacher phase, the two top students are picked and given the task of engaging with the other students during the learner phase I. All of the students engaged in random interaction throughout Learner phase II to raise their level of knowledge. The ITLBO can successfully avoid a local optimum due to the appropriate balancing of exploration and exploitation.
4.1. Literature review
The ITLBO is a teaching-learning-based optimization modification that has been successfully used in several technical applications. As a result, it may be claimed that ITLBO employs the fundamental idea of TLBO. Using the principles of the conventional school teaching and learning process as inspiration, Rao (2015) suggested a unique TLBO [43]. In this approach, the offered courses serve as the design variables and the population of interest is the class of students. The best person in the population is selected as a teacher in the TLBO algorithm's rounds, and the remaining individuals are changed into students. In TLBO, there is just one teacher who teaches the students and puts a lot of effort into helping them learn more [44]. The instructor stage and the learner stage are the two stages that makeup TLBO, just like with the ITLBO. A teacher tries to improve the class's average grade during the teacher stage. The amended solutions from each student may be written as follows:
where xnmt stands for the outcome of the teacher's instruction to the mth student, n stands for the nth class and is 3, and m stands for the mth student. The mth student in the nth class at the kth iteration is denoted as xnmk. The xntk is the teacher's accomplished result for the nth class at the kth iteration, and rd is a random integer between 0 and 1. Tf is a teaching factor that chooses the average outcome that has to be improved; it is chosen at random with equal probability, and it is stated as
Tf = 1/2, andMnkis the average outcome of the nth class at the kth iteration with the expression
where Ps = 45 is the population of each class.
All of the acceptable function values are retained after the teacher stage and used as input during the learner stage. Every instructor and student will be considered as a learner throughout the learner stage. Interacting with any of the random learners allowed the single learner to increase their knowledge. The update of each student may be expressed as follows if the arbitrary learner has greater knowledge than the single one:
where xnml stands for the outcome of the mth single in the nth class at the kth iteration. The learners chosen arbitrarily are xi and xj. If xnml yields a greater function value, accept it. The learner phase's final acceptable function values are all retained, and these values serve as the input for the teacher phase of the subsequent iteration. Untill the termination criteria are met, repeat the instructor and learner phases.
4.2. Summary of ITLBO
With this innovative heuristic method, global optimums may be reached with less computation and with more consistency. The ITLBO uses several courses to find the best answer, with an instructor and a class of pupils in each class [45]. Each educator, whether a teacher or a student, interacts with a network of individuals. As already mentioned, the idea behind this algorithm is TLBO with improvements. The remaining answer is revised as follows by using (44):
where f stands for the fitness function. If (59), offers a greater function value, that value is accepted. Every teacher works to increase the knowledge of the pupils they are responsible for teaching in this way. Through conversation, if someone learns that others have more useful knowledge, their current solution will be modified based on that information, leading to a better solution, as follows
where xnml stands for the outcome of the mth single in the nth class at the kth iteration. xnmb may be stated as follows to represent the best solution updated from the people at the kth iteration:
xnmk stands for the collection of people with whom the mth learner engaged during the kth iteration of the nth class, and it may be written as follows:
where pij stands for the probability of interaction among the ith and the jth individuals, k stands for the iteration number, kmax = 120 is the maximum iteration, and Cp = 0.75 is the probability coefficient (0 < Cp < 1). Based on (60), the remaining solution is updated as
The ITLBO features a strong and reliable global search function, and it is also used to fine-tune the FSMC controller's coefficients. The FSMC controller's settings are adjusted via the ITLBO. The ITLBO method is used to discover the best AFSMC controller settings under typical operation circumstances. Each iteration of the optimization model will take into account the controllable variables of the HIMG system, i.e., the fitness functions and associated solutions, with each solution standing in for either a teacher or a pupil in the ITLBO. In this work, the ITLBO uses three classes for broader explorations, allowing each teacher to independently direct his or her students in that class, increasing the chance of finding a higher-quality optimal solution, or a guaranteed greater capacity for global searching. Additionally, the student can learn from other students in any class with a probability. These interactions, which come from several classes and dynamics, enable further exploitation during optimal searching.
4.3. Objective function
The reference frequency deviation under standard operating conditions is used to create the objective function. In terms of the error to improve the controller gain settings and the adaptive control system parameters, the following objective function is used in this study
The related limits are as follows:
All the parameters for AFSMC need to be optimized.
The goal of these ITLBO-optimized FSMC (AFSMC) controller is to achieve the set frequency values with the least amount of settling time, and to overshoot.
5.
Result analysis
The HIMG system was modeled and simulated in a MATLAB environment [21]. The FSMC controller's settings were set to operate under the same circumstances by the same objective function. All parameters of the proposed AFSMC (ITLBO-FSMC), FSMC and SMC along with discussed the system data are presented in Appendix-I.
The ITLBO proposed method has been employed to resolve this optimization difficulty and to determine the controllers' ideal set of gain settings. This search procedure has a strong stabilizer and can operate efficiently across a broad range of operating conditions. Before settling on this optimal set of controller values, the ITLBO algorithm was run several times. The work was tested and simulated using the acquired values. All of the data show that the suggested controllers significantly increase system stability.
Case-1: FdRs of the HIMG due to step load perturbation
In this case, the outputs of wind and solar energy are held constant at 0.015 pu and 0.01 pu, respectively, while the HIMG is exposed at t = 0 s to a step load perturbation of 0.01 pu. The FSMC, SMC, and controllers' HIMG frequency responses were contrasted with the recommended AFSMC controllers. The HIMG frequency response determined for various controllers is shown in Figure 5(a). From Figure 5(a), it has been revealed that there is an improved FdR of the HIMG for the suggested control approach. Figure 6 depicts the trajectory of the AFSMC parameter vectors, Δdg and Δev, which correspond to the various dispatchable units (b). The power outputs of the PV and WT systems are depicted in Figure 5(b). The comparative FdR transient parameters for each control system are shown in Table 1.
The Settling time (ST) and Peak (P) values for the suggested control strategy were improved by a maximum of 20.20% and 69.33%, respectively, according to Table 1. These findings show the proposed method's stronger performance for damping all oscillations with an early settling time. The comparative FdR transient parameters for each control system in terms of rise time (RT), damping ratio (DR), natural frequency (NF) and time constant (TC) are shown in Table 1.
Case-2: FdRs of the HIMG due to random load perturbation using dispatchable units
According to random load perturbation (RLP) of 0.01 pu at t = 0.55 s, and -0.02 pu at t = 3.25 s, FdRs of the HIMG in this situation are produced. To reduce frequency variations, only the dispatchable DG units are taken into account in this situation. Units that cannot be dispatched are not included. The comparative FdRs in Figure 6(a) make it abundantly evident that the proposed AFSMC outclasses the other control systems in relation to the FdR of the HIMG and superior FdR transient parameters. In this case, the power output of the EV is displayed in Figure 6(b). The relative power outputs of the DG and FC for the suggested method with and without the EV are shown in Figure 6(c)–(d), respectively.
Case-3: FdRs of the HIMG due to RLP using variable solar energy
In this case, the variable Ppv is taken into account while the FdRs of the HIMG are subject to the RLP pattern of -0.005 pu at t = 0.35 s, and 0.01 pu at t = 2.52 s. The suggested controller's and other controllers' frequency responses were contrasted. The frequency responses of several controllers were depicted in Figure 7(a). The power output of the EV is displayed in Figure 7(b). The relative power outputs of the DG and FC for the suggested method with and without the EV are shown in Figure 7(c)–(d), respectively.
6.
Conclusions
This study demonstrated the frequency stabilization of an HIMG, including EVs, by using an AFSMC controller. The benefit of the ITLBO algorithm has been shown and proven by applying the algorithm as a better tuning approach for optimally setting the controlling gain parameters. An HIMG is taken into account, which consists of loads, storage systems, EVs, wind farms, solar farms, FCs and diesel generators. Three distinct scenarios and instances have been used to simulate and study the effects of various situations on the primary frequency establishment. The outcomes allow for the drawing of certain conclusions.
1) The proposed approach of frequency control works effectively in a MG when RES penetration is strong. The adoption of EVs affects the frequency regulation capacity. When the V2G method was active for EVs, the frequency was well stabilized within the allowable margin, in contrast to when the V2G method was deactivated.
2) Various HIMG operation situations have been considered to validate the suggested controller's viability. In each case, the controller's performance has been compared to that of other well-known controllers. All the factors were considered in this proposed HIMG controller and provide a substantial performance improvement.
3) According to the simulation findings, the suggested controller performs very well in terms of achieving better performance index values corresponding to each situation than the controller applied in [24]. The proposed control approach also provides a low overshoot and settling time. Low internal resistance, the unpredictability of produced output and imbalanced system conditions are the significant difficulties that MGs have faced recently.
4) Due to the limited adoption and the fact that its maximum benefits of battery and ESS in industrial settings, the potential applications of this type of technology during the present transitional time are expected to bring successful outcomes.
5) The major limitation of the method approaches substantial financial investments. Further research is needed to deploy the HIMG.
Conflict of interest
The authors declare that there is no conflict of interest.
Appendix-I
HIMG parameter values: f = 50 Hz; 𝑀 = 0.25 pu/s; 𝐷 = 0.015 pu/Hz; Tt = 0.015 s; Tdg = 0.5 s; Ti = 0.04 s; Tc = 0.002 s; Tfc = 0.25s; Tbt = 0.1 s; Tpv = 1.5 s; Tfc = 4 s; Twt = 1.8 s; Tev = 1 s; Emxag = 1.161; Emnag = 1.032; Ncon = 86; Nconin = 80; NconI = 14; NconO = 20. The Controller parameter values: K = 1; p = 1.25.
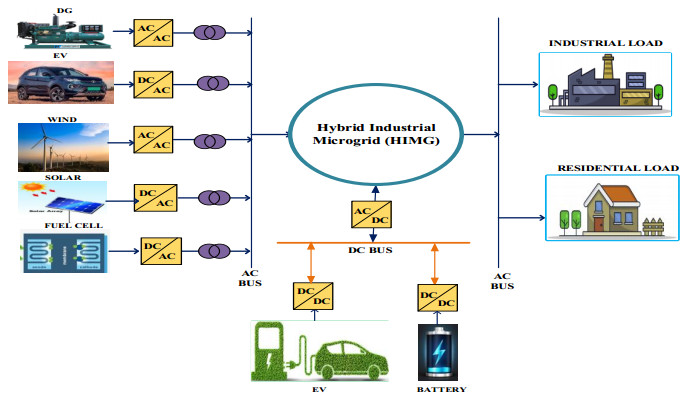









 Analysis of the modeling of the hybrid industrial microgrid made up of various energy sources (DG, WT, PV, EVs, FC and battery) has been studied in detail in this work.
Analysis of the modeling of the hybrid industrial microgrid made up of various energy sources (DG, WT, PV, EVs, FC and battery) has been studied in detail in this work. DownLoad:
DownLoad:










