Figure 1.
Equivalent model of the primary side of the distribution network.
When a fault occurs on a distribution line, transient fault signals fade quickly, leaving only a short period of time for measurement and sampling. In addition, timing discrepancies between multiple measuring devices affect the accuracy of fault localization. This study proposes a method for fault detection in distribution lines based on an auxiliary inductance approach, where auxiliary inductors are introduced after the trip to provide steady-state fault data for localization. For asymmetrical short-circuit faults, the fault voltage is calculated from current and voltage measurements at both ends of the line, and the ratio of positive to negative sequence voltages is used to compensate for the phase angle and generate fault location functions. For symmetrical short-circuit faults, the voltage ratio between two faulted phases eliminates asynchronous angles, facilitating the derivation of fault location functions. Simulation results show that this method achieves high accuracy and is robust to differences in fault location, transition resistance, fault types, and synchronous angles.
Citation: Weiji Zhou, Jun Lin, Zekun Long, Feifei Liu, Mingfei He. Research on fault location method for distribution lines based on additional inductance strategy[J]. AIMS Energy, 2025, 13(2): 250-264. doi: 10.3934/energy.2025010
| [1] | Pooja Khandare, Sanjay Deokar, Arati Dixit . Relay Coordination and Optimization techniques using DWT-Differentiation Algorithms for Fault Detection in Microgrid. AIMS Energy, 2020, 8(4): 563-579. doi: 10.3934/energy.2020.4.563 |
| [2] | Abdul Matin Ibrahimi, K Narayanan, Mohammed Elsayed Lotfy, Mir Sayed Shah Danish, Mikaeel Ahmadi, Tomonobu Senjyu . Transients outrush current analysis and mitigation: A Case study of Afghanistan North East power system. AIMS Energy, 2019, 7(4): 493-506. doi: 10.3934/energy.2019.4.493 |
| [3] | Stefania Conti, Santi A. Rizzo, Nunzio Salerno, Giuseppe M. Tina . Distribution network topology identification based on synchrophasor. AIMS Energy, 2018, 6(2): 245-260. doi: 10.3934/energy.2018.2.245 |
| [4] | Arqum Shahid, Ahsan Ali, Faheem Ashiq, Umer Amir Khan, Muhammad Ilyas Menhas, Sajjad Manzoor . Comparison of resistive and inductive superconductor fault current limiters in AC and DC micro-grids. AIMS Energy, 2020, 8(6): 1199-1211. doi: 10.3934/energy.2020.6.1199 |
| [5] | Zeid Al Qaisi, Qais Alsafasfeh, Ahmad Harb . Stability impact of integrated small scale hybrid (PV/Wind) system with electric distribution network. AIMS Energy, 2018, 6(5): 832-845. doi: 10.3934/energy.2018.5.832 |
| [6] | Tung-Sheng Zhan, Yih-Der Lee, Jheng-Lun Jiang . Optimal OCR coordination in a high penetration distribution power system using a refined immune algorithm with an auto-tuning reproductive mechanism. AIMS Energy, 2024, 12(6): 1225-1263. doi: 10.3934/energy.2024056 |
| [7] | Jinhua Tian, Yueyuan Zhang, Yanan Gao, Yu Qin, Bihan Fan, Cheng Zhang, Qiqi Zang . Distributed optimization and scheduling strategy for source load storage distribution grid based on alliance chain. AIMS Energy, 2024, 12(5): 946-967. doi: 10.3934/energy.2024044 |
| [8] | Mohammad Aman YAQOBI, Hidehito Matayoshi, Natarajan Prabaharan, Hiroshi Takahashi, Ashraf M. Hemeida, Senjyu Tomonobu . Interconnected standalone DC microgrid fault protection based on Self-Adaptive DC fault current limiter with hybrid solid state circuit breaker. AIMS Energy, 2021, 9(5): 991-1008. doi: 10.3934/energy.2021045 |
| [9] | Katherin Indriawati, Bambang L. Widjiantoro, Ali Musyafa . Design of sensor and actuator fault tolerant control system on wind turbine benchmark for Region II. AIMS Energy, 2019, 7(2): 111-126. doi: 10.3934/energy.2019.2.111 |
| [10] | Abdulrahman J. Babqi, NasimUllah, Ahmed Althobaiti, Hend I. Alkhammash, Asier Ibeas . Current model predictive fault-tolerant control for grid-connected photovoltaic system. AIMS Energy, 2022, 10(2): 273-291. doi: 10.3934/energy.2022015 |
When a fault occurs on a distribution line, transient fault signals fade quickly, leaving only a short period of time for measurement and sampling. In addition, timing discrepancies between multiple measuring devices affect the accuracy of fault localization. This study proposes a method for fault detection in distribution lines based on an auxiliary inductance approach, where auxiliary inductors are introduced after the trip to provide steady-state fault data for localization. For asymmetrical short-circuit faults, the fault voltage is calculated from current and voltage measurements at both ends of the line, and the ratio of positive to negative sequence voltages is used to compensate for the phase angle and generate fault location functions. For symmetrical short-circuit faults, the voltage ratio between two faulted phases eliminates asynchronous angles, facilitating the derivation of fault location functions. Simulation results show that this method achieves high accuracy and is robust to differences in fault location, transition resistance, fault types, and synchronous angles.
As distribution network topologies grow increasingly complex, enhancing automation levels and ensuring both reliability and user satisfaction in power supply have become critical objectives [1,2,3]. Accurate and prompt fault localization methods are essential for expediting line repairs and maintaining power supply dependability. For single-phase earth faults, the fault current is typically minimal, whereas other fault types generate larger fault currents that decay rapidly, leaving a narrow window for effective fault information extraction. This challenge is compounded by the limited availability of universal fault localization techniques applicable across all fault scenarios [4,5]. Currently, methods for finding faults in distribution networks are widely divided into traveling wave and impedance approaches. The traveling wave approach confronts issues such as difficulty in detecting wave reflections, stringent requirements for high-speed sampling equipment, and positional blind spots [6,7,8,9]. In contrast, the impedance method takes advantage of the neutral-point low-current grounding commonly used in medium-voltage distribution networks in China. Under single-phase earth fault conditions, the system can operate for 1–2 hours in a fault state, presenting a prolonged steady phase. However, other fault types trigger immediate protective actions, resulting in a brief transient phase. Based on the nature of fault information employed, the impedance method is further divided into transient-based [10,11,12] and steady state–based approaches [13,14,15]. Using double-end data minimizes errors caused by transition resistance and achieves high accuracy, making it a preferred choice for fault localization in distribution networks [16]. The transient approach examines fault-induced transient signals characterized by large amplitudes, which facilitates monitoring, though the signals decay quickly, limiting the effective analysis window. In [11], a time-domain method was introduced for locating single-phase earth faults by analyzing specific moments, which simplifies computations and enables rapid localization. However, it demands synchronized double-end data and high-performance sampling devices, making it less cost-effective. In [12], it was highlighted that most distribution network metering devices, such as feeder and transformer terminals, rely on local synchronization. Transmission introduces a timing error of 1~3 ms. To mitigate errors from unsynchronized data, voltage and current conditions are relaxed, transforming the localization problem into an optimization model. Nonetheless, this adjustment cannot entirely negate the influence of data asynchrony in principle.
The steady-state approach primarily examines stable signals during faults, where the fault electrical quantities exhibit low amplitude yet remain consistent and cost-effective. In [16], formulating a fault location equation based on zero-sequence signals captured during the steady-state phase following a single-phase earth fault was suggested. Under low-current grounding systems, the relatively large zero-sequence impedance results in a measurable zero-sequence voltage for the fault phase. However, while the double-end method helps locate faults, it neglects the influence of unsynchronized data. To address this issue, a non-synchronous phase angle difference at both ends, forming positive and negative sequence networks, was introduced in [17]. Since positive and negative sequence phase angle deviations in the same circuit are identical, these differences can be eliminated from fault location equations, mitigating non-synchronism effects in principle. This technique is straightforward and reliable, avoiding complex iterations or searches. Nevertheless, in cases where the interval between fault occurrence and protection action is brief, higher harmonics complicate the accurate measurement of positive and negative sequence quantities. In small-current grounding systems, protection typically remains inactive post-fault, enabling effective detection of steady-state components once harmonics dissipate. However, in systems with high zero-sequence impedance, negative sequence voltages are minimal, making precise measurement challenging and limiting fault location accuracy. Additionally, these methods are generally restricted to single-phase earth faults, as the rapid three-phase changes in other fault types hinder the acquisition of steady-state data [18,19,20]. In [20], it was proposed to install limiting resistors post-fault to reduce fault currents, allowing the affected line to operate temporarily with the fault. This enables secondary measurement equipment to conduct fault analysis, though current research on fault location using this approach remains limited.
In summary, extracting fault information after distribution network failures is challenging, and most existing algorithms struggle to fully resolve non-synchronism issues. To overcome these limitations, this study introduces a fault location method for overhead lines incorporating additional inductance. By adding inductance following line tripping, the short-circuit current is constrained, extending the fault operation period and enhancing the amplitude and measurement window of negative sequence components. This provides steady-state positive and negative sequence quantities for fault location. Utilizing double-end data, the method theoretically eliminates non-synchronism effects, improving localization accuracy. Finally, simulations conducted with PSCAD/EMTDC validate the method's reliability and precision.
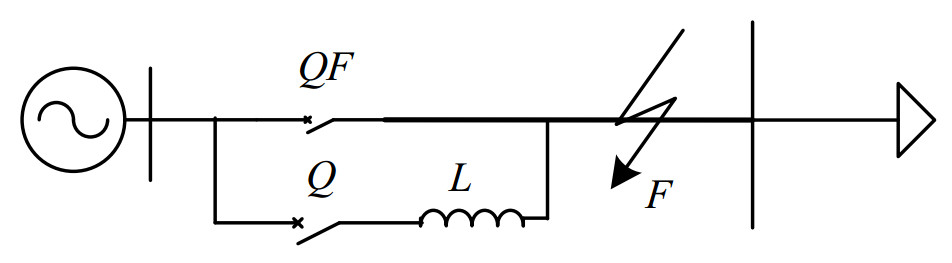
In order to solve the problem of determining the amount of power in distribution lines during faults, this study proposes a system that combines control and protection measures with algorithmic solutions. An auxiliary inductor is connected in parallel with the bus breaker to activate the faulted line after the breaker trip. With this setup, steady-state electrical quantities can be obtained for distance measurements. The equivalent model of the primary side of the line under fault conditions is shown in Figure 1.
In Figure 1, L is the system auxiliary inductor, Q is the auxiliary switch, and QF is the line circuit breaker.
The cooperation scheme utilizing auxiliary inductance operates as follows: (1) During normal operation, both QF and the auxiliary switch Q remain in an open position, with the inductance in an inactive state. (2) When a fault occurs under the small current grounding method at the power system neutral point, QF is tripped by the protective system (with the current setting determined based on the original fault current of the line), and the QF circuit breaker disconnects. In the event of a single-phase-to-earth fault, the alteration in fault current is insignificant and remains below the prescribed threshold, thereby enabling the line to function with the fault for a designated period. If distance measurement is required, QF is tripped, and switch Q is closed. (3) Upon closing switch Q, the additional inductance is connected, and the faulted line enters the steady-state phase following the transient process (referred to as the post-protection steady-state). Once the steady-state fault information has been collected, the auxiliary switch Q may be opened to allow for maintenance, or if deemed an instantaneous fault, the line circuit breaker may be closed to resume operation.
The use of steady-state fault data, after protection has been applied using the symmetrical component method, has shown that for faults other than single-phase to earth, the power supply remains intact. When the inductance is connected, a higher fault current flows through the line. In addition, the introduction of the inductance can reduce the fault current in the faulted phase. The voltage and current of the positive and negative sequence electrical quantities derived from the three-phase line provide crucial information about the fault event. In the case of a single-phase-to-earth fault, after the inductance has been connected and with the power supply still operational, the fault current entering the fault point remains relatively low. In such a scenario, the power supply is maintained through the positive sequence network, allowing the effective measurement of a significant positive sequence electrical quantity on the faulted phase [21]. Figure 2 illustrates the equivalent negative sequence network of the line for the negative sequence component.
In Figure 2, ZS2, Z2, and Zeq2 represent the equivalent negative-sequence impedance on the power supply side, the negative-sequence impedance of the line, and the equivalent negative-sequence impedance at the fault point, respectively. Uf2 denotes the negative-sequence source.
As illustrated in the figure, the negative-sequence voltage decreases progressively from the fault point toward the power-side grounding point, with the voltage measured at point 2 being higher than that at point 1. Consequently, point 2 is selected as the first electrical measurement point in this study. In the absence of additional inductance, the negative-sequence network impedance along the line is composed of ZS2 and Z2, with points 1 and 2 treated as equivalent. The negative-sequence voltage, derived from the three-phase voltage at the end of the line, is divided by ZS2. When ZS2 is small, the amplitude of the negative-sequence voltage at the first end also decreases, which may obscure fault information. Therefore, incorporating additional inductance helps to increase the amplitude of the negative-sequence voltage, enhancing the clarity of the fault signal.
Following a system failure, the equivalent circuit representing the network in its faulty state under the cooperative scheme using auxiliary inductors is shown in Figure 3.
In Figure 3, L represents the additional inductance, while IL represents the current passing through inductance L during the fault. ES refers to the power supply at the moment of the fault. Z1 is the line impedance preceding the fault point on the line, ZS represents the system's equivalent impedance at the measurement point, and Rf is the transition resistance at the fault location.
After activation of the protection strategy described in this article, the current flowing through the additional inductance will not undergo a sudden change that may cause a transient overvoltage due to operation, but the withstand voltage of the distribution lines is generally designed to withstand lightning over voltages greater than the operational overvoltage at that time, so no special protective devices are required. In the event of a permanent fault occurring after system operation, IL is limited by the inductance of the connection. In the event of a three-phase short-circuit fault, the transition resistance at the busbar is effectively zero. This is due to the fact that the line is completely short-circuited after the inductance and the short-circuit current IL is:
| IL=ESjω0L+ZS | (1) |
In Eq (1), ω0 is the system frequency. Based on Eq (1), the additional inductance L is obtained as:
| L=ESILjω0−ZSjω0 | (2) |
In this approach, once the inductor is connected, the line continues to operate with the fault for a specific duration. To maintain the safety of the line, the current during this period must not exceed 1.2 times the rated current. Moreover, in order to ensure the accurate measurement of electrical quantities following a fault, it is essential that the line current is of a sufficient magnitude to exceed the minimum detection value of the current transformer. In consequence, the potential range of potential values for IL is as follows:
| Ic≤IL≤1.2Ie | (3) |
In Eq (3), Ie is the rated current, and Ic denotes the smallest amplitude measurable by the current transformer. Considering the uncertainties associated with the fault location, as well as the attenuating influence of line resistance and supplementary inductance on the amplitude of the line current, it is recommended that IL be set to approximately 1.2 times Ie.
The feeder terminal unit (FTU) plays a crucial role in enabling device-level coordination, supporting cooperative operational schemes. Following a fault event, the system can transition into a steady-state process by activating an inductor, allowing distance measurement to be performed using steady-state data. Within this cooperative framework, this study employs a distance measurement approach based on steady-state data. Compared to methods relying on transient signal analysis at specific instants, the proposed method imposes fewer demands on sampling equipment, offers superior economic viability, extends the effective measurement duration, and simplifies the assessment of electrical quantities.
By adjusting the parameters of the added inductance, the post-fault short-circuit current can be regulated to approximate the rated value. This adjustment facilitates the calibration of the measuring transformer and reduces measurement errors. For asymmetrical faults occurring within the system, the inclusion of inductance enhances the magnitude of the negative sequence component, enabling accurate measurement of its steady-state value during distance evaluation. This allows both positive and negative sequence components to be utilized for correcting timing discrepancies. During various asymmetrical fault scenarios, the line can continue operating with the fault temporarily. Under such conditions, the positive and negative sequence networks remain equivalent, permitting the application of a unified distance measurement equation.
In this study, a lumped parameter π-type equivalent circuit is adopted on both sides of the fault location to analyze the steady-state performance after the activation of protective measures. The occurrence of an asymmetrical fault on the transmission line is examined by applying the symmetrical components method to evaluate the positive and negative sequence networks, which share identical sequence impedances under fault conditions, as illustrated in Figure 4.
In Figure 4, K represents the ratio of the distance lSF from the S terminal to the fault point F relative to the total line length lSN; C1 and Z1 denote the total capacitance and impedance of the line, which can be derived from the total line length and per-unit length parameters. US1, US2, IS1, and IS2 correspond to the positive sequence voltage, negative sequence voltage, and currents at the S-terminal of the faulted line, with the voltages measured after the inductance is applied. UN1 and UN2 represent the positive and negative sequence voltages at the N-terminal of the line. These values can all be synthesized from the fundamental components of the three-phase electrical quantities, and the recorded data are expressed in the frequency domain. ISC1, ISC2, INC1, and INC2 are the equivalent earth capacitance currents of the positive and negative sequences at both ends of the line. ES1 refers to the power supply during the fault event. ZS1 and ZN1 represent the positive sequence resistances on the power supply side and the load side, respectively. These resistances are difficult to determine during a fault and are not critical, as they can be disregarded in the derivation.
In Figure 4, the parameter K denotes the ratio of the distance lSF, measured from the S terminal to the fault point F, to the total line length lSN. The symbols C1 and Z1 represent the overall capacitance and impedance of the transmission line, respectively, which are determined based on the total line length and per-unit-length characteristics. US1, US2, IS1, and IS2 signify the positive and negative sequence voltages and currents at the S terminal of the faulted line, where the voltages are recorded following the application of inductance. UN1 and UN2 correspond to the positive and negative sequence voltages observed at the N terminal. These quantities are synthesized from the fundamental components of three-phase electrical signals and are represented in the frequency domain. Additionally, ISC1, ISC2, INC1, and INC2 denote the equivalent earth capacitance currents for the positive and negative sequences at both ends of the transmission line. The term ES1 refers to the power source during the fault condition. The parameters ZS1 and ZN1 indicate the positive sequence impedances on the source side and load side, respectively. While these impedances are challenging to measure during fault events, their precise values are not critical and can be omitted from the derivation process.
The sequence voltages at the fault point F can be derived from the sequence voltages at both ends of the transmission line, the sequence currents at the bus side, and the line impedance. These electrical quantities, measured at the S and N terminals, provide the necessary data to calculate the positive and negative sequence voltages at the fault location.
| {˙USF1=˙US1−(˙IS1−˙ISC1)Z1K˙UNF1=˙UN1+(˙IN1+˙INC1)Z1(1−K)˙USF2=˙US2−(˙IS2−˙ISC2)Z1K˙UNF2=˙UN2+(˙IN1+˙INC1)Z1(1−K)˙IN1=˙UN1/ZN1˙IN2=˙UN2/ZN1 | (4) |
In Eq (4), USF1, UNF1, USF2, and UNF2 represent the positive and negative sequence voltages at the fault point, derived from the measurement data at the S and N ends, respectively.
The voltage at the fault point, derived from the steady-state voltages and currents at both the S and N terminals within the positive and negative sequence networks, remains constant. This allows the fault distance to be determined using either the positive or negative sequence electrical quantities separately. However, to apply dual-ended data for fault distance calculation, synchronization between the data from both ends is necessary. With the meter at the S end serving as the reference time, there exists a time synchronization error ranging from 1 to 3 ms between the meter at the N end and the meter at the S end. If the phase angles of the voltages at both ends are calculated at the same moment, this timing error impacts the accuracy of the measured phase angles, as noted in reference [17]. We define the phase angle affected by this timing error as the unsynchronized phase angle δd, which allows the voltage at the N end to be represented as:
| ˙U′Nn=˙UNnejδd | (5) |
In Eq (5), n = 1, 2 represent the positive and negative sequences, respectively. It denotes the synchronized data at the N terminal.
When data from both ends are synchronized, the fault point voltages calculated at each end are identical. As a result, from Eqs (6) and (7), we can derive:
| ˙US1−(˙IS1−˙US1jωC1K/2)Z1K=˙UN1ejδdD1 | (6) |
| ˙US2−(˙IS2−˙Us2jωC1K/2)Z1K=˙UN2ejδdD1 | (7) |
| D1=1+[(1−K)Z1+1/ZN1]jωC1(1−K)/2 | (8) |
Dividing Eq (6) by Eq (7) yields:
| ˙US1−(˙IS1−˙US1jωC1K/2)Z1K˙US2−(˙IS2−˙US2jωC1K/2)Z1K=˙UN1ejδd˙UN2ejδd=˙UN1˙UN2 | (9) |
At this juncture, it is possible to eliminate the phase angle error, and by simplifying Eq (9), we can obtain a quadratic equation in complex numbers as follows:
| {K+2aK+b=0a=˙UN1˙IS2−˙UN2˙IS1jωC1(˙US1˙UN2−˙UN1˙US2)b=2/jωC1Z1 | (10) |
By solving Eq (10), the ratio K, representing the fault distance relative to the total cable length, is obtained. While solving the quadratic complex equation might lead to an erroneous root, K should logically be a real number and cannot exceed 1, given practical constraints. However, errors inevitably arise in the measurement of electrical quantities, as well as during the calculation of sequence components concerning amplitude and phase angle, which influence the solution. Therefore, a formula for determining K is proposed as follows:
| {−δl≤Re(K)≤1+δl−1−δl≤Im(K)≤1+δl | (11) |
Here, δl represents the ratio of the maximum permissible error in the results to the total length of the line. Since medium and low voltage distribution network lines are generally shorter in distance, an accuracy requirement of 5% is reasonable; however, this can be adjusted based on the specific conditions of different lines.
The application and resolution of Eq (10) are limited to cases of asymmetrical faults. In symmetrical faults, such as three-phase short circuits, the negative sequence component does not exist in the faulted line, with only the positive sequence component remaining. Under these circumstances, the voltages and currents of phases A and B at the S terminal, along with the voltage at the N terminal, can replace the positive and negative sequence components in the earlier expressions. Following this substitution, the analytical method and resulting equations remain fundamentally unaltered, allowing for similar correction of phase angle deviations. Further discussion on this topic is beyond the scope of this paper.
To evaluate the effectiveness of the proposed method, simulations were conducted using PSCAD/EMTDC. A model of a 10 kV distribution network system was developed, as illustrated in Figure 5.
The voltage source is represented by an equivalent impedance of 0.55 + j0.32 Ω [22]. The fault occurs in 0.3 s. After 0.2 s, circuit-breaker QF1 is tripped by protection or manual operation (i.e., the inductor is connected when the circuit-breaker operates at 0.5 s). Switch K closes, connecting the inductor, and 0.5 s after it is connected, the switch opens, disconnecting the inductor. It is calculated that the additional inductance value is 0.1 h. The line parameters per unit length are provided in Table 1.
| Line parameters | Numerical value |
| Positive sequence resistance | 0.1700 Ω/km |
| Positive sequence inductance | 1.2096 mH/km |
| Positive sequence capacitance | 0.27 uF/km |
| Zero-sequence resistance Zero-sequence inductance |
0.23 Ω/km 5.4749 mH/km |
| Zero-sequence capacitance | 2.5 uF/km |
DownLoad:
CSV
To validate the single-phase earth fault analysis presented in Section 2.1, when a metallic fault occurs at the mid-point of a 10 km line, the steady-state negative sequence voltages at measurement points 1 and 2, calculated from the three-phase voltages, are shown in Figure 6.
As shown in Figure 6, the inductor is connected at 0.5 s. After a brief period, the three-phase voltages are recorded. A Fourier transform is subsequently employed to compute the steady-state negative sequence voltage. The negative sequence voltage at point 2 is significantly greater than that at point 1. The voltage at point 2 at this stage can be used for distance measurement calculations.
All measurement data in this article are in the frequency domain and are subjected to a Fourier transform, from which the fundamental voltage and current phasor values can be obtained. The data are input into MATLAB for calculation. For instance, if the feeder 1 is set with a fault distance of 2,000 m, and a single-phase grounding fault occurs with a transition resistance of 10 Ω, the equation coefficients at this point are a = 43,853.886 + 19,618.485i, and b = –17,541.835 – 7,847.663i. By substituting these coefficients into the equation, the solutions are obtained: k1 = 0.200343 + 0.000383i, and k2 = –8.770797×104 – 3.9236970×104i. According to Eq (11), k2 can be excluded, and k1 is the real root, indicating that the distance of the fault point from the beginning is 2,003.243 m. The accuracy of the method proposed in this article is verified in several aspects below.
To evaluate the effectiveness of the method proposed in this paper, a comparison is made between the steady-state method and a fast transient time-domain technique for locating faults in distribution networks. The distance measurement results for various types of short-circuit faults are presented in Table 2, with a transition resistance of 10 Ω in these scenarios.
| Fault location/km | Fault type | Transient time-domain method/km | Steady-state method/km |
| 2 | Single-phase grounding | 2.0027 | 2.0034 |
| Two-phase short circuit | 1.9987 | 2.0012 | |
| Two-phase grounding | 2.0047 | 2.0011 | |
| Three-phase short circuit | 2.0015 | 2.0032 | |
| 5 | Single-phase grounding | 5.0082 | 5.0152 |
| Two-phase short circuit | 5.0061 | 5.0008 | |
| Two-phase grounding | 5.0083 | 5.0015 | |
| Three-phase short circuit | 4.9821 | 5.0082 | |
| 7 | Single-phase grounding | 7.0081 | 6.9812 |
| Two-phase short circuit | 7.0192 | 7.0055 | |
| Two-phase grounding | 6.9921 | 7.0062 | |
| Three-phase short circuit | 7.0255 | 6.9852 |
DownLoad:
CSV
The evaluation of the distance measurement results for the distribution lines, as shown in Table 2, indicates that the proposed steady-state method achieves a maximum absolute error of 18.8 m, a maximum relative error of 0.36%, and an average relative error of 0.12%. For single-phase earth faults, the average relative error is recorded at 0.24%. In comparison, the transient time domain method gives a maximum absolute error of 25.5 m, a maximum relative error of 0.38%, and an average relative error of 0.20%, with an average relative error of 0.13% for single-phase earth faults. The relatively lower accuracy of the steady-state method for single-phase earth faults can be explained by the reduced magnitudes of the steady-state fault current and the negative sequence voltage. However, for other fault types, the steady-state method achieves superior accuracy in distance measurement, surpassing the transient method. Furthermore, the proposed method consistently maintains a relative error of less than 1%, regardless of fault type or location, ensuring compliance with the required accuracy standards for fault distance estimation.
To evaluate the accuracy of the proposed methodology and the influence of the transition resistance on the fault location estimation, Table 3 shows the fault location results for different transition resistances. In these cases, the fault location is 5 km, and the fault type is a two-phase short circuit.
| Transition resistance/Ω | Transient time-domain method/km | Relative error | Steady-state method/km | Relative error |
| 10 | 5.0061 | 0.12% | 5.0008 | 0.016% |
| 100 | 5.0095 | 0.19% | 5.0034 | 0.068% |
| 500 | 5.0462 | 0.92% | 4.9975 | 0.050% |
DownLoad:
CSV
Analyzing the ranging results under different transition resistances, it is evident that the steady-state method outlined in this paper gives relatively small relative errors over a range of transition resistances, thus meeting the requirements of fault ranging. In contrast, the transient time-domain method experiences higher measurement errors, as an increase in contact resistance reduces the fault current. However, the method presented in this paper is less affected by changes in contact resistance due to the current-limiting effect of the additional inductance. This helps to amplify the negative sequence component and minimize the effect of junction resistance on the measurement.
To confirm the reliability of the distance measurement approach outlined in this study under various non-synchronous phase angles, considering the timing error mentioned above, which ranges from 1 to 3 ms, the range of non-synchronous phase angles is approximately 0–54 degrees. The simulation results of various fault location algorithms under various non-synchronous phase angles are shown in Table 4.
| Asynchronous phase angle/° | Transient time-domain method/km | Relative error | Steady-state method/km | Relative error |
| 54 | 5.5215 | 10.63% | 4.9958 | 0.084% |
| 25 | 5.1215 | 2.43% | 5.0046 | 0.092% |
| 0 | 5.0095 | 0.19% | 5.0034 | 0.068% |
| 25 | 4.7862 | 4.27% | 5.0089 | 0.178% |
| 54 | 5.6862 | 13.72% | 5.0012 | 0.024% |
DownLoad:
CSV
A comparison of the distance measurement results obtained using the two methods reveals, as shown in Table 4, that the algorithm that neglects phase angle corrections experiences a maximum relative error of 13.72% under conditions of severe timing errors. This underscores the substantial influence of timing errors on phase angle determination, ultimately compromising the precision of distance measurement. Conversely, the steady-state approach proposed in this study demonstrates robust resistance to timing errors, preserving a high level of measurement accuracy.
To address the challenges of fault information extraction and timing discrepancies in distribution networks, which affect the accuracy of distance measurement, this paper presents a fault-handling strategy using an auxiliary inductor. Within this framework, a fault distance calculation method is applied using asynchronous data from both ends of the line. The effectiveness and advantages of the proposed algorithm are validated by simulation results. The auxiliary inductor-based fault location technique is independent of transition resistance, fault type, and fault distance, maintains high accuracy over a range of asynchronous angles, and satisfies fault location requirements. Compared to conventional transient-based methods, the approach presented here offers greater adaptability to varying transition resistances and asynchronous angles. However, for practical lines with intermittent arcing faults where multiple transient processes occur, achieving steady-state data may require extending the duration of the auxiliary inductor connection.
This study focuses primarily on the analysis of traditional radial distribution networks. For meshed networks and distribution systems incorporating distributed energy resources, where circuit breakers are installed at both ends of the line, future investigations are expected to address the coordinated operation of these circuit breakers. Such efforts could facilitate the further development of a fault location methodology for distribution lines using an auxiliary inductor.
The successful completion of this paper would not have been possible without the support of the Chinese Postdoctoral Research Station (Grant No. 357939), the Xinjiang Uygur Autonomous Region Major Science and Technology Project (Grant No. 2022294467) and the Tianchi Talent Program of Xinjiang Uygur Autonomous Region (2025, Mingfei He). We are grateful to both for their invaluable contributions.
The authors declare that they have no known competing financial interests or personal relationships that could have influenced the research presented in this paper.
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Zhou Weiji (First Author): Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Software, Validation, and Writing—original draft. Lin Jun: Investigation, Resources, and Project administration. Long Zekun: Investigation, Resources, and Project administration. Liu Feifei: Investigation, Resources, and Project administration. He Mingfei (Corresponding Author): Conceptualization, Methodology, Visualization, Project administration, Funding acquisition, and Writing—review & editing.
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
| [1] |
Shu HC, Dai Y, An N, et al. (2023) Grounding electrode line fault location method based on simulation after test and deduction. Electr Power Syst Res 215: 108952. https://doi.org/10.1016/j.epsr.2022.108952 doi: 10.1016/j.epsr.2022.108952
|
| [2] |
Li Y, Wei X, Lin J, et al. (2023) A robust fault location method for active distribution network based on self-adaptive switching function. Int J Elec Power 148: 109007. https://doi.org/10.1016/j.ijepes.2023.109007 doi: 10.1016/j.ijepes.2023.109007
|
| [3] |
Liang Y, He A, Yuan J, et al. (2023) An accurate fault location method for distribution lines based on data fusion of outcomes from multiple algorithms. Int J Elec Power 153: 109290. https://doi.org/10.1016/j.ijepes.2023.109290 doi: 10.1016/j.ijepes.2023.109290
|
| [4] |
Wen J, Qu X, Liu J, et al. (2024) A novel fault location method for the active distribution network based on dynamic quantum genetic algorithm. Electr Eng 106: 4719–4735. https://doi.org/10.1007/s00202-024-02244-8 doi: 10.1007/s00202-024-02244-8
|
| [5] |
Mansourlakouraj M, Hosseinpour H, Livani H, et al. (2022) Waveform measurement unit-based fault location in distribution feeders via short-time matrix pencil method and graph neural network. IEEE Trans Ind Appl 59: 2661–2670. https://doi.org/10.1109/TIA.2022.3231586 doi: 10.1109/TIA.2022.3231586
|
| [6] |
Hu K, Cai Y, Cai Z, et al. (2022) Fault location method based on structure-preserving state estimation for distribution networks. Iet Gener Transm Dis 16: 3004–3015. https://doi.org/10.1049/gtd2.12492 doi: 10.1049/gtd2.12492
|
| [7] |
Bayati N, Mortensen LK, Savaghebi MSHR (2022) A localized transient-based fault location scheme for distribution systems. Sensonrs 22: 2723. https://doi.org/10.3390/s22072723 doi: 10.3390/s22072723
|
| [8] |
Wang C, Li P, Xu X, et al. (2022) A DC fault location method of multiterminal flexible DC distribution network. Math Probl Eng 2022: 8120857. https://doi.org/10.1155/2022/8120857 doi: 10.1155/2022/8120857
|
| [9] |
Rezaei D, Gholipour M, Parvaresh F (2022) A single-ended traveling-wave-based fault location for a hybrid transmission line using detected arrival times and TW' s polarity. Electr Pow Syst Res 210: 108058. https://doi.org/10.1016/j.epsr.2022.108058 doi: 10.1016/j.epsr.2022.108058
|
| [10] |
Kim SH (2022) Dimensionless impedance method for the transient response of pressurized pipeline system. Eng Appl Comp Fluid 16: 1641–1654. https://doi.org/10.1080/19942060.2022.2108500 doi: 10.1080/19942060.2022.2108500
|
| [11] |
Duarte N, Conti AD, Alipio R (2021) Assessment of ground-return impedance and admittance equations for the transient analysis of underground cables using a full-wave FDTD method. IEEE Trans Power Deliver 37: 3582–3589. https://doi.org/10.1109/TPWRD.2021.3131415 doi: 10.1109/TPWRD.2021.3131415
|
| [12] |
Won CY (2023) A virtual impedance-based flying start considering transient characteristics for permanent magnet synchronous machine drive systems. Energies 16: 1172. https://doi.org/10.3390/en16031172 doi: 10.3390/en16031172
|
| [13] |
Gomis-Bellmunt O, Song J, Cheah-Mane M, et al. (2022) Steady-state impedance mapping in grids with power electronics: What is grid strength in modern power systems? Int J Elec Power 136: 107635. https://doi.org/10.1016/j.ijepes.2021.107635 doi: 10.1016/j.ijepes.2021.107635
|
| [14] |
Monteiro FMDS, De Souza JV, Asada EN (2023) Analytical method to estimate the steady-state voltage impact of non-utility distributed energy resources. Electr Pow Syst Res 218: 109190. https://doi.org/10.1016/j.epsr.2023.109190 doi: 10.1016/j.epsr.2023.109190
|
| [15] |
Aquib M, Parth N, Doolla S, et al. (2023). An adaptive droop scheme for improving transient and steady-state power sharing among distributed generators in islanded microgrids. IEEE Trans Ind Appl 59: 5136–5148. https://doi.org/10.1109/TIA.2023.3272873 doi: 10.1109/TIA.2023.3272873
|
| [16] |
Wang S, Nie X, Li T, et al. (2024) Fast millimeter-wave three-dimensional holographic reconstruction based on target accurate distance. Opt Eng 63: 054104. https://doi.org/10.1117/1.OE.63.5.054104 doi: 10.1117/1.OE.63.5.054104
|
| [17] |
Deng LW, Lu JP, Shi JW, et al. (2020) A fault location method for hybrid lines based on two-terminal asynchronous data. Power Syst Technol 45: 1574–1580. https://doi.org/10.13335/j.1000-3673.pst.2020.0044a doi: 10.13335/j.1000-3673.pst.2020.0044a
|
| [18] |
Xie C, Li F, Fan Y, et al. (2019). Adaptive three-phase reclosing scheme of transmission lines without shunt reactors using additional capacitors. High Voltage Eng 45: 1811–1818. https://doi.org/10.13336/j.1003-6520.hve.20190604017 doi: 10.13336/j.1003-6520.hve.20190604017
|
| [19] |
Xiang L (2021) Key technology and application of primary and secondary fusion in distribution network. New Technol New Prod China 446: 66–68. https://doi.org/10.13612/j.cnki.cntp.2021.16.022 doi: 10.13612/j.cnki.cntp.2021.16.022
|
| [20] |
Liu J, Zhang Z, Rui J, et al. (2020) Adaptive reclosing of distribution lines based on primary and secondary device coordination. Power Syst Protec Control 48: 26–32. https://doi.org/10.19783/j.cnki.pspc.202084 doi: 10.19783/j.cnki.pspc.202084
|
| [21] |
Wang B, Cai L, Dong X, et al. (2017) A comprehensive analysis for asymmetrical short-circuit fault of electric power system with neutral-point unground. Prot Control Mod Pow 45: 149–153. https://doi.org/10.7667/PSPC160115 doi: 10.7667/PSPC160115
|
| [22] |
Hao W, Meng Z, Zhang Y, et al. (2023) Optimization model of the distribution network system by considering multi-types distributed power generation. J Jilin University 8: 1–11. https://doi.org/10.13229/j.cnki.jdxbgxb.20230119 doi: 10.13229/j.cnki.jdxbgxb.20230119
|
Figures(6) / Tables(4)
Weiji Zhou, Jun Lin, Zekun Long, Feifei Liu, Mingfei He. Research on fault location method for distribution lines based on additional inductance strategy[J]. AIMS Energy, 2025, 13(2): 250-264. doi: 10.3934/energy.2025010
| Line parameters | Numerical value |
| Positive sequence resistance | 0.1700 Ω/km |
| Positive sequence inductance | 1.2096 mH/km |
| Positive sequence capacitance | 0.27 uF/km |
| Zero-sequence resistance Zero-sequence inductance |
0.23 Ω/km 5.4749 mH/km |
| Zero-sequence capacitance | 2.5 uF/km |
DownLoad:
CSV
| Fault location/km | Fault type | Transient time-domain method/km | Steady-state method/km |
| 2 | Single-phase grounding | 2.0027 | 2.0034 |
| Two-phase short circuit | 1.9987 | 2.0012 | |
| Two-phase grounding | 2.0047 | 2.0011 | |
| Three-phase short circuit | 2.0015 | 2.0032 | |
| 5 | Single-phase grounding | 5.0082 | 5.0152 |
| Two-phase short circuit | 5.0061 | 5.0008 | |
| Two-phase grounding | 5.0083 | 5.0015 | |
| Three-phase short circuit | 4.9821 | 5.0082 | |
| 7 | Single-phase grounding | 7.0081 | 6.9812 |
| Two-phase short circuit | 7.0192 | 7.0055 | |
| Two-phase grounding | 6.9921 | 7.0062 | |
| Three-phase short circuit | 7.0255 | 6.9852 |
DownLoad:
CSV
| Transition resistance/Ω | Transient time-domain method/km | Relative error | Steady-state method/km | Relative error |
| 10 | 5.0061 | 0.12% | 5.0008 | 0.016% |
| 100 | 5.0095 | 0.19% | 5.0034 | 0.068% |
| 500 | 5.0462 | 0.92% | 4.9975 | 0.050% |
DownLoad:
CSV
| Asynchronous phase angle/° | Transient time-domain method/km | Relative error | Steady-state method/km | Relative error |
| 54 | 5.5215 | 10.63% | 4.9958 | 0.084% |
| 25 | 5.1215 | 2.43% | 5.0046 | 0.092% |
| 0 | 5.0095 | 0.19% | 5.0034 | 0.068% |
| 25 | 4.7862 | 4.27% | 5.0089 | 0.178% |
| 54 | 5.6862 | 13.72% | 5.0012 | 0.024% |
DownLoad:
CSV
| Line parameters | Numerical value |
| Positive sequence resistance | 0.1700 Ω/km |
| Positive sequence inductance | 1.2096 mH/km |
| Positive sequence capacitance | 0.27 uF/km |
| Zero-sequence resistance Zero-sequence inductance |
0.23 Ω/km 5.4749 mH/km |
| Zero-sequence capacitance | 2.5 uF/km |
| Fault location/km | Fault type | Transient time-domain method/km | Steady-state method/km |
| 2 | Single-phase grounding | 2.0027 | 2.0034 |
| Two-phase short circuit | 1.9987 | 2.0012 | |
| Two-phase grounding | 2.0047 | 2.0011 | |
| Three-phase short circuit | 2.0015 | 2.0032 | |
| 5 | Single-phase grounding | 5.0082 | 5.0152 |
| Two-phase short circuit | 5.0061 | 5.0008 | |
| Two-phase grounding | 5.0083 | 5.0015 | |
| Three-phase short circuit | 4.9821 | 5.0082 | |
| 7 | Single-phase grounding | 7.0081 | 6.9812 |
| Two-phase short circuit | 7.0192 | 7.0055 | |
| Two-phase grounding | 6.9921 | 7.0062 | |
| Three-phase short circuit | 7.0255 | 6.9852 |
| Transition resistance/Ω | Transient time-domain method/km | Relative error | Steady-state method/km | Relative error |
| 10 | 5.0061 | 0.12% | 5.0008 | 0.016% |
| 100 | 5.0095 | 0.19% | 5.0034 | 0.068% |
| 500 | 5.0462 | 0.92% | 4.9975 | 0.050% |
| Asynchronous phase angle/° | Transient time-domain method/km | Relative error | Steady-state method/km | Relative error |
| 54 | 5.5215 | 10.63% | 4.9958 | 0.084% |
| 25 | 5.1215 | 2.43% | 5.0046 | 0.092% |
| 0 | 5.0095 | 0.19% | 5.0034 | 0.068% |
| 25 | 4.7862 | 4.27% | 5.0089 | 0.178% |
| 54 | 5.6862 | 13.72% | 5.0012 | 0.024% |
