Hybrid B-spline collocation method with particle swarm optimization for solving linear differential problems

1.   Introduction

Ordinary differential equations (ODEs) are often used to model many practical applications in the fields of applied mathematics, physics, chemistry, and engineering. Generally, ODEs can be classified into two types: linear and non-linear ODEs. An ODE is said to be linear if the dependent variables and all their derivatives are of degree one, respectively. In contrast with the non-linear ODE, the dependent variables and their derivatives can be of degree greater than one and/or with any multiplication between the variables and derivatives. The general form of the $n$th-order ODE can be written as

for some $n\in\mathbb{N}, n\geq 2$, where $y$ is a function of $x$, $y'(x)$ is the first derivative with respect to $x$, and $y^n(x)$ is the $n$th derivative with respect to $x$. In this paper, a second-order linear two-point BVP will be considered in the following form:

where $\alpha, b, \alpha_1, \alpha_2$ are real numbers. Note that the boundary conditions in Eq (1.2) are called the Dirichlet conditions where are the most common type of boundary conditions and will be considered in this study. Moreover, Dirichlet boundary conditions ensure that the continuity of the solution will be obtained ^[1]. To solve physical problems is sometimes very challenging and requires extensive effort. Therefore, it is recommended to use numerical solutions for solving real-life application problems. Several numerical techniques, including the variational approach ^[2], finite difference method (FDM) ^[3,4,5], finite element method (FEM) ^[3,5], finite volume method (FVM) ^[3,5], and the shooting method (LSM) ^[4], have been applied to the two-point BVP solutions.

The cubic B-spline interpolation method (CBI) was proposed by ^[5] to solve for two-point BVP solutions. This study can be considered as a breakthrough as it gives the fundamental idea of the B-spline collocation method. Based on the computed maximum errors, it can be concluded that this method was more precise than the methods by ^[3]. Various numerical techniques based on CBI have been extensively used since then to solve both linear and nonlinear BVPs ^[6,7,8]. The cubic trigonometric B-spline collocation method (CTBSM) and extended cubic B-spline collocation method (ECBSM) were investigated by ^[9] as solutions to linear two-point BVPs. In comparison with the CBSM, the CTBSM produced better results when dealing with trigonometric problems. A hybrid version of the CBSM and CTBSM schemes has been presented in ^[10] to address nonlinear two-point BVPs. This research was proven to give promising results when the free parameter $\gamma$ was optimized. This is a crucial step in order to produce results with high accuracy.

In 2019, an improved method to solve singular BVPs of second order was constructed by leveraging an extended cubic B-spline basis ^[11]. A variety of third-order Emden-Flower-type problems were solved using a new cubic B-Spline approximation (NCBSA) by ^[12]. For the solutions of non-linear higher-order Korteweg-de Vries equations, a new CBS approximation was provided using the Taylor series method ^[13]. A novel quintic B-spline approximation was applied to solve Boussinesq equations ^[14]. Septic- and nonic-order splines have also been developed and applied to surfaces as tensor product schemes ^[15,16,17]. The convexity of the closed shapes was also discussed in ^[16]. Many authors and researchers have used higher-order numerical schemes to solve ODEs and PDEs, but these schemes have shown computationally higher costs and inefficiency in building the solutions for a large subsequent matrix system with unknown constants due to the rigidity they possess, as compared to the spline approximations.

The CHBSM has been shown to be the superior method for approximating second-order linear BVPs compared to other spline methods ^[10]. The main reason for this is because the CHBSM has a free parameter, $\gamma$, which is optimized using the brute force method initially proposed in ^[9]. To our knowledge, the best optimization method specifically for the CHBSM has not been found. Instead, the optimization approach by ^[18] for parameter $\lambda$ in the ECBSM was adopted and applied to the CHBSM. According to this approach, Newton's method was chosen and implemented for the minimization process. This method was proven to give promising results ^{[6,9,10,19,20]} and thus became the reference of this study.

An optimization algorithm is a process or technique designed to identify the optimal solution or set of solutions to a problem by maximizing or minimizing a specific objective function ^[33]. Particle swarm optimization (PSO) is a widely adopted, straightforward, and efficient technique. It belongs to the population-based algorithms which were inspired by population group behavior. PSO was originally discovered by ^[21] when the authors observed the social behavior of a flock of birds. Since then, PSO has been extensively used to optimize various types of problems mostly in the field of engineering ^[22]. For instance, the one-dimensional nonlinear Schrödinger equation was effectively solved using PSO with an exponential B-spline ^[22]. The authors then introduced the use of the exponential modified cubic B-spline differential quadrature method (Expo-MCB-DQM) with PSO to tackle Sine–Gordon equations ^[23]. The method significantly enhanced the stability and accuracy of the solution compared to earlier methods. To find the optimal parameter value of the radial basis functions for solving PDEs, the "PSO with Kansa's method" based on collocation techniques was integrated, and its performance superiority was demonstrated through numerical results ^[24].

As an application in geometric modeling and computer-aided design, scattered data points were effectively fitted with ball B-spline curves using PSO ^[25]. The PSO algorithm has also been applied into developable surfaces for shape optimization. A highly accurate developability GHT-Bézier surface was visualized in ^[26] where the authors applied PSO to find the optimum shape control parameters of the surface. However, there is a major lack of study on the implementation of PSO in numerical approximations, specifically in the B-spline collocation method. This is because most research opt to modify their basis functions ^[27,28] or use the aforementioned brute force with Newton's method, instead of using an optimization approach. This issue has motivated us to explore PSO as a potential optimization method for spline approximations. Therefore, the primary objective of this paper is to incorporate the use of the PSO technique to obtain an optimized value of the free parameter, $\gamma$, in the OCHBSM for solving linear second-order BVPs.

This paper is organized as follows: Section 2 introduces the basis functions of the cubic hybrid B-spline approach and explains the formation of the collocation method. It also details the integration of particle swarm optimization (PSO) with the CHBSM. Section 3 provides a few numerical examples of linear two-point boundary value problems (BVPs) where both the proposed method and existing approaches such as the CBSM and CTBSM were applied. The results are then analyzed and discussed in Section 4. Finally, the conclusion of the study with suggestions for future work are presented in Section 5.

2.   Methodology

The basis function of the cubic hybrid B-spline method is presented in this section. Subsequently, a collocation method is formed, namely the CHBSM. A particle swarm optimization approach is employed to optimize the free parameter in the CHBSM, which is called the OCHBSM.

2.1.   Cubic hybrid B-spline

The hybrid B-spline is defined as the linear combination of the B-spline function, $B_j^k(x)$, and the trigonometric B-spline function, $T_j^k(x)$. The $j$-th hybrid B-spline basis function of $k$-th order is defined in ^[20] as:

It is important to point out that the value of the parameter $\gamma$ in Eq (2.1) has significant importance in the hybrid B-spline basis functions. When $\gamma = 1$, the basis function is reduced to the B-spline basis function and when $\gamma = 0$, the basis function becomes the trigonometric B-spline basis function. The relationship between the order, $k$, and degree, $d$, of a basis function is defined by $k = d+1$ ^[29]. For instance, if a B-spline function of degree $d = 4$, is used, the value of $k$ will be 5, as the order is simply the degree plus one. In our study, B-spline basis functions of degree $d = 3$, were used; hence, the order $k = d+1 = 4$ was substituted. However, it is possible to use other values of $k$, as a B-spline curve can also be defined by the control points, $n$. Based on ^[29], a B-spline curve can be constructed up to order $n+1$ by adjusting the locality of the B-spline. Subsequently, the cubic hybrid B-spline basis can be obtained by substituting $k = 4$ into Eq (2.1) resulting in

The definitions of $B_j^4 (x)$ and $T_j^4 (x)$ in ^[20] are as follows:

where $h = \frac{(b-a)}{n}$, $\delta (x_j, x) = \sin \frac{x-x_j}{2}, \theta(x_j, x) = \sin \frac{x_j-x}{2}$, and $\varphi = \sin(\frac{h}{2})\sin (h) \sin(\frac{3h}{2})$.

2.2.   Collocation method

This section explains the collocation method of the cubic hybrid B-spline. An approximate solution of Eq (1.2) using the CHBSM can be written as:

where $C_j(x)$ are the unknown real coefficients and $H_j^4 (x)$ are the cubic hybrid B-spline basis functions presented in Eq (1.2). The term $f(x)$ is the continuous function in the domain $[x_0, x_n]$ located at the right-hand side of the BVP. Analogous to the CBSM and CTBSM, there are three nonzero terms at each knot, $x_j$, namely $H_j^4 (x)$, $H_{j-2}^{4} (x)$, and $H_{j-1}^{4}(x)$ due to the local support property of the B-spline basis. The values are tabulated in Table 1.

The values of $h_j$ for $j = 1, 2, 3, ..., 6$ are as follows:

Suppose $S(x)$ is the approximated solution for the analytical solution $y(x)$ in Eq (1.2). We can replace $y(x)$ and its derivatives by substituting $S(x)$ and its corresponding derivatives. By substituting $x_j$ and applying the the boundary conditions into Eq (1.2), it can be rewritten as:

for $j = 0, 1, ..., n-1$. Thus, the approximated solution in Eq (2.5) and its derivatives with respect to $x$, and the three nonzero terms at each knot $x_j$, given in Table 1, are substituted into Eq (2.5) yielding

where

and

Equations (2.7)–(2.9) are then substituted into Eq (1.2) giving

Collecting the terms that contain $C_{j-3}$, $C_{j-2}$, and $C_{j-1}$ from Eq (2.11) leads to

with boundary conditions

Equations (2.12)–(2.14) result in a tri-diagonal matrix system of size $(n+3)(n+3)$. This system can be denoted as $BC_j = F$. The matrix $C$ is a column matrix of the coefficients $C = (C_0, C_1, \dots, C_{n-1}, C_n)$, and the right-hand-side matrix is the function $F = (\alpha_1, f(x_0), f(x_1), \dots, f(x_n), \alpha_2)^T$ where the coefficients of matrix $B$ are presented as follows:

where

for $j = 0, 1, \dots, n-1.$ The values of the unknown $C_j$ for $j = 0, 1, \dots, n-1$ can be obtained by solving the matrix system using

and are substituted in Eq (1.2) to get the approximated solution of the second-order linear two-point BVP in Eq (2.5). Note that matrix $B$ is a square matrix where the determinant is nonzero. Hence, it is a non-singular matrix such that the inverse of it exists.

2.3.   Optimization of $\gamma$

The accuracy level of the approximated solutions of second-order linear two-point BVPs using the CHBSM is highly dependent on the value of the free parameter $\gamma$. This section explains the method of determining $\gamma$ with the use of swarm optimization, namely particle swarm optimization, after establishing the collocation method in the previous section. This method is a simple and direct method which can be applied to the splines. Figure 1 and Algorithm 1 show the flowchart and process of the proposed OHCBSM, respectively.

PSO is an evolutionary computation method similar to the genetic algorithm (GA). It was proposed by ^[21] in 1995. In PSO, swarms called particles can be defined as $P_i \in [a, b]$ where $i = 1, 2, 3, \dots, D$ and $a, b \in R$ where $D$ is the dimension. Each particle has its own velocity and position which are randomly initialized at the start. Each particle has to maintain its positions pbest, known as the local best position, and gbest, known as the global best position, among all the particles. The following equations are used to update the position and velocity of the particle ^[30].

We are given that $V_i$ is the velocity, $X_i$ is the particle position, pbest is the personal best particle position, and gbest is the global best particle position. $r_1$ and $r_2$ are two random numbers ranging from $[0, 1]$ where $c_1$ and $c_2$ are the cognitive coefficients. When selecting parameters for PSO, the goal is to balance exploration (searching broadly) and exploitation (focusing on promising areas) by adjusting factors such as population size, inertia weight, $w$, and cognitive coefficients, based on the problem's complexity, in order to achieve fast convergence to a near-optimal solution while avoiding local optima.

In this study, the parameters are initialized as follows: number of particles (population size, $N$) = 20, weight inertial coefficient, $w = 0.9$, cognitive coefficient, $c_1$ = 2, social coefficient, $c_2$ = 2, number of iterations = 50, lower bound = -2, and upper bound = 8. The population size chosen is small (i.e., 20), as our problem is less complex. Generally, complex problems require a larger population size to explore a wider search space while simpler problems may require a smaller population. The inertia weight, $w$, controls the exploration of particles whether to move further across the search space or to focus on areas near the best solution, and the given range is between 0 and 1 ^[31]. According to most research, the standard inertia weight implemented in PSO is $w = 0.9$, which is closer to 1 to encourage further exploration of particles in the search space ^[32]. Moreover, a recent work ^[33] showed that the results obtained using the stated inertia weight are reliable.

For cognitive and social coefficients, they are typically set equal (e.g., $c_1 = c_2 = 2$) in many standard implementations such as in ^[33,34], but tuning these values can help in fine-tuning the balance between exploration and exploitation. Other values are also possible, but large values can lead to instability whereas very small values might slow down convergence. Adjusting these coefficients can significantly affect the algorithm's performance in finding optimal solutions. Based on our test run, the errors converge more quickly as the number of iterations increases. Hence, we simply choose a large number of iterations where the errors will be significantly small.

The values of upper and lower boundaries are adopted from ^[9] which states that the boundary values of $\gamma$ must be between -2 and 8 to satisfy the B-spline properties. Eq (2.12) with boundary conditions in Eq (2.13) and Eq (2.14) is the fitness function for $x_j$ for $j = 0, 1, 2, \dots, n$. The values of pbest and gbest are constantly updated for each iteration. The work by ^[30] discussed PSO in greater detail. To determine the accuracy of the scheme, the maximum absolute error $L_{_{_{_{\infty}}}}$ and the Euclidean norm $L_{2}$ are calculated as follows:

The maximum percentage error and improvement percentage can also be calculated to further verify the accuracy and efficiency of our proposed method using the following formulas, respectively.

The numerator of the maximum percentage error in Eq (2.23) corresponds to $L_{_{_{_{\infty}}}}$ in Eq (2.22), which represents the maximum difference between the approximated solution $S(x_j)$ and the analytical solution $y(x_j)$. Meanwhile, Eq (2.24) is used to compute the error improvement between the two methods, where the initial error is defined as the maximum percentage error of the CBSM or CTBSM, and the new error corresponds to the maximum percentage error of our proposed method.

3.   Results and discussion

In this section, four numerical examples were studied to demonstrate the accuracy of the proposed method. The results obtained are compared with the analytical solution of each example. Our approach shows significant improvements over Caglar's method ^[5] in both accuracy and usability. For all examples, PSO was iterated several times to determine the optimal parameter value, $\gamma$. A value is considered optimal when the associated errors are smaller than those from previous results. Unlike prior methods, our approach considered the value of $\gamma$ at each knot, allowing for enhanced local control. We recorded the optimized $\gamma$ values at each knot and calculated their average, which was then used in Eq (2.2).

Example 1. ^[4]

Consider the following linear equation:

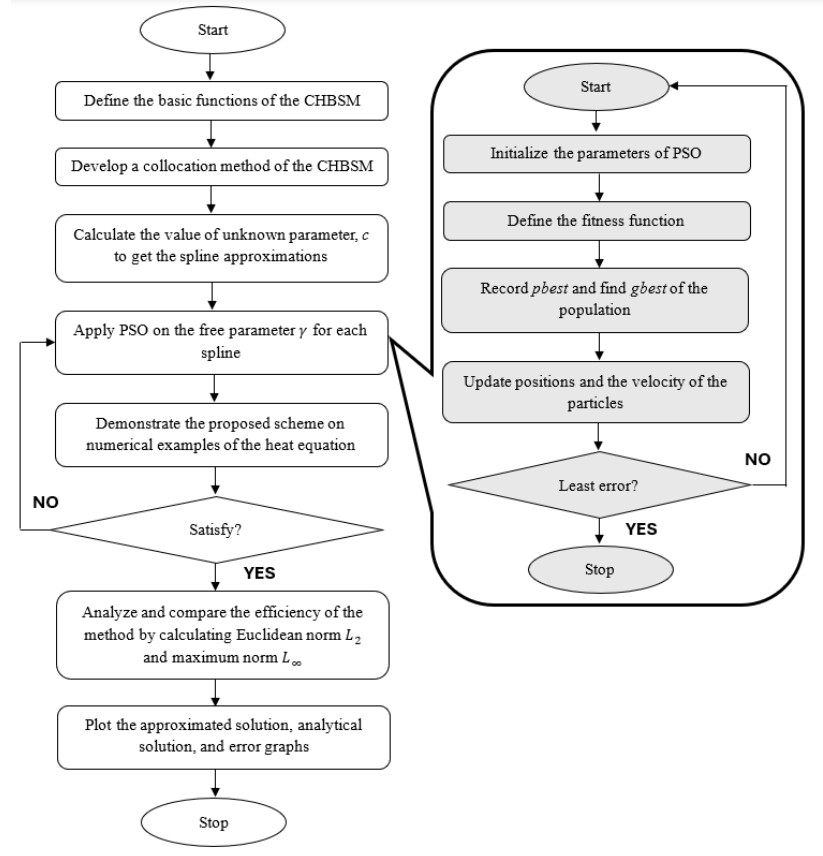
The analytical solution is given by $xe^{x-1}$. Figure 2(a) compares the approximated and analytical solutions using the OCHBSM with $n = 10,$ showing that the approximated solution closely matches the analytical one as both solutions overlapped, indicating minimal errors. Figure 2(b) shows the errors for the approximated solutions using the CBSM, CTBSM and OCHBSM. It is evident that the approximation error is smallest for the OCHBSM, followed by the CBSM and CBTSM. The smaller error for the OCHBSM suggests that its approximated solution is closest to the analytical solution compared to the other methods.

Table 2 presents the absolute errors and norms upon applying the CBSM, CTBSM, CHBSM with brute force optimization ^[35], and OCHBSM with PSO optimization on Example 1 where Table 3 displays the chosen value of parameter $\gamma$ using PSO in the OCHBSM at each knot. According to Table 2, the maximum absolute error $L_{_{_{_{\infty}}}}$ and the Euclidean norm $L_{2}$ for the OCHBSM are $4.95596\times 10^{-6}$ and $9.93104\times 10^{-6}$, respectively, which are the lowest compared to other methods. Additionally, the results from the CBSM and CTBSM are consistent with those reported in ^[35]. Evidently, our proposed method produced better approximations compared with the earlier methods.

Example 2. ^[36]

Consider the following linear equation with a trigonometric function:

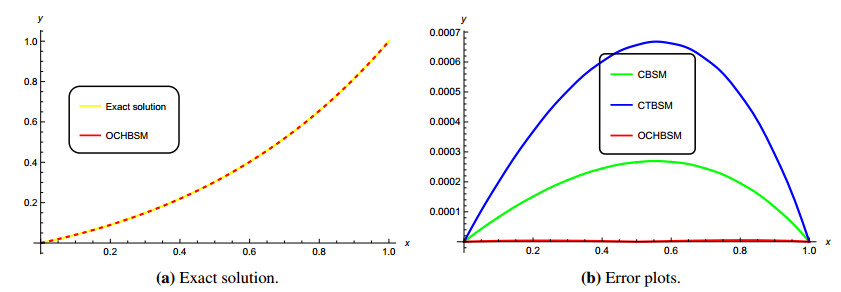
The analytical solution is given by $\sin{\pi x}$. Figure 3(a) illustrates the analytical solution and approximated solution for the OCHBSM with $n = 10$. Again, both solutions overlap each other, indicating a good agreement between the approximated and the analytical solutions. The comparison of the errors between the proposed method, CBSM, and CTBSM is shown in Figure 3(b). As observed in the figure, the OCHBSM has the smallest approximation error, followed by the CTBSM and CBSM. While the CTBSM performs slightly better than the CBSM for equation problems involving trigonometric functions, the performance of the OCHBSM exceeded both earlier methods in giving the best approximation to the analytical solution.

Table 4 presents the absolute errors and norms upon applying the CBSM, CTBSM, and proposed OCHBSM on Example 2 and Table 5 displays the value of parameter $\gamma$ chosen using PSO in the OCHBSM at each knot. According to Table 4, the maximum absolute error $L_{_{_{_{\infty}}}}$ and the Euclidean norm $L_{2}$ for the OCHBSM are $3.95268\times 10^{-7}$ and $8.83843\times 10^{-7}$, respectively. Both errors are the smallest compared to the other methods. Besides that, the results of the CBSM and CTBSM agree with those found in ^[19,37].

Example 3. ^[18]

Consider another linear equation:

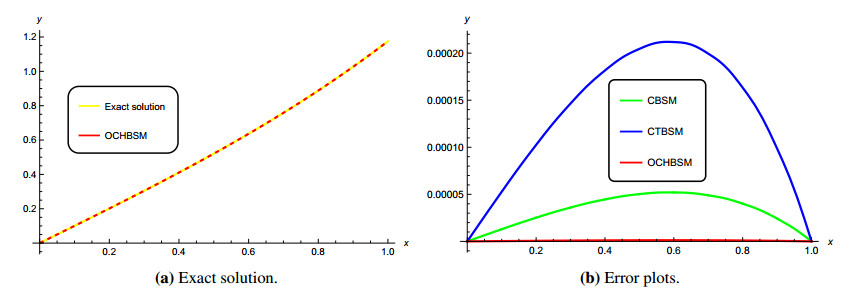
The analytical solution is given by $\sinh{x}$. Again, from Figure 4(a) and Figure 4(b), it was observed that our presented method is more precise than the earlier methods, the CBSM and CTBSM.

Table 6 lists the absolute errors and norms upon applying the CBSM, CTBSM, and OCHBSM on Example 3 and Table 7 reports the values of the parameter $\gamma$ involved. From Table 6, the maximum absolute error $L_{_{_{\infty}}}$ and the Euclidean norm $L_{2}$ are found to be $1.23029\times 10^{-6}$ and $2.78941\times 10^{-6}$, respectively, which are the lowest among the methods evaluated. The results tabulated for the CBSM and CTBSM match with those reported in ^[5,37].

Example 4. ^[38]

To further test the efficacy of the proposed method, we will consider a linear system as follows:

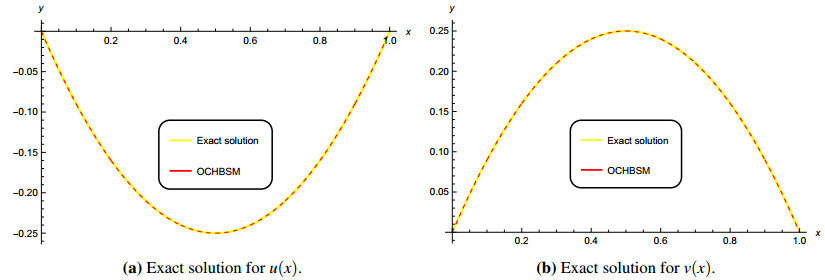
The analytical solution is given by $x^{2}-x$ for $u(x)$ and $x-x^{2}$ for $v(x)$. Figure 5(a) and Figure 5(b) illustrate the approximated analytical solutions for $u(x)$ and $v(x)$, respectively. The close overlap of these results indicates good approximations, as corroborated by Table 8.

The numerical results are tabulated in Table 8. From the table, the results for the CBSM and CTBSM are consistent with those presented in ^[38,39]. On the other hand, the parameter values $\gamma$ at each knot for $u(x)$ are listed in Table 9. The average of these optimized values was calculated to be $9.38154 \times 10^{-5}$. It is important to highlight that the solutions for $u(x)$ and $v(x)$ are negatives of each other. Therefore, to derive the approximation for $v(x)$, it is adequate to apply a negative sign to $u(x)$. For simplicity, the same value of $\gamma$ is used to approximate the solutions of $v(x)$, resulting in results similar to $u(x)$ except for the number signs. For this reason, the results of $v(x)$ were not tabulated.

The maximum absolute error, $L_{_{\infty}}$, for the functions $u(x)$ and $v(x)$ is recorded in Table 10 for $n = 10$ and $n = 21$. It should be noted that the maximum absolute errors for both $u(x)$ and $v(x)$ are the same, as $u(x)$ is the negative of $v(x)$, leading to identical error values. At $n = 21$, the results obtained using the CBSM method align with those reported in ^[38]. The CBSM provides the best results due to the absence of trigonometric functions in the problem; in cases involving trigonometric functions, the OCHBSM method would produce the smallest maximum absolute error. For $n = 10$, the parameter $\gamma$ is $9.38154\times 10^{-5}$ as indicated in Table 9, while for $n = 21$, $\gamma$ is $1.65796\times 10^{-4}$ upon applying PSO.

For comparative analysis, the computational time and maximum percentage error alongside the improvement percentage for each method are computed and summarized in Tables 11 and 12, respectively. It is important to note that two different software platforms, MATLAB R2024a and Mathematica 14.0, were employed in this study. For the OCHBSM, the B-spline collocation method was implemented in Mathematica 14.0 while the PSO algorithm was executed in MATLAB R2024a. Therefore, the computational times reported may not be entirely accurate, as they were calculated separately in each software and subsequently combined. Additionally, each iteration of PSO for each spline may vary due to the initialization of random numbers, $r_1$ and $r_2$, within the range [0, 1]. To mitigate this variability, the PSO algorithm was run three times for each spline, and the average computational time was recorded.

For methods other than the OCHBSM, all computations were performed exclusively in Mathematica software. As shown in Table 11, it is expected that the computational time for the OCHBSM is higher than that of CBSM and CTBSM, due to the inclusion of two basis functions and an additional optimization method. Thus, the computational work for the OCHBSM is approximately double, as both the CBSM and CTBSM must be computed prior to the OCHBSM. Although the execution time for the OCHBSM is slightly higher than the other two methods, the difference in computational time is minimal, typically on the order of a few seconds. That said, one can anticipate that as problem complexity increases, the computational time for the OCHBSM will also rise, but this is justified by the improved accuracy it offers.

From Table 12, the OCHBSM exhibits the lowest maximum percentage error and a significantly higher improvement percentage compared to the CBSM and CTBSM across all examples, except for Example 4. This discrepancy is likely due to the absence of trigonometric functions in the equation for Example 4. It needs to be highlighted that the percentage improved in the table was calculated based on the difference between the maximum percentage error of the CBSM or CTBSM, and the new error, which corresponds to the maximum percentage error of our proposed method, as shown in Eq (2.24). The exact value is determined by using the $L_{\infty}$ norm as given in Eq (2.22) to obtain the knot value where the error is the biggest. Hence, it is possible that the knot chosen in computing the exact value differs for each method, which can be seen in Example 4. In this example, the $L_{\infty}$ norm was attained at knot $x = 0.1$ for the CBSM and OCHBSM while the knot value $x = 0.5$ was recorded for the CTBSM. These values are then substituted into the analytical and approximated solutions to get the corresponding values. On average, an improvement percentage of $99.828352\% \approx 99.83\%$ was achieved, indicating that our method outperforms the compared methods significantly though the differences of improvement between the CBSM and CTBSM are quite small. Therefore, these results support the claim of the accuracy and efficiency of the proposed method.

4.   Conclusions

In conclusion, this study demonstrated the effectiveness of particle swarm optimization (PSO) to optimize the free parameter, $\gamma$, in the cubic hybrid B-spline collocation method (CHBSM). The numerical results showed that the OCHBSM outperformed traditional B-spline methods, including the CBSM and CTBSM, in approximating second-order linear BVPs. This superior performance is attributed to the flexibility provided by the free parameter in the OCHBSM. However, the CBSM was able to solve linear systems of BVPs in Example 4 more accurately than the CTBSM and our proposed method. This is probably due to the lack of trigonometric functions in the particular example. According to ^[18], the CTBSM can offer better approximations than the CBSM for problems involving trigonometric functions due to the existence of trigonometric basis functions. Since the OCHBSM is a linear combination of trigonometric B-spline basis functions, it is expected that the OCHBSM would also provide improved solutions for problems involving trigonometric functions. A limitation of this study is the use of a fixed set of initialized parameters for the PSO. Consequently, the results may vary for different sets of initial parameters, potentially leading to different values of $\gamma$ and, possibly, improved results. Additionally, the proposed method was applied only to linear second-order BVPs. Therefore, future work may focus on extending the PSO approach to more complex problems such as non-linear PDEs or to other spline methods with multiple free parameters or a significantly large number of nodes. On top of that, factors such as the order of the non-linear problems, the type of boundary conditions, and the selection of PSO parameters are important considerations for future improvements. Further exploration of alternative optimization techniques, such as whale optimization, could also enhance the performance of the OCHBSM.

Author contributions

Seherish Naz Khalid Ali Khan: Conceptualization, Formal Analysis, Investigation, Methodology, Software, Visualisation, Writing–original draft; Md Yushalify Misro: Project administration, Supervision, Writing–review and editing. All authors have read and approved the final version of the manuscript for publication.

Acknowledgments

This research was supported by the Ministry of Higher Education Malaysia through the Fundamental Research Grant Scheme (FRGS/1/2023/STG06/USM/03/4) and the School of Mathematical Sciences, Universiti Sains Malaysia. The authors are very grateful to the anonymous referees for their valuable suggestions.

Conflict of interest

The authors declare that they have no conflicts of interest.

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.