Radical scavenging capacity of RuBisCO bioactive peptides derived from Dunaliella salina and Spirulina platensis: An in silico and in vitro study

1.   Introduction

In population dynamics, harvesting is quite common and always visible in ecology. In the natural or human haphazardness, harvesting reduces species due to hunting, fishing, disease, war, environmental effects like natural disasters, competition among the species for the same resources, limited living space and limited food supply. For the optimal use of limited natural resources, and to maintain the balance of the ecological system, it is crucial to know the threshold of harvesting. The study of harvesting is very effective both in ecology and economics. Population models with a harvesting effect greatly impact various industries that drive the economy, like fisheries, forestry, plants and poultry.

In ^[1], the authors delineated two species harvesting strategies where the populations are harvested independently at constant rates. The largest amount of secure harvesting may be much less than what would be considered from the perspective of a local analysis for the equilibrium point. The global behavior of predator-prey systems was investigated in the presence of constant harvesting and the preservation of either or both species ^[2,3,4,5]. The result is analogous to the characteristics of an unharvested system with several parameters. The combined impacts of harvesting and discrete-time delay on the predator-prey system were studied in ^[6], where a comparative analysis of stability behavior has been offered without time delay.

Notably, the regular diffusion strategy could be more challenging to analyze; see ^{[7,8,9,10,11,12]} and references therein.

Several scenarios can happen when harvesting is applied to a single or interacting species with different diffusive strategies ^[13,14,15]. Previously, the single species with spatio temporal harvesting was considered to investigate the persistence and extinction of a population ^[13]. In contrast, the harvesting effort was focused on by using a time-independent cropped function for two competitive populations in ^[15]. The model is a modified reaction-diffusion model, known as the directed diffusion model, where species diffuse according to the smooth spatial function. Also, the resource distribution of the model is described as per capita available resources. A non-homogeneous Gilpin–Ayala diffusive equation was studied for single species by considering a spatially distributed harvesting map ^[16,17]. The study emphasized the crucial concept in the ecological system that a perfect mathematical model cannot be gained since we cannot include all of the effective parameters in the model ^[18]. Moreover, the model will never be able to forecast ecological catastrophes.

This study gives a transparent idea about real-life frameworks of the competitive population in the population ecology. To design the mathematical model, we are taking into account that the harvesting rate is proportional to the intrinsic growth rate such that the harvesting functions are $E_{1}(\boldsymbol{x})\propto r(\boldsymbol{x})$ and $E_{2}(\boldsymbol{x}) \propto r(\boldsymbol{x})$ which implies that $E_{1}(\boldsymbol{x}) = \mu r(\boldsymbol{x})$ and $\; E_{2}(\boldsymbol{x}) = \nu r(\boldsymbol{x})$, where $\mu$ and $\nu$ are coefficients of proportionality which are non-negative. The model equations are

where $u(t, \boldsymbol{x})$ and $v(t, \boldsymbol{x})$ represent the population densities of two competing species which are non-negative, with corresponding dispersal rates $d_{1}$ and $d_{2}$, respectively. The harvesting coefficients of populations $u, \; v$ are $\mu, \; \nu$, respectively. Hence the harvesting functions are $E_{1}(\boldsymbol{x}) = \mu r(\boldsymbol{x})$ and $\; E_{2}(\boldsymbol{x}) = \nu r(\boldsymbol{x})$, respectively. To analyze the model, we have simplified the model into a more compact profile in a later section.

Let us now consider the initial conditions $u_{0}(\boldsymbol{x})\geq 0$ and $v_{0}(\boldsymbol{x})\geq 0$, $\boldsymbol{x}\in\overline{\Omega}$, and these initial conditions are positive in an open nonempty subdomain of $\Omega$. The carrying capacity and intrinsic growth rate are denoted by $K(\boldsymbol{x})$ and $r(\boldsymbol{x})$, respectively. The function $K(\boldsymbol{x})$ is continuous as well as positive on $\overline{\Omega}$ and $r(\boldsymbol{x})\geqslant 0$, where $\boldsymbol{x}\in\overline\Omega$; moreover, $r(\boldsymbol{x})$ is positive in an open nonempty subdomain of $\Omega$. The notation $\Omega$ is a bounded region in $\mathbb{R}^{n}$, i.e., typically, $n = \{1, 2, 3\}$, with the smooth boundary $\partial \Omega\in C^{2+\alpha}, \; 0 < \alpha < 1$, and where $\eta$ represents the unit normal vector on $\partial \Omega$. The zero Neumann boundary condition indicates that no individual crosses the boundary of the habitat, or that individuals going in and out at any location from the boundary stay equal at all times. The Laplace operator $\Delta: = \sum_{i = 1}^n \partial^{2}/ \partial x_{i}^{2}$ in $\mathbb{R}^{n}$ implies the random motion of the species.

Now, we modify the system (1.1) in such a technique that the harvesting rate is expedited and easier to complete the analysis. The first equation of the model (1.1) can be written in the following way:

Let $K_{1}(\boldsymbol{x}) = (1-\mu)K(\boldsymbol{x})$ and $r_{1} = 1-\mu$. Then, we obtain

After applying same framework for the second equation of the system (1.1), we finally obtain the modified version of the main model:

where $K_{1}(\boldsymbol{x}) = (1-\mu)K(\boldsymbol{x}), K_{2}(\boldsymbol{x}) = (1-\nu)K(\boldsymbol{x}), r_{1} = 1-\mu$ and $r_{2} = 1-\nu$.

In the present study, the main objectives and findings are as follows:

● We study the impact of the harvesting of two species in a spatially non-homogeneous environment on their interaction, where the harvesting rate varies for each population. The competition arises for the same resources, limited food supply and limited living space; predators make the prey species their food.

● We prove that the solution to the initial value problem for positive initial conditions approaches $(u_s(x), \; v_s(x))$ globally in time.

● This study aims to illustrate the persistence-extinction story-line due to the harvesting rates between two competitive species.

● We have established the result to describe when they can coexist or when one species will drive the other to extinction.

● If the harvesting rate does not exceed the intrinsic growth rate and imposes conditions on $\mu$ and $\nu$, coexistence is possible.

● We also present some numerical results both in one and two dimensional cases. We find the evolution of system energy for species densities with a periodic space and time dependent intrinsic growth rate and carrying capacity. Also, the system energy versus time is plotted for both short-time and long-time evolution with the harvesting coefficients.

We solve (1.1) numerically by using a stable backward Euler, decoupled and linearized fully discrete time-stepping algorithm in a finite element setting and examine whether the theoretical results are supported by giving several numerical experiments. To the best of our knowledge, the modeling, theoretical and numerical results presented in this manuscript are novel.

The rest of the paper is organized as below. In Section 2, the existence and uniqueness of the solution of (1.1) are proven. In Section 3, stability analysis of the equilibrium points is given for the conditions when the intrinsic growth rate exceeds the harvesting rates, one harvesting rate exceeds the intrinsic growth rate and both harvesting rates exceed the intrinsic growth rate. To support the theoretical findings, several numerical experiments are given in Section 4. Finally, a concluding summary and future research directions are discussed in Section 5.

2.   Existence and uniqueness

Now we detach each equation to delineate the existence and uniqueness of the paired system. Consider the following system:

The results of single species are also discussed in ^{[19,20,21,22]}. Note that the proofs of Lemmas 7 and 8 are analogous to the proofs in ^[19]. The statements and proofs of Lemmas 7 and 8 can be found in Appendix A. It is also noted that all single-species results are available in Appendix A, and we will recall the results where necessary.

The following result demonstrates the existence and the uniqueness of solutions to a paired system (1.2).

Theorem 1. Let $K_1(\boldsymbol{x}), K_2(\boldsymbol{x}) > 0$, which implies that $\mu, \nu\in[0, 1)$, and $r(\boldsymbol{x}) > 0$ on $\boldsymbol{x}\in \overline{\Omega}$. When $u_0(\boldsymbol{x}), \; v_0(\boldsymbol{x})\in C(\Omega)$, the model (1.2) has a unique solution $(u, v)$. Further, if both initial functions $u_0$ and $v_0$ are non-negative and nontrivial, $u(t, \boldsymbol{x}) > 0$ and $v(t, \boldsymbol{x}) > 0$ for $t > 0$.

Proof. Take into account the following system with $\mu, \nu\in[0, 1):$

where $K_{1}(\boldsymbol{x}) = (1-\mu)K(\boldsymbol{x}) > 0, \; K_{2}(\boldsymbol{x}) = (1-\nu)K(\boldsymbol{x}) > 0, \; r_{1} = 1-\mu > 0$ and $\; r_{2} = 1-\nu > 0$ since $\mu, \nu\in[0, 1)$.

We utilize the existence-uniqueness theorem for parabolic paired, systems which is discussed in ^[23], and methods which are similar to the proof of ^[21], to show the existence of nontrivial time-dependent solutions. We choose the following constants:

and use the notations of proven results as discussed in ^[23] to denote

Then, it is simple to establish that the following conditions of the theorem are satisfied:

The conditions of (2.3) satisfy the conditions of the parabolic coupled systems in ^[23] for the functions $f_1$ and $f_2$ defined above. As a result, we come to the theorem conclusion that for any nontrivial $(u_0(\boldsymbol{x}), v_0(\boldsymbol{x}))$ such that

where $C \left([0, \infty) \times\overline{\Omega}\right)$ is the class of continuous functions on $[0, \infty) \times\overline{\Omega}$; a unique solution $(u(t, \boldsymbol{x}), v(t, \boldsymbol{x}))$ for the system (2.2) exists and remains in ${\bf S}_\rho$ for all $(t, \boldsymbol{x})\in [0, \infty) \times\overline{\Omega}$. Thus, $(u(t, \boldsymbol{x}), v(t, \boldsymbol{x}))$ is a unique and positive solution.

Let us establish the existence result for (1.1) for $0\leq\nu < 1\leq\mu$.

Theorem 2. Assume that $0\leq\nu < 1\leq\mu$, and let the initial conditions be $u_0\geq 0$ and $\; v_0\geq 0$; therefore, the model (1.1) has a unique, positive, time-dependent nontrivial solution.

Proof. The system (1.1) can be written as

Recalling the theoretical results as vindicated in ^[23] and the methods parallel to the proof in ^[22], to show the existence of nontrivial time-dependent solutions, let us choose the following constants:

Note that the definitions of $\rho_u$ and $\rho_v$ are analogous to those in ^[22]. Let us denote

Then, it is simple to establish that the following conditions of the theorem are satisfied:

The conditions (2.6) are valid based on the analysis presented in ^[23] for the functions $f_1$ and $f_2.$ Therefore, we come to the theorem conclusion that for any nontrivial $(u_0(\boldsymbol{x}), v_0(\boldsymbol{x}))$ such that

where $C \left([0, \infty) \times\overline{\Omega}\right)$ is the class of continuous functions on $[0, \infty) \times\overline{\Omega}$; a unique solution $(u(t, \boldsymbol{x}), v(t, \boldsymbol{x}))$ for the system (2.5) exists and remains in ${\bf S}_\rho$ for all $(t, \boldsymbol{x})\in [0, \infty) \times\overline{\Omega}$. Thus, $(u(t, \boldsymbol{x}); v(t, \boldsymbol{x}))$ is a unique and positive solution.

Let us establish the existence result for (1.1) for $0\leq\mu < 1\leq\nu$.

Theorem 3. Assume that $0\leq\mu < 1\leq\nu$ and the initial conditions are $u_0\geq$ and $\; v_0\geq 0$; therefore, the model (1.1) has a unique, positive, time-dependent nontrivial solution.

Proof. The proof is analogous to that of Theorem 2.

Remark 1. In the next section, the residuum of the main results is presented. We need several preliminary and auxiliary results to prove the theoretical results for the two species populations, which are presented in Appendix A. It is also noted that the main body of the paper contains only the leading and significant findings.

3.   Main results (global stability analysis)

When investigating the consequences of competition between two competitive species, it is a vital task to check the stability analysis of the semi-trivial equilibrium, namely, one should evaluate $(u^*(\boldsymbol{x}), 0),$$\; (0, v^*(\boldsymbol{x}))$, the trivial solution $(0, 0)$ and the nontrivial stationary solution, which implies the coexistence $(u_s, v_s)$.

3.1.   When the intrinsic growth rate exceeds the harvesting rate

The following section describes the case of the intrinsic growth rate transcending harvesting rate such that $\mu, \nu \in [0, 1)$. Given that $E_{1}(\boldsymbol{x}) = \mu r(\boldsymbol{x}), \; E_{2}(\boldsymbol{x}) = \nu r(\boldsymbol{x})$, where $\mu, \nu$ belongs to $[0, 1)$ then obviously $0\leq E_1(\boldsymbol{x}) < r(\boldsymbol{x})$ and $0\leq E_2(\boldsymbol{x}) < r(\boldsymbol{x})$. We investigate two possible cases: $\mu\leq\nu$ and $\mu\geq \nu$.

Lemma 1. Assume that $\mu, \nu \in [0, 1)$, which implies that $r_{1} > 0$, $r_{2} > 0$ and $K_{1}(\boldsymbol{x})$ and $K_{2}(\boldsymbol{x})$ are positive on $\overline{\Omega}$. Therefore, the trivial steady state $(0, 0)$ of the model (1.2) is an unstable repelling equilibrium.

Proof. Let the linearized system (1.2) near the trivial equilibrium be given as

The corresponding eigenvalue problems are given below:

Using the variational characterization of eigenvalues according to ^[19], we obtain the principal eigenvalue by choosing the eigenfunction $\psi = 1:$

Analogously, utilizing the variational characterization of eigenvalues according to ^[19], we obtain the principal eigenvalue by the choosing the eigenfunction $\phi = 1:$

Thus, the trivial equilibrium $(0, 0)$ is unstable. Now, we prove that the trivial steady state $(0, 0)$ is a repeller. The proof can be found in ^[20] and ^[24].

The following case demonstrates the result for the outcome of the competition when the intrinsic growth rate exceeds the harvesting rate for $0\leq\mu \leq\nu < 1$.

3.1.1.   Case: $\mu\leq\nu$

The semi-trivial steady state $(u^*, 0)$ is unstable whenever $\mu\leq \nu$, as shown in the following lemma.

Lemma 2. Let $\mu, \nu \in [0, 1)$, where $\mu \leq \nu$. Thus, there exists $\nu_1$ for a certain $\mu$ such that, for all $\nu \in [\mu, \nu_1)$, the equilibrium $(u^*, 0)$ is unstable for the system (1.2).

Proof. The analogous case $\mu = \nu$ was discussed in ^[25], where the species have a common carrying capacity. Thus, we discuss the case that $\mu < \nu$. Linearization of the second equation from (1.2) near the stationary solution $(u^*(\boldsymbol{x}), 0)$ gives

The corresponding eigenvalue problem is represented as follows:

The principal eigenvalue of this system is given by ^[19]:

We assume that $\Psi$ is the principal eigenfunction for the problem (3.3) with the principal eigenvalue $\sigma_1$. This value is positive whenever the numerator of (3.4) is positive, leading to

Since the denominator on the right-hand side of (3.5) is positive, to have a positive eigenvalue, we assume that

Multiplying both sides by $(1-\nu)$ gives

Therefore, we have

Here, in the above inequality, the left-hand-side $(1-\nu)\in (0, 1]$ whenever $\nu\in [0, 1)$ and the right-hand side is positive since the numerator and denominator have a square term and there is no negative term because the parameter $d_2$ is positive. Therefore, we can say that the right-hand side of the above inequality belongs to $(0, 1)$ since the right-hand side is less than the left-hand side and positive, where the left-hand side of the above inequality is $(1-\nu)\in (0, 1]$.

Rearrange the above inequality to obtain

Note that and left-hand side of the above inequality belongs to $(0, 1)$ as explained above. We define

which implies that $\nu_1 > \nu$ since the right-hand side is greater than $\nu$. Hence, we obtain that $\mu\leq\nu < \nu_1$. Therefore, there exists $\nu_1$ for a fixed $\mu$ such that, for all $\nu \in [\mu, \nu_1)$, the equilibrium $(u^*, 0)$ is unstable.

In the following lemma, we prove that the steady state $(0, v^*)$ is unstable whenever $\mu\leq \nu$.

Lemma 3. Let $\mu, \nu\in[0, 1)$, where $\mu \leq \nu$, and let there exist $\nu_1$ for a certain $\mu$ as long as $\nu \in [\mu, \nu_1)$. Thus, the steady state $(0, v^*)$ is unstable in the system (1.2).

Proof. The case that $\mu = \nu$ was discussed in ^[25]. Thus, here we only discuss the case that $\mu < \nu$. Linearizing the first equation of (1.2) in the neighborhood of $(0, v^*)$, we obtain

The corresponding eigenvalue problem is

The principal eigenvalue of this problem is given by ^[19]:

For $\nu\in[0, 1)$, take into account the eigenfunction $\psi(\boldsymbol{x}) = \sqrt{(1-\nu)K(\boldsymbol{x})} = \sqrt{K_2(\boldsymbol{x})}$. Then, the principle eigenvalue becomes

Note that $\nu \in [\mu, \nu_1)$, $\nu_1$ is defined in Lemma 2. We introduce a constant $c: = \dfrac{1-\mu}{1-\nu} > 1$ as long as $\mu < \nu$; further, it is true for every $0\leq \mu \leq \nu < 1$, and it is definitely true for $0\leq \mu \leq \nu < \nu_1 < 1$ because $\nu_1 \in [0, 1)$, which means that $\mu, \nu, \nu_1 \in [0, 1)$; it implies that $c > 1$ for any values in $[0, 1)$.

Let us now estimate the principal eigenvalue in the following way:

which can be rewritten as

Introducing the constant $c$, we have

We want to show that the numerator of the right-hand-side fraction in (3.8) is positive. From Lemma 13, we have

Note that, since $c > 1$, we obtain

Therefore, the numerator of the inequality (3.8) is positive. Thus, the principal eigenvalue is positive:

which completes the proof.

In the following theorem, we prove that the equilibrium $(u_s, v_s)$ is globally stable for the system (1.2) whenever $\mu\leq \nu$ by using Lemmas 1, 2 and 3.

Theorem 4. Suppose that $\mu, \nu \in [0, 1)$, where $\mu \leq \nu$. There exists $\nu_1$ for a certain $\mu$ such that, for all $\nu \in [\mu, \nu_1)$, the equilibrium $(u_s, v_s)$ of the system (1.2) is globally stable.

Proof. We consider that $0\leq \mu \leq\nu < 1$. Lemma 2 demonstrates that there is a number $\nu_1\in[0, 1)$ such that, whenever $\nu\in [\mu, \nu_1)$, the steady state $(u^*, 0)$ is unstable. Lemma 3 illustrates that the steady state $(0, v^*)$ is unstable. Lemma 1 demonstrates that the trivial steady state $(0, 0)$ is unstable and a repeller. We extract two results established in ^[24]. Hence, there exists a globally stable coexistence solution.

We get symmetrical results by exchanging $\mu$ and $\nu$, which means that $0\leq\nu \leq\mu < 1$. The following results can be obtained:

● When $\mu \geq \nu$, where $\mu, \nu\in [0, 1)$. There exists a value $\mu_1$ for a certain $\nu$ such that, for all $\mu \in [\nu, \mu_1)$, the steady state $(0, v^*(\boldsymbol{x}))$ of (1.2) is unstable.

● When $\mu \geq \nu$, where $\mu, \nu\in [0, 1)$, there exists a value $\mu_1$ for a certain $\nu$ for all $\mu \in [\nu, \mu_1)$. Thus, the steady state $(u^*(\boldsymbol{x}), 0)$ of the system (1.2) is unstable.

● Global coexistence solution: When $\mu \geq \nu$, where $\mu, \nu\in [0, 1)$. Thus, there exists a value $\mu_1$ for a certain $\nu$ for all $\mu \in [\nu, \mu_1)$; the coexistence steady state of the system (1.2) is globally stable.

3.2.   When one harvesting rate exceeds the intrinsic growth rate

In the present section, we examine the outcomes of two competitive species when one harvesting rate in the system (1.1) surpasses the corresponding intrinsic growth rate, which means that there are two possible scenarios that can arise, namely, $E_1(\boldsymbol{x}) \geq r(\boldsymbol{x})$ or $E_2(\boldsymbol{x}) \geq r(\boldsymbol{x})$ such that $0\leq \nu < 1\leq\mu$ or $0\leq\mu < 1\leq\nu,$ respectively.

First, we depict the result on the impact of competition when one harvesting function exceeds the respective intrinsic growth function for the case that $0\leq\nu < 1\leq\mu$.

3.2.1.   Case $\nu < 1\leq\mu$

The following lemma shows that there is no coexistence state when $0\leq\nu < 1\leq\mu$.

Lemma 4. Suppose that $0\leq\nu < 1\leq\mu$; thus, there is no nontrivial stationary solution $(u_s, v_s)$ for the model (2.5) or (1.1).

Proof. Take into account that there is a nontrivial stationary solution $(u_s(\boldsymbol{x}), v_s(\boldsymbol{x}))$, where $u_s\geq 0$ and $\; v_s\geq 0$ for all $\boldsymbol{x}\in\Omega$. The coexistence solution is to satisfy the following system of equations:

Now, integrating the first equation over $\Omega$ and utilizing the boundary conditions yields

The integrand is non-positive for all $\boldsymbol{x} \in\Omega$ whenever $\mu\geq 1$ and $u_s\not\equiv 0$ (which holds by our assumption of $u_s$ being a nontrivial coexistence solution). Hence, there is no coexistence state, $(u_s, v_s).$

Next, we delineate that $(0, v^*)$ is the only possible nontrivial stationary solution for the system (2.5) for any nontrivial non-negative initial conditions.

Lemma 5. Suppose that $\mu \geq 1$ then $(0, v^*(\boldsymbol{x}))$ is the only nontrivial stationary solution of (2.5) and (1.1).

Proof. We assume that there exists a nontrivial equilibrium other than $(0, v^*(\boldsymbol{x}))$. Since there is no coexistence in the system according to Lemma 4, the other possible solution of such type is $(u^*(\boldsymbol{x}), 0)$, where $u^*(\boldsymbol{x}) \geq 0$ on $\Omega$ and satisfies the following boundary value problem for $\mu = 1$:

Now, integrating and applying the boundary conditions yields

which is not true for a nontrivial $u^*(\boldsymbol{x}) \geq 0$. Therefore, we arrive at a contradiction, and the only nontrivial stationary solution is $(0, v^*(\boldsymbol{x}))$, where the function $v^*(\boldsymbol{x})$ satisfies the second equation given Lemma 13. The same procedure is applicable for $\mu > 1$. Thus, $(0, v^*(\boldsymbol{x}))$ is the only nontrivial stationary solution of (1.1) for $\mu\geq 1$.

The following lemma proves that $(0, 0)$ of the system (2.5) (equivalent to (1.1)) is unstable but not a repeller when the harvesting rate $E_1(\boldsymbol{x})$ surpasses or is equal to the intrinsic growth rate $r(\boldsymbol{x})$. Note that the proof is parallel with ^[21].

Lemma 6. Consider the case that $0\leq \nu < 1\leq\mu$. Thus, the trivial steady state $(0, 0)$ of the model (1.1) is unstable, but it is not a repeller.

Proof. First, we assume that $\mu > 1$ and the system (1.2) is linearized near the trivial equilibrium:

The corresponding eigenvalue problems are

Consider $\psi_1$ and $\phi_1$ as two eigenfunctions (that can be chosen positive) with corresponding principal eigenvalues of (3.11): $\gamma_1$ and $\sigma_1$, respectively ^[19]. Integrating (3.11) by using the boundary conditions yields

and

respectively. Thus, the steady state $(0, 0)$ is unstable.

Therefore, for $0\leq \nu < 1\leq\mu,$ the steady state $(0, 0)$ is unstable but not a repeller.

The next result shows the global stability for the solution $(0, v^*(\boldsymbol{x}))$ of the system (1.1) when the harvesting coefficient satisfies $0\leq\nu < 1\leq \mu$, as obtained by using Lemmas 4, 5 and 6.

Theorem 5. Let $0\leq\nu < 1\leq \mu$. Thus, the stationary solution $(0, v^*(\boldsymbol{x}))$ of the system (1.1) is globally asymptotically stable.

Proof. From Lemma 6, the solution $(0, 0)$ is unstable and there is no coexistence solution according to Lemma 4. According to Lemma 5, the remaining non-negative steady state is $(0, v^*(\boldsymbol{x}))$. This solution is unique by the positivity and uniqueness proofs; see Lemmas 9 and 10. Recall the definition of ${\bf S}_\rho$ from (2.7):

where

Using the result in ^[23], we obtain the time-dependent solution $(u(t, \boldsymbol{x}), v(t, \boldsymbol{x}))$ of (1.1), and the solution will converge to the equilibrium $(0, v^*(\boldsymbol{x}))$ as $t\rightarrow \infty$ for any initial conditions from ${\bf S}_\rho$, which completes the proof.

Symmetrically, the steady state $(u^*(\boldsymbol{x}), 0)$ of the model (1.1) is globally asymptotically stable when $\mu < 1\leq\nu$.

3.3.   When both harvesting rate exceed the intrinsic growth rate

Finally, in this section, we examine the case when both harvesting rates exceed the intrinsic growth rate; symbolically, $\mu, \nu\geq 1$.

3.3.1.   Case $\mu, \nu\geq 1$

Theorem 6. Let $\mu, \nu\geq 1$. Thus the trivial solution $(0, 0)$ of the model (1.1) is globally asymptotically stable.

Proof. The reasoning from the proof of Lemma 6 applies here directly, and it shows that the solution $(u(t, \boldsymbol{x}), v(t, \boldsymbol{x}))$ gradually converges to the trivial solution, which completes the proof.

Biologically, the result of Theorem 6 is valid since more harvesting than growth significantly reduces the density of both populations, and, as a continuation, populations will tend to extinction.

4.   Numerical results

In this section, we represent numerical experiments by using the finite element method to support the theoretical results. Here, $\|u\|_{L^2}: = \sqrt{\int_\Omega u^2(t, \textbf{x})d\textbf{x}}$ is the $L^2$ norm, whereas $\|u\|_{L^1}: = \int_\Omega |u(t, \textbf{x})|d\textbf{x}$ is the $L^1$ norm. In finite element simulations, we deal with finite-dimensional space, where all norms are equivalent. Therefore, using either $L^1$ or $L^2$ norms, the outcomes and decisions will be similar. But, we used $L^2$-norm square with a scaling factor of $\frac{1}{2}$ so that it looks like the kinetic energy. The usual $L^2(\Omega)$ inner product is denoted by $(., .)$. We define the Hilbert space for our problem as

The conforming finite element space is denoted by $X_h\subset X$, and we assume a regular triangulation $\tau_h(\Omega)$, where $h$ is the maximum triangle diameter. We consider the following fully discrete, decoupled and linearized scheme of the system (1.1):

For all experiments, we consider the diffusion coefficients $d_{1} = d_{2} = 1$, a unit square domain $\Omega = (0, 1)\times(0, 1)$ and $P_2$ finite element and structured triangular meshes. We define the energy of the system at time $t$ for the species densities $u$ and $v$ as

respectively. The 2D code is written in Freefem++ ^[26].

4.1.   Stationary carrying capacity

In this section, we will consider the stationary carrying capacity together with both constant and space-dependent intrinsic growth rates.

4.1.1.   Experiment 1: Constant intrinsic growth rate

In this experiment, we consider the carrying capacity of the system

with a constant intrinsic growth rate $r(\boldsymbol{x})\equiv 1.2$. We ran several simulations for various values of the harvesting coefficients $\mu$ and $\nu$. In Figures 1–4, we considered the initial population densities $u_0 = v_0 = 1.8$ with time step size $\Delta t = 0.1$.

In Figure 1, we present the contour plots for the species densities $u$ and $v$ at time $t = 1.6$ with fixed harvesting coefficients $\mu = 1.5$ and $\nu = 0.08$. A co existence is observed at the moment.

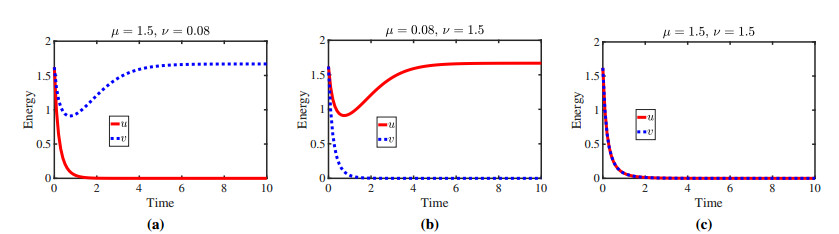
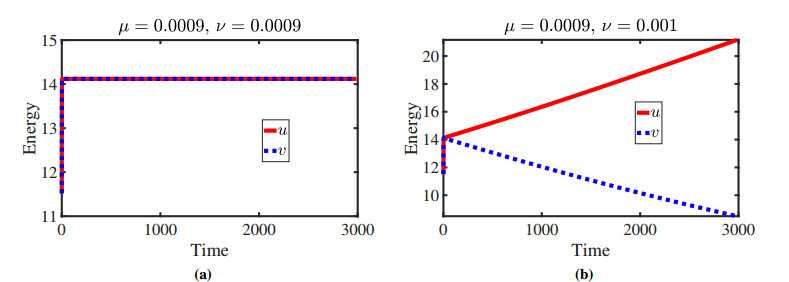
We also plotted the energy of the system for the species densities $u$ and $v$ versus time for three different combinations of the harvesting coefficient pairs $(\mu, \nu)$ in Figure 2. We consider the harvesting parameter $\mu = 1.5 > \nu = 0.08$ in Figure 2(a), and thus observe that the species $u$ will die away shortly while the species $v$ survives. The opposite scenario is observed in Figure 2(b), where $\mu = 0.08 < \nu = 1.15$ is considered. This is because one harvesting coefficient is significantly bigger than the other and exceeds the intrinsic growth rate; that is why one species becomes extinct in a short period of time. The results in Figure 2(a) and (b) support Theorems 2 and 3, respectively. In Figure 2(c), though the harvesting coefficients are the same ($\mu = \nu = 1.5$), both exceed the intrinsic growth rate; thus, extinction in both species is observed in short-time evolution.

In Figure 3, we plot the energy of the system versus time for the species density $u$, and $v$ with the coefficients of harvesting (a) $\mu = 0.0006$, and $\nu = 0.0$, and (b) $\mu = 0.0$, and $\nu = 0.0006$. We observe the harvesting impact as an extinction of the species $u$ in (a), and the species $v$ in (b).

In Figure 4, we plot the energy of the system for both species versus time, keeping fixed the harvesting parameter $\mu = 0.0009$ while varying $\nu$. We ran the simulation until $t = 2000$ for each case. In Figure 4(a), since $\mu > \nu$, as time grows, the species density for $v$ remains bigger than that for $u$, whereas, the scenario is opposite in Figures 4(b)–(f) because $\mu < \nu$. A possible coexistence is exhibited in Figure 4(a), (c) and (d), which supports Theorem 4. There is a possible threshold from extinction to the persistence of both populations. In Figure 4(b), (e) and (f), the long-run results show that, when $\mu < \nu$, a possible extinction and evolution of multiple thresholds can exist.

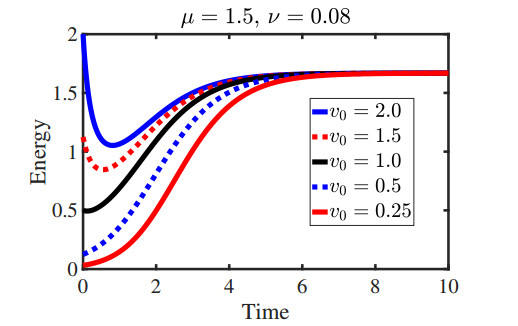
In Figure 5, we show the population density $v(t, \boldsymbol{x})$ versus time for various values of the initial condition $v_0$. In all cases, we considered the initial densities for both species to be the same and omitted the results for $u$. We observe a unique solution as time grows if the initial conditions are positive.

From Figure 6(a), we observe that, when the harvesting parameters do not exceed the intrinsic growth rate, a nontrivial solution exists, i.e., there is the co-existence of the two species. In Figure 6(b), we observe that the population density of the first species remains bigger than the second species because $\mu < \nu$. Ultimately, the second species will die out because of the competition between them.

4.1.2.   Experiment 2: Space-dependent intrinsic growth rate

In this experiment, we consider the carrying capacity and the intrinsic growth rate as

respectively, along with the equal initial population densities $u_0 = v_0 = 1.2$. The system energy versus time is plotted until $t = 3000$ in Figure 6(a) and (b) for two different harvesting parameter pairs.

4.2.   Non-stationary carrying capacity

In this section, we consider a time-dependent periodic system carrying capacity together with constant and time-dependent intrinsic growth rates.

4.2.1.   Experiment 3: Constant intrinsic growth rate

In this experiment, we consider the time-dependent carrying capacity

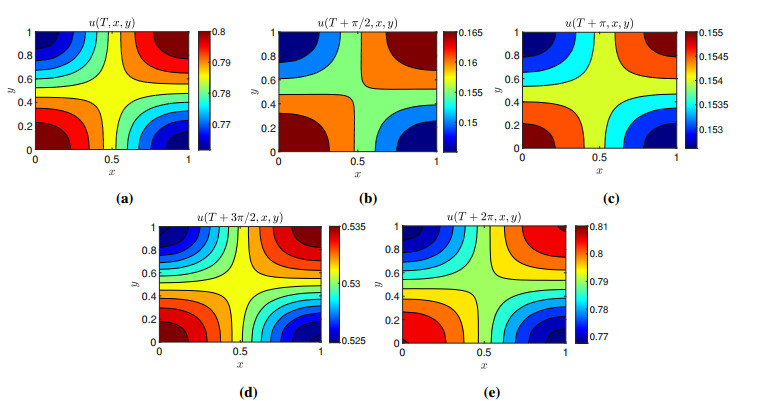
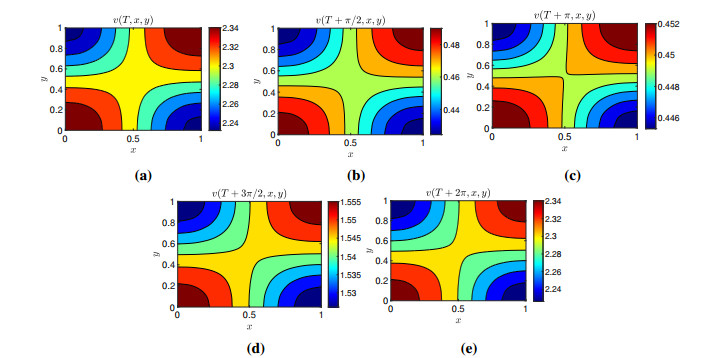
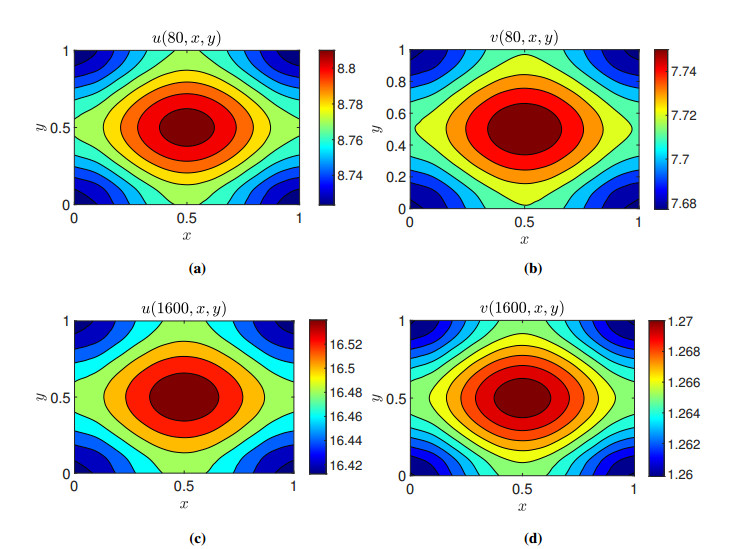
harvesting coefficients $\mu = 0.0009$, and $\nu = 0.0025$, intrinsic growth rate $r(\boldsymbol{x})\equiv 1.0$ and initial conditions $u_0 = 0.5$ and $v_0 = 1.5$ for the species $u$ and $v$, respectively. We have a fixed time $t = T = 13.74$ and draw the contour plots at $t = T, T+\pi/2, T+\pi, T+3\pi/2$ and $T+2\pi$ for the species densities $u$ and $v$ in Figures 7 and 8, respectively. From Figures 7 and 8, we observe quasiperiodic behavior in both species and their coexistence.

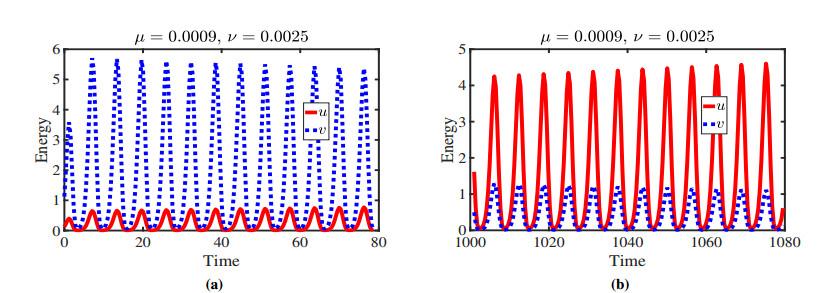
We have also plotted the energy of the system for species densities $u$ and $v$ versus time in Figure 9. We observe a clear co-existence of the two populations and change their density quasiperiodically over time. Since, in this case, $\mu < \nu$, the amplitude of the species density $u$ increases, while it decreases for $v$, consuming more resources by population $u$ and enjoying the best possible habitat.

4.2.2.   Experiment 4: Exponentially varying carrying capacity

In this experiment, we consider the carrying capacity

together with the constant intrinsic growth rate $r(\boldsymbol{x})\equiv 1$, initial population density $u_0 = v_0 = 1.6$ and harvesting coefficients $\mu = 0.0009$ and $\nu = 0.0025$.

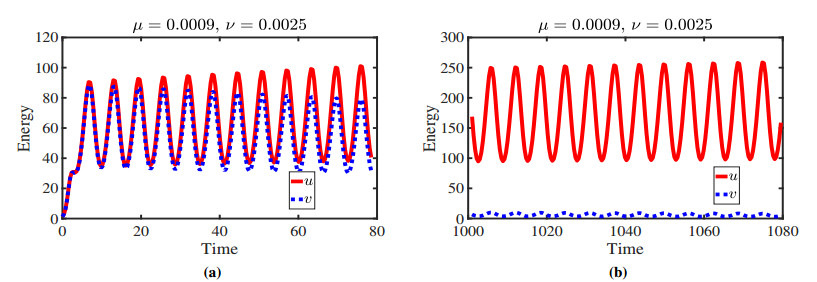
In Figure 10, the system energy versus time is plotted for both short-time and long-time evolution with the harvesting coefficients $\mu = 0.0009$, and $\nu = 0.0025$. We observe the periodic population densities for both species, and that, eventually, the species $v$ dies out while the species $u$ continues to exist.

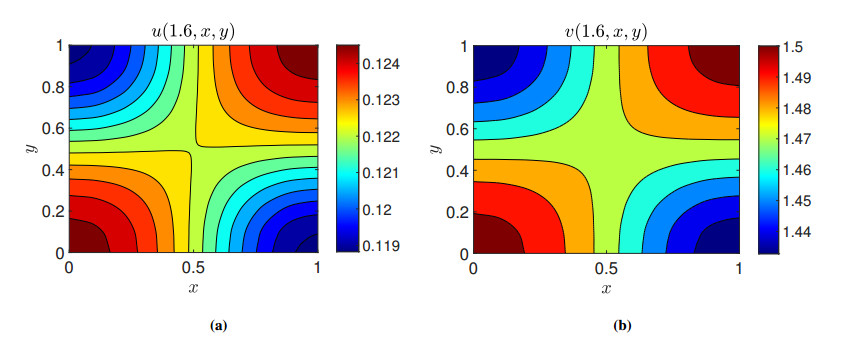
In Figure 11, we present the contour plots for both species at times $t = 80$ and $t = 1600$. It is observed that the highest population density is at $(0.5, 0.5)$ and there is a coexistence of both species though the population density of the species $u$ remains bigger than the species $v$ at every place. This is the effect of the different harvesting parameters.

5.   Conclusions

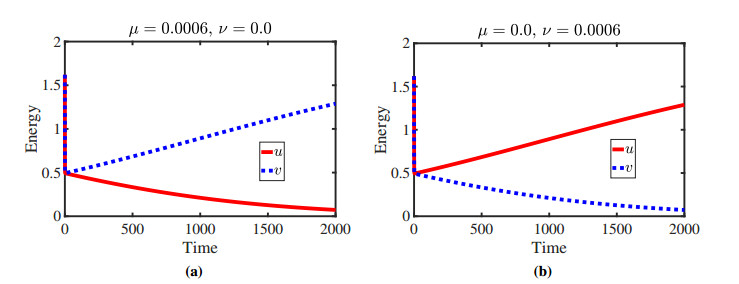
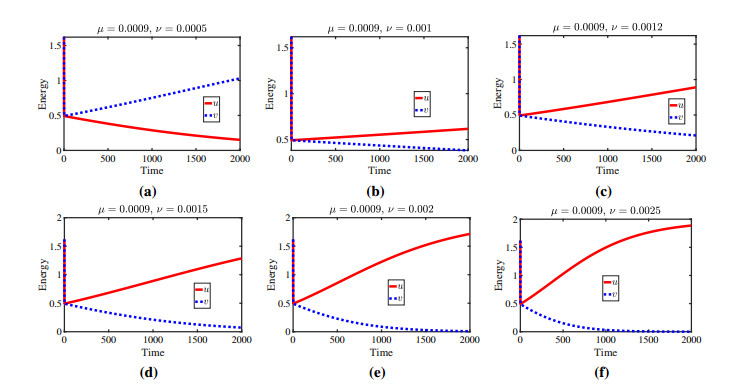
In this paper, we have studied two competing species in spatially heterogeneous environments. We observed various scenarios for several harvesting rates. When the harvesting rate does not surpass the intrinsic growth rate, which means that $\mu, \nu \in [0, 1)$ and imposes conditions on $\mu$ and $\nu$, so coexistence is possible. For small values of $\mu$ and $\nu$, prey and predator populations coexist, which is observed analytically and numerically. We estimated the threshold of the harvesting coefficient when coexistence is possible; consider the following:

$({\rm{i}})$ When we fix $\mu = 0.0009,$ the threshold of $\nu$ is 0.5, so species $v$ tends to extinction. Notably, we can get another entry of $\nu$ by choosing any other values of $\mu\in [0, 1)$.

$({\rm{ii}})$ Analogously, we can determine the threshold of $\mu$ when $\nu$ is fixed, which has been demonstrated in Theorem 5.

Further, only one species becomes extinct when their harvesting rate is greater than their growth rate and other species persist when the harvesting rate is less than their growth rate. Both species become extinct when their harvesting rate exceeds the growth rate and the systems (1.1) and (1.2) converge to the trivial solution. From these analytical and numerical observations, we can conclude that both species coexist when the harvesting rate is less than their growth rate. Both species die out if the harvesting rate exceeds their intrinsic growth rate.

The model (1.1) is a well-known Lotka-Volterra competition model. Also, it is a predatory system as a special case; in some scenarios, two species fight for the same resources and limited space, and in another scenario or environment, one species attacks another species because of the limitation of food. Moreover, we have the harvesting term depending on the intrinsic growth rate, which is more realistic and biologically feasible. The study can be extended for experimental research on intra- or inter-specific competitive populations. This study is appropriate for application to various farms, wild animal persistence and river-ocean ecologies with seasonal change; in particular, the model is applicable to two-species phytoplankton populations ^[27]. Finally, there are two open problems for future studies. Consider and analyze the problem (1.2) for the following cases ^[28]:

● Predator-prey dynamics while $\mu < 0$ and $\nu > 0$. Various lines of evidence attest to the importance of predation, such as the evidence of research on diversity, the ubiquity of anti-predator adaptations, and the impact of interacting with predators and prey in a population circle.

● Symbiotic (mutualism) model when $\mu < 0$ and $\nu < 0$. Mutualism refers to a relationship between two species of organisms that benefit from the association.

Acknowledgments

The authors thank the anonymous reviewers for their suggestions, which have significantly improved the quality of the manuscript. The author M. Kamrujjaman was partially supported by the University Grants Commission and the Bose Center for Advanced Study and Research in Natural Sciences, University of Dhaka. Also, the author Muhammad Mohebujjaman was supported by the National Science Foundation grant DMS-2213274 and University Research grant Texas A & M International University.

Conflict of interest

The authors declare no conflict of interest.

Appendix A.   Auxiliaries of single species

In the first appendix, we have a few preliminary and auxiliary results for single-species populations.

Lemma 7. ^[21] Consider that the parameters are positive on $\overline{\Omega}$ and the initial condition of (2.1) is a nonnegative continuous function $u_0(\boldsymbol{x})\in C(\Omega), \; u_0(\boldsymbol{x})\geq 0$ in $\Omega$, and $u_0(\boldsymbol{x}) > 0$ in some open, bounded, nonempty domain $\Omega_1 \subset \Omega$. Thus, there exists a unique positive solution of the system (2.1).

Lemma 8. ^[21] Consider the problem (2.1); then, there exists a function $u^*(\boldsymbol{x}) > 0$ that is a unique equilibrium solution of (2.1). Further, for any initial condition $u_0(\boldsymbol{x})\geq 0, \; u_0(\boldsymbol{x})\not\equiv 0$, the solution $u(t, \boldsymbol{x})$ satisfies the condition

uniformly for $\boldsymbol{x}\in \overline{\Omega}$.

Now, take into account the next following problem for the population density $v = v(t, \boldsymbol{x})$:

Lemma 9. ^[21] Consider the initial condition of (A.1) as a continuous non-negative function $v_0(\boldsymbol{x})\in C(\Omega), \; v_0(\boldsymbol{x})\geq 0$ in $\Omega$, and $v_0(\boldsymbol{x}) > 0$ in some open, bounded, nonempty domain $\Omega_1 \subset \Omega$. Therefore, there exists a unique positive solution of the system (A.1).

Lemma 10. ^[21] Consider the problem (A.1); thus, there exists a function $v^*(\boldsymbol{x}) > 0$ which is a unique stationary solution of (A.1). Further, for any initial condition $v_0(\boldsymbol{x})\geq 0, \; v_0(\boldsymbol{x})\not\equiv 0$, the solution $v(t, \boldsymbol{x})$ satisfies the condition

uniformly for $\boldsymbol{x}\in \overline{\Omega}$.

Stationary solutions and preliminaries:

Let the following problem have a stationary solution $u^*(\boldsymbol{x})$ where $v$ is zero in (1.2):

Analogously, the following problem has a stationary solution $v^*(\boldsymbol{x})$ when $u$ is zero in (1.2)

The following preliminary results are also discussed in ^{[15,25,29,30]}.

Lemma 11. Let $u^{*}$ be a positive solution of (A.2) and $v^{*}$ be a positive solution of (A.3); let $K_{1}(\boldsymbol{x})$ satisfy $d_{1}\Delta K_{1}(\boldsymbol{x})\not\equiv 0$ and $K_{2}(\boldsymbol{x})$ satisfy $d_{2}\Delta K_{2}(\boldsymbol{x})\not\equiv 0$ on $\Omega$. Thus,

and

respectively.

Proof. First, we set $v = 0$ and $u = u^{*}$ in the first equation of (1.2), and, utilizing the boundary conditions, as well as integrating over $\Omega$, we obtain

Adding and subtracting $K_1$ in (A.6), we have

Rewriting

we have

Simplifying (A.9), we obtain

Analogously, the result (A.5) is justified.

Lemma 12. Assume that $u^{*}(\boldsymbol{x})$ is a positive solution of (A.2). Moreover, if $K_{1}(\boldsymbol{x})\not\equiv const$, then

Proof. The proof is analogous to that of Lemma 11.

Lemma 13. Assume that $v^{*}(\boldsymbol{x})$ is a positive solution of (A.3). Moreover, if $K_{2}(\boldsymbol{x})\not\equiv const$, then

Proof. The proof is analogous to that of Lemma 11.