Thyroid function and hematological alterations in cardiac catheterization workers: a pre-post observational study on x-ray exposure

1.   Introduction

Industry 4.0 has led to advanced technologies led by artificial intelligence to lead the change of production methods at an unprecedented speed. In this context, the importance of machinery fault diagnosis as an indispensable key link in industrial production is becoming more and more significant. Along with advances in the Internet of Things (IoT) and big data technologies, the sensors are increasingly being deployed as core components of the Industry 4.0 infrastructure, providing powerful technical support to accurately monitor system status. Nevertheless, as the working environment of engineering systems is complicated and changeable with multiple interfering factors, a single sensor cannot fully reflect the system status, which is prone to misjudgment or omission, and cannot meet the requirements of engineering systems for high-precision diagnosis. Besides, certain faults may manifest themselves in multiple features, whereas it is difficult to distinguish different features accurately based on single sensor data, leading to diagnostic difficulties. Therefore, how to effectively integrate and utilize multi-sensor data to provide reliable data support for the stable operation of the system and fault prevention has become a crucial research topic.

Data-driven fault diagnosis methods have been widely used for accurate diagnosis of bearing faults in the field of intelligent manufacturing. There are many data-driven fault diagnosis methods, and the traditional method is to directly start from the time-domain signal, and establish the feature selection model and diagnostic model based on processing the signal by Fourier transform ^[1], variational modal decomposition ^[2], wavelet transform and other methods. Nonetheless, this method only extracts the time-frequency features of the measurement information to describe the fault information, which neglects the spatial relationship of the signal and fails to capture the local modes, leading to the limitation of feature expression. Meanwhile, methods of time-domain feature and frequency-domain feature extraction tend to be insensitive to signal variations and cannot effectively deal with complex nonlinear signal variations, resulting in poor performance in certain complex situations. In addition, the additional establishment of feature selection models increases the workload.

With the rapid development of machine learning technology, deep learning has been widely used in machinery fault diagnosis due to its advantage of automatically learning hierarchical representations utilizing multiple hidden layers to characterize faults from massive input data ^[3,4,5]. In deep learning-based fault diagnosis, vibration signals and their feature images are widely used as input samples to realize intelligent recognition of the data to be measured from the perspective of image processing. Several studies have utilized continuous wavelet transform ^[6,7,8], Gramian angular difference field (GADF) ^[9,10], S-transform ^[11], simultaneous compressed wavelet transform (SWT) ^[12], Markov transfer field ^[13], signal image mapping (STIM) ^[14], constant Q-nonstationary Gabor transform (CQ-NSGT) ^[15], compressed sensing (CS) ^[16] and other methods to convert one-dimensional vibration signals into time-frequency images in preparation for fully extracting the spatial features of the signals. Convolutional neural network (CNN), as a representative deep learning network, has shown great potential in the field of rotating machinery fault diagnosis ^[17,18] and reported good results ^[19,20,21]. However, since time-frequency signals usually have complex spatiotemporal features, traditional deep neural networks may encounter problems such as gradient vanishing or gradient explosion when processing, resulting in networks that are difficult to train or are poorly trained. Instead, Resnet introduces residual connectivity, which allows the network to learn the residuals and thus train the deep network easier. This residual connectivity helps the information to pass better, allowing the network to better capture complex features in time-frequency signals, improving the performance and generalization of the network. Although the image-based classification method can deal with the 2D time-frequency image of the signal, it is unable to directly extract the time-domain features and frequency-domain features of the signal, resulting in the loss of some important information.

In summary, in order to solve the problems of incomplete information, difficult diagnosis under complex working conditions, and low diagnostic accuracy faced by single information source in bearing fault diagnosis, this paper constructs a new bearing fault diagnosis model based on multi-sensor and multimodal information fusion to realize accurate fault diagnosis of bearings. To start, this paper realizes the fusion of multi-sensor signals by auto-encoder. On this basis, the fused 1D vibration signals are transformed into 2D time-frequency images using the continuous wavelet transform technique and input to the Resnet network for preliminary diagnostic analysis. Meanwhile, 14 time-frequency statistical features are employed as substitutes for the fused one-dimensional signals, and the improved 1DCNN model based on the residual block and attention mechanism (1DCNN-REA) model is introduced to further improve the diagnostic accuracy. In order to give full play to the advantages of the Resnet model and the 1DCNN-REA model, this paper further adopts the TPE algorithm to achieve the fusion of the two, aiming to improve the performance of a single model in bearing fault diagnosis by complementing each other's strengths, and realize the multimodal information fusion fault diagnosis.

The rest of this article is organized as follows. Section Ⅱ introduces the related theories and techniques. In Section Ⅲ, the proposed Resnet-1DCNN-REA model is detailed. Real-world applications are presented in Section Ⅳ. Finally, Section Ⅴ concludes this article.

2.   Relevant preparations

2.1.   Auto-encoder

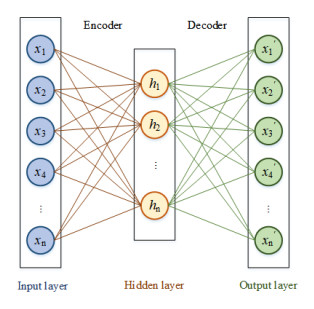
Auto-encoder can be divided into two steps: encoder and decoder. The former compresses the high-dimensional input into a low-dimensional latent vector representation, and the latter aims to recover the data based on the latent vectors ^[22]. Figure 1 shows the structure of the auto-encoder.

Figure 1.  The architecture of the auto-encoder.

DownLoad: Full-Size Img PowerPoint

Since the auto-encoder is trained on a large amount of data under the normal state with the goal of minimizing the reconstruction error, the auto-encoder that completes the training has a good ability to recover the normal signal. Its mathematical expression is as follows ^[23].

where, $x$ is input, $b$ and $W$ denote the deviation and weight of the neural network, respectively, $h$ is the hidden layer, and $\sigma$ represents the nonlinear transformation function. $z$ is the reconstructed result of original input signal $x$, and $r$ is reconstruction error.

2.2.   CWT

Because the joint representation of time-frequency images in the time and frequency domains contains more complex structural distribution information than one-dimensional vibration signals ^[24], it is capable of reflecting fault characteristics more comprehensively. Furthermore, the convolutional structure of Resnet aims to process 2D input data, so it is necessary to convert one-dimensional vibration signals into two dimensions. CWT serves as a time-frequency conversion method that can effectively convert one-dimensional vibration signals into two-dimensional time-frequency spectra and can be directly used in convolutional layers ^[25].

For a 1-D vibration signal sequence $s\left(t\right)$, the CWT is expressed as

where $a$ and $b$ are the scale and shifting variables, respectively, ${\mathit{\Psi}}$ represents the mother wavelet function, $CWT\left(a, b\right)$ represents the wavelet coefficients, and $*$ is the complex conjugate operator. It is crucial to choose a suitable mother wavelet for CWT. Commonly used mother wavelet functions include Haar, Morlet, Meyer, Symlet, and so on ^[26].

As shown in Figure 2, multiple random points are selected on the original vibration signal, and each random point serves as the starting point for intercepting samples of the same length. Then, the sample segments are converted to time-frequency images by CWT. The complex Gaussian wavelet function is selected for the CWT, with a scale range of [100, 1000].

Figure 2.  The process of converting vibration signals into images. (a) Inner race fault (b) Rolling element fault (c) Outer race fault.

DownLoad: Full-Size Img PowerPoint

2.3.   Resnet

In deep learning, the training of neural networks grows more difficult as the depth of the network increases. This is mainly due to the fact that in the training of networks based on stochastic gradient descent, the multilayer back propagation of error tends to lead to dispersion or disappearance of gradient. Meanwhile, Resnet came along to solve this problem by using residual blocks to make the network deeper without overfitting, and its accuracy and precision far exceed that of traditional network models ^[27]. It is widely used for a variety of vision tasks, and competitive results can be obtained with only a few parameters ^[28].

Resnet is almost similar to other CNN models, consisting of convolution, pooling, activation mapping, and fully-connected layers. The only major difference between Resnet and other CNN is the connection of the input layer to the end of the residual block. Figure 3 illustrates a schematic structure of the conventional and residual modules. The architecture of Resnet34 starts with convolution and max-pooling operations, using kernels of (7^*7) and (3^*3) pixels in size, respectively, to perform the convolution operation. Thereafter, four stages with different numbers of residual blocks are introduced to perform the convolution operation using kernels of size (3^*3) pixels as shown in Table 1. While passing from one point to the next, the depth of the channel is doubled with the size of the input samples halved ^[29].

Figure 3.  Schematic structure of conventional and residual modules. (a) Conventional module (b) Residual module.

DownLoad: Full-Size Img PowerPoint

Table 1.  The architecture of Resnet34.

Layer Name	Output size	Convolution layer
Conv1	112$\times \ $112	7$\times \ $7, 64, stride 2
Conv2_x	56 $\times$ 56	$\text{3}\ \times \ \text{3}$ max pooling, stride 2
		$\left[\begin{array}{c}\text{3}\ \times \ \text{3, 64}\\ \text{3}\ \times \ \text{3, 64}\end{array}\right]\ \times \ \text{3}$
Conv3_x	28$\times \ $28	$\left[\begin{array}{c}\text{3}\ \times \ \text{3,128}\\ \text{3}\ \times \ \text{3,128}\end{array}\right]\ \times \ \text{4}$
Conv4_x	$\text{14}\ \times \ \text{14}$	$\left[\begin{array}{c}\text{3}\ \times \ \text{3,256}\\ \text{3}\ \times \ \text{3,256}\end{array}\right]\ \times \ \text{6}$
Conv5_x	7$\times \ $7	$\left[\begin{array}{c}\text{3}\ \times \ \text{3,512}\\ \text{3}\ \times \ \text{3,512}\end{array}\right]\ \times \ \text{3}$
	1$\times \ $1	Average pooling, fc, softmax

---

 | Show Table

DownLoad: CSV

The network structure of Resnet34 is shown in the Table 1.

2.4.   1DCNN-REA

CNN is a feed-forward neural network with convolutional computation and deep structure which enables it to represent learning and classify the input information according to its hierarchical structure. 1DCNN architectures are similar to 2DCNN, which usually consist of five layered structures: input layer, convolutional layer, pooling layer, fully connected layer, and output layer ^[30].

The convolutional layer is the core of 1DCNN, which serves to perform feature extraction, usually using multiple layers of convolution to obtain deeper features. The expression of the convolutional layer is as follows:

where W is the convolution kernels, j represents the number of kernels, and M denotes the channel number of input ${X}_{i}^{l-1}$. $b$ is the bias corresponding to the kernel, $f\left(\right)$ is the activation function, and $*$ represents the convolution operator.

The main function of the pooling layer is to perform feature compression to retain the main features while simplifying the network computation. Pooling is divided into maximum pooling and average pooling, where average pooling is calculated according to the size of the predetermined pooling window, and the maximum pooling method selects the largest parameter within the predetermined window as the output value ^[31]. The paper employs average pooling methods. The role of the fully connected layer is to achieve classification, and each of its nodes is connected to each node in the previous layer to synthesize the features extracted above. The output of the last fully connected layer is the classification result. The expression of the fully connected layer is as follows:

Although 1DCNN has achieved good results in the field of fault diagnosis, traditional convolutional neural networks consider each bearing fault feature channel equally important during the convolutional pooling process, while in reality, the information carried by each feature is of different importance. Simply think that each fault feature channel is the same lack of reasonableness, and most of the studies have ignored this point. Therefore, this paper introduces the attention mechanism module, which focuses on the important regions and ignores the unimportant information. In addition, in order to facilitate the learning of the residual information of the data and improve the learning ability and training effect of the model, this paper introduces the residual module in the 1DCNN model. The structure of the proposed 1DCNN with residual and attention block (1DCNN-REA) model is shown in Figure 4.

Figure 4.  The architecture of the proposed 1DCNN-REA network.

DownLoad: Full-Size Img PowerPoint

2.5.   TPE

TPE is a Bayesian optimization algorithm in which a set of optimal values can be obtained by iteratively adjusting the hyperparameters of the model. It can be expressed as:

where $f\left(x\right)$ represents the objective function to minimize, $X$ represents the search space, and ${x}^{*}$ represents optimal hyperparameter settings.

TPE works by defining a surrogate function that is based on the loss probability representation of previous trials ^[32]. It divides the trials into good $g\left(x\right)$ and bad $b\left(x\right)$ trial groups based on predetermined quantized values of losses from finished trials. The boundary between good and bad trial groups is represented by loss 𝑦 with 𝑦∗ representing the loss boundary. If $y < {y}^{*}$, the trial is in $g\left(x\right)$, otherwise the trial is in $b\left(x\right)$. These trial groups are then utilized to define an expected improvement (EI) function derived from the Bayes theorem. The function can be expressed as:

Using the definitions above and by substituting $\gamma = p(y < {y}^{*})$, the simplification is:

3.   The proposed diagnosis method

The framework of the proposed bearing fault diagnosis method based on multisource and multimodal information fusion in this paper is shown in Figure 5. First, the raw data obtained from multi-sensor acquisition is preprocessed with minimum-maximum normalization, based on which, this paper establishes a multisource information fusion model based on auto-encoder to obtain multi-sensor fused signals, which contributes to obtaining more comprehensive fault characterization information. Then, the fused signal is subjected to sliding segmentation. Specifically, the signal acquired in the 0.05 s time period is taken as a sample sequence since the sampling frequency is 25.6 kHz, i.e., each segment contains 1280 sample points. Meanwhile, the sample segments are generated by sliding segmentation at intervals of 500 sample points. The division of the training set and test set is carried out in 8:2.

Figure 5.  Flowchart of the proposed method.

DownLoad: Full-Size Img PowerPoint

For the obtained samples, a Resnet-based fault diagnosis model is established on the one hand. The one-dimensional signal samples are transformed into two-dimensional images using continuous wavelet transform to show more intuitively the changes of the signals in the time and frequency domains, which are then inputted into the Resnet34 network for fault diagnosis. On the other hand, a fault diagnosis model based on 1DCNN-REA is established. Specifically, the statistical features of the samples are extracted from both time and frequency domains to capture the key statistical information of the signals and provide effective feature vectors for subsequent classification. Finally, the prediction results of the two models are combined to fully utilize the advantages of both models. With the TPE algorithm for optimization, the integrated model with the best diagnostic results is obtained by setting the weight parameter for each basic model and performing a decision fusion:

where ${P}_{pred}\left(x\right)$ is the predicted category; ${P}_{1DCNN-REA}\left(x\right)$ is the probability of the category predicted by the 1DCNN-REA model; ${P}_{Resnet}$ is the probability of the category predicted by the Resnet model; $m$ is the weight coefficient assigned to the 1DCNN-REA model; and $n$ is the weight coefficient assigned to the Resnet model.

4.   Experiments

4.1.   Dataset preparation

In order to verify the effectiveness of the proposed method, a fault simulation test was conducted on the test rig shown in Figure 6. The test rig consists of motor, coupling, inertia wheel, conveyor belt, conveyor belt drive mechanism, crank linkage mechanism, gearbox, and reciprocating mechanism with spring. The MB ER-10K deep groove ball bearing mounted close to the motor side was taken as the object of study, and localized cracks with width and depth of 0.2 mm were implanted on the outer race, inner race, and rolling element surfaces of the bearing, respectively, and the three types of bearing faults obtained included inner race fault (IRF), outer race fault (ORF), and rolling element fault (REF). The motor speed was 900 r/min and the bearings were operated under no alternating load conditions while the signals were collected at a frequency of 25.6 kHz using an accelerometer with a sensitivity of 10.2 (mV/ms^-2)/100 (mV/g).

Figure 6.  Schematic diagram of the test rig.

DownLoad: Full-Size Img PowerPoint

4.2.   Evaluation indicators

For multi-category classification, multiple evaluation metrics are required and the confusion matrix is shown in Table 2 ^[33]. In order to comprehensively evaluate the effectiveness of the proposed method in bearing fault diagnosis and to compare with other models, accuracy, precision, and F1-score are chosen to evaluate the performance of the selected model.

Table 2.  Confusion matrix.

		True class
		Positive	Negative
Predicted class	Positive	True positive (TP)	False positive (FP)
	Negative	False Negative (FN)	True Negative (TN)

---

 | Show Table

DownLoad: CSV

The formula for each indicator from the confusion matrix is as follows.

4.3.   Time-Frequency features extraction

In this study, the time-frequency statistical features of the signals are extracted from the integrated perspective of time and frequency domains to characterize the information contained in the signals, as shown in the Table 3. Among them, 11 time-domain features and 3 frequency-domain features are included, specifically, ${f}_{1}$–${f}_{11}$ are time-domain features and ${f}_{12}–{f}_{14}$ are frequency-domain features.

Table 3.  Time-frequency domain features.

Name	Definitions	Name	Definitions
Maximum value	${f}_{1}=\mathrm{m}\mathrm{a}\mathrm{x}\left(X\right)$	Crest factor	${f}_{8}=\frac{{f}_{1}}{{f}_{4}}$
Minimum value	${f}_{2}=\mathrm{m}\mathrm{i}\mathrm{n}\left(X\right)$	Impulse factor	${f}_{9}=\frac{max\left|X\right|}{\frac{1}{N}\sum _{i=1}^{N}\left|{x}_{i}\right|}$
Mean value	${f}_{3}=\frac{1}{N}\sum\limits_{i=1}^{N}{x}_{i}$	Shape factor	${f}_{10}=\frac{\sqrt{\frac{1}{N}\sum _{i=1}^{N}{x}_{i}^{2}}}{\frac{1}{N}\sum _{i=1}^{N}\left|{x}_{i}\right|}$
Root mean square	${f}_{4}=\sqrt{\frac{1}{N}\sum\limits_{i=1}^{N}{x}_{i}^{2}}$	Margin factor	${f}_{11}=\frac{max\left|X\right|}{\frac{1}{N}\sum _{i=1}^{N}\sqrt{\left|{x}_{i}\right|}}$
Kurtosis	${f}_{5}=\frac{N\sum _{i=1}^{N}{\left({x}_{i}-{f}_{3}\right)}^{4}}{{\left[\sum _{i=1}^{N}{\left({x}_{i}-{f}_{3}\right)}^{2}\right]}^{2}}$	Center of gravity frequency	${f}_{12}=\frac{\sum _{k=1}^{K}{f}_{k}A\left(k\right)}{\sum _{k=1}^{K}A\left(k\right)}$
Skewness	${f}_{6}=\frac{\sqrt{N}\sum _{i=1}^{N}{\left({x}_{i}-{f}_{3}\right)}^{3}}{\sqrt[3]{{\left[\sum _{i=1}^{N}{\left({x}_{i}-{f}_{3}\right)}^{2}\right]}^{2}}}$	Root mean square frequency	${f}_{13}=\sqrt{\frac{\sum _{k=1}^{K}{f}_{k}^{2}A\left(k\right)}{\sum _{k=1}^{K}A\left(k\right)}}$
Peak-to-peak value	${f}_{7}={f}_{1}-{f}_{2}$	Frequency standard deviation	${f}_{14}=\sqrt{\frac{\sum _{k=1}^{K}A\left(k\right){[{f}_{k}-{f}_{12}]}^{2}}{\sum _{k=1}^{K}A\left(k\right)}}$

---

 | Show Table

DownLoad: CSV

4.4.   Results and discussion

4.4.1.   Multisource information fusion based on auto-encoder

This paper constructs an auto-encoder model to realize multisource information fusion from different sensors. During the construction process, in order to measure the accuracy of the model in reconstructing the input data, we chose the mean square error (MSE) as the loss function, which aims to minimize the mean squared difference between the model's predicted values and the true values, thus ensuring that the model can capture the intrinsic structure of the data more accurately. In the choice of activation function, we adopt the parametric rectified linear unit (PReLU). As an improved version of ReLU, it not only inherits the nonlinear characteristics of ReLU, but also can effectively alleviate the dead ReLU problem, so as to improve the expressive ability and training efficiency of the model. As for the optimizer, we choose the Adam optimizer, which combines the adaptive learning rate adjustment and momentum strategy to dynamically adjust the learning rate of each parameter and accelerate the convergence based on the historical gradient information, which enables the model to find the optimal solution faster during the training process. In addition, we set the learning rate to 0.01, an initial value that shows good performance in most scenarios, which facilitates the model to enter a stable learning state quickly in the early stage of training.

To visually assess the effectiveness of the training process, we recorded the training loss after each training round and plotted the corresponding loss images, as shown in Figure 7. The horizontal axis accurately represents the progression of training epochs, while the vertical axis clearly indicates the magnitude of the loss values. Observing the training loss curve, it is evident that the training loss consistently decreases as the number of training rounds increases, indicating that the model is continuously optimizing its internal parameters to reconstruct the input data more accurately. However, in the latter half of the training, it is noticeable that the training loss curve begins to flatten, suggesting that the model may have reached a relatively stable state. This plateau indicates that it has become increasingly challenging for the model to further reduce the loss values in the current training environment.

Figure 7.  Auto-encoder based data fusion training loss. (a) Inner race fault (b) Rolling element fault (c) Outer race fault.

DownLoad: Full-Size Img PowerPoint

To investigate the performance of the auto-encoder-based data fusion method, we visualize the original and fused data using the t-distributed stochastic neighbor embedding (t-SNE) technique, as illustrated in Figure 8(a), (b). Figure 8(a) clearly demonstrates that the original samples are nearly indistinguishable in 2D space. In contrast, after fusing the raw data with the auto-encoder, the inner race fault samples are almost completely separated from the other two fault types. This outcome indicates that the auto-encoder-based data fusion method effectively aids in distinguishing different fault types, facilitating accurate diagnosis of the three subsequent fault categories.

Figure 8.  t-SNE visualization results. (a) Original data (b) Auto-encoder based fused data.

DownLoad: Full-Size Img PowerPoint

4.4.2.   Multimodal bearing fault diagnosis based on Resnet-1DCNN-REA

On the basis of converting one-dimensional vibration signals into two-dimensional images using continuous wavelet transform, this paper utilizes deep learning models to recognize and classify the images. Specifically, this study compares the diagnostic performance of two models, Resnet and CNN, on two-dimensional vibration signal images. From a series of experiments, the specific values of the two models on the three key indexes of accuracy, precision and F1-score were obtained, as shown in Table 4.

Table 4.  Comparison of experimental results between Resnet and 2DCNN.

	Accuracy	Precision	F1-score
Resnet	0.9822	0.9830	0.9820
2DCNN	0.8434	0.8442	0.8435

---

 | Show Table

DownLoad: CSV

First, from the accuracy point of view, the Resnet model achieved higher accuracy on the test set. This shows that the Resnet model is able to determine more accurately whether an image contains fault information or not when recognizing fault features in an image. Second, the precision metric reflects the proportion of instances predicted by the model to be positive samples that are actually positive samples. In this metric, Resnet also performs well, indicating that the Resnet model has higher reliability in predicting faulty images and can reduce the possibility of false alarms. Finally, the F1-score, which is the reconciled average of precision and recall, combines the model's accuracy and completeness rates. On F1-score, the Resnet model also outperforms the CNN model, which further proves the overall superiority of Resnet in fault diagnosis tasks. This may be due to the fact that the Resnet model adopts the residual learning idea, which is capable of constructing deeper network structures and thus extracting richer image features. In addition, the residual connectivity in the Resnet model helps to alleviate the gradient vanishing problem and improve the training efficiency and stability of the model.

In order to more intuitively show the difference in the effect of the two models, we draw a bar chart for comparison. As shown in Figure 9, it can be clearly seen that the Resnet model is significantly higher than the CNN model in the three metrics of accuracy, precision, and F1-score. This result fully proves the effectiveness and superiority of Resnet model in image fault diagnosis task. Furthermore, this study compares and analyzes the fault diagnosis performance of two different models with a visual presentation of their results using confusion matrix plots, as shown in Figure 10. The results show that the Resnet model has a recognition accuracy of more than 96% for all three evaluated fault types. On the contrary, the 2DCNN model, while showing reasonable performance, has a maximum recognition accuracy of only 88.72% for the same fault patterns. This implies that the Resnet model exhibits higher recognition accuracy and better classification results in fault diagnosis tasks.

Figure 9.  Comparison results of Resnet and 2DCNN model effects.

DownLoad: Full-Size Img PowerPoint

Figure 10.  Confusion matrix of Resnet and 2DCNN models. (a) Resnet (b) 2DCNN.

DownLoad: Full-Size Img PowerPoint

Combining the residual module and the attention mechanism, this paper builds a 1DCNN-REA model aiming to improve the adequate extraction of fault information. The variation curves of training accuracy and validation accuracy with the number of iterations are shown in Figure 11(a), and the variation curves of training loss and validation loss with the number of iterations are shown in Figure 11(b). Based on the time-frequency statistical characteristics of the signal, the 1DCNN-REA model is utilized for fault diagnosis, and the confusion matrix obtained is shown in Figure 12.

Figure 11.  1DCNN-REA model effect. (a) Accuracy curve (b) Loss curve.

DownLoad: Full-Size Img PowerPoint

Figure 12.  Confusion matrix of 1DCNN-REA model.

DownLoad: Full-Size Img PowerPoint

In this paper, we provide a comprehensive evaluation of the proposed method using an experimental dataset containing three fault types for the bearing fault diagnosis problem. By comparing with traditional machine learning models such as support vector machine (SVM) and random forest (RF), as well as common deep learning models such as long short-term memory network (LSTM) and gated recurrent unit (GRU), we analyze in depth the performance of the different models in bearing fault diagnosis with the results shown in Tables 5–7. These tables show the results of ablation experiments on the proposed method in addition to the comparison experimental results of different methods, which comprehensively analyze the performance of different methods from multiple perspectives.

Table 5.  Comparison of classification accuracy results for different models.

Fault diagnosis model	Test accuracy			Average classification accuracy
	ORF	REF	IRF
DBN	0.5532	0.7179	0.9777	0.7456
SVM	0.8670	0.8359	0.8659	0.8563
RF	0.9894	0.6872	1.0000	0.8879
LSTM	0.8138	0.9949	1.0000	0.9359
GRU	0.8457	0.9846	1.0000	0.9431
1DCNN(No_res_att)	0.7340	1.0000	1.0000	0.9110
1DCNN(No_att)	0.7606	1.0000	1.0000	0.9199
1DCNN(No_res)	0.7660	1.0000	1.0000	0.9217
Proposed method (1DCNN-REA)	1.0000	0.8667	1.0000	0.9537

---

 | Show Table

DownLoad: CSV

Table 6.  Comparison of classification precision results for different models.

Fault diagnosis model	Test precision			Average classification precision
	ORF	REF	IRF
DBN	0.6933	0.6167	0.9459	0.7472
SVM	0.8359	0.8717	0.8611	0.8563
RF	0.7530	0.9853	1.0000	0.9123
LSTM	0.9935	0.8472	1.0000	0.9448
GRU	0.9815	0.8688	1.0000	0.9483
1DCNN(No_res_att)	1.0000	0.7959	1.0000	0.9292
1DCNN(No_att)	1.0000	0.8125	1.0000	0.9349
1DCNN(No_res)	1.0000	0.8159	1.0000	0.9361
Proposed method (1DCNN-REA)	0.8785	1.0000	1.0000	0.9594

---

 | Show Table

DownLoad: CSV

Table 7.  Comparison of classification F1-score results for different models.

Fault diagnosis model	Test F1-score			Average classification F1-score
	ORF	REF	IRF
DBN	0.6154	0.6635	0.9615	0.7423
SVM	0.8512	0.8534	0.8635	0.8559
RF	0.8552	0.8097	1.0000	0.8855
LSTM	0.8947	0.9151	1.0000	0.9353
GRU	0.9086	0.9231	1.0000	0.9427
1DCNN(No_res_att)	0.8466	0.8864	1.0000	0.9093
1DCNN(No_att)	0.8640	0.8966	1.0000	0.9186
1DCNN(No_res)	0.8675	0.8986	1.0000	0.9205
Proposed method (1DCNN-REA)	0.9353	0.9286	1.0000	0.9536

---

 | Show Table

DownLoad: CSV

As an example, Table 5 demonstrates the classification accuracy and average accuracy of various models for different types of faults. The table reveals significant differences in the performance of the models across fault types. Specifically, for the diagnosis of ORF, the proposed method achieves a classification accuracy of 100%, representing an improvement of 80.77% over deep belief network (DBN), 15.34% over SVM, 1.07% over RF, 22.88% over LSTM, and 18.25% over GRU, all of which demonstrate lower accuracy. Furthermore, from the perspective of model classification accuracy, traditional machine learning models such as SVM and RF outperform the common deep learning models LSTM and GRU. In terms of REF diagnosis, it is similarly observed that different models exhibit varying levels of accuracy. The SVM model, a traditional machine learning approach, demonstrates a classification accuracy of 83.59%. In contrast, the RF model achieves only 68.72% accuracy for this fault type, which is significantly lower than SVM. This discrepancy may be attributed to the limitations of RF in handling complex fault diagnosis tasks. Nevertheless, the deep learning models LSTM and GRU perform exceptionally well in diagnosing this fault type. The LSTM model achieves an accuracy of 99.49%, which is nearly perfect for classification. The GRU model, a variant of LSTM, offers a more streamlined structure and faster training speed while maintaining a high accuracy of 98.46%. It is important to note that the diagnostic accuracy of our proposed model for this fault type is 86.67%, which, while slightly lower than that of the LSTM model, is still higher than that of SVM and RF. Considering the advantages of the proposed model in diagnosing other fault types, its average diagnostic accuracy across the three fault types is superior to that of the other models, making the accuracy of 86.67% competitive. For the diagnosis of IRF, the accuracy of the SVM model is only 86.59%, the DBN model reaches 97.77%, while all other models achieve 100%.

The comparison results of the precision rates for various models diagnosing the three types of faults, as presented in Table 6, indicate that for the ORF fault type, despite the variations in diagnostic precision rates among models such as DBN, SVM, RF, LSTM, and GRU, our model demonstrates its effectiveness with a precision rate of 87.85%. Notably, in diagnosing REF and IRF fault types, the precision rate of the proposed model achieves 100%, showcasing exceptional reliability and precision.

The categorized F1-score as well as the average F1-score for the various models across the three fault types are presented in Table 7. The data in the table indicates that the proposed method achieves excellent F1-scores for all three fault types, with an average F1-score that surpasses those of the other models compared. This suggests that the proposed method effectively balances precision and recall in fault diagnosis, resulting in more comprehensive and accurate fault detection. Compared to the other models, the proposed method clearly demonstrates a significant advantage in terms of F1-score.

In order to clarify the different contributions of the attention mechanism module and the residual module to improve model performance, we designed three sets of ablation experiments. In the first group of experiments, we removed both the attention mechanism module and the residual module to establish a baseline. The second set of experiments removed only the attention mechanism module, thus allowing us to isolate and quantify its impact on model performance. In the third set of experiments, we excised only for the residual module while retaining the attention mechanism and performed a similar performance evaluation. To ensure the comprehensiveness of our findings, we conducted these ablation experiments with different datasets and experimental configurations. The experimental results clearly show that when tested individually, each module improves the overall performance of the model to varying degrees. Notably, the performance degradation observed after removing either module emphasizes the indispensability of both components of the proposed method. This comprehensive analysis validates the strategic integration of the attention mechanism and the residual module, emphasizing their synergistic effects in enhancing the model's capabilities.

The proposed method enables the model to focus on the more important parts of the input data by introducing an attention mechanism module. In the ablation experiments, we find that the model performs poorly in processing complex data without the attention mechanism module or without the residual module. This demonstrates the effectiveness of the attention mechanism and the residual module in improving model performance. In addition, we also noticed interactions between different modules, specifically, the performance of the model was further improved when the attention mechanism module was used in conjunction with the residual module. This suggests that when designing the method, we need to fully consider the synergies between the modules in order to achieve optimal performance.

To present the experimental results more intuitively, we visualized the accuracy, precision, and F1-score, as illustrated in Figures 13–15. The graphs clearly demonstrate that the overall performance of the proposed model surpasses that of the comparison models. The average accuracy, precision, and F1-score curves for the four models—SVM, RF, LSTM, and GRU—show a gradual increase. Compared to these five machine learning models, the proposed model in this paper exhibits superior diagnostic performance. The results of the ablation experiments reveal a decline in model performance with both single-module and two-module ablation compared to the full model. Notably, the model with two-module ablation experiences the most significant performance degradation, suggesting an interdependence between the two modules in the proposed model, which collectively influence overall performance. A comparison between the models with single-module and two-module ablation indicates that the model with only one module removed still outperforms the model with both modules removed. This finding further substantiates the independent contribution of each module to the overall performance of the proposed method.

Figure 13.  Diagnosis accuracy of different models for different faults.

DownLoad: Full-Size Img PowerPoint

Figure 14.  Diagnosis precision of different models for different faults.

DownLoad: Full-Size Img PowerPoint

Figure 15.  Diagnosis F1-score of different models for different faults.

DownLoad: Full-Size Img PowerPoint

To better assess the uncertainty of the models, this paper trains and tests each model using ten random initializations, calculating the standard deviation of the classification accuracies for comparison. The experimental results are presented in Table 8. It is evident that the standard deviation of the proposed 1DCNN-REA model is 0.0067, which is significantly smaller than that of the other models (e.g., 0.1314 for GRU and 0.0667 for RF). This indicates that the performance of the 1DCNN-REA model is much more stable, with almost no significant fluctuations under varying random initial conditions.

Table 8.  Comparison of standard deviation of accuracy for different models.

Fault diagnosis model	Standard deviation	Fault diagnosis model	Standard deviation
SVM	-	1DCNN(No_res_att)	0.0282
RF	0.0667	1DCNN(No_att)	0.0261
LSTM	0.0286	1DCNN(No_res)	0.0180
GRU	0.1314	Proposed method (1DCNN-REA)	0.0067
DBN	0.0152

---

 | Show Table

DownLoad: CSV

To enhance the effectiveness of fault diagnosis, this paper employs the TPE optimization algorithm to integrate the ResNet-based fault diagnosis model with the 1D CNN-REA-based fault diagnosis model, resulting in an integrated model. The integrated model is validated using experimental datasets and compared to the diagnostic effectiveness of the individual models, with the results presented in Table 9. The diagnostic accuracy of the integrated model is 0.72% higher than that of the single ResNet-based fault diagnosis model and 3.73% higher than that of the single 1D CNN-REA-based fault diagnosis model, demonstrating the efficacy of model integration.

Table 9.  Comparison of classification accuracy results of different models.

Fault diagnosis model	Resnet	1DCNN-REA	The proposed ensemble model
Accuracy	98.22%	95.37%	98.93%

---

 | Show Table

DownLoad: CSV

This paper employs the integrated model to conduct ten experiments with random initialization for both model training and testing. The standard deviation of the model's accuracy is calculated to be 0.0013, indicating that the model demonstrates a high level of stability. In Eq (8), the values of m and n are 0.3364 and 0.6636, respectively. When utilizing the integrated model to diagnose three types of bearing faults, the resulting confusion matrix is illustrated in Figure 16. The figure indicates that the integrated model exhibits superior diagnostic performance across all three fault types. However, it is evident that the model performs better than the IRF for diagnosing ORF faults, while it is relatively less effective for diagnosing REF faults. This outcome suggests that the integrated model displays varying sensitivities to the features of different fault types, demonstrating a heightened ability to capture the characteristics of ORF faults, thereby allowing for more accurate identification of this fault type.

Figure 16.  Confusion matrix of the proposed ensemble model.

DownLoad: Full-Size Img PowerPoint

5.   Conclusions

Aiming at the problem of multi-information fusion, this paper proposes a novel Resnet-1DCNN-REA bearing fault diagnosis method based on multisource and multimodal information fusion. The proposed method utilizes auto-encoder to fuse the multi-sensor signals, as well as provides a more comprehensive and richer feature representation by integrating the multimodal information of time-frequency statistical information and image features to improve the understanding and analysis of signals by the fault diagnosis system. In addition, the accuracy and robustness of bearing fault diagnosis under complex working conditions are improved through integrating the advantages of different models to make up for the limitations of their respective methods.

In order to verify the effectiveness of the proposed model, this paper utilizes real experimental data for detailed validation. The effectiveness of the proposed auto-encoder-based multisource information fusion model is demonstrated by visualizing the data distribution before and after multi-source data fusion. By comparing the results of the experiments with those of the ablation experiments, we observe that the proposed 1DCNN-REA model and the integrated model demonstrate a high degree of accuracy in the diagnosis of three types of faults, namely, outer race fault, inner race fault, and rolling element fault. Notably, the integrated model attains a remarkable fault diagnosis accuracy of 98.93%, underscoring its superiority and reliability in the domain. Compared to other diagnostic models, the proposed model exhibits superior diagnostic performance across several classification evaluation metrics, including accuracy, precision, and F1 score. Additionally, it demonstrates greater stability, thereby confirming its enhanced performance capabilities. This result shows that the bearing fault diagnosis model based on multi-sensor information fusion established in this paper can predict and diagnose bearing faults more accurately, which not only improves the technical level of bearing fault diagnosis, but also provides reference for fault diagnosis in other fields.

The proposed method involves image computation, resulting in greater complexity compared to traditional machine learning algorithms such as SVM, and RF, and others like LSTM networks and 1DCNN. In future research, we will focus on reducing computational requirements through techniques such as model compression, pruning, and quantization to enhance the model's efficiency. In addition, future research will be devoted to further optimizing the feature extraction and classification models and expanding the scope of application of the method to cope with more complex and variable industrial environments.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This research was funded by the National Natural Science Foundation of China (Grant No. 72371013 & 71971013) and the Fundamental Research Funds for the Central Universities (YWF-23-L-933). The study was also sponsored by the Teaching Reform Project and Graduate Student Education and Development Foundation of Beihang University.

Conflict of interest

The authors declare there is no conflict of interest.