Research on crude oil price forecasting based on computational intelligence

1.   Introduction

Because the social and economic environment are more complex than ever, many practical decision making problems are difficult to solve, and it is a need for us to develop multiple criteria/ attribute decision making methods to deal with various problems. Recent years, multi-criteria decision making (MCDM) and multi-attribute decision making (MADM) methods have been received great attention in solving various engineering problems ^[1,2,3,4,5]. In actual decision process, many qualitative attributes (criteria, indicators) in practical decision-making problems are difficult to quantify ^[6]. Some of these attributes are inherently ambiguous, such as the evaluation index of "problem-solving ability" in human resources management, which is itself ambiguous. The fuzziness of evaluation attributes is due to the influence of subjective and objective factors such as decision maker's time, energy and incomplete understanding of objective things, such as "safety and reliability" as an evaluation index in aircraft type selection. Zadeh ^[7] proposed the concept of fuzzy sets to solve these fuzzy phenomena in real-life problems. Because Zadeh's fuzzy sets can better depict the fuzziness of the objective things themselves and the fuzziness of human thinking, the fuzzy multi-attribute decision-making methods based on fuzzy sets have been greatly developed and applied in various fields ^[8,9].

Zadeh's fuzzy set has only one degree of membership and can only reflect two aspects of information, which results in some limitations in many real decision making problems. For example, with the increasing complexity of social and economic activities, decision makers often hesitate to some extent or show a certain degree of lack of knowledge in decision-making, which make the evaluation results show three aspects: support, against and hesitation. Because Zadeh's fuzzy set has only one degree of membership and can only reflect two aspects of information, it is difficult to describe the above situation better. So Atanassov ^[10,11] extended Zadeh's theory of fuzzy set, and put forward the concept of intuitionistic fuzzy (IF) set and interval-valued intuitionistic fuzzy (IVIF) set. Compared with Zadeh's fuzzy set, IF set and IVIF set can describe the concept of "either one or the other" by adding a non-membership parameter and considering the information of membership degree, non-membership degree and hesitation degree. Therefore, they can better describe the hesitation and uncertainty degree of decision makers' judgments, and then they can describe the model of objective things more delicately. Because IF sets and IVIF sets are more flexible than fuzzy sets in dealing with fuzziness and uncertainty, they are widely used in decision-making field ^{[12,13,14,15,16,17]}. Some other extensions of Zadeh's fuzzy set are also proposed and attached great attention to many authors. For example, picture fuzzy set ^[18], single valued neutrosophic set ^[19], intuitionistic fuzzy soft set ^[20,21,22], Pythagorean fuzzy soft set ^[23], interval type-2 fuzzy set ^[24] and q-rung orthopair fuzzy set ^[25,26] are all very famous successful extensions of Zadeh's fuzzy set.

In order to use the concept of intuitionistic fuzzy sets to define an uncertain quantity or a quantity difficult to quantify, some scholars put forward the concept of continuous intuitionistic fuzzy numbers. For example, Shu et al. ^[27] first introduced the concept of intuitionistic triangular fuzzy number and applied it to fault tree analysis. On this basis, Wang and Zhang ^[28] developed the concept of intuitionistic trapezoidal fuzzy number (ITFN). In recent years, the ITFNs have attracted many scholars' attention ^[29,30,31].

Distance measure is an important information measure in the study of intuitionistic fuzzys. But there are few distance formulas for ITFNs proposed in documents. Wang and Zhang ^[28] proposed a distance formula for two ITFNs. But we find that Wang and Zhang’s distance formula exists shortcomings, for example, $\tilde A$ = < [0.2, 0.3, 0.4, 0.5], 0.1, 0.7 > and $\tilde B$ = < [0.4, 0.6, 0.8, 1.0], 0.1, 0.9 > are two ITFNs. When we use Wang and Zhang’s distance formula, we obtain the distance of $\tilde A$ and $\tilde B$ is 0, which is counter-intuitive. Then this paper will proposed a new distance to overcome this shortcomings.

Most of the existing MADM models under intuitionistic trapezoidal fuzzy environment are based on the expected utility theory assuming that decision makers are completely rational. However, in the real MADM process, decision makers often have subjective risk preferences for alternatives, so it is important to consider the real-life attitude of decision makers in the MADM model. The prospect theory, first proposed by Kahneman and Tversky ^[32], is a challenge to expected utility theory, as it explains the phenomena that expected utility theory can not explain. It is more in line with the actual decision-making mode of human beings to introduce the cumulative prospect theory into the fuzzy decision model ^[33,34].

There are few documents discussed the application of prospect theory in intuitionistic trapezoidal fuzzy MADM problems. Chen et al. ^[35] developed a decision making method combining with parameter estimation and score functions for solving the MADM problem under intuitionistic trapezoidal fuzzy environment. But they defined a prospect value function of ITFNs based on the difference of score functions between ITFN. In prospect theory, a prospect value function is mainly defined by distance, which can get a well discrimination ^[36]. Thus this paper will first propose a new distance for ITFNs, then use it to define prospect values, and furthermore develop a new decision-making method for solving MADM problem under intuitionistic trapezoidal fuzzy environment with incomplete information based on cumulative prospect theory.

2.   Preliminaries

2.1.   ITFNs and prospect theory

Some basic concepts and properties of ITFN and cumulative prospect theory are reviewed. To overcome the limitation of Zadeh’s fuzzy set, Atanassov proposed the concept of intuitionistic fuzzy set, which is illustrated in Definition 1.

Definition 1 ^[10]. Let $X$ be a given universal set, a set $A = \{ < {x_i}, {\mu _A}({x_i}), {\upsilon _A}({x_i}) > |{x_i} \in X\} $is called an intuitionistic fuzzy set, where ${\mu _A}({x_i})$ and ${\upsilon _A}({x_i})$ are the membership degree and non-membership degree of ${x_i}$, respectively. Here, $0 \leqslant {\mu _A}({x_i}) + {\upsilon _A}({x_i}) \leqslant 1$ for any${x_i} \in X$ and an index ${\pi _A}({x_i}) = 1 - {\mu _A}({x_i}) - {\upsilon _A}({x_i})$ is called the hesitancy degree of ${x_i}$. For convenience, if there is only one element in $X$, we call $A$ intuitionistic fuzzy number.

In order to use the concept of intuitionistic fuzzy sets to define an uncertain quantity or a quantity difficult to quantify, Wang and Zhang ^[28] introduced the concept of ITFN, which is illustrated in Definition 2.

Definition 2. Let $a, b, c, d \in R$, $0 \leqslant {\mu _{\tilde A}} \leqslant 1$, $0 \leqslant {\upsilon _{\tilde A}} \leqslant 1$ and${\mu _{\tilde A}} + {\upsilon _{\tilde A}} \leqslant 1$. A fuzzy number $\tilde A = < [a, b, c, d]; {\mu _{\tilde A}}, {\upsilon _{\tilde A}} > $ is called an ITFN, if its membership degree and non-membership degree functions are (^[28]).

and

respectively.

To rank the order of ITFNs, Wang and Zhang ^[29] introduced the concepts of the score and accuracy functions of an ITFN$\tilde A = < [a, b, c, d]; {\mu _{\tilde A}}, {\upsilon _{\tilde A}} > $, which is similar to that concepts of intuitionistic fuzzy numbers. Based on score function $S(\tilde A) = \frac{1}{4}(a + b + c + d) \times ({\mu _{\tilde A}} - {\upsilon _{\tilde A}})$ and accuracy function $H(\tilde A) = \frac{1}{4}(a + b + c + d) \times ({\mu _{\tilde A}} + {\upsilon _{\tilde A}})$. Score function $S(\tilde A)$ can represent a support degree if we choose a vote case as example, while accuracy function$H(\tilde A) = \frac{1}{4}(a + b + c + d) \times (1 - {\pi _{\tilde A}})$can reflect the deterministic information of $\tilde A$ in some degree. Thus Wang and Zhang ^[29] proposed a ranking rule as in Definition 3.

Definition 3 ^[29]. Let $\tilde A = < [a, b, c, d]; {\mu _{\tilde A}}, {\upsilon _{\tilde A}} > $ be an ITFN. Then the score and accuracy functions of $\tilde A$ are $S(\tilde A)$ and $H(\tilde A)$, respectively. Then for two ITFN$\tilde A$and $\tilde B$,

(1) If $S(\tilde A) > S(\tilde B)$, then $\tilde A > \tilde B$

(2) If $S(\tilde A) = S(\tilde B)$ and

(ⅰ) $H(\tilde A) = H(\tilde B)$, then $\tilde A = \tilde B$;

(ⅱ) $H(\tilde A) > H(\tilde B)$，then $\tilde A > \tilde B$.

As a very useful tool for describing the number of fuzzy numbers, $\alpha $-cut set is very important for studing the properties of fuzzy numbers. Let $\tilde A = < [{a_1}, {a_2}, {a_3}, {a_4}]; {\mu _{\tilde A}}, {\upsilon _{\tilde A}} > $ be an ITFN, and the corresponding $\alpha $-cut is ${\tilde a_\alpha } = \{ x|{\mu _{\tilde a}}(x) \geqslant \alpha \} $, $\beta $-cut is ${\tilde a_\beta } = \{ x|{\upsilon _{\tilde a}}(x) \leqslant \beta \} $. Here $0 \leqslant \alpha \leqslant {\mu _A}$, ${\upsilon _A} \leqslant \beta \leqslant 1$ and $0 \leqslant \alpha + \beta \leqslant 1$. By straightforward calculation, we can get

Prospect theory, firstly proposed by Kahneman and Tversky ^[32], can objectively reflect decision makers’ behavior and the theory has been developed into solving MADM problems ^[33,34]. This paper will use the prospect theory to determine weights of indices with the help of a new distance measure of ITFNs. Some key elements of prospect theory are the prospect value and value function, which are given in the following definitions.

Definition 4 ^[32]. Prospect value, determined by value functions and decision weight, is defined as follows:

where $\pi ({p_j})$ is the probability weight function which is monotone increasing with respect to ${p_j}$, and $\nu (x)$ is the value function.

Definition 5. Value function, first proposed by Kahneman and Tversky ^[32], has the following formula

where $\nu (x)$ comes from the subjective feeling of the decision maker and the variable $x$ is the gains ($x > 0$) or the losses ($x < 0$), parameters $\alpha, \beta \in (0, 1)$ are the concave-convex degree of the region value power function of the gains and the losses, respectively. $\theta $ shows that the region value power function is more steeper for the losses than for the gains, and $\theta > 1$ means the losses aversion.

Definition 6. The probability weight, proposed by Kahneman and Tversky ^[32] has the following form:

where $\gamma > 0$ is a parameter measuring degree of curvature.

2.2.   A new distance measure for ITFNs

Let $A$ and $B$ be two fuzzy numbers. Scholars have constructed many distance formulas of $A$ and $B$, such as Euclidian distance, Hamming distance ^[37]. Grzegorzewski ^[38] proposed a new distance formula as follows:

Let $A$ and $B$ be two fuzzy number, the corresponding $\alpha $-cuts are $[{({A_L})_\alpha }, {({A_U})_\alpha }]$ and $[{({B_L})_\alpha }, {({B_U})_\alpha }]$, respectively. The distance measure of $A$ and $B$ is defined as

The distance formula (7) has received great attention, for the reason that many authors used it to obtain nearest interval, triangular and trapezoidal approximation of a fuzzy number preserving ambiguity ^[39,40]. Motivated by the distance formula (7), this section will construct a new distance formula for ITFNs.

For two any ITFNs $\tilde A$ and $\tilde B$, the most existing distance formulas $d(\tilde A, \tilde B)$ could not consider the influence of $\alpha - {\rm{cut}}$ and $\beta - {\rm{cut}}$, which are two important concepts of fuzzy sets. There exist limitations of most distance formulas when we use them to discriminate some intuitionistic fuzzy numbers ^[41]. This section will consider the $\alpha - {\rm{cut}}$ and $\beta - {\rm{cut}}$ into the construction of the new distance formula. The new distance measure of $\tilde A$ and $\tilde B$ is constructed as follows:

Lemma 1. (Cauchy-Schwarz Inequality) Let $f(x)$ and $g(x)$ be two integral functions on [$a, b$], then

By straightforward calculation, we have the following result seen in Lemma 2.

Lemma 2. For four positive real numbers:$x_1, x_2, y_1, y_2,$ then

Lemma 3. Let $f_1,f_2,g_1,g_2$ and $g$ are real functions of variable $x$, and they are integral on [$a,b$], set

Then

Proof.

According to Lemma 1 and Lemma 2, we have

Then we can easily complete the proof.

Theorem 1. Let $\tilde A$, $\tilde B$ and $\tilde C$ be three ITFNs, then $d(\tilde A, \tilde B)$ is a distance measure of $\tilde A$ and $\tilde B$. That is, the following three conditions are satisfied: (ⅰ)$d(\tilde A, \tilde B) \geqslant 0$; (ⅱ)$d(\tilde A, \tilde B) = d(\tilde B, \tilde A)$ and (ⅲ)$d(\tilde A, \tilde B) \leqslant d(\tilde A, \tilde C) + d(\tilde B, \tilde C)$.

Proof. Obviously, (ⅰ) and (ⅱ) are true. Now we prove (ⅲ). Set，

where

According to Lemma 3 and ${d_3}(\tilde A, \tilde B)$ is a formula of Minkowski distance, we can immediately get (ⅲ).

Therefore $d(\tilde A, \tilde B)$ is a distance measure of $\tilde A$ and $\tilde B$.

Let $\tilde A$ and $\tilde B$ be two ITFNs, where $\tilde A = < [{a_1}, {a_2}, {a_3}, {a_4}]; {\mu _{\tilde A}}, {\upsilon _{\tilde A}} > $ and $\tilde B = < [{b_1}, {b_2}, {b_3}, {b_4}]; {\mu _{\tilde B}}, {\upsilon _{\tilde B}} > $. Let ${S_1} = 1 + {\mu _{\tilde A}} - {\upsilon _{\tilde A}}$ and ${S_2} = 1 + {\mu _{\tilde B}} - {\upsilon _{\tilde B}}$. Then Wang and Zhang’s distance measure ^[28] of $\tilde A$ and $\tilde B$ is

Example 1. Let us consider two ITFNs = < [0.2, 0.3, 0.4, 0.5], 0.1, 0.7 > and = < [0.4, 0.6, 0.8, 1.0], 0.1, 0.9 > . Then, using Wang and Zhang’s distance measure (11), we obtain the distance of and is 0, which is counter-intuitive. Here we use the proposed distance formula (8) to calculate the distance between them. According to Eq (3), we have

Substituting them into formula (8), we can easily get the calculation result $d(\tilde A, \tilde B) = 2.2917$. This result shows that the proposed distance formula has a better discrimination ability than Wang and Zhang’s distance measure (11).

Definition 7 ^[34]. Let two $\tilde A$ and $\tilde B$ be two then we can define the value function of $\tilde B$ by using $\tilde A$ as a reference point as follows:

Where $d(\tilde A, \tilde B)$ is the distance of $\tilde A$ and $\tilde B$.

3.   A new decision making method based on prospect theory

In real-life decision-making problems, different attitudes are often accompanied by different decision results due to different conditions and external environments of decision-makers. Some scholars have considered the influence of different attitudes of decision-makers for solving MADM problems under interval number and triangular fuzzy number environment. But few literature considered the behavior factors of decision maker in solving MADM problem in which attribute values are expressed by ITFNs.

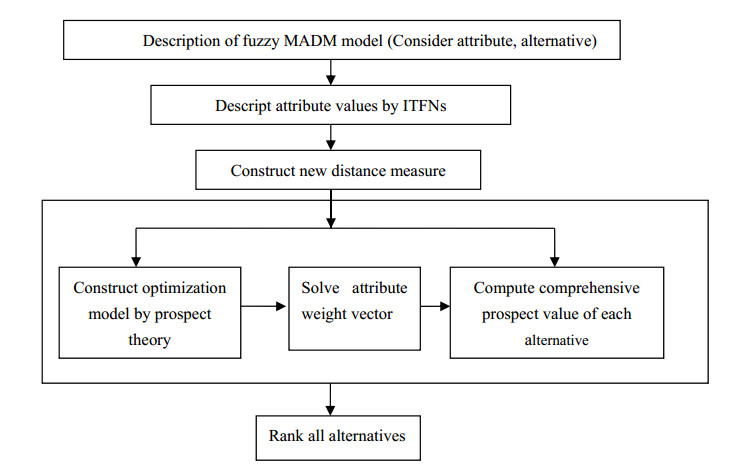
In this section, we will propose a new decision method of intuitionistic trapezoidal fuzzy model, which takes the decision maker's attitude into consideration based on prospect theory combining with the new distance measure of ITFNs. The detail decision process is shown in the Figure 2.

Now, we first introduce the intuitionistic trapezoidal fuzzy multi-attribute decision making problem as follows:

(ⅰ) Alternative set $\{ {A_1}, {A_2}, ..., {A_m}\} $ and attribute set $O = \{ {o_1}, {o_2}, ..., {o_n}\} $;

(ⅱ) Because the importance of different attributes is often different, and ${w_j}$ is the importance degree of attribute ${o_j}$, and they satisfy $\sum\limits_{j = 1}^n {{w_j}} = 1$ and ${w_j} \geqslant 0, $ $j = 1, 2, ..., n$.

(ⅲ) For alternative ${A_i}$, the evaluation value of ${A_i}$ with respect to ${o_j}$ is an ITFN ${\tilde a_{ij}} = < [{a_{ij1}}, {a_{ij2}}, {a_{ij3}}, {a_{ij4}}]; {\mu _{{{\tilde a}_{ij}}}}, {v_{{{\tilde a}_{ij}}}} > $, then one can get a fuzzy decision making matrix $\tilde A = {({\tilde a_{ij}})_{m \times n}}$.

(ⅳ) The weight information is partially known, and the set of incomplete information is defined as $H$.

The task of decision maker is to give a rational ranking result for given alternatives. Now we develop a new decision making method based on prospect theory combining with the new distance measure. The specific decision-making steps are as follows:

Step 1. Normalize $\tilde A = {({\tilde a_{ij}})_{m \times n}}$ to $\tilde R = {({\tilde r_{ij}})_{m \times n}}$.

In order to eliminate the influence of different physical dimensions on decision results, it is necessary to standardize the decision matrix. Set $M = \{ 1, 2, ..., m\}, N = \{ 1, 2, ..., n\} $. ${I_1}$ and ${I_2}$ represent the subscript sets of benefit type and cost type respectively. The matrix $\tilde A = {({\tilde a_{ij}})_{m \times n}}$ is transformed into a normalized matrix $\tilde R = {({\tilde r_{ij}})_{m \times n}}$ by using the following formulas, where ${\tilde r_{ij}} = < [{r_{ij1}}, {r_{ij2}}, {r_{ij3}}, {r_{ij4}}]; {\mu _{{{\tilde r}_{ij}}}}, {v_{{{\tilde r}_{ij}}}} > $,

and

Step 2. Define the positive ideal solution (PIS) and negative ideal solution (PIS).

PIS is defined as ${\tilde r^ + } = \{ \tilde r_1^ +, \tilde r_2^ +, ..., \tilde r_n^ + \} $and NIS is defined as ${\tilde r^ - } = \{ \tilde r_1^ -, \tilde r_2^ -, ..., \tilde r_n^ - \} $, where $\tilde r_j^ + = < (1, 1, 1, 1), 1, 0 > $ and $\tilde r_j^ - = < (0, 0, 0, 0), 0, 1 > $.

Step 3. Determine the gain and loss values of the attributes of each alternative.

When the NIS is taken as the reference point, the alternative ${A_i}$ is better than the NIS. For the decision maker, he/she is faced with benefits. According to the prospect theory, he/she is averse in risk at this time. Then the positive prospect value is defined by ${v^ + }({r_{ij}}) = {(d({\tilde r_{ij}}, r_j^ -))^\alpha }$, where

The distance decision matrix from the alternative ${x_i}$ to the negative ideal point is obtained as follows:

When the PIS is taken as the reference point, the alternative ${A_i}$ is inferior to the PIS. For the decision maker, he/she is faced with loss. According to the prospect theory, he/she is pursuing risk averse at this time. At this time, the negative prospect value is defined by ${v^ - }({\tilde r_{ij}}) = - \theta {(d({\tilde r_{ij}}, r_j^ +))^\beta }$, where

Then the distance decision matrix from the alternative ${x_i}$ to the positive ideal point is obtained as follows:

Step 4. Determine the positive prospect and negative prospect values.

When the NIS is taken as the reference point, the alternative ${A_i}$ is better than the NIS. For the decision maker, he is faced with benefits. According to the prospect theory, the decision maker is risk averse at this time. At this time, the positive prospect value is defined by ${v^ + }({r_{ij}}) = {(d({\tilde r_{ij}}, r_j^ -))^\alpha }$ and abbreviated by $v_{ij}^ + $.

When the PIS is taken as the reference point, the alternative ${A_i}$ is inferior to the PIS. For the decision maker, he is faced with loss. According to the prospect theory, the decision maker is pursuing risk at this time. At this time, the negative prospect value is defined by ${v^ - }({\tilde r_{ij}}) = - \theta {(d({\tilde r_{ij}}, r_j^ +))^\beta }$ and abbreviated by $v_{ij}^ - $.

Step 5. Compute the comprehensive prospect value of ${x_i}$.

Assume that ${\pi ^ + }({w_j})$ and ${\pi ^ - }({w_j})$ are the prospect weight functions, which represent the weights of decision maker facing to the gains and losses, respectively. Then the comprehensive prospect value, noted by ${V_i}$, of alternative ${A_i}$ is the sum of positive prospect values and negative prospect values. Then we can get

Where

and $v_{ij}^ + $ and $v_{ij}^ - $are the value functions. According to ^[34], in this paper we will adopt the parameter values as follows:

Step 6. Determine the optimal attribute weights.

Let $w = ({w_1}, {w_2}, ..., {w_n})$ and$w \in H$. For each alternative${A_i}$, its comprehensive prospect value is always the larger the better, so we need maximum $V = ({V_1}, {V_2}, ..., {V_m})$ under weights information. Then we can construct the following optimization model

Because of the fair competition among the alternatives, we establish the following optimization model

The optimal weight vector ${w^ * } = (w_1^ *, w_2^ *, ..., w_n^ *)$ can be obtained by MATLAB or Lingo software.

Step 7. Calculate the optimal comprehensive prospect value of each alternative $A_i(i=1,2,3,…,m)$ as

By sorting $V_i^ * $ $(i = 1, 2, ..., m)$ from large to small, the sorting results and the optimal scheme of the whole alternative set can be obtained.

4.   An illustrated example

Taking the example ^[29] of supplier selection for an engine parts manufacturing company to illustrate the performance of the proposed method. There are five alternative suppliers${A_1}, {A_2}, {A_3}, {A_4}, {A_5}$, and the five evaluation attributes: supply capability (${o_1}$), delivery capability (${o_2}$), service quality (${o_3}$), influence (${o_4}$), scientific research strength (${o_5}$). Decision makers give the intuitionistic trapezoidal decision matrix provided in Table 1. The attributes’ weight information of given by decision makers is partially known, $H = {\rm{\{ (}}{w_1}, {w_2}, \ldots, {w_5})|0.10 \leqslant {w_1} \leqslant 0.15, 0.10 \leqslant {w_2}{\rm{, }}{w_5} \leqslant 0.30, $ $0.05 \leqslant {w_3} \leqslant 0.20, $ $0.08 \leqslant {w_4} \leqslant 0.18, {w_2} \geqslant {w_5} \geqslant {w_1} \geqslant {w_4} \geqslant {w_3}\} $. Our task is to determine the best supplier.

Now we give the detail calculation steps of this example.

Step 1. Normalize $\tilde A$ by the normalization formulas (13)–(15), we can get $\tilde R$ shown in Table 2.

Step2. Determine the PIS ${\tilde r^ + } = (\tilde r_1^ +, \tilde r_2^ +, ..., \tilde r_5^ +)$, where $\tilde r_j^ + = < (1, 1, 1, 1), 1, 0 > $ and NIS${\tilde r^ - } = (\tilde r_1^ -, \tilde r_2^ -, ..., \tilde r_5^ -)$, where $\tilde r_j^ - = < (0, 0, 0, 0), 0, 1 > $ for all $j = 1, 2, ..., 5$.

Step3. Calculate the distance measures between each attribute of alternative ${A_i}$ with that of positive and negative ideal points, and these values are shown in Tables 3 and 4.

Step 4. Calculate ${v^ + }({r_{ij}})$ and${v^ - }({\tilde r_{ij}})$, and we can get the positive prospect matrix and negative prospect matrix as shown in Tables 5 and 6.

Step 5. Set ${\gamma ^ + } = 0.61, {\gamma ^ - } = 0.69$. Because of solving the nonlinear optimization model (23), we first choose the initial point ${w_0}$ = (0.15;0.25;0.10;0.10;0.20). With the help of matlab software, the optimal weight vector is obtained as ${w^ * } = (0.15, 0.30, 0.10, 0.15, 0.30)$.

Step 6. Calculate the optimal comprehensive prospect value of each alternative ${A_i}$, and we get $V_1^ * = $ –1.7631, $V_2^ * = $ –0.9588, $V_3^ * = $ –1.7610, $V_4^ * = $ –1.8069, $V_5^ * = $ –2.0599.

Step 7. According to the order of the optimal comprehensive prospect value, the ranking result is: ${A_2} > {A_3} > {A_1} > {A_4} > {A_5}$. Therefore, the optimal alternative is ${A_2}$.

In Example 1, the optimal alternative is in consistent with the ranking results of Wang and Zhang ^[29], but other alternatives’ order is different. The reason is that the they didn’t consider psychological factors of decision makers in the decision process.

5.   Conclusion

Most of the existing MADM models under intuitionistic trapezoidal fuzzy environment are based on the expected utility theory assuming that decision makers are completely rational. However, in the actual MADM process, decision makers often have subjective risk preferences, such as psychological and behavioral factors for alternatives. So it is important to consider the risk attitude of decision makers in the decision process. Prospect theory can describe human's psychological behavior under uncertain conditions more truthfully, and it can explain the phenomena that expected utility theory can not explain. Our decision making method is considering the psychological factors of decision makers based on prospect theory. The main contribution of this article is as follows:

This article firstly constructs a new distance formula of ITFNs, and the distance measure can well recognize the difference between two TIFNs. Then aiming at the problem of MADM with incomplete attribute weight information and attribute evaluation values expressed by ITFNs, a new MADM method based on prospect theory combining with the new proposed distance formula is developed. According to the distance formula, the value function of ITFNs is given, and the positive and negative ideal solutions are taken as reference, based on these, we adopt different ways to deal with "gain" and "loss" so that decision makers can get more accurate decision weights. The intuitionistic trapezoidal fuzzy MADM method based on prospect theory proposed in this paper has the characteristics of clear concept, simple calculation process and easy software implementation, and can be easily applied in practice.

The proposed decision making method can be used to solve other MADM problems, such as the investment decision, project evaluation, etc. Also, the proposed method has its limitation: How to determine the most suitable values of parameters in prospect theory. In the future, we will further develop similar constructing method proposed in this paper into the study of new distance formulas for trapezoidal fuzzy neutrosophic number, which is a useful generalized intuitionistic fuzzy number.

Acknowledgments

This research was financially supported by National Natural Science Foundation of China (No.71661012), Key Projects of Science Research of Jiangxi Educational Committee (Grant No. GJJ170496 and GJJ160629). The authors are grateful to the reviewers for their careful reading of the manuscript and the suggestions which are helpful to the improvement of the paper.

Conflict of interest

The authors declared that they have no conflicts of interest to this work.