Differential equations of the neutral delay type: More efficient conditions for oscillation

1.   Introduction

In this article, we study the oscillatory nature of solutions of the neutral differential equations (NDE)

and

where $\iota \geq \iota _{0},$ $z\left(\iota \right) = x\left(\iota \right) +p\left(\iota \right) x\left(h\left(\iota \right) \right),$ and $\alpha$ is a ratio of two odd natural numbers. We use the following assumptions:

(A1) The functions $\varrho,$ $p$ and $q$ are continuous on $\left[ \iota _{0}, \infty \right)$ and satisfy the conditions:

$\varrho \left(\iota \right) > 0,$ $\varrho ^{\prime }\left(\iota \right) > 0,$ $0 < p\left(\iota \right) < 1,$ $q\left(\iota \right) > 0,$ and $q$ does not vanish identically on any half-line $\left[ \iota _{\ast }, \infty \right),$ for $\iota _{\ast }\geq \iota _{0}$.

(A2) $h$ and $g$ are continuous delay functions on $\left[ \iota _{0}, \infty \right)$ and fulfill the conditions:

$h\left(\iota \right),$ $g\left(\iota \right) \leq \iota$ $g^{\prime }\left(\iota \right) \geq 0$ and $\lim_{\iota \rightarrow \infty }h\left(\iota \right) = \lim_{\iota \rightarrow \infty }g\left(\iota \right) = \infty$.

Moreover, we consider the canonical case, that is,

By a solution of Eq (1.1) or (1.2), we mean a real function $x\in C^{m-1}\left(\left[ \iota _{x}, \infty \right) \right)$ for some $\iota _{x}\geq \iota _{0}$, which has the property $\varrho \cdot \left(z^{m-1}\right) ^{\alpha }\in C^{1}\left(\left[ \iota _{x}, \infty \right) \right)$ and $x$ satisfies Eq (1.1) on $\left[ \iota _{x}, \infty \right)$, for $m = 2, 4$. Only solutions that satisfy the condition $\sup \{\left\vert x\left(\iota \right) \right\vert :\iota \geq \iota _{\ast }\} > 0, \ $for all $\iota _{\ast }\geq \iota _{x}$, will receive our attention. A solution of Eq (1.1) is called non-oscillatory if it is eventually positive or eventually negative; otherwise, it is called oscillatory.

Since the creation of the differentiation concept, ordinary differential equations have been utilized to model physical phenomena. As a result of the observation that most of the natural and physical phenomena contain a delay in time (different times), the so-called delay differential equations (DDE) have been established, which take into account the temporal memory of the phenomena. DDEs are functional differential equations in one independent variable, frequently time $\iota$, and they contain late times as the highest derivative in them is on the solution without delay.

The property of oscillation is widespread in many physical, natural, and even social phenomena, so the study of oscillatory properties for solutions of differential equations is an interesting issue not only for its applied importance, but because it also contains many interesting analytical issues.

Sturm's paper ^[1] is one of the pioneering papers that contributed to the establishment of oscillation theory. He devised the comparative technique, which couples the oscillatory properties of solutions to one differential equation to another. Then, Kneser ^[2] completed the work in this field and deduced the type of solutions that have been known by his name so far. In 1921, Fite ^[3] presented the first results that included the oscillation of the solutions of differential equations with deviating arguments. Since then, many results, techniques, and approaches have been presented that have contributed to the development of oscillation theory, most of which have been compiled in monographs ^[4,5,6,7,8].

Neutral differential equations are a type of functional differential equation in which the highest derivative occurs on the solution with and without delay. This type of equation appears as a result of modeling many phenomena, such as electric networks containing lossless transmission lines (as in high speed computers), vibrating masses, and variational problems with time delays, see ^[9]. Interest in studying the qualitative behavior of DDE is increasing as a result of the creation of new models and the tremendous technical and scientific growth that the world is currently witnessing in engineering, biology, and physics, see ^{[10,11,12,13]}.

Baculikova and Dzurina in ^[14] studied the oscillation of NDE

when $\alpha \geq \beta,$ $g\ $and $h$ nondecreasing, $h\left(g\left(\iota \right) \right) = g\left(h\left(\iota \right) \right)$. In ^[15,16,17], the oscillatory behavior of NDE

have been studied. Liu et al. ^[15], investigated the asymptotic behavior of (1.4), when $\alpha \geq \beta$, $\varrho ^{\prime }\left(\iota \right) > 0$ and $g^{\prime }\left(\iota \right) > 0$. Wu et al. ^[16] and Zeng et al. ^[17] obtained oscillation criteria for (1.4), which develops the criteria in ^[15]. Grace et al. ^[18] developed criteria with more than one approach to test the oscillation of solutions of second-order NDEs. Recently, Pátíková and Fiš narová ^[19] used an improved Riccati substitution to obtain the oscillation criteria of (1.1). Jadlovská ^[20] provided sharp criteria to check the oscillation of the solutions of (1.1).

In 1998, Zafer ^[21] studied the oscillatory behavior of the NDE

where there are $w,$ $h\in {\bf{C}}^{1}\left(\left[ \iota _{0}, \infty \right), \left[ 0, \infty \right) \right)$ such that $w\left(\iota \right) > 0$, $w^{\prime }\left(\iota \right) > 0$, and

Later, Karpuz et al. ^[22] and Zhang et al. ^[23] used the principle of comparison to obtain an oscillation criterion for the NDE

In ^[24], Zhang and Yan developed criteria of an iterative nature to test the oscillation of (1.5). Agarwal et al. ^[25] used the Riccati technique to study the oscillatory behavior of the NDE (1.5).

In 2012, Zhang et al. ^[26] examined the asymptotic behavior of

in the noncanonical case. The results in ^[26] made sure that all nonoscillatory solutions of Eq (1.6) converge to zero. Zhang et al. ^[27] improved the results in ^[26]. By imposing the following conditions

Baculikova et al. ^[28] studied the oscillatory properties of

in the canonical and noncanonical cases. Recently, there have been some studies concerned with the canonical case of Eq (1.6), see for examples ^[29,30,31].

In this paper, we derive new monotonic features of the second-order NDE (1.1). We then use these features to obtain optimized oscillation parameters. We use more than one approach to obtain oscillation parameters. Moreover, in the last section, we set new criteria that ensure the oscillation of solutions of the fourth order NDE (1.2). The new criteria are an extension and development of relevant previous studies.

2.   Oscillation results for the second-order equation

In this section, we set out to investigate the monotonic properties and oscillatory behavior of solutions to Eq (1.1).

2.1.   Preliminary results

Before looking at the oscillation of the DDE, it is known that determining the signs of derivatives of $x$ or $z$ is important and necessary. Establishing relationships between derivatives of various orders is also crucial, although doing so may impose further limitations on the study. The most influential factor in the relationships between derivatives is the monotonic properties of the solutions of these equations. Therefore, improving these properties or finding new properties of an iterative nature greatly affects the qualitative study of solutions to these equations.

The following notations will be required when presenting the results: $\mathcal{P}_{s}:$ The set of all eventually positive solutions of (1.1)$,$ $h_{0}\left(\iota \right) : = \iota,$ $h_{i} = h\circ h_{i-1},$ for $i = 1, 2, ...$,

and

Lemma 2.1. The following properties are satisfied for each $x\in \mathcal{P} _{s}$:

for $\iota \geq \iota _{1}\geq \iota _{0}$.

Proof. Assuming that $x\in \mathcal{P}_{s}$, we find, by taking into account (C2), that $x\circ h,$ $x\circ g$ and $z$ are also eventually positive. Hence, from Eq (1.1), the function $\varrho \cdot \left(z^{\prime }\right) ^{\alpha }$ is decreasing, and so $\varrho \cdot \left(z^{\prime }\right) ^{\alpha }$ is of fixed sign.

For the proof of $\left({\mathrm{P1}}\right)$, we should consider two cases:

Case 1: $\varrho \left(\iota \right) \left(z^{\prime }\left(\iota \right) \right) ^{\alpha }\geq 0$. Then, $z^{\prime }\left(\iota \right) \geq 0$, and $z$ is non-decreasing.

Case 2: $\varrho \left(\iota \right) \left(z^{\prime }\left(\iota \right) \right) ^{\alpha } < 0$. Because $z$ is positive and decreasing, there existis a constant $L$ such that $\varrho \left(\iota \right) \left(z^{\prime }\left(\iota \right) \right) ^{\alpha }\leq -L^{2} < 0$ for $\iota \geq \iota _{1}$. Therefore, $z^{\prime }\left(\iota \right) \leq -L^{2/\alpha }\varrho ^{-1/\alpha }\left(\iota \right)$. By integrating this inequality from $\iota _{1}$ to $\infty$ and using the canonical condition (1.3), we obtain $z\left(\iota _{1}\right) = \infty$, a contradiction.

Now, we have $z$ is increasing for $\iota \geq \iota _{1}$. Thus,

Then, $\left(\frac{1}{\mu _{\iota _{1}}}z\right) ^{\prime } = \frac{1}{\mu _{\iota _{1}}^{2}}\left(\mu _{\iota _{1}}z^{\prime }-\varrho ^{-1/\alpha }z\right) \leq 0$, (property $\left({\mathrm{P2}}\right)$).

Here, the proof ends.

Lemma 2.2. Assume that $x\in \mathcal{P}_{s}$. Then,

Proof. Assume that $x\in \mathcal{P}_{s}$. Based on the relationship between $x$ and $z$, we obtain $x = z-p\cdot \left(x\circ h\right)$. Thus, $\left(x\circ h\right) = \left(z\circ h\right) -\left(p\circ h\right) \cdot \left(x\circ h_{2}\right)$. By substitution, we get

By repeating this procedure, we arrive at

Hence,

From Lemma 2.1, we obtain that $\left({\mathrm{P1}}\right)$ and $\left({\mathrm{P2}}\right)$ hold. Therefore, $\left(z\circ h_{2i}\right) \geq \left(z\circ h_{2i+1}\right)$, and

for $\iota \geq \iota _{1}$. Then, (2.3) reduce to

Now, Eq (1.1) becomes $\left(\varrho \left(\iota \right) \left(z^{\prime }\left(\iota \right) \right) ^{\alpha }\right) ^{\prime }\leq -q\left(\iota \right) \widetilde{p}\left(g\left(\iota \right), m\right) z^{\alpha }\left(g\left(\iota \right) \right)$.

Here, the proof ends.

Lemma 2.3. Assume that

and

Then, the following properties are satisfied for each $x\in \mathcal{P}_{s}$:

Proof. Assuming that $x\in \mathcal{P}_{s}$, we find, by taking into account (C2), that $x\circ h,$ $x\circ g$ and $z$ are also eventually positive.

From Lemma 2.1, we have that $\left({\mathrm{P1}}\right)$ and $\left({\mathrm{P2}}\right)$ hold.

Now, we have $z/\mu _{\iota _{1}}$ is positive and decreasing. Then, $z/\mu _{\iota _{1}}\rightarrow c\geq 0$ as $\iota \rightarrow \infty$.

When, unlike property $\left({\mathrm{P3}}\right)$, we assume that $c > 0$, we find that there is a $\iota _{1}\geq \iota _{0}$ such that $z/\mu _{\iota _{1}}\geq c$ for $\iota \geq \iota _{1}.$ Thus, by integrating (2.2) from $\iota _{1}$ to $\iota$, we obtain

From (2.4), we arrive at

a contradiction. Then, $c = 0$.

Next, using (2.1), (2.2), (2.4) and the fact that $\left(\varrho ^{1/\alpha }\left(\iota \right) z^{\prime }\left(\iota \right) \right) ^{\prime }\leq 0$, we find

Here, we define the function $\phi : = \left(1-k\right) z-\mu _{\iota _{1}}\cdot \varrho ^{1/\alpha }\cdot z^{\prime }$. By differentiating and using (2.7), we get

Now, we will prove that $\phi \left(\iota \right) > 0$. If we assume the contrary, then we find that $\left(1-k\right) z\leq \mu _{\iota _{1}}\cdot \left(\varrho ^{1/\alpha }\cdot z^{\prime }\right)$, and so $z/\mu _{\iota _{1}}^{1-k}$ is increasing. We note from $\left({\mathrm{P3}}\right)$ that $\lim_{\iota \rightarrow \infty }\varrho ^{1/\alpha }\left(\iota \right) z^{\prime }\left(\iota \right) = 0$. Thus, by integrating (2.2) over $\left[ \iota, \infty \right)$, we arrive at

Hence, from (2.4) and $\left({\mathrm{P2}}\right)$, we arrive at

and hence $\mu _{\iota _{1}}\cdot \varrho ^{1/\alpha }\cdot z^{\prime }\geq z$, which contradicts (2.1). Thus, $\phi \left(\iota \right) > 0$, and then $z/\mu _{\iota _{1}}^{1-k}$ is decreasing.

Next, from (2.4) and (2.8), we have

which, with $\left({\mathrm{P4}}\right)$ and (2.5), gives

Hence, $\mu _{\iota _{1}}\cdot \varrho ^{1/\alpha }\cdot z^{\prime }\geq k^{1/\alpha }\, \delta ^{k}\, z$, and then $z/\mu _{\iota _{1}}^{\sqrt[\alpha ] {k}\, \delta ^{k}}$ is increasing.

Here, the proof ends.

Lemma 2.4. Assume that $x\in \mathcal{P}_{s}$, (2.4) and (2.5) hold. Then,

where

Proof. Proceeding as in the proof of Lemma 2.2, we arrive at (2.3). From Lemma 2.3, we have that $\left({\mathrm{P4}}\right)$ and $\left({\mathrm{P5}}\right)$ hold. Then, we get

and

for $i = 0, 1, ...$. Thus, (2.3) transforms into

which together with (1.1) gives (2.9).

Here, the proof ends.

In the following lemma, we formulate Eq (1.1) in linear form.

Lemma 2.5. Assume that (2.4) and (2.5) hold. If $x\in \mathcal{P}_{s}$, then

where

Proof. Assuming that $x\in \mathcal{P}_{s}$, we find, by taking into account (C2), that $x\circ h,$ $x\circ g$ and $z$ are also eventually positive. From Lemmas 2.1 and 2.3, we have that $\left({\mathrm{P1}}\right)$–$\left({\mathrm{P5}}\right)$ hold.

From Lemma 2.4, we have that (2.9) holds. Then,

Assume first that $\alpha \geq 1$. Using $\left({\mathrm{P4}}\right)$, we get that $\left(1-k\right) z\geq \mu _{\iota _{1}}\cdot \left(\varrho ^{1/\alpha }\cdot z^{\prime }\right)$. From the facts that $g\left(\iota \right) \leq \iota$, $\left({\mathrm{P4}}\right)$ and (2.5), we obtain

which with (2.11) gives

Assume now that $\alpha < 1$. Using $\left({\mathrm{P5}}\right)$ and (2.5), we arrive at

which with (2.11) gives

Combining (2.12) and (2.13), we get that (2.10) holds.

Here, the proof ends.

2.2.   Oscillation criteria

Using the results in the previous section, we introduce new oscillation criteria for Eq (1.1) in the following theorems:

Theorem 2.1. Assume that (2.4) and (2.5) hold. Then, Eq (1.1) is oscillatory if

Proof. On the basis of assuming the contrary, we assume that $x\in \mathcal{P}_{s}$. It follows from Lemmas 2.1 and 2.3 that $\left({\mathrm{P1}} \right)$–$\left({\mathrm{P5}}\right)$ hold.

From Lemma 2.5, we have that (2.10) holds. Integrating (2.10) from $\iota$ to $\infty$ and using $\left({\mathrm{P3}}\right)$, we obtain

and so

Integrating once again from $\iota _{1}$ to $\iota$, we arrive at

Hence,

Using $\left({\mathrm{P4}}\right)$ and $\left({\mathrm{P5}}\right)$, we conclude that

Taking $\lim \sup_{\iota \rightarrow \infty }$ of the previous inequality, we arrive at a contradiction with (2.14).

Here, the proof ends.

Theorem 2.2. Assume that (2.4) and (2.5) hold. Then, Eq (1.1) is oscillatory if

Proof. On the basis of assuming the contrary, we assume that $x\in \mathcal{P}_{s}$. It follows from Lemmas 2.1 and 2.3 that $\left({\mathrm{P1}} \right)$–$\left({\mathrm{P5}}\right)$ hold. From Lemma 2.5, we have that (2.10) holds.

Using $\left({\mathrm{P4}}\right)$, we have $\left(1-k\right) z\geq \mu _{\iota _{1}}\cdot \left(\varrho ^{1/\alpha }\cdot z^{\prime }\right)$, which (2.10) gives

Then, $\varrho ^{1/\alpha }\cdot z^{\prime }$ is a positive solution of the delay differential inequality of first-order (2.16). It follows from Theorem 1 in ^[32] that the delay differential equation

has also a positive solution. From Theorem 2 in ^[33], Eq (2.17) is oscillatory under condition (2.15), a contradiction.

Here, the proof ends.

Theorem 2.3. Assume that (2.4) and (2.5) hold. Then, Eq (1.1) is oscillatory if there is a $\rho \in \left(\left[ \iota _{1}, \infty \right), \mathbb{R} ^{+}\right)$ such that

Proof. On the basis of assuming the contrary, we assume that $x\in \mathcal{P}_{s}$. It follows from Lemma 2.3 that $\left({\mathrm{P4}}\right)$ holds. From Lemma 2.5, we have that (2.10) holds.

Now, we define the function $w: = \rho \cdot \left(\left(\varrho ^{1/\alpha }\cdot z^{\prime }\right) /z\right)$. Then $w\geq 0$, for $\iota \geq \iota _{1}$. It follows from (2.10) that

by using the fact that $\, \varrho w-Bw^{2}\leq \frac{1}{4}\varrho ^{2}B^{-1}$. Thus, from $\left({\mathrm{P4}}\right)$, we get

Integrating (2.19) from $\iota _{1}$ to $\iota$, we arrive at

Taking $\lim \sup_{\iota \rightarrow \infty }$ of the previous inequality, we arrive at a contradiction with (2.18).

Here, the proof ends.

Remark 2.1. Using formula (2.2) instead of (2.9), we can obtain the same oscillation criteria by replacing $\widehat{q}$ with $\widetilde{q}$. It is also easy to verify that $\widetilde{p}\left(\iota, 0\right) = \left(1-p\left(\iota \right) \right) ^{\alpha }$.

Corollary 2.1. Assume that (2.5) hold and

Then, equation

is oscillatory if there is a $\rho \in \left(\left[ \iota _{1}, \infty \right), \mathbb{R} ^{+}\right)$ such that

where

Theorem 2.4. Assume that (2.4) and (2.5) hold. Then, Eq (1.1) is oscillatory if

where $\beta = \left(\alpha /\left(\alpha +1\right) \right) ^{\alpha +1}$.

Proof. On the basis of assuming the contrary, we assume that $x\in \mathcal{P}_{s}$. It follows from Lemmas 2.1 and 2.3 that $\left({\mathrm{P1}}\right)$–$\left({\mathrm{P5}}\right)$ hold.

We define $w: = \left(\varrho ^{1/\alpha }\cdot z^{\prime }\right) ^{\alpha }/z^{\alpha }$, then

which with $\left({\mathrm{P2}}\right)$ gives

Integrating (2.21) from $\iota _{1}$ to $\iota$, we have

Using the inequality

we obtain

Taking $\lim \sup_{\iota \rightarrow \infty }$ of the previous inequality, we arrive at a contradiction with (2.20).

Here, the proof ends.

Corollary 2.2. Assume that (2.5) hold. Then, Eq (1.1) is oscillatory if

Proof. It is easy to note that condition (2.23) guarantees both conditions (2.4) and (2.20).

Example 2.1. Consider the NDE

where $\, \iota > 0$, $\, p_{0}\in \left[ 0, 1\right)$, $q_{0} > 0$, $a\in \left(0, 1\right)$, and $0 < b < \min \left\{ 1, \sqrt[\alpha ]{\frac{1}{\alpha }q_{0}} \left(1-p_{0}\right) \right\}$. It is easy to check that $h_{i} = a^{i}\iota$, and

By choosing $\delta = 1/b$, and $k = \frac{1}{\alpha }A_{0, m}q_{0}b^{\alpha }$, we have that (2.4) and (2.5) hold. Then

and

Hence, condition (2.14) becomes

Moreover, condition (2.15) becomes

On the other hand, by choosing $\rho \left(\iota \right) = \iota$, condition (2.18) reduces to

Remark 2.2. Corollary 1 in ^[19] confirms that Eq (2.24) is oscillatory if

Using Theorem 6 in ^[18], we get that (2.24) is oscillatory if

where $\kappa = \left(\alpha /\left(\alpha +\left(1-p_{0}\right) ^{\alpha }q_{0}b^{\alpha }\right) \right) ^{\alpha }$. Consider the special case of (2.24) when $p_{0} = 1/2$, $a = 0.9$, and $\alpha = 1$, namely,

It is easy to check that $A_{0, m} = 0.62696$, $k = 0.62696q_{0}b$, and

Applying conditions (2.25)–(2.27), we obtain that (2.28) is oscillatory if one of the following conditions is satisfied:

or

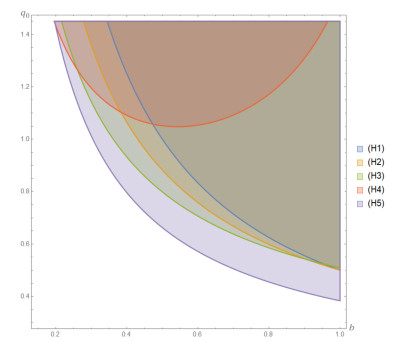
Figure 1 shows a comparison of regions where conditions (H1)–(H5) are satisfied for Eq (2.28). It is easy to see that our criterion (H5) provides the best results for the oscillation of (2.28). For example, we find that criterion (H5) ensures that the equation

is oscillatory, while the rest of the criteria fail to do so. Figure 2 shows the lower bounds of the regions in which condition (H5) is satisfied for $m = 0, 1, 5$.

3.   Oscillation results for the fourth-order equation

The following notations will be required when presenting the results: $\mathcal{F}_{s}:$ The set of all eventually positive solutions of (1.2),

and

Lemma 3.1. ^[38] If $H\in C^{r}\left([\iota _{0}, \infty), \left(0, \infty \right) \right)$, $H^{\left(j\right) }\left(\iota \right) > 0$ for $j = 1, 2, ..., r$, and $H^{\left(r+1\right) }\left(\iota \right) \leq 0$, then $H\left(\iota \right) \geq \frac{1}{r}\iota H^{\prime }\left(\iota \right)$, eventually.

The following lemma determines the sign of the derivatives of the positive solutions of (1.2), which comes directly from applying Lemma 2.2.1 in ^[35] to Eq (1.2).

Lemma 3.2. The following properties are satisfied for each $x\in \mathcal{F} _{s}$:

Lemma 3.3. Assume that $x\in \mathcal{F}_{s}$. If $z^{\prime \prime }\left(\iota \right) > 0$, eventually, then,

On the other hand, if $z^{\prime \prime }\left(\iota \right) < 0$, eventually, then

for all $\epsilon \in \left(0, 1\right)$.

Proof. Assume that $x\in \mathcal{F}_{s}$ and $z^{\prime \prime }\left(\iota \right) > 0$ for $\iota \geq \iota _{1}$. By using Lemma 3.1 with $H = z$ and $r = 3$, we get that $z\geq \frac{1}{3}\iota \, z^{\prime }$. Next, proceeding as in the proof Lemma 2.2, we arrive at (2.3). Using the facts that $z^{\prime }\left(\iota \right) > 0$ and $\left({\mathrm{F1}} \right)$, we obtain $\left(z\circ h_{2i}\right) \geq \left(z\circ h_{2i+1}\right)$ and

Then, (2.3) becomes

which together with (1.2) gives $\left({\mathrm{F2}}\right)$.

Next, assume that $z^{\prime \prime }\left(\iota \right) < 0$ for $\iota \geq \iota _{1}$. Then, there is $\iota _{2} > \iota _{1}$ such that

for all $\iota \geq \iota _{2}$ and $\epsilon \in \left(0, 1\right)$. Using the previous fact and $z^{\prime }\left(\iota \right) > 0$, (2.3) reduces to

which together with (1.2) gives $\left({\mathrm{F4}}\right)$.

Here, the proof ends.

3.1.   Oscillation criteria

Lemma 3.4. Assume that $x\in \mathcal{F}_{s}$, and there is a $\rho \in C\left(\left[ \iota _{0}, \infty \right), \left(0, \infty \right) \right)$ such that

Then $z^{\prime \prime }\left(\iota \right) < 0$, eventually.

Proof. Assume that $x\in \mathcal{F}_{s}$. From Lemma 3.2, we have that $\left({\mathrm{i}}\right)$ and $\left({\mathrm{ii}}\right)$ hold.

Suppose the contrary that $z^{\prime \prime }\left(\iota \right) > 0$ for $\iota \geq \iota _{1}$. Then, we find

Hence, $z^{\prime \prime }/\mu _{\iota _{1}}$ is decreasing, and so

Moreover, from $\left({\mathrm{F1}}\right)$, we get

Now, we define the function

Then, from $\left({\mathrm{F2}}\right)$, (3.2) and (3.3), we find

By using inequality (2.22), we obtain

By integrating this inequality from $\iota _{1}$ to $\iota$, we conclude that

which contradicts (3.1).

Here, the proof ends.

Theorem 3.1. Assume that $g^{\prime }\left(\iota \right) > 0$ and there is a $\rho \in C\left(\left[ \iota _{0}, \infty \right), \left(0, \infty \right) \right)$ such that (3.1) holds. Then, Eq (1.2) is oscillatory if the equation

is oscillatory.

Proof. Assume the contrary that $x\in \mathcal{F}_{s}$. From Lemma 3.2, we have that $\left({\mathrm{H1}}\right)$ and $\left({\mathrm{H2}}\right)$ hold. It follows from Lemma 3.4, $z^{\prime \prime }\left(\iota \right) < 0$, eventually. By integrating $\left({\mathrm{F4}}\right)$ twice from $\iota$ to $\infty$, we conclude that

We define the function $\omega = z^{\prime }/\left(z\circ g\right)$. Then, from (3.5), we find

and so,

In view of ^[36,37], Eq (3.4) has a non-oscillatory solution if and only if there exists a function $\omega$ satisfying (3.6), a contradiction.

Here, the proof ends.

3.2.   Comparison with previous results

In the following, we review some theorems from previous studies that dealt with the oscillation of the NDE

by using different techniques, so that we can compare our results with them.

Theorem 3.2. [21,Theorem 2] Suppose that

Then (3.7) is oscillatory.

Theorem 3.3. [22,23,Corollary 1] Suppose that

Then (3.7) is oscillatory.

Theorem 3.4. [24,Theorem 2] Suppose that there exists a $m\in \mathbb{Z} ^{+}$ such that

where $\eta \left(\iota \right) = \max \left\{ g\left(s\right), s\in \left[ \iota _{0}, \iota \right] \right\}$, $\eta _{-1}\left(\iota \right) = \sup \left\{ s\geq \iota _{0}:\eta \left(s\right) = \iota \right\}$, $\eta _{-\left(i+1\right) } = \eta _{-1}\left(\eta _{-i}\left(\iota \right) \right)$, $\, G\left(\iota \right) = \frac{1}{6}q\left(\iota \right) g^{3}\left(\iota \right) \left(1-p\left(g\left(\iota \right) \right) \right)$

and

Then (3.7) is oscillatory.

Theorem 3.5. [25,Theorem 2.1] Suppose that there exist $\theta _{1},$ $\theta _{2}\in {\bf{C}}^{1}\left(\left[ \iota _{0}, \infty \right), \left(0, \infty \right) \right)$ such that

and

Then (3.7) is oscillatory.

Example 3.1. Consider the NDE

where $\iota > 0$, $p_{0},$ $a,$ $b\in \left(0, 1\right)$, and $q_{0} > 0$. It is easy to check that

By choosing $\rho \left(\iota \right) = \iota ^{3}$, condition (3.1) reduce to

which is satisfied if $q_{0}L_{3}b^{3} > \frac{9}{2}$. From Theorem 3.1, Eq (3.8) is oscillatory if the equation

is oscillatory. Using Corollary 2.1, Eq (3.10) is oscillatory if $q_{0} > 3/\left(2L_{1/\epsilon }b\right)$. Therefore, Eq (3.8) is oscillatory if

Remark 3.1. Consider the NDE (3.8). By applying Theorems 3.2–3.5, we get respectively the following results:

$–$ Eq (3.8) is oscillatory if

$–$ Eq (3.8) is oscillatory if

$–$ We have $\eta \left(\iota \right) = b\iota,$ $G\left(\iota \right) = q_{0}b^{3}\left(1-p_{0}\right) \frac{1}{6\iota }$ and

Then Eq (3.8) is oscillatory if

$–$ By choosing $\theta _{1}\left(\iota \right) = \iota ^{3}$ and $\theta _{2}\left(\iota \right) = \iota$, Eq (3.8) is oscillatory if

From the aforementioned, we observe that

(1) Since $L_{c}\geq \left(1-p_{0}\right)$, criterion (C1) is an improvement of (C4).

(2) Criterion (C3) is an improvement of (C2).

(3) The results of Theorem 3.4 are the same as those of Theorem 3.3, although Theorem 3.3 is easier to apply.

(4) Setting $a = 0.9$ and $p = 0.8$, Figure 3 shows the lower bounds of $q_{0}$ values at which criteria (C1), (C3) and (C4) are satisfied. We note that (C3) provides the best results for the oscillation of (3.8) when $b\in \left(0, 0.476\right)$, and (3.11) provides the best results for the oscillation of (3.8) when $b\in \left(0.476, 1\right)$.

4.   Conclusions

In this work, the oscillatory behavior of second- and fourth-order half-linear neutral differential equations is studied in the canonical case. For the second-order equation, we obtained improved monotonic properties based on establishing a new relationship between the solution and its corresponding function. We then used the new relationships and properties to infer a set of oscillation criteria by using different methods. At the end of this part of the paper, we presented examples and remarks that illustrate the importance of the results and compare them with relevant results in the literature. For the fourth-order equation, after obtaining new relationships between $x$ and $z$ in each case of positive solutions, we introduced a new criterion to test the oscillation of the studied equation. Then, we reviewed some previous theorems in the literature and compared our results with them using an example.

We notice through the results that improving the relationship between the solution and the corresponding function of the neutral differential equations contributes to obtaining new monotonic properties for the positive solutions of these equations, which in turn leads to the development of oscillation criteria. It would be interesting to extend this improvement to higher-order differential equations in the non-canonical case.

Acknowledgments

Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R157), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Conflict of interest

The authors declare no conflict of interest.