Global dynamics of multiple delays within-host model for a hepatitis B virus infection of hepatocytes with immune response and drug therapy

1.   Introduction

Hepatitis B virus (HBV) infection is a significant worldwide health issue. It is a liver infection caused by the hepatitis B virus. Generally, the infection is classified as either acute or chronic and can lead to more serious long-term complications, such as liver inflammation, cirrhosis or liver cancer ^[1]. According to World Health Organisation (WHO) reports, HBV infection is mostly notified in Africa, Southern Europe, Asia and Latin America. 257 million people were living with chronic HBV infection in 2015 ^[2] and about 887,000 people died. In extremely endemic areas, hepatitis B is most commonly spread from mother to child at birth or transmitted through contact with the blood or other body fluids of an infected person. From the global epidemic situation, it is essential to have some effective prevention and treatment measures for hepatitis B infection.

HBV can replicate within hepatocytes without causing direct cell damage, this can be seen in those who are asymptomatic HBV carriers. Approximately 5-10% of HBV-infected adults may progress to a chronic state. The immune responses to HBV antigens are responsible for both disease pathogenesis and viral clearance. The adaptive immune response specifically the virus-specific cytotoxic T lymphocytes (CTL) is shown to play a key role in eliminating the infected cells and inhibiting viral replication ^{[3,4,5,6,7,8,9,10,11]}. Another adaptive immune response is the antibodies, which are produced by the B cells, that neutralize virus particles and prevent the reinfection of cells ^[10,12]. Further, the body's immune response would take time from being attacked by viruses to the cell becoming productively infected, therefore time delay regarding to this circumstance should not be ignored ^{[13,14,15,16,17,18,19,20]}. In addition, HBV infections have shown some time delay in virus amplification and spreading through the liver ^[21].

People with chronic hepatitis B infection are recommended to have some medication to reduce the risk of disease progression, prevent transmission to others and decrease the risk of complications of hepatitis B. There are two main types of drugs which are standard PEGylated interferon (PEG-IFN) and nucleoside analogues (NAs). IFN has a role in suppressing viral protein synthesis, preventing viral infection of cells and degradation of viral mRNA. The NAs play a role in elongating DNA in order to inhibit HBV replication ^[21,22,23]. In addition, in some cases, the treatment may include antiviral medications (e.g. lamivudine, adefovir, entecavir) and the interferon alfa-2b injection ^[24]. However, mentioned drugs can hardly clear the viral covalently closed circular DNA (cccDNA) which is responsible for the persistence of HBV ^[25,26]. The alternative therapies have been recently in clinical trials and proposed, they base on viral gene silencing by controlling the RNA interference (RNAi) pathway which suppresses HBV replication and may result in disabling cccDNA during chronic infection ^[25,26]. With the fact mentioned above, although the HBV vaccines are widely used, safe and effective and there are some drugs that could cure and greatly reduce the viral burden ^[27,28], there are limitations against chronic infection. Hence, HBV infection is still a major health problem around the world.

Mathematical models have been shown to greatly contribute to a better understanding of HBV infection. The work by Nowak et al. ^[29] is one of the earliest models about the HBV infection of hepatocytes consisting of three variables which are the concentration of uninfected cells, infected cells and free virus particles. There are a number of mathematical models that have been proposed after that (e.g. ^{[30,31,32,33,34,35,36,37,38,39]}). Some models involve treatments or drug efficacy (e.g. ^[38,40,41]). In some studies, the time delay has been considered. The models which involve the time delay from being infected to the release of free virus particles and free movement of virus particles in the liver are of the works by Gourley et al., 2008 ^[42]; Xie et al., 2010 ^[43]; Guo and Cai, 2011 ^[16]; Wang et al., 2008 ^[44]. Further, some studies involve the effect of humoral immunity or CTL-mediated cellular immunity e.g. the work by Yousfi et al., 2011 ^[34] and Fisicaro et al., 2009 ^[45]. Recently, Sun et al., 2017 ^[46] proposed a delay model with 6 variables including exposed state, CTL and alanine aminotransferases (ALT), where the delay was put on the CTL process. In 2015, Manna and Chakrabarty, 2015 ^[47] proposed a model which included the intracellular HBV DNA-containing capsids and a delay in the production of the infected hepatocytes. Later on, Guo et al., 2018 ^[48] extended the work of Manna and Chakrabarty, 2015 ^[47] by adding a delay during the time when the infected cells create new intracellular HBV DNA-containing capsids due to the penetration by the virus. Furthermore, Aniji et al., 2020 ^[49] proposed the model involves a delay as a time between antigenic stimulation and the production of CTL including a delay during the decay of CTL. With the important role of antibodies against HBV infection, Meskaf et al., 2017 ^[18], Sun et al., 2017 ^[46] and Allali et al., 2018 ^[50] had added antibodies as variables into their models. In addition, some researchers have developed HBV models which involve both diffusion and delay (e.g. ^[51,52]). Among the above studies, in some studies drug therapies have also been applied in the models e.g the work by Hattaf et al., 2009 ^[53], Manna and Chakrabarty, 2018 ^[54] and in particular Danane and Allali, 2018 ^[20] had included the drug therapies in their delay model. Further, some researchers have proposed models involving infection in the form of fractional differential equations (e.g. ^[55,56]).

In this paper, we have developed a model for HBV infection which incorporates the intracellular HBV DNA-containing capsids, CTL and antibodies with a time delay from being attacked by the virus to being infected hepatocytes and a time delay in the antigenic stimulation generating CTL. Further, two drug therapies, i.e., blocking new infection and inhibiting viral production have been applied in the model. The structure of the paper starts with a description of the proposed model in section 2, followed by the model properties, the basic reproduction number, three equilibrium states and their global stability. In section 3, the numerical simulations are presented and discussed. Finally, we end this paper with conclusions in section 4.

2.   Model formulation

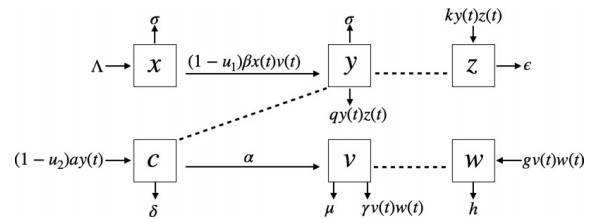
We have developed a delay model describing the hepatitis B virus (HBV) dynamics involving immune response and drug therapy by extending the work of Danane and Allali, 2018 ^[20] by adding the delay time that an antigenic stimulation generating CTL, which is $\tau_{2}$ in our model. This is because we take into account the fact that the antigenic stimulation generates CTL cells may require a time lag and in this model, we assume that CTL produced depends on infected cells. This model is described by a system of delay differential equations (2.1), it includes six variables: the concentration of uninfected hepatocytes $x(t)$, infected hepatocytes $y(t)$, intracellular HBV DNA-containing capsids $c(t)$, free viruses $v(t)$, antibodies $w(t)$, and CTL $z(t)$. The uninfected hepatocytes $x(t)$ are produced at a constant rate $\Lambda$ and die at a rate $\sigma$. The infection of hepatocytes in this model incorporates the uninfected become infected hepatocytes by the free virus with a rate $\beta$ with involvement of the efficiency of drug therapy in blocking new infection $u_{1}$. The $e^{-m\tau_{1}}$ is the probability of surviving hepatocytes in the time period from $t-\tau_{1}$ to $t$, where $m$ is a constant rate of the death average of infected hepatocytes which are still not virus-producing cells. Time $\tau_{1}$ is the delay in the productively infected hepatocytes. This infection term is represented by the nonlinear term $(1-u_{1})e^{-m\tau_{1}}\beta x(t)v(t)$. The infected hepatocytes $y(t)$ are eliminated by the CTL, $z(t)$, with a rate $q$ and die at a rate $\sigma$, which has the same rate as the mortality rate of uninfected hepatocytes as we assume there is no increase in death rate of infected hepatocytes due to an infection. The production of intracellular HBV DNA-containing capsids $c(t)$ incorporates the efficiency of drug therapy in inhibiting viral production $u_{2}$ with a production rate $a$, described by the term $(1-u_{2})ay(t)$. The intracellular HBV DNA-containing capsids are transmitted into the bloodstream to become free viruses at a rate $\alpha$ and are decomposed at a rate $\delta$. The free viruses are reduced by the neutralization rate of antibodies $\gamma$ and die at a rate $\mu$. The antibodies are enhanced in response to the free viruses at a rate $g$ and decay at a rate $h$. Further, the second time delay in this model cannot be ignored for the immune response, that is the activation of CTL producing antigens may require a period of time $\tau_ {2}$. Therefore, we propose the form $ky(t-\tau_{2})z(t-\tau_{2})$ and the CTL decay at the rate $\epsilon$. The flow chart of the model is presented in Figure 1.

This model can be written into a form of system of delay differential equations as follows:

with initial condition

for $\tau_{1} > 0$ and $\tau_{2} > 0$. Here, $0 < u_{1} < 1$ and $0 < u_{2} < 1$.

2.1.   Model analysis

2.1.1.   Initial conditions

The Banach space of continuous functions mapping the interval $[-\tau, 0]$ into $R^{6}_{+}$ is defined by $C = C([-\tau, 0], R^{6}_{+})$, where $\tau = \max[\tau_{1}, \tau_{2}]$. For any $\varphi\in C([-\tau, 0], R^{6}_{+})$ by the fundamental theory of functional differential equations (see ^[59]) there exists a unique solution $\textbf{P}(t, \varphi) = ((x(t, \varphi), y(t, \varphi), c(t, \varphi), v(t, \varphi), w(t, \varphi), z(t, \varphi))$ of the system (2.1), which satisfies $\textbf{P}_{0} = \varphi$. The initial conditions are given by $x(\theta)\geq0, y(\theta)\geq0, c(\theta)\geq0, v(\theta)\geq0, w(\theta)\geq0, z(\theta)\geq0$ with $\theta\in[-\tau, 0]$ and $y(0), c(0), v(0), w(0), z(0) > 0$.

2.1.2.   Non-negative and boundedness of solution

For system (2.1) to be epidemiologically meaningful, we prove that all state variables are non-negative. Since it is irrational to have a negative hepatocytes density and system (2.1) describes the dynamics of HBV infection of hepatocytes, we show that all state variables stay non-negative and the solutions of system (2.1) with non-negative initial conditions will remain non-negative for fall $t > 0$. The following lemma is applied.

Lemma 1. Given that the initial solutions and parameters of system (2.1) are non-negative, the solutions $x(t), y(t), c(t), v(t), w(t)$ and $z(t)$ stay non-negative for all $t > 0$.

Proof. Consider the first equation in system (2.1) we have,

We multiply both sides of the differential equation by the integrating factor which is defined as

Multiply equation (2.3) by $I$, we have

We integrate both side between $0$ and $t$, then

Thus, $\quad \ \ x(t) = (e^{-\int_{0}^{t} (\sigma+(1-u_{1})\beta v(s)) \ ds})(x(0)+\int_{0}^{t} (e^{\int_{0}^{t} (\sigma+(1-u_{1})\beta v(s)) \ ds})\Lambda ds)$, leads to $x(t)\geq0$.

Similarly,

Therefore, $x(t)\geq0, \ y(t)\geq0, \ c(t)\geq0, \ v(t)\geq0, \ w(t)\geq0, \ z(t)\geq0$ for all $t > 0$ given that $x(0)\geq0, \ y(0)\geq0, \ c(0)\geq0, \ v(0)\geq0, \ w(0)\geq0, \ z(0)\geq0$.

Theorem 1. Under the given initial conditions, all solutions of system (2.1) are non-negative and bounded for all $t\geq0$.

Proof. First, we use the following function to help determining the boundness of the solutions of system (2.1):

By differentiating (2.7) with respect to $t$ and with system (2.1), we have

Let $Q = \min(\sigma, \frac{\sigma}{2}, \epsilon, \delta, \mu, h).$

Thus, we have

By integrating both sides,

By taking $t\rightarrow \infty$, we have

Hence, we have that $N(t)$ is bounded, which leads to the variables $x(t), y(t), c(t), v(t), w(t)$ and $z(t)$ are bounded.

2.1.3.   The steady states of system

In this section, we compute steady states of system (2.1). There are five steady states as follows.

1. The infection-free steady state $\label{eqpointE0} E_{0} \ \text{is} \ (x_{0}, y_{0}, c_{0}, v_{0}, w_{0}, z_{0}) = \bigg(\frac{\Lambda}{\sigma}, 0, 0, 0, 0, 0\bigg)$.

2. The immune-free steady state $E_{1}$ is $(x_{1}, y_{1}, c_{1}, v_{1}, 0, 0)$ where

$x_{1} = \frac{\sigma\mu(\alpha+\delta)}{(1-u_{1})(1-u_{2})\beta e^{-m\tau_{1}}a\alpha}, y_{1} = \frac{(\alpha+\delta)c_{1}}{(1-u_{2})a}, c_{1} = \frac{\sigma\mu}{(1-u_{1})\beta\alpha}(R_{0}-1), v_{1} = \frac{\alpha c_{1}}{\mu}$. $E_{1}$ exists when $R_{0} > 1$.

3. The immune-activated infection steady state $E_{2}$ is ($x_{2}, y_{2}, c_{2}, v_{2}, w_{2}, z_{2}$) where

$x_{2} = \frac{\Lambda g}{\sigma g+(1-u_{1})\beta h}, y_{2} = \frac{\epsilon}{k}, c_{2} = \frac{(1-u_{2})a\epsilon}{k(\alpha+\delta)}, v_{2} = \frac{h}{g}, w_{2} = \frac{(1-u_{2})a\epsilon\alpha g}{(\alpha+\delta)\gamma hk}-\frac{\mu}{\gamma},$

$z_{2} = \frac{(1-u_{1})\beta\Lambda hke^{-m\tau_{1}}}{(\sigma g+(1-u_{1})\beta h)q\epsilon}-\frac{\sigma}{q}$. $E_{2}$ exists when $\frac{(1-u_{2})a\epsilon\alpha g}{(\alpha+\delta) hk} > \mu$ and $\frac{(1-u_{1})\beta\Lambda hke^{-m\tau_{1}}}{(\sigma g+(1-u_{1})\beta h)\epsilon)} > \sigma$.

4. The andibody-free steady state $E_{3}$ is $(x_{3}, y_{3}, c_{3}, v_{3}, 0, z_{3})$ where

$x_{3} = \frac{\Lambda}{\sigma-(1-u_{1})\beta v_{3}}, y_{3} = \frac{\epsilon}{k}, c_{3} = \frac{(1-u_{2})ay_{3}}{\alpha+\delta}, v_{3} = \frac{\alpha c_{3}}{\mu}, w_{3} = 0$,

$z_{3} = \frac{(1-u_{1})\beta e^{-m\tau_{1}}x_{3}v_{3}-\sigma y_{3}}{qy_{3}}$. $E_{3}$ exists when $\sigma > (1-u_{1})\beta v_{3}$ and $(1-u_{1})\beta e^{-m\tau_{1}}x_{3}v_{3} > \sigma y_{3}$.

5. The CTL-free steady state $E_{4}$ is $(x_{4}, y_{4}, c_{4}, v_{4}, w_{4}, 0)$ where

$x_{4} = \frac{\Lambda}{\sigma-(1-u_{1})\beta v_{4}}, y_{4} = \frac{(1-u_{1})\beta e^{-m\tau_{1}}x_{4}v_{4}}{\sigma}, c_{4} = \frac{(1-u_{2})ay_{4}}{(\alpha+\delta)}, v_{4} = \frac{h}{g}, w_{4} = \frac{\alpha c_{4}-\mu v_{4}}{\gamma v_{4}}, z_{4} = 0$.

$E_{4}$ exists when $\sigma > (1-u_{1})\beta v_{4}$ and $\alpha c_{4} > \mu v_{4}$.

2.1.4.   The basic reproduction number ($R_{0}$)

To calculate $R_{0}$, we used the next-generation matrix method by van den Driessche et al., 2002 ^[60] and we obtain

Then we have

By substituting the infection-free equilibrium point (2.1.3) in the Jacobian matrices above, we get

Next,

The next generation matrix is

The basic reproduction number is given by $\rho(FV^{-1})$, thus

2.1.5.   Local stability of infection-free equilibrium point

Theorem 2. (local stability at $E_{0}$) If $R_{0} < 1$, then the infection-free equilibrium point ($E_{0}$) is locally asymptotically stable. Otherwise, it is unstable.

Proof. The Jacobian matrix of system (2.1) at $E_{0}$ is

From Jacobian matrix above, we have the characteristic equation as

Thus, $\lambda_{1} = -\epsilon < 0, \ \lambda_{2} = -h < 0, \ \lambda_{3} = -\sigma < 0$.

Since, $x_{0} = \frac{\Lambda}{\sigma}$ and $R_{0} = \frac{(1-u_{1})(1-u_{2})\beta e^{-m\tau_{1}}\Lambda a\alpha}{\sigma^{2} \mu(\alpha+\delta)}$, we write the rest of the term as

For $R_{0} < 1$, if $\lambda$ has a non-negative real part then the modulus of the left-hand side of equation (2.19) satisfies

Consider the modulus of the right-hand side of equation (2.19),

which is contradiction. Hence, when $R_{0} < 1$, the real part of $\lambda$ has no non-negative real part and the infection-free state $E_{0}$ is locally asymptotically stable.

For $R_{0} > 1$, we let

Then,

and $\lim_{\lambda\rightarrow \infty} h(\lambda) = +\infty.$

By the continuity of $h(\lambda)$, there exists at least one positive root of $h(\lambda) = 0$. Thus, the infection-free equilibrium point, $E_{0}$ is unstable when $R_{0} > 1$. This completes the proof.

2.1.6.   Global stability of infection-free equilibrium point

Theorem 3. If $R_{0} < 1$, the infection-free equilibrium point ($E_{0}$) is globally asymptotically stable.

Proof. Let the Lyapunov functions be

where $L$ is positive definite. The derivative of $L$ along the solutions of the system (2.1) is

Since,

We obtain that $\frac{dL}{dt} < 0$ when $R_{0} < 1$ and $\frac{dL}{dt} = 0$ at $E_{0}$. Therefore, $E_{0}$ is globally asymptotically stable when $R_{0} < 1$.

2.1.7.   Local stability of the immune-free equilibrium point

Theorem 4. (local stability at $E_{1}$) If $1 < R_{0} < 1+\inf\{A_{1}, A_{2}\}$,

where $A_{1} = \frac{(1-u_{1})(1-u_{2})\epsilon a\beta\alpha}{k\sigma\mu(\alpha+\delta)}$ and $A_{2} = \frac{(1-u_{1})h\beta}{g\sigma}$, then the immune-free equilibrium point ($E_{1}$) is locally asymptotically stable. If $R_{0} > 1+\inf\{A_{1}, A_{2}\}$, then $E_{1}$ is unstable.

Proof. We first set $det(J(E_{1})-\lambda I) = 0$ to find eigenvalues, then we obtain $det(J(E_{1})-\lambda I)$

By calculating above expression, we have characteristic equation as

where

Therefore, it gives $\lambda_{1} = ky_{1}(t-\tau_{2})e^{-\lambda\tau_{2}}-\epsilon$ and $\lambda_{2} = gv_{1}-h$.

First, we consider

For $\tau_{2} = 0$, If $1 < R_{0} < 1+\frac{(1-u_{1})(1-u_{2})\epsilon a\beta\alpha}{k\sigma\mu(\alpha+\delta)}$. Then, we have $\lambda_{1} = ky_{1}-\epsilon$, since $y_{1} = \frac{\sigma\mu(\alpha+\delta)(R_{0}-1)}{(1-u_{1})(1-u_{2})\beta\alpha a}$.

Thus,

Thus, $\lambda_{1} < 0.$ This shows that $\lambda_{1} < 0$ for $\tau_{2} = 0$. Next, we consider the case when $\tau_{2} > 0$. By letting $\lambda_{1} = \omega i \ (\omega > 0)$ be a purely imaginary root for some $\omega > 0$, we have

Thus, this implies that $\epsilon = ky_{1}\cos(\omega\tau_{2})$ and $\omega = -ky_{1}\sin(\omega\tau_{2})$.

Then,

Since $1 < R_{0} < 1+\frac{(1-u_{1})(1-u_{2})\epsilon a\beta\alpha}{k\sigma\mu(\alpha+\delta)}$, then

Thus, $\omega^{2} < 0$ which is contradiction.

Next, suppose that $\lambda_{1} = b+\omega i$ where $b$ is positive real number and $\omega > 0$, we can write

Then, the magnitude of $h$ is as follows when $b$ is positive real number,

Since

Substituting $y_{1}$ into (2.36), we have

Thus, $\vert h \rvert < \epsilon$ implie that $h\in B(0, \epsilon)$. If $h = D+Ci$ where $D > 0$, then $h$ is complex number in the right-half of complex plane. However, if $h-\epsilon = D+Ci-\epsilon$, then $D-\epsilon$ is negative real part. Therefore, we have $h-\epsilon$ is a complex number in the left-half of complex plane, then consider the left hand side of the equation (2.35) as

Since we suppose that $b > 0$ and $\lambda_{1} = h-\epsilon$, then $\lambda_{1}$ will be a complex number on the right-half of complex plane. We have

By assumption $b > 0$, but $D-\epsilon < 0$. This is contradiction, because $b$ can not be a positive real part.

Therefore, $\lambda_{1}$ has a negative real part, when $1 < R_{0} < 1+\frac{(1-u_{1})(1-u_{2})\epsilon a\beta\alpha}{k\sigma\mu(\alpha+\delta)}$.

Next, we consider $\lambda_{2} = gv_{1}-h$. If $1 < R_{0} < 1+\frac{h(1-u_{1})\beta}{g\sigma}$, then

Thus, $\lambda_{2} < 0.$ Therefore, $\lambda_{2}$ is negative when $1 < R_{0} < 1+\frac{h(1-u_{1})\beta}{g\sigma}$.

Then, we consider the characteristic equation where $\tau_{1} > 0$,

where $a_{1}-a_{6}$ are defined in (2.33).

Thus, we have

Suppose $(2.40)$ has a purely imaginary root $\lambda = i\omega \ (\omega > 0)$, by substituting $\lambda = i\omega$ into $(2.41)$ and separating the real and imaginary parts, we have

Since $\vert e^{-i\omega\tau_{1}}\rvert = \vert\cos(-\omega\tau_{1})+i\sin(-\omega\tau_{1})\rvert = \sqrt{\cos^{2}(\omega\tau_{1})+\sin^{2}(\omega\tau_{1})} = 1$, then we have

Thus, we have

and

Thus, equation (2.42) becomes

We let $X = \omega^{2}$ and define a function $G(X)$ as the left-hand side of (2.45), the above equation can be simplified to

Therefore, if the characteristic equation (2.40) has a purely imaginary root $(\lambda = i\omega)$, it is equivalent to the fact that $G(X) = 0$ has a positive real root $(X = \omega^{2})$.

Theorem 5. If $G(X) = 0$ has no positive real roots, then the positive equilibrium point $E_{1}$ is locally asymptotically stable for any $\tau_{1} > 0$.

Proof. If $G(X) = 0$ has no positive real roots, we obtain that $X$ can be zero or negative root. Since $X = \omega^{2}$, so $\omega$ can be either zero or $bi$ for $b > 0$. But from the hypothesis that $\omega > 0$, we then have $\omega = bi$, implying that (2.40) have negative roots i.e. $\lambda = \omega i = (bi)i = -b$. Therefore, the equilibrium $E_{1}$ is locally asymptotically stable for any $\tau_{1} > 0$ when $G(X) = 0$ has no positive real roots.

Next, we consider $E_{1}$ being locally asymptotically stable for $[0, \tau^{0}_{1})$ such that $\tau^{0}_{1} = \min\{\tau^{j}_{1_n}\rvert1\leq n \leq\tilde{n}\}$ where $\tilde{n}$ is the number of roots of $G(X)$.

Substituting $\lambda = i\omega$ into $(2.40)$, we obtain the real part as

and the imaginary part as

Next, we solve for $\cos(\omega\tau_{1})$ and $\sin(\omega\tau_{1})$ from equation (2.48) and (2.49). Assuming that $G(X) = 0$ has $(1\leq\tilde{n}\leq4)$ positive real roots, denoted by $X_{n}(1\leq n\leq\tilde{n})$. As $\sqrt{X_{n}} = \omega$, (2.49) then becomes

Thus,

Substituting (2.50) into (2.48), we have

Then, substitute (2.51) into (2.50), gives

Let

Therefore, for the imaginary root $\lambda = i\omega$ of (2.40), we have two sequences as follows:

where $1\leq n\leq \tilde{n}$ and $j = 0, 1, 2, 3, ...$

Assuming $\tau^{(0)}_{1_n} = \min\{\tau^{(j)}_{1_n}\rvert1\leq n \leq\tilde{n}, j = 0, 1, 2\}$, i.e., $\tau^{(0)}_{1_{n}}$ is the minimum value associated with the imaginary solution $i\omega_{0}$ of the characteristic equation (2.40). Therefore, the characteristic equation $(2.40)$ has a pair of purely imaginary roots $\pm i\sqrt{X_{n}}$.

For every integer $j$ and $1\leq n\leq\tilde{n}$, define $\lambda^{(j)}_{n}(\tau_{1}) = \alpha^{(j)}_{n}(\tau_{1})+i\omega^{(j)}_{n}(\tau_{1})$ as the root of $(2.40)$ near $\tau^{(j)}_{1_n}$, satisfying $\alpha^{(j)}_{1_n}(\tau^{(j)}_{1_n}) = 0$ and $\omega^{(j)}_{n}(\tau^{(j)}_{1_n}) = \sqrt{X_{n}}$.

Theorem 6. If $G(X) = 0$ has some positive real roots, then $E_{1}$ is locally asymptotically stable for $\tau_{1}\in[0, \tau^{(0)}_{1_n})$, when $\tau^{(0)}_{1_n} = min\{\tau^{(j)}_{1_n}\rvert1\leq n \leq\tilde{n}, j = 0, 1, 2, ...\}.$

Proof. For $\tau^{(0)}_{1_n} = \min\{\tau^{(j)}_{1_n}\leq n\leq\tilde{n}, j = 0, 1, 2, ...\}$, $G(X) = 0$ has no positive real roots when $\tau_{1}\in[0, \tau^{(0)}_{1_n})$, which means that all the roots of $(2.40)$ have strictly negative real part when $\tau_{1}\in[0, \tau^{(0)}_{1_n})$. Therefore, $E_{1}$ is locally asymptotically stable for $\tau_{1}\in[0, \tau^{(0)}_{1_n})$.

Theorem 7. If $X_{n_0}$ is a simple root of $G(X) = 0$, then there is a Hopf bifurcation for the system as $\tau_{1}$ increases past $\tau^{(0)}_{1_{n_{0}}}$.

Proof. The characteristic equation (2.40) can be written into the following form:

where $f_{0}(\lambda) = \lambda^{4}+a_{1}\lambda^{3}+a_{2}\lambda^{2}+a_{3}\lambda+a_{4}$ and $f_{1}(\lambda) = a_{5}\lambda+a_{6}$, and $f_{0}(\lambda)$ and $f_{1}(\lambda)$ are continuously differentiable to $\lambda$.

Next, we determine sign$\bigg\{\frac{dRe(\lambda)}{d\tau_{1}}\bigg\rvert_{\tau_{1} = \tau^{(0)}_{1_{n}}}\bigg\}$, where sign is the sign function and $Re(\lambda)$ is the real part of $\lambda$. We assume that $\lambda(\tau_{1}) = v(\tau_{1})+i\omega(\tau_{1})$ is the solution of (2.40) with respect to $\tau_{1}$. Suppose that one of the roots of (2.54) is $\lambda(\tau_{1}) = \alpha(\tau_{1})+i\omega(\tau_{1})$, satisfying $\alpha(\tau_{1_{0}}) = 0$ and $\omega(\tau_{1_{0}}) = \omega_{0}$ for a positive real number $\tau_{1_{0}}$.

Let

Since

Then,

And since $f_{1}(i\omega) = a_{5}(i\omega)+a_{6} = a_{5}i\omega+a_{6}$,

Then, $\frac{d\vert f_{1}(i\omega)\rvert^{2}}{d\omega} = 2a^{2}_{5}\omega$.

Thus, we have

Because $\vert f_{0}(i\omega_{0})\rvert^{2} = \vert f_{1}(i\omega_{0})\rvert^{2}$, we have

Next, differentiate both sides of (2.54) with respect to $\tau_{1}$, we have

We can write (2.61) as

Since $f_{0}(i\omega_{0})+f_{1}(i\omega_{0})e^{-i\omega_{0}\tau_{1}} = 0$, we obtain that

From (2.60) and (2.63), we have

When $Re(\lambda) = \alpha^{(j)}_{n}(\tau_{1})$, we have

As $X_{n_{0}}$ is a simple root of $G(X) = 0$, we know $\dot{G}(X_{n_{0}})\neq0$. From (2.65), we know $\bigg(\frac{d\alpha^{(0)}_{n_{0}}}{d\tau_{1}}\bigg\rvert_{\tau_{1} = \tau^{(0)}_{1_{n}}}\neq0\bigg)$. If $\frac{d\alpha^{(0)}_{n_{0}}}{d\tau_{1}}\bigg\rvert_{\tau_{1} = \tau^{(0)}_{1_{n}}} < 0$, then we obtain that the root of (2.40) has positive real part when $\tau_{1}\in[0, \tau^{(0)}_{1_{n_{0}}})$ which contrasts to Theorem 6. Hence, we can see that $\frac{d\alpha^{(0)}_{n_{0}}}{d\tau_{1}}\bigg\rvert_{\tau_{1} = \tau^{(0)}_{1_{n}}} > 0$. When $\tau_{1} = \tau^{(0)}_{1_{n_{0}}}$, except for the pair of purely imaginary root, the remaining roots of (2.40) have strictly negative real parts, so the system has Hopf bifurcation. This completes the proof.

2.1.8.   Global stability of the immune-free equilibrium point

Theorem 8. The immune-free equilibrium point $E_{1}$ is globally asymptotically stable when $1 < R_{0} < 1+\inf\{A_{1}, A_{2}\}$, where $A_{1} = \frac{(1-u_{1})(1-u_{2})\epsilon a\beta\alpha}{k\sigma\mu(\alpha+\delta)}$ and $A_{2} = \frac{(1-u_{1})h\beta}{g\sigma}$.

Proof. We consider the function $G(x) = x-1-\ln x \ (x > 0)$. Note that $G(x)\geq0, \forall x$ and that $G(x) = 0$ if and only if $x = 1$. We define a Lyapunov function $L_{1}$ as follows:

Since $\frac{dx_{1}}{dt} = 0$, then $\Lambda = \sigma x_{1}+(1-u_{1})\beta x_{1}v_{1}$. Therefore,

Since $c_{1} = \frac{(1-u_{2})ay_{1}}{\alpha+\delta}$, we have $\frac{(1-u_{1})(1-u_{2})\beta x_{1}v_{1}ayc_{1}}{(\alpha+\delta) c_{1}c} = \frac{(1-u_{1})\beta x_{1}v_{1}yc_{1}}{y_{1}c}$ and $v_{1} = \frac{\alpha c_{1}}{\mu}$ then $\frac{(1-u_{1})\beta x_{1}v_{1}\mu v_{1}}{\alpha c_{1}} = (1-u_{1})\beta x_{1}v_{1}$ and $\frac{dy_{1}}{dt} = 0$, we have $(1-u_{1})\beta x_{1}v_{1} = \sigma y_{1}e^{m\tau_{1}}$.

Then,

Substituting $x_{1} = \frac{\sigma\mu(\alpha+\delta)}{(1-u_{1})(1-u_{2})\beta e^{-m\tau_{1}}a\alpha}, c_{1} = \frac{(1-u_{2})ay_{1}}{\alpha+\delta}$ and $v_{1} = \frac{\alpha c_{1}}{\mu}$ into $\frac{(1-u_{1})(1-u_{2})\beta x_{1}v_{1}ay}{(\alpha+\delta)c_{1}} = \sigma e^{m\tau_{1}}y$. We have $v_{1} = \frac{\sigma (R_{0}-1)}{(1-u_{1})\beta}$ from $1 < R_{0} < 1+\frac{(1-u_{1})g\beta}{g\sigma}$ then $v_{1} < \frac{h}{g}$ and $y_{1} = \frac{(\alpha+\delta)\sigma\mu(R_{0}-1)}{(1-u_{1})(1-u_{2})\beta a\alpha}$ from $1 < R_{0} < \frac{(1-u_{1})(1-u_{2})\epsilon a\beta\alpha}{k\sigma\mu(\alpha+\delta)}$, we have $y_{1} < \frac{\epsilon}{k}$. Then,

We obtain that $\frac{dL}{dt} < 0$ when $1 < R_{0} < 1+\inf\{A_{1}, A_{2}\}$, where $A_{1} = \frac{(1-u_{1})(1-u_{2})\epsilon a\beta\alpha}{k\sigma\mu(\alpha+\delta)}$ and $A_{2} = \frac{(1-u_{1})h\beta}{g\sigma}$ and $\frac{dL}{dt} = 0$ at $E_{1}$. Therefore, $E_{1}$ is globally asymptotically stable when $1 < R_{0} < 1+\inf\{A_{1}, A_{2}\}$, where $A_{1} = \frac{(1-u_{1})(1-u_{2})\epsilon a\beta\alpha}{k\sigma\mu(\alpha+\delta)}$ and $A_{2} = \frac{(1-u_{1})h\beta}{g\sigma}$.

2.1.9.   Global stability of the immune-activated infection equilibrium point

Theorem 9. The immune-activated infection equilibrium point $E_{2}$ is globally asymptotically stable when $R_{0} > 1$ and $A > B$ (where $A$ and $B$ are defined in the proof).

Proof. We consider the function $G(x) = x-1-\ln x \ (x > 0)$. Note that $G(x)\geq 0, \forall x$ and that $G(x) = 0$ if and only if $x = 1$. We define a Lyapunov function $L_{2}$ as follows:

Then,

Since $\frac{dx_{2}}{dt} = 0$ then $\Lambda = \sigma x_{2}+(1-u_{1})\beta x_{2}v_{2}$ and $y_{2} = \frac{\epsilon}{k}$, we have

From

we have

Then,

And since, $\frac{dv_{2}}{dt} = 0$, $\gamma w_{2} = \frac{\alpha c_{2}-\mu v_{2}}{v_{2}}$ and $v_{2} = \frac{h}{g}$, then

Let $A = \sigma\frac{(x-x_{2})^{2}}{x}-(1-u_{1})\beta x_{2}v_{2}\bigg(4-\frac{x_{2}}{x}-\frac{y_{2}}{y}\frac{x(t-\tau_{1})v(t-\tau_{1})}{x_{2}v_{2}}-\frac{cv_{2}}{c_{2}v}-\frac{c_{2}y}{cy_{2}}+\ln\frac{x(t-\tau_{1})v(t-\tau_{1})}{xv}\bigg)- \ qe^{m\tau_{1}}y_{2}z_{2}\bigg(2-\frac{y_{2}}{y}-\frac{y(t-\tau_{2})z(t-\tau_{2})}{y_{2}z}+\ln\frac{y(t-\tau_{2})z(t-\tau_{2})}{yz}\bigg)+ \ 2qe^{m\tau_{1}}y_{2}z_{2}$ and $B = qe^{m\tau_{1}}yz_{2}+\frac{qe^{m\tau_{1}}y^{2}_{2}z_{2}}{y}$. Thus, the global stability of immune-activated steady state equilibrium point is globally asymptotically stable when $R_{0} > 1$ and $A > B$.

Next, we perform numerical simulation for system (2.1) to confirm global stability of the three above equilibrium points.

Case I: infection-free equilibrium point

In this case, we used $\beta = 3\times10^{-13}$, then the infection-free equilibrium point $(E_{0} = (368.6455, 0, 0, 0, 0, 0))$ is globally asymptotically stable when $R_{0} = 2.9178\times10^{-10} < 1$ as shown in Figure 2.

Case II: immune-free equilibrium point

In this case, $1 < R_{0} = 1.3616 < \inf\{A_{1}, A_{2}\} = 2.1932$ at $\beta = 0.0014$ and $k = 0.001$ the immune-free equilibrium point $(270.7360, 92.6698, 56.8294, 5.6829, 0, 0)$ is globally asymptotically stable as shown in Figure 3.

Case III: immune-activated infection equilibrium point

The last critical point is the immune-activated infection equilibrium is globally asymtotically stable when $R_{0} = 13.6164 > 1$ as shown in Figure 4. We use $a = 1.5$, then $E_{2} = (168.0870, 50,306.6211, 18.7500, 44.0279, 30.7616)$.

3.   Numerical simulation

In this section, the numerical simulations of the system (2.1) are performed with the use of parameters values from Table 1. We divide the results into 4 cases as follows to investigate the impact of drug therapy ($u_{1}$ and $u_{2}$) and to explore the dynamics of model in the different values of time delays.

(i) when $u_{1}$ varies and $\tau_{1} = \tau_{2} = 0$

(ii) when $u_{2}$ varies and $\tau_{1} = \tau_{2} = 0$

(iii) when $\tau_{1}$ varies and $\tau_{2} = 5$

(iv) when $\tau_{2}$ varies and $\tau_{1} = 5$.

(i) when $u_{1}$ varies and $\tau_{1} = \tau_{2} = 0$.

Figure 5 (a)–(f) shows the dynamics of the concentration of the uninfected hepatocytes, infected hepatocytes, intracellular HBV DNA-containing capsid, free viruses, antibodies, and CTL, respectively where they are treated by $u_{1}$ and $u_{2}$ representing the efficiency of drug therapy in blocking new infection and the efficiency of drug therapy in inhibiting viral production, respectively. We choose $u_{1}$ = 0.2, 0.4, 0.6 and $u_{2}$ = 0.5. From Figure 5(a), we can see that a larger value of $u_{1}$ can slow down the decline of the concentration of uninfected hepatocytes when compare with the smaller $u_{1}$. At the end, they tend to reach the same equilibrium value. Figures 5(b) and 5(c) give a similar pattern, the concentration of infected hepatocytes and intracellular HBV DNA-containing capsids rises since the beginning for all values of $u_{1}$. Figure 5(b) shows that the greater value of $u_{1}$, the smaller the peak of the concentration of infected hepatocytes with a slightly slower time for the peak to occur. In the case when $u_{1} = 0.2$ and $0.4$, it tends to give the second peak in the period of 80th to 150th day, whereas when $u_{1} = 0.6$ there is no second peak. Further, it reaches a lower equilibrium value when compared with a smaller $u_{1}$. The difference between Figure 5(c) and Figure 5(b) is that the first peak of all three cases are at the same level. At the start in Figure 5(d), the concentration of free viruses decreases for a few days and goes up sharply to reach a peak. When $u_{1}$ increases, the peak height is smaller, respectively with a slower time for the peak to occur and reaches the smaller equilibrium value. Further, for the case $u_{1} = 0.2$ and $0.4$, the second peak is observed between 50th-150th day. Figure 5(e) shows interesting results i.e. there are two peaks of the concentration of antibodies when $u_{1} = 0.2$ and $0.4$, where their second peak is larger than their first peak. Only one peak of the concentration of antibodies is obtained for $u_{1} = 0.6$. Time for the peak to occur is slightly slower when $u_{1}$ increases. The dynamics tend to reach a lower equilibrium value with the larger value of $u_{1}$. Interestingly, Figure 5(f) shows a significant reduction of the concentration of CTL and a slower time for the peak to occur when $u_{1}$ increases. Further, in the case of $u_{1} = 0.2$, on the 100th day, the concentration of CTL rises again to reach a small peak ranging the period of 50 days then goes down to zero. Overall, from the results above $u_{1}$ has been shown to play a main role in significantly reducing the concentration of infected hepatocytes, free viruses and CTL.

(ii) when $u_{2}$ varies and $\tau_{1} = \tau_{2} = 0$

In Figure 6, the value of $u_{2}$ is varied by choosing $u_{2} = 0.2, 0.4, 0.6$ and $u_{1} = 0.5$. In Figure 6(a), our results show that with an increase of $u_{2}$, the concentration of uninfected hepatocytes decreases slightly slower than the concentration of the smaller $u_{2}$ and it tends towards the same equilibrium value at the end. Figure 6(b) demonstrates double peaks of the concentration of infected hepatocytes where the higher value of $u_{2}$, the lower peak height for both peaks. It reaches a peak at 1000 cells/ml in the case $u_{2} = 0.2$, whereas it reaches a peak at less than 900 cells/ml for $u_{2} = 0.6$. After the first peak, they drop down to between 200-300 cells/ml and gradually rise up again as the second peak on approximately 100th day. Figure 6(c) gives a very interesting result i.e. with $u_{2} = 0.2, 0.4$ and $0.6$, the concentration of intracellular HBV DNA-containing capsids go up to reach the peak at 800 cells/ml, 600 cells/ml and 400cells/ml, respectively. Although when $u_{2} = 0.2$ and $u_{2} = 0.4$, it tends to give the second peak in the period of 100th to 150th day, with $u_{2} = 0.6$ there is no second peak. Further, with the larger value of $u_{2}$, it tends to reach a lower equilibrium value. Figure 6(d) shows a significant decrease of the concentration of free viruses when $u_{2}$ increases, and the time for the peak to occur is slightly slower. Figure 6(e) shows the concentration of antibodies increases from the beginning for all $u_2$ values, there is a double peak for $u_{2} = 0.2$, it reaches the first peak at 400 cells/ml on the 45th day and slightly declines to 350 cells/ml then it rises up again to the higher second peak. At $u_{2} = 0.4$, the double peak is smaller than the case of $u_{2}$ and than its first peak. With a higher value of $u_{2}$, the concentration of antibodies decreases largely, respectively and tends to reach a lower equilibrium value. Figure 6(f) shows that when $u_{2}$ increases, the concentration of CTL decreases significantly, and the time for the peak to occur is slightly slower, respectively. On the whole, from the results above $u_{2}$ has been shown to play a main role in greatly reducing the concentration of intracellular HBV DNA-containing capsids, free viruses, antibodies and CTL.

(iii) when $\tau_{1}$ varies and $\tau_{2} = 5$

In Figure 7, we vary the value of $\tau_{1}$ where $\tau_{2}$ is 5. From Figure 7 (a), we can see that the dynamics of concentration of uninfected hepatocytes hardly changed when $\tau_{1}$ varies. Figures 7(b) and 7(c) show a similar pattern, the concentration of infected hepatocyte and intracellular HBV DNA-containing capsids go up since the beginning for all values of $\tau_{1}$. They show that the higher the value of $\tau_{1}$, the smaller the peak and the longer it takes for the peak to appear. Further, it reaches a lower equilibrium value when compared with a smaller $\tau_{1}$. Figure 7(d) shows double peaks in the concentration of free viruses, the lower peak height for both peaks obtained with the larger value of $\tau_{1}$. They drop down after the first peak, then gradually rise to the second peak, which occurs between the 150th and 250th day. Finally, it tends to reach a lower equilibrium value when $\tau_{1}$ increases. Figures 7(e) and 7(f) show that in the case when $\tau_{1}$ increases, the concentration of antibodies and CTL decrease with a slower time for the peak to occur, respectively. In summary, the result above $\tau_{1}$ has shown to have an impact to a reduction in the concentration of infected hepatocytes, intracellular HBV DNA-containing capsids, free viruses, antibodies and CTL. Also, the epidemic peak occurs slower when $\tau_{1}$ increases. (iv) when $\tau_{2}$ varies and $\tau_{1} = 5$.

When $\tau_{2}$ increases, the concentration of uninfected hepatocytes drops faster on the first 100th day, as shown in Figure 8(a). After that, however, the concentration of uninfected hepatocytes tends to decrease slower than in the case of smaller $\tau_{2}$. Figure 8(b) and 8(c) give a similar pattern when $\tau_{2}$ increases, the concentration of infected hepatocytes and intracellular HBV DNA-containing capsids largely increase, with a slower time for the peak to occur. Interestingly, with $\tau_{2} = 0.5$, there are two peaks occurred, whereas only one peak observed in case $\tau_{2} = 5$ and $15$. Further, with $\tau_{2} = 15$ it reaches a lower equilibrium value when compared to $\tau_{2} = 0.5$, and $5$. When $\tau_{2}$ increases, the concentration of free viruses increases to almost the same level of the peak as shown in Figure 8(d). However, it tends to give the second peak for case $\tau_{2} = 0.5$ and $5$, while in case $\tau_{2} = 15$ there is only one peak. At the start in Figure 8(e), when $\tau_{2}$ increases, the concentration of antibodies significantly increases with a slower time for the peak to occur, with $\tau_{2} = 0.5$, after the 70th day, it goes up again to the small second peak at a smaller level. On the other hand, Figure 8(f) shows a large reduction of the concentration of CTL with a slower time for the peak to occur, when $\tau_{2}$ increases. Further, in the case $\tau_{2} = 0.5$, on the 80th day, it tends to rise to give the second peak ranging the period of 70 days then goes down to zero. On the whole, from the results above, $\tau_{2}$ has shown to give an impact in boosting up the concentration of infected hepatocytes, intracellular HBV DNA-containing capsids, free viruses, and antibodies with a longer period of an epidemic time. However, it shows to play a main role in greatly reducing the concentration of CTL. This means that the delay of antigenic stimulation generating CTL causes a longer duration with a large quantity of the hepatitis B virus infection.

4.   Conclusion

In this paper, different from other existing models we propose multiple delays within-host model for HBV infection with 6 variables consisting of the uninfected hepatocytes, infected hepatocytes, intracellular HBV-DNA containing capsids, free viruses, antibodies, and cytotoxic T-lymphocyte (CTL). We incorporate the two delays which are the delay in the productively infected since viruses attack and an additional delay in an antigenic stimulation generating CTL. The model also involves two drug therapies. We have proved that all solutions are non-negative and bounded. Three equilibrium states are determined in this model i.e. infection-free, the immune-free and the immune-activated infection. The basic reproduction number is determined and becomes the threshold in determining the stability of the infection-free equilibrium point. Further, the global stability of immune-free and immune-activated infection equilibrium points are analyzed and presented in Theorem 8 and 9, respectively. Our numerical simulations have shown that both drug therapies play a key role in reducing an HBV infection overall. From Figure 7, we obtain that $\tau_{1}$ affects the time for the peak to occur i.e. it is slower when $\tau_{1}$ increases. Also, a smaller epidemic is observed in a larger value of $\tau_{1}$. In addition, the results of Figure 8 obtained, they show that the greater the delay in an antigenic stimulation generating CTL ($\tau_{2}$), the more severe HBV infection occurs. Our findings have confirmed the great role of both drug therapies in reducing HBV infection as shown in the work of Danane and Allali, 2018 ^[20]. However, the greater the delay in an antigenic stimulation generating CTL cells has been shown to make the HBV infection more severe, this can be found in the work of Sun and Liu, 2017 ^[46] that this time delay gives a big effect on the model dynamics. Overall, including both adaptive immune responses which are CTL and antibodies with time delays would make this model more realistic and this could bring better understanding of HBV infection. As a future work, it might be reasonable to include spatial components and diffusion for viruses into the model.

Acknowledgments

This work has been supported by the Department of Mathematics, Faculty of Science, Naresuan University, Thailand. Pensiri Yosyingyong has been funded by a DPST scholarship from the Thai government.

Conflict of interest

The authors declare there is no conflict of interest.