Effects of vaccination on mitigating COVID-19 outbreaks: a conceptual modeling approach

1.   Introduction

The pandemic of Coronavirus Disease 2019 (COVID-19) has given rise to an unprecedented public health crisis globally since the onset of the epidemic. As of June 9, 2022, over 533.7 million people in the world have been diagnosed with COVID-19 and more than 6.3 million have died. Thanks to the rapid progress in the development of the COVID vaccine. The vaccines are highly effective at preventing serious infection, hospitalization, and death from the disease. In many epidemic regions/countries, vaccination coverage rising has gradually reduced the economic and social disruptions caused by the pandemic. However, the progressively emerging SARS-CoV-2 variants, breakthrough infections and vaccine hesitancy have complicated the transmission and spread of COVID-19 infection, and posed new challenges for disease control. As a consequence, the developed COVID vaccines have raised important questions that remain unanswered or only partially answered regarding mitigating COVID-19 pandemic. For example, how effective vaccination coverage will be in the prevention and control of COVID-19 outbreaks and how vaccination coverage should be implemented in a region (e.g., a city, a state or a country) in short and long runs to protect the population there?

Many mathematical models have been published to study vaccination effects against the COVID-19 pandemic (see e.g., ^{[5,6,7,8,9,10,11,12]} and the references therein). For instance, Roy et al. ^[13] employed an SEIRD (susceptible-exposed-infected-recovered-dead) model to study the strategy of vaccination coverage in New York State. Saad-Roy et al. ^[6] applied a compartmental model of the SIR type to investigate a variety of scenarios of transmission and vaccine immunity. Amaral et al. ^[14] used a data-driven methodology (built upon an SIR-type model) to study the impact of vaccination rate against the COVID-19 in Brazil. The impulsive vaccination strategy was discussed by Etxeberria-Etxaniz et al. ^[15], whereas the mass vaccination was studied by Rachaniotis et al. ^[9] in Greece, Moghadas et al. ^[16] and Lin et al. ^[17] in the US and Shim ^[10] in South Korea. Goh et al. ^[18] proposed a country-specific model to compute the COVID-19 vaccination coverage needed to achieve herd immunity. Although the aforementioned works have provided valuable insights in disease prevention, most of these studies have been focused on the single or double doses of COVID-19 vaccine. In addition, none of these works have conducted a thorough mathematical analysis to study the transmission and spread of the disease with the inclusion of vaccination. This motivates our work on quantifying the impact of vaccination against COVID-19 outbreaks in a conceptual modeling study aiming to help us better understand the vaccination strategies in mitigating the disease.

The goal of this work is to predict the effectiveness of vaccination against the COVID-19 pandemic in short and long runs. To that end, we propose a compartmental model which extends a so-called SEIRD model with the inclusion of the vaccinated group, then we analyze the dynamics of this model under periodic vaccination programs and homogeneous disease transmission. Finally, to study the impact of vaccination, we fit our model to multiple COVID-19 waves in four locations including Hong Kong (SAR) China, Singapore, Japan, and South Korea as vaccine findings in reducing infection and mortality have shown to be spatially heterogeneous, and then forecast the prevalence of COVID-19 by the end of 2022 and in the future.

2.   Model

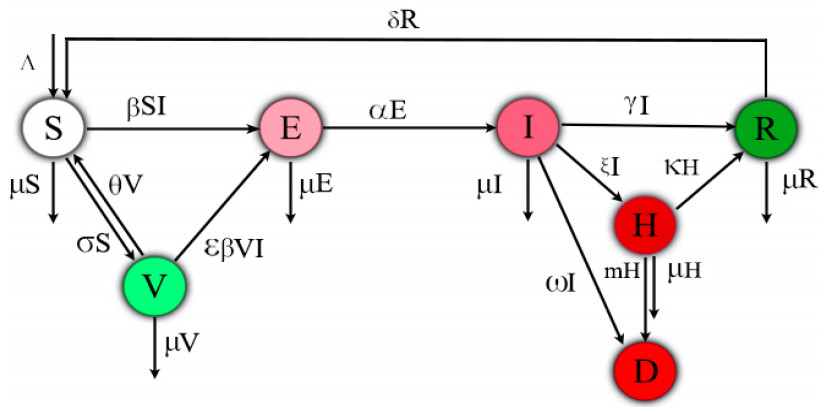
To study the impact of vaccination programs on the ongoing COVID-19 pandemic, we extend the previous susceptible-exposed-infectious-hospitalized-recovered-dead (SEIRD) model ^[1,2,3,4]. Our model is built upon the classical susceptible-exposed-infected-recovered (SEIR) compartmental framework by incorporating the birth and death of the population, disease-induced mortality and waning immunity induced by vaccine and infection, and adding a vaccinated compartment ($V$) to capture the vaccination. In the model, we divide the human population into seven compartments: susceptible ($S$), vaccinated ($V$), exposed ($E$), infected ($I$), hospitalized ($H$), disease-induced dead/removed ($D$) and recovered ($R$). Susceptible individuals can become exposed after contacting with infected people. Exposed individuals can progress to the infectious compartment after the latency period. Infectious individuals can move to the hospitalized compartment, which comes from either mild or severe cases. Infectious individuals can recover or be removed due to treatment or disease-induced death and then enter compartment $D$. Here $V$ is the number of vaccinated individuals. We assumed that (i) susceptible individuals are vaccinated at time $t$ at a rate $\sigma(t)$, (ii) $100\times {\epsilon} \%$ of vaccinated individuals can become infected; (iii) the vaccinated people can regain susceptibility and come back to the $S$ compartment at the rate of $\theta$ due to the waning of vaccine-induced immunity. Besides, clinical and epidemiological evidence indicates that there are some individuals who never develop symptoms (see, e.g., ^[19,20] and references therein). However, there is no asymptomatic case data currently available. So, we synthesize asymptomatic and symptomatic transmission into an overall transmission route in our model. Our model, illustrated by a flow chart in Figure 1, can be written as:

The definition of the model parameters is provided in Table 1. The parameter $\Lambda$ represents the population influx, $\mu$ is the natural death rate of human individuals, $\alpha^{-1}$ is the latent period between exposure and infection, $\omega$ is the disease-induced death rate, $\gamma$ (resp. $\kappa$) is the recovery rate from infection (resp. hospitalization), $\xi$ is the rate of hospitalization, $\theta$ (resp. $\delta$) is the rate of waning immunity induced by the vaccine (resp. infection), and $\delta$ is the removal rate of the virus from the environment. The function $\beta(t)$ is the time-dependent transmission rate. The function $\sigma(t)$ measures the rate at which susceptible individuals are vaccinated at time $t$. The vaccination is imperfect and it only has a degree of protection. Let $\epsilon = 1-d\in (0, 1)$, where $d$ is the vaccine efficacy. Moreover, we assume that

(H1) $\beta(t)$ is a positive continuous function.

(H2) $\sigma(t)$ is a nonnegative continuous function.

(H3) All parameters are positive.

3.   Analysis

To gain more analytical insight into our model, we conduct a mathematical analysis for a special case of this model (2.1) based on the following assumptions.

$1)$ Transmission rate $\beta(t)$ is assumed to be constant $\beta$.

$2)$ Suppose that the vaccination program is provided on a regular basis, and we assume that $\sigma(t)$ is $T$-periodic, where $T$ is the vaccination period.

Then our original model (2.1) is reduced to a system of periodic ordinary differential equations.

3.1.   Basic reproduction number

First, we derive the basic reproduction number $\mathcal{R}_0$, a key indicator of the severity of the infection.

To study the disease-free steady state (DFS), we set $E = I = H = R = D = 0$ and it leads to the following linear periodic system

is cooperative and strongly subhomogeneous (see, e.g., [27, Section 2.3]). It follows from [27, Theorem 2.3.2] that there exists a unique $T$-periodic positive solution

which is globally attractive in ${\mathbb{R}}^2$.

By the theory of asymptotically periodic semiflows (see, e.g., [27, section 3.2] or ^[28]), it is easy to verify that when $E(t) = I(t) = 0$,

Hence, the DFS of model (2.1) is given by $\mathcal{E}^0: = (S^*(t), V^*(t), 0, 0, 0, 0, 0, 0)$. Linearizing model (2.1) at its DFS $\mathcal{E}^0$, we obtain the following periodic linear equations in terms of disease variables $E$ and $I$:

where

Define

Since $\mathbb{V}$ is a constant matrix, the evolution operator, $Y(t, s)$, $t\ge s$, of the linear $T$-periodic model

is its fundamental matrix; i.e., for each $s\in{\mathbb{R}}$, $Y(t, s)$ satisfies

where $I$ is the $2\times 2$ identity matrix. More specifically, if $\chi\ne \alpha +\mu$,

and if $\chi = \alpha+\mu$ (i.e., $\gamma+\xi+\omega+\mu = \alpha+\mu$ which is equivalent to $\gamma+\xi+\omega = \alpha$),

Let $C_T$ be the ordered Banach space of all $T$-periodic functions from $\mathbb{R}$ to $\mathbb{R}^2$, which is equipped with the maximum norm $\|\cdot\|$ and the positive cone $C_T^+: = \{\psi\in C_T:\psi(t)\geq 0, \ \forall \ t\in \mathbb{R}\}$.

Suppose that $\psi(s)\in C_T$ is the initial distribution of infected individuals. Then $\mathbb{F}(s)\psi(s)$ is the distribution of the new infections produced by the infected individuals who were introduced at time $s$. Given $t\geq s$, then $Y(t, s)\mathbb{F}(s)\psi(s)$ gives the distribution of those infected individuals who were newly infected at time $s$ and remain in the infected compartments at time $t$. It follows that

gives the distribution of accumulative new infections at time $t$ produced by all those infected individuals $\psi(s)$ introduced at time previous to $t$. We define a linear operator $L:C_T\rightarrow C_T$ by

which is referred to as the next generation operator. Motivated by the concept of next generation operators in ^{[29,30,31,32,33]}, the basic reproduction number is defined as the spectral radius of $L$; that is, $\mathcal{R}_0: = r(L)$.

In the special case where model (2.1) is autonomous, i.e., $\beta(t) = \beta$, $\sigma(t)\equiv \sigma$, $N^*_{{\epsilon}}(t)\equiv\frac{\Lambda ({\epsilon} \sigma+\theta+\mu)}{\mu (\sigma+\theta+\mu)}$, the basic reproduction number is reduced to

It is clear that $\mathcal{R}_0$ is a strictly decreasing function of the constant rate of vaccination $\sigma$ as ${\epsilon} < 1$. This indicates that increasing vaccination rate could reduce the risk of infection.

3.2.   Threshold dynamics

In this subsection, we establish threshold dynamics of the disease in terms of the basic reproduction number $\mathcal{R}_0$.

Before proceeding, we need to review some basic results related to a monodromy matrix. Let $M(t)$ be a continuous, cooperative, irreducible, and $T$-periodic $m\times m$ matrix function. Suppose $\Phi_{{M}(\cdot)}(t)$ is the monodromy matrix of the linear ordinary differential system

and $r(\Phi_{{M}(\cdot)}(T))$ is the spectral radius of $\Phi_{{M}(\cdot)}(T)$. By [34, Lemma 2] or [35, Theorem 1.1]), it follows that $\Phi_{M(\cdot)}(t)$ is a matrix with all entries positive for each $t > 0$. In view of the Perron-Frobenius theorem, $r(\Phi_{{M}(\cdot)}(T))$ is the principal eigenvalue of $\Phi_{{M}(\cdot)}(T)$ in the sense that it is simple and admits a positive eigenvector.

By [32, Theorem 2.1], we have the following result.

Lemma 3.1.

1) If $r\left(\Phi_{\frac{\mathbb{F}(\cdot)}{\mu}-\mathbb{V}}(T)\right) = 1$ has a positive solution $\mu = \mu_*$, then $\mu_*$ is an eigenvalue of operator $L$, and $\mathcal{R}_0 > 0$.

2) If $\mathcal{R}_0 > 0$, then $\mu = \mathcal{R}_0$ is the unique solution of $r\left(\Phi_{\frac{\mathbb{F}(\cdot)}{\mu}-\mathbb{V}}(T)\right) = 1$.

3) $\mathcal{R}_0 = 0$ if and only if $r\left(\Phi_{\frac{\mathbb{F}(\cdot)}{\mu}-\mathbb{V}}(T)\right) < 1$ for all $\mu > 0$.

It is usually difficult to compute $\mathcal{R}_0$ using the model (3.6). The part 2) of the above result, in particular, provides an alternative approach to numerically evaluating $\mathcal{R}_0$.

Moreover, by [32, Theorem 2.2], the following statement holds.

Lemma 3.2. ([32, Theorem 2.2])

Thus, the DFS $\mathcal{E}^0(t)$ is locally asymptotically stable if $\mathcal{R}_0 < 1$, and unstable if $\mathcal{R}_0 > 1$.

The following result is an immediate consequence of [36, Lemma 2.1].

Lemma 3.3. ([36, Lemma 2.1]) Let ${\lambda} = \frac{\ln\left[r(\Phi_{M(\cdot)}(T))\right]}{T}$. Then there exists a positive $T$-periodic function $v(t)$ such that $e^{\lambda t}v(t)$ is a solution of model (3.8).

Define

Recall that $\mathbb{F}$ and $\mathbb{V}$ are defined in model (3.4). Let

If $\eta = 0$, it is clear that $\mathbb{F}_0 = \mathbb{F}$ and $\lambda_0 = \frac{1}{T}\ln\big[r(\Phi_{\mathbb{F}(\cdot)-\mathbb{V}}(T))\big]$.

Let $\mathbb{X} = \mathbb{R}^7_{+}$. Note that $\mathbb{X}$ is positively invariant for model (2.1). By [37, Theorem 5.2.1], for every $x^0 = (S^0, V^0, E^0, I^0, H^0, R^0, D^0)\in \mathbb{X}$, model (2.1) has a unique local nonnegative solution $w(t, x^0) = (S(t, x^0), V(t, x^0), E(t, x^0), I(t, x^0), H(t, x^0), R(t, x^0), D(t, x^0))\in \mathbb{X}$ for $t\ge 0$ with initial $w(0, x^0) = x^0$.

The following theorem establishes the global stability of the DFS $\mathcal{E}^0$ when $\mathcal{R}_0 < 1$.

Theorem 3.4. If $\mathcal{R}_0 < 1$, the DFS, $\mathcal{E}^0$, of model (2.1) is globally attractive; i.e.,

where $w^*(t) = (S^*(t), V^*(t), 0, 0, 0, 0, 0).$

Proof. By $\mathcal{R}_0 < 1$, it follows from Lemma 3.2 that $r(\Phi_{\mathbb{F}(\cdot)-\mathbb{V}}(T)) < 1$ and hence $\lambda_0 < 0$. By continuity, there exists $\eta_0 > 0$ such that

In view of the global attractivity of $(S^*(t), V^*(t))$ in model (3.1), there exists $t_0 > 0$ such that

It follows from Lemma 3.3 that there exists a positive $T$-periodic solution $v_{\eta_0}(t)$ such that $\bar{v}(t) = c e^{\lambda_{\eta_0}(t-t_0)}v_{\eta_0}(t)$ is a solution of model (3.8) with $M(t) = \mathbb{F}_{\eta_0}(t)-\mathbb{V}$. Here constant $c$ is chosen such that $(E(t_0), I(t_0))\le \bar{v}(t_0) = cv_{\eta_0}(t_0)$.

In view of model (3.12),

for $t\ge t_0$. Thus

The comparison principle implies that

Since $\lambda_{\eta_0} < 0$, it follows that

This implies that $S(t)$ and $V(t)$ in model (2.1) is asymptotic to model (3.1). By the theory of asymptotically periodic semiflows (see, e.g., ^[28] or [27, section 3.2]), it follows that $\lim_{t\to\infty}(S(t)-S^*(t)) = \lim_{t\to\infty}(V(t)-V^*(t)) = 0$. Then $H(t)$ is asymptotic to

and hence it follows from the theory of asymptotically periodic semiflows ^[28] that $\lim_{t\to\infty}H(t) = 0$.

Similarly one can verify that $\lim_{t\to\infty}R(t) = \lim_{t\to\infty}H(t) = 0$. This completes the proof.

Let $N(t) = S(t)+V(t)+E(t)+I(t)+H(t)+R(t)$ denote the total population size at time $t$. By model (2.1),

It follows from the comparison principle that $N(t)$ is ultimately bounded. By the positivity of the solution, we see that $w(t)$ is ultimately bounded for $w = S, V, E, I, H, R$. Hence the solutions of model (2.1) admits a connected global attractor in $\mathbb{X}$ that attracts all positive orbits in $\mathbb{X}$.

When $\mathcal{R}_0 > 1$, we assume that waning of infection-induced immunity is negligible, i.e., $\delta = 0$, for simplicity. In this case, the first four equations of model (2.1) are decoupled from the rest, and hence it suffices to consider the following system

Let $\mathbb{Y} = \mathbb{R}^4_{+}$. Let $Q(t): \mathbb{Y}\to \mathbb{Y}$ denote the solution map of model (3.18); i.e., for any $z^0\in \mathbb{Y}$,

where $u(t, z^0)$ is the unique solution of model (3.18) with initial $u(0, z^0) = z^0$. Then $\widehat{Q} = Q(T)$ is the

Poincaré map associated with model (2.1) and

Moreover, $\big\{\widehat{Q}^n: \mathbb{Y}\to \mathbb{Y}\big\}_{n\ge 0}$ defines a discrete-time dynamical system that admits a global attractor in $\mathbb{Y}$. Let

and

If the waning of infection-induced immunity is neglected (i.e., $\delta = 0$), we have the following persistent result when $\mathcal{R}_0 > 1$.

Theorem 3.5. Suppose that $\delta = 0$ (i.e., the waning of infection-induced immunity is neglected). If $\mathcal{R}_0 > 1$, the solutions of model (3.18) are uniformly persistent; that is, there exists some constant $c > 0$ such that any solution $u(t, z_0) = (S(t, z_0), V(t, z_0), E(t, z_0), I(t, z_0))$ of model (3.18) with $z_0\in \mathbb{Y}_0$ satisfies $\liminf_{t\to\infty}E(t)\ge c$ and $\liminf_{t\to\infty}I(t)\ge c$, and model (3.18) admits at least one positive $T$-periodic solution.

Proof. Recall that the Poincaré map $\widehat{Q}:\mathbb{Y}\to \mathbb{Y}$ associated with model (3.18) has a global attractor in $\mathbb{Y}$. Now we proceed to prove that $\widehat{Q}$ is uniformly persistent with respect to $(\mathbb{Y}_0, {\partial}\mathbb{Y}_0)$. It is easy to verify that $\mathbb{Y}_0$ and ${\partial}\mathbb{Y}_0$ are positively invariant under the solution flow of model (3.18) satisfying $\mathbb{Y}_0\cup {\partial}\mathbb{Y}_0 = \mathbb{Y}$, $\mathbb{Y}_0\cap {\partial}\mathbb{Y}_0 = \emptyset$, and ${\partial}\mathbb{Y}_0$ is relatively closed in $\mathbb{Y}$.

Since $\mathcal{R}_0 > 1$, it follows from Lemma 3.2 that $r(\Phi_{\mathbb{F}(\cdot)-\mathbb{V}}(T)) > 1$. Thus,

and $\lim_{\eta\to 0}\lambda_{\eta} = \lambda_0 > 0$, where $\lambda_{\eta}$ is defined in model (3.10). Hence, we can choose $\eta_1 > 0$ sufficiently small such that $\lambda_{\eta_1} > 0$. By Lemma 3.3, model (3.18) has a positive $T$-periodic solution $v_{\eta_1}(t)$ such that $\underline{v}(t) = e^{\lambda_{\eta_1}t}v_{\eta_1}(t)$ is a solution of model (3.8) with $M(t) = \mathbb{F}_{\eta_1}(t)-\mathbb{V}$.

In view of $\lim_{\phi\to \mathcal{E}^0}\|Q(t)\phi-Q(t)\mathcal{E}^0\| = 0$ uniformly for $t\in [0, T]$, there exists $\rho = \rho(\eta_1)\in (0, \eta_1)$ such that for any $\phi\in \mathbb{Y}_0$ with $\|\phi-\mathcal{E}^0\| < \rho$, we have $\|Q(t)\phi-Q(t)\mathcal{E}^0\| < \underline{\eta}: = \eta_1/(1+{\epsilon} \eta_1)$ for all $t\in [0, T].$ We further claim the following result.

Claim.

Suppose, by contradiction, that $\limsup_{n\to\infty}\|\widehat{Q}^n\psi-\mathcal{E}^0\| < \rho$ for some $\psi\in \mathbb{Y}_0$. Then there exists $N\in\mathbb{N}$ such that $\|\widehat{Q}^n\psi-\mathcal{E}^0\| < \rho$ for all $n\ge N$. For any $t\ge NT$, there exist $m\ge N$ and $t'\in [0, T)$ such that $t = mT+t'$, and hence $\|Q(t)\psi-Q(t)\mathcal{E}^0\| = \|Q(t')\big(\widehat{Q}^m(\psi)\big)-Q(t')\mathcal{E}^0\| < \underline{\eta}$. It then follows that $S(t) > S^*(t)-\underline{\eta}$, $V(t) > V^*(t)-\underline{\eta}$, $E(t) < \underline{\eta}$ and $I(t) < \underline{\eta}$ for $t\ge NT$, which implies that $S(t)+{\epsilon} V(t)\ge S^*(t)-\underline{\eta}+{\epsilon}(V^*(t)-\underline{\eta}) < /p > < p > = N_{{\epsilon}}^*(t)-\eta_1$, $E(t) < \eta_1$, and $I(t) < \eta_1$ for $t\ge NT$. Then we have

for $t\ge NT$. Since $\psi\in \mathbb{Y}_0$, $E(t, \psi) > 0$ and $I(t, \psi) > 0$ for $t\ge 0$. Thus we can choose ${k} > 0$ sufficiently small such that $(E(NT, \psi), I(NT, \psi))^T\ge {k}\underline{v}(NT)$. It follows from the comparison principle that $(E(t, \psi), I(t, \psi))^T\ge k \underline{v}(t) = k e^{\lambda_{\eta_1} t}v_{\eta_1}(t)$ for $t\ge NT$. Since $\lambda_{\eta_1} > 0$, $\lim_{t\to\infty}E(t, \psi) = \lim_{t\to\infty}I(t, \psi) = \infty$, which contradicts the boundedness of the solutions of model (3.18). This proves the claim.

The result of this claim implies that $\mathcal{E}^0$ is an isolated invariant set for the Poincaré map $\widehat{Q}$ in $\mathbb{Y}_0$ and $W^s(\mathcal{E}^0)\cap \mathbb{Y}_0 = \emptyset$, where $W^s(\mathcal{E}^0)$ of the stable set of $\mathcal{E}^0$ with respect to $\widehat{Q}$. Define

For any given $\psi\in M_{\partial}$, $\widehat{Q}^n(\psi)\in \partial \mathbb{Y}_0$ for $n\ge0$. Thus, for each $n\in\mathbb{N}$, either $E(nT, \psi) = 0$ or $I(nT, \psi) = 0$. Using the last two equations in system model (3.18), we see that $E(t, \psi) = 0$ or $I(t, \psi) = 0$ for all $t\ge 0$. Case 1. Suppose $I(t, \psi)\equiv 0$ for $t\ge 0$. By the third equation of model (3.18), ${dE}/{dt} = -(\alpha+\mu)E$ for $t\ge 0$ and hence $\lim_{t\to\infty}E(t) = 0$. It follows from the theory of asymptotically periodic semiflows (see, e.g., [27, Section 3.2]) that $\lim_{t\to\infty}(S(t)-S^*(t)) = \lim_{t\to\infty}(V(t)-V^*(t)) = 0$.

This implies that

Case 2. Suppose $I(t, \psi)\not\equiv 0$ for $t\ge 0$. In this case, $E(t, \psi)\equiv 0$ for all $t\ge 0$. Moreover, there exists $t_0\ge 0$ such that $I(t_0, \psi) > 0$. By the fourth equation of model (3.18), $I(t, \psi) > 0$ for $t\ge t_0$. Using the fourth equation of model (3.18), we see that $\lim_{t\to\infty}I(t) = 0$. By the theory of asymptotically periodic semiflows (see, e.g., [27, Section 3.2]), it follows that $\lim_{t\to\infty}(S(t)-S^*(t)) = \lim_{t\to\infty}(V(t)-V^*(t)) = 0$, which shows that model (3.20) holds. Therefore, every orbit in $M_{\partial}$ approaches $\mathcal{E}^0$ as $t\to\infty$, and $\mathcal{E}^0$ is acyclic for $\widehat{Q}$ in $\partial \mathbb{Y}_0$. By the acyclicity theorem on uniform persistence for maps (see [27, Theorem 3.1.1]), it follows that $\widehat{Q}: \mathbb{Y}\to\mathbb{Y}$ is uniformly persistent with respect to $(\mathbb{Y}_0, \partial \mathbb{Y}_0)$; namely, there exists some constant $c > 0$ such that any solution $u(t, \phi) = (S(t), V(t), E(t), I(t))$ of model (3.18) with $\phi\in \mathbb{Y}_0$ satisfies $\liminf_{t\to\infty}E(t)\ge c$ and $\liminf_{t\to\infty}I(t)\ge c$. Furthermore, by [27, Theorem 1.3.6], it follows that $\widehat{Q}$ has a fixed point $\hat{u}(0) = (\hat{S}(0), \hat{V}(0), \hat{E}(0), \hat{I}(0))\in \mathbb{Y}_0$. By the first equation of model (3.18), $\hat{S}(t) = e^{-\int_0^tb(s_1)ds_1}\left[\hat{S}(0)+ \int_0^te^{\int_0^{s_2}b(s_1)ds_1}a(s_2)ds_2\right],$ where $a(t) = \Lambda+\theta V(t)\ge \Lambda > 0$ and $b(t) = \beta I(t)+(\sigma(t)+\mu)$, and hence $\hat{S}(t) > 0$ for all $t > 0$. By the second equation of model (3.18), $\hat{V}(t) = e^{-\int_0^td(s_1)ds_1}\left[\hat{V}(0)+ \int_0^te^{\int_0^{s_2}d(s_1)ds_1}g(s_2)ds_2\right],$ where $g(t) = \sigma(t)S(t) > 0$ and $d(t) = {\epsilon} \beta I+\theta+\mu$. Thus, $\hat{V}(t) > 0$ for all $t > 0$. Additionally, $\hat{E}(0) > 0, \ \hat{I}_I(0) > 0$. By [37, Theorem 4.1.1] as generalized to nonautonomous systems, the irreducibility of the cooperative matrix

implies that $(\hat{E}(t), \hat{I}(t))\gg 0, \ \forall \ t > 0.$ We show that $(\hat{S}(t), \hat{V}(t), \hat{E}(t), \hat{I}(t))\gg 0, \ \forall \ t > 0$ which gives us is a positive $T$-periodic solution of the system. It completes the proof.

4.   Case studies

To illustrate the usage of the proposed model (2.1) in the evaluation of the long-term impact of vaccination, we perform a case study for COVID-19 epidemics, which is to show that (1) the model is appropriate that can be well fitted to multiple waves of COVID data and (2) this conceptional modeling approach can be useful for investigating the effects of vaccinations on this severe and long-lasting pandemic.

We now apply our model to study the COVID-19 epidemics in four locations, including Hong Kong (SAR) China, Singapore, Japan, and South Korea. We use the COVID-19 datasets published by the World Health Organization (WHO) and other sources ^[38,39] for the daily confirmed cases and daily vaccination data (fully vaccinated and third-dose vaccination) in each location. We convert daily cases to weekly data (since daily data includes weekday effects which we do not model). We assume a constant reporting ratio $p$, i.e., only $p$ proportion infections are confirmed as cases (later we estimate $p$ and the estimates fall in [0.3, 0.5] which is reasonable). Vaccination data are typically in the form per capita, namely the proportion of the population vaccinated, which cannot be directly incorporated into the model. We need the proportion of susceptible that are vaccinated daily. Susceptible individuals are among the group of unvaccinated. Given the daily vaccinated, we can estimate the proportion of the population that are unvaccinated. We convert vaccination (per capita) data to vaccination per unvaccinated ^[3,17,40]. Similarly, we convert vaccination daily (per capita) data to vaccination proportion per fully vaccinated, and move the proportion from $V$ class to $R$ class.

Following the previous works ^[3,4], we set the base parameter values as $\alpha = 0.5$ per day, $\gamma = 0.3$ per day, $\xi = 0.03267$ per day, $\omega = 0.0006658$ per day, $\kappa = 0.07917$ per day, $m = 0.004167$ per day, $\mu = 0.00003424$ per day, $\sigma(t) = 0.3\%$ per day, $\theta = 365$ per day, $\epsilon = 0.1$, $\delta = 182.5$ per day, and $\Lambda = \mu N$ where $N$ is the total population size of a location, where the references of these base parameter values are provided in Table 1. In data fitting, we use actual daily reported proportion of population received the second dose to fit $\sigma(t)$.

Additionally, due to the immune evasion of the Omicron variant, we assume $\zeta$ proportion of recovered and $\zeta$ proportion of vaccinated losing immunity protection and joining a susceptible pool, i.e., $V\rightarrow (1-\zeta)V$, $R\rightarrow (1-\zeta)R$ and $S\rightarrow S+\zeta(V+R)$, when the Omicron variant evaded and dominated in a location. We compare four timings of this transition for each location: December 31, 2021, January 12, 2022, January 24, 2022, and February 5, 2022, for Hong Kong and South Korea, and November 24, 2021, December 6, 2021, December 18, 2021, and December 31, 2021, for Singapore and Japan to reflect the observation that the Omicron wave took off early in Singapore and Japan. We estimate $\zeta$ and $\beta$. We assume that $\beta$ is time-varying and modeled as an exponential cubic spline function with $n_{\beta}$ nodes uniformly distributed over the entire period of the study. We assume $\zeta$ in the range $[0.3, 0.6]$. Since the study period (January 23, 2020 – May 9, 2022) is relatively short, the population size $N$ at each location is roughly constant and hence in the data fitting, we set $\Lambda = \mu = 0$.

By employing the method of iterated filtering, we use our model to fit the multiple waves in each location in terms of weekly cases starting on January 23 2021. Our simulation is implemented with an R software package named partially observed Markov process (POMP) using maximum-likelihood-based iterated filtering technique ^[41]. A nice feature of our proposed model (2.1) is that it allows time-varying transmission rate, $\beta(t)$, which was set as an exponential cubic spline ^{[42,43,44,45,46,47]} to account for the simultaneous impact of all of the all-possible interventions. For more detailed information regarding the model fitting procedure, we refer the readers to Appendix A for an outline of the model fitting procedure, Appendix B for a pseudo code, and ^[43,48] for the theoretical basis and technique details of the general methodology and numerical implementation via examples.

Our model fitting is reasonably well, and the result is displayed in Figure 2. In top half of each panel, the green and blue curves show the daily data of fully vaccinated (second dose) coverage and booster (third dose) coverage. The brown curve shows the proportion of population that are temporally immunized via infection or vaccination. The drop in the brown curve shows the immune evasion, i.e., a proportion of immunized lose protection (moving to $S$) due to the immune evasion ability of Omicron variant. In the bottom half, the red circles show the observed weekly cases, and the black curve (and gray region) shows the median (and 95% range) of $1,000$ model simulation. The blue curve with cross shows the estimated transmission rate. We used $n_{\beta} = 19$ notes in the cubic spline and we fitted 120 weeks of data. After May 9, 2022, we forecast the trend of COVID-19 till the end of the year. We assume the $\beta(t)$ will stable at the maximum value before May 9, 2022, after a transition, till the end of the year, while the second-dose coverage will reach 92% and the third-dose vaccination coverage will increase by 14% at the current level by the end of the year (2022). Our model framework sets a baseline model for the investigation of the long term trend.

In what follows, our investigation will be focused on the effects of vaccination against COVID-19 pandemic. We assume that the transmission rate $\beta(t)$ is kept at the constant level after May 9, 2022, and its value is taken to be the estimated value of $\beta(t)$ on that date (which is obtained from the data fitting). Before presenting the vaccination rate $\sigma(t)$, we need to introduce an auxiliary function. Let $f(t) = \dfrac{\sigma_{max}}{1+e^{2(t-0.4T)}}$ for $0\le t\le T$ where $\sigma_{max}$ is the maximal value of vaccination rate and $T$ is the vaccination period. It is apparent that $f(t)$ is a monotonically increasing function.

Let $0 < dt\ll T$ be given. We set $\sigma(t)$ as follows.

where $t_1 = T-dt$. The midnight blue curve in Figure 3(a) illustrates function $\sigma(t)$ when vaccination coverage reaches $C_{max} = 92\%$ by the end of $T = 6$ months, with $dt = 10^{-4}T$. In this case, $\sigma_{max}$ is required to be $0.72\%$ per day to achieve $92\%$ coverage by the end of the vaccination period. One can see from these figures that vaccination rate $\sigma(t)$ slowly increases in the beginning, then follows an exponential growth to approach its maximal value $\sigma_{max}$ until $t_1$, and finally linearly decay back to $f(0)$ by the end of the period $T$. The red curve in Figure 3(a) plots the respective vaccination coverage as a function of time, which is a $T$-periodic increasing function and reaches its maximal value $C_{max}$ at $T$. Figure 3(b) displays how $\sigma_{max}$ is shaped by the period $T$ with varied levels of vaccination coverage $C_{max}$. It shows that (a) when $C_{max}$ is fixed, $\sigma_{max}$ is a decreasing function of period $T$; (b) when the value of $T$ is fixed, $\sigma_{max}$ is an increasing function of $C_{max}$. This indicates that (i) to achieve a certain level of vaccination coverage by the end of the period, the longer the vaccination period, the lower the maximal vaccination rate; (ii) on the other hand, if the vaccination period is kept constant, the higher the vaccination coverage, the more demanding requirement for the vaccination rate per day. For instance, if the final vaccination coverage is $60\%$ (i.e., $C_{max} = 60\%$), $\sigma_{max} = 0.73\%$, $0.47\%$, $0.24\%$ per day when $T = 4, 6,$ and $12$ months, respectively. whereas if vaccination coverage is $92\%$ (i.e., $C_{max} = 92\%$), $\sigma_{max} = 1.10\%$, $0.73\%$, $0.37\%$ per day when $T = 4, 6,$ and $12$ months, respectively.

Figure 4 illustrated the dynamics of model (2.1). Particularly, it shows that when $\mathcal{R}_0 < 1$, the disease dies out; when $\mathcal{R}_0 > 1$, the disease persists. This verifies our analytical results (Theorems 3.2 and 3.2) by numerical simulation.

To study the impact of vaccinations on the prevention and control of the disease, we compute the basic reproduction number $\mathcal{R}_0$ for these four locations as the vaccination period $T$ increases. The value of $\mathcal{R}_0$ is numerically evaluated by using part 2 of Lemma 3.1. The result is plotted in Figure 5. For the displayed curves in each panel, the vaccination coverage is $60\%, 80\%$ and $92\%$ by the end of the vaccination period, respectively, from top to bottom. It shows that $\mathcal{R}_0$ is an increasing function of $T$. This indicates that the longer the vaccination period, the higher risk of infection we may have to expect. Furthermore, there appears to be a critical value of vaccination period $T$, denoted as $T^c$, such that $\mathcal{R}_0 < 1, \mathcal{R}_0 = 1$, and $\mathcal{R}_0 > 1$ are equivalent to $T < T^c, T = T^c$, and $T < T^c$, respectively. In particular, our result predicts that $T^c = 4.1$ (resp. $T^c = 5.1$, $T^c = 5.8$) months for Hong Kong when maximal vaccination coverage $C_{max}$ can achieve $60\%$ (resp. $80\%$, $92\%$). This indicates that if vaccination coverage is $60\%$, the optimal vaccination period for Hong Kong is expected to be about $4.1$ months, which indicates that if vaccination coverage will reach $60\%$ by the end of the vaccination period, the time between subsequent vaccinations should not be longer than $4.2$ months for disease control in Hong Kong. Whereas if vaccination coverage is higher, then the optimal vaccination period may be longer. For instance, if $C_{max}$ is $80\%$ or $90\%$, the corresponding vaccination period $T^c$ would expect to be $5.1$ or $5.8$ months. For Japan, $T^c = 5.3$ (resp. $T^c = 6.7$, $T^c = 7.5$) months when $C_{max}$ can achieve $60\%$ (resp. $80\%$, $92\%$). In contrast, the optimal vaccination period $T^c$ may have to be shortened for Singapore and South Korea. Especially, $T^c = 3.1, 4.0$ and $4.4$ months for Singapore and $T^c = 2.6, 3.1$ and $3.5$ months for South Korea, when $C_{max}$ is $60\%$, $80\%$ and $92\%$, respectively. This indicates that the fourth-dose vaccination is very likely to be needed, particularly for the high-risk groups, this September (2022) in South Korea, October in Singapore and November in Hong Kong; whereas for Japan, the fourth dose may wait until early of next year (2023) if vaccination coverage can reach $92\%$ by the end of vaccination period.

5.   Discussion and conclusions

The transmission and spread of COVID-19 involve complex biological and socioeconomic processes. The underlying mechanisms for COVID-19 outbreaks vary from place to place. In this work, we have attempted to use mathematical modeling and data fitting to investigate the multiple COVID-19 waves in four different locations (Hong Kong, Singapore, Japan and South Korea) in the East Asia and Southeast Asia, with an aim to better understand the impact of vaccinations on this severe and long-lasting epidemic of COVID-19.

If we assume that the basic reproduction number $\mathcal{R}_0$ will stable at the maximum value before May 9, 2022 after a transition, till the end of the year, while the second-dose coverage will reach 92% and the third-dose vaccination coverage will increase by 14% at the current level by the end of the year (2022), we can forecast the trend of the COVID-19 in these four locations. The trends are different across the four locations. Hong Kong will reach a low level of daily cases in summer and expect a bounce back at the end of the year. Japan will reach a low level at the end of the year, Singapore and South Korea will not reach a low level and see a bounce back at the end of the year. This indicates that a fourth dose among the high-risk group is probably needed by the end of the year. On the other hand, we numerically compute the basic reproduction number $\mathcal{R}_0$, and our result shows that the longer of the vaccination period or the lower of the vaccination coverage, the higher risk of infection. More specifically, our findings indicate that the fourth-dose vaccination is very likely to be needed for the high-risk groups this September (of 2022) in South Korea, October in Singapore and November in Hong Kong; for Japan, the fourth dose may wait until early of next year (2023) provided that vaccination coverage can reach $92\%$ by the end of the vaccination period.

There are several limitations in our work. First, as it has been suggested by the clinical and epidemiological evidence from COVID-19 literature, the asymptomatic transmission may play an important role in the SARS-CoV-2 transmission. Since we modeled aggregated cases and the data for asymptomatic cases are currently not available, we synthesize asymptomatic and symptomatic transmission into an overall transmission route. For our present study, this simplification allows us to make the model analytically more trackable. We plan to investigate asymptomatic transmission and the related problems in our future study. Secondly, our mathematical epidemic model is a non-autonomous system, for which there is no general theory to define or compute the basic reproduction number. Thus, our analysis is focused on a special case where the model is a periodic system. Thirdly, more compartments could be added to the model for a representation of the different population sets and environmental components. For example, it would be interesting to introduce an age structure into the model to represent the fact that different age groups exhibit different disease risks, with the elderly being the most vulnerable. Fourthly, it may be more realistic to consider a multi-strain model to account for the new variants of SARS-CoV-2, particularly the Omicron variant that is contributing to a surge in cases throughout the world at present. Additionally, we assume that the transmission rate $\beta$ is kept constant to forecast the trend of COVID-19 in the long term, which however is not quite realistic since disease transmission and spread are spatiotemporally heterogeneous in reality. Such complications haven't been explored in the current work, which will provide interesting topics for future research.

In conclusion, we proposed a simple SEIR type of epidemic model to study the effects of vaccination on mitigating COVID-19 outbreaks. We fit this model to reported COVID-19 cases in four locations (i.e., Hong Kong, Singapore, Japan and South Korea) and reconstructed the basic reproduction number $\mathcal{R}_0$. We gained a qualitative idea of the long-term impact of vaccination. Our findings indicate that a fourth dose among high-risk group is likely needed by the end of the year. At the next step, we plan to associate the reconstructed $\mathcal{R}_0$ with government control measures and possible voluntary social distancing in each location.

Acknowledgments

DH acknowledges the support from the Research Grants Council of the Hong Kong Special Administrative Region, China (HKU C7123-20G).

Data availability statement

The data used to support the findings of this study are available from the corresponding author upon request.

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix

A.   Model fitting

To evaluate the long-term impact of vaccination, we fit our model (2.1) to the real COVID epidemic data in four locations: Hong Kong (SAR) China, Singapore, Japan, and South Korea. The time series of daily confirmed cases and daily deaths in each of these locations is modeled as a partially observed Markov process (POMP, also referred to as a hidden Markov process). The algorithm of iterated filtering ^[41,49] is utilized for the data fitting, implemented numerically in an R software package known as POMP via maximizing the log likelihood function.

In particular, model (2.1) has time-varying transmission rate $\beta(t)$. Following the previous studies (e.g., see ^[3,4,47] and the references therein), we define $\beta(t)$ as an exponential cubic splines: $\beta(t) = \exp(\text{cubic splines}),$ which has $n_{\beta}$ nodes evenly spaced over the entire epidemic period $T_s$ of the study. We simulate deaths weekly and fit it to the weekly reported mortality data. Let $\Delta t$ be the reporting period, and $\Delta t$ would be one week in this case. Based on the daily data, we simulate weekly deaths $D_{t+\Delta t}$ as

where $m$ is the disease induced death rate of hospitalized individuals (see Table 1), and $H(s)$ is obtained by numerically solving model (2.1) for a given value of unknown parameters. This gives us a time-series death data $\{D_1, D_2, \cdots, D_{T_s}\}$. For each week $t \; (1\le t\le T_s)$, we denote $Z_t$ to be the weekly reported deaths of that week. We assume that $Z_t$ follows a negative binomial distribution, more specifically,

Here NB represents negative binomial distribution. $\tau$ is an over-dispersion parameter which will be estimated. Basically parameter $\tau$ is a measurement of noise due to surveillance and heterogeneity among individuals.

When $\tau = 0$, the above negative binomial distribution reduces to a Poisson distribution. Let $\Theta$ denote the vector of unknown parameters. Let $D_{1:T_s}$ denote time-series data for deaths. Hence the likelihood of the week, $\ell_t(\Theta): = \ell(\Theta|D_{1:T_s}, \tau),$ will be the probability of observing $Z_t$ given $D_{1:T_s}$ and $\tau$, which is a function of $\Theta$ and can be directly calculated. The overall likelihood function is

Then the method of iterated filtering is used to estimate model parameter $\Theta$ by maximizing the log likelihood function, $\ln\Big(L(\Theta)\Big)$.

B.   Pseudo-code for modeling fitting procedure

For self completeness, a pseudo-code for modeling fitting procedure from ^[3] is included:

$(1)$ Prepare the data.

$(2)$ Set up the model and provide an initial guess for the values of model parameters to be fitted.

$(3)$ Employ pfilter of the POMP package to calculate log likelihood of model given data.

$(4)$ Apply mif function of the POMP package to obtain the maximum likelihood estimate of parameters.

$(5)$ Repeat (3) and (4) until maximum log likelihood estimation converges.

$(6)$ Use simulate function of the POMP package to perform the model simulation.

For a step-by-step instruction and hands-on examples on the methodology, we refer the readers to https://kingaa.github.io/sbied/.