Dynamics of toxoplasmosis in the cat's population with an exposed stage and a time delay

1.   Introduction

The Internet of Things (IoT), as an "interconnected network of things", involves a variety of different businesses, often with different priorities. For security surveillance, facial data is more important than human data; for smart homes, infrared sensing data is more important than temperature and humidity; and the differentiation of different data by importance in the process of collecting data is an issue that must be considered in wireless sensor networks. The MAC protocol defines how the node occupies the wireless channel to send data during data collection and enables differentiated priority services by setting the MAC. Polling control systems, as a reservation-based scheduling control model, are widely used in wireless sensor networks for their fairness, non-competition, reliability, efficiency and high quality of service ^[1,2,3]. Depending on the service strategy, they are usually classified as gated, exhaustive and limited services. The gated service system is where the server services the information groupings reached before accessing the site; the exhaustive service system is where the server services all the information groupings in the site; and the limited services system is where the server services up to K information groupings. Each of the three service strategies has its own advantages, with limited services fairness being the best, exhaustive service latency being the lowest and gated service being moderate. In recent years, with the rapid development of the Internet of Things, the need for differentiated priority and high quality of multiple services has become increasingly important. The traditional one-level polling control system is unable to differentiate priorities ^[4,5]. Therefore, many researchers have improved it, breaking away from the idea of a single polling control strategy and proposing a hybrid service strategy, which allows the system to be more optimized, more flexible and more targeted.

Lv et al. ^[6] divided each service cycle into a polling period and a contention period. Polling is performed according to the latest access time in the polling period, and backoff counts are assigned to each site in each contention period, thus reducing the waste of resources caused by polling idle sites and conflicts, and reducing latency. The literature ^[7,8] set the polling priority by packets and energy packets to adjust the packet delivery rate. Siddiqui et al. ^[9] used adaptive and dynamic polling MAC to integrate two cross-layer schemes: dynamic channel polling and packet concatenation, which enables synchronization between the management source and receiver and greatly improves the packet delivery rate. Yang et al. ^[10] investigated a two-level hybrid polling control strategy based on a combination of discrete-time symmetric and asymmetric, with an exhaustive service policy for the central site and an asymmetric gated service for the ordinary sites. The system, although well differentiated in terms of priority, failed to guarantee fairness for the ordinary sites. Han et al. ^[11] introduced a multi-priority mechanism and reduced the length of the time slot occupied by the collision of information packets to meet the service quality requirements of different priority services and improve the system throughput rate, effectively alleviating the channel congestion phenomenon and improving the system performance of wireless Ad Hoc networks. Yang et al. ^[12] combined polling order with access policies including gated and exhaustive service and proposed a new priority-based parallel scheduling polling MAC protocol in WSN to implement a priority-based scheme while reducing overhead time through parallel scheduling. Mercian A et al. ^[13] introduced two gated traffic control protocols to adapt the service policy. Ding et al. ^[14] proposed a multi-level priority polling MAC protocol for the practical requirements of multi-priority transmission control for multiple users in tactical data chain systems, and controls the arrival rate of user messages at all levels by means of a priority weight matrix P. The demand for multi-priority transmission control of each user in the system is satisfied, and the feature of diversified control functions of the polling MAC protocol is realized. Guan et al. ^[15] proposed a two-level polling control system relying on the site state based on a two-level polling model for hybrid services, which satisfies both differentiated priorities and avoids idle queries. Jiang et al. ^[16] analyzed the strategic services of customers of different priority levels under the join or reject dilemma at two information levels. Mu et al. ^[17] proposed a two-level polling system with multi-level gated services, which is controlled using the number of levels of gated services and provides for the development needs of service diversity and elastic services in resource allocation.

In the above polling control systems, discrete-time analysis is used to analyze the polling system, which is computationally complex and difficult. Therefore, in order to reduce the computational difficulty and simplify the solution process, the Laplace transform is used to analyze the first-order and second-order characteristics. Mao et al. ^[18] proposed a continuous-time two-level exhaustive polling access MAC protocol for priority services and real-time requirements in the IoT, with an exhaustive service policy for both priority and normal users. Yang et al. ^[19] proposed a two-level polling service model with differentiated priorities. In this model, gated service is used for low priority sites and exhaustive service is used for high priority sites. In the case of high priority to low priority, the transfer service is processed in parallel with the transfer query to reduce the time spent by the server during the query transition and improve the efficiency of the polling system. This guarantees the quality of service for the low priority sites and provides high-quality service for the high priority sites. In order to ensure the fairness of ordinary sites, we propose a two-level priority polling system controlled by an exhaustive-limited services policy, which optimizes the polling system scheduling mechanism to accommodate the service quality requirements of services of different priority levels in the system under certain resources, providing guaranteed services to high priority central sites and more fair limited services to low priority ordinary sites.

In the above study, the system properties were solved using traditional mathematical calculations and iterative simulations were performed. This method is less efficient, more difficult to calculate and more time-consuming. With the rapid development of society and economy, the scale of the network is gradually expanding, which puts higher requirements on the deployment and maintenance of the network. Traditional methods no longer meet the real-time deployment requirements.

Nowadays, with the increasing volume of data and rising complexity of data access. Researchers work to integrate machine learning and artificial intelligence algorithms more closely with computer networks. Machine learning is the process of using computer programming to learn from historical data and make predictions about new data. Gupta et al. ^[20] discussed the most advanced methods based on federated learning models for game theory applications in wireless communication. Research on maximization of benefits, authentication, privacy management, trust management and threat detection are discussed. Boobalan et al. ^[21] proposed the combination of federated learning and industrial internet for resource, privacy and data management. Guarino et al. ^[22] investigated the capability of state-of-art single-modal and multimodal Deep Learning-based classifiers in telling the specific app, the activity performed by the user, or both. On this basis, a novel multimodal solution for early traffic classification is newly proposed, using contextual inputs as additional modes. It is demonstrated that the training time is shorter using a variant where the contextual input does not depend on the payload information. Liu et al. ^[23] proposed AR-GAIL, an adaptive routing protocol based on generative adversarial imitation learning, which can select the route with the lowest end-to-end delay according to the network conditions. It can be seen that machine learning has been widely applied in computer networks. Thus, we use neural networks to predict the two-level polling control system.

The methods such as support vector machine (SVM) ^[24,25,26], linear regression ^[27,28,29], deep neural networks (DNN) ^[30,31,32], boosting ^[33], bagging ^[34], recurrent neural network (RNN) ^[35,36,37], long short-term memory (LSTM) ^[38,39,40], artificial neural network (ANN) ^[41,42,43] and back propagation (BP) neural networks ^[44,45,46] are commonly used in predictive analysis to make use of historical data to make predictions on new data. LSTM, as a special type of RNN network, is able to transfer the characteristics of the previous node to the current node, has better performance advantages and is widely used in predictive analysis. Hou et al. ^[47] constructed a deep convolutional neural network with long and short-term memory (CNN-LSTM) in order to extract the spatio-temporal characteristics of temperature and the correlation between meteorological elements, and used kriging interpolation to spatially visualize the simulated and predicted temperatures. It is demonstrated that CNN-LSTM has higher temperature simulation, prediction accuracy and generalization ability. Zhang et al. ^[48] improved the quality of service of IoT by analyzing the large amount of data generated by industrial IoT and designing LSTM network models to predict the operation of devices. Shu et al. ^[49] used LSTM to learn individual-level actions and then integrated individual-level actions into group activities, proposing a LSTM-in-LSTM model that also enables group activity recognition by modelling person-level actions and group-level activities. Shu et al. ^[50] predicted data transmission in wireless sensing networks through a combination of LMS filters and LSTM, thus reducing energy consumption.

Media access control protocols for wireless sensor networks mainly consist of traditional competitive and non-competitive protocols. The two types of protocols correspond to the distributed function DCF and the point coordinated function PCF, respectively. DCF provides distributed contention-based channel access for asynchronous data transmission through a carrier listening multiple access/conflict avoidance (CSMA/CA) control strategy; PCF provides contention-free service for real-time services through a polling control strategy. In IEEE802.11, the PCF protocol uses the limited K = 1 polling control method, but this method is not flexible for the case of load burst and load with priority. Therefore, in order to solve the shortcomings of PCF in wireless sensor networks and the problems of multi-service transmission and improving fairness in the Internet of Things, a continuous-time exhaustive-limited (K = 2) two-level polling control system is proposed. First, a mathematical model is developed using probabilistic generating functions and Markov chains to derive the first-order and second-order characteristics. Second, simulation experiments are carried out using MATLAB. Third, performance prediction using LSTM neural network with attention mechanism is performed to verify the feasibility of the method.

2.   System model

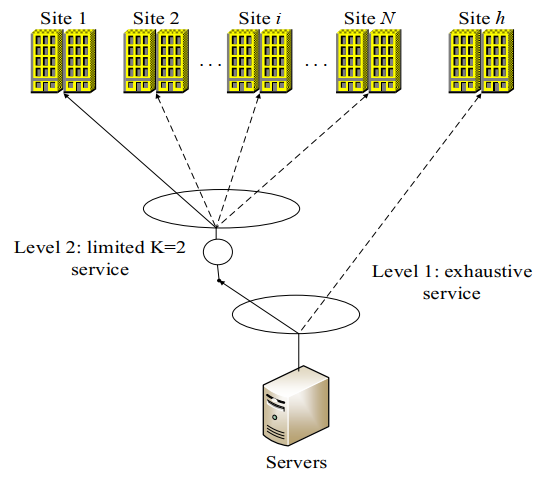
As shown in Figure 1, the two-level polling control system consists of a relay node (server) and N + 1 collection nodes (sites), where the first level is a central site and the second level is N ordinary sites. The first level central site uses exhaustive service policy to serve users, denoted by the subscript h, while the second level ordinary site uses limited K = 2 service policy to serve low priority service users, denoted by the serial number $i(i = 1, 2, ..., N)$. Usually the sensor nodes in a wireless sensor network collect the required physical information depending on their functionality, and then the relay nodes receive the information from each node according to a pre-agreed MAC protocol, and finally send it to the end nodes. The system service principle: The server gives priority to the central site h in accordance with the exhaustive service strategy, until all the information in the central site is sent in groups, and then transfers to the low-priority i common site for service according to the limited K = 2 strategy. When the service is over, the server transfers to the central site again, and then starts to serve the i + 1 common site after the service is over. Server from the central site to the common site conversion, piggyback query common site, improve system efficiency. The order of enquiry services is shown in Figure 2. The mathematical method is expressed as $h \to 1 \to h \to 2 \to... \to i \to h \to i + 1 \to... \to N \to h \to 1$. Average queue length, average delay and average cycle time are commonly used to measure the performance of a system. Under the same conditions, the smaller the average queue length and average delay, the better the system performance, the faster it runs and the more efficient it is.

2.1.   System working conditions

It is assumed that the data transfer between the sites is normal and that the server's memory does not overflow with data, etc. Based on the system model, combined with the control mechanism and transmission characteristics of the polling system, the following system operating conditions are defined:

(1) The arrival process of message groupings into each site within any time slot is to satisfy a Poisson distribution independent of each other, with the arrival rate of the ordinary site being ${\lambda _i}$, and the arrival rate of the central site being ${\lambda _h}$.

(2) The time at which the server transmits the grouping of messages in the common site i of the service satisfies a mutually independent, identically distributed probability distribution. The Laplace transform (LST) of the random variable is ${B_i}(s)$, the mean is $\beta = - {B'}(0)$ and the second order origin moment is ${v}_{\beta } = {B}^{"}(0)$. The LST of the packet from service central site h is ${B_h}(s)$, the mean is ${\beta _h} = - B_h'(0)$ and the second order origin moment is ${v}_{h} = {B}_{h}^{"}(0)$.

(3) The time taken by the server to send data from the ordinary site i to the time taken to move to the central site to send data satisfies a mutually independent and identically distributed probability distribution. The LST of its random variable is ${R_i}(s)$, the mean is $\gamma = - R'(0)$ and the second-order origin moment is ${v}_{\gamma } = {R}_{i}^{"}(0)$.

(4) The sites in the service system have a large capacity and do not suffer from packet loss.

(5) The server serves groups of information in the site on a first-come, first-served (FCFS) basis.

2.2.   Definition of variables

In order to analyze the system model, the following random variables are defined, as shown in Table 1.

Set the server to poll common site $i(i = 1, 2, ..., N)$ at time ${t_n}$. The number of message packets waiting to be sent in common site i is ${\xi _i}(n)$, and the number of message packets defining the central site h is ${\xi _h}(n)$. The random variable for the whole system is $\left\{ {{\xi _1}(n), {\xi _2}(n), ..., {\xi _i}(n), ...., {\xi _N}(n), {\xi _h}(n)} \right\}$. The server provides a transfer service for the common site i according to limited K = 2 service policy. The server ends service to site i after a transfer time ${u_i}$ to start the service central site, and the number of message packets entering site j during time ${u_i}$ is ${\mu _j}({u_i})$. At time ${t_{n*}}$, the server queries the central site for the number of message groupings and the random variable of the system is $\left\{ {{\xi _1}(n*), {\xi _2}(n*), ..., {\xi _i}(n*), ...., {\xi _N}(n*), {\xi _h}(n*)} \right\}$. At time ${t_{n + 1}}$, after the central site has finished serving, the server moves again to the common site i + 1 for service, where the state variable is $\left\{ {{\xi _1}(n + 1), {\xi _2}(n + 1), ..., {\xi _i}(n + 1), ...., {\xi _N}(n + 1), {\xi _h}(n + 1)} \right\}$.

According to the above analysis, the relationship between the three moments is ${t_n}$ < ${t_{n*}}$ < ${t_{n + 1}}$. The state of the model at the moment ${t_{n + 1}}$ does not depend on the state at the moment ${t_n}$ and is only related to the state at the moment ${t_{n*}}$. That is, this system state variable has the same essential properties as the state variable in the basic model of polling system. Under stable conditions of the system, this Markov process is homogeneous, aperiodic, irreducible and ergodic and has a unique steady-state distribution ^[51,52]. After analysis, the system is an N-dimensional Markov chain. Assume that when the system is stable, the server state is (a, b), with probability ${p_{ab}}$, a and b can take the values 0, 1; and since the system is a single-server system, it cannot take a value of 1 at the same time. Here, a value of 1 for a indicates that the server is serving the central site and a value of 0 for a indicates that the server is serving an ordinary site or not performing service; conversely, a value of 0 for b indicates that the server services or does not service the central site, and a value of 1 for b indicates that the server services the common site. That is, when the state (0, 1) becomes (1, 0), it means that the server has changed from servicing the normal site to the service central site. If when the state is (1, 0) becomes (0, 1) it means that the server changes from serving the service central site to serving the ordinary site. The state transition process is shown in Figure 3.

2.3.   Probability generating functions

According to the above operating conditions and variable definitions of the system, the system reaches stability under condition $\sum {_{i = 1}^N{\lambda _i}\beta } + {\lambda _h}{\beta _h} = \sum {_{i = 1}^N{\rho _i} + } {\rho _h} < 1$ ^[53]. Define the probability generating function ${G_i}({z_1}, {z_2}, ..., {z_N}, {z_h})$ of the system state variables at time ${t_n}$, expressed in Eq (1).

Similarly define the probability generating function ${G_i}_h({z_1}, {z_2}, ..., {z_N}, {z_h})$ of the state variables of the system at time $t_n^*$, expressed in Eq (2).

According to $t_n^*$ and ${t_{n + 1}}$ moments, the server according to the corresponding service policy service central site and ordinary site i + 1, resulting in the relationship of Eq (3).

The server polls the service central site at time $t_n^*$. The probability generating function of the system state variable is represented by Eq (4).

The state variables of the system at time ${t_{n + 1}}$ is represented by Eq (5).

where, ${H_h}(s) = B(s + {\lambda _h}(1 - {H_h}(s)))$.

2.4.   main notation

The notations used in the text are shown in Table 2 (arranged in the order in which they appear in the text).

3.   System characterization

3.1.   Average queue length

Average queue length: At time ${t_n}$, the server starts transmitting data to site i. The average number of packets stored in the memory of site j is ${g_i}(j)$, then:

The above Eqs (4)–(6) gives Eq (7), which represents the average queue length at the central site

where, ${\rho _h} = {\lambda _h}{\beta _h}, {\rho _i} = {\lambda _i}{\beta _i}$.

3.2.   Average cycle

The query period of the system is the statistical average of the time taken by the server to complete a service for the N + 1 sites in the system according to the corresponding service policy, i.e. the average time taken by the server to query the same site twice. Therefore, the query period $\theta {\text{ }}$ of a continuous-time two-level polling system is shown in Eq (8).

3.3.   System throughput

System throughput is expressed as the number of packets of information that can be served by that system per unit of time, as shown in Eq (9).

3.4.   Second-order characteristics

Equations (10) and (11) represent the second order partial derivative of the system state probability generating function.

The expressions (4) and (5) of the probability generating function can be substituted to calculate the second-order partial derivatives to obtain a system of second-order characteristic parametric equations, and after simplification, the second-order characteristic quantities ${g_i}(i)$ and ${g_{ih}}(h, h)$ of the probability distribution of the length of the information group queue are obtained, as shown in Eqs (12) and (13).

${g_i}(i)$ denotes the average queue length at the common site.

3.5.   Average delay

In this paper, we study a continuous-time two-level polling control system, and by considering the literature ^[54], we can derive the average waiting delay in this polling control system for service according to the exhaustive service policy and the limited service policy as shown in Eqs (14) and (15).

In a two-level polling system, the time between when a message packet enters the site memory and when it is sent out is the waiting delay of the message packet. $E({w_i})$ is the average delay at the common site and $E({w_h})$ is the average delay at the central site. The average delay can be derived from the expressions calculated above.

Equation (16) is the average delay for a common site.

Equation (17) is the average delay at the central site.

The specific time delay can be found by substituting ${g_{ih}}(h, h)$ and ${g_{ih}}(h)$ in the above.

3.6.   Simulation experiments and analysis

Based on the above analysis and calculations, it can be seen that the limited model used in this paper is different in complexity from the other two models. Models on limited services require second-order derivation when solving for theoretical values of performance metrics such as average queue length, which makes the computation more difficult. In contrast, the exhaustive and gated services require only first-order derivation to find the length. The MATLAB2019b platform was used to carry out simulation experiments under the stable conditions of System $\sum {_{i = 1}^N} {\lambda _i}{\beta _i} + {\lambda _h}{\beta _h} = \sum {_{i = 1}^N{\rho _i} + {\rho _h}} < 1$ to verify the feasibility of the theoretical analysis and the reliability of the system. The simulation experiment generates a Poisson distributed random sequence satisfying the arrival rates of ${\lambda _i}$ and ${\lambda _h}$ for the common and central sites respectively using the exprnd () function to simulate the number of message packets arriving per unit time at each site. The greater the arrival rate, the greater the number of packets of information that arrive. The more data that is queued up when keeping the channel transmission rate and processing capacity consistent. Service time and conversion time are used as important indicators of polling efficiency. Typically, the service time variable is used to record the cumulative time spent processing data in the system. For each unit of data reduction, the service time variable accumulates one service time. Use ${\beta _i}$ and ${\beta _h}$ to denote the service time between the common site and the central site, with larger ${\beta _i}$ and ${\beta _h}$ indicating weaker data processing capacity and lower throughput, and vice versa. For the transition time ${\gamma _i}$, the larger the ${\gamma _i}$, the longer the system takes to poll a cycle and the less efficient it is; the smaller the ${\gamma _i}$, the shorter the system takes to poll a cycle and the more efficient it is. In order to improve the accuracy of the model, the simulation experiment was set up for 100,000 Monte Carlo statistics, that is, a cycle count of 100,000. The simulation experiments were carried out according to the flow chart shown in Figure 4. During the simulation, all were in the ideal state, that is, all message packets were sent successfully with a packet loss and retransmission rate of 0.

3.6.1.   Performance analysis

In the experiment, the arrival rate of information packets and the number of network stations were changed to analyze the changes in the average queue length, average delay, average cycle time and throughput of the two-level polling system. Figures 5 and 6 shows the variation pattern of average queue length and delay with load. The graph shows that the number of fixed network sites, service time and query time for both common sites and central sites, the theoretical values basically match the simulated values, the error is within a small range and the length and delay are positively correlated with the load, proving that the system is feasible. The two graphs are analyzed horizontally, the length and delay of the common site change in tandem, the longer the length, the greater the corresponding time delay. In the longitudinal view, the length and time delay of the common site are much larger than that of the central site. As the load increases, the distinction becomes increasingly clear. It shows that the model is able to differentiate between different priority services with significant results. From the control mechanism, it is clear that the two-level polling control model divides the N + 1 sites into N normal sites and one central site. When polling all sites, the central site is given N opportunities to use the exhaustive service policy service, and the normal site has only limited service. Thus, according to the number of services, the length and time delay of the common site are greater than that of the central site. Therefore, multiple times service central site, to ensure the quality of service of the central site, to meet the demand of real-time central site within the system.

The relationship between average cycle time and arrival rate is shown in Figure 7. The relationship between arrival rate and cycle time is explored by varying the number of sites. Regardless of the number of sites, the average cycle time of the system increases as the arrival rate increases. When the arrival rate and number of sites are small, the system takes less time to poll for a week, allowing access to all sites to be completed quickly, with better stability and faster cycle response characteristics. From the up and down distribution of the four curves, the four curves did not cross when the grouping of messages kept increasing. The period of the system was vertically distributed with the number of stations, i.e. the number of stations was also an important factor affecting the period, and when the arrival rate was certain, the larger the number of stations, the longer the period. Overall, the error between the theoretical and simulated values is small, indicating that the system is stable.

Figure 8 depicts the variation pattern between the system throughput and the arrival rate of grouped messages at a site. As shown in the figure, system throughput increases linearly with arrival rate. On the other hand, for increasing the arrival rate, the average delay also increases accordingly, so the delay performance should be used as a constraint while considering how to improve the throughput.

3.6.2.   Comparative analysis

To further analyze the performance of a continuous-time exhaustive-limited (K = 2) two-level polling control system. The model in this paper is compared with the literature ^[54] one-level limited K = 2 model, the literature ^[55] one-level limited K = 1 model and the literature ^[56] one-level exhaustive model, as shown in Figures 9 and 10. The three models are set to have the same network size, that is, the same number of total station points. Looking at Figures 9 and 10, the relationship between length and delay can be seen in (a): one-level limited K = 1 > one-level limited K = 2 > two-level common site > two-level central site; The relationship between length and delay from (b): one-level exhaustive service > common site > central site. Therefore, with the same parameters, the average length and delay of the common site of this paper's model are smaller than those of the one-level model, which not only differentiates priorities, but also reduces the length and delay of the common site and improves the quality of service, indicating that the central site affects the performance of the two-level polling control system.

Figures 11 and 12 explore the variation of this paper's model from the exhaustive-limited K = 1 model and the gated-exhaustive model. Keeping the wireless terminal N and service time the same, the length and latency of the exhaustive-limited K = 1 are greater than the exhaustive-limited K = 2 model for both the normal and central sites, indicating that increasing the qualified K value optimizes system performance. Looking at the gated- exhaustive service model, although the performance of the common site is better than the model in this paper, for the central site, gated-exhaustive > exhaustive-limited K = 1 > exhaustive-limited K = 2, indicating that the model in this paper has a higher priority.

Further analyzing the average length, the three two-level models basically overlap when the business volume is low (i.e., the arrival rate is low), at which point the desired requirements can be met regardless of which model is chosen. However, as the volume of service increases, the gap between the models slowly increases, at which point the ordinary site length of the gated- exhaustive service model and the exhaustive-limited K = 2 service model are essentially the same, with smaller enhancements. In contrast, the central site of the gated- exhaustive service model grows faster (i.e., the slope becomes larger) for the length as the volume of service increases. Analyzing Figure 12 average delay, it is clear that the delay of the exhaustive-limited K = 1 service model is much larger than the other two models (i.e., the system performance is much lower than that of the other two models), and therefore the model is generally not used, regardless of whether the business volume is large or small. Exhaustive-limited K = 2 service model where performance improves with the number of information groupings per service for the limited service. Observing the gated- exhaustive service and exhaustive-limited K = 2 service models, it can be seen that the arrival rate is less than 0.008, and the difference in delay between the two common sites is small. Common sites choose to limited services, improving the fairness of the whole system. At high business volumes, there is no situation where only one of the sites is served, leaving the others waiting for a long time. Conversely, the delay at the central site, because of the use of gated service, is greater than exhaustive service at the central site from start to finish. Although the performance of the model in this paper is slightly worse than the gated- exhaustive model at the common site, the overall improvement is more at the central site. In summary, it is better to choose the exhaustive-limited K = 2 service model proposed in this paper.

4.   Performance prediction of two-level polling control system based on LSTM and attention mechanism for wireless sensor networks

With the increase in network size, dense site access and large amount of data acquisition, network deployment becomes more difficult. Therefore, a neural network is chosen to predict and analyze the performance of the system, which helps to reduce the difficulty of network deployment. In the above, a continuous-time exhaustive-limited K = 2 two-level model is proposed, the first-order and second-order characteristics are accurately resolved and simulations are carried out. Next, the performance of the system is predicted by building a LSTM +attention model to further validate the correctness and feasibility of the solution. In addition, data under known arrival rates are used to predict data under unknown arrival rates and observe the trends.

4.1.   Principle of the LSTM + attention mechanism model

For time series problems, it is difficult for traditional neural networks to make predictions on unknown data using known data, while RNN, as a kind of neural network with better processing effect on time series data, can effectively retain the information of the previous data step and continuously cycle the data. However, its performance in predicting longer sequences is often unsatisfactory, limited by the limitations of the RNN structure, with problems such as gradient disappearance, gradient explosion and long-term dependence during backpropagation calculations ^[57]. Then, as time accumulates, the residuals that need to be passed back in the network will fall exponentially, affecting the network weight update and failing to reflect the long-term memory effect of RNN. Therefore, in order to solve the above problems, a prediction model with LSTM + attention mechanism is proposed. the model of LSTM + attention mechanism is shown in Figure 13. One of the attention mechanism modules is shown in Figure 14.

At the heart of the LSTM neural network is the cell state. The LSTM differs from the RNN in that it adds a conveyor belt of information, and its branch less conveyor belt structure is designed so that the information remains largely unchanged as it passes through the entire cell. The LSTM consists of four major components: An oblivion gate, an input gate, an output gate and a memory storage unit. In this case, the forgetting, input and output gates implement the control of the cell state, selectively adding or removing information to the cell state. It works as follows:

1) Determine the missing information. The forgetting gate controls the information passed through by the Sigmoid activation function, using the input ${x_t}$ at time $t$ and the implicit layer state ${h_{t - 1}}$ at time $t - 1$ to obtain a value of ${f_t}$ between 0 and 1, where 0 indicates complete forgetting and 1 indicates complete invariance. Finally, the information in ${C_{t - 1}}$ is determined based on the value of ${f_t}$, as shown in Eq (18).

In Eq (18), $\sigma$ denotes the Sigmoid activation function, ${w_f}$ denotes the weight coefficient of ${h_{t - 1}}$ in the forgetting gate and feature extraction process, ${u_f}$ denotes the weight coefficient of ${x_t}$ in the forgetting gate and feature extraction process and ${b_f}$ denotes the forgetting gate bias value.

2) Determine the new information to be stored. First, the input gate determines the updated value; Finally, a new candidate value ${a_t}$ is created using the tanh function, as shown in Eqs (19) and (20).

In Eqs (19) and (20), ${i_t}$ denotes the value of the input gate, ${a_t}$ denotes the temporary cell state, ${w_i}$ and ${w_a}$ denote the weight coefficients of ${h_{t - 1}}$ in the input gate and feature extraction process, ${u_i}$ and ${u_a}$ denote the weight coefficients of ${x_t}$ in the input gate and feature extraction process, ${b_i}$ and ${b_a}$ denote the input gate bias values.

3) Determine the old cell state to update. Updating the old cell state is the process of updating the cell state at time $t - 1$ to the current cell state. The updated cell state is obtained using the cell state at time $t - 1$ to determine the discarded information through the forgetting gate, plus the candidate values generated through the input gate, as shown in Eq (21).

In Eq (21), ${C_t}$ denotes the cell state at the current moment and $\otimes$ denotes the vector product.

4) Determine the LSTM output value. In two steps, the output value of the cell state is determined from the activation function; the current cell state is passed through the tanh function to obtain a value between –1 and 1; finally, it is multiplied by the output value, as shown in Eqs (22) and (23).

In Eqs (22) and (23), ${O_t}$ denotes the value of the output gate, ${h_t}$ denotes the output value at the current moment, ${w_o}$ denotes the weight coefficient of ${h_{t - 1}}$ in the output gate and feature extraction process, ${u_o}$ denotes the weight coefficient of ${x_t}$ in the output gate and feature extraction process, ${b_o}$ denotes the output gate bias value.

5) Determine the output values for the entire model, as shown in Eq (24).

4.2.   Model building

Average queue length and average delay are often used as important metrics to assess system performance, with smaller average length and lower delay indicating better system performance and more efficient service. To solve the polling system performance prediction problem. First, expand the scale of the experiment to obtain the average length and time delay as the arrival rate changes; second, abstract the relationship between arrival rate and length into a time series prediction problem, that is, the average length and time delay of customers under different business volumes are constituted into a series of discrete data in chronological order; finally, build a neural network model and perform statistical analysis on the known data series to achieve effective prediction. The experimental model was completed by building the TensorFlow framework in python 3.9 environment. Root mean square error (RMSE) was used in the experiments to assess the accuracy of the predicted data and the reliability of the model, and the calculation is shown in Eq (25).

In Eq (25), N denotes the total number of data sets, ${y_t}$ denotes the true value and ${y_p}$ denotes the predicted value.

To prevent overfitting, the Dropout strategy was used, i.e. some of the neurons in the hidden layer were randomly removed at each iteration, thus avoiding overfitting to a certain extent. During the training process, the first-order moment estimation and second-order moment estimation of Adaptive moment estimation (Adam) are used to update the weights of the network for the purpose of optimizing the network. The flow of this Adam algorithm is shown in Table 3.

In order to simplify the network and improve the computational efficiency, the overall network structure is designed as one input layer, one hidden layer (the number of neurons in the hidden layer is 32), one fully connected layer, attention layer and one output layer, and the network structure is shown in Figure 15.

4.3.   Data preparation and problem description

The performance of polling systems is usually measured using first-order and second-order characteristics. One of the first-order characteristics is the average queue length and the second-order characteristic is the average delay. In communication, the system service volume is complex, and different service volumes correspond to different length and delay, and data sets with different length and delays can be obtained by varying the amount of service volume. As there are no readily available data sets for research analysis. Therefore, based on the mathematical analysis in 3.1–3.5 above, MATLAB was used to simulate the data set at different arrival rates. In practice, changes in arrival rates also affect changes in load, and the system load is denoted as $\rho = \lambda \beta$. When the service rate is certain, the system load capacity is limited, as shown by the length increasing with the load.

In order to meet the actual communication effect, under the condition of system stability, the arrival rate is set to increase from small to large according to the step size of 0.0001, that is, the system traverses the three states of idle, balanced and blocked successively to improve the generalization ability of the model. In the experiments, 200 sets of data were used for prediction. The data processing was carried out in such a way that the arrival rate corresponded to the time series, that is, the data were represented as a time series $M = \{ {m_0}, {m_1}, ...{m_{T - 1}}\}$. ${m_T}$ denotes the value of time step T. For prediction, the data set was divided into training and test sets, with the division share being 75 and 25%. To improve the training efficiency and smooth out the solution process, the minmax function was used for normalization, scaling the data to between [0~1], Eq (26) is the normalized expression.

In Eq (26), ${y_{gyh}}$ is the normalized value, $y$ is the actual value, ${y_{\max }}$ is the maximum value in the data and ${y_{\min }}$ is the minimum value in the data.

The two-level polling system prediction problem can be simply expressed as follows: the average length at arrival rate $i + 1$ is $y(i + 1)$. N historical data (that is, the average length at the previous N arrival rates) is used as input and is represented by the matrix Q. As in Eq (27).

Equation (28) is a time series representation of the matrix Q.

Predicting the next data from the known data is represented by Eq (29).

Furthermore, the performance prediction of a two-level polling control system based on LSTM and attention mechanisms for wireless sensor networks can be divided into five steps:

Step 1: Data collection. Simulate a dataset of average queue length and average delay at different arrival rates.

Step 2: Data processing. Import the collected data, divide the training set and test set, perform normalization, etc.

Step 3: Modeling and parameter tuning. After data processing, the network model is built and the experimental parameters are dynamically adjusted.

Step 4: Predictive analysis. The model is trained to make predictions on it, and then the known data is predicted on the unknown data by taking a sliding window operation.

Step 5: Evaluate the model. The data is back-normalized and the prediction curves are compared with the simulation curves. Evaluate the predictive performance of the system and thus verify the feasibility.

5.   Projection and analysis of results

5.1.   Predictive analysis

In the experiment, a dataset of 200 sets of average queue length and average delay was obtained by varying the arrival rate; second, the sample size was expanded for analysis and comparison, and the prediction results are shown in Figures 16 and 17.

From Figures 16 and 17, it can be seen that the prediction curves for the common site and the central site basically fit the simulation curves, and the error between the predicted and simulated values is small, indicating that the model can accurately predict the two-level polling system. As in the above analysis, both the length and the delay increase with the arrival rate, and the length and time delay of the central site are much less than those of the common site. Thus, the model is shown to be able to differentiate priorities well.

Figures 18 and 19 show the loss function curves for the average queue length and average delay in a two-level polling control system. The loss function is used as a measure of how similar the predicted values of a model are to the simulated values. The larger the loss function, the less robust the model is and the worse the performance. As can be seen from Figure 18 and 19, the loss decreases rapidly from 0 to 25 epochs. From 25 to 50 epochs, the loss decreases slowly until it approaches 0. The losses in both length and delay converge around 0 for both normal and central sites, indicating that the experimentally set parameters are the best ones under the model.

In order to assess the operational status of the model and the performance of the system, the network model is adjusted to predict future data using known data. Lengths and delays at low arrival rates are used to predict lengths and delays at high arrival rates, i.e., the output of the network is re-fed using loops. In the experiments, the average length and delay for an unknown step size of 50 was predicted, as shown in Figures 20 and 21. It can be seen that the unknown prediction trends for average length and delay are the same as the known data prediction trends, both increasing with increasing arrival rates and increasing differentiation, in line with the theoretical analysis. To some extent, the model has shown that it can predict two-level polling systems very well. The impact of load on system performance is generally fully considered when studying polling systems. The greater the arrival rate of message packets at a fixed service time, the greater the average queue length. Therefore, when encountering high traffic volumes in the design of specific communication systems, consider increasing the number of servers to ease the pressure on individual servers. Also, to evaluate system performance, network parameters can be deployed to record low traffic data to predict high traffic data.

5.2.   Comparative analysis

To verify the generalizability and generalization of the model, the arrival rate was varied to obtain data of different sample sizes for prediction. As shown in Figures 22 and 23, the graphs represent the prediction curves at sample sizes of 200,254 and 381. It can be concluded that the prediction curves for different sample sizes follow the same trend as the simulation curves and the errors remain within manageable limits. The prediction errors under different sample models are shown in Table 4. The model fits well regardless of the increase in sample size, indicating that increasing the sample size does not affect the model's predictive effectiveness.

There are also many mainstream prediction models in machine learning, such as: BP neural networks, SVM, autoregressive sliding average ARMA models and informer neural networks. In order to accurately compare the prediction results of LSTM and attention mechanism, LSTM neural networks and BP neural networks were selected for comparison. Predictions were made using the same common site length dataset on different neural network models. The experiment shows that the LSTM + attention prediction error = 0.0012, while the LSTM network prediction error = 0.0055 and the BP network prediction error = 0.05125. The prediction error of LSTM + attention mechanism is the smallest, indicating that the introduction of attention mechanism can improve the accuracy of deep neural network models in predicting two-level polling systems. In summary, the LSTM +attention model not only fits the data well, but also accurately captures the trends of the two-level polling system.

6.   Conclusions

With the increase of network size and communication volume in the IoT, many different services are involved, and the importance of different services to the user is usually not consistent. When data is collected by wireless sensor networks, the data is not prioritized according to importance, which affects the user experience. Therefore, a continuous-time exhaustive-limited (K = 2) two-level polling system model that distinguishes between different priority levels is proposed to address this problem. In order to improve the computational efficiency and to quickly evaluate the performance of the polling system, we use LSTM + attention mechanism for performance prediction. A two-level mathematical model is built, performance metrics such as length, delay and period are analyzed and simulation experiments are carried out on MATLAB; the relationship between length and delay and arrival rate is abstracted into a time series problem and a network model is built for prediction; the sample size was varied to verify the generalizability of the model and to compare it with LSTM neural network and BP neural network. The results show that the simulated values are basically consistent with the expected values, the predicted curves are basically fitted with the simulated curves and the length and time delay of the common site are larger than those of the central site. It is shown that the new model is able to differentiate service priorities well and has better system performance, which is suitable for polling control mechanisms in wireless sensor networks. LSTM and attention mechanism are used to predict the performance of polling systems more accurately and can be applied as a new method to other polling system performance studies. In addition to performing two-level polling system predictions, future extensions to multi-level multidimensional polling systems and asymmetric polling systems can be pursued, build more applicable models.

The polling system has been an important scheduling control method in the MAC layer of wireless sensor networks, as they can provide conflict-free access to information and provide delay guarantees for delay-sensitive services. Thus, traditional ultra-dense wireless sensor networks are recommended as a complement to cellular networks, 5G ultra-high cellular networks are proposed based on MIMO communication technology, and it is believed that the Exhaustive-Limited K = 2 two-level polling control system will certainly have a prominent role in 5G or 6G optimization and improvement. In addition, the TinyOS system can be used to design the acquisition MAC protocol based on polling control, and the wireless sensor network can be accessed to the cloud platform using WI-FI access to collect the data indicators of the surrounding environment and display them in real time.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The Wu Zhonghai Expert Workstation Project in Yunnan Province (Project No.202305AF150045), and Yang Zhijun's Industry Innovation Talents Project of Yunnan Xingdian Talents Support Plan (Certificate No.: YNWR-CYJS-2020-017).

Conflict of interest

All authors declare no conflicts of interest in this paper.