A combined functional dorsal nerve model of the foot

1.   Introduction

Fractional calculus $(\mathbb{FC})$, also known as non-integer calculus, has been widely studied in recent over the past decades (beginning $1695$) in fields of applied sciences and engineering. $\mathbb{FC}$ deals with fractional-order integral and differential operators, which establishes phenomenon model as an increasingly realistic tool for real-world problems. In addition, it has been properly specified the term "memory" particularly in mathematics, physics, chemistry, biology, mechanics, electricity, finance, economics and control theory, we recommend these books to readers who require to learn more about the core ideas of fractional operators ^{[1,2,3,4,5,6]}. However, recently, several types of fractional operators have been employed in research education that mostly focus on the Riemann-Liouville ($\mathbb{RL}$) ^[3], Caputo ^[3], Hadamard ^[3], Katugampola ^[7], conformable ^[8] and generalized conformable ^[9]. In 2017, Jarad et al. ^[10] introduced generalized $\mathbb{RL}$ and Caputo proportional fractional derivatives including exponential functions in their kernels. After that, in 2021, new fractional operators combining proportional and classical differintegrals have been introduced in ^[11]. Moreover, Akgül and Baleanu ^[12] studied the stability analysis and experiments of the proportional Caputo derivative.

Recently, one type of fractional operator that is popular with researchers now is proportional fractional derivative and integral operators ($\mathbb{PFDO}$s/$\mathbb{PFIO}$s) with respect to another function; for more details see ^[13,14]. For $\alpha > 0$, $\rho \in (0, 1]$, $\psi \in \mathcal{C}^{1}([a, b])$, $\psi^{\prime} > 0$, the $\mathbb{PFIO}$ of order $\alpha$ of $h\in L^{1}([a, b])$ with respect to $\psi$ is given as:

where $\Gamma(\alpha) = \int_{0}^{\infty} s^{\alpha-1} e^{-s} ds$, $s > 0$, and

The Riemann-Liouville proportional fractional derivative ($\mathbb{RL}$-$\mathbb{PFD}$) of order $\alpha$ of $h \in \mathcal{C}^{n}([a, b])$ with respect to $\psi$ is given by

with $n = [\alpha]+1$, where $[\alpha]$ denotes the integer part of order $\alpha$, ${_{}^{\rho}}\mathbb{D}^{n, \psi} = \underbrace{{_{}^{\rho}}\mathbb{D}^{\psi}\cdot{_{}^{\rho}}\mathbb{D}^{\psi}\cdots {_{}^{\rho}}\mathbb{D}^{\psi}}_{{\rm{n times}}}$, and ${_{}^{\rho}}\mathbb{D}^{\psi}[h(t)] = (1 - \rho) h(t) + \rho h^{\prime}(t))/\psi^{\prime}(t)$. The $\mathbb{PFD}$ in Caputo type is given as in

The relation of $\mathbb{PFI}$ and Caputo-$\mathbb{PFD}$ which will be used in this manuscript as

Moreover, for $\alpha$, $\beta > 0$ and $\rho \in (0, 1]$, we have the following properties

Notice that if we set $\rho = 1$ in (1.1), (1.3) and (1.4), then we have the $\mathbb{RL}$-fractional operators ^[3] with $\psi(t) = t$, the Hadamard fractional operators ^[3] with $\psi(t) = \log t$, the Katugampola fractional operators ^[7] with $\psi(t) = t^{\mu}/\mu$, $\mu > 0$, the conformable fractional operators ^[8] with $\psi(t) = (t-a)^{\mu}/\mu$, $\mu > 0$ and the generalized conformable fractional operators ^[9] with $\psi(t) = t^{\mu+\phi}/(\mu+\phi)$, respectively. Recent interesting results on $\mathbb{PFO}$s with respect to another function could be mention in ^{[15,16,17,18,19,20,21,22,23,24,25]}.

Exclusive investigations in concepts of qualitative property in fractional-order differential equations ($\mathbb{FDE}$s) have recently gotten a lot of interest from researchers as existence property ($\mathbb{EP}$) and Ulam's stability ($\mathbb{US}$). The $\mathbb{EP}$ of solutions for $\mathbb{FDE}$s with initial or boundary value conditions has been investigated applying classical/modern fixed point theorems ($\mathbb{FPT}$s). As we know, $\mathbb{US}$ is four types like Hyers-Ulam stability $(\mathbb{HU})$, generalized Hyers-Ulam stability $(\mathbb{GHU})$, Hyers-Ulam-Rassias stability $(\mathbb{HUR})$ and generalized Hyers-Ulam-Rassias stability $(\mathbb{GHUR})$. Because obtaining accurate solutions to fractional differential equations problems is extremely challenging, it is beneficial in various of optimization applications and numerical analysis. As a result, it is requisite to develop concepts of $\mathbb{US}$ for these issues, since studying the properties of $\mathbb{US}$ does not need us to have accurate solutions to the proposed problems. This qualitative theory encourages us to obtain an efficient and reliable technique for solving fractional differential equations because there exists a close exact solution when the purpose problem is Ulam stable. We suggest some interesting papers about qualitative results of fractional initial/boundary value problems ($\mathbb{IVP}$s/$\mathbb{BVP}$s) involving many types of non-integer order, see ^{[26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43]} and references therein.

We are going to present some of the researches that inspired this manuscript. In recent years, pantograph equation ($\mathbb{PE}$) is a type of proportional delay differential equation emerging in deterministic situations which first studied by Ockendon and Taylor ^[44]:

The problem (1.8) has been a broad area of applications in applied branchs such as science, medicine, engineering and economics that use the sake of $\mathbb{PE}$s to model some phenomena of the problem at present which depend on the previous states. For more evidences of $\mathbb{PE}$s, see ^{[45,46,47,48,49,50,51]}. There are many researches of literature on nonlinear fractional differential equations involving a specific function with initial, boundary, or nonlocal conditions, for examples in $2013$, Balachandran et al. ^[52] discussed the initial nonlinear $\mathbb{PE}$s as follows:

where $u_{0}\in \mathbb{R}$, ${^{C}}\mathbb{D}^{\alpha}$ denotes the Caputo fractional derivative of order $\alpha$ and $h \in \mathcal{C}([0, 1] \times \mathbb{R}^2, \mathbb{R})$. $\mathbb{FC}$ and $\mathbb{FPT}$s were applied to discuss the existence properties of the solutions in their work. In $2018$, Harikrishman and co-workers ^[53] examined the existence properties of $\psi$-Hilfer fractional derivative for nonlocal problem for $\mathbb{PE}$s:

where ${^{H}}\mathbb{D}_{a^+}^{\alpha, \beta; \psi}$ represents the $\psi$-Hilfer fractional derivative of order $\alpha$ and type $\beta \in [0, 1]$, $\mathbb{I}_{a^+}^{1-\gamma; \psi}$ is $\mathbb{RL}$-fractional integral of order $1-\gamma$ with respect to $\psi$ so that $\psi^{\prime} > 0$ and $h \in \mathcal{C}([a, b] \times \mathbb{R}^2, \mathbb{R})$. Asawasamrit and co-workers ^[54] used Schaefer's and Banach's $\mathbb{FPT}$s to establish the existence properties of $\mathbb{FDE}$s with mixed nonlocal conditions ($\mathbb{MNC}$s) in $2019$. In 2021, Boucenna et al. ^[55] investigated the existence and uniqueness theorem of solutions for a generalized proportional Caputo fractional Cauchy problem. They solved the proposed problem based on the decomposition formula. Amongst important fractional equations, one of the most interesting equations is the fractional integro-differential equations, which provide massive freedom to explain processes involving memory and hereditary properties, see ^[56,57].

Recognizing the importance of all parts that we mentioned above, motivated us to generate this paper which deals with the qualitative results to the Caputo proportional fractional integro-differential equation ($\mathbb{PFIDE}$) with $\mathbb{MNC}$s:

where ${_{}^{C\rho}}\mathbb{D}_{a^+}^{q, \psi}$ is the Caputo-$\mathbb{PFDO}$ with respect to another increasing differentiable function $\psi$ of order $q = \{\alpha, \beta_j\}$ via $0 < \beta_j < \alpha \leq 1$, $j = 1, 2, \ldots, n$, $0 < \rho\leq 1$, $0 < \lambda < 1$, ${_{}^{\rho}}\mathbb{I}_{a^+}^{p, \psi}$ is the $\mathbb{PFIO}$ with respect to another increasing differentiable function $\psi$ of order $p = \{\omega, \delta_r\} > 0$ for $r = 1, 2, \ldots, k$, $0 < \rho\leq 1$, $\gamma_i, \kappa_j, \sigma_r, {A} \in\mathbb{R}$, $0 \leq a\leq \eta_i, \xi_j, \theta_r \leq T$, $i = 1, 2, \ldots, m$, $f \in \mathcal{C}(\mathcal{J}\times \mathbb{R}^4, \mathbb{R})$, $\mathcal{J} = [a, T]$. We use the help of the famous $\mathbb{FPT}$s like Banach's, Leray-Schauder's nonlinear alternative and Krasnoselskii's to discuss the existence properties of the solutions for (1.11). Moreover, we employ the context of different kinds of $\mathbb{US}$ to discuss the stability analysis. The results are well demonstrated by numerical examples at last section.

The advantage of defining $\mathbb{MNC}$s of the problem (1.11) is it covers many cases as follows:

● If we set $\kappa_{j} = \sigma_{r} = 0$, then (1.11) is deducted to the proportional multi-point problem.

● If we set $\gamma_{i} = \sigma_{r} = 0$, then (1.11) is deducted to the $\mathbb{PFD}$ multi-point problem.

● If we set $\gamma_{i} = \kappa_{j} = 0$, then (1.11) is deducted to the $\mathbb{PFI}$ multi-point problem.

● If we set $\alpha = \rho = 1$, (1.11) emerges in nonlocal problems ^[58].

This work is collected as follows. Section $2$ provides preliminary definitions. The existence results of solutions for (1.11) is studied in Section $3$. In Section $4$, stability analysis of solution for (1.11) in frame of $\mathbb{HU}$, $\mathbb{GHU}$, $\mathbb{HUR}$ and $\mathbb{GHUR}$ are given is established. Section $5$ contains the example to illustrate the theoretical results. In addition, the summarize is provided in the last part.

2.   Preliminaries

Before proving, assume that $\mathcal{E} = \mathcal{C}(\mathcal{J}, \mathbb{R})$ is the Banach space of all continuous functions from $\mathcal{J}$ into $\mathbb{R}$ provided with $\Vert u \Vert = \sup_{t\in \mathcal{J}}\{|u(t)|\}$. The symbol ${_{}^{\rho}}\mathbb{I}_{a^+}^{q, \psi} [F_u(s)(c)]$ means that

where $q = \{\alpha, \alpha-\beta_j, \alpha+\delta_r\}$, $c = \{t, \eta_i, \xi_j, \theta_r\}$, and

In order to convert the considered problem into a fixed point problem, (1.11) must be transformed to corresponding an integral equation. We discuss the following key lemma.

Lemma 2.1. Let $0 < \beta_j < \alpha \leq 1$, $j = 1, 2, \ldots, n$, $\rho > 0$, $\delta_r$, $> 0$, $r = 1, 2, \ldots, k$ and $\Omega \neq 0$. Then, the Caputo-$\mathbb{PFIDE}$ with $\mathbb{MNC}$s:

is equivalent to the integral equation

where

Proof. Suppose $u$ is the solution of (2.2). By using (1.5), the integral equation can be rewritten as

where $c_{1} \in\mathbb{R}$. Taking ${_{}^{C\rho}}\mathbb{D}_{a^+}^{\beta_j, \psi}$ and ${_{}^{\rho}}\mathbb{I}_{a^+}^{\delta_r, \psi}$ into (2.5) with (1.6) and (1.7), we obtain

Applying the nonlocal conditions in (2.2), we have

Solving the above equation, we get the value

where $\Omega$ is given as in (2.4). Taking $c_1$ in (2.5), we obtain (2.3).

On the other hand, it is easy to show by direct computing that $u(t)$ is provided as in (2.3) verifies (2.2) via the given $\mathbb{MNC}$s. The proof is done.

3.   Existence results

By using Lemma $2.1$, we will set the operator $\mathcal{K}:\mathcal{E}\to\mathcal{E}$

where $\mathcal{K}_1$, $\mathcal{K}_2 : \mathcal{E} \to \mathcal{E}$ defined by

Notice that $\mathcal{K}u = \mathcal{K}_1u + \mathcal{K}_2u$. It should be noted that (1.11) has solutions if and only if $\mathcal{K}$ has fixed points. Next, we are going to examine the existence properties of solutions for (1.11), which is discussed by employing Banach's $\mathbb{FPT}$, Leray-Schauder's nonlinear alternative and Krasnoselskii's $\mathbb{FPT}$. For the benefit of calculation in this work, we will provide the constants:

3.1.   Uniqueness property

Firstly, the uniqueness result for (1.11) will be stidied by applying Banach's $\mathbb{FPT}$.

Lemma 3.1. (Banach contraction principle ^[59]) Assume that $\mathcal{B}$ is a non-empty closed subset of a Banach space $\mathcal{E}$. Then any contraction mapping $\mathcal{K}$ from $\mathcal{B}$ into itself has a unique fixed point.

Theorem 3.2. Let $f \in \mathcal{C}(\mathcal{J}\times\mathbb{R}^{4}, \mathbb{R})$so that:

$(H_1)$ there exist constants $\mathbb{L}_1 > 0$, $\mathbb{L}_2 > 0$, $0 < \mathbb{L}_3 < 1$ so that

$\forall u_i$, $v_i$, $w_i$, $z_i \in \mathbb{R}$, $i = 1, 2$, $t\in \mathcal{J}$.

If

then the Caputo-$\mathbb{PFIDE}$ with $\mathbb{MNC}$s (1.11) has a unique solution on $\mathcal{J}$, where (3.4) and (3.5) refers to $\Theta(T, \omega)$ and $\Lambda$.

Proof. First, we will convert (1.11) into $u = \mathcal{K}u$, where $\mathcal{K}$ is given as in (3.1). Clearly, the fixed points of $\mathcal{K}$ are solutions to (1.11). By using the Banach's $\mathbb{FPT}$, we are going to prove that $\mathcal{K}$ has a $\mathbb{FP}$ which is a unique solution of (1.11).

Define $\sup_{t\in J}|f(t, 0, 0, 0, 0)| : = M_1 < \infty$ and setting $B_{r_1} : = \{u \in \mathcal{E} : \Vert u \Vert \leq r_1\}$ with

where $\Omega$, $\Theta(T, \omega)$ and $\Lambda$ are given as in (2.4), (3.4) and (3.5). Clearly, $B_{r_1}$ is a bounded, closed and convex subset of $\mathcal{E}$. We have divided the method of the proof into two steps:

Step I. We prove that $\mathcal{K}B_{r_1} \subset B_{r_1}$.

For each $u \in B_{r_1}$, we obtain

From the assumption $(H_1)$, it follows that

Then

This implies that

By using the fact of $0 < e^{\frac{\rho-1}{\rho} \left(\psi(t)-\psi(s) \right)} \leq 1$, $a \leq s < t \leq T$, it follows that

which implies that $\Vert \mathcal{K}u \Vert \leq r_1$. Thus, $\mathcal{K}B_{r_1} \subset B_{r_1}$.

Step II. We prove that $\mathcal{K}:\mathcal{E}\to \mathcal{E}$ is contraction.

For each $u$, $v \in \mathcal{E}$, $t \in \mathcal{J}$, we obtain

From $(H_1)$ again, we can compute that

Then

By inserting (3.9) into (3.8), one has

also, $\Vert \mathcal{K}u - \mathcal{K}v\Vert \leq (2\mathbb{L}_1+\mathbb{L}_2\Theta(T, \omega))/(1-\mathbb{L}_{3}) \Lambda \Vert u-v\Vert$. It follows from $[(2\mathbb{L}_1+\mathbb{L}_2\Theta(T, \omega))/(1-\mathbb{L}_{3})]\Lambda < 1$, that $\mathcal{K}$ is contraction. Then, (from Lemma $3.1$), we conclude that $\mathcal{K}$ has the unique fixed point, that is the unique solution to (1.11) in $\mathcal{E}$.

3.2.   Existence property via Leray-Schauder's type

Next, Leray-Schauder's nonlinear alternative is employed to analyze in the second property.

Lemma 3.3. (Leray-Schauder's nonlinear alternative ^[59]) Assume that $\mathcal{E}$ is a Banach space, $C$ is a closed and convex subset of $M$, $X$ is an open subset of $C$ and $0 \in X$. Assume that $F: \overline{X}\to C$ is continuous, compact (that is, $F(\overline{X})$ is a relatively compact subset of $C$) map. Then either $(i)$ $F$ has a fixed point in $\overline{X}$, or $(ii)$ there is $x\in\partial X$ (the boundary of $X$ in $C$) and $\varrho \in (0, 1)$ with $z = \varrho F(z)$.

Theorem 3.4. Assume that $f \in \mathcal{C}(\mathcal{J}\times\mathbb{R}^{4}, \mathbb{R})$ so that:

$(H_2)$ there exists $\Psi \mathcal{C}(\mathbb{R}^+, \mathbb{R}^+)$ and $\Psi$ is non-decreasing, $p$, $f \in \mathcal{C}(\mathcal{J}, \mathbb{R}^{+})$, $q\in \mathcal{C}(\mathcal{J}, \mathbb{R}^{+}\cup \{0\})$ so that

where $p_0 = \sup_{t\in \mathcal{J}}\{p(t)\}$, $f_0 = \sup_{t\in \mathcal{J}}\{f(t)\}$, $q_0 = \sup_{t\in \mathcal{J}}\{q(t)\} < 1$.

$(H_3)$ there exists a constant $N > 0$ so that

where $\Theta(T, \omega)$ and $\Lambda$ are given as in (3.4) and (3.5).

Then the Caputo-$\mathbb{PFIDE}$ with $\mathbb{MNC}$s (1.11) has at least one solution.

Proof. Assume that $\mathcal{K}$ is given as in (3.1). Next, we are going to prove that $\mathcal{K}$ maps bounded sets (balls) into bounded sets in $\mathcal{E}$. For any $r_2 > 0$, assume that $B_{r_2} : = \{u \in \mathcal{E} : \Vert u \Vert \leq r_2\} \in \mathcal{E}$, we have, for each $t\in \mathcal{J}$,

It follows from $(H_2)$ that

Then, we have

For any $a \leq s < t \leq T$, we have $0 < e^{\frac{\rho-1}{\rho} \left(\psi(t)-\psi(s) \right)} \leq 1$, then

which leads to

Now, we will prove that $\mathcal{K}$ maps bounded sets into equicontinuous sets of $\mathcal{E}$.

Given $\tau_1 < \tau_2$ where $\tau_1$, $\tau_2 \in \mathcal{J}$, and for each $u \in B_{r_2}$. Then, we obtain

Clearly, which independent of $u \in B_{r_{2}}$ the above inequality, $\vert (\mathcal{K}u)(\tau_2) - (\mathcal{K}u)(\tau_1) \vert \to 0$ as $\tau_2 \to \tau_1$. Hence, by the Arzelá-Ascoli property, $\mathcal{K} : \mathcal{E} \to \mathcal{E}$ is completely continuous.

Next, we will prove that there is $\mathcal{B} \subseteq \mathcal{E}$ where $\mathcal{B}$ is an open set, $u \neq \varrho \mathcal{K}(u)$ for $\varrho \in (0, 1)$ and $u \in \partial \mathcal{B}$. Assume that $u\in\mathcal{E}$ is a solution of $u = \varrho \mathcal{K}u$, $\varrho \in (0, 1)$. Hence, it follows that

which yields

Consequently,

By $(H_3)$, there is $N$ so that $\|u\| \neq N$. Define

Note that $\mathcal{K} : \overline{\mathcal{Q}} \to \mathcal{E}$ is continuous and completely continuous. By the option of $\mathcal{Q}$, there is no $u \in \partial \mathcal{Q}$ so that $u = \varrho \mathcal{K}u$, $\exists\varrho \in (0, 1)$. Thus, (by Lemma $3.3$), we conclude that $\mathcal{K}$ has fixed point $u\in\overline{\mathcal{Q}}$ which verifies that (1.11) has at least one solution.

3.3.   Existence property via Krasnoselskii's fixed point theorem

By applying Krasnoselskii's $\mathbb{FPT}$, the existence property will be achieved.

Lemma 3.5. (Krasnoselskii's fixed point theorem ^[60]) Let $\mathcal{M}$ be a closed, bounded, convex and nonempty subset of a Banach space. Let $K_1$, $K_2$ be the operators such that $(i)$ $K_1x+K_2y \in \mathcal{M}$ whenever $x, y \in \mathcal{M}$; $(ii)$ $K_1$ is compact and continuous; $(iii)$ $K_2$ is contraction mapping. Then there exists $z \in \mathcal{M}$ such that $z = K_1z+K_2z$.

Theorem 3.6. Suppose that $(H_1)$ holds and $f \in\mathcal{C}(\mathcal{J}\times\mathbb{R}^{4}, \mathbb{R})$ so that:

$(H_4)$ $\exists g \in \mathcal{C}(\mathcal{J}, \mathbb{R}^+)$ so that

If

then the Caputo-$\mathbb{PFIDE}$ with $\mathbb{MNC}$s (1.11) has at least one solution.

Proof. Define $\sup_{t \in \mathcal{J}} \vert g(t) \vert = \Vert g \Vert$ and picking

we consider $B_{r_3} = \left\{ u \in \mathcal{E}: \Vert u \Vert \leq r_3 \right\}$. Define $\mathcal{K}_1$ and $\mathcal{K}_2$ on $B_{r_3}$ as (3.2) and (3.3).

For any $u, v \in B_{r_3}$, we obtain

This implies that $\mathcal{K}_1u+\mathcal{K}_2v \in B_{r_3}$, which verifies Lemma $3.5$ (i).

Next, we are going to show that Lemma $3.5$ (ii) is verified.

Assume that $u_n$ is a sequence so that $u_n \to u \in \mathcal{E}$ as $n \to \infty$. Hence, we get

Since $f$ is continuous, verifies that $F_{u}$ is also continuous. By the Lebesgue dominated convergent theorem, we have

Therefore,

Thus, implies that $\mathcal{K}_1u$ is continuous. Also, the set $\mathcal{K}_1B_{r_3}$ is uniformly bounded as

Next step, we will show the compactness of $\mathcal{K}_1$.

Define $\sup \{\vert f(t, u, v, w, z) \vert; (t, u, v, w, z) \in \mathcal{J}\times \mathbb{R}^4\} = f^* < \infty$, thus, for each $\tau_1, \tau_2 \in \mathcal{J}$ with $\tau_1 \leq \tau_2$, it follows that

Clearly, the right-hand side of the above inequality is independent of $u$ and $\left \vert (\mathcal{K}_1u)(\tau_2)-(\mathcal{K}_1u)(\tau_1) \right \vert \to 0$, as $\tau_2 \to \tau_1$. Hence, the set $\mathcal{K}_1B_{r_3}$ is equicontinuous, also $\mathcal{K}_1$ maps bounded subsets into relatively compact subsets, which implies that $\mathcal{K}_1B_{r_3}$ is relatively compact. By the Arzelá-Ascoli theorem, then $\mathcal{K}_1$ is compact on $B_{r_3}$.

Finally, we are going to show that $\mathcal{K}_2$ is contraction.

For each $u$, $v \in B_{r_{3}}$ and $t \in \mathcal{J}$, we get

Since (3.10) holds, implies that $\mathcal{K}_2$ is contraction and also Lemma $3.5$ (iii) verifies.

Therefore, the assumptions of Lemma $3.5$ are verified. Then, (by Lemma $3.5$) which verifies that (1.11) has at least one solution.

4.   Stability results

This part is proving different kinds of $\mathbb{US}$ like $\mathbb{HU}$ stable, $\mathbb{GHU}$ stable, $\mathbb{HUR}$ stable and $\mathbb{GHUR}$ stable of the Caputo-$\mathbb{PFIDE}$ with $\mathbb{MNC}$s (1.11).

Definition 4.1. The Caputo-$\mathbb{PFIDE}$ with $\mathbb{MNC}$s (1.11) is called $\mathbb{HU}$ stable if there is a constant $\Delta_{f} > 0$ so that for every $\epsilon > 0$ and the solution $z\in \mathcal{E}$ of

there exists the solution $u\in \mathcal{E}$ of (1.11) so that

Definition 4.2. The Caputo-$\mathbb{PFIDE}$ with $\mathbb{MNC}$s (1.11) is called $\mathbb{GHU}$ stable if there is a function $\Phi \in \mathcal{C}(\mathbb{R}^{+}, \mathbb{R}^{+})$ via $\Phi(0) = 0$ so that, for every solution $z\in \mathcal{E}$ of

there is the solution $u\in \mathcal{E}$ of (1.11) so that

Definition 4.3. The Caputo-$\mathbb{PFIDE}$ with $\mathbb{MNC}$s (1.11) is called $\mathbb{HUR}$ stable with respect to $\Phi \in \mathcal{C}(\mathcal{J}, \mathbb{R}^{+})$ if there is a constant $\Delta_{f, \Phi} > 0$ such that for every $\epsilon > 0$ and for any the solution $z\in \mathcal{E}$ of (4.3) there is the solution $u\in \mathcal{E}$ of (1.11) so that

Definition 4.4. The Caputo-$\mathbb{PFIDE}$ with $\mathbb{MNC}$s (1.11) is called $\mathbb{GHUR}$ stable with respect to $\Phi \in \mathcal{C}(\mathcal{J}, \mathbb{R}^{+})$ if there is a constant $\Delta_{f, \Phi} > 0$ so that for any the solution $z\in \mathcal{E}$ of

there is the solution $u\in \mathcal{E}$ of (1.11) so that

Remark 4.5. Cleary, (i) Definition $4.1$ $\Rightarrow$ Definition $4.2$; (ii) Definition $4.3$ $\Rightarrow$ Definition $4.4$; (iii) Definition $4.3$ for $\Phi(t) = 1$ $\Rightarrow$ Definition $4.1$.

Remark 4.6. $z\in \mathcal{E}$ is the solution of (4.1) if and only if there is the function $w\in \mathcal{E}$ (which depends on $z$) so that: $(i)$ $|w(t)|\leq \epsilon$, $\forall t \in \mathcal{J}$; $(ii)$ ${_{}^{C\rho}}\mathbb{D}_{a^+}^{\alpha, \psi}[z(t)] = F_{z}(t) + w(t)$, $t\in \mathcal{J}$.

Remark 4.7. $z\in \mathcal{E}$ is the solution of (4.3) if and only if there is the function $v\in \mathcal{E}$ (which depends on $z$) so that: $(i)$ $|v(t)|\leq \epsilon \Phi(t)$, $\forall t \in \mathcal{J}$; $(ii)$ ${_{}^{C\rho}}\mathbb{D}_{a^+}^{\alpha, \psi}[z(t)] = F_{z}(t) + v(t)$, $t\in \mathcal{J}$.

4.1.   $\mathbb{HU}$ stability and $\mathbb{GHU}$ stability

From Remark $4.6$, the solution of

can be rewritten as

Firstly, the key lemma that will be applied in the presents of $\mathbb{HU}$ stable and $\mathbb{GHU}$ stable.

Lemma 4.8. Assume that $0 < \epsilon, \rho \leq 1$. If $z\in \mathbb{E}$ verifies (4.1), hence $z$ is the solution of

where $\Lambda$ is given as in (3.5).

Proof. By Remark 4.6 with (4.8), it follows that

where $\Lambda$ is given by (3.5), from which (4.9) is achieved.

Next, we will show the $\mathbb{HU}$ and $\mathbb{GHU}$ stability results.

Theorem 4.9. Suppose that $f \in \mathcal{C}(\mathcal{J}\times\mathbb{R}^4, \mathbb{R})$. If $(H_{1})$ is verified with (3.6) trues. Hence the Caputo-$\mathbb{PFIDE}$ with $\mathbb{MNC}$s (1.11) is $\mathbb{HU}$ stable as well as $\mathbb{GHU}$ stable on $\mathcal{J}$.

Proof. Assume that $z\in \mathcal{E}$ is the solution of (4.1) and assume that $u$ is the unique solution of

By using $|x-y|\leq |x|+|y|$ with Lemma 4.8, one has

where $\Lambda$ is given as in (3.5). This offers $|z(t)-u(t)|\leq\Delta_{f}\epsilon$, where

Then, the Caputo-$\mathbb{PFIDE}$ with $\mathbb{MNC}$s (1.11) is $\mathbb{HU}$ stable. In addition, if we input $\Phi(\epsilon) = \Delta_{f}\epsilon$ via $\Phi(0) = 0$, hence (1.11) is $\mathbb{GHU}$ stable.

4.2.   The $\mathbb{HUR}$ stability and $\mathbb{GHUR}$ stability

Thanks of Remark $4.7$, the solution

can be rewritten as

For the next proving, we state the following assumption:

$(H_5)$ there is an increasing function $\Phi\in \mathcal{C}(\mathcal{J}, \mathbb{R}^+)$ and there is a constant $n_{\Phi} > 0$, so that, for each $t\in J$,

Lemma 4.10. Assume that $z\in \mathcal{E}$ is the solution of (4.3). Hence, $z$ verifies

where $\Lambda$ is given as in (3.5).

Proof. From (4.11), we have

where $\Lambda$ is given by (3.5), which leads to (4.13).

Finally, we are going to show $\mathbb{HUR}$ and $\mathbb{GHUR}$ stability results.

Theorem 4.11. Suppose $f \in \mathcal{C}(\mathcal{J}\times\mathbb{R}^4, \mathbb{R})$. If $(H_{1})$ is satisfied with (3.6) trues. Hence, the Caputo-$\mathbb{PFIDE}$ with $\mathbb{MNC}$s (1.11) is $\mathbb{HUR}$ stable as well as $\mathbb{GHUR}$ stable on $\mathcal{J}$.

Proof. Assume that $\epsilon > 0$. Suppose that $z\in \mathcal{E}$ is the solution of (4.6) and $u$ is the unique solution of (1.11). By using the triangle inequality, Lemma 4.8 and (4.11), we estamate that

where $\Lambda$ is given as in (3.5), verifies that $|z(t)-u(t)| \leq \Delta_{f, \Phi}\epsilon \Phi(t)$, where

Then, the Caputo-$\mathbb{PFIDE}$ with $\mathbb{MNC}$s (1.11) is $\mathbb{HUR}$ stable. In addition, if we input $\Phi(t) = \epsilon \Phi(t)$ with $\Phi(0) = 0$, then (1.11) is $\mathbb{GHUR}$ stable.

5.   Numerical examples

This part shows numerical instances that demonstrate the exactness and applicability of our main results.

Example 5.1. Discussion the following nonlinear Caputo-$\mathbb{PFIDE}$ with $\mathbb{MNC}$s of the form:

Here, $\alpha = 1/2$, $\rho = 2/3$, $\psi(t) = \sqrt{t}$, $\lambda = 1/\sqrt{3}$, $\omega = 3/4$, $a = 0$, $T = 1$, $m = 2$, $n = 3$, $k = 2$, $\gamma_{i} = (i+1)/2$, $\eta_{i} = (2i+1)/5$, $i = 1, 2$, $\kappa_j = (2j-1)/5$, $\beta_{j} = (2j+1)/20$, $\xi_{j} = j/4$, $j = 1, 2, 3$, $\sigma_{r} = r/3$, $\delta_{r} = r/(r+1)$, $\theta_{r} = (r+1)/4$, $r = 1, 2$. By using Python, we obtain that $\Omega \approx 2.4309\neq 0$ and $\Lambda \approx 4.042711$.

(I) If we set the nonlinear function

For any $u_i$, $v_i$, $w_i$, $z_i\in \mathbb{R}$, $i = 1, 2$ and $t\in [0, 1]$, one has

The assumption $(H_1)$ is satisfied with $\mathbb{L}_{1} = \mathbb{L}_2 = \mathbb{L}_3 = \frac{1}{27}$. Hence

All conditions of Theorem $3.2$ are verified. Hence, the nonlinear Caputo-$\mathbb{PFIDE}$ with $\mathbb{MNC}$s (5.1) has a unique solution on $[0, 1]$. Moreover, we obtain

Hence, from Theorem 4.9, the nonlinear Caputo-$\mathbb{PFIDE}$ with $\mathbb{MNC}$s (5.1) is $\mathbb{HU}$ stable and also $\mathbb{GHU}$ stable on $[0, 1]$. In addition, by taking $\Phi(t) = e^{\frac{\rho-1}{\rho}\psi(t)}\left(\psi(t)-\psi(0)\right)$, we have

Thus, (4.12) is satisfied with $n_\Phi = \frac{2\sqrt{2}}{\sqrt{3\pi}} > 0$. Then, we have

Hence, from Theorem 4.11, the nonlinear Caputo-$\mathbb{PFIDE}$ with $\mathbb{MNC}$s (5.1) is $\mathbb{HUR}$ stable and also $\mathbb{GHUR}$ stable.

(II) If we take the nonlinear function

we have

From the above inequality with $(H_2)$–$(H_3)$, we get that $p(t) = 1 /4^{t+2}$, $\Psi\left(\vert u \vert +\vert v \vert \right) = \vert u \vert +\vert v \vert +1/2$ and $h(t) = q(t) = 1 / 2^{t+3}$. So, we have $p_0 = 1/16$ and $h_0 = q_0 = 1/8$. From all the datas, we can compute that the constant $N > 0.432489$. All assumptions of Theorem $3.4$ are verified. Hence, the nonlinear Caputo-$\mathbb{PFIDE}$ with $\mathbb{MNC}$s (5.1) has at least one solution on $[0, 1]$. Moreover,

Hence, from Theorem 4.9, the nonlinear Caputo-$\mathbb{PFIDE}$ with $\mathbb{MNC}$s 5.1 is $\mathbb{HU}$ stable and also $\mathbb{GHU}$ stable on $[0, 1]$. In addition, by taking $\Phi(t) = e^{\frac{\rho-1}{\rho}\psi(t)}\left(\psi(t)-\psi(0)\right)^{\frac{1}{2}}$, we have

Thus, (4.12) is satisfied with $n_\Phi = \frac{\sqrt{3\pi}}{2\sqrt{2}} > 0$. Then, we have

Hence, from Theorem 4.11, the nonlinear Caputo-$\mathbb{PFIDE}$ with $\mathbb{MNC}$s 5.1 is $\mathbb{HUR}$ stable and also $\mathbb{GHUR}$ stable on $[0, 1]$.

(III) If we set the nonlinear function

For $u_i$, $v_i$, $w_i$, $z_i\in \mathbb{R}$, $i = 1, 2$ and $t\in [0, 1]$, we have

The assumption $(H_4)$ is satisfied with $\mathbb{L}_{1} = \mathbb{L}_2 = \frac{1}{16}$, $\mathbb{L}_{3} = \frac{1}{8}$ and

which yields that

Then

All assumptions of Theorem $3.6$ are verified. Hence the nonlinear Caputo-$\mathbb{PFIDE}$ with $\mathbb{MNC}$s (5.1) has at least one solution on $[0, 1]$.

Furthermore, we get

Hence, from Theorem 4.9, the nonlinear Caputo-$\mathbb{PFIDE}$ with $\mathbb{MNC}$s (5.1) is $\mathbb{HU}$ stable and also $\mathbb{GHU}$ stable on $[0, 1]$. In addition, by taking $\Phi(t) = e^{\frac{\rho-1}{\rho}\psi(t)}\left(\psi(t)-\psi(0)\right)^{2}$, we have

Thus, (4.12) is satisfied with $n_\Phi = \frac{8\sqrt{6}}{15\sqrt{\pi}} > 0$. Then, we have

Hence, from Theorem 4.11, the nonlinear Caputo-$\mathbb{PFIDE}$ with $\mathbb{MNC}$s (5.1) is $\mathbb{HUR}$ stable and also $\mathbb{GHUR}$ stable on $[0, 1]$.

Example 5.2. Discussion the following linear Caputo-$\mathbb{PFIDE}$ with $\mathbb{MNC}$s of the form:

By Lemma $2.1$, the implicit solution of the problem (5.2)

where

We consider several cases of the following function $\psi(t)$:

(I) If $\psi(t) = t^{\alpha}$ then the solution of linear Caputo-$\mathbb{PFIDE}$ with $\mathbb{MNC}$s (5.2) is given as in

where

(II) If $\psi(t) = \frac{\sin t}{\alpha}$ then the solution of linear Caputo-$\mathbb{PFIDE}$ with $\mathbb{MNC}$s (5.2) is given as in

where

(III) If $\psi(t) = e^{\alpha t}$ then the solution of linear Caputo-$\mathbb{PFIDE}$ with $\mathbb{MNC}$s (5.2) is given as in

where

(IV) If $\psi(t) = \frac{\ln(1+t)}{\alpha}$ then the solution of linear Caputo-$\mathbb{PFIDE}$ with $\mathbb{MNC}$s (5.2) is given as in

where

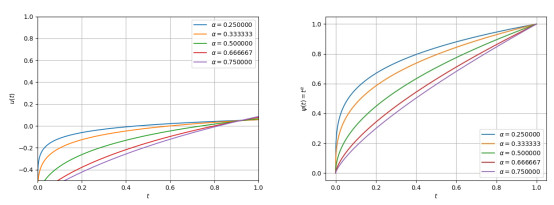
Graph representing the solution of the problem (5.2) with various values $\alpha$ via many the functions $\psi(t) = t^{\alpha}$, $\psi(t) = \frac{\sin t}{\alpha}$, $\psi(t) = e^{\alpha t}$ and $\psi(t) = \frac{\ln(1+t)}{\alpha}$ is shown as in Figures 1–4 by using Python.

6.   Conclusions

The qualitative analysis is accomplished in this work. The authors proved the existence, uniqueness and stability of solutions for Caputo-$\mathbb{PFIDE}$ with $\mathbb{MNC}$s which consist of multi-point and fractional multi-order boundary conditions. Some famous theorems are employed to obtain the main results such as the Banach's $\mathbb{FPT}$ is the important theorem to prove the uniqueness of the solution, while Leray-Schauder's nonlinear alternative and Krasnoselskii's $\mathbb{FPT}$ are used to investigate the existence results. Furthermore, we established the various kinds of Ulam's stability like $\mathbb{HU}$, $\mathbb{GHU}$, $\mathbb{HUR}$ and $\mathbb{GHUR}$ stables. Finally, by using Python, numerical instances allowed to guarantee the accuracy of the theoretical results.

This research would be a great work to enrich the qualitative theory literature on the problem of nonlinear fractional mixed nonlocal conditions involving a particular function. For the future works, we shall focus on studying the different types of existence results and stability analysis for impulsive fractional boundary value problems.

Acknowledgments

B. Khaminsou was supported by the International Science Programme PhD. Research Scholarship from National University of Laos (NUOL). W. Sudsutad was partially supported by Ramkhamhaeng University. C. Thaiprayoon and J. Kongson would like to thank for funding this work through the Center of Excellence in Mathematics (CEM), CHE, Sri Ayutthaya Road, Bangkok, 10400, Thailand and Burapha University.

Conflict of interest

On behalf of all authors, the corresponding author states that there is no conflict of interest.