Statistical modelling for a new family of generalized distributions with real data applications

1.   Introduction

Fractional calculus is a main branch of mathematics that can be considered as the generalisation of integration and differentiation to arbitrary orders. This hypothesis begins with the assumptions of L. Euler (1730) and G. W. Leibniz (1695). Fractional differential equations (FDEs) have lately gained attention and publicity due to their realistic and accurate computations ^{[1,2,3,4,5,6,7]}. There are various types of fractional derivatives, including Riemann–Liouville, Caputo, Grü nwald–Letnikov, Weyl, Marchaud, and Atangana. This topic's history can be found in ^[8,9,10,11]. Undoubtedly, fractional calculus applies to mathematical models of different phenomena, sometimes more effectively than ordinary calculus ^[12,13]. As a result, it can illustrate a wide range of dynamical and engineering models with greater precision. Applications have been developed and investigated in a variety of scientific and engineering fields over the last few decades, including bioengineering ^[14], mechanics ^[15], optics ^[16], physics ^[17], mathematical biology, electrical power systems ^[18,19,20] and signal processing ^[21,22,23].

One of the definitions of fractional derivatives is Caputo-Fabrizo, which adds a new dimension in the study of FDEs. The new derivative's feature is that it has a nonsingular kernel, which is made from a combination of an ordinary derivative with an exponential function, but it has the same supplementary motivating properties with various scales as in the Riemann-Liouville fractional derivatives and Caputo. The Caputo-Fabrizio fractional derivative has been used to solve real-world problems in numerous areas of mathematical modelling for example, numerical solutions for groundwater pollution, the movement of waves on the surface of shallow water modelling ^[24], RLC circuit modelling ^[25], and heat transfer modelling ^[26,27] were discussed.

Rach (1987), Bellomo and Sarafyan (1987) first compared the Adomian Decomposition method (ADM) ^{[28,29,30,31,32]} to the Picard method on a variety of examples. These methods have many benefits: they effectively work with various types of linear and nonlinear equations and also provide an analytic solution for all of these equations with no linearization or discretization. These methods are more realistic compared with other numerical methods as each technique is used to solve a specific type of equations, on the other hand ADM and Picard are useful for many types of equations. In the numerical examples provided, we compare ADM and Picard solutions of multidimentional fractional order equations with Caputo-Fabrizio.

The fractional derivative of Caputo-Fabrizio for the function $x\left(t\right)$ is defined as ^[33]

and its corresponding fractional integral is

where $x\left(t\right)$ be continuous and differentiable on [0, T]. Also, in the above definition, the function $B\left(\alpha \right) > 0$ is a normalized function which satisfy the condition $B\left(0\right) = B\left(1\right) = 0.$ The relation between the Caputo–Fabrizio fractional derivate and its corresponding integral is given by

2.   Construction of the algorithm

In this section, we will introduce a multidimentional FDE subject to the initial condition. Let $\alpha \in \; (0, 1]$, $0 < \alpha _{1} < \alpha _{2} < ..., \alpha _{m} < 1,$ and $m$ is integer real number,

where $x = x\left(t\right), t\in J = \left[ 0, T\right], T\in R^{+}, x\in C\left(J\right)$.

To facilitate the equation and make it easy for the calculation, we let $x\left(t\right) = c_{0}+X\left(t\right)$ so Eq (2.1) can be witten as

the algorithm depends on converting the initial condition from a constant $c_{0}$ to 0.

Let $^{CF}D^{\alpha }X = y\left(t\right)$ then $X = \; ^{CF}I^{\alpha }y,$ so we have

Substituting in Eq (2.2) we obtain

Assume $f$ satisfies Lipschtiz condition with Lipschtiz constant$\ L$ given by,

which implies

The solution algorithm of Eq (2.4) using ADM is,

where $a\left(t\right)$ pocesses all free terms in Eq (2.4) and $A_{n}$ are the Adomian polynomials of the nonlinear term which takes the form ^[34]

where $f\left(S_{n}\right) = \sum_{i = 0}^{n}A_{i}$. Later, this accelerated formula of Adomian polynomial will be used in convergence analysis and error estimation. The solution of Eq (2.4) can be written in the form,

lastly, the solution of the Eq (2.4) takes the form

At which we convert the parameter to the initial form $y$ to $x$ in Eq (2.10), so we have the solution of the original Eq (2.1).

3.   Convergence analysis

3.1.   Existence and uniqueness

Define a mapping $F:E\rightarrow E$ where $E = \left(C\left[ J\right], \left\Vert \cdot \right\Vert \right)$ is a Banach space of all continuous functions on $J$ with the norm $\left\Vert x\right\Vert = \underset{t\epsilon J}{\text{ }\max\limits } \; x\left(t\right)$.

Theorem 3.1. Equation (2.4) has a unique solution whenever $0 < \phi < 1$ where $\phi = L\left(\sum_{i = 0}^{m}\frac{\left[ \left(\alpha-\alpha _{i}\right) \left(T-1\right) \right] +1}{B\left(\alpha -\alpha_{i}\right) }\right)$.

Proof. First, we define the mapping $F:E\rightarrow E$ as

Let $y$ and $z\in E$ are two different solutions of Eq (2.4). Then

which implies that

under the condition $0 < \phi < 1,$ the mapping $F$ is contraction and hence there exists a unique solution $y\in C\left[ J\right]$ for the problem Eq (2.4) and this completes the proof.

3.2.   Proof of convergence

Theorem 3.2. The series solution of the problem Eq (2.4)converges if $\left\vert y_{1}\left(t\right) \right\vert < c$ and $c$ isfinite.

Proof. Define a sequence $\left\{ S_{p}\right\}$ such that $S_{p} = \sum_{i = 0}^{p}y_{i}\left(t\right)$ is the sequence of partial sums from the series solution $\sum_{i = 0}^{\infty }y_{i}\left(t\right),$ we have

So

From Eq (2.7) we have

let $S_{p}, S_{q}$ be two arbitrary sums with $p\geqslant q$. Now, we are going to prove that $\left\{ S_{p}\right\}$ is a Caushy sequence in this Banach space. We have

let $p = q+1$ then,

From the triangle inequality we have

Since $0 < \phi < 1, p\geqslant q$ then $\left(1-\phi ^{p-q}\right) \leq 1$. Consequently

but $\left\vert y_{1}\left(t\right) \right\vert < \infty$ and as $q\rightarrow \infty$ then, $\left\Vert S_{p}-S_{q}\right\Vert \rightarrow 0$ and hence, $\left\{ S_{p}\right\}$ is a Caushy sequence in this Banach space then the proof is complete.

3.3.   Error estimate

Theorem 3.3. The maximum absolute truncated error Eq (2.4)is estimated to be $\underset{t\epsilon J}{\max }\left\vert y\left(t\right)-\sum_{i = 0}^{q}y_{i}\left(t\right) \right\vert \leq \frac{\phi ^{q}}{1-\phi }\underset{t\epsilon J}{\max }\left\vert y_{1}\left(t\right) \right\vert$

Proof. From the convergence theorm inequality (Eq 3.1) we have

but, $S_{p} = \sum_{i = 0}^{p}y_{i}\left(t\right)$ as $p\rightarrow \infty$ then, $S_{p}\rightarrow y\left(t\right)$ so,

so, the maximum absolute truncated error in the interval $J$ is,

and this completes the proof.

4.   Numerical examples

In this part, we introduce several numerical examples with unkown exact solution and we will use inequality (Eq 3.2) to estimate the maximum absolute truncated error.

Example 4.1. Application of linear FDE

A Basset problem in fluid dynamics is a classical problem which is used to study the unsteady movement of an accelerating particle in a viscous fluid under the action of the gravity ^[36]

Set

Equation (4.1) will be

Appling Eq (2.3) to Eq (4.2), and using initial condition, also we take a = 1, b = 1/2,

Appling ADM to Eq (4.3), we find the solution algorithm become

Appling Picard solution to Eq (4.2), we find the solution algorithm become

From Eq (4.4), the solution using ADM is given by $y\left(t\right) = \underset{q\rightarrow \infty }{Lim}{_{i = 0}^{q} y_{i}} \left(t\right)$ while from Eq (4.5), the solution using Picard technique is given by $y\left(t\right) = \; \underset{i\rightarrow \infty }{ Lim} \; y_{i}\left(t\right)$. Lately, the solution of the original problem Eq (4.2), is

One the same processor (q = 20), the time consumed using ADM is 0.037 seconds, while the time consumed using Picard is 7.955 seconds.

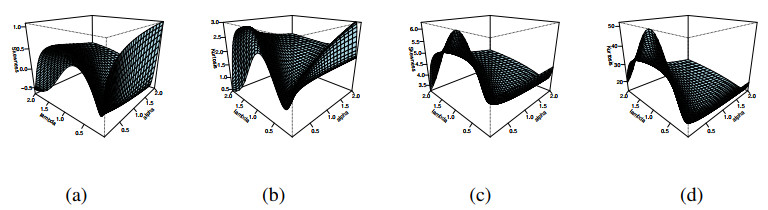
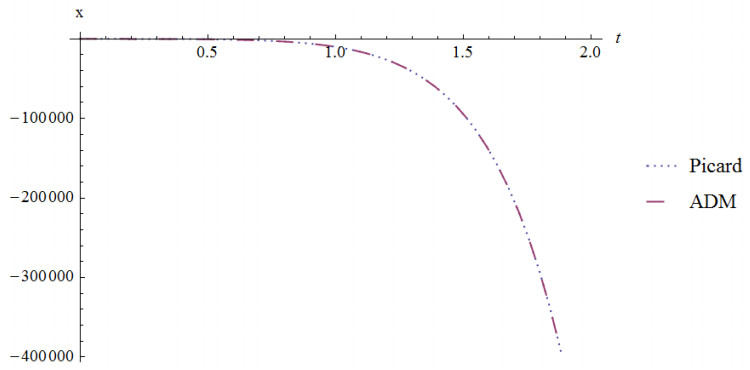
Figure 1 gives a comparison between ADM and Picard solution of Ex. 4.1.

Example 4.2. Consider the following nonlinear FDE ^[35]

Appling Eq (2.3) to Eq (4.6), and using initial condition,

Appling ADM to Eq (4.7), we find the solution algorithm will be become

at which A$_{\text{i}}$ are Adomian polynomial of the nonliner term $\left(^{CF}I^{1/2}y\right) ^{2}.$

Appling Picard solution to Eq (4.7), we find the the solution algorithm become

From Eq (4.8), the solution using ADM is given by $y\left(t\right) = \underset{q\rightarrow \infty }{Lim}{_{i = 0}^{q}y_{i}} \left(t\right)$ while from Eq (4.9), the solution using Picard technique is given by $y\left(t\right) = \underset{i\rightarrow \infty }{Lim} y_{i}\left(t\right)$. Finally, the solution of the original problem Eq (4.7), is.

One the same processor (q = 2), the time consumed using ADM is 65.13 seconds, while the time consumed using Picard is 544.787 seconds.

Table 1 showed the maximum absolute truncated error of of ADM solution (using Theorem 3.3) at different values of m (when t = 0:5; N = 2):

Figure 2 gives a comparison between ADM and Picard solution of Ex. 4.2.

Example 4.3. Consider the following nonlinear FDE ^[35]

Appling Eq (2.3) to Eq (4.10), and using initial condition,

Appling ADM to Eq (4.11), we find the solution algorithm become

at which A$_{\text{i}}$ are Adomian polynomial of the nonliner term $\left(^{CF}I^{1/2}y\right) ^{2}.$

Then appling Picard solution to Eq (4.11), we find the solution algorithm become

From Eq (4.12), the solution using ADM is given by $y\left(t\right) = \underset{q\rightarrow \infty }{Lim}{_{i = 0}^{q}y_{i}} \left(t\right)$ while from Eq (4.13), the solution is $y\left(t\right) = \underset{i\rightarrow \infty }{Lim}y_{i}\left(t\right)$. Finally, the solution of the original problem Eq (4.11), is

One the same processor (q = 4), the time consumed using ADM is 2.09 seconds, while the time consumed using Picard is 44.725 seconds.

Table 2 showed the maximum absolute truncated error of of ADM solution (using Theorem 3.3) at different values of m (when t = 0:5; N = 4):

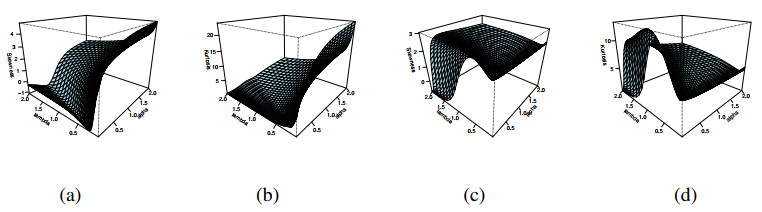
Figure 3 gives a comparison between ADM and Picard solution of Ex. 4.3 with $\alpha = 1$.

Example 4.4. Consider the following nonlinear FDE ^[35]

Appling Eq (2.3) to Eq (4.10), and using initial condition,

Appling ADM to Eq (4.15), we find the solution algorithm become

where A$_{\text{i}}$ are Adomian polynomial of the nonliner term $\left(^{CF}I^{\alpha }y\right) ^{4}.$

Then appling Picard solution to Eq (4.15), we find the solution algorithm become

From Eq (4.16), the solution using ADM is given by $y\left(t\right) = \underset{q\rightarrow \infty }{Lim}{_{i = 0}^{q}y_{i}} \left(t\right)$ while from Eq (4.17), the solution using Picard technique is $y\left(t\right) = \underset{i\rightarrow \infty }{Lim} y_{i}\left(t\right)$. Finally, the solution of the original problem Eq (4.14), is

One the same processor (q = 3), the time consumed using ADM is 0.437 seconds, while the time consumed using Picard is (16.816) seconds. Figure 4 shows a comparison between ADM and Picard solution of Ex. 4.4 $at \; \alpha = 0.7, \; \alpha _{1} = 0.1, \alpha _{2} = 0.3, \alpha _{3} = 0.5.$

5.   Conclusions

The Caputo-Fabrizo fractional deivative has a nonsingular kernel, and consequently, this definition is appropriate in solving nonlinear multidimensional FDE ^[37,38]. Since the selected numerical problems have an unkown exact solution, the formula (3.2) can be used to estimate the maximum absolute truncated error. By comparing the time taken on the same processor (i7-2670QM), it was found that the time consumed by ADM is much smaller compared with the Picard technique. Furthermore Picard gives a more accurate solution than ADM at the same interval with the same number of terms.

Conflict of interest

The authors declare there is no conflict of interest.