Extended dynamic mode decomposition for cyclic macroeconomic data

1.   Introduction

For many decades, business cycles remain among the most interesting and fruitful research areas in macroeconomics. There have been numerous studies which attempt to: (a) model business cycles; (b) shed light into the interconnection between business cycles and other economic features (for instance, inflation, rate of unemployment, technological shocks etc); and (c) understand the behaviour of business cycles (for instance, dominant frequencies, main business cycle drivers etc). Indicatively, we refer to Angeletos et al.(2020), Barsky and Sims (2011), Beaudry et al.(2020), Bloom et al.(2018), Dekimpe and Deleersnyder (2018), Galí (1999), Galí (2015), Hicks (1950), Jaimovich and Rebelo (2009), Justiniano et al.(2010), Jump and Stockhammer (2022), Lucas (1975), Michaillat and Saez (2022), Piiroinen and Raghavendra (2019), Puu (1989). Due to the complexity of the subject, many studies focus on specific types of economies which share similar characteristics. It is also clear that business cycles and its characteristic features (i.e. length, severity, amplitude, frequencies) are deeply connected with financial stability (or financial crises).

The growing complexity of economies has created new challenges in studying the business cycles. The data, which have to be analyzed and understood in order to reveal their information about the financial risk, are usually complex, non-linear and multi-dimensional. On the other hand, data science and machine learning have provided new techniques which allow us to monitor and analyze big and unbalanced data and retain all the information available (see for example Angeletos et al. 2020).

The main objective of the present paper is to apply data-driven and machine learning methods from the theory of Koopman operators and Extended Dynamic Mode Decomposition in the study and analysis of the business cycles. Although these techniques are extensively used in dynamical systems and control theory, especially in the case of non-linear or unknown dynamics, they are (to the best of our knowledge) underutilized in financial or economic studies.

Roughly speaking, the core idea underlying the Koopman operator theory (initiated in Koopman, 1931) in the following. Assume that we have a dynamical system, $\dot{{\bf x}(t)} = f({\bf x}(t))$, where ${\bf x}(t)\in \mathcal{M}$, which describes the evolution in time of the state variables ${\bf x}(t)$. The dynamics $f$ of the system may be non-linear or even unknown. The Koopman operator $\mathcal{K}$ acts on observables of the dynamical system, where the term observable refers to functions $g\colon \mathcal{M} \to \mathbb{C}$. More precisely, the operator updates every observable according to the evolution of the dynamical system. Therefore, it "lifts" the dynamical system from the state space to spaces of functions defined on the state space. The Koopman operator is linear and captures the dynamics of the original system. Furthermore, this linearization is global, in the sense that it does not hold in the are of a fixed point or a periodic orbit. Hence, methods from the operator theory, such as spectral analysis (von Neumann, 1932; Halmos and von Neumann, 1942; Halmos, 1951; Mezić, 2005), can be utilized in the analysis of the dynamical system.

The Koopman formalism is linear, albeit infinite-dimensional. Therefore, although theoretically it is easier to analyze the Koopman operator, its computation, as well as its spectral analysis, is always impossible, with only a few exceptions. Consequently, one wishes to find finite approximations of this operator. This issue remains a challenge in the area of dynamical systems. The first attempts towards this direction have had limited success. The most effective way for obtaining finite dimensional approximations of the Koopman operator is the Dynamic Mode Decomposition (DMD) (Rowley et al.2009; Schmid, 2010) and its generalization, the extended-DMD (EDMD). Both methods, in their numerical versions, are based on data, they are easy to implement, mainly relying on least squares regression, and computationally and mathematically flexible, enabling numerous extensions and applications (see, for instance, Brunton and Kutz, 2019). The final outcome is a finite dimensional linear dynamical system, which is necessarily defined in some augmented state space, and it approximates the original system. However, there is no guarantee that the resulting models will have good approximation properties.

Indeed, a clear drawback of the EDMD algorithm is the need to make an a priori choice of a finite set of observables (which is called a dictionary). It is well-known that the choice significantly impacts the approximation quality of the spectral properties of the system (see Williams et al.2015; Williams et al.2015; Korda and Mezić, 2018). For high-dimensional and highly non-linear systems, it is often not easy to make a judicious selection without prior information of the dynamics.

As it has been mentioned, our primary purpose is to apply the above described combination of Koopman operators and EDMD to study the business cycle. This approach also incorporates data-driven algorithms and machine learning methods, such as the Gaussian interpolation method. The final result is a linear model in some augmented state space whose projection is expected to approximate the trajectories of the business cycle. We are interested in examine whether the linear model has good approximation properties or not. It is also worth mentioning that the augmented state space contains several functions (observables) which are naturally indicated by the model, but they have not used in economic studies so far, since they do not seem to have some structural counterpart in the theory.

For simplicity of the presentation, and because we are mainly interested in the applicability of the method in the case of business cycle and not in specific data, we will not use real data in our study. Instead, we make use of a business cycle non-linear model to produce the data needed for applying the method. However, we would like to stress once again that the Koopman operator and EDMD approach can also be applied to real data of business cycles with no essential modifications. We choose the particular approach because one of our goals is to examine the strength of the proposed model and to which extend the linear model that is obtained is capable of approximating the trajectories of the original model.

More specifically, we consider the multiplier-accelerator model which initiated by Samuelson in $1939$. The original model of Samuelson was a linear two-dimensional model and it was capable of producing cycles only under a very restrictive choice of the parameters of the model. A non-linear model which is used in our work can be found in Puu (1989). The Samuelson-Hicks-Goodwin-Puu (SHGP) model (Samuelson, 1939; Hicks, 1950; Goodwin, 1951; Puu (1989)) is a non linear continuous dynamical model whose main merit is that in the appropriate parameter space sector predicts intrinsically business cycles which in the phase space are structurally stable limit cycles. This model is relatively simple and elegant. One of its characteristics is that it produces the business cycle without the use of exogenous shocks.

We approximate the SHGP dynamics which exhibits a limit cycle with two methods. In the first method, we extend, in continuous time, the two-dimensional state space of the SHGP model to a nine-dimensional linear space of observables $\mathrm{Obs}$ and we so obtain an EDMD finite approximation of the Koopman operator of the SHGP model. The elements of the vector of the residuals of the approximation do not tend to zero in the neighbourhood of the limit cycle and, as a result, the trajectories of the ensuing linear dynamical system are a good approximation to the flow of the SHGP model only for a short time span of the horizon.

The second method is data-driven, it applies in discrete time, and it requires a finite number of snapshots of the system as it evolves in time. We define data matrices with columns the values of a finite set of observables at the aforementioned snapshots. The finite approximation to the Koopman operator in this method is the shift operator which moves forward in unit time steps the vectors of observables and is determined with least squares minimization. In both methods, it is the dynamics of the linear dynamical system determined by the finite approximation to the Koopman operator which compares with the dynamics of the SHGP model. In the second method by augmenting appropriately the set of observables with more elements we are able to obtain an even better approximation, compared to the one we obtained with the first method, to the trajectories in the phase space of the SHGP model.

Business cycle is a complex topic in economics which is non linear depends on several parameters and it is difficult to analyze. Furthermore, there is a plethora of data available for every economy. The latest developments in machine learning and computer science have provided new data-based methods for analyzing such phenomena and revealing underlying structures and correlations. The data-driven approach of Koopman operators in combination with EDMD are ideal for system that combine those characteristics. Therefore, it is natural to apply this methods to the study of the business cycle.

There have been other papers in the literature on DMD and business cycles, albeit with different focus. Hua et al.(2015) used DMD to extract cyclic activity in financial markets whereas in Kuttichira et al. 2017a, 2017b proposed a method for stock price prediction using DMD. In Mann and Kutz (2015), the application of an algorithmic trading strategy is demonstrated based upon DMD.

This paper is organized as follows: In Section 2 we give the bare essentials of the Koopman operator theory and of the associated EDMD method.In Section 3, we remind the numerical EDMD algorithm which implements the finite-dimensional approximations of Section 2. In Section 4, we propose a method, based on Gaussian process interpolation, for training the linear system that is used to approach the non-linear one. In Section 5 we give all the necessary theoretical prerequisites of the SHGP model. In Section 6 we apply the EDMD method to the SHGP model in continuous time. In Section 7 we apply the numerical EDMD algorithm to the SHGP model in discrete time. In Sections 8 and 9 we study the eigenstructure of the linear model that have been obtained in Section 7. In Section 11 we use more complex periodic data. We explain how this method can be applied to this data and we also describe a more general approach that can be used in real data. Finally, in Section 10, we apply the interpolation-based method to the SHGP model and Section 12 concludes the paper.

2.   Koopman operator theory and EDMD

We consider a continuous dynamical system

defined on some manifold $\mathcal{M}\subseteq \mathbb{R}^d$, through the function $f\colon \mathcal{M} \to T\mathcal{M}$. The flow map $\Phi(t, {\bf x}_0)$ describes the evolution of the system in time $t\ge 0$ with initial condition ${\bf x}_0$, i.e. $\Phi(t, {\bf x}_0)$ is the state of the system when we start from initial condition ${\bf x}_0$ after time $t$.

Alternatively, we may consider a discrete dynamical system

defined by some function $f\colon \mathcal{M} \to \mathcal{M}$. In this case, we denote the flow map by $\Phi(n, {\bf x}_0)$. Discrete systems are often more natural, especially when we consider measurements from data. Furthermore, continuous system give rise to discrete ones by considering sampling in some time-step $\Delta t$.

Any function $g\colon \mathcal{M} \to \mathbb{C}$ is called an observable of the system. We assume now that $\mathcal{F}$ is a function space which is closed under composition with the flow $\Phi(t, {\bf x}_0)$. The Koopman operator $\mathcal{K}^t\colon \mathcal{F} \to \mathcal{F}$ updates every observable $g\in \mathcal{F}$ according to the flow of the dynamical system, i.e. $\mathcal{K}^t(g) = g\circ \Phi(t, \cdot)$. It is clear that when we refer to the Koopman operator, we actually refer to a set of operators $(\mathcal{K}^t)_{t\ge 0}$. However, in accordance with the literature, we will use the term Koopman operator. In the case of discrete systems, the definition is similar and simpler. The Koopman operator is defined as $\mathcal{K}(g) = g\circ \Phi(1, \cdot)$. It should also be pointed out that in many applications the function $f$ defining the system is measurable and the space $\mathcal{F}$ is the Hilbert space of square integrable complex-valued functions on $\mathbb{R}^d$.

The Koopman operator associated to a dynamical system is clearly linear and the research has shown that its spectral decomposition characterizes the behaviour of the dynamical system. Hence, this type of operators offer a linear representation of the original system which is also global, that is it does not valid only in some area of a fixed point or a periodic orbit. However, this operator is inevitably infinite dimensional and in the majority of cases it is impossible to be calculated. Consequently, several methods have been developed for approximating the Koopman operator and its spectral properties with finite dimensional linear operators. Dynamic mode decomposition (DMD) and Extended dynamic mode decomposition (EDMD) have been proved very useful and they are the more successful methods in this direction. These approaches, in their numerical versions, depend on data and their aim is to produce a linear model which best fits the spatial measurements from one time to the next. This model is not only linear but also finite dimensional and it is not defined in the state space $\mathcal{M}$ but on some augmented space $\overline{\mathcal{M}}$ of dimension bigger than $\mathcal{M}$. Hence, we somehow exchange linearity with dimensionality. Although the original system is non-linear, one expects that this approach will be rich enough to capture the spectral analysis of the Koopman operator and the trajectories of the original system at some specific part of the state space.

This type of approximation (DMD method) involves the following steps.

${\rm{(a)}}$ For a given non-linear dynamical system

define a set of observables $\{\psi_1, \psi_2, \ldots, \psi_m\}$ (this set is called a dictionary) and consider the linear space $\widetilde{\mathcal{F}}$ spanned by these functions.

${\rm{(b)}}$ If $\widetilde{\mathcal{F}}$ is invariant with respect to the Koopman operator $\mathcal{K}$, then the restriction of $\mathcal{K}$ to $\widetilde{\mathcal{F}}$ gives a finite dimensional linear operator which can provide information about the eigenstructure of $\mathcal{K}$.

${\rm{(c)}}$ However, it is extremely rare to find a finite dimensional invariant space of observables. Consequently, we have to consider the orthogonal projection of $\mathcal{K}$ to $\widetilde{\mathcal{F}}$.

Koopman operator theory and EDMD is a systematic way to address problems from systems and model identification, model expansion and model reduction by using tools from Operator Theory and AI. In elementary terms, flows of dynamical systems $\Phi(t, {\bf x}_0)$ are decomposed as

where $m_i(t)$ are modes of a linear system, i.e combinations of exponentials, trigonometric and polynomial functions and $g_i({\bf x}_0)$ depend on the basis of EDMD which is taken from a superset of observables called dictionary.

The quality of this approximation depends on the selection of observables, i.e the dictionary, which for complex non-linear systems is created via AI and machine learning methods.

3.   Data-driven EDMD algorithm for the Koopman operator of non-linear or unknown dynamics

We next give a brief description of the EDMD algorithm for the Koopman operator which numerically implements the approximations described in Section 2. We assume again that we have a dynamical system of the form (1), i.e. $\dot{{\bf x}} = f({\bf x})$, ${\bf x}\in \mathbb{R}^n$, where the dynamics $f$ are non-linear or even unknown. We cannot expect to obtain a linear approximation of the same dimension $n$ and hence, we need to construct an augmented state space. This algorithm consists of the following steps.

$1.$ Initially, we need data from the original system. We assume that $k$ trajectories of the original system are executed and they start from different initial conditions ${\bf x}_{0j}$, $j = 1, \ldots, k$. Each trajectory is witnessed for some time horizon $T$ and sampling points are collected at a fixed time interval $\Delta t$. Hence, $\frac{T}{\Delta t}$ points of each trajectory are collected. It should however be noted that uniform sampling in time is not necessary and one may consider different sampling methods for collecting the data. Finally, our data are given by

$2.$ We next choose number a $m$ and some set $\phi_1, \ldots, \phi_m$ of observables, which is called a dictionary. This step is very important. A suitable dictionary leads to good approximation properties while a "bad" choice may result in false conclusions. The choice of the dictionary remains a challenge in the theory of Koopman operators and dynamical systems.

The augmented (or lifted) stated space consists of vectors of the form

where ${\bf \phi}({\bf x}) = \left[ \phi_1({\bf x}), \ldots, \phi_m({\bf x}) \right]^T$. Hence, this space has dimension $m+n$. As it is expected, if we wish to approximate the original non-linear system with a linear one, we have to pay in dimensions. The number $m$ of additional coordinates varies and depends on the behaviour of the original system. If our data indicate that the dynamical system, although non-linear, has a "smooth" behaviour, then it suffices to consider only a few additional coordinates. For systems with extreme behaviour and complex trajectories, the number $m$ should be large enough to obtain good approximation properties (if this is possible). Each trajectory of the original system corresponds to a trajectory in the lifted space. Therefore, the collected data $\left(\left({\bf x}_{js}\right)_{s = 0}^{n_0} \right)_{j = 1}^k$ correspond to data in the augmented state space which have the form

for initial values ${\bf y}_{j0}$, $j = 1, 2\ldots, k$. For any $j = 1, 2, \ldots, k$, we set

$3.$ Finally, a best-fit (finite dimensional) linear operator $\widetilde{{\bf A}} \in \mathbb{R}^{(n+m)\times (n+m)}$ is obtained such that ${\bf \mathcal{Y}}_{j, [1, n_0]} \approx \widetilde{{\bf A}} {\bf \mathcal{Y}}_{j, [0, n_0-1]}$ for all $j = 1, \ldots, k$. The matrix $\widetilde{{\bf A}}$ is constructed with least square regression methods. For instance, one may consider

The (finite dimensional) linear operator $\widetilde{{\bf A}}$ can now be used to approximate the trajectories of the original dynamical system. More precisely, given initial condition ${\bf x}_0\in \mathbb{R}^n$, one has to move into the lifted space and to consider the initial condition ${\bf y} = [{\bf x}_0, {\bf \phi}({\bf x}_0)]^T$. Then, the trajectory $\left\{{\bf y}_n\right\}$ of the linear system ${\bf y}_{n+1} = \widetilde{{\bf A}} \cdot {\bf y}_n$ can also be obtained. The projection of this trajectory to the first $n$ coordinates gives rise to an approximation of the trajectory of the original system, provided that the choice of dictionary is proven to be suitable.

Roughly speaking, the above approach has the following characteristics. (a) If we isolate one of the trajectories, starting at the point ${\bf x}_{0j}$, then we expect that we will be able to reproduce the trajectory of the original non-linear dynamics with a finite dimensional linear operator whose dimensions are rather small. (b) However, if we consider another trajectory, starting at a different point, then it is highly likely that the linear operator that approximates the previous one may not be able to catch the new orbit. Therefore, if we consider many different trajectories, then, in order to obtain as accurate results as possible, we may have to consider liner operators with much bigger dimensions. In other words, we have to pay in dimensions, if we wish to have good approximations.

4.   EDMD and learned approximations to Koopman operator

Motivated by the above observations of the previous section, we now propose a methodology for obtaining relatively good approximations using however operators with low dimensions. The core idea in this approach is to replace the matrix ${\bf A}$ with a matrix whose entries are functions rather than numbers and to train these functions with some machine learning technique. In this approach, it is expected that a smaller numbers of observables are needed to obtain good approximations.

More precisely, this methodology consists of the following steps.

$1.$ We again execute $k$ trajectories of the dynamical system with initial conditions ${\bf x}_{0j}$, $j = 1, \ldots, k$. We collect the data as above. Again, it is not necessary to perform a uniform sampling.

$2.$ We again consider some dictionary, i.e. a set of observables ${\bf \phi} = \left(\phi_1, \phi_2, \ldots, \phi_m\right)$. These measurements may be linear or non-linear and they may also contain the original state ${\bf x}$.

$3.$ For each trajectory, we consider the matrices

Then, we find a best-fit linear operator that maps ${\bf \mathcal{Y}}$ to ${\bf \mathcal{Y}}'$ by solving the regression problem

As far, the method coincide with the previous one. The difference is that we apply the method for each trajectory separately and thus we have obtained a set of linear operators ${\bf A}^j$ corresponding to the initial conditions ${\bf x}_{0j}$, $j = 1, \ldots, k$. The linear system produced by each one of these operators is expected to provide a good approximation of the corresponding trajectory. However, it may present poor performance in other trajectories under different initial conditions.

To overcome this inconvenience, we consider for every $i, r = 1, 2, \ldots, m$, the set of points $\left({\bf x}_{0j}, a_{ir}^j \right)_{j = 1}^k$ which associated each initial condition ${\bf x}_{0j}$ with the $(i, r)$-entry of the matrix ${\bf A}^j$. Applying Gaussian interpolation process, we find a function $a_{ir}({\bf x}_0)$ (${\bf x}_0 \in \mathcal{M}$ should be interpreted as the initial condition) which best fits the points that we have considered.

Consequently, the matrix

is constructed whose entries are functions on the state space $\mathcal{M}$. Given some initial condition ${\bf x}_0 \in \mathcal{M}$, one may consider the linear system produced by the matrix ${\bf A}({\bf x}_0)$ for the specific choice of ${\bf x}_0$. The projection of this linear system is expected to have good approximations properties at least along the trajectory of the original system with initial condition ${\bf x}_0$.

5.   The SHGP model

At the beginning of the thirties, the Great Depression shook the very foundations of the modern world, causing great damage to virtually all advanced countries and laying a responsibility on the international economics community to explain these frightening recurring downward movements in the level of production and to possibly find a cure for them.

Culmination of the efforts to explain these recurring downward movements led to the advent of Samuelson's Samuelson (1939) multiplier-accelerator model in 1939 which gave birth to modern business cycle theory. As demonstrated by Samuelson, the interplay between the multiplier analysis and the principle of acceleration may generate temporary business cycles.

Samuelson's model is based on the Keynesian multiplier, which is a consequence of assuming that consumption intentions depend on the level of economic activity, and the accelerator theory of investment, which assumes that investment intentions depend on the pace of growth in economic activity.

Samuelson's multiplier-accelarator model clearly displays the limitations of linear analysis. The model is capable of either producing exponentially damped or exponentially explosive change, but nothing else. Hicks Hicks (1950) and Goodwin Goodwin (1951) convincingly argued that Samuelson's model conforms better to reality if the linear investment function in it is replaced by a nonlinear investment function.

Puu a few years later Puu (1989) suggested a model which also includes a nonlinear investment function. Puu's model subdues the models suggested by Hicks Hicks (1950) and Goodwin Goodwin (1951) and it is epitomized in the following system of differential equations

The meaning of the symbols $Y,$ $s$ and $v$ is as follows: $Y$ denotes the income. Savings, $S$, are a given proportion $s$ of the income. Investments, denoted $I$, are by definition the rate of change of capital stock. Thus: $I = v \frac{dY}{dt}$ and $S = sY.$

One can easily show that the dynamical system (2), (3) has one equilibrium point at $(Y, I) = (0, 0).$ A linearization of the system at $(Y, I) = (0, 0)$ yields

If $r_{1}$ and $r_{2}$ are the roots of the characteristic polynomial of the matrix $\left[ \begin{array}{cc} - s & - v s \\ \ \ 1 & -1 + v \end{array} \right]$ we easily find that

If $v-1-s > 0$ equation (5) implies that $Re(r_{1}) > 0, \ Re(r_{2}) > 0$. Therefore, the equilibrium point (0, 0) is unstable and the dynamical system exhibits Puu (1989) a stable limit cycle. If $v-1-s < 0$ equation (5) implies that $Re(r_{1}) < 0, \ Re(r_{2}) < 0$ and consequently the equilibrium point (0, 0) is stable and the dynamical system does not possess Puu (1989) any limit cycle.

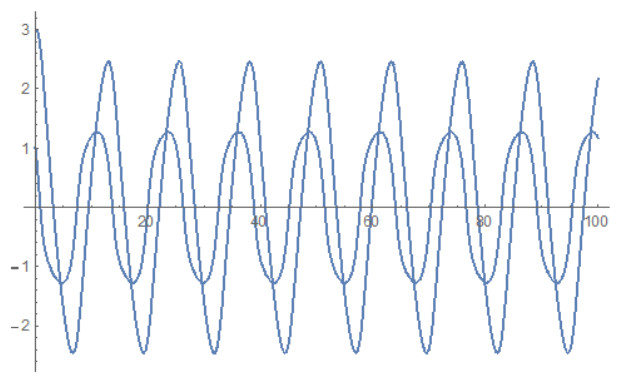
For example, by choosing $Y(0) = 3$, $I(0) = 1$, and $v = 2$ and $s = 0.3$, by numerically integrating (2), (3) we obtain for $Y(t)$ and $I(t)$ the plots shown in Figure 1.

By plotting in phase space $I$ against $Y$ we obtain the diagram of Figure 2.

The main feature of the SHGP model which also constitutes its main merit is that in the appropriate parameter space sector predicts intrinsically business cycles which in the phase space are structurally stable limit cycles. The SHGP model cannot be solved in closed form. We approximate the SHGP dynamics in the presence of a limit cycle with two methods. The first method is model based and it is given in section 6. The second method is data driven and it is given in Section 7.

6.   Koopman operator and observables for the non-linear business cycle model

In this section, we extend, in continuous time, the two-dimensional state space of the SHGP model to a finite-dimensional linear space of observables $\mathrm{Obs}$ and we so obtain an EDMD finite approximation of the Koopman operator of the SHGP model.

We consider the following set of observables (dictionary):

For instance, $Z_{10} = I$, $Z_{01} = Y$, $Z_{20} = I^2$, $Z_{11} = IY$, $Z_{02} = Y^2$ and so on. Substituting $\dot{Y}$ from Equation (2) to Equation (3) and after some calculations, we obtain

Hence,

Similarly,

It follows that the space $\mathrm{Obs}$ generated by the observables $(Z_{kr})_{k, r = 0}^\infty$ is invariant. The above equations can be written in the following form

In matrix form

Hence, we may approximate the non-linear dynamical system with the following linear one:

Figure 3 shows the eigenvalues of the $15\times 15$ approximation of the Koopman operator. We observe the appearance of eigenvalues whose real part is $1$ or close to $1$. On the other hand, there are no eigenvalues with small real part, i.e. eigenvalues which is imaginary numbers. This implies that the linear dynamical system has trajectories that diverge to infinity and it cannot give the limit cyclic behaviour. Hence, it can be used for short term predictions of $Y$ and $I$. Finally, Figure 4 shows the "true" $Y(t)$ and $I(t)$ and compares them with the corresponding functions obtained by the previous approximation. It is clear that for short term, one has good approximations. However, the solutions obtained with the aforementioned method do not exhibit the cyclic limit behaviour of the "true" solutions $Y(t)$ and $I(t)$.

The fact that one has short term good approximation of the "true" $Y(t)$ and $I(t)$ can be attributed to the fact the elements of the vector of residuals which appear in (8) do not tend to zero at the neighbourhood of the limit cycle.

7.   Extended Dynamic Mode Decomposition and trajectories of the business cycle

In this section we find a data-driven EDMD finite approximation of the Koopman operator of the SHGP model. We consider a finite number of snapshots of the system as it evolves in time. We define data matrices with columns the values of a finite set of observables at these snapshots. The finite approximation to the Koopman operator in this method is the shift operator which moves forward in unit time steps the vectors of the observables and it is determined with least square fit.

The task is to approximate these trajectories (shown in Figure 5) via EDMD through discretization in the Horizon $[0, 40]$. We performed Sampling of $401$ points within this horizon together with the enhancement of state space from $2$ to $15$ dimensions as described by the following vector of observables:

This gives rise to an $X_{[0,400]} \in \mathbb{R}^{15\times 401}$ observation matrix of the specific trajectories, in the extended state space. The final step of the EDMD is the solution of the following matrix equation by matrix inversion:

"A" is the system matrix of a linear system in a 15-dim state space that may be used as an alternative description for the above periodic trajectories defining the limit cycle of the original nonlinear system. The location of the poles of the linear system as well as the distribution of their modulus' are depicted in Figure 6.

By using A and the same initial conditions we reconstruct Y in the horizon [0, 40] which is shown in the following graph where the periodic features of the trajectories are preserved and apparent as shown in Figure 7.

Furthermore the comparison of this trajectory with the original data used to "train" $A$ is shown in Figure 8.

This demonstrates

${\rm{(a)}}$ the strong approximating power of the discrete EDMD method for a single trajectory;

${\rm{(b)}}$ the existence of small deviations from the ideal data only at the peaks and troughs;

${\rm{(c)}}$ sustained oscillation for an horizon of at least $[0,100]$ and then emergence of slow decay with time as shown in Figure 9 of the EDMD approximation in the extended horizon of $[0,800]$ (out of sample).

We note that the much better approximating power of the discrete EDMD method, given in this section, as compared with the approximating power of the continuous EDMD method given in section 5 is made intelligible by the different nature of the two methods. In the continuous EDMD method we approximate ab initio the non-linear SHGP model (2), (3) by a linear model (8) and it is this linear model which we integrate. The residuals of the linear approximation which appear in (8) not only do they not tend to zero in the vicinity of the limit cycle but also they propagate and become bigger when we integrate (8). On the contrary, the data used in this section in order to construct the matrices $X_{[0,400]}, \ \in X_{[1,401]}$ and thereby to derive the matrix $A$ are obtained by integrating the exact Equations (2), (3) and not a finite approximation of them.

Continuous EDMD from Discrete EDMD

Given the better approximating power of the discrete EDMD method as compared with the continuous EDMD method we can use the finite approximation $A$ to the Koopman operator derived from the discrete EDMD in Section 7 to obtain a more efficient finite approximation $\overline{A}$ to the Koopman operator in the continuous EDMD by requiring

where $\Delta t$ is the time step which separates the snapshots of the system in the discrete EDMD in Section 7. Solving equation (8), we obtain the matrix $\overline{A}$. This can be used in Equation (8) to gibe better results in the continuous case.

8.   Discrete EDMD with different initial conditions

To demonstrate the efficacy of the discrete EDMD we calculate the finite approximations of the Koopman operator with discrete EDMD for various initial conditions inside and outside the limit cycle. This set of initial conditions is described by the line segment $\{ (1-t)(1, 1)+t(3, 3), \ t = 0.01k, \ k = 0, 1, ..., 100\}.$ For these operators-finite approximations to the Koopman operator we calculate the eigenvalues and a selection of the distribution of their magnitudes. These are depicted in the Figures 10 and 11.

We note that all these operators have an eigenvalue with modulus very close to $1$; it is the oscillatory mode which leads to the limit cycle in the phase space. The other eigenvalues with various degrees of volatility in their magnitudes, as depicted in Figure 11, are responsible for the transient state which drives the SHGP system towards the limit cycle.

Finally, a plot of the frequency corresponding on the average highest eigenvalue is shown in Figure 13.

We observe that the range of values and the variances of the larger eigenvalues (that shape the dominant frequency of the cycle) is much less than that of the smaller eigenvalues (that control the transient behaviour of the trajectories). A plot of the average modulus of eigenvalues by size is given in Figure 12.

We note that this mode which leads to the limit cycle dies off in a very slow pace well beyond of the time horizon of the 40 years.

9.   Evolution of the eigenvalues' location of the EDMD operator on the same $I, Y$ trajectory but with variable initial conditions

As we have shown in Section 7, the (finite-dimensional) linear operator (matrix) obtained from data with the EDMD method has strong approximation properties for a single trajectory of the non-linear dynamical system of the business cycle. We have also studied the eigenvalues of this operator, and we have observed the existence of eigenvalues in the unit circle, giving the periodic part of the solutions, and the existence of eigenvalues located away from the unit circle, corresponding to the transient part of the business cycle.

In this section, we focus on a single trajectory of $Y$ and $I$ and we examine the evolution of the eigenvalues of the EDMD operators which are obtained from different initial conditions (on the same trajectory).

We start with $t = 0$ and the initial condition $Y = 30, I = 30$ which is located away from the business cycle and the trajectory in the horizon $[0, 40]$ contains a significant transient part. The EDMD operator has eigenvalues located close to the unit circle (capturing the periodic part of the trajectory) and some eigenvalues away form it capturing the transient part. The eigenvalues in the complex plane are shown in Figure 14.

We considered now the window of the horizon to move to $[2, 42]$ on the same orbit as before. The new trajectory segment moves deeper into the business cycle and captures more of the cyclic part. Thus the new EDMD operator eigenvalues approach further the unit circle (see Figure 15). Finally moving the window to $[30, 70]$, i.e. for initial condition at $t = 30$, the trajectory segment is fully periodic and thus the EDMD eigenvalues are on the unit circle (see Figure 15).

10.   The use of EDMD with varying initial conditions by interpolating EDMD matrices

So far we have demonstrated the use of state space augmentation by EDMD methods, as a new form of linear representation and a tool for numerical simulations of the business cycle dynamic model with cubic nonlinearity. If the initial conditions as well as the horizon are both fixed, then the results (proximity of flows) are satisfactory and are achieved with a moderate state space augmentation from $2$ to $15$ in dimension. However, the use of a single EDMD matrix for a range of initial conditions seems intractable without significantly increasing the dimension of the state space. In this section we propose to interpolate EDMD matrices each of which fits a single trajectory starting from an initial condition in a set of predefined points of the state space. Here for the specific example we study, we consider a segment of initial conditions $S_{[0, 1]} = \{(1-r)(1, 1)+r(3, 3) \mid r \in [0, 1]\}$ parametrized by $r \in [0, 1]$. This set parametrises a large part of the flows of the business cycle system in the proximity of the attractor from both its inside and outside. We sample $101$ equidistant points of this segment and calculated $101$ EDMD matrices $A_r$, $r \in \{0, 0.01, 0.02, \ldots, 1\}$ approximating the trajectories starting from these $101$ initial conditions. The purpose now is to interpolate these finite set matrices to a continuum of matrices $A_r$ with $r\in [0, 1]$ so as we have an EDMD matrix for every initial condition in $S_{[0, 1]}$. By plotting each entry of EDMD matrices $A_r$ against $r\in \{0, 0.01, 0.02, \ldots, 1\}$ we observe that the graphs vary significantly as shown in the following figures, a fact that suggests the use of a generic method of interpolation. Here we consider the Gaussian process interpolation method recently popularized in the machine learning community and created a $15\times 15$ matrix of interpolatory functions covering all $S_{[0, 1]}$. The results for three (out of $15^2$) representative entries are shown in Figure 16.

The plots of Figure 16 show the existence of an overshoot of the values of the entries of the matrices $A_r$ when $r$ located between $0.05$ and $0.2$. The Gaussian process interpolation traces all the values of the entries correctly within the domain $r \in [0, 1]$ apart from (possibly) the segment $r\in [0.05, 0.2]$. This segment is a neighborhood of the intersection of $S_{[0, 1]}$ with the attractor and, there, it seems that this generic interpolatory method may fail for some of the entries of $A_r$. Figure 17 demonstrates the cyclic path of the business cycle system along with the segment $S_{[0, 1]}$ of initial conditions and the exceptional subset of $S_{[0, 1]}$ which is located in the vicinity of the attractor.

With this in mind, we proceeded to fit $15^2 = 225$ interpolatory gaussian process functions corresponding to every entry of $A_r$. Thus for every initial condition in $S_{[0, 1]}$ we may calculate an EDMD matrix $A_r$. Next we demonstrate some results on the performance of this method by comparing the real trajectories with those taken by the EDMD interpolatory matrices both starting from various initial conditions in $S_{[0, 1]}$. The two trajectories are plotted in the same graph for comparison purposes. The results are shown in Figure 18

11.   Application to real data

To apply the dynamic modelling approach presented for data arising from SH data to more general cyclic data given by a time series $I(t)$ one has to introduce an auxiliary variable $Y(t)$ by exponentially smoothing and scaling $I$ and then to consider an EDMD basis of the form $I^k Y^\lambda$, $k, \lambda \in \mathbb{N}^*$. This approach poses some conceptual and numerical challenges which will appear in the sequel.

The easiest approach to fit such dynamic models to data with noise or not is to consider basis of the form $I, \dot{I}, \ddot{I}, \ldots, I^{(n)}$ for continuous data, or $I, L(I), L^2(I), \ldots, L^n(I)$ for discrete data and to explore linear relationships between them for $n$ large enough. This can be extended to vector or matrix data ${\bf G}_k$ and the minimum order of dynamics required (which reflects the complexity of the data) is determined ny the rank $p$ of the infinite Hankel matrix ${\bf H}_{\infty \times \infty } (G)$, where

This leads to a minimal state space triple $({\bf C}, {\bf A}, {\bf B})$ where ${\bf A}\in \mathbb{R}^{p \times p}$. The matrix ${\bf A}$ reflects the dynamics of the data with respect to the selected basis. In the case of cyclic data, ${\bf A}$ contains the essential modes as described by the Fourier frequencies. ${\bf C}$ is a selection matrix which describes the linear observables, i.e. the time series to be modelled. Furthermore, the pairs $({\bf C}, {\bf A})$ and $({\bf A}, {\bf B})$ are observable and controllable respectively.

For a given set of observables, i.e. time series, the minimal triple $({\bf C}, {\bf A}, {\bf B})$ can be constructed in a variety of ways (hence, it is not unique). Nevertheless, there is a similarity equivalence between these triples that leaves the object ${\bf C}({\bf I}-\lambda {\bf A})^{-1}{\bf B}$ invariant.

For a set of observed time series $S = \{ I_1, I_2, \ldots, I_k \}$ one has to extend $S$ to $\overline{S} = \{ f_j(I_1, I_2, \ldots, I_k) \}_{j = k+1}^{p+\lambda} \bigcup S$. $B$ is a single $(p+\lambda) \times 1$ vector of initial values of the observables basis $\overline{S}$, ${\bf C} = \left[ I_k, 0_{k\times (p+\lambda)-k} \right]$ and ${\bf A}$ is a transition matrix to be calculated with EDMD methods.

For the case of a single time series $I_1$, which is the case in this paper, as we mentioned in the beginning of the present section, we select a basis $\{ I, Y, I^k Y^\lambda \}_{k = 1, \lambda = 1}^{p_1 p_2}$, with $p_1\cdot p_2 +2 \ge p$. We demonstrate this use with the following toy example. For simplicity purposes, we consider a time series formed by exactly two Fourier frequencies and no noise as shown in Figure 19(a).

If the two frequencies are observable, one can easily model this time series as a sum of the outputs of two independent harmonic oscillators, that is, the output of a four state dynamical system.

In this respect, in a time horizon $t\in [0, 50]$, we sample $I(t)$ in $510$ points creating a time series $I_t$ and also subsequently an exponentially smoothed time series $Y_t$. We calculate the transition matrix $A$ with matrix pseudo-inversion and we assess the results with two metrics: (a) The sum of squares of errors of all variables in the selected basis; (b) The sum of squares of errors only for the target variable. We insert and delete basis variables of the form $I^k Y^\lambda$ according to whether they improve or not the two metrics. Finally, we end up to the following basis

Figure 20 shows the eigenvalues of the $6\times 6$ matrix ${\bf A}$.

The estimated time series $\hat{I_k}$ is calculated by

The two plots of $\hat{I_k}$ and $I_k$ are shown in Figure 21.

Therefore, to correct the inaccuracy of the modes of $\hat{I_k}$ and to reestablish periodicity, we may either

${\rm{(a)}}$ project the modes of ${\bf A}$, located close to the unit circle, to the unit circle by radial projection keeping the same eigenstructure of ${\bf A}$; or

${\rm{(b)}}$ improve EDMD pseudo-inversion by weighted least squares by optimizing transition on all significant peaks and monotonic parts of the time series.

Furthermore, we may reduce the states to four by extracting only the observable part of ${\bf A}$. To this end, we applied a radial correction to the eigenvalues of ${\bf A}$ which resulted to a new estimation $\hat{I_k}$ which is almost identical to $I_k$ as it was required (see Figure 22).

In the case of real periodic data with richer spectrum and stochastic noise the application of the projection method used in the above example is challenging. A plain EDMD method utilizing the aforementioned procedure produces poor results. The least one must require is a modified EDMD construction that forces the location of the modes of ${\bf A}$ towards the unit circle. This is a demanding problem which can however suboptimally calculated in two stages as follows.

${\rm{(a)}}$ Calculate ${\bf A}$ by pseudo-inversion as ${\bf A} = {\bf \mathcal{Y}}' {\bf \mathcal{Y}}^{-1}$ and let ${\bf T}$ be a real eigenframe of ${\bf A}$, i.e. ${\bf A} = {\bf T}^{-1}{\bf \Lambda} {\bf T}$, where ${\bf \Lambda}, {\bf T}$ are all real matrices.

${\rm{(b)}}$ Then, consider the orthogonal procrustes problem

where ${\bf U}{\bf U}^T = {\bf U}^T {\bf U} = {\bf I}$ and ${\bf \mathcal{Y}}_2 = {\bf T} {\bf \mathcal{Y}}_1'$, ${\bf \mathcal{Y}}_1 = {\bf T}{\bf \mathcal{Y}}$.

The solution ${\bf U}$ in closed form is given by ${\bf U} = {\bf V}_1 {\bf V}_2$ where ${\bf V}_1 {\bf \Sigma} {\bf V}_2$ is the SVD of ${\bf \mathcal{Y}}_2 {\bf \mathcal{Y}}_1^T$. Then, a suboptimal EDMD solution of the original problem, i.e. $\underset{{\bf A}}{\min} \|{\bf \mathcal{Y}}' -{\bf A} {\bf \mathcal{Y}} \|$ under the condition that $\mathrm{spec}({\bf A}) \subseteq S_1$ is given by ${\bf A} = {\bf T}^{-1} {\bf U} {\bf T}$. All the linear observables induced by the transition matrix ${\bf A}$ will be periodic by construction and hence $\hat{I}_k$ is also periodic. Finally, given the minimality conditions above, the obtained $\hat{I}_k$ is expected to be close to the original time series $I(t)$.

12.   Conclusions

We have applied the theory of Koopman operators combined with EDMD in order to study the trajectories and phase portrait of business cycles. Towards this aim, we have utilized the Samuelson-Hicks model. The original model is a linear and two-dimensional and it is not capable of producing cycles, except some rare cases. A non-linear version which was the base of our investigation, can be found in Puu (1989). This model, despite being relatively simple, is convincing and distinguished for its elegance. The periodic behaviour of $Y$ and $I$ is an endogenous characteristic of the model as it follows from the equations themselves and not from some exogenous shock. Latest studies, utilizing the strength of computers and programming, incorporate data from a plethora of economic variables. However, Samuelson's multiplied-accelerator model remains a standard reference and a topic of several studies and research.

Our primary purpose is to approximate the two-dimensional, non-linear model with a linear dynamical system which will be able to capture the main features of the business cycle and it will be more suitable for prediction and control. In order to achieve this goal, we have to pay in dimensions. Koopman operator has established as a standard tool for deriving a global linear representation of a non-linear dynamical system, which is valid in the whole state space and not only near fixed points or periodic orbits. This operator captures the dynamics of the original system and it is linear. Nevertheless, it is infinite dimensional and it is usually not possible to calculate. Consequently, the very next challenge is to obtain "successful" finite dimensional approximations of this operator.

Our first attempt is described in Section 6. We choose a set of observables, namely the set $\{Z_{kr}\}_{k, r\ge 0}$ which contains all possible products of $Y$ and $I$. These functions may not have some true structural counterpart in the the theory and, to the best of out knowledge, may have not been utilized so far. However, our choice is induced by the form of the system of differential equations describing the model, since this set of observables is invariant with respect to the Koopman operator.

We next have to consider a finite subset (which is called a dictionary) of the aforementioned observables and the subspace they span. This step is very crucial. In the ideal case where the finite subspace spanned by the dictionary is invariant with respect to the Koopman operator, one can project the Koopman operator and obtain a finite approximation. This can be then used to calculate eigenvalues, modes etc.

However, as it was demonstrated in Section 6, the finite subsets of $\{Z_{kr}\}_{k, r\ge 0}$ do not produce subspaces close to being Koopman invariant. Therefore, the generated finite dimensional linear operators can not capture the trajectories of the business cycle, except some small time horizon. Consequently, they can be used only for short time analysis.

The second approach, along with its characteristics, main approximation results and properties, is analyzed in Sections 7, 8, 9 and 10. This approach also uses the same dictionary, however it depends on data and measurements. The main idea is to approximate the Koopman operator with a finite dimensional matrix which best fits the high-dimensional data and advances spatial measurements from one time to the next. The obtained linear system can then be used to approximate the trajectories of the original non-linear system.

It should be pointed out that in our analysis we used data from the model itself. That is, we integrated numerically the system of differential equations and we obtained some trajectories of the non-linear system. Then, we consider data from these trajectories. However, the aforementioned EDMD approach can also be applied to real data and it has the advantage that it can also be used in the case where the dynamics are unknown.

Our result exhibit that the second approach gives good approximation results if we consider one trajectory and finite time horizon (which is a realistic scenario). We also have studied the eigenstructure of the resulting linear system. In contrast to the original Samuelson's linear model which has only two modes, our augmented linear system has much more modes and a rich eigencontent. The complex eigenvalues of the matrix are located close to the number $1$ and on an arc of the unit circle symmetrical with respect to $1$. These eigenvalues correspond to the periodic part of the business cycle. We have also witnessed the existence of eigenvalues which are away from the unit circle and which actually correspond to the transient part of the business cycle. However, when we move the time window these eigenvalues disappear, as it was expected.

The previous approach has good approximation properties when we consider one trajectory in finite time horizon. In order to obtain results for several trajectories we applied the Gaussian interpolation method. In particular, in Section 10, we considered a segment of initial conditions. We sampled this segment and we calculated the corresponding EDMD matrices. Then, we applied the interpolation method for each one entries of these matrices. This approach enabled to obtain good approximation properties for trajectories with different initial conditions.

Finally, in Section 11 we apply the Koopman and EDMD approach to more complex periodic data and we also described a general method that can be applied to real data. If we wish to apply the method to real data, we should include a relatively small number of observables so that the algorithm to be robust. The basis of observables is constructed by adding and deleting observables so that a suitable choice is achieved. Furthermore, the method should be modified as it was described at the end of Section 11.

Conflict of interest

The authors declare no conflicts of interest in this paper.

Acknowledgments

The authors would like to thank the anonymous referees for their helpful comments.