A new hybrid ensemble machine-learning model for severity risk assessment and post-COVID prediction system

1.   Introduction

The exploration of dynamic systems through mathematical models, particularly within the framework of Caputo-Fabrizio fractional-order models, has garnered significant attention in recent years due to its relevance to attractivity, stability, and periodic chaos in discrete dynamical systems. Through a series of research endeavors, including investigations into Caputo-Fabrizio fractional-order fuzzy competitive neural networks (CF-FCNNs, ^[1]), almost automorphic fuzzy neural networks ^[2], multi-delay fractional-order differential equations ^[3], and stochastic inertial neural networks with spatial diffusions ^[4], researchers have made strides in understanding the dynamics and convergence properties of these systems. These works have contributed new theories, methods, and computational techniques, shedding light on the existence of unique bounded asymptotically almost periodic solutions, global exponential stability, synchronization phenomena, and random periodicity. Collectively, these findings offer valuable insights into the behavior of difference equation systems and their applications across various scientific and engineering domains. Moreover, within the broader realm of mathematical frameworks, rational difference equations and systems emerge as powerful tools for capturing the evolution of discrete dynamical systems. Recently, there has been a noteworthy surge in mathematicians' interest in the intricate dynamics exhibited by rational difference equations and systems of difference equations. This research area has proven exceptionally fruitful, significantly contributing to the foundational theory surrounding the qualitative behavior of nonlinear rational difference equations and systems. Studying rational difference equations and systems is essential for several reasons. First, these equations serve as powerful tools for modeling dynamic systems across various fields, including electrical networks, biology genetics, sociology, probability theory, statistical analyses, stochastic time series, finance, economics, and more. Notably, references such as Ghezal et al. ^[5,6,7,8] offer insights into asymmetric time series models, while Ghezal et al. ^[9,10,11] provide valuable contributions to stochastic volatility time series models. Additionally, Ghezal et al. ^{[12,13,14,15,16]}, as well as works by Elaydi ^[17], Grove and Ladas ^[18], Kocic and Ladas ^[19], and Kulenovic and Ladas ^[20], serve as exemplary references showcasing the diverse applications of these equations across various fields. By understanding the behavior of rational difference equations and systems, researchers can gain valuable insights into the underlying mechanisms governing complex phenomena observed in real-world systems. Second, rational difference equations and systems offer a versatile framework that can capture nonlinear interactions, delays, and other intricate dynamics present in many practical scenarios. This flexibility allows for the development of mathematical models that accurately represent the complexities of dynamic systems. Moreover, the study of rational difference equations and systems presents both theoretical challenges and practical applications. Analyzing the asymptotic stability and long-term behavior of solutions to rational difference equations and systems can be particularly challenging but is also rewarding in terms of understanding system behavior and making predictions. Additionally, advancements in the theory of rational difference equations and systems contribute to the advancement of mathematical knowledge and its applications. By developing new methods and techniques for analyzing rational difference equations and systems, researchers can expand the boundaries of mathematical theory and enhance our ability to model and predict the behavior of complex systems.

This paper rigorously explores and analyzes the qualitative behaviors of solutions, placing particular emphasis on both local and global stability within a specific form of a system of rational difference equations, outlined as follows:

where $s$ is a fixed positive integer. The system is initialized with conditions denoted as $\xi_{-v}$, and $\psi_{-v}$, $v\in\left\{ 0, 1, \ldots, 2s+1\right\}$, and it is crucial that these initial conditions are real and nonzero.

Understanding the stability of dynamic systems is not only about unraveling intricate behaviors but also discerning the fundamental elements governing their equilibrium. Interestingly, the solution form of some solvable type difference equations and systems can even be expressed in terms of well-known integer sequences such as Fibonacci numbers, Lucas numbers, generalized Fibonacci numbers, etc. Our aim in this paper is to show that system (1.1) is solvable by deriving its closed-form formulas elegantly and to describe the behavior and periodicity of well-defined solutions to system (1.1). One of the reasons that makes this study interesting is that the solution of system (1.1) is expressed in terms of co-balancing numbers. This investigation delves into the fascinating interplay between global stability and co-balancing numbers within the solutions of rational difference equations. As mathematical structures intimately linked to equilibrium states, co-balancing numbers offer a unique lens through which we can interpret and analyze the stability of the system. The specific number 7 holds significance in our study due to its relevance to the underlying mathematical framework and the properties of the system under investigation. However, we acknowledge that the rationale behind the selection of this particular number is that the solution of system (1.1) is expressed in terms of co-balancing numbers, enabling us to obtain real, non-complex solutions. Numerous researchers have dedicated their efforts to unraveling the qualitative nuances of solutions to rational difference equations, exploring aspects such as global attractivity, boundedness, and periodicity, shedding light on the rich and multifaceted nature of nonlinear mathematical models. For instance, Ghezal ^[21] investigated the convergence of positive solutions to a rational system of $4(k+1)-$order difference equations given by:

where $k$ is a fixed positive integer. El-sayed ^[22] contributed to the exploration by investigating the behavior of solutions to the nonlinear difference equation:

In ^[23], Ghezal et al. explored the solvability of a bilinear system of difference equations with coefficients dependent on the Jacobsthal sequence. They studied the local stability of the positive solutions. Simșek et al. ^[24] investigated the solution of the following difference equation

In ^[25], the solution forms for the following nonlinear difference equations were elucidated:

Additionally, Zhang et al. ^[26] conducted an examination on the boundedness and global asymptotic stability of positive solutions within the system of nonlinear difference equations

where $s$ is a fixed positive integer. Furthermore, Zhang et al. ^[27] delved into the dynamics of a system governed by the nonlinear difference equations

In a demonstration by Okumuș ^[28], it was shown that the following two-dimensional system of difference equations can be successfully solved:

Our paper provides a comprehensive investigation into the local and global stability of a system of rational difference equations, elucidating its connection to co-balancing numbers. This work distinguishes itself through its thorough exploration of the intricate dynamics of mathematical models and their stability properties, with a particular emphasis on the broader implications of global stability. By delving into the role of co-balancing numbers, the paper reveals their significance in achieving equilibrium within the solutions of rational difference equations, thereby enriching our understanding of dynamic systems. In comparison to existing works such as ^[28] which focus on investigating the solutions, stability characteristics, and asymptotic behavior of rational difference equations associated with Tribonacci numbers, our paper broadens the scope to examine the broader implications of global stability and its connection to co-balancing numbers. This broader perspective offers a more comprehensive understanding of the dynamics and equilibrium properties of dynamic systems. Moreover, while ^[26,27] concentrate on studying the behavior and stability of specific systems of rational difference equations, our paper extends this analysis to explore the broader concept of global stability and its relationship with co-balancing numbers. Additionally, while ^[25] and ^[23] delve into the solutions and local stability of specific types of difference equations associated with Fibonacci and Jacobsthal sequences, respectively, our paper broadens the scope to examine the broader implications of global stability and its connection to co-balancing numbers. This extension enhances our understanding of the stability properties of rational difference equations and offers valuable insights into the factors influencing their equilibrium behavior.

Recent advancements in computational methods for solving nonlinear evolution equations and partial differential equations (PDEs) have led to the development of innovative techniques such as the bilinear residual network method and the bilinear neural network method. While these methods primarily focus on obtaining exact analytical solutions for nonlinear PDEs, their underlying principles and computational frameworks share similarities with approaches used to solve systems of difference equations. Both systems of difference equations and PDEs describe the evolution of dynamic systems over discrete or continuous domains, respectively, and often exhibit nonlinear behavior. The computational methods proposed in the referenced works ^{[29,30,31,32]} leverage neural network architectures and advanced mathematical techniques to tackle the complexities inherent in solving nonlinear equations. Although the specific applications discussed in these references pertain to PDEs, the principles and methodologies underlying these methods can be adapted and extended to address systems of difference equations. By leveraging the flexibility and efficiency of neural networks and tensor-based approaches, researchers can explore new avenues for solving systems of difference equations, advancing our understanding of discrete dynamical systems and their behaviors. Therefore, while the referenced works focus on PDEs, their methodologies and computational frameworks hold promise for addressing challenges in systems of difference equations and related areas of research.

This paper not only contributes to the academic understanding of mathematical modeling but also provides valuable insights for practitioners in fields where dynamic systems play a crucial role. Through a synthesis of theoretical exploration and illustrative examples, we aim to elucidate the profound implications of global stability and co-balancing numbers in the realm of rational difference equations. For further insights into the system of rational difference equations and related results, researchers can explore the extensive body of work referenced in Abo-Zeid ^[33], Elsayed et al. ^[34,35,36], Kara ^[37], Berkal and Abo-Zeid ^[38], as well as the contributions by Ghezal and Zemmouri ^[39,40,41]. These references offer valuable insights into various aspects of rational difference equations, including global behavior, solution structures, periodicity, and stability properties. Additionally, Kara's investigation ^[37] provides further exploration into the dynamics of exponential-form difference equation systems.

2.   Preliminaries

We begin by recalling co-balancing numbers as defined in ^[42,43], which will be instrumental in our analysis of the solution to the system of difference equations (1.1).

Definition 2.1. A positive integer $n$ is termed a balancing number if

for some $r\in\mathbb{N}$. Here, $r$ is referred to as the balancer corresponding to the balancing number $n$. ^[44] demonstrated in a joint study that the balancing numbers satisfy the following recurrence relation:

with $B_{0} = 0$ and $B_{1} = 1$. The Binet formula is $B_{n} = \left. \left(\tau^{n}-\kappa^{n}\right) \right/ \left(\tau-\kappa\right)$ for all $n\geq0,$ where $\kappa = 3-2\sqrt{2}\ $and $\tau = 3+2\sqrt{2}.$

Definition 2.2. The quotient of two consecutive terms of balancing numbers tends to a, that is, $\lim B_{n+1}/B_{n} = \tau$.

Definition 2.3. After a slight modification to (2.1), we call a natural number $n$ a co-balancing number if it satisfies:

and if the pair $(n, r)\in$ $\mathbb{N}$ is a solution to (2.2), then $n$ is called the co-balancing number and $r$ is termed the co-balancer associated with $n$.

Definition 2.4. The co-balancing sequence is defined by $(b_{n})$ for $n\in\mathbb{N}$, where

with $b_{1} = 0$ and $b_{2} = 2$. The Binet formula for $b_{n}$ is given by $b_{n} = -1/2+\left. \left(\tau^{n-1/2}-\kappa^{n-1/2}\right) \right/ \left(\tau-\kappa\right)$ for all $n\geq0.$

3.   Dynamics of the system of difference equations (1.1)

Our exploration of the solutions for system (1.1) involves a nuanced analysis of two distinct cases: one where $s = 0$, and another where $s > 0$.

3.1.   Second-order: $s=0$

When $s = 0$, system (1.1) takes on the following form

In this context, we endeavor to derive closed-form solutions for system (3.1). To achieve this, we utilize the following change of variables, denoted by

which transforms system (3.1) into its equivalent counterpart:

To further simplify the last system, we sum and subtract the two equations and introduce a new variable transformation:

Therefore, we arrive at an equivalent system given by: $\forall n\geq0,$

Through this, we can deduce closed-form expressions as outlined in the following three Lemmas.

Lemma 3.1. Consider the linear difference equation (3.5) with initial values $x_{-2}$, $x_{-1}$, and $x_{0}\in\mathbb{R}$. The general solution $\left\{ x_{n}, \mathit{\text{}}n\geq-2\right\}$ is delineated by the following expression:

where $\left(B_{n}, n\geq1\right)$ represents the sequence of balancing numbers.

Proof. We commence the proof by employing the characteristic polynomial of Eq (3.5):

The roots of this equation are $\lambda_{1} = 1,$ $\lambda_{2} = \kappa,$ $\lambda_{3} = \tau$. Consequently, the closed form of the general solution for difference equation (3.5) is expressed as:

Here, $x_{-2}$, $x_{-1}$, and $x_{0}$ denote initial values satisfying:

By solving the standard system and conducting subsequent calculations, we obtain:

Hence, we derive the following expression:

and after further calculations and simplification, we arrive at:

The lemma is thereby proven.

Lemma 3.2. Consider the linear difference equation (3.6) with initial values $y_{-2}$, $y_{-1}$, and $y_{0}\in\mathbb{R}$. The general solution $\left\{ y_{n}, \mathit{\text{}}n\geq-2\right\}$ can be succinctly expressed as:

Proof. To establish the solution for the difference equation (3.5), we begin by utilizing its characteristic polynomial:

The roots of this polynomial are denoted as $\lambda_{1} = -1,$ $\lambda _{2} = -\kappa,$ $\lambda_{3} = -\tau$, then the closed form of the general solution for this difference equation is expressed as:

Here, $y_{-2}$, $y_{-1}$, and $y_{0}$ are defined by the standard system:

Upon solving the standard system and conducting subsequent calculations, the coefficients $\vartheta_{1}$, $\vartheta_{2}$ and $\vartheta_{3}$ are determined as follows:

Consequently, the final expression for $y_{n}$ is given by:

Further simplification yields the key result:

Thus, the lemma is effectively proven.

Lemma 3.3. Consider the system of linear difference equations (3.3) with initial values $u_{-2}$, $u_{-1}$, $u_{0},$ $v_{-2}$, $v_{-1}$, and $v_{0}\in\mathbb{R}$. The general solution $\left\{ \left(u_{n}, v_{n}\right), \mathit{\text{}}n\geq-2\right\}$ can be succinctly expressed as:

Proof. Through the equivalent linear systems (3.5) and (3.6) and by employing the conversely defined change of variables (3.4), $u_{n+1}$ is represented as $\left. \left(x_{n+1}+y_{n+1}\right) \right/ 2$ and$\ v_{n+1}\ $ is represented as $\left. \left(x_{n+1}-y_{n+1}\right) \right/ 2$. The subsequent application of Lemmas 3.1 and 3.2 allows us to deduce the closed-form solution for system (3.3) as:

By applying the variable substitution defined in (3.4) once again, the desired results can be obtained. Hence, the lemma is effectively demonstrated.

Below, we derive a main result specific to this subsection and present it in the form of a theorem.

Theorem 3.1. Consider the system of nonlinear difference equations (3.1) with initial values $\xi_{-1}$, $\xi_{0}$, $\psi_{-1}$, and $\psi_{0}\in\mathbb{R}$. The general solution $\left\{ \left(\xi_{n}, \psi_{n}\right), \mathit{\text{}}n\geq-1\right\}$ can be succinctly expressed as:

Proof. The proof of this theorem relies on Lemma 3.2 and employs the change of variables (3.2). Consequently, we establish the following relationships denoted as

then, for all $n$,

The remaining details are straightforward and omitted for brevity.

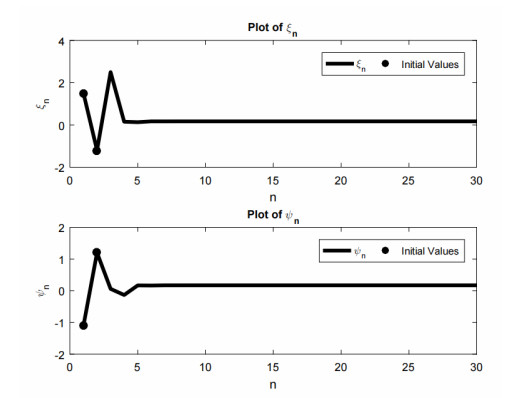
Example 3.1. Consider the system (3.1) with initial values $\xi_{-1} = 1.50$, $\xi_{0} = -1.20$, $\psi_{-1} = -1.10$, and $\psi_{0} = 1.20$. Figure $1$ presents a graphical depiction of the sustained dynamics within this system.

3.2.   $2\left(s+1\right)$-order: $s > 0$

For a $2\left(s+1\right)$-order system with $s > 0$, our aim is to deduce closed-form solutions for system (1.1). This system is viewed as an extension of system (3.1), represented as follows for all $n\geq 0$:

for $m\in\left\{ 0, 1, \ldots, s\right\} \ $and $n\in\mathbb{N}.$ Introducing the notations$:$ $\Phi_{n}^{\left(s\right) }\left(m\right) = \xi_{\left(s+1\right) n-m},$ $\Psi_{n}^{\left(s\right) }\left(m\right) = \psi_{\left(s+1\right) n-m},$ for $m\in\left\{ 0, 1, \ldots, s\right\}$ and $n\geq0$, we can derive $\left(s+1\right) -$systems analogous to system (3.1),

for $m\in\left\{ 0, 1, \ldots, s\right\}.$ Based on this discussion, we present the first main result.

Theorem 3.2. Consider the system of nonlinear difference equations (1.1) with initial values $\xi_{-v}\in\mathbb{R}$ and $\psi_{-v} \in\mathbb{R}$, $v\in\left\{ 0, 1, \ldots, 2s+1\right\}$. The general solution $\left\{ \left(\xi_{n}, \psi_{n}\right), \mathit{\text{}}n\right\}$ can be succinctly expressed as: for $m\in\left\{ 0, 1, \ldots, s\right\},$

Proof. Utilizing the $\left(s+1\right) -$systems analogous to system (3.1) and applying Theorem 3.1, we conclude the proof of Theorem 3.2.

In the preceding outcome, the solutions of system (1.1) were represented using a balancing sequence, whereas the next result was articulated using a co-balancing sequence.

Corollary 3.1. Consider the system of nonlinear difference equations (1.1) with initial values $\xi_{-v}\in\mathbb{R}$, and $\psi_{-v}\in\mathbb{R}$, $v\in\left\{ 0, 1, \ldots, 2s+1\right\}$. The general solution $\left\{ \left(\xi_{n}, \psi_{n}\right), \mathit{\text{}}n\right\}$ can be succinctly expressed as: for $m\in\left\{ 0, 1, \ldots, s\right\},$

where $\left(b_{n}, n\geq1\right)$ represents the sequence of co-balancing numbers.

Proof. The proof of this corollary establishes the following relation between balancing and co-balancing numbers: $2B_{n} = b_{n+1}-b_{n}$. Further details have been omitted.

Remark 3.1. The general solution to the system of nonlinear difference equations (1.1) with initial values $\xi_{-v}\in\mathbb{R}$ and $\psi_{-v} \in\mathbb{R}$, $v\in\left\{ 0, 1, \ldots, 2s+1\right\}$ is of paramount importance. The general solution $\left\{ \left(\xi_{n}, \psi_{n}\right), \text{ }n\right\}$ can be succinctly expressed as follows: for $m\in\left\{ 0, 1, \ldots, s\right\}$, for every $n$, $\xi_{\left(s+1\right) \left(2n\right) -m}$, $\xi_{\left(s+1\right) \left(2n+1\right) -m}$, $\psi_{\left(s+1\right) \left(2n\right) -m}$, and $\psi_{\left(s+1\right) \left(2n+1\right) -m}$ can be expressed using the proposed formulas, where $(B_{n})$ and $(b_{n})$ represent balancing and cobalancing numbers. This remark illustrates the method by which solutions to the complex system of difference equations can be accurately expressed, highlighting the importance of employing co-balancing numbers in this context.

Corollary 3.2. Consider the following nonlinear difference equation

where $s$ is a fixed positive integer with initial values $\xi_{-v} \in\mathbb{R}$, $v\in\left\{ 0, 1, \ldots, 2s+1\right\}$. The general solution $\left\{ \xi_{n}, \mathit{\text{}}n\right\}$ can be succinctly expressed as: for $m\in\left\{ 0, 1, \ldots, s\right\},$

Proof. The proof of the general solution for the nonlinear difference equation is derived from Theorem 3.2 when $\xi_{-v} = \psi_{-v}$ for $v\in\left\{ 0, 1, \ldots, 2s+1\right\}$.

Example 3.2. Consider the system (1.1) with $s = 1$ and initial values $\xi _{-4} = 1.50$, $\xi_{-3} = 1.20,$ $\xi_{-2} = 0.30$, $\xi_{-1} = 0.40$, $\xi _{0} = 0.50,$ $\psi_{-4} = -1.10$, $\psi_{-3} = -1.20$, $\psi_{-2} = -1.30$, $\psi_{-1} = -1.40$, and $\psi_{0} = -1.50$. Figure $2$ presents a graphical depiction of the sustained dynamics within this system.

Example 3.3. Consider the system (1.1) with $s = 2$ and initial values $\xi _{-v} = 1-\sqrt{v}$ and $\psi_{-v} = -1.2\exp\left(v\right) +2,$ $v\in\left\{ 0, 1, \ldots, 6\right\}$. Figure $3$ presents a graphical depiction of the sustained dynamics within this system.

3.3.   Stability of system (1.1)

In this subsection, we first determine the equilibrium points and then proceed to analyze the local and global stability of the solutions of system (1.1). The system has three positive equilibrium points:

which are solutions to the standard system:

The following theorem provides information on the local stability of the equilibrium point $\underline{\Lambda}_{2}$ of system (1.1).

Theorem 3.3. The positive equilibrium point $\underline{\Lambda}_{2}$ of system (1.1) is locally asymptotically stable.

Proof. In order to analyze the local stability of system (1.1) around the equilibrium point $\underline{\Lambda}_{2},$ we employ linearized equations. Let $\forall n\geq0,$ $\underline{\mathbf{\xi}}_{n+1} = \Gamma\left(\underline{\mathbf{\xi}}_{n}\right),$ where $\underline{\mathbf{\xi}} _{n}: = \left(\underline{\mathbf{x}}_{n}^{\prime}, \underline{\mathbf{y}} _{n}^{\prime}\right) ^{\prime},$ $\underline{\mathbf{x}}_{n} = \left(x_{n}^{\left(1\right) }, x_{n}^{\left(2\right) }, \ldots, x_{n}^{\left(2s+2\right) }\right) ^{\prime},$ $\underline{\mathbf{y}}_{n} = \left(y_{n}^{\left(1\right) }, y_{n}^{\left(2\right) }, \ldots, y_{n}^{\left(2s+2\right) }\right) ^{\prime},$

The mapping $\Gamma$ is defined as:

where

The partial derivatives of $\Gamma_{1}\left(.\right)$ (resp., $\Gamma _{2}\left(.\right)$) with respect to its components are given by:

Given the symbols introduced earlier, we can express the linearized system around the equilibrium point $\underline{\Lambda}_{2}$ as: $\Gamma\left(\underline{\mathbf{\xi}}_{n}\right) = \chi_{s}\underline{\mathbf{\xi}}_{n}$, where $\chi_{s}$ is the stability matrix defined as:

Upon performing initial computations, we find that the characteristic polynomial of $\chi_{s}$ is given by:

where $I_{4\left(s+1\right) \times4\left(s+1\right) }$ is the identity matrix of size $4\left(s+1\right) \times4\left(s+1\right)$. By analyzing the characteristic polynomial, we can determine the eigenvalues of $\chi_{s}$. After conducting meticulous calculations, we ascertain that the roots of $\chi_{s}$ satisfy $\lambda^{2s+2} = \left(\sqrt{17}-4\right) \left(70\sqrt{2}-99\right)$ or $\lambda^{2s+2} = \left(\sqrt{17}+4\right) \left(99-70\sqrt{2}\right)$. This implies that all the moduli of every eigenvalue of $\chi_{s}$ are less than one. Therefore, the positive equilibrium point $\underline{\Lambda}_{2}$ of system (1.1) is concluded to be locally asymptotically stable.

Theorem 3.4. Consider the system of nonlinear difference equations (1.1) with initial values $\xi_{-v}\in\mathbb{R}$, and $\psi_{-v}\in\mathbb{R}$, $v\in\left\{ 0, 1, \ldots, 2s+1\right\}$.

1) Every positive solution $\left\{ \left(\xi_{n}, \psi_{n}\right), \mathit{\text{}}n\right\}$ of this system converges to the equilibrium point $\underline{\Lambda}_{2}$ as $n\longrightarrow\infty$.

2) The positive equilibrium point $\underline{\Lambda}_{2}$ of system (1.1) is globally asymptotically stable.

Proof. (ⅰ) Let $\left\{ \left(\xi_{n}, \psi_{n}\right), \text{ }n\right\}$ be a positive solution of system (1.1). We are interested in calculating the limit of the sequences $\left(\xi_{\left(s+1\right) \left(2n\right) -m}\right)$, $\left(\xi_{\left(s+1\right) \left(2n+1\right) -m}\right),$ $\left(\psi_{\left(s+1\right) \left(2n\right) -m}\right)$, and$\left(\psi_{\left(s+1\right) \left(2n+1\right) -m}\right),$ for $m\in\left\{ 0, 1, \ldots, s\right\}$. To proceed with this calculation, let's start by analyzing the behavior of $\xi_{\left(s+1\right) \left(2n\right) -m}$ as $n$ approaches infinity.

From the given limits: $\lim_{n}\dfrac{B_{2n}}{B_{2n+1}} = \kappa,$ $\lim _{n}\dfrac{B_{2n-1}}{B_{2n+1}} = \kappa^{2},$ $\lim_{n}\dfrac{B_{2n-2} }{B_{2n+1}} = \kappa^{3},$ and $\lim_{n}\dfrac{1}{B_{2n+1}} = 0$, we get

for $m\in\left\{ 0, 1, \ldots, s\right\}.$ The same approach can be applied to $\left(\xi_{\left(s+1\right) \left(2n+1\right) -m}\right),$ $\left(\psi_{\left(s+1\right) \left(2n\right) -m}\right)$, and$\left(\psi_{\left(s+1\right) \left(2n+1\right) -m}\right),$ for $m\in\left\{ 0, 1, \ldots, s\right\}.$

(ⅱ) The proof of the second assertion follows directly from Theorem 3.3 and the first assertion.

Remark 3.2. Throughout the examples in this paper, Figures $1$–3 demonstrate that the equilibrium point $\underline{\Lambda}_{2}$ of system (1.1) is globally asymptotically stable.

4.   Conclusions

This study provided a comprehensive exploration of the dynamics of a system of rational difference equations, investigating both local and global stability aspects. The findings underscored the intricate relationship between stability properties and co-balancing numbers, revealing their significant impact on achieving equilibrium within the solutions of rational difference equations. By examining the role of co-balancing numbers, we gained insights into the interplay between global stability and co-balancing numbers, enhancing our understanding of dynamic systems' mathematical structures. Moreover, this article serves as a valuable resource for mathematicians, researchers, and scholars interested in the intersection of global stability and co-balancing sequences within rational difference equations. The consistently demonstrated global asymptotic stability of the equilibrium point, supported by examples and figures throughout the paper, underscores the significance of the findings. Further research in this direction holds promise for uncovering additional nuances in the intricate relationship between stability and co-balancing numbers within mathematical modeling.

In the realm of integrable systems, the quest for analytical solutions to nonlinear PDEs has long been a challenge due to the absence of a universal method. However, recent breakthroughs in symbolic computation, particularly through the application of neural networks proposed by Zhang et al. ^{[45,46,47,48]}, have opened a new avenue for the analytical treatment of nonlinear PDEs. These innovative approaches pave the way for symbolic computation to tackle the complexities of nonlinear PDEs, laying the groundwork for a universal method for obtaining analytical expressions. While the focus of these works is primarily on obtaining exact solutions for PDEs, the underlying methodologies and principles can inspire new ideas for future work. A potential open problem that arises from this research is the exploration of applying similar computational techniques to systems of difference equations. By adapting the neural network architectures and symbolic computation methods employed in solving nonlinear PDEs, researchers can investigate the feasibility of obtaining analytical solutions for systems of difference equations, thus advancing our understanding of discrete dynamical systems and their behaviors. This interdisciplinary approach holds promise for addressing longstanding challenges in the field and opens avenues for further exploration at the intersection of computational mathematics and dynamical systems theory.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors extend their appreciation to the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research at King Faisal University, Saudi Arabia, for financial support under the annual funding track $\left[5964\right].$

Conflict of interest

The authors declare there is no conflicts of interest.