Conditional Ulam stability and its application to von Bertalanffy growth model

1.   Introduction

Metabolism can be divided into catabolism and anabolism. It is known that body weight depends on their balance. In this paper, we consider the von Bertalanffy growth model

for $t\ge 0$, where $w$ denotes mass (body weight) and $a > 0$ and $b > 0$ are the coefficients of anabolism (synthesis) and catabolism (destruction), respectively. Bertalanffy ^[1] proposed this equation as a model for fish growth and suggested that the exponent $\frac{2}{3}$ is appropriate. Many studies in biology on the von Bertalanffy growth model have shown that the solution to the equation is a good representation of fish weight growth, e.g., ^[2,3]. Many generalizations about the von Bertalanffy growth model have been reported. For example, see ^[4,5] and the references cited therein. In many cases, trying to describe a real phenomenon using a mathematical model requires a very complicated model, and the match may still not be perfect. Although it is not possible to build a mathematical model that exactly matches the original phenomenon, the references above suggest that even a simple model may produce a fairly close match. In the present paper, a mathematical model that completely describes the original phenomenon is simply referred to as the real phenomenon. The present study focuses on the following problem. Under the assumption that the difference between a real phenomenon and its mathematical model (von Bertalanffy growth model) is less than a constant $\varepsilon > 0$, is there always a solution for the mathematical model that is close to the solution for the real phenomenon? This problem is a kind of perturbation problem, but note that $\varepsilon > 0$ does not have to be small. A concept related to this proposed by Ulam has recently evolved into an important field of study in differential equations. See ^[6]. Many results have been reported for linear differential equations. For example, for first-order linear differential equations, Onitsuka ^[7] and Onitsuka and Shoji ^[8] studied constant coefficient equations, Fukutaka and Onitsuka ^[9,10] studied periodic coefficient equations, and Popa and Rașa ^[11], Wang, Zhou and Sun ^[12] and Zada, Shah and Shah ^[13] studied variable coefficient equations, for second-order linear differential equations, see ^[14,15,16], and for fractional differential equations, see ^[17,18], and the references cited therein. Nonlinear differential equations have not received as much attention because in many cases it is necessary to solve the solution concretely. When the solution cannot be found, the Lipschitz condition and the fixed point theorems are used. For example, for the results obtained using the Lipschitz condition, see ^{[19,20,21,22]}, and for the fixed point approaches, see ^[23,24,25]; however, in such cases, the detailed behavior of the solution is not clarified. In 2018, Popa, Rașa, and Viorel ^[26] researched the stability of the logistic model

for $t\ge 0$. They proposed conditional Ulam stability and developed a stability theory for nonlinear equations. The present author ^[27] considered the conditional Ulam stability of the equation

for $t\ge 0$, and applied it to the logistic model

for $t\ge 0$, where $P$ denotes population size and $r > 0$ and $K > 0$ are the intrinsic growth rate and the carrying capacity, respectively.

Conditional Ulam stability is defined as follows. Let $\left[0, T_w\right)$ be the maximal existence interval for the solution $w$. Define the class $\mathcal{C}$ as

Let $M\subseteq (0, \infty)$. The nonlinear differential equation

is conditionally Ulam stable on $\left[0, \min\left\{T_w, T_{\phi}\right\}\right)$ in the class $\mathcal{C}$ if there exists a constant $N > 0$ such that for every $\varepsilon \in M$ and every approximate solution $\phi\in \mathcal{C}$ that satisfy

there exists a solution $w\in \mathcal{C}$ of Equation (1.2) such that

We call such $N$ an Ulam constant for Equation (1.2) on $\left[0, \min\left\{T_w, T_{\phi}\right\}\right)$. If $M = (0, \infty)$ and $D = \mathbb{R}$, then this definition is exactly the same as that for the standard Ulam stability.

The main result in this paper is as follows.

Theorem 1. Equation (1.1) is conditionally Ulam stable on $[0, \infty)$, with $M = \left(0, \frac{a}{3}\left(\frac{2a}{3b}\right)^2\right]$, in the class $\mathcal{C} = \left\{ w\in C^1[0, \infty) : w(0) \ge \left(\frac{2a}{3b}\right)^3 \right\}$ and with an Ulam constant $N = \frac{3}{b}\left(\frac{19}{12}\right)^{\frac{5}{2}}$.

If we can estimate the error between a real phenomenon and its mathematical model, we can then conclude that the multiplication of the error and an Ulam constant is the magnitude of the difference between the solutions. Hence, the Ulam constant indicates the accuracy of the mathematical model.

The rest of this paper is organized as follows. In Section 2, we investigate the behavior of the approximate solutions of a special Bertalanffy model using the comparison principle. In Section 3, we deal with conditional Ulam stability for the special model. In Section 4, we apply the obtained result to the von Bertalanffy growth model and complete the proof of Theorem 1. To explain the theorem, numerical simulations are performed. Finally, in Section 5, we give the conclusions.

2.   Approximate solutions of $\frac{dz}{d\tau} = z^{\frac{2}{3}}-z$

Let $\tau: = bt$ and $z: = \left(\frac{b}{a}\right)^3w$. Then, Equation (1.1) is reduced to the nonlinear differential equation

for $\tau \ge 0$. In Section 4, it will be shown that this transformation reduces the conditional Ulam stability of Equation (1.1) to that of Equation (2.1). Let $\delta > 0$ be given and let $z_0\in \mathbb{R}$. Now, we consider the perturbed equations

and

for $\tau\ge 0$, where $f\in C[0, \infty)$. Let

We can see that the right-hand side of Equations (2.1), (2.2), (2.3), and (2.4) is continuously differentiable with respect to $z > 0$, $\zeta > 0$, $x > 0$, and $y > 0$, respectively. Hence, if a positive initial condition (2.5) is given, then the local existence and uniqueness of the solutions are guaranteed in the positive domain. However, we must pay attention to the global existence of the solutions. By limiting the initial values, the existence of the global solutions is guaranteed. The following result is derived using the comparison principle.

Proposition 2. Let $z \in C^1\left[0, T_{z}\right)$, $\zeta \in C^1\left[0, T_{\zeta}\right)$, $x \in C^1\left[0, T_{x}\right)$, and $y \in C^1\left[0, T_{y}\right)$ be the solutions of Equations (2.1), (2.2), (2.3), and (2.4) with (2.5), respectively. If

then $T_{z} = T_{\zeta} = T_{x} = T_{y} = \infty$ and

for $\tau\in (0, \infty)$.

Proof. Assume that

Define $F(z): = z^{\frac{2}{3}}-z$ for $z\in \mathbb{R}$. Then, $F(0) = F(1) = 0$ holds; that is, $z = 0$, $1$ are the equilibrium points of Equation (2.1). From $\frac{dF}{dz}(z) = \frac{2}{3}z^{-\frac{1}{3}}-1$, we see that $\frac{dF}{dz}(z) > 0$ on $\left[0, \frac{8}{27}\right)$; $\frac{dF}{dz}\left(\frac{8}{27}\right) = 0$; $\frac{dF}{dz}(z) < 0$ on $\left(\frac{8}{27}, \infty\right)$. This implies that the function $F(z)$ takes the maximum value $\frac{4}{27}$ when $z = \frac{8}{27}$. Moreover, we see that $F(z) > 0$ on $(0, 1)$ and $F(z) < 0$ on $(1, \infty)$.

First, we will prove $\frac{8}{27} \le x(\tau)$ for all $\tau\ge 0$. Now, we consider the function $F(z)-\delta$. If $\delta = \frac{4}{27}$, then

holds; that is, $z = \frac{8}{27}$ is the unique equilibrium point of Equation (2.3). Hence, $x(\tau) \equiv \frac{8}{27}$ is the unique global solution of Equation (2.3) with $x(0) = \frac{8}{27}$. Because of the uniqueness of the solutions, $x(0) > \frac{8}{27}$ implies $\frac{8}{27} < x(\tau)$ for $\tau\ge 0$. Next, we consider the case $0 < \delta < \frac{4}{27}$. In this case, we have

This indicates that Equation (2.3) has two positive equilibrium points $E_1$ and $E_2$ that satisfy $F(E_1)-\delta = F(E_2)-\delta = 0$ and

Because $F(x)-\delta > 0$ for $\frac{8}{27} \le x < E_2$, we see that $x' > 0$ for $\frac{8}{27} \le x < E_2$. Therefore, integrating this inequality yields

for $\tau\ge 0$. Based on this and the uniqueness of the solutions, we see that $x(0) \in \left[\frac{8}{27}, E_2\right)$ implies

for $\tau\ge 0$. Thus, if $x(0) \in \left[\frac{8}{27}, E_2\right)$, then $T_x = \infty$. $x(\tau) \equiv E_2$ is a global unique solution of Equation (2.3). On the other hand, because $F(x)-\delta < 0$ holds for $E_2 < x$, we have $x' < 0$ for $E_2 < x$. Thus, if $x(0) \in (E_2, \infty)$, then

for $\tau\ge 0$, and so if $x(0) \in (E_2, \infty)$, then $T_x = \infty$. Hence, $\frac{8}{27} \le x(0)$ implies the global existence of the solution $x$ of Equation (2.3) and $\frac{8}{27} \le x(\tau)$ for all $\tau\ge 0$.

Next, we will prove $x(\tau) \le \zeta(\tau) \le y(\tau)$ for $\tau\ge 0$. Let $\psi(\tau): = \zeta(\tau)-x(\tau)$ for $\tau\ge 0$. By way of contradiction, we suppose that there exists $\sigma_1 \ge 0$ such that $\psi(\sigma_1) < 0$. Because $\psi$ is continuously differentiable and $\psi(0) = 0$, we can choose $0 \le \tau_1 \le \sigma_1$ such that $\psi(\tau_1) = 0$ and

for $\tau_1 < \tau \le \sigma_1$. Then, we have

for $\tau_1 < \tau \le \sigma_1$. This implies that

and thus

for $\tau_1 < \tau \le \sigma_1$. This contradicts the fact that $\psi(\tau) < 0$ for $\tau_1 < \tau \le \sigma_1$. Therefore, we have $x(\tau) \le \zeta(\tau)$ for $\tau\ge 0$. Using the same technique, we obtain $\zeta(\tau) \le y(\tau)$ for $\tau\ge 0$.

Next, we will show that $x(\tau) < z(\tau) < y(\tau)$ for $\tau > 0$. Let $\omega(\tau): = z(\tau)-x(\tau)$ for $\tau\ge 0$. From the above inequality with $f(\tau)\equiv 0$, we see that $\omega(\tau)\ge 0$ for $\tau\ge 0$. By $\omega(0) = 0$, we have

This together with the continuous differentiability of $\omega$ implies that $\omega$ takes a positive value near $\tau = 0$. By way of contradiction, we suppose that there exists $\sigma_2 > 0$ such that $\omega(\sigma_2) = 0$ and $\omega(\tau) > 0$ for $0 < \tau < \sigma_2$. Then, we have

and so

for $0 < \tau < \sigma_2$. Integrating this inequality from $\frac{\sigma_2}{2}$ to $\sigma_2$ yields

This contradicts $\omega(\sigma_2) = 0$. Hence, we have $x(\tau) < z(\tau)$ for $\tau > 0$. Using the same technique, we see that $z(\tau) < y(\tau)$ for $\tau > 0$.

Finally, we will show that $y(\tau)$ is bounded above for $\tau\ge 0$. We consider the function $F(z)+\delta$, where $F(z) = z^{\frac{2}{3}}-z$. For any $0 < \delta \le \frac{4}{27}$, we have

and so Equation (2.4) has two equilibrium points $E_3$ and $E_4$ that satisfy $F(E_3)+\delta = F(E_4)+\delta = 0$ and

We have only to prove that the solution $y$ of Equation (2.4) with $y(0) > E_4$ is bounded above for $\tau\ge 0$. Because of the uniqueness of the solutions, any solution of Equation (2.4) with $y(0) \le E_4$ is below the solution $y$ of Equation (2.4) with $y(0) > E_4$. Because $y(t) \equiv E_4$ is a global unique solution of Equation (2.4) and $y' = F(y)+\delta < 0$ holds for $y > E_4$, we see that

for $\tau \ge 0$. Therefore, $y(\tau)$ is bounded above for $\tau\ge 0$. Hence, combining this with the inequality $\frac{8}{27} \le x(\tau) \le \zeta(\tau) \le y(\tau)$ for $\tau\ge 0$, we conclude that $T_{z} = T_{\zeta} = T_{y} = \infty$. The proof is now complete.

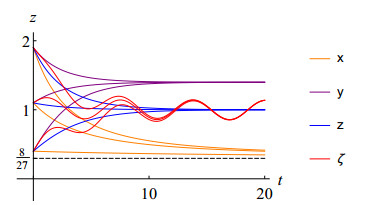
Figure 1 shows a sketch of the claim in Proposition 2. Three initial points, namely $z_0 = 0.4$, $1.1$, and $1.9$, are selected. $x$, $y$, and $z$ each converge to a constant, but $\zeta$ does not necessarily converge to a constant.

Remark 3. Now, we consider the case $\delta > \frac{4}{27}$. For $\gamma > 0$, let $\delta = \frac{4}{27}+\gamma$. From the first paragraph in the proof of Proposition 2, we see that

where $F(x) = x^{\frac{2}{3}}-x$ for $x\in \mathbb{R}$. This indicates that

and thus $x(\tau)$ takes a negative value when $\tau > \frac{x(0)}{\gamma}$. Unfortunately, we see that Equation (2.3) does not have a real solution for $\tau > \frac{x(0)}{\gamma}$ because it includes $x^{\frac{3}{2}}$. This means that the solution of Equation (2.3) will disappear at least after this time. Therefore, we note that we cannot discuss Ulam stability for global solutions when $\delta > \frac{4}{27}$. For this reason, we can conclude that $\delta = \frac{4}{27}$ is the threshold.

Remark 4. Now, we consider the case $\delta = \frac{4}{27}$ and $x(0) < \frac{8}{27}$. From the first paragraph in the proof of Proposition 2, we see that

This indicates that

and thus

for $\tau \ge 0$ because $F(x)$ is increasing on $\left[0, \frac{8}{27}\right)$. Integrating this inequality yields

for $\tau \ge 0$. From $F(x(0))-\delta < 0$, this inequality indicates that the solution $x(\tau)$ will hit the positive $\tau$-axis and it will take a negative value when

Therefore, for the same reason as that given in Remark 3, the solution $x(\tau)$ of Equation (2.3) will disappear at least after this time. Therefore, we note that we cannot discuss Ulam stability for global solutions when $\delta = \frac{4}{27}$ and $x(0) < \frac{8}{27}$. For this reason, we can conclude that $x(0) = \frac{8}{27}$ is the threshold.

3.   Conditional Ulam stability for $\frac{dz}{d\tau} = z^{\frac{2}{3}}-z$

In this section, we will prove the following result. This theorem is the core of this study.

Theorem 5. Suppose that $0 < \delta\le \frac{4}{27}$ and $z_0 \ge \frac{8}{27}$. Let $z \in C^1\left[0, T_{z}\right)$ and $\zeta \in C^1\left[0, T_{\zeta}\right)$ be the solutions of Equations (2.1) and (2.2) with (2.5), respectively. Then, $T_{z} = T_{\zeta} = \infty$ and

for $\tau\in [0, \infty)$.

Before discussing the proof of this theorem, we will give some technical inequalities.

Lemma 6. Define the function

for $X > 0$. Then, $\frac{dG}{dX}(X) < 0$ for $X > 0$.

Proof. If $X > 0$, then

holds. Hence, the proof is complete.

Lemma 7. Define the function

for $\tau\ge 0$. Then, $H(\tau) < -\frac{4}{19}$ for $\tau\ge 0$.

Proof. By a simple calculation, we have

for $\tau\ge 0$, which implies that

for $\tau\ge 0$. This completes the proof.

Proposition 8. Suppose that $0 < \delta\le \frac{4}{27}$ and $z_0 \ge \frac{8}{27}$. Let $z \in C^1\left[0, T_{z}\right)$, $x \in C^1\left[0, T_{x}\right)$, and $y \in C^1\left[0, T_{y}\right)$ be the solutions of Equations (2.1), (2.3), and (2.4) with (2.5), respectively. Then, $T_{z} = T_{x} = T_{y} = \infty$ and

and

hold for $\tau\in (0, \infty)$.

Proof. By Proposition 2, we have $T_{z} = T_{x} = T_{y} = \infty$ and

for $\tau\in (0, \infty)$. Because the proofs of the two inequalities in Proposition 8 are the same, only the first one is shown here. For convenience, we write

for $\tau\in (0, \infty)$. Because we can solve Equation (2.1), we have

for $\tau\in (0, \infty)$. Using this with Lemma 6, we obtain

for $\tau\in (0, \infty)$. Now, note that

Hence, this together with Lemma 7 implies that

for $\tau\in (0, \infty)$. This completes the proof.

Proof of Theorem 5. Suppose that

Let $z \in C^1\left[0, T_{z}\right)$, $\zeta \in C^1\left[0, T_{\zeta}\right)$, $x \in C^1\left[0, T_{x}\right)$, and $y \in C^1\left[0, T_{y}\right)$ be the solutions of Equations (2.1)–(2.4), with (2.5), respectively. Then, by Proposition 2, we see that $T_{z} = T_{\zeta} = T_{x} = T_{y} = \infty$ and

for $\tau\in (0, \infty)$. Because

holds, we see that

for $\tau\in (0, \infty)$. Define $\rho_1(\tau): = y(\tau)-z(\tau)$ and $\rho_2(\tau): = z(\tau)-x(\tau)$ for $\tau\in (0, \infty)$. Then, we have

and

for $\tau\in (0, \infty)$. Noticing that $\rho_1(\tau)$ and $\rho_2(\tau)$ are positive and using Proposition 8, we get the inequality

for $\tau\in (0, \infty)$ and $i\in \{1, 2\}$, where

This implies that

and so

for $\tau\in (0, \infty)$ and $i\in \{1, 2\}$. We need to estimate the above integral. It is easy to verify that

for $\tau \ge s$. Using this with the inequality $12 < \left(e^{-\frac{1}{3}\tau}-4\right)^2+3 < 19$ for $\tau > 0$, we have

for $\tau\in (0, \infty)$. Hence, combining this estimation with (3.1) and (3.2), we obtain

for $\tau\in (0, \infty)$. When $\tau = 0$ this inequality is true. Therefore, for all $\tau\in [0, \infty)$, this inequality holds.

Using Theorem 5, we immediately obtain the following result.

Theorem 9. Equation (2.1) is conditionally Ulam stable on $[0, \infty)$, with $M = \left(0, \frac{4}{27}\right]$, in the class $\mathcal{C} = \left\{ w\in C^1[0, \infty) : w(0) \ge \frac{8}{27} \right\}$ and with an Ulam constant $N = 3\left(\frac{19}{12}\right)^{\frac{5}{2}}$.

4.   Application to von Bertalanffy growth model

In this section, we apply the obtained result to the von Bertalanffy growth model. We can establish the following result.

Theorem 10. Suppose that $0 < \varepsilon\le \frac{a}{3}\left(\frac{2a}{3b}\right)^2$ and $w_0 \ge \left(\frac{2a}{3b}\right)^3$. Let $w \in C^1\left[0, T_{w}\right)$ and $\phi \in C^1\left[0, T_{\phi}\right)$ be the solutions of eEquation (1.1) and the inequality

with $w(0) = \phi(0) = w_0$, respectively. Then, $T_{w} = T_{\phi} = \infty$ and

for $t\in [0, \infty)$.

Proof. Suppose that

Let $\phi \in C^1\left[0, T_{\phi}\right)$ satisfy the condition $\phi(0) = w_0$ and the inequality

for $0 \le t\le T_{\phi}$. Now, using the transformations $\tau : = bt$ and $\zeta : = \left(\frac{b}{a}\right)^3 \phi$, we obtain the inequality

for $0 \le \tau\le T_{\zeta} = bT_{\phi}$. Let $\delta : = \frac{1}{a}\left(\frac{b}{a}\right)^2 \varepsilon$. Then, $0 < \delta \le \frac{4}{27}$ and

hold. Next, we consider the solution $z \in C^1[0, T_z)$ of Equation (2.1) with

By Theorem 5, we see that $T_{\phi} = T_{\zeta} = T_{z} = \infty$ and $|\zeta(\tau)-z(\tau)| < 3\left(\frac{19}{12}\right)^{\frac{5}{2}}\delta$ for all $\tau\ge 0$. Let $w(t): = \left(\frac{a}{b}\right)^3z(\tau)$. Then, the above inequality indicates that

for $t \ge 0$. Moreover,

holds for $t\ge 0$; that is, $w(t)$ is a global and unique solution of Equation (1.1) with the condition

This completes the proof.

Proof of Theorem 1. Theorem 10 immediately implies the conditional Ulam stability for Equation (1.1). The proof of Theorem 1 is now complete.

Hereafter, we present some examples. We consider the perturbed von Bertalanffy model

where $a > 0$, $b > 0$, and $p(t)$ is a continuous function. Let $a = 3$ and $b = 2$. Note that

Suppose that $0 < \varepsilon\le 1$, $w_0 \ge 1$, and $|p(t)|\le\varepsilon$ for $t\ge0$. Let $w \in C^1\left[0, T_{w}\right)$ and $\phi \in C^1\left[0, T_{\phi}\right)$ be the solutions of Equations (1.1) and (4.1) with $w(0) = \phi(0) = w_0$, respectively. Then, by Theorem 10, $T_{w} = T_{\phi} = \infty$ and

for $t\in [0, \infty)$.

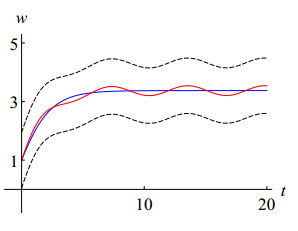
Now, we consider the case $p(t) = 0.2 \cos t$ for $t\ge0$. $\varepsilon = 0.2$ and Equation (1.1) is conditionally Ulam stable by Theorem 1. Figure 2 is a numerical simulation of the behavior of the solution curves of Equations (1.1) and (4.1) with $a = 3$, $b = 2$, and $w(0) = 1$. If we can measure the error (in this case, $\varepsilon = 0.2$) between the real phenomenon and its mathematical model, we can determine the accuracy of the fish growth model (in this case, $\frac{3}{10}\left(\frac{19}{12}\right)^{\frac{5}{2}}\approx 0.946351$). We consider the case $p(t) = -1.1$ for $t\ge0$. By means of Remark 3, the solution of Equation (4.1) will disappear when it hits the $t$-axis. See Figure 3.

Hereafter, we regard Equations (4.1) and (1.1) as the real phenomenon and its mathematical model, respectively. Seasonal fluctuations must be taken into account for fish growth. It should be assumed that the error between the real phenomenon and its mathematical model is also affected by seasonal fluctuations. In other words, $p(t)$ in Equation (4.1) is required to have periodicity. However, since it is not possible to create a real phenomenon, here we will approximate $p(t)$ using the following settings: Assume that the average error values in spring, summer, autumn, and winter are $p_1$, $p_2$, $p_3$, and $p_4$, respectively. Then, $p(t)$ can be written as follows:

where $T_1$, $T_2$, $T_3$, and $T_4$ are the spans of the spring, summer, autumn, and winter periods, respectively. $p(t)$ is a periodic function with period $T_1+T_2+T_3+T_4$. However, because it is not a continuous function, we cannot use our theorem directly. Therefore, we treat the above step function as a continuous function by approximating it with a Fourier series. Let $m$ be a sufficiently large natural number. Then, $p(t)$ is approximated by

where

and $\alpha_0$, $\alpha_n$, and $\beta_n$ are Fourier coefficients:

$p_m(t)$ is a continuous periodic function with period $2L = T_1+T_2+T_3+T_4$. In addition, we can easily calculate the maximum value of $|p_m(t)|$. Let

Assume that $0 < \varepsilon_m\le \frac{a}{3}\left(\frac{2a}{3b}\right)^2$ and $w_0 \ge \left(\frac{2a}{3b}\right)^3$. Let $w$ and $\phi$ be the solutions of Equations (1.1) and (4.1) with $w(0) = \phi(0) = w_0$, respectively. Then, by Theorem 10, we see that

for $t\in [0, \infty)$. Hence, we can conclude that if we regard Equations (4.1) and (1.1) as the real phenomenon and its mathematical model, respectively, then the magnitude of the error between the solutions of the real phenomenon and its mathematical model is less than $\frac{3}{b}\left(\frac{19}{12}\right)^{\frac{5}{2}}\varepsilon_m$.

5.   Conclusions

This is the first study of conditional Ulam stability for the von Bertalanffy growth model. This study considered the conditions for the global existence of approximate solutions to $\frac{dz}{d\tau} = z^{\frac{2}{3}}-z$ and clarified that a magnitude correlation holds between the approximate solutions. The combination of this relationship with some special inequalities established conditional Ulam stability for the above equation. It was clearly shown that the conditions related to the initial value and $\delta > 0$ are thresholds. The obtained result was applied to the von Bertalanffy growth model, for which conditional Ulam stability was established. Finally, numerical simulations were presented to explain the results. This study expands the potential of Ulam stability for growth models.

Acknowledgments

The author is supported by the Japan Society for the Promotion of Science (JSPS) KAKENHI (grant number JP20K03668).

Conflict of interest

The author declares no conflicts of interest.