On a generalization of fractional Langevin equation with boundary conditions

1.   Introduction

In multibody systems, the demand for lightweight designs requires researchers and designers to account for the impact of the link flexibility of the mechanisms. However, research on link flexibility has mainly focused on planar mechanisms and robotic arms, whereas there have been fewer studies focused on rigid flexible spatial parallel mechanisms with non-linear coupling effects. The parallel mechanism with rigid links and flexible spatial links is widely used in aerospace, industrial production, and other practical engineering fields. In particular, in the field of industrial production, robots with fewer degrees of freedom have been widely used ^[1,2,3,4,5]. Ideally, all the components should be set as rigid links for dynamics analysis, but at high speeds, the slender links will be elastically deformed, and the flexible deformation of the links and the coupling effects with the rigid links will have an important impact on the dynamic performance of the system. Therefore, it is of great significance to derive a reasonable dynamics model ^[6,7,8,9] of the rigid–flexible spatial parallel mechanisms with nonlinear coupling effects for analyzing the forces acting on a system and ensuring the trajectory accuracy of the end-effector.

The absolute nodal coordinate formulation (ANCF) ^{[10,11,12,13]} and the floating frame of reference (FFR) formulation ^[14,15] are widely used methods for establishing dynamics models of flexible multibody systems. The advantages of the former include the mass matrix being constant and the centrifugal and Coriolis forces being zero. However, the stiffness matrix is highly complicated and inefficient for use in calculating the dynamics solutions. In the FFR formulation, the coupling effects between the rigid and flexible coordinates are included in the dynamics ^[1,16,17,18], which can be applied with modal reduction techniques. There are two sets of coordinate systems in the FFR formulation. The first set is used to define the configuration of the local coordinate system, whereas the second set is applied to describe the configuration of the deformed body. Lugrís et al. ^{[19,20,21,22]} provide detailed derivations for the inertia terms, shape integrals, and elastic forces of planar mechanisms based on the FFR formulation. For instance, the dynamic performance of the rigid–flexible coupling of a hub-beam was considered in Liu and Liu ^[23]. Long et al. ^[24] presented a new method for determining the dynamics of a parallel robot with a flexible platform. In Zhang et al. ^[25,26], flexible multibody dynamics models of planar parallel robots were established, and the coupling effects were analyzed. Liu et al. ^[27] verified the importance of thermoplastic coupling using a rigid–flexible–thermal coupling model and a simulation verification. In Liu et al. ^[28], Lagrange's equations were applied to analyze the dynamic characteristics of a spatial parallel manipulator with a rigid end-effector and three flexible kinematic chains. Han et al. ^[29] implemented dynamics analysis and a simulation of a flexible beam element using the ANCF and FFR methods.

This paper makes six new contributions:

1) By setting the local coordinate system of the flexible spatial links as a non-centroid coordinate system, the influence of the coupling term in the inertia tensor on the dynamic performance of the system is considered.

2) Unlike previous models, this model uses the FFR method to determine the dynamics while accounting for the coupling effects between the rigid and flexible coordinates and the micro-displacement of the end effector. This allows the elastic vibrations and motion errors of the system to be more accurate.

3) Since the coupling term in the inertia tensor has an important influence on the dynamic performance of the system, it is considered in this analysis by setting the local coordinate system of the flexible spatial link as a non-centroid coordinate system. This coupling term was not taken into account in previous studies.

4) Three typical models were compared. The FFR model was established using the FFR formulation and Lagrange's equations, and simulation code was written in MATLAB. The FEA model was implemented using a co-simulation of SOLIDWORKS, ANSYS, and ADAMS. The ideal rigid–body model, which was established based on Lagrange's equations of the first kind, and an analytical solution were obtained.

5) The dynamics equation of the FFR model is a highly coupled, highly nonlinear, high-index differential-algebraic equation. The mass matrix is no longer a symmetric matrix, and the stiffness matrix is no longer a constant matrix. Converting the dynamics equation into a pure differential equation to obtain a numerical solution avoids the problem of numerical divergence caused by the inaccurate estimation of the initial value of the Lagrange multiplier and the new solution problem caused by the expansion of the model.

6) The results indicate that the FFR model is more accurate for calculating the influence of the flexible deformation on the dynamic performance of the spatial parallel robot. The recursive formulas are also applicable to other flexible spatial links.

2.   FFR formulation of flexible spatial link

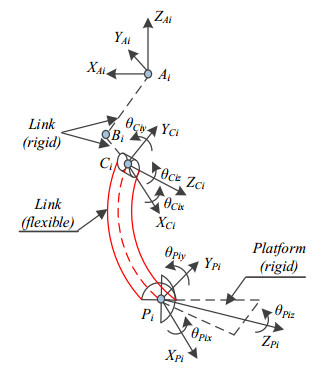
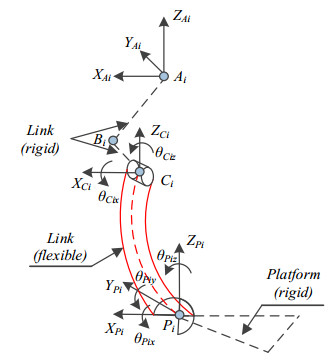
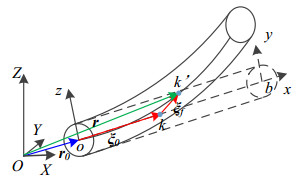
As depicted in Figure 1, the O-XYZ system is a global coordinate system that defines the large rigid-body displacement, and the o-xyz system is a local coordinate system that defines the small deformation body displacement.

By using the FFR formulation, the absolute position vector of point k on the flexible link can be written as

where ${{\boldsymbol{r}}_0}$ is the origin vector of the $o - xyz$ system, ${{\boldsymbol{\xi }}_0}(x, y, z)$ defines the vector of the point $k$ in $o - xyz$ in the undeformed state, and ${{\boldsymbol{\xi }}_f}$ represents the vector of point $k$ relative to the $o - xyz$ system in the deformed state. o and b are the two nodes of the spatial beam element. The rotation matrix ${\boldsymbol{R}}$ from the $o - xyz$ system to the $O - XYZ$ system is given by Eq (2). In particular, when the flexible link is a spatial link, matrix ${\boldsymbol{R}}$ includes more than one transformation angle ${\theta _i}(i = 1, \ldots n)$ as follows

The finite element method was employed to discretize the deformation field of the flexible spatial link. The displacement vector of any point k on the flexible spatial link caused by the deformation can be expressed as

where ${{\boldsymbol{q}}_f}$ represents the node displacement vector of the spatial beam element in the local coordinate system, and N represents the shape function. The specific expression of ${{\boldsymbol{q}}_f}$ is follows

where ${x_o}$, ${y_o}$, ${z_o}$, ${x_b}$, ${y_b}$, and ${z_b}$ represent deformation displacement vectors along the three coordinate axes at the nodes. ${\theta _{ox}}$, ${\theta _{oy}}$, ${\theta _{oz}}{\rm{ }}$, ${\theta _{bx}}$, ${\theta _{by}}$, and ${\theta _{bz}}$ represent the rotational displacement vectors around the three coordinate axes at the nodes.

It is assumed that the deformation displacement along the axis is described using a first-order polynomial, and a cubic polynomial interpolation function is used to describe the elastic angular deformation.

1) Axial interpolation function

Assuming that the axial interpolation function is a linear function, it can be written as

According to the boundary conditions

2) Horizontal interpolation function

Assuming that the axial interpolation function is a linear function, it can be written as

According to the boundary conditions

The axial and horizontal displacements corresponding to nodes $o$ and $b$ can be obtained by solving Eq (6) and Eq (8), therefore, the shape function ${\boldsymbol{N}}$ can be expressed as

where $e = x/L$, ${x_o} = e$, ${y_o} = {z_o} = 1 - 3{e^2} + 2{e^3}$, ${\theta _{by}} = - {\theta _{bz}} = L(- {e^2} + {e^3})$, ${y_b} = {z_b} = 3{e^2} - 2{e^3}$, ${\theta _{oy}} = - {\theta _{oz}} = L(e - 2{e^2} + {e^3})$, ${x_b} = 1 - e$.

3.   Spatial rigid–flexible coupling dynamics modeling

Lagrange's equations are typically used to derive the dynamics equations as follows ^[30]

where the $T$ is the kinetic energy, $V$ represents the potential energy, ${\boldsymbol{C}}$ represents constraint equations, vectors ${\boldsymbol{q}}$ and ${\boldsymbol{Q}}$ are the generalized coordinates of the generalized external forces, and ${\boldsymbol{\lambda }}$ is a Lagrange multiplier vector.

3.1.   Kinetic energy of each kinematic chain

3.1.1.   Kinetic energy of flexible spatial link

For the spatial flexible links, translational and rotational kinetic energy must be included.

1) Translational kinetic energy of flexible spatial link

The translational kinetic energy of the flexible spatial link based on the energy principle is as follows

where $\rho$ is the density of the material. The global position vector ${{\boldsymbol{r}}_k}$ is equal to

The velocity vector of the flexible spatial link is computed from Eq (12), yielding the following equation

The matrix ${\boldsymbol{H}}$ and generalized velocity vector $\dot{\boldsymbol{q}}$ can be expressed as

where ${{\boldsymbol{I}}_0}$ is a 3 × 3 identity matrix, and ${{\boldsymbol{I}}_1}, {{\boldsymbol{I}}_2}, ..., {{\boldsymbol{I}}_{n + 1}}$ can be expressed as follows:

By means of Eq (11), the translational kinetic energy of the flexible spatial link may be written as

where $A$ represents the cross-sectional area of the flexible spatial link. The mass matrix ${{\boldsymbol{M}}_{f - T}}$ of the translational kinetic energy is expressed in the following compact form

where ${{\boldsymbol{M}}_{tt}}$ represents the purely translational inertia terms, ${{\boldsymbol{M}}_{ff}}$ is the purely flexible component, ${{\boldsymbol{M}}_{t{\theta _n}}}(n = 1, 2, \ldots j)$ is the coupling term containing the translational and rotational coordinates, ${{\boldsymbol{M}}_{tf}}$ represents the coupling term between translational coordinates and flexible coordinates, ${M_{{\theta _n}{\theta _n}}}(n = 1, 2, \ldots j)$ is the purely rotational component, and ${{\boldsymbol{M}}_{{\theta _n}f}}(n = 1, 2, \ldots j)$ is the coupling term between rotational coordinates and flexible coordinates.

The matrix ${{\boldsymbol{M}}_{tt}}$ is a constant matrix, and ${\rm{ }}{{\boldsymbol{M}}_{ff}}, {\rm{ }}{{\boldsymbol{M}}_{t{\theta _n}}}, {\rm{ }}{M_{{\theta _n}{\theta _n}}}, {\rm{ }}{{\boldsymbol{M}}_{tf}}, {\rm{ }}{{\boldsymbol{M}}_{{\theta _n}f}}$ can be written as

When the flexible spatial link degenerates into a rigid spatial link, the deformation coordinates of the flexible link are zero (${{\boldsymbol{q}}_f} = 0$). Hence, the translational kinetic energy of the rigid spatial link can be further written as

2) Rotational kinetic energy of flexible spatial link

The rotational kinetic energy of the flexible spatial link is defined as

where ${\boldsymbol{\theta }}\left({x, t} \right)$ is the absolute rotation angle of the micro-segment with a distance x and a width dx from the local coordinate system origin in actual motion, and $d{{\boldsymbol{J}}_c} = \rho {\boldsymbol{J}}dx$ is the area moment of inertia around the center of mass.

The link area moment of inertia in the O-XYZ system can be expressed as

where $\bar {\boldsymbol{J}} = \left[{\begin{array}{*{20}{c}} {{I_x}} & {} & {} \\ {} & {{I_y}} & {} \\ {} & {} & {{I_z}} \end{array}} \right]$, ${I_x}$, ${I_y}$, and ${I_z}$ represent the respective area moments of inertia of the flexible spatial link with respect to the local coordinate axes $x$, $y$ and $z$ the rotational kinetic energy of the flexible spatial link can be written as

where ${{\boldsymbol{M}}_{f - R}}$ is the mass matrix corresponding to the rotational kinetic energy and is expressed as follows

The matrices ${{\boldsymbol{m}}_{rr}}, {\rm{ }}{{\boldsymbol{m}}_{ff}}, {\rm{ }}{{\boldsymbol{m}}_{r{\theta _n}}}, {\rm{ }}{{\boldsymbol{m}}_{rf}}, {\rm{ }}{m_{{\theta _n}{\theta _n}}}$, and ${{\boldsymbol{m}}_{{\theta _n}f}}$ can be written as

When the flexible spatial link degenerates into a rigid spatial link, the deformation coordinates of the flexible link are zero (${{\boldsymbol{q}}_f} = 0$). Hence, the rotational kinetic energy of the rigid spatial link can be further written as

3) Total kinetic energy of flexible spatial link

The total kinetic energy of the flexible spatial link is calculated as follows:

The total kinetic energy of the rigid spatial link is calculated as follows:

However, the generalized coordinates of the flexible spatial link are expressed in the $o - xyz$ system, and they must be expressed in the $O - XYZ$ system. Therefore, the transformation relationships from ${{\boldsymbol{q}}_f}$ to ${{\boldsymbol{u}}_m}$ are expressed as follows

where ${\boldsymbol{B}}$ is given by

Substituting Eqs (28) and (29) into Eq (26), the total kinetic energy of the flexible spatial link in the $O - XYZ$ system is

The specific forms of ${{\boldsymbol{\dot{\bar{q}}}}_{\boldsymbol{i}}}$ and ${{\boldsymbol{M}}_{O - f}}$ are shown in Appendix 1. Since the mass matrix in the $o - xyz$system is a symmetric matrix, but the total mass matrix of the system must be converted to the $O - XYZ$ system for representation, so it needs to be multiplied by the transform matrix ${\boldsymbol{B}}$, and because the matrix ${\boldsymbol{B}}$ is a asymmetry matrix. Therefore, the system mass matrix is no longer a symmetric matrix.

3.1.2.   Total kinetic energy of each kinematic chain

By assembling the differential equations of the rigid and flexible links, the kinetic energy of each kinematic chain can be expressed as

where ${\boldsymbol{\bar q}}$ represents the generalized coordinates of the kinematic chain, and ${{\boldsymbol{M}}_i}$ represents the mass matrix of the kinematic chain.

3.2.   Generalized forces of each kinematic chain

3.2.1.   Generalized elastic forces of each kinematic chain

According to the virtual work principle, the elastic force virtual work of any beam element in the flexible spatial link can be written as

where $\sigma$ and $\varepsilon$ represent stress and strain vectors, respectively. For linear isotropic materials, ${\boldsymbol{\sigma }} = E{\mathit{\pmb{\varepsilon }}}$, and the strain–displacement relationship is ${\mathit{\pmb{\varepsilon }}} = {\boldsymbol{DN}}{q_f}$. Substituting ${\boldsymbol{\sigma }} = E{\mathit{\pmb{\varepsilon }}}$ and ${\mathit{\pmb{\varepsilon }}} = {\boldsymbol{DN}}{q_f}$ into Eq (32), the beam element stiffness matrix can be written as

where $E$ and ${\boldsymbol{D}}$ represent the partial differential operator of the strain–displacement and the shear modulus of the flexible spatial link, respectively. The specific expression of ${{\boldsymbol{k}}_f}$ is shown in Appendix 1.

Because the rigid links cannot produce generalized elastic forces, the stiffness matrix of the kinematic chain in the $o - xyz$ system can be expressed as

Since ${{\boldsymbol{k}}_f}$ is a constant matrix, ${{\boldsymbol{k}}_i}$ is also a constant matrix, but the total stiffness matrix of the system must be converted to the $O - XYZ$ system for representation, so it needs to be multiplied by the transform matrix ${\boldsymbol{B}}$, and because the matrix ${\boldsymbol{B}}$ is a time-varying related to generalized coordinates. Therefore, the system stiffness matrix is no longer a constant matrix, and its specific form ${{\boldsymbol{K}}_i}$ is shown in Appendix 1.

The generalized elastic forces of the kinematic chain may be expressed by deriving the elastic potential energy relative to the elastic coordinates

where $V_e^i$ represent the elastic potential energy of the kinematic chain i.

3.2.2.   Generalized external forces of each kinematic chain

Based upon the aforementioned generalized forces, the generalized forces of the kinematic chain due to gravity of the spatial parallel robot can be written as

The virtual work of the robotic actuated force (torque) can be written as

The robotic actuated force (torque) of the kinematic chain can be derived by differentiation as

By means of Eq (10), the matrix form of the dynamics equations of the kinematic chain can be obtained as follows

where ${\boldsymbol{Q}}_V^i$ includes the Coriolis and centrifugal force matrices of the kinematic chain, which can be written as

3.3.   Dynamics equations of spatial rigid flexible coupling model

The dynamics equations of the spatial rigid–flexible coupling model can be expressed by assembling the dynamics equations of the kinematic chain and the constraint equations as follows

where ${\boldsymbol{M}}$ and ${\boldsymbol{K}}$ are the mass and stiffness matrices of the spatial rigid–flexible coupling model, respectively, ${{\boldsymbol{\hat F}}_g}$ and ${{\boldsymbol{\hat Q}}_F}$ are the generalized gravitational and robotic actuated force (torque), respectively, ${{\boldsymbol{\hat Q}}_V}$ represents the Coriolis and centrifugal forces, ${\boldsymbol{\hat q}}$ and ${\boldsymbol{\hat C}}_{{\boldsymbol{\hat q}}}^T$ are generalized coordinates and constraint Jacobian matrix of the spatial rigid–flexible coupling model, respectively. Among them, the constrained Jacobian matrix ${\boldsymbol{\hat C}}_{{\boldsymbol{\hat q}}}^T$ can be obtained by deriving the generalized coordinates from the constrained equations.

The matrices ${\boldsymbol{M}}$, Kand ${\boldsymbol{\hat q}}$ can be expressed as

where n and m represent the number of the rigid and flexible coordinates of the spatial parallel robot, respectively.

4.   Numerical examples

4.1.   Physical description

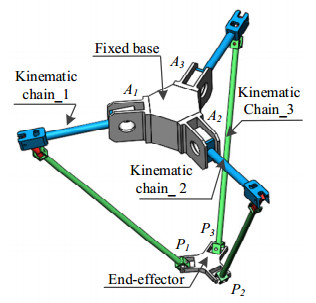
A typical 3-RRRU spatial parallel robot with rigid links and flexible spatial links is shown in Figure 2.

This robot has three triangular symmetric kinematic chains. It is composed of ten parts, a driving link A_iB_i (i = 1, 2, 3), an intermediate link B_iC_i (i = 1, 2, 3), a passive link C_iP_i (i = 1, 2, 3), and the end-effector P₁P₂P₃. The fixed base and driving links are connected by a revolute pair A_i (i = 1, 2, 3), whereas joints B_i (i = 1, 2, 3) and C_i (i = 1, 2, 3) are passive revolute pairs. The end-effector and passive links are connected by universal joints. Among these ten parts, the passive link C_iP_i (i = 1, 2, 3) is a slender link that will be elastically deformed under high-speed motion. Therefore, it is treated as a flexible-body, and the other parts are treated as a rigid body. The link C_iP_i (i = 1, 2, 3) can perform arbitrary movements in space. However, the component connected to it is a rigid component, so the end-effector can only perform translational movement along three coordinate axes.

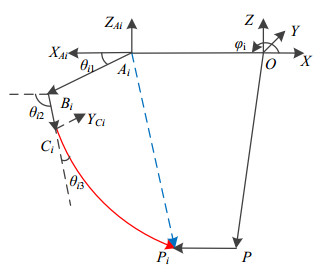
The joint variables of the robotic kinematic chain with rigid links and flexible spatial links is illustrated in Figure 3.

The global coordinate system O-XYZ is attached to the geometric center of the fixed base. The Z-axis is perpendicular to the fixed base, and the X-axis is opposite to the undeformed neutral axis of each link. The local coordinate is fixed at the upper joint of each link. The driving link AiBi (i = 1, 2, 3) and intermediate link BiCi (i = 1, 2, 3) are in the same plane, the rotating axis in the global coordinate system is the Y-axis, but the rotation axis of passive link CiPi (i = 1, 2, 3) is the Z-axis. Therefore, the passive link CiPi (i = 1, 2, 3) is a spatial link.

The lengths of components A_iB_i, B_iC_i, and C_iP_i (i = 1, 2, 3) are L₁, L₂, and L₃, respectively.${\theta _{i1}}$, ${\theta _{i2}}$ and ${\theta _{i3}}$ are the angles between the rotation axis and links A_iB_i, B_iC_i, and C_iP_i (i = 1, 2, 3) in the local coordinate system, respectively. φ_i (i = 1, 2, 3) denotes the angle between the coordinate system $O - XYZ$ and ${A_i} - {X_{Ai}}{Y_{Ai}}{Z_{Ai}}(i = 1, 2, 3)$ in the Z direction, and ${Z_{Ai}}$ is parallel to $Z$.

4.2.   The dynamic analysis and comparison of the three robotic models

To ensure the correctness of the derived dynamic equations, it is necessary to verify the influence of the flexible deformation on the system by comparing the end-effector motion trajectories in the FFR and the ideal rigid-body models and to verify the accuracy of the derived formula by comparing the motion trajectory deviations of the FFR and FEA models relative to that of the ideal rigid-body model. The dynamics equations of the three models were established using Lagrange's equations of the first kind and solved by numerical integration.

4.2.1.   FFR model of robotic dynamics

1) Dynamic equations of the spatial flexible link

Dynamics models can be established using the dynamics equations derived in section 2 and 3. First, by means of Eq (12), the vector ${{\boldsymbol{r}}_k}$ is described as follows:

where ${{\boldsymbol{\xi }}_0} = {\left[{\begin{array}{*{20}{c}} x & y & z \end{array}} \right]^T}$, ${{\boldsymbol{\xi }}_f}{\boldsymbol{ = N}}{{\boldsymbol{q}}_f}$.

The absolute rotation angle vector can be written as

Figures 4 and 5 show the flexible coordinates in the $o - xyz$ and $O - XYZ$ systems, respectively.

By means of Eq (28), the relationship between the generalized coordinates ${{\boldsymbol{q}}_f}$ and ${{\boldsymbol{u}}_i}$ can be obtained.

Finally, the translational and rotational kinetic energies of the flexible spatial link of the 3-RRRU spatial parallel robot can be obtained by substituting Eqs (43) and (44) into Eqs (11) and (20), respectively, and the total kinetic energy of the flexible spatial link in the global coordinate system can be obtained according to Eq (30), as follows:

where $\dot{\overline{\boldsymbol{q}}}_{i} = \frac{d\left(\left[\begin{array}{llll} \boldsymbol{\theta}_{i 1} & \boldsymbol{\theta}_{i 2} & \boldsymbol{\theta}_{i 3} & \boldsymbol{u}_{m} \end{array}\right]\right)}{d t}.$

2) Dynamic equations of rigid components

Because the driving link A_iB_i (i = 1, 2, 3) is purely rotated, its rotational kinetic energy is

The intermediate link B_iC_i (i = 1, 2, 3) has both translational and rotational kinetic energy, and its kinetic energy is expressed as follows

The kinetic energy of each kinematic chain can be obtained by substituting Eqs (45)–(47) into Eq (31).

The potential energy of rigid component of the kinematic chain can be written as

The generalized gravitational force ${\boldsymbol{F}}_g^i$ of the kinematic chain can be obtained by substituting Eq (48) into Eq (36).

The generalized coordinates and the driving force of the C_iP_i (i = 1, 2, 3) can be expressed as

The actuated torque ${\boldsymbol{Q}}_F^i$ of the robotic system can be obtained by substituting Eq (49) into Eq (38).

However, the elastic deformation of the flexible links will cause positional errors in the kinetic trajectory of the end-effector, Therefore, the micro-displacement and micro-rotation generalized coordinates of the end-effector can be assumed to be $\Delta {\boldsymbol{P}} = \left[{\Delta P\begin{array}{*{20}{c}} {_x} & {\Delta {P_y}} & {\Delta {P_z}} \end{array}} \right.\;\left. {\Delta P\begin{array}{*{20}{c}} {_{\theta x}} & {\Delta {P_{\theta y}}} & {\Delta {P_{\theta z}}} \end{array}} \right]$, the actual kinetic trajectory ${\boldsymbol{P}}' = \left[{\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{P_x}'} & {{P_y}'} & {{P_z}'} \end{array}} & {{P_{\theta x}}'} & {{P_{\theta y}}'} \end{array}} \right.$${\rm{ }}\left. {{P_{\theta z}}'} \right]$, the ideal motion trajectory ${\boldsymbol{P}} = [{P_x}{\rm{ }}{P_y}{\rm{ }}{P_z}{\rm{ }}{P_{\theta x}}\left. {{\rm{ }}{P_{\theta y}}{\rm{ }}{P_{\theta z}}{\rm{ }}} \right]$, and the relationship between ${\boldsymbol{P}}'$, $\Delta {\boldsymbol{P}}$ and$\mathrm{ } \;{\boldsymbol{P}}$ can be expressed as

where ${{\boldsymbol{U}}_P} = \left[{\begin{array}{*{20}{c}} 1 & {} & {} & 0 & {{P_z}} & { - {P_y}} \\ {} & 1 & {} & { - {P_z}} & 0 & {{P_x}} \\ {} & {} & 1 & {{P_y}} & { - {P_x}} & 0 \end{array}} \right]$.${{\boldsymbol{U}}_P}$ represents geometrical constraint relationship ^[31] between the actual kinetic trajectory and ideal kinetic trajectory of the end-effector. Thus, the kinetic and potential energy of the end-effector can be written as

3) Constraint relationship

The constraint equations are defined as follows.

(1) Constraint equation of the length of link B_iC_i (i = 1, 2, 3)

(2) Constraint equation for the distance between point P_i (i = 1, 2, 3) and P

(3) Constraint equation for joint C_i (i = 1, 2, 3) can be expressed by the position vector of the rigid joint C_i (i = 1, 2, 3) equal to the position vector of the flexible joint C_i (i = 1, 2, 3)

(4) Constraint equation for joint P_i (i = 1, 2, 3) can be expressed by the position vector of the rigid joint P_i (i = 1, 2, 3) equal to the position vector of the flexible joint P_i (i = 1, 2, 3)

The constraint equations can be written as

The velocity constraint matrix and the angular velocity constraint matrix can be obtained by calculating the first and second derivative of the position constraint matrix $\hat C$with respect to time t, the specific expression are as follows

The Eq (56), $T_O^i, {\rm{ }}{\boldsymbol{Q}}_F^i, {\rm{ }}$${\boldsymbol{F}}_g^i$ and Eq (51) are substituted into Eq (41) to obtain the matrix form of the system dynamics equations of the spatial rigid–flexible coupling model.

4) Numerical solution

The FFR model of the spatial parallel robot with rigid links and flexible spatial links was established using the FFR formulation. The number of generalized coordinates for the FFR model was 42, which included 12 rigid and 30 flexible coordinates. By means of Eq (41), the dynamics equations can be rewritten as

where ${\boldsymbol{\hat Q}} = {{\boldsymbol{\hat Q}}_F} + {{\boldsymbol{\hat Q}}_V} - {\boldsymbol{K\hat q}} - {{\boldsymbol{\hat F}}_g}.$

Since the Eq (59) in this study were differential algebraic equations with a high index of 3, and numerical divergence occurred readily. Therefore, to obtain the solution, they were combined with the acceleration Eq (58) to solve.

Because the dynamics solution was obtained at the acceleration level, as the number of iterations increased, it was possible to calculate the position and velocity constraint equation errors. Therefore, positional and velocity violations were eliminated using the Baumgarte stabilization method, which can be expressed as follows

where $\alpha$ and $\beta$ are system feedback control parameters, ${{\mathit{\pmb{\varepsilon }}}_1}$ and ${{\mathit{\pmb{\varepsilon }}}_2}$ represent the displacement and velocity constraint stabilization parameters, respectively, expressed as follows

It is necessary to estimate the initial values of the generalized position coordinate vector ${\boldsymbol{\hat q}}$ and the Lagrange multiplier vector ${\boldsymbol{\hat \lambda }}$. ${\boldsymbol{\hat q}}$ can be estimated based on the initial position of the rigid-body dynamics, but it is much more difficult for ${\boldsymbol{\hat \lambda }}$. Therefore, the numerical calculation was performed by reducing the index to 1. Equation (59) can be rewritten in the following form

Multiplying both sides of Eq (62) by ${{\boldsymbol{\hat C}}_{{\boldsymbol{\hat q}}}}$ yields the following

Vector ${\boldsymbol{\hat \lambda }}$ can be obtained by combining Eqs (60) and (63). Vector ${d^2}{\boldsymbol{\hat q}}/d{t^2}$ can be obtained by substituting ${\boldsymbol{\hat \lambda }}$ into Eq (62). Vectors ${\boldsymbol{\hat q}}$ and $d{\boldsymbol{\hat q}}/dt$ were obtained by utilizing the Newmark $\beta$ method.

where $h$ is the step size. Computational programs were written in MATLAB to perform dynamic simulation of the FFR model.

5) Frequency solution

By means of Eq (41), the free vibration equations of the 3-RRRU spatial parallel robot with rigid links and flexible spatial links can be written as

According to the modal analysis theory ^[32], the natural frequency and modal expressions of the system can be obtained as

When the mass matrix is a non-singular matrix, let ${\boldsymbol{S}} = {{\boldsymbol{M}}^{{\boldsymbol{ - 1}}}}{\boldsymbol{K}}$, then Eq (66) can be rewritten as

where ${\omega _m}$ is the natural angular frequency of the system, and ${f_m}$ is the natural frequency of the system.

4.2.2.   Ideal rigid-body model of robotic dynamics

Ideally, the spatial links C_iP_i (i = 1, 2, 3) of the spatial parallel robot can be treated as a rigid body, and the kinetic energy ${T_{{C_i}{P_i}}}$ can be directly calculated using Eq (27). The specific expression is

The potential energy of the spatial link C_iP_i (i = 1, 2, 3) can be obtained by the work–energy theorem, and its expression is as follows:

The kinetic and potential energies of the end-effector can be calculated as

Therefore, the dynamic model of the ideal rigid-body can be established by introducing the kinetic and potential energy of each rigid link into the Lagrange equations of the first kind, which can be solved by numerical methods.

4.2.3.   FEA model of robotic dynamics

To compare and verify with the FFR model, the structural features and numerical solution methods of the FEA model are the same as the FFR model. When the spatial parallel mechanism is simulated by finite element software, there are many factors affecting its dynamic characteristics. Therefore, the following assumptions must be made before establishing a FEA model of a spatial rigid–flexible coupled parallel robot.

1) The elastic deformation of the spatial slender link during system operation will have an important impact on the dynamic performance of the system. Therefore, in the FEA model, the spatial link is considered to be a flexible body, and the other links are considered to be rigid bodies for analysis.

2) Each pair of components are connected by a rigid motion pair.

3) There is negligible friction between pairs.

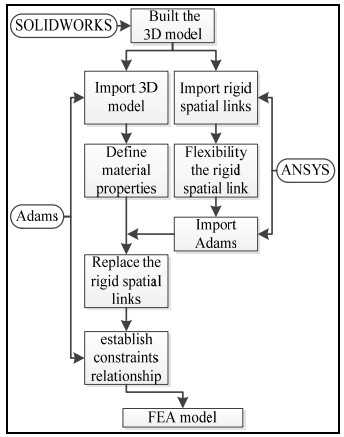
The FEA model was implemented using a co-simulation of three software packages: ANSYS, SOLIDWORKS, and ADAMS. The workflow of the co-simulation using these three software packages is shown in Figure 6.

First, the 3D model was established in SOLIDWORKS and imported into finite element analysis software in the STP file format. Second, the deformation of the flexible spatial link ${{\rm{C}}_i}{{\rm{P}}_i}(i = 1, 2, 3)$ is described by the FEA method. The bodies of the flexible spatial links were meshed with SOLID 185 units and contained 48,598 elements and 63,659 nodes. The model was saved as a flexible neutral file (.mnf) and imported into ADAMS through the ADAMS connection module in ANSYS. Finally, the constraint relationship of the FEA model was defined based on the actual physical prototype in ADAMS, and the material properties are shown in Table 1. The dynamics equations were deduced using Lagrange's equations, and an integral solver (SI2, GSTIFF) was used for the simulation analysis in ADAMS, and the solution accuracy is 10^-4.

The simulation time was set to 5 s, and the step size was 0.001 s. To verify the correctness of the rigid–flexible coupled model, the results of the fully rigid inverse dynamics model were loaded into the rigid–flexible coupled model based on the same driver. The validity of the model was determined by examining the movement trends and trajectory errors of the two types of models.

5.   Simulation results and analysis

To validate the presented method, a circular trajectory of the geometric center point of the end-effector was used to carry out the simulation. The circle defined in the plane ${P_z} = - 0.7{\rm{ m}}$ with a radius of 0.1 m can be written as

where $\omega$ represents the angular velocity of the end-effector, which was set to 2 rad/s. The shearing modulus G = 8 × 10⁴ MPa. The geometric properties of all the parts are shown in Table 2, and the solution accuracy is 10^-4. When the dynamic analysis was performed on an ideal rigid-body model, the material properties of all parts were steel.

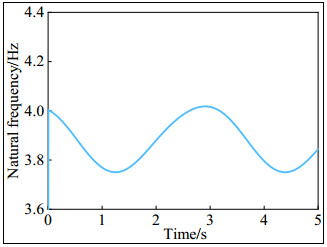
The relationship of the natural frequency of the spatial parallel robot with rigid links and flexible spatial links with time can be solved by MATLAB software programming, and the result is shown in Figure 7.

In order to verify the correctness of natural frequency by using the derived dynamics model, based on the FEA simulation model, the natural frequency of the system is analyzed through the ADAMS/Vibration module. The results are shown in Table 3.

It can be seen from Table 3 that the first 6 natural frequencies in the vibration simulation model are all 0, that is, the rigid body mode corresponding to the system. Therefore, the minimum natural frequency of the system appears at the 7th order, and the corresponding natural frequency is 2.21E-005Hz. The minimum natural frequency of the derived dynamics model calculated by Eq (67) is 3.72E-005Hz. Due to the large number of elements of the flexible spatial link and the system's assembly errors, the minimum natural frequency of the simulation model is smaller than the derived dynamics model, but the two values are basically the same, thus verifying the correctness of the establishment of the dynamics model.

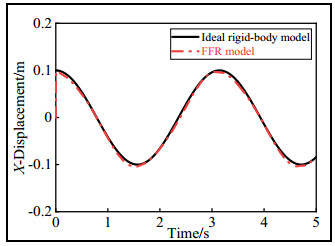
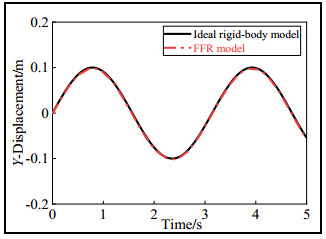
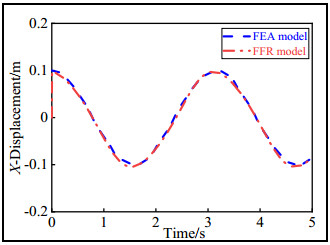
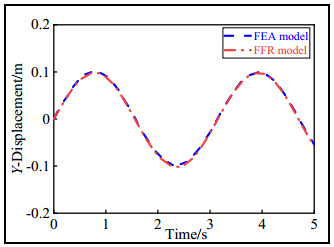
A comparison of the displacement of the end-effector between the ideal rigid-body and FFR models is shown in the figures below. The displacement trajectories of the geometric center point of the end-effector in the X and Y directions with time are shown in Figures 8 and 9, respectively.

As shown in Figures 7 and 8, the trajectory trends of the end-effector of the ideal rigid-body and FFR models were basically the same, but the FFR model predictions yielded certain range of fluctuations relative to the ideal rigid-body model trajectory. The maximum deviations of the fluctuations are shown in Table 4. The fluctuations reached a maximum at the peak point of the motion trajectory.

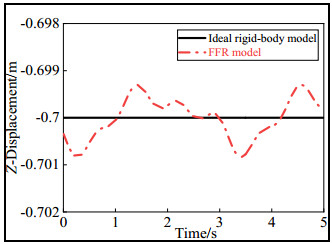
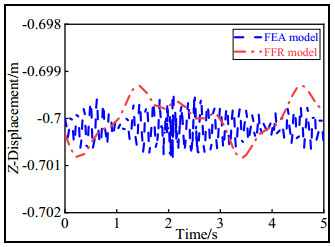
The displacement of the geometric center of the end-effector in the Z direction is shown in Figure 9.

As shown in Figure 10, when the end-effector was moving in a plane, the Z-direction displacement of the rigid system did not change, and the rigid flexible coupling system floated between −0.70083 and −0.6993 m.

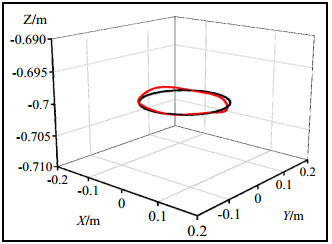
The circular motion trajectories of the end-effector of the ideal rigid-body and FFR models on the three planes are shown in Figure 11.

Figure 11 shows that the motion trajectory of the ideal rigid-body model was an ideal circular curve, but the FFR model was no longer an ideal circular curve. This was because the elastic deformation of the flexible spatial links in the FFR model affected the dynamic performance of the system. Therefore, the elastic deformation of the flexible spatial links cannot be ignored, and it is necessary to establish a dynamic model that follows rigid–flexible coupling dynamics.

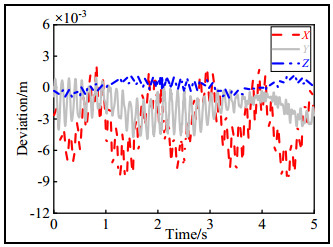
Figures 12 and 13 show the displacement differences of the end-effector between the FFR and FEA models in the X and Y directions, respectively.

As shown in Figures 12 and 13, the FFR and FEA models exhibited the same trends and fluctuated within a certain range. This was because the FFR and FEA models considered the elastic deformation of the flexible spatial links. The maximum fluctuations of both models in the X and Y directions mainly appeared at the peaks of the trajectories. However, compared to the FEA model, the ranges of the FFR model's values in the X and Y directions were −0.008942 to 0.0022 m and −0.00471 to 0.000805 m, respectively.

The displacements of the end-effector for the FFR and FEA models in the Z direction are shown in Figure 14.

As shown in Figure 14, the motion trajectories of the FFR and the ideal rigid-body models both fluctuated within a certain range, and the range of the FFR model was larger than that of the ideal rigid-body model. The floating values in the Z direction were −0.00099 to 0.00125 m.

The comparison of the deviations of the end-effector of the FFR model relative to the FEA model in the X, Y, and Z directions is shown in Figure 15.

As shown in Figure 15, the deviations of the end-effector in the X, Y, and Z directions showed periodic variations. The error fluctuations in the X direction were the largest, followed by those in the Y direction, and the error changes in the Z axis were the smallest. This was related to the relative position of the geometric center of the end-effector and the global coordinate system.

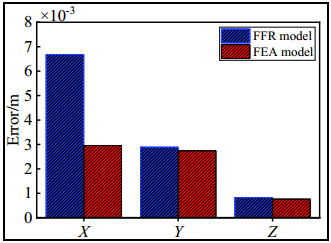
The comparison of the maximum deviations of the motion trajectories of the end-effector of the FFR and FEA models in the X, Y, and Z directions relative to the ideal rigid-body model are shown in Figure 16.

As shown in Figure 16, the maximum deviations of the motion trajectory of the end-effector of the FFR model relative to the ideal rigid-body in the X, Y, and Z direction were larger than those of the FEA model. The deviations of the trajectories between the FFR and FEA models relative to the ideal rigid-body in the X, Y, and Z directions were 0.00372, 0.00015, and 0.000066 m, respectively. This was because the FFR model accounted for the micro-displacement of the end-effector in the dynamic modeling process and strengthened the influence of the flexible spatial link deformation on the dynamic performance of the system by ignoring damping. In addition, the FFR model further considered the nonlinear coupling effects of the rigid links and flexible spatial links. Therefore, the FFR model could more accurately describe the nonlinear deformation of the flexible links and the robotic rigid–flexible coupling effects during the motion, resulting in fluctuations in the trajectory compared to the trajectories of the other two methods.

6.   Conclusions

Compared with an ideal rigid-body model, the FFR and FEA models exhibited a range of fluctuations in the X, Y, and Z directions because they considered flexible deformation of the spatial links, and the results were consistent with actual observations. The peak values of the end-effector were larger for the FFR than those obtained using the FEA model. This occurred because the FFR model considered not only the deformation of the spatial flexible links, but also the nonlinear coupling effects between the rigid and flexible spatial links and the micro-displacement of the end-effector. The FFR model could more accurately describe the influence of the flexible links on the spatial parallel robot. Because the effectiveness of the dynamics equations was verified, this method can be used for the dynamics modeling of other flexible spatial links where the nonlinear coupling effects cannot be neglected.

Acknowledgements

The work described in this paper was supported by the National Key Research and Development Project (No. 2017YFB1303502), the Tianjin Research Program of Application Foundation and Advanced Technology (No.17JCYBJC18300, No.18JCYBJC87900, and No.17JCQNJC04200), the Tianjin Municipal Education Commission Research Project (Grant No. 2017KJ259 and 2017KJ260), and the National Undergraduate Training Programs for Innovation and Entrepreneurship (No.20181006 0013).

Conflict of interest

The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.

Appendix.   1

Natation

A cross-sectional area

B transformation matrix to convert from local coordinate system to global coordinate system

C constraint equations

E elastic modulus

${\boldsymbol{F}}_{elastic}^i$ elastic force of flexible link of kinetic chain

${\boldsymbol{F}}_g^i$ elastic force of kinematic chain

G shearing modulus

I_x, I_y, I_z area moments of inertia of spatial flexible link with respect to the local coordinate x, y, and z axes

k_f stiffness matrix of flexible spatial link

K stiffness matrix of system

L length

M mass matrix

N shape function

P trajectory of the geometric center point of the end-effector

q_f generalized elastic coordinate

q generalized coordinate of kinematic chain in reference system

$\bar {\boldsymbol{q}}$ generalized coordinate of kinematic chain in global system

$\hat {\boldsymbol{q}}$ generalized coordinate of system in global system

$\dot {\boldsymbol{\hat q}}$ generalized velocity vector of system in global system

$\ddot {\boldsymbol{\hat q}}$ generalized acceleration vector of system in global system

Q generalized external vector

$\boldsymbol Q_\boldsymbol F^\boldsymbol i$ robotic actuated force (torque) of kinetic chain

$\boldsymbol Q_\boldsymbol V^\boldsymbol i$ Coriolis and centrifugal forces

r_k position vector of an arbitrary point

r₀ position vector of the reference

R transformation matrix

T kinetic energy

u_m elastic generalized coordinate in global coordinate system

V potential energy

$\alpha, \beta$ system feedback control parameters

${{\boldsymbol{\xi }}_0}$ undeformed state in the reference system

${\boldsymbol \xi _f}$ deformed state in the reference system

$\boldsymbol \theta$ absolute angle

${{\boldsymbol{\varepsilon }}_1}$ displacement constraint stabilization parameters

${{\boldsymbol{\varepsilon }}_2}$ velocity constraint parameters

ω angular velocity vector defined in global coordinates

Appendix.   2

where $G$ represents the shear modulus of the flexible spatial link, ${I_p} = \int_A {({y^2} + {z^2})} {\rm{ }}dA$, ${I_y} = \int_A {{z^2}} dA$ and ${I_z} = \int_A {{y^2}} dA$