A new vertex distinguishing total coloring of trees

1.   Introduction

The problem of vertex distinguishing colorings can be traced to two articles ^[3] and ^[4]. Burris and Schelp ^[3] introduced a proper edge $k$-coloring of a simple graph $G$ is called a vertex distinguishing edge $k$-coloring ($k$-vdec, or vdec for short) if for any two distinct vertices $u$ and $v$ of $G$, the set of the colors assigned to the edges incident with $u$ differs from the set of the colors assigned to the edges incident with $v$. The minimum number of colors required for all vertex distinguishing colorings of $G$ is denoted by $\chi \, '_s(G)$. Let $n_d(G)$ denote the number of all vertices of degree $d$ in $G$, or $n_d = n_d(G)$ if no confusion. Furthermore, Burris and Schelp presented the following conjecture: Let $G$ be a simple graph having no isolated edges and at most one isolated vertex, and let $k$ be the smallest integer such that $(^k_d)\geq n_d$ for all $d$ with respect to $\delta(G)\leq d\leq \Delta(G)$. Then $k\leq \chi \, '_s(G)\leq k+1$. The above Conjecture is known for some families of graphs, including complete graphs, complete bipartite graphs and many trees ^[3]. Later it has been proved for graphs of large maximum degree ^[1] and for $G$ a union of cycles or a union of paths ^[2]. Therefore, the most challenging cases seem to occur when $G$ has small maximum degree which is at least three. In this paper we show some results on trees to confirm positively Burris-Schelp Conjecture.

Graphs mentioned here are undirected, finite and simple, and graph colorings are proper (so we omit the term "proper" hereafter). We use standard terminology and notation of graph theory, and introduce a new total coloring with two vertex distinguishing constraints. Let $f$ be a total coloring of a simple graph $G$ from $V(G)\cup E(G)$ to $\{1, 2, \dots, k\}$, and let $C(u, f)$ be the set of the colors assigned to the edges incident with $u$. If $f$ holds simultaneously

then we call call $f$ a (2)-vertex distinguishing total $k$-coloring, and write $k$-(2)-vdc for short. The minimum number $k$ of colors required for which $G$ admits a $k$-(2)-vdc is denoted by $\chi''_{2s}(G)$. Clearly, an edge coloring obtained by removing the colors assigned to vertices from a $k$-(2)-vdc of $G$ is just a $k$-vdec of $G$, which implies that $\chi'_s(G)\leq \chi''_{2s}(G)$. We say a color $a$ is missing at a vertex $u$ means $a\not\in C(u, f)\cup \{f(u)\}$. A leaf is a vertex of degree one, and a $k$-degree vertex is one of degree $k$ at least two. The set of neighbors of a vertex $u$ of $G$ is denoted by $N_G(u)$, or $N(u)$ if no confusion; the degree $d_G(u)$ of $u$ is equal to $|N_G(u)|$. $D(G)$ stands for the diameter of $G$. The shorthand notation $[m, n]$ stands for an integer set $\{m, m+1, \dots, n\}$ with $n > m\geq 0$. Let $P_n$ be a path on $n$ vertices. In the present work, we will show the following:

Theorem 1. Let $T$ be a tree with $n_2(T)\leq n_1(T)$ and $|T|\geq 3$. Then $\chi\, ''_{2s}(T) = n_1(T)+2$ if $T\cong P_3, P_4$; $\chi\, ''_{2s}(T) = n_1(T)+1$ if $T\not\cong P_3, P_4$ and $n_1(T) = \Delta(T)$ or $D(T) = 3$; and $\chi\, ''_{2s}(T) = n_1(T)$ for otherwise.

2.   Basic lemmas

Lemma 2. Let $T$ be a tree with $n_2(T)\geq n_1(T)$. Then there exists a $2$-degree vertex such that one of its neighbors is either a leaf or a vertex of degree $2$.

Proof. Suppose (reductio and absurdum) that each 2-degree vertex $x$ is not adjacent to a leaf and has its neighborhood $N(x) = \{x_1, x_2\}$ such that $d_T(x_i)\geq 3$ for $i = 1, 2$. Then we have $n_2\leq \sum\limits_{d = 3}^{\Delta}n_d$ by the assumption. Applying the formula $n_1 = 2+\sum\limits_{d = 3}^{\Delta}(d-2)n_d$ shown in ^[5], we have $n_1\geq 2+n_d$ for $d\geq 3$, and

which shows that $\sum\limits_{d = 3}^{\Delta}n_d\leq \frac{1}{2}(n_1+n_3)-1$. It immediately deduces that

which contradicts to the hypothesis.

Lemma 3. Let $T$ be a tree with $D(T) = 3$. Then $\chi\, ''_{2s}(T) = n_1(T)+2$ for $|V(T)| = 4$, and $\chi\, ''_{2s}(T) = n_1(T)+1$ for $|V(T)|\geq 5$.

Proof. Observe that each tree of diameter 3, also, is a double star $DS_{m+1, n+1}$ obtained by joining two centers of two complete bipartite graphs $K_{1, m}$ and $K_{1, n}$. When $n = m = 1$, $T$ is a path of length 3 with $n_1(T) = n_2(T)$, and we can verify $\chi\, ''_{2s}(T) = n_1(T)+2$ by simply assigning colors to the edges and vertices of $T$. For $m+n\geq 3$, let $V(K_{1, m}) = \{s, s_1, s_2, \dots, s_m\}$ and $E(K_{1, m}) = \{ss_1, ss_2, \dots, ss_m\}$; $V(K_{1, n}) = \{t, t_1, t_2, \dots, t_n\}$ and $E(K_{1, n}) = \{tt_1, tt_2, \dots, tt_n\}$, where $s$ and $t$ are the centers. Then $V(DS_{m+1, n+1}) = V(K_{1, m})\cup V(K_{1, n})$ and $E(DS_{m+1, n+1}) = E(K_{1, m})\cup E(K_{1, n})\cup \{st\}$. Suppose that $f$ is a $k$-(2)-vdc of $DS_{m+1, n+1}$ such that $k = \chi\, ''_{2s}(DS_{m+1, n+1})$. Since $C(s_i, f)\neq C(s_j, f)$ and $C(t_i, f)\neq C(t_j, f)$ for $i\neq j$, $C(s_i, f)\neq C(t_l, f)$ for $i\neq l$, and $C(s, f)\neq C(t, f)$, $k\geq m+n+1$. This $k$-(2)-vdc $f$ can be exactly defined by setting $f(ss_i) = i$ for $i\in [1, m]$, and $f(s_i) = i-1$ for $i\in [2, m]$, $f(s_1) = m$; $f(s) = m+2$, $f(st) = m+1$, $f(t) = 1$; $f(tt_j) = m+1+j$ for $i\in [1, n]$, and $f(t_j) = m+j$ for $i\in [2, n]$, $f(t_1) = m+n+1$.

Lemma 4. For $n\geq 2$, a $2$-star, denoted as $K^{(2)}_{1, 2n}$, is a tree on $1+2n$ vertices such that every leaf of $K_{1, n}$ is joined a new vertex out of $K_{1, n}$ by an edge. Then $\chi\, ''_{2s}(K^{(2)}_{1, 2n}) = n+1$.

Proof. Suppose that $K_{1, n}$ has its own vertex set $V(K_{1, n}) = \{w, w_1, w_2, \dots, w_n\}$ and edge set $E(K_{1, n}) = \{ww_1, ww_2, \dots, ww_n\}$. By the definition of a $2$-star $K^{(2)}_{1, 2n}$, we have $V(K^{(2)}_{1, 2n}) = V(K_{1, n})\cup S$, where $S = \{z_1$, $z_2$, $\dots$, $z_n\}$ with $S\cap V(K_{1, n}) = \emptyset$, and edge set $E(K^{(2)}_{1, 2n}) = E(K_{1, n})\cup \{w_1z_1$, $w_2z_2$, $\dots$, $w_nz_n\}$. Clearly, $n_1(K^{(2)}_{1, 2n}) = n$, each $z_i$ is a leaf of $K^{(2)}_{1, 2n}$ for $i\in [1, n]$. It is clear that $\chi\, ''_{2s}(K^{(2)}_{1, 2n})\geq n+1$. It is straightforward to define an $(n+1)$-(2)-vdc $f$ of $K^{(2)}_{1, 2n}$ as follows: $f(w) = n+1$; $f(ww_i) = i$ for $i\in [1, n]$; $f(w_iz_i) = i-1$ for $i\in [2, n]$, and $f(w_1z_1) = n$; $f(w_i) = i+1$ for $i\in [1, n-1]$, and $f(w_n) = 1$; $f(z_i) = i$ for $i\in [3, n]$, and $f(z_1) = f(z_2) = n+1$.

Lemma 5. Let $T$ be a tree with $n_2(T)\leq n_1(T)$ and $|T|\geq 3$. If $\Delta(T) = n_1(T)$, then $\chi\, ''_{2s}(T) = n_1(T)+2$ for $\Delta(T) = 2$, and $\chi\, ''_{2s}(T) = n_1(T)+1$ for $\Delta(T)\geq 3$.

Proof. Write $n_i = n_i(T)$ for $i\in [\delta, \Delta]$, where $\delta = \delta(T)$ and $\Delta = \Delta(T)$. By a formula $n_1 = 2+\sum\limits_{3\leq d\leq \Delta}(d-2)n_d$ in ^[5] and $\Delta = n_1$, we have $n_\Delta = 1$ and $n_d = 0$ for $3\leq d\leq \Delta-1$. Thus, $T$ is called a spider having its body $w$ with $d_T(w) = \Delta$ and legs $P_i = ww_{i, 1}w_{i, 2}\cdots w_{i, k_i}$ for $k_i\geq 1$ and $i\in [1, \Delta]$. When $k_i = 2$ for $i\in [1, \Delta]$, $T = K^{(2)}_{1, 2\Delta}$ is a $2$-star. When $\Delta(T) = 2$, $T$ is a path of length 2 or 3, hence it easily gets that $\chi\, ''_{2s}(T) = n_1+2$. For $\Delta(T)\geq 3$, we show $\chi\, ''_{2s}(T) = n_1(T)+1$ in the following. If $T$ is a $2$-star, we are done by Lemma 4. By induction on the order of spiders, and assume that $T$ is not a $2$-star.

Observe that there exists some $k_i = 1$ since $T$ is not a $2$-star and $n_2(T)\leq n_1(T)$. Without loss of generality, set $k_1 = 1$, then we have a tree $T_1 = T-w_{1, 1}$ with $n_1(T_1) = n_1-1$ and $\Delta(T_1) = \Delta-1$.

When $n_2(T_1)\leq n_1(T_1)$, by induction hypothesis, $T_1$ has a $p_1$-(2)-vdc $f$ with $\chi\, ''_{2s}(T_1) = p_1 = n_1(T_1)+1$. Then we can extend $f$ to an $(n_1+1)$-(2)-vdc $g$ of $T$ as follows: $g(z) = f(z)$ for $z\in (V(T)\setminus \{w_{1, 1}\})\cup (E(T)\setminus\{ww_{1, 1}\})$, $g(ww_{1, 1}) = p_1+1$, $g(w_{1, 1})\in [1, p_1]\setminus \{f(w)\}$.

When $n_1(T_1) = n_2(T_1)-1 = n_2-1$, we meet every $k_j\leq 2$ for $j\in [2, \Delta]$. In this case, $T_1$ is a spider with $\chi\, ''_{2s}(T_1) = n_1(T_1)+1 = n_1$, the lemma holds. For some $k_i\geq 3$ with $k_i\neq k_1$, we can take a tree $T_2 = T_1-w_{i, k_i-1}+w_{i, k_i-2}w_{i, k_i}$, here $w_{i, k_i-2}\neq w$. Clearly, $n_1(T_2) = n_2(T_2) = n_2-1$, so $T_1$ has a $p_2$-(2)-vdc $f\, '$ with $\chi\, ''_{2s}(T_2) = p_2 = n_1(T_2)+1 = n_1(T_1)+1 = n_1$ by induction hypothesis. We define a $(n_1+1)$-(2)-vdc $g\, '$ of $T$ by setting $g\, '(z) = f\, '(z)$ for $z\in (V(T)\setminus \{w_{1, 1}, w_{i, k_i-1}\})\cup (E(T)\setminus\{ww_{1, 1}, w_{i, k_i-2}w_{i, k_i-1}, w_{i, k_i-1}w_{i, k_i}\})$; $g\, '(ww_{1, 1}) = p_2+1$, $g\, '(w_{1, 1})\in [1, p_2]\setminus \{f\, '(w)\}$; $g\, '(w_{i, k_i-2}w_{i, k_i-1}) = p_2+1$, $g\, '(w_{i, k_i-1})\in [1, p_2]\setminus \{f\, '(w_{i, k_i-2}), f\, '(w_{i, k_i-2}w_{i, k_i}), f\, '(w_{i, k_i})\}$; and $g\, '(w_{i, k_i-1}w_{i, k_i}) = f\, '(w_{i, k_i-2}w_{i, k_i})$.

This completes the proof.

3.   Proof of Theorem 1

Let $n_i = n_i(T)$ for $i = 1, 2$, and $N(w) = N_T(w)$ for $w\in V(T)$. If $T$ is a path of length 2 or 3, then it is not hard to prove that $\chi\, ''_{(2)s}(T) = n_1+2$. According to Lemmas 3–5, we will show that $\chi\, ''_{(2)s}(T) = n_1$ by induction on the order of trees. Assume that $T$ is not a $2$-star, and suppose that $n_2\leq n_1$, $\Delta(T) < n_1$ and $D(T)\geq 5$ in the following discussion.

Case A. There exists a leaf $v$ having a neighbor $u$ with $d_T(u)\geq 4$. Let $T\, ' = T-v$. Then $n_1(T\, ') = n_1-1$, $n_2(T\, ') = n_2$ and $D(T\, ') = D(T)\geq 5$. If $\Delta(T\, ') = n_1(T\, ')$, then $T\, '$ is a spider, which means that $d_{T\, '}(u) = \Delta(T\, ')$, and hence $\Delta(T) = n_1$, a contradiction. Hence, $\Delta(T\, ') < n_1(T\, ')$.

Case A.1. $n_1(T\, ')\geq n_2(T\, ')$. By induction hypothesis, there is a total coloring $\theta_{T\, '}:V(T\, ')\cup E(T\, ')\rightarrow [1, b\, ']$ such that $\chi\, ''_{2s}(T\, ') = b\, ' = n_1(T\, ') = n_1-1$. It is straightforward to define an $n_1$-(2)-vdc $\theta:V(T)\cup E(T)\rightarrow [1, b\, ']\cup \{b\, '+1\}$ by setting $\theta(z) = \theta_{T\, '}(z)$ for $z\in (V(T)\cup E(T))\setminus \{uv, v\}$, $\theta(uv) = b\, '+1$ and $\theta(v) = a$, where the color $a\in [1, b\, ']$ is missing at $u$.

Case A.2. $n_1(T\, ') = n_2(T\, ')-1$. By Lemma 2, $T\, '$ has a 2-degree vertex $x$ with its neighborhood $N_{T\, '}(x) = \{x_1, x_2\}$ having $d_{T\, '}(x_1)\leq 2$. Note that $d_{T\, '}(x) = d_{T}(x)$ and $d_{T\, '}(x_1) = d_{T}(x_1)$. We get a tree $T_1 = T\, '-x+x_1x_2$. Clearly, $n_1(T_1) = n_1(T\, ') > \Delta(T\, ') = \Delta(T_1)$, $n_2(T_1) = n_2(T\, ')-1$ and $D(T_1)\geq D(T\, ')-1 = D(T)-1$. If $D(T_1) = 4$, and $n_2(T_1) = n_2(T\, ')-1 = n_1(T\, ') = n_1(T_1)$, then we have $n_1(T_1) = \Delta(T_1) = \Delta(T\, ') < n_1(T_1)$, a contradiction. Hence $D(T_1)\geq 5$. By induction hypothesis, $T_1$ admits a (2)-vdc $\theta_{T_1}:\; V(T_1)\cup E(T_1)\rightarrow [1, b_1]$ such that $\chi\, ''_{2s}(T_1) = b_1 = n_1(T_1) = n_1-1$. We define a total coloring $\theta$ of $T$ as: $\theta(z) = \theta_{T_1}(z)$ for $z\in V(T)\cup E(T)\setminus \{v, uv, x, xx_1, xx_2\}$; $\theta(uv) = b_1+1$ and $\theta(v) = a$, where the color $a\in [1, b_1]$ is missing at $u$; $\theta(xx_2) = b_1+1$, $\theta(xx_1) = \theta_{T_1}(x_1x_2)$, and $\theta(x)\in [1, b_1]\setminus \{\theta_{T_1}(x_1x_2), \theta_{T_1}(x_1), \theta_{T_1}(x_2)\}$. It is not hard to check that $\theta$ holds (DC). Therefore, $\theta$ is a desired $n_1$-(2)-vdc.

Case B. There is a leaf $v$ having a 3-degree neighbor $u$ in $T$, and Case A does not appear.

Case B.1. $v\, '$ is another leaf in the neighborhood $N(u) = \{v, v\, ', u\, '\}$, and $T$ has a 2-degree vertex $x$ having its neighborhood $\{x_1, x_2\}$ such that $x_1$ is a leaf of $T$.

We have a tree $T_1 = T-\{v, v\, ', x\}+x_1x_2$. Clearly, $n_1(T_1) = n_1-1$ and $n_2(T_1) = n_2-1$. We shall frist discuss two subcases $D(T_1) = 3$ or $4$ as below.

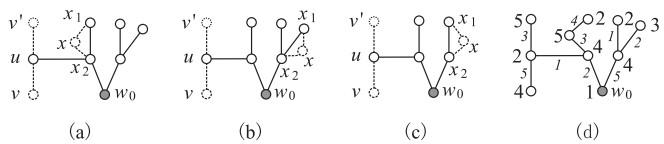
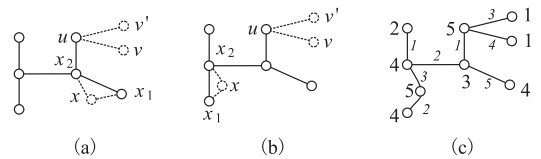
Case B.1.1. If $D(T_1) = 3$, then $T_1$ is one of two trees shown in Figure 1(a) and 1(b). So, $n_1 = 5$, $D(T) = 5$. Then $T$ admits a $5$-(2)-vdc shown in Figure 1(c).

Case B.1.2. If $D(T_1) = 4$, let $w_0$ be the center of $T_1$. We consider $d _{T_1}(w_0) = 2$. So, $T_1$ is one of Figure 2(a), 2(b) and 2(c), which implies the structural of $T$. To determine $\chi\, ''_{2s}(T)$, we give a $5$-(2)-vdc of $T$ by the graph shown in Figure 2(d).

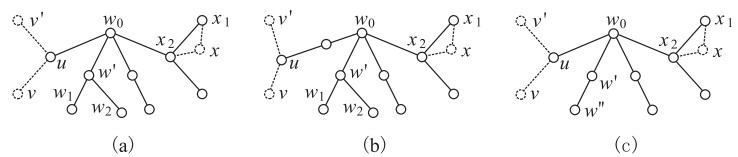
When $D(T_1) = 4$ and $d_{T_1}(w_0)\geq 3$, $T$ is as one taken from Figure 3(a) and 3(b). We take a vertex $w\, '\in N(w_0)\setminus \{u, x_2\}$ such that $d_{T_1}(w\, ')\leq d_{T_1}(z)$ for $z\in N(w_0)\setminus \{u, x_2\}$.

If $d_{T_1}(w\, ') = 3$ (see Figure 3(a) or 3(b)), we take another tree $T\, '_1 = T-\{w\, ', w_1, w_2\}$, where $w_1, w_2\in N(w\, ')$. Notice that $n_1(T\, '_1) = n_1-2$, $n_2(T\, '_1) = n_2$, $D(T\, '_1) = D(T)$ and $n_1(T\, '_1) > \Delta(T\, '_1)\geq n_2(T\, '_1)$. By induction hypothesis, we get a (2)-vdc $\theta_{T\, '_1}:\; V(T\, '_1)\cup E(T\, '_1)\rightarrow [1, b\, '_1]$ such that $\chi\, ''_{(2)s}(T\, '_1) = b\, '_1 = n_1(T\, '_1)$. We can extend the total coloring $\theta_{T\, '_1}$ to an $n_1$-(2)-vdc $\theta$ of $T$ as follows: $\theta(z) = \theta_{T\, '_1}(z)$ for $z\in V(T)\cup E(T)\setminus \{uv, w\, ', w_1, w_2, w_0w\, ', w\, 'w_1, w\, 'w_2\}$; $\theta(uv) = b\, '_1+1$; and $\theta(w_0w\, ') = b\, '_1+1$, $\theta(w\, 'w_1) = \theta_{T\, '_1}(uv)$, $\theta(w_1) = \theta(w_2) = \theta_{T\, '_1}(v)$, $\theta(w\, 'w_2) = b\, '_1+2$, and $\theta(w\, ')\in [1, b\, '_1]\setminus \{\theta_{T\, '_1}(v), \theta_{T\, '_1}(w_0), \theta_{T\, '_1}(uv)\}$.

If $d_{T_1}(w\, ') = 2$ (see Figure 3(c)), then we get a tree $T\, '_2 = T-\{w\, ', w\, ''\}$, where $w\, ''\in N(w\, ') = \{w_0, w\, ''\}$. Hence, $n_1(T\, '_2) = n_1-1$, $n_2(T\, '_2) = n_2-1$, $D(T\, '_2) = D(T)$, $n_1(T\, '_2) > \Delta(T\, '_2)\geq n_2(T\, '_2)$. By induction hypothesis, there is a (2)-vdc $\theta_{T\, '_2}:\; V(T\, '_2)\cup E(T\, '_2)\rightarrow [1, b\, '_2]$ such that $\chi\, ''_{2s}(T\, '_2) = b\, '_2 = n_1(T\, '_2)$. Thereby, we define an $n_1$-(2)-vdc $\theta$ of $T$ in the way that $\theta(z) = \theta_{T\, '_2}(z)$ for $z\in V(T)\cup E(T)\setminus \{uv, w\, ', w\, '', w_0w\, ', w\, 'w\, ''\}$; $\theta(uv) = b\, '_2+1$; and $\theta(w_0w\, ') = b\, '_2+1$, $\theta(w\, 'w\, '') = \theta_{T\, '_2}(uv)$, $\theta(w\, '') = \theta_{T\, '_2}(v)$, and $\theta(w\, ')\in [1, b\, '_2]\setminus \{\theta_{T\, '_2}(v), \theta_{T\, '_2}(w_0), \theta_{T\, '_2}(uv)\}$.

Case B.1.3. When $D(T_1)\geq 5$, by induction hypothesis, $T_1$ has a (2)-vdc $\theta_{T_1}:\; V(T_1)\cup E(T_1)\rightarrow S_1 = [1, b_1]$ such that $\chi\, ''_{2s}(T_1) = b_1 = n_1(T_1) = n_1-1$. Notice that $u$ is a leaf of $T_1$. So, we can extend $\theta_{T_1}$ to a total coloring $\theta$ of $T$ as follows: $\theta(z) = \theta_{T_1}(z)$ for $z\in V(T)\cup E(T)\setminus \{v, v\, ', u, uv, uv\, ', x, xx_1, xx_2\}$, and $\theta(uu\, ') = \theta_{T_1}(u\, ')$, $\theta(u\, ') = b_1+1$, $\theta(uv\, ') = \theta_{T_1}(uu\, ')$, $\theta(v\, ') = \theta(v) = \theta_{T_1}(u)$, $\theta(uv) = b_1+1$, $\theta(u)\in S_1\setminus \{\theta_{T_1}(u), \theta_{T_1}(u\, '), \theta_{T_1}(uu\, ')\}$; $\theta(xx_1) = \theta_{T_1}(x_1x_2)$, and $\theta(xx_2) = b_1+1$; $\theta(x)\in S_1\setminus \{\theta_{T_1}(x_1), \theta_{T_1}(x_1x_2), \theta_{T_1}(x_2)\}$ such that $C(x, \theta)\cup \{\theta(x)\}\neq C(u\, ', \theta)\cup \{\theta(u\, ')\}$. Hence, according to (DC), $\theta$ is a desired $n_1$-(2)-vdc of $T$.

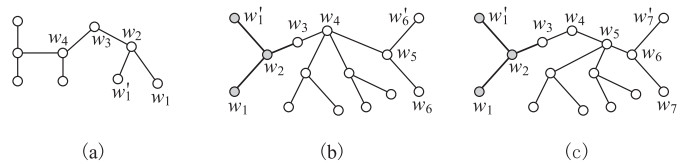
Case B.2. $T$ does not have a 2-degree vertex being adjacent to a leaf of $T$. Let $P = w_1w_2\cdots w_{m-1}w_m$ be a longest path of $T$, where $m$ is the diameter $D(T)$ of $T$. So, $d_T(w_2) = 3 = d_T(w_{m-1})$ by the hypothesis of Case B, thus, $w_2$ is adjacent to two leaves $w_1, w\, '_1$, and $w_{m-1}$ is adjacent to two leaves $w_m, w\, '_m$.

Case B.2.1. If $n_2 = 0$, then we take a tree $H_1 = T-w_1$, and we get $n_1(H_1) = n_1-1$ and $n_2(H_1) = n_2+1 = 1$. Notice that $D(H_1) = D(T)$, $n_1(H_1)\geq 3 > n_2(H_1)$. By induction hypothesis, $H_1$ admits a 2-vdc $\theta_{H_1}:\; V(H_1)\cup E(H_1)\rightarrow [1, a_1]$ such that $\chi\, ''_{2s}(H_1) = a_1 = n_1(H_1)$. We define an $n_1$-(2)-vdc $\theta$ of $T$ as follows: $\theta(z) = \theta_{H_1}(z)$ for $z\in V(T)\cup E(T)\setminus \{w_1, w_1w_2\}$, and $\theta(w_1w_2) = a_1+1$, $\theta(w_1)\in [1, a_1]\setminus \{\theta_{H_1}(w_2)\}$.

Case B.2.2. When $n_2\geq 1$ and $d_{T}(w_3) = 2$, we take a tree $H_2 = T-\{w_1, w\, '_1, w_2\}$. Notice that $w_3$ is a leaf of $H_2$, $n_1(H_2) = n_1-1$, $n_2(H_2) = n_2-1$. If $D(H_2) = 3$, then $T$ is shown in Figure 4(a). It is easy to show that $\chi\, ''_{2s}(T) = n_1$ by assigning appropriately colors to the vertices and edges of $T$. If $D(H_2) = 4$, then $T$ is one of Figure 4(b) and 4(c). Without loss of generality, $T$ is Figure 4(b), so we can select a tree $H_3 = T-w_6$ such that $D(H_3) = D(T)$, $n_1(H_3) = n_1-1\geq 3$, $n_2(H_3) = n_2+1 = 2$. Thereby, $H_3$ has a (2)-vdc $\theta_{H_3}:\; V(H_3)\cup E(H_3)\rightarrow [1, a_3]$ such that $\chi\, ''_{(2)s}(H_3) = a_3 = n_1(H_3)$. We define an $n_1$-(2)-vdc $\theta$ of $T$ as follows: $\theta(z) = \theta_{H_3}(z)$ for $z\in V(T)\cup E(T)\setminus \{w_6, w_5w_6\}$, and $\theta(w_5w_6) = a_3+1$, $\theta(w_6)\in [1, a_3]\setminus \{\theta_{H_3}(w_5)\}$.

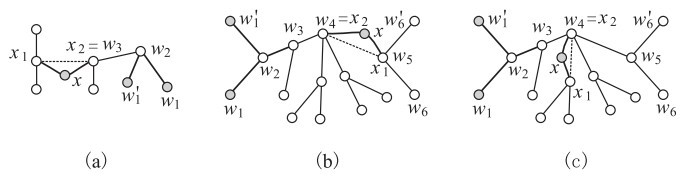
Case B.2.3. When $n_2\geq 1$ and $d_{T}(w_3)\geq 3$, let $x$ be a 2-degree vertex of $T$ having its own neighborhood $N(x) = \{x_1, x_2\}$ with $d_T(x_i)\geq 2$ for $i = 1, 2$. Consider a tree $H_4 = T-\{w_1, w\, '_1, x\}+x_1x_2$. Clearly, $D(H_4)\geq D(T)-2\geq 3$. If $D(H_4) = 3$, then $T$ must be one shown in Figure 5(a), hence $\chi\, ''_{2s}(T) = n_1$ by assigning appropriately colors to the vertices and edges of $T$.

If $D(H_4) = 4$, then $T$ is one of trees shown in Figure 5(b) and 5(c), say, $T$ is shown in Figure 5(b). We have a tree $H_5 = T-w_1$ such that $D(H_5) = D(T)$, $n_1(H_5) = n_1-1\geq 3$, $n_2(H_5) = n_2+1 = 2$. By induction hypothesis, there is a (2)-vdc $\theta_{H_5}:\; V(H_5)\cup E(H_5)\rightarrow [1, a_5]$ with $\chi\, ''_{2s}(H_5) = a_5 = n_1(H_5) = n_1-1$, and we can extend it to an $n_1$-(2)-vdc $\theta$ of $T$ by setting $\theta(z) = \theta_{H_5}(z)$ for $z\in V(T)\cup E(T)\setminus \{w_1, w_1w_2\}$, and $\theta(w_1w_2) = a_5+1$, $\theta(w_1)\in [1, a_5]\setminus \{\theta_{H_5}(w_2)\}$.

Case C. Both Case A and Case B are false. In other words, each leaf is adjacent to a 2-degree vertex in $T$. Thereby, $n_1 = n_2$.

Case C.1. Each 2-degree vertex $x$ has its neighborhood $N(x) = \{x_1, x_2\}$ such that $d_T(x_1) = 1$ and $d_T(x_2)\geq 3$, and no two 2-degree vertices have a common neighbor. Let $Q = p_1p_2\cdots p_m$ be a longest path in $T$ with $m = D(T)$. Then $d_T(p_3)\geq 3$ and $d_T(p_{m-2})\geq 3$ since $n_2 = n_1$. Notice that $d_T(x)\leq 2$ for $x\in N(p_3)\setminus \{p_2, p_4\}$ (resp. $x\in N(p_{m-2})\setminus \{p_{m-3}, p_{m-1}\}$) since $x\not \in V(Q)$, and furthermore this vertex $x$ is neither a leaf (Case B has been assumed to appear) nor a 2-degree vertex (by the assumption of this subcase and $n_2 = n_1$). We confirm the latter subcase does not exist in the following.

Case C.2. Since Case C.1 does not exist, $n_2 = n_1$, $n_1 > \Delta(T)$ and $D(T)\geq 5$, there exists a subgraph $H$ having $V(H) = \{w, u\}\cup V\, '$ with $r\geq 2$, $V\, ' = \{y_i, x_i:i\in [1, r]\}$ and $E(H) = \{wu, uy_i, y_ix_i:i\in [1, r]\}$, where $d_T(w)\geq 3$, moreover, every $y_i$ is a 2-degree vertex and every $x_i$ is a leaf for $i\in [1, r]$. Then we consider a tree $T_1 = T-V\, '$.

If $D(T_1) = 1$, then $w$ is a leaf of $T$ which contradicts to the hypothesis of Case C. If $D(T_1) = 2$, then $T$ is a $2$-star, which conflicts with $D(T)\geq 5$. If $D(T_1) = 3$, then $T_1$ is a path of length 3, and hence $n_1 = \Delta(T)$, a contradiction. If $D(T_1) = 4$, then $d_T(w) = 2$ and $n_1 = n_2+1$, a contradiction.

For $D(T_1)\geq 5$, notice that $n_1(T_1) = n_1-r+1$ and $n_2(T_1) = n_2-r$, and $u$ is a leaf of $T_1$. By induction hypothesis, $T_1$ admits a (2)-vdc $\theta_{T_1}:\; V(T_1)\cup E(T_1)\rightarrow S^* = [1, b_1]$ having $\chi\, ''_{2s}(T_1) = b_1 = n_1(T_1) = n_1-(r-1)$. We define a (2)-vdc $\theta$ of $T$ as follows:

$\theta(z) = \theta_{T_1}(z)$ for $z\in V(T_1)\cup E(T_1)\setminus \{u, uw\}$;

$\theta(uy_i) = b_1+i$ for $i\in [1, r-1]$, and $\theta(uy_r) = \theta_{T_1}(uw)$;

$\theta(y_jx_j) = b_1+j-1$ for $j\in [2, r]$, and $\theta(y_1x_1) = \theta_{T_1}(uw)$;

$\theta(w) = b_1+1$, $\theta(uw) = \theta_{T_1}(w)$; $\theta(x_i) = \theta_{T_1}(u)$ for $i\in [1, r]$; and

$\theta(u) = a\in S^*\setminus \{\theta_{T_1}(w), \theta_{T_1}(uw)\}$; $\theta(y_i) = a\, '\in S^*\setminus \{\theta_{T_1}(u), \theta_{T_1}(uw), a\}$ for $i\in [1, r]$.

Therefore, Theorem 1 follows from the principle of induction.

Corollary 6. Let $G$ be a connected graph having cycles, $p$ vertices and $q$ edges. If $n_2(G)\leq 2(q-p+1)+n_1(G)$, then $\chi\, ''_{2s}(G)\leq 1+ 2(q-p+1)+n_1(G)$.

Proof. Let $H$ be a spanning tree of $G$. Then we can construct another tree $T$ of $G$ by deleting each edge $uv\in E\, ' = E(G)\setminus E(H)$, and adding two new vertices $u\, ', v\, '$ by joining $u\, '$ with $u$ and $v\, '$ with $v$, respectively. Clearly, $n_1(T) = 2(q-p+1)+n_1(G)$, $n_2(T) = n_2(G)$, $D(T)\geq 4$ and $\Delta(T) = \Delta(G)$. On the other hand, each $k$-(2)-vdc $\theta$ of $G$ with $k = \chi\, ''_{2s}(G)$ corresponds to a total coloring $\varphi$ of $T$ by setting $\varphi(x) = \theta(x)$ for $x\in V(G)\cup (E(G)\setminus E\, ')$; $\varphi(uu\, ') = \varphi(vv\, ') = \theta(uv)$, $\varphi(u\, ') = \theta(v)$ and $\varphi(v\, ') = \theta(u)$ for $uv\in E\, '$. In general, this total coloring $\varphi$ is not a $(2)$-vdc of $T$. Hence, $\max\{\varphi(x):x\in V(T)\cup R(T)\} = k\leq \chi \, ''_{2s}(T)$. This corollary follows from Lemmas 3–5 and Theorem 1.

Corollary 7. Let $T$ be a spanning tree of a connected graph $G$, and $G[E^*]$ be an induced graph over the edge subset $E^* = E(G)\setminus E(T)$. Then $\chi\, ''_{2s}(G)\leq \chi\, ''_{2s}(T)+\chi\, '(G[E^*])$, where $\chi\, '(H)$ is the chromatic index of a graph $H$.

4.   Conclusions and further works

A $k$-vdtc of a graph $G$ is a total coloring $f: V(G)\cup E(G)\rightarrow [1, k]$ such that $C(w, f)\cup \{f(w)\}\neq C(z, f)\cup \{f(z)\}$ for distinct $w, z\in V(G)$, and $\chi\, ''_s(G)$ is the least number $k$ of colors required for which $G$ has a $k$-vdtc. For $2\leq m\leq n$, by Lemma 3, the difference $\chi\, ''_{2s}(DS_{m+1, n+1})-\chi\, ''_{s}(DS_{m+1, n+1}) = m+n+1-(n+1) = m$ can be as large as we expect.

For a $k$-(2)-vdc $f$ of a graph $G$, let $S_i = \{f(x) = i:\; x\in V(G)\cup E(G)\}$ for $i\in [1, k]$. We call this coloring $f$ to be an equitable $k$-(2)-vdc of $G$ if two sizes of $S_i$ and $S_j$ differ at most one. Again, the smallest number $k$ of colors required for which $G$ has an equitable $k$-(2)-vdc is denoted as $\chi \, ''_{2es}(G)$. Clearly, $\chi \, ''_{2s}(G)\leq \chi \, ''_{2es}(G)$. We have shown that $\chi \, ''_{2s}(H) = \chi \, ''_{2es}(H)$ for every $2$-star or every double star $H$. As further work we present a problem: Is there $\chi \, ''_{2s}(T) = \chi \, ''_{2es}(T)$ for a tree $T$ having $D(T)\geq 4$ and $n_1(T)\neq \Delta(T)$? And we conjecture that: Let $T$ be a tree with $2n_2(T)\leq (n_1(T)+k-1)^2$. Then $\chi \, ''_{2s}(T)\leq n_1(T)+k$.

Acknowledgments

Bing Yao was supported by the National Natural Science Foundation of China under Grant No. 61662066; Zhi-xiang Yin was supported by the National Natural Science Foundation of China under Grant Nos. 61672001 and 62072296.

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.