Figure 1.
Residual stresses distribution in a welding joint (a) σx and (b) σy.
One of the most important negative consequence in the fusion welding processes is the generation of tensile residual stresses in welded joints. The main goals of this work are to determine the optimal combination of welding parameters to minimize the residual stress level and the influence of each welding parameter in that feature to weld 6082-T6 aluminum alloy plates using the GMAW welding process. To achieve these goals was implemented the Taguchi orthogonal array (L27) to define the design of numerical and experimental tests. All combinations were simulated in the Simufactwelding 6.0 software, from which it was possible to obtain the values of maximum residual stresses. The data treatment was carried out, reaching the combination of levels for each parameter. With ANOVA analysis was found that the parameter with the greatest influence in the residual stress generation was the welding speed, while the parameter with the least influence was the torch angle. Also, to minimize the residual stresses it was observed that the optimal combination of welding parameters is welding current intensity of 202 A, welding speed of 10 mm/s, and 30° of inclination of the angular torch. The two simulations that resulted in the highest and lowest residual stresses were validated experimentally by the hole drilling method to measure the residual stresses.
Citation: Sharlane Costa, Maria S. Souza, Manuel B. César, José Gonçalves, João E. Ribeiro. Experimental and numerical study to minimize the residual stresses in welding of 6082-T6 aluminum alloy[J]. AIMS Materials Science, 2021, 8(2): 271-282. doi: 10.3934/matersci.2021018
| [1] | Harish Mooli, Srinivasa Rao Seeram, Satyanarayana Goteti, Nageswara Rao Boggarapu . Optimal weld bead profiles in the conduction mode LBW of thin Ti–6Al–4V alloy sheets. AIMS Materials Science, 2021, 8(5): 698-715. doi: 10.3934/matersci.2021042 |
| [2] | Ehsan Harati, Paul Kah . Laser welding of aluminum battery tab to variable Al/Cu busbars in Li-ion battery joint. AIMS Materials Science, 2022, 9(6): 884-918. doi: 10.3934/matersci.2022053 |
| [3] | N. S. Biradar . Effect of transverse mechanical arc oscillation on hot cracking (solidification & liquation) and weld metal properties of AA2014 T6 TIG welds. AIMS Materials Science, 2016, 3(4): 1544-1560. doi: 10.3934/matersci.2016.4.1544 |
| [4] | Paul Kah, Pavel Layus, Benoit Ndiwe . Submerged arc welding process peculiarities in application for Arctic structures. AIMS Materials Science, 2022, 9(3): 498-511. doi: 10.3934/matersci.2022029 |
| [5] | Utpal K. Dhar, Md. Farabi Rahman, Mustafa Oguzhan Ayanoglu, Ahammad Abdullah . Welding on C67 steel grade sheet: Influence of the parameters and post welding heat treatment. AIMS Materials Science, 2023, 10(3): 453-464. doi: 10.3934/matersci.2023025 |
| [6] | Muhammad Awwaluddin, Sri Hastuty, Djoko Hadi Prajitno, Makmuri, Budi Prasetiyo, Yudi Irawadi, Jekki Hendrawan, Harry Purnama, Eko Agus Nugroho . Effect of Yttrium on corrosion resistance of Zr-based alloys in Ringer's lactate solution for biomaterial applications. AIMS Materials Science, 2024, 11(3): 565-584. doi: 10.3934/matersci.2024028 |
| [7] | Francois Njock Bayock, Paul Kah, Kibong Marius Tony . Heat input effects on mechanical constraints and microstructural constituents of MAG and laser 316L austenitic stainless-steel welded joints. AIMS Materials Science, 2022, 9(2): 236-254. doi: 10.3934/matersci.2022014 |
| [8] | Shashi Bahl, Tarunpreet Singh, Virinder Kumar, Shankar Sehgal, Ashok Kumar Bagha . A systematic review on recent progress in advanced joining techniques of the lightweight materials. AIMS Materials Science, 2021, 8(1): 62-81. doi: 10.3934/matersci.2021005 |
| [9] | Rafael R. Lucas, Rita C.M. Sales-Contini, Francisco J.G. da Silva, Edson C. Botelho, Rogério P. Mota . Plasma electrolytic oxidation (PEO): An alternative to conventional anodization process. AIMS Materials Science, 2024, 11(4): 684-711. doi: 10.3934/matersci.2024035 |
| [10] | Pawan Kumar, B B Verma . Propagation of corrosion induced fatigue crack in aluminum alloy. AIMS Materials Science, 2022, 9(3): 512-521. doi: 10.3934/matersci.2022030 |
One of the most important negative consequence in the fusion welding processes is the generation of tensile residual stresses in welded joints. The main goals of this work are to determine the optimal combination of welding parameters to minimize the residual stress level and the influence of each welding parameter in that feature to weld 6082-T6 aluminum alloy plates using the GMAW welding process. To achieve these goals was implemented the Taguchi orthogonal array (L27) to define the design of numerical and experimental tests. All combinations were simulated in the Simufactwelding 6.0 software, from which it was possible to obtain the values of maximum residual stresses. The data treatment was carried out, reaching the combination of levels for each parameter. With ANOVA analysis was found that the parameter with the greatest influence in the residual stress generation was the welding speed, while the parameter with the least influence was the torch angle. Also, to minimize the residual stresses it was observed that the optimal combination of welding parameters is welding current intensity of 202 A, welding speed of 10 mm/s, and 30° of inclination of the angular torch. The two simulations that resulted in the highest and lowest residual stresses were validated experimentally by the hole drilling method to measure the residual stresses.
Aluminum alloys gathers wide range of acceptance and potential application in automobile, aerospace, ship building industries, off shore structures and construction of bridges due to the low weight, superior strength to weight ratio and other anti-corrosive properties of this material [1]. Compared to steel, the main advantages of aluminum alloys are the high strength-to-weight ratio, the excellent corrosion resistance and reduced maintenance, which compensate their higher price compared to steel [2,3,4]. For example, 6xxx series Al-alloys are widely used due to the excellent physical and chemical properties, such as corrosion resistance, good formability and weldability [5]. The aluminum alloy studied in this work is 6082-T6, which is an extruded medium to high strength Al–Mg–Si alloy that contains manganese to increase ductility and toughness. The T6 condition is obtained through artificial ageing at a temperature of approximately 180 ℃ [6]. The most important advantages of 6082 aluminum alloys are low specific weight, high corrosion resistance and superior thermal conductivity [7,8].
One of the most common welding techniques for aluminum alloys is gas-metal arc welding (GMAW), which offers advantages such as deep penetration, smooth weld bead, high welding speed, large metal deposition rate, lower spatter, lower distortion and shrinkage, and lesser probability of porosity and fusion defects and the possibility to be robotized [9,10,11,12]. This process, due to the high temperatures involved, causes thermomechanical distortion and generation of residual stresses [13], which can lead to a premature collapse of the welded structure. In this way the mechanical properties of welding joints may determine the performance and service life of a welded structural part. Thus, the welding quality of aluminum alloy should be carefully considered [14].
In recent years, extensive studies [15] have been reported to investigate the influence of shielding gas on metal transfer [16], the influence of different wire-electrodes on metallurgical characterization [17], and effects of processing parameters (such as gas mixtures [18] and preheating [19]) on mechanical properties of GMAW process [20]. However, the basic parameters in robot welding, such as electric current, torch angle and welding speed, also need attention. Despite of many advantages in the GMAW process, there are still some shortcomings needing to be resolved, such as the welded distortion [21] and the generation of residual stresses [13].
To understand these behaviors in welds, three types of studies can be used: analytical, experimental and numerical. Among the analytical solutions, Rosenthal [22] proposed, for the first time, an analytical solution in 1946, of a semi-infinite body for thin and thick plates based on constant properties of the material. In 1999, Nguyen [23] showed an analytical solution based on Green's vector function using a Gaussian double-ellipsoidal thermal distribution. Goldak et al. [24] presented a numerical solution in the form of a semi-ellipsoidal and double-ellipsoidal heat source (applied methodology), more recently, Nasiri and Enzinger [25] proposed an analytical solution for heating flux in welding called adaptive function. These authors measured temperature values close to the melting line and determined the relative error less than 5% concerning the experimental method.
In this work, a set of numerical simulations based on experimental validation were implemented. It is important to notice that experimental analysis is extremely important to predict the reduction of mechanical properties induced by welding [26]. This prediction can be made by computational methods, due to the advancement of technology, through the Finite Element Method (FEM). It is possible to simulate a weld bead and approximate what the result will be, such as residual stresses and distortions [27,28,29,30].
Despite the capabilities of finite element software, it is important to perceive the discrepancy in computational results in relation to the experimental results. For this, we conducted a study of a corner welding of two aluminum bars 6082-T6 and validate the numerical results with the experimental ones. This study intends to observe the influence of certain welding parameters like electric current, torch angle and welding speed with three different levels each in the values of residual stresses. To perform the combinations of levels for the different parameters resorted to an orthogonal array of Taguchi L27 resulting 27 different combinations. The 27 combinations were simulated using the Software Simufacwelding® 6.0, from which it was possible to recall the values of the maximum principal stresses (MaxPS).
The residual stress plays an important role in crack initiating and propagating in the metal parts [31]. Residual stresses are those stresses that remain after deformation with all external forces removed [32], occurs in materials and mechanical components during manufacture from many processes like plastic deformation or forming, machining or welding processes, among others [33,34]. Both material and deposition process may produce a residual stress, which may be particularly critical in applications where a large mismatch exists between thermal, structural and mechanical properties of the layers and substrates [32]. That is, the state of a residual stress depends both, on the previous processes it underwent and also on the properties of the material that relate to the mechanical process.
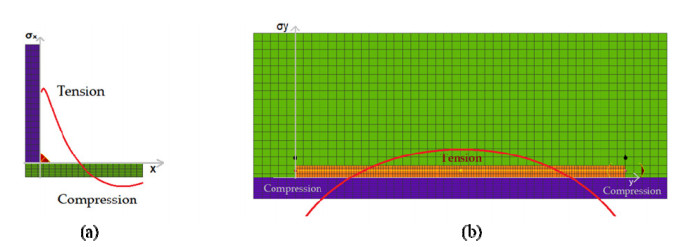
For particular case of welding process, residual stresses are caused by the application of intense heat or thermal loading at the weld joint, which causes plasticity of the material underneath and immediately surrounding the weld arc, but the nearby cooler material remains elastic and acts to constrain the heated material. The thermal cycle imposed on any welded object causes thermal expansions and contractions to occur which vary with time and location. Because this expansion is not uniform, stresses appear when hot regions near the weld are restrained by cooler regions further away. Plastic deformations, occurring as a result of these stresses lead to residual stresses in the object after the temperatures have returned to ambient levels [35]. In the welding process, tensile and compressive stresses may arise along the sheet and along the weld bead. The typical distribution of both longitudinal (a) and transverse (b) residual stresses in welding joints can be shown in Figure 1 [36].
In the present work, the influence of the main welding parameters on the residual stress amplitude in the welding corner joint is analyzed. For this, an orthogonal array of tests was developed by Taguchi, L27, where it is possible to combine different levels for the defined parameters. Table 1 shows the levels used for each parameter.
| Nº | Symbol | Parameters | Units | Levels | ||||
| 1 | 2 | 3 | ||||||
| 1 | A | Welding current | (A) | 163 | 181 | 202 | ||
| 2 | B | Welding speed | (mm/s) | 10 | 13 | 16 | ||
| 3 | C | Torch angle | (o) | 30º | 45º | 60º |
DownLoad:
CSV
In this case, a L27 array was used to define the combination of parameters. The numerical simulations were carried out using SymufactWelding® software version 6.0 using a double ellipsoid model for energy distribution transferred from the heat source to the component [24].
The double ellipsoid model (Figure 2) and transversal section cord (Figure 3) were previously calibrated with experimental welding (Figure 4) which, in this, case was used a robot. The measurements are obtained from metallographic samples of welding cord as shown in Figure 5.
Having the dimensions of the experimental cords for all combinations, these values were used in the simulations. The numerical model shown in Figure 6 corresponds to the model projected in the SymufactWelding® software, where the plates to be welded, the weld bead, and the fixing devices were inserted, in the same orientation and position of the experimental tests.
Figure 6 shows the studied process model. The model configuration is specified as: two components (plates), 1 bearing, 2 clamps, 1 robot, and the arc welding process. Other specifications related to the material, welding parameters, trajectories and assembly have also been specified. As input conditions in the SymufactWelding® software, the values of voltage (V), current (A), speed (mm/s) and torch angle (º) were used, as shown in Table 2. The mesh pattern used in the simulations is shown in Figure 7.
| Simulation | Current (A) | Speed (mm/s) | Torch angle (º) | Voltage (V) | MaxPS (MPa) |
| 1 | 163 | 10 | 30 | 22.6 | 75.4138 |
| 2 | 163 | 10 | 45 | 22.6 | 72.7757 |
| 3 | 163 | 10 | 60 | 22.6 | 62.2036 |
| 4 | 163 | 13 | 30 | 22.6 | 78.6806 |
| 5 | 163 | 13 | 45 | 22.6 | 82.6118 |
| 6 | 163 | 13 | 60 | 22.6 | 76.7528 |
| 7 | 163 | 16 | 30 | 22.6 | 94.3697 |
| 8 | 163 | 16 | 45 | 22.6 | 85.5548 |
| 9 | 163 | 16 | 60 | 22.6 | 84.5229 |
| 10 | 181 | 10 | 30 | 23.4 | 70.9412 |
| 11 | 181 | 10 | 45 | 23.4 | 73.7608 |
| 12 | 181 | 10 | 60 | 23.4 | 61.0019 |
| 13 | 181 | 13 | 30 | 23.4 | 73.8837 |
| 14 | 181 | 13 | 45 | 23.4 | 74.4494 |
| 15 | 181 | 13 | 60 | 23.4 | 71.9547 |
| 16 | 181 | 16 | 30 | 23.4 | 78.6379 |
| 17 | 181 | 16 | 45 | 23.4 | 85.487 |
| 18 | 181 | 16 | 60 | 23.4 | 85.7779 |
| 19 | 202 | 10 | 30 | 23.8 | 61.0982 |
| 20 | 202 | 10 | 45 | 23.8 | 62.5565 |
| 21 | 202 | 10 | 60 | 23.8 | 54.5618 |
| 22 | 202 | 13 | 30 | 23.8 | 80.4348 |
| 23 | 202 | 13 | 45 | 23.8 | 76.0197 |
| 24 | 202 | 13 | 60 | 23.8 | 73.9517 |
| 25 | 202 | 16 | 30 | 23.8 | 79.484 |
| 26 | 202 | 16 | 45 | 23.8 | 77.2585 |
| 27 | 202 | 16 | 60 | 23.8 | 79.3789 |
DownLoad:
CSV
After all simulations completed, the values of the maximum principal stress (MaxPS) were withdrawn at various points along the x-axis, Figure 7.
The maximum values of the residual stresses for each simulation are presented in Table 2.
The simulation required 8 h on a virtual machine cluster (HPC) with 64 GB of RAM. The average value of the residual stresses (MaxPS) for each parameter is presented in Table 3. Based on the results is possible to determine the combination that minimizes the residual stresses. In this case, the combination that minimizes the residual stress is A3B1C1 (202 A, 10 mm/s and 30º). On the other hand, the combination that maximizes the residual stress is A1B3C3 (163 A, 16 mm/s and 60º).
| Parameters | Level | MaxPS |
| A | 1 | 79.21 |
| 2 | 75.10 | |
| 3 | 71.64 | |
| B | 1 | 66.03 |
| 2 | 76.53 | |
| 3 | 83.39 | |
| C | 1 | 72.23 |
| 2 | 76.72 | |
| 3 | 76.99 |
DownLoad:
CSV
The goal of the analysis of variance (ANOVA) is to determine which design welding parameters affect meaningfully the residual stresses. In Table 4 it is possible to observe the ANOVA analysis for MaxPS residual stresses. Thus, for MaxPS residual stresses the most influent parameter is welding speed (65%) followed by the welding current with a contribution of 12%, and the torch angle with 6%. The possible reason for such an observation could be that with the increase in welding speed, the rate of heat input is higher than the rate of heat dissipation. This effect results in greater heating located in the melting zone and thermal incompatibility, which causes the formation of residual stresses. That is, if the heat source moves faster, there will be less time for the heat transfer to occur with the surrounding material. This effect has already been proven analytically by Zasa et al. [37].
| Source | DF | SQ | MS | F-value | P-value | Contribution (%) |
| Current (A) | 2 | 258.6 | 129.3 | 7.14 | 0.005 | 12% |
| Welding speed (mm/s) | 2 | 1374.5 | 687.27 | 37.93 | 0 | 65% |
| Torch angle (º) | 2 | 128.5 | 64.27 | 3.55 | 0.048 | 6% |
| Error | 20 | 362.4 | 18.12 | |||
| Total | 26 | 2124 |
DownLoad:
CSV
Where DF is the degree of freedom, SQ is the sum of squares and MS the mean squares.
In order to validate the numerical simulations, was implemented an experimental procedure to welding a specimen using a robot (Yaskawa MA2010 with a DX200 controller) and the welding machine (Fronius TransPuls 4000 CMT R). After the welding of each specimen the residual stress was measured. As the main objective of this work is to validation the combination to minimize (simulation 19) and maximize (simulation 9) the level of residual stresses. The residual stresses were measured with the hole-drilling technique (Figure 8) using the RS-200 milling guide that is a high-precision instrument for analyzing residual stresses (Figure 9). To measure the strain relaxation resorted to a special rosette of strain gages, that was located immediately ahead the weld bead, at x axis direction, and 50 millimeters in y direction at half cord.
The residual stresses values were determined using H-Drill software. The residual stresses are determined from the strain values measured in the strain gauges (Table 5).
| MaxPS (MPa) | Error | |||
| Numerical | Experimental | |||
| S_09 | 85 | 106 | 20% | |
| S_19 | 61 | 67 | 9% |
DownLoad:
CSV
The numerical simulations of GMAW welding process with SymufactWelding® software proved to be a useful and powerful tool for the calculation of residual stresses in the weld joints with 6082-T6 aluminum alloy.
The Taguchi method allows the determination of the combination of welding parameters to minimize and maximize the value of residual stresses. The optimal combination that minimizes the MaxPS residual stresses is A3B1C1, i.e., a welding current of 202 A, a welding speed of 10 mm/s and 30° for the torch angle. On the other hand, A1B3C3 combination was the one that maximizes MaxPS, i.e., 163 A, 16 mm/s and 60° for the welding current, welding speed and torch angle, respectively.
The ANOVA analysis was successful in identifying the influence of each parameter on the variation of residual stresses. In the case of MaxPS, the welding speed was the most influent parameter (65%) while the angle torch was the least important parameter (6%).
The numerical simulations were validated with experimental tests and were proved that the numerical results are relatively close to the experimental data, but not on the security side. The relative error in the measurements is 20% in combination 19 and 9% in combination 9.
This work has been supported by FCT-Fundação para a Ciência e Tecnologia within the R & D Units Project Scope: CIMO (UIDB/00690/2020).
The authors declare that there are no conflicts of interest.
| [1] |
Hazari HR, Balubai M, Kumar DS, et al. (2019) Experimental investigation of TIG welding on AA 6082 and AA 8011. Mater Today Proc 19: 818-822. doi: 10.1016/j.matpr.2019.08.137
|
| [2] | Mazzolani FM (1994) Aluminium Alloy Structures, 2 Eds., London: CRC Press. |
| [3] | Mazzolani FM (2002) Design criteria for aluminium structures: Technology, codification and applications, In: Mazzolani FM, Aluminium Structural Design, Vienna: Springer. |
| [4] |
Zhao Y, Zhai X, Wang J (2019) Buckling behaviors and ultimate strength of 6082-T6 aluminum alloy columns with square and circular hollow sections under eccentric compression-Part Ⅱ: Parametric study, design provisions and reliability analysis. Thin Wall Struct 143: 106208. doi: 10.1016/j.tws.2019.106208
|
| [5] |
Marioara CD, Andersen SJ, Jansen J, et al. (2001) Atomic model for GP-zones in a 6082 Al-Mg-Si system. Acta Mater 49: 321-328. doi: 10.1016/S1359-6454(00)00302-5
|
| [6] |
Moreira PMGP, De Jesus AMP, Ribeiro AS, et al. (2008) Fatigue crack growth in friction stir welds of 6082-T6 and 6061-T6 aluminium alloys: A comparison. Theor Appl Fracture Mec 50: 81-91. doi: 10.1016/j.tafmec.2008.07.007
|
| [7] |
Dubourg L, Ursescu D, Hlawka F, et al. (2005) Laser cladding of MMC coatings on aluminium substrate: influence of composition and microstructure on mechanical properties. Wear 258: 1745-1754. doi: 10.1016/j.wear.2004.12.010
|
| [8] |
Canel T, Zeren M, Sınmazçelik T (2019) Laser parameters optimization of surface treating of Al 6082-T6 with Taguchi method. Opt Laser Technol 120: 105714. doi: 10.1016/j.optlastec.2019.105714
|
| [9] |
Leoni F, Sandness L, Grong Ø, et al. (2019) Mechanical behavior of gas metal arc AA6082-T6 weldments. Procedia Struct Integrity 18: 449-456. doi: 10.1016/j.prostr.2019.08.187
|
| [10] |
Kumar R, Dilthey U, Dwivedi DK, et al. (2009) Thin sheet welding of Al 6082 alloy by AC pulse-GMA and AC wave pulse-GMA welding. Mater Design 30: 306-313. doi: 10.1016/j.matdes.2008.04.073
|
| [11] | Castner HR (1994) Gas Metal Arc Welding Fume Generation Using Pulsed Current. American Welding Society. |
| [12] |
Palani PK, Murugan N (2006) Selection of parameters of pulsed current gas metal arc welding. J Mater Process Tech 172: 1-10. doi: 10.1016/j.jmatprotec.2005.07.013
|
| [13] | Smartt HB (1993) Transfer of heat and mass to the base metal in gas-metal arc welding, In: Olson DL, Siewert TA, Liu S, et al., Welding, Brazing and Soldering, ASM International, 6: 25-29. |
| [14] |
Zhu C, Cheon J, Tang X, et al. (2018) Molten pool behaviors and their influences on welding defects in narrow gap GMAW of 5083 Al-alloy. Int J Heat Mass Tran 126: 1206-1221. doi: 10.1016/j.ijheatmasstransfer.2018.05.132
|
| [15] |
Huang L, Hua X, Wu D, et al. (2019) A study on the metallurgical and mechanical properties of a GMAW-welded Al-Mg alloy with different plate thicknesses. J Manuf Process 37: 438-445. doi: 10.1016/j.jmapro.2018.12.017
|
| [16] |
Ogino Y, Hirata Y, Murphy AB (2016) Numerical simulation of GMAW process using Ar and an Ar-CO2 gas mixture. Weld World 60: 345-353. doi: 10.1007/s40194-015-0287-3
|
| [17] |
Li D, Yang D, Zhang G, et al. (2018) Microstructure and mechanical properties of welding metal with high Cr-Ni austenite wire through Ar-He-N2 gas metal arc welding. J Manuf Process 35: 190-196. doi: 10.1016/j.jmapro.2018.07.026
|
| [18] |
Mvola B, Kah P (2017) Effects of shielding gas control: welded joint properties in GMAW process optimization. Int J AdvManuf Tech 88: 2369-2387. doi: 10.1007/s00170-016-8936-2
|
| [19] |
Zhu C, Tang X, He Y, et al. (2018) Effect of preheating on the defects and microstructure in NG-GMA welding of 5083 Al-alloy. J Mater Process Tech 251: 214-224. doi: 10.1016/j.jmatprotec.2017.08.037
|
| [20] | Kamble AG, Rao RV (2017) Effects of process parameters of GMAW on bead geometry, tensile strength, hardness, microstructure and thermo-mechanical simulation of AISI 202 steel. J Manuf Process 24: 413-428. |
| [21] |
Minh PS, Phu TV (2014) Study on the structure deformation in the process of gas metal arc welding (GMAW). AJME 2: 120-124. doi: 10.12691/ajme-2-4-4
|
| [22] | Rosenthal D (1946) The theory of moving sources of heat and its application of metal treatments. Trans ASME 68: 849-866. |
| [23] | Nguyen NT, Ohta A, Matsuoka K, et al. (1999) Analytical solutions for transient temperature of semi-infinite body subjected to 3-D moving heat sources. Weld J 78: 265-s. |
| [24] |
Goldak J, Chakravarti A, Bibby M (1984) A new finite element model for welding heat sources. Metal Mater Trans B 15: 299-305. doi: 10.1007/BF02667333
|
| [25] |
Nasiri MB, Enzinger N (2019) Powerful analytical solution to heat flow problem in welding. Int J Therm Sci 135: 601-612. doi: 10.1016/j.ijthermalsci.2018.08.003
|
| [26] |
Wang T, Hopperstad OS, Lademo OG, et al. (2007) Finite element analysis of welded beam-to-column joints in aluminium alloy EN AW 6082 T6. Finite Elem Anal Design 44: 1-16. doi: 10.1016/j.finel.2007.08.010
|
| [27] | Lu J (1996) Handbook of Measurement of Residual Stresses, The Fairmont Press, 5-70. |
| [28] |
Deng D (2009) FEM prediction of welding residual stress and distortion in carbon steel considering phase transformation effects. Mater Design 30: 359-366. doi: 10.1016/j.matdes.2008.04.052
|
| [29] |
Deng D, Murakawa H (2006) Numerical simulation of temperature field and residual stress in multi-pass welds in stainless steel pipe and comparison with experimental measurements. Comp Mate Sci 37: 269-277. doi: 10.1016/j.commatsci.2005.07.007
|
| [30] |
Leggatt RH (2008) Residual stresses in welded structures. Int J Pres Ves Pip 85: 144-151. doi: 10.1016/j.ijpvp.2007.10.004
|
| [31] |
Yu QM, Cen L (2017) Residual stress distribution along interfaces in thermal barrier coating system under thermal cycles. Ceram Int 43: 3089-3100. doi: 10.1016/j.ceramint.2016.11.119
|
| [32] |
Oladijo OP, Venter AM, Cornish LA, et al. (2012) X-ray diffraction measurement of residual stress in WC-Co thermally sprayed coatings onto metal substrates. Surf Coat Tech 206: 4725-4729. doi: 10.1016/j.surfcoat.2012.01.044
|
| [33] |
Ribeiro J, Monteiro J, Vaz M, et al. (2009) Measurement of residual stresses with optical techniques. Strain 45: 123-130. doi: 10.1111/j.1475-1305.2008.00421.x
|
| [34] | Bradley GR, James MN (2000) Geometry and microstructure of metal inert gas and friction stir welded aluminium alloy 5383-H321[Dissertation]. University of Plymouth, 1-78. |
| [35] | Francis JD (2001) Welding simulations of aluminum alloy joints by finite element analysis[Dissertation]. Virginia Tech, Blacksburg. |
| [36] |
Li JG, Wang SQ (2017) Distortion caused by residual stresses in machining aeronautical aluminum alloy parts: Recent advances. Int J Adv Manuf Tech 89: 997-1012. doi: 10.1007/s00170-016-9066-6
|
| [37] |
Zaza D, Ciavarella M, Zurlo G (2021) Strain incompatibility as a source of residual stress in welding and additive manufacturing. Eur J Mech A-Solid 85: 104147. doi: 10.1016/j.euromechsol.2020.104147
|
| 1. | Glauco Nobrega, Maria Sabrina Souza, Manuel Rodríguez-Martín, Pablo Rodríguez-Gonzálvez, João Ribeiro, Parametric Optimization of the GMAW Welding Process in Thin Thickness of Austenitic Stainless Steel by Taguchi Method, 2021, 11, 2076-3417, 8742, 10.3390/app11188742 | |
| 2. | Rebai Billel, Contribution to study the effect of (Reuss, LRVE, Tamura) models on the axial and shear stress of sandwich FGM plate (Ti–6A1–4V/ZrO2) subjected on linear and nonlinear thermal loads, 2023, 10, 2372-0484, 26, 10.3934/matersci.2023002 | |
| 3. | Lucas Martins Garcia, Verônica Teixeira Noronha, João Ribeiro, Effect of Welding Orientation in Angular Distortion in Multipass GMAW, 2021, 5, 2504-4494, 63, 10.3390/jmmp5020063 | |
| 4. | Qiang Wang, Zhandong Wan, Tianyi Zhao, Yue Zhao, Dongyang Yan, Guoqing Wang, Aiping Wu, Tensile properties of TIG welded 2219-T8 aluminum alloy joints in consideration of residual stress releasing and specimen size, 2022, 18, 22387854, 1502, 10.1016/j.jmrt.2022.03.059 | |
| 5. | Inês S. Afonso, Manuel Rodríguez Martín, João E. Ribeiro, Effect of Welding Sequence in Angular Distortion on Butt Joint GMAW Process, 2022, 12, 2076-3417, 10402, 10.3390/app122010402 | |
| 6. | V. V. Kvasnytskyi, A. O. Perepichai, O. V. Prokhorenko, O. A. Slyvinskyi, I. M. Lagodzinskyi, Numerical Simulation of the Stress-Strain State of a PAW-MIG-Welded 1561 Aluminum Alloy Butt Joint Produced Under Different Process Modes, 2024, 56, 0039-2316, 258, 10.1007/s11223-024-00645-5 | |
| 7. | Yang Hu, Weichi Pei, Hongchao Ji, Rongdi Yu, Shengqiang Liu, Tungsten Inert Gas Welding of 6061-T6 Aluminum Alloy Frame: Finite Element Simulation and Experiment, 2024, 17, 1996-1944, 1039, 10.3390/ma17051039 | |
| 8. | JiaYuan Luo, Chao Tan, Xin Li, Yuhang Tang, Influence of welding residual stress and welding method on fracture properties of welded joints, 2024, 238, 0954-4062, 1629, 10.1177/09544062231187208 |
Figures(9) / Tables(5)
Sharlane Costa, Maria S. Souza, Manuel B. César, José Gonçalves, João E. Ribeiro. Experimental and numerical study to minimize the residual stresses in welding of 6082-T6 aluminum alloy[J]. AIMS Materials Science, 2021, 8(2): 271-282. doi: 10.3934/matersci.2021018
| Nº | Symbol | Parameters | Units | Levels | ||||
| 1 | 2 | 3 | ||||||
| 1 | A | Welding current | (A) | 163 | 181 | 202 | ||
| 2 | B | Welding speed | (mm/s) | 10 | 13 | 16 | ||
| 3 | C | Torch angle | (o) | 30º | 45º | 60º |
DownLoad:
CSV
| Simulation | Current (A) | Speed (mm/s) | Torch angle (º) | Voltage (V) | MaxPS (MPa) |
| 1 | 163 | 10 | 30 | 22.6 | 75.4138 |
| 2 | 163 | 10 | 45 | 22.6 | 72.7757 |
| 3 | 163 | 10 | 60 | 22.6 | 62.2036 |
| 4 | 163 | 13 | 30 | 22.6 | 78.6806 |
| 5 | 163 | 13 | 45 | 22.6 | 82.6118 |
| 6 | 163 | 13 | 60 | 22.6 | 76.7528 |
| 7 | 163 | 16 | 30 | 22.6 | 94.3697 |
| 8 | 163 | 16 | 45 | 22.6 | 85.5548 |
| 9 | 163 | 16 | 60 | 22.6 | 84.5229 |
| 10 | 181 | 10 | 30 | 23.4 | 70.9412 |
| 11 | 181 | 10 | 45 | 23.4 | 73.7608 |
| 12 | 181 | 10 | 60 | 23.4 | 61.0019 |
| 13 | 181 | 13 | 30 | 23.4 | 73.8837 |
| 14 | 181 | 13 | 45 | 23.4 | 74.4494 |
| 15 | 181 | 13 | 60 | 23.4 | 71.9547 |
| 16 | 181 | 16 | 30 | 23.4 | 78.6379 |
| 17 | 181 | 16 | 45 | 23.4 | 85.487 |
| 18 | 181 | 16 | 60 | 23.4 | 85.7779 |
| 19 | 202 | 10 | 30 | 23.8 | 61.0982 |
| 20 | 202 | 10 | 45 | 23.8 | 62.5565 |
| 21 | 202 | 10 | 60 | 23.8 | 54.5618 |
| 22 | 202 | 13 | 30 | 23.8 | 80.4348 |
| 23 | 202 | 13 | 45 | 23.8 | 76.0197 |
| 24 | 202 | 13 | 60 | 23.8 | 73.9517 |
| 25 | 202 | 16 | 30 | 23.8 | 79.484 |
| 26 | 202 | 16 | 45 | 23.8 | 77.2585 |
| 27 | 202 | 16 | 60 | 23.8 | 79.3789 |
DownLoad:
CSV
| Parameters | Level | MaxPS |
| A | 1 | 79.21 |
| 2 | 75.10 | |
| 3 | 71.64 | |
| B | 1 | 66.03 |
| 2 | 76.53 | |
| 3 | 83.39 | |
| C | 1 | 72.23 |
| 2 | 76.72 | |
| 3 | 76.99 |
DownLoad:
CSV
| Source | DF | SQ | MS | F-value | P-value | Contribution (%) |
| Current (A) | 2 | 258.6 | 129.3 | 7.14 | 0.005 | 12% |
| Welding speed (mm/s) | 2 | 1374.5 | 687.27 | 37.93 | 0 | 65% |
| Torch angle (º) | 2 | 128.5 | 64.27 | 3.55 | 0.048 | 6% |
| Error | 20 | 362.4 | 18.12 | |||
| Total | 26 | 2124 |
DownLoad:
CSV
| MaxPS (MPa) | Error | |||
| Numerical | Experimental | |||
| S_09 | 85 | 106 | 20% | |
| S_19 | 61 | 67 | 9% |
DownLoad:
CSV
| Nº | Symbol | Parameters | Units | Levels | ||||
| 1 | 2 | 3 | ||||||
| 1 | A | Welding current | (A) | 163 | 181 | 202 | ||
| 2 | B | Welding speed | (mm/s) | 10 | 13 | 16 | ||
| 3 | C | Torch angle | (o) | 30º | 45º | 60º |
| Simulation | Current (A) | Speed (mm/s) | Torch angle (º) | Voltage (V) | MaxPS (MPa) |
| 1 | 163 | 10 | 30 | 22.6 | 75.4138 |
| 2 | 163 | 10 | 45 | 22.6 | 72.7757 |
| 3 | 163 | 10 | 60 | 22.6 | 62.2036 |
| 4 | 163 | 13 | 30 | 22.6 | 78.6806 |
| 5 | 163 | 13 | 45 | 22.6 | 82.6118 |
| 6 | 163 | 13 | 60 | 22.6 | 76.7528 |
| 7 | 163 | 16 | 30 | 22.6 | 94.3697 |
| 8 | 163 | 16 | 45 | 22.6 | 85.5548 |
| 9 | 163 | 16 | 60 | 22.6 | 84.5229 |
| 10 | 181 | 10 | 30 | 23.4 | 70.9412 |
| 11 | 181 | 10 | 45 | 23.4 | 73.7608 |
| 12 | 181 | 10 | 60 | 23.4 | 61.0019 |
| 13 | 181 | 13 | 30 | 23.4 | 73.8837 |
| 14 | 181 | 13 | 45 | 23.4 | 74.4494 |
| 15 | 181 | 13 | 60 | 23.4 | 71.9547 |
| 16 | 181 | 16 | 30 | 23.4 | 78.6379 |
| 17 | 181 | 16 | 45 | 23.4 | 85.487 |
| 18 | 181 | 16 | 60 | 23.4 | 85.7779 |
| 19 | 202 | 10 | 30 | 23.8 | 61.0982 |
| 20 | 202 | 10 | 45 | 23.8 | 62.5565 |
| 21 | 202 | 10 | 60 | 23.8 | 54.5618 |
| 22 | 202 | 13 | 30 | 23.8 | 80.4348 |
| 23 | 202 | 13 | 45 | 23.8 | 76.0197 |
| 24 | 202 | 13 | 60 | 23.8 | 73.9517 |
| 25 | 202 | 16 | 30 | 23.8 | 79.484 |
| 26 | 202 | 16 | 45 | 23.8 | 77.2585 |
| 27 | 202 | 16 | 60 | 23.8 | 79.3789 |
| Parameters | Level | MaxPS |
| A | 1 | 79.21 |
| 2 | 75.10 | |
| 3 | 71.64 | |
| B | 1 | 66.03 |
| 2 | 76.53 | |
| 3 | 83.39 | |
| C | 1 | 72.23 |
| 2 | 76.72 | |
| 3 | 76.99 |
| Source | DF | SQ | MS | F-value | P-value | Contribution (%) |
| Current (A) | 2 | 258.6 | 129.3 | 7.14 | 0.005 | 12% |
| Welding speed (mm/s) | 2 | 1374.5 | 687.27 | 37.93 | 0 | 65% |
| Torch angle (º) | 2 | 128.5 | 64.27 | 3.55 | 0.048 | 6% |
| Error | 20 | 362.4 | 18.12 | |||
| Total | 26 | 2124 |
| MaxPS (MPa) | Error | |||
| Numerical | Experimental | |||
| S_09 | 85 | 106 | 20% | |
| S_19 | 61 | 67 | 9% |
