Studying on the impact of media coverage on the spread of COVID-19 in Hubei Province, China

1.   Introduction

Since the end of the 20th century, the emergence and recurrence of infectious diseases in the world have increased significantly. At present, about 30 new diseases have been found, including the outbreak of severe acute respiratory syndrome (SARS) and avian influenza in November 2003 ^[1]. SARS first broke out in Shunde, Guangdong Province on November 16, 2002. It spreads widely in six months and finally spreads to 32 countries and regions. According to the statistics released by the World Health Organization on August 15, 2003, as of August 7, 2013, there were 8422 cases of SARS in the world ^[2]. The Corona Virus Disease 2019 (COVID-19) has also spread rapidly to other provinces and neighbor countries since the first case of pneumonia in Wuhan, China. In December 2019, the epidemic was mainly spread by small-scale exposure, and began to spread one month later. However, the onset time of confirmed cases reached the peak from February 10 to 13, which means that the epidemic has been effectively controlled. The time of return to work of Wuhan and its surrounding areas based on the actual data according to the propagation rules of COVID-19 were analyzed ^[3]. The model of infectious disease transmission and control were established for COVID-19 ^[4,5]. Based on the real data of Hubei Province, the unknown parameters of network model were determined by statistical calculation and parameter estimation, the optimal time for resumption of work in Wuhan and surrounding areas was analyzed, and it was evaluated for the impact of early resumption of work on the risk of secondary outbreak. However, with arrival of the resumption of work time and the new term begin, we still need to prepare for the rebound of COVID-19, and we still can not relax our protection and vigilance. Since the epidemic situation in China has been effectively controlled, the situation in Japan and South Korea is not optimistic ^[6]. Since the implementation of various prevention and control measures in China, the epidemic situation has been effectively controlled. Why is it spreading so fast overseas? The reason is that people pay less attention to the early warning and risk of the media.

The influence of social media on the spread of infectious diseases was studied ^{[7,8,9,10,11,12,13,14]}. Yi Wang et al. ^[15] proposed an SIS network model to investigate the influence of media coverage on disease transmission. They found the media coverage reduces the transmission rate between susceptible and infected individuals. It was found that media coverage plays an important role in reducing the contact rate of infectious diseases and effectively reduces the transmission rate of infectious diseases. Based on a simple SIS model, The paper studied the influence of media on the control of infectious diseases by promoting the awareness of infectious disease prevention through media ^[11], The conclusion showed that the spread of infectious diseases could be controlled through the media awareness project. A non-linear SIS model was proposed by A.K. Misra et al. ^[16]. They found the spread of an infectious disease can be controlled by using awareness programs but the disease remains endemic due to immigration. Weike Zhou et al. ^[17] Proposed a deterministic dynamic model to test the interaction between disease progression and media coverage. They investigated the effectiveness of media reporting on mitigating the spread of COVID-19. The findings suggested that media coverage can be considered as an effective way to mitigate the disease spreading during the initial stage of an outbreak. Similar to the above work, A series of studies with different emphases to explore the impact of the dynamics models were carried out with the awareness of infectious disease prevention ^[11,13,14].

COVID-19 broke out during the Spring Festival in 2020^[18], and Wuhan city was closed on January 23, 2020^[19]. However, the strategies of restricting the population shift in other regions were gradually implemented after January 23. Then, the nationwide epidemic prevention and control has begun to enter a state of emergency, and media coverage has gradually increased. So how media information contains and affects the change of epidemic situation is a valuable research problem based on the COVID-19 epidemic situation in Hubei Province, in this paper an SIHRS epidemic model with the effect of media coverage will be proposed to analyze the impact of media coverage for the spread of COVID-19 epidemic.

The framework of this paper is as follows. In section 2, an SIHRS epidemic model with the effect of media coverage will be proposed. In section 3, with the basic reproduction number, the globally asymptotically stable of two equilibria will be proved. In section 4, based on the reported COVID-19 epidemic data of Hubei Province from January 26 to February 13, numerical simulations will be used to verify the analysis results. In the last section, the results of this paper were discussed.

2.   The model with media coverage

Based on the clinical progress, epidemiological status and control measures taken by the government for COVID-19 epidemic situation, an SIHRS epidemic model with the effect of media coverage is proposed. As closely following up the suspected cases, we classify the population into four categories: the susceptible $S(t)$, the actively isolated susceptible $S_{m}(t)$, the infectious (the latent patient) $I(t)$, the hospitalized (the confirmed patient) $H(t)$ and the recovered $R(t)$, thus $S(t)+S_{m}(t)+I(t)+H(t)+R(t) = N(t)$. $M(t)$ indicates the effective accumulated information driven by media coverage about COVID-19 epidemic in a certain area at time $t$. In particular, the infectious $I(t)$ include the exposed, the asymptomatic infectious and symptomatic infectious, they are infectious and can infect susceptible individuals. We also call $I(t)$ the latent patient, who are not the confirmed patient. $H(t)$, all of them are in the hospital for isolation treatment, and they will not infect the susceptible. The recovered $R(t)$ will re-enter into the actively isolated susceptible $S_{m}(t)$ due to loss of immunity. So the dynamical model is described as

where, all the parameters are described as shown in Table 1.

The unit of $b, \mu_{0}$ is per day, the unit of $u$ is bit per person per day, and the unit of other parameters is per person per day.

3.   Stability analysis

According to system (2.1), the feasible region of the system is as follows:

It can be verified that $\Omega$ is a positive invariant set of system (2.1).

The basic reproduction number $R_0$ is defined by the method of next generation matrix ^[21], and $R_0 = \frac{b\beta}{d_1(\alpha+d_1)}$. Two equilibria can be calculated from system (2.1), namely a disease-free equilibrium

and a unique endemic equilibrium

where $S^* = \frac{(\alpha+d_1)}{\beta}$, $S_m^* = \frac{1}{q+d_1}\left(\frac{pu(\alpha+d_1)}{\mu_0\beta}+\frac{\gamma_1\gamma_2}{\gamma_2+d_1}\right)H^*$, $I^* = \frac{\gamma_1+d_1+d_2}{\alpha}H^*$, $R^* = \frac{\gamma_1}{\gamma_2+d_1}H^*$, $M^* = \frac{u}{\mu_0}H^*$, $H^* = \frac{b}{A}\left(1-\frac{1}{R_0}\right)$, and $A = \frac{\beta\mu_0 (q+d_1)(d_1+\gamma_2)(\gamma_1+d_1+d_2)(\alpha+d_1)+\alpha pud_1(\alpha+d_1)(d_1+\gamma_2)-\alpha\beta\gamma_1\gamma_2\mu_0 q}{\alpha\beta\mu_0 (q+d_1)(d_1+\gamma_2)}\;\;\; > 0$. If $R_0 > 1$, then $H^* > 0$, $S^* > 0$, $S_m^* > 0$, $I^* > 0$, $R^* > 0$, $M^* > 0$. Thus we have the following theorem.

Theorem 3.1 If $R_{0} < 1$, system (2.1) has a unique disease-free equilibrium $E_{0}$, and it is globally asymptotically stable; If $R_{0} > 1$, the disease-free equilibrium $E_{0}$ is unstable.

Proof. The Jacobian matrix $J$ of system (2.1) at the disease-free equilibrium $E_{0}$ is

The characteristic equation about $E_{0}$ is given by

where $D = \frac{b \beta}{d_1}-\alpha-d_1$. If $R_{0} < 1$, then we have $\lambda_i < 0$, $i = 1, 2, 3, 4, 5, 6$, thus all the eigenvalues of Eq (3.4) are negative. Hence the disease-free equilibrium $E_{0}$ is locally asymptotically stable.

If $R_{0} > 1$, then $\lambda_6 = \frac{b \beta}{d_1}-\alpha-d_1 > 0$. The disease-free equilibrium $E_{0}$ is unstable.

In order to determine the global stability of the disease-free equilibrium point, and define the Lypunov function $V = \frac{1}{2}I^2$, then we have

If $R_{0} < 1$, then $\frac{b\beta}{d_1}-(\alpha+d_1) = (\alpha+d_1)(R_0-1) < 0$. And we have $\frac{dV}{dt}\leq 0$, $\frac{dV}{dt} = 0$ if and only if $I = 0$. Hence if $R_{0} < 1$, the maximum positive invariant set of function $V$ in $\left\{(S, S_m, I, H, R, M)\in \Omega:\dot{V} = 0\right\}$ is $E_0$. By using the principle of Lasalle invariant principle, we can see that the disease-free equilibrium of system (2.1) is globally asymptotically stable when $R_{0} < 1$.

Theorem 3.2 If $R_{0} > 1$, the limiting system of (2.1) has a unique endemic equilibrium $(L^{*}, H^{*}, R^{*})$, which is globally asymptotically stable.

Proof. we investigate the globally asymptotic stability of the endemic equilibrium of system (2.1). It shows that, as $t\rightarrow+\infty$, we have $S(t)\rightarrow\frac{b}{d_1}$, and the limiting system ^[24] of (2.1) shown as

The dynamics of system (3.6) can be explored on this restricted region $\Omega_1$, where

Motivated by the method in ^[22], define

where $x_1 = I(t), x_2 = H(t), x_3 = R(t)$, then $f:R^3_+\rightarrow R^3_+$ is a continuously differentiable map. Obviously, $f(0) = 0$, $f(x)\geq 0$ for all $x\in\Omega_1$ and $x_{i} = 0, i = 1, 2, 3$. Since $\frac{\partial f_i(x)}{\partial x_i}\geq 0(i\neq j), x\in\Omega_1$. So $f$ is cooperative on $\Omega_1$.

For every $\theta\in(0, 1)$ and $x\in\Omega_1$, we have $f_{i}(\theta x)\geq\theta f(x), i = 1, 2, 3$. Therefore $f$ is strictly sublinear on $\Omega_1$. A straightforward calculation of $Df(x)$ gives

Obviously, $|D(f(x))|\neq 0$, it is irreducible on $\Omega_1$, and the stability modulus is $s(Df(0)) = max\{Re\lambda; det(\lambda-Df(0)) > 0\}$. By Corollary 3.2 in ^[22], we obtain that the endemic equilibrium $(I^{*}, H^{*}, R^{*})$ of system (3.6) is globally asymptotically stable.

Theorem 3.3 If $R_{0} > 1$, system (2.1) has a unique endemic equilibrium $E_{*}$, which is globally asymptotically stable.

Proof. From formula (3.2), we know that there is a unique endemic equilibrium $E_*$ when $R_0 > 1$. Set $\phi(t):R^+\rightarrow R^6_+$, and let it be a solution semi-flow of system (2.1), and $\phi(t)$ is a finite set. Assume $\omega$ be an internal propagation chain set of $\phi(t)$.

Obviously, there are only two equilibrium points for the system. If $R_{0}\leq 1$, there is a disease-free equilibrium $E_{0}$. If $R_{0} > 1$, there is a unique endemic equilibrium point $E_{*}$.

Next, we prove that $\omega$ has only one endemic equilibrium, that is $\omega = \{E_{*}\}$. If the above conclusion is not true, then $\omega = \{E_{0}\}$. Therefore there are

If $R_{0} > 1$, the spectral radius $s(M_1)$ is defined as the eigenmatrix $FV^{-1}$ of the system (2.1) at $E_{0}$. Choose any one $\varepsilon > 0$ small enough to make $s(M_1+\varepsilon M_2) > 0$, where $M_2 = diag(\sigma_1, \sigma_2, \sigma_3, \sigma_4, \sigma_5, \sigma_6)$. Then there is one $t'$, for any $t > t'$. So that

where $N^* = \frac{b}{d_1}$. Hence, we have

Let $v$ is a positive eigenvector of $M_1+\varepsilon M_2$ associated with $s(M_1+\varepsilon M_2)$, then choose an arbitrarily small number $\eta$ satisfying $I\geq \eta v$. According to the comparison theorem, we have

Therefore, if $t\rightarrow \infty$, this is contrary to the hypothesis

then the only positive equilibrium solution $E_{*}$ of the system is globally asymptotically stable.

4.   Numerical simulation

Since the number of confirmed cases in most regions were reported from January 23, and the data of first three days are not very accurate, so the data of Hubei Province and Wuhan City from January 26 to February 13 are used for parameter estimation. $H_{Wuhan}$ and $H_{Hubei}$ represent the cumulative number of confirmed cases in Wuhan and Hubei from January 26 to February 13, respectively ^[23].

Data set:

$H_{Wuhan}$ = [1590, 1905, 2261, 2639, 3215, 4109, 5142, 6384, 8351, 10117, 11618, 13603, 14982, 16902, 18454, 19558, 32994, 35991, 37914].

$H_{Hubei}$ = [2714, 3554, 4586, 5806, 7153, 9074, 11177, 13522, 16678, 19665, 22112, 24953, 27100, 29631, 31728, 33366, 48206, 51986, 54406].

Parameters setting:

Permanent population of Hubei $N_{Hubei} = 5.917\times 10^7$ and permanent population of Wuhan $N_{Wuhan} = 9.08\times 10^6$. In order to limit the flow of population, Wuhan was closed down from January 23, In this paper, the main factors of population migration are medical workers, social volunteers, government officials and so on. Therefore, we set $b^{Wuhan} = 0.002N_{Wuhan}, d^{Wuhan}_1 = 0.001$. The information is obtained from Baidu map migration big data^[25]. Although other cities in Hubei Province also take corresponding measures to restrict population flow, it is far less intense than the control measures of Wuhan. In addition, after the proposal of 'one province one city'^[26], the people from all other parts of the country have made great efforts to help the people in Hubei, so we set $b^{Hubei} = 0.003N_{Hubei}, d^{Hubei}_1 = 0.001$.

To quantify the amount of information reported by the media on confirmed cases, we define the following function. If $x\geq 1$, $f(x) = \log_2x$, which is defined by Shannon entropy^[20]. If $0\leq x < 1$, $f(x) = 0$. The essence of each confirmed case is an information source symbol, so $f(H(t)$ is the amount of information generated by all confirmed cases.

According to reference ^[3], set $\alpha = 0.1923$, $\gamma_1 = 0.05$, $\gamma_2 = 0.02$, $d_2 = 0.024$, $p = 0.008$, $q = 0.1$, $u = 1$, $\mu_0 = 0.02$.

Initial conditions of the system for Wuhan: $S_m(0) = 0.9N_{Wuhan}$, $I(0) = 4109$, $H(0) = 1590$, $R(0) = 42$, $M(0) = 70$, $Sum_H(0) = H(0)$, $S(0) = N_{Wuhan}-S_m(0)-I(0)-H(0)$. Initial conditions of the system for Hubei: $S_m(0) = 0.9N_{Hubei}$, $I(0) = 9074$, $H(0) = 2714$, $R(0) = 47$, $M(0) = 70$, $Sum_H(0) = H(0)$, $S(0) = N_{Hubei}-S_m(0)-I(0)-H(0)$.

Simulation results 1:

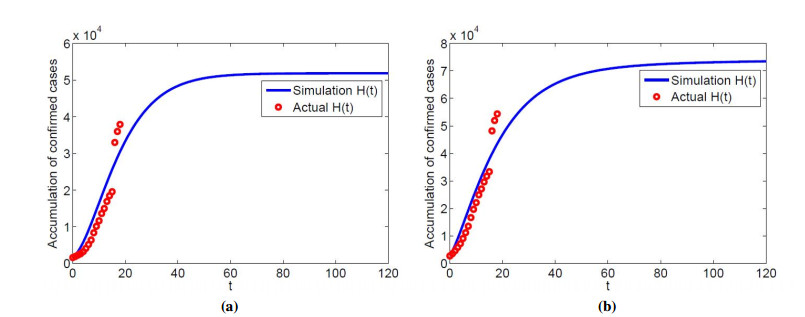
Standard incidence and infection rate of disease spread $\beta = c\cdot \beta^c$, $c$ is contact rate, and $c = 13$^[3]. $\beta^c$ is the probability of infection per person per exposure. According to $H_{Wuhan}$ and $H_{Hubei}$ dataset, the probabilities of each contact infection in Wuhan and Hubei are obtained by data fitting. The fitting effect of confirmed cases accumulation in Wuhan is shown as Figure 1(a). $\beta_{Wuhan}^c = 5.62\times 10^{-10}$ can be obtained, and then $R_0^{Wuhan} = 0.689$ can be calculated. The fitting effect of confirmed cases accumulation in Hubei is shown as the Figure 1(b). $\beta_{Hubei}^c = 1.44\times 10^{-10}$ can be obtained, and then $R_0^{Hubei} = 1.723$ can be calculated.

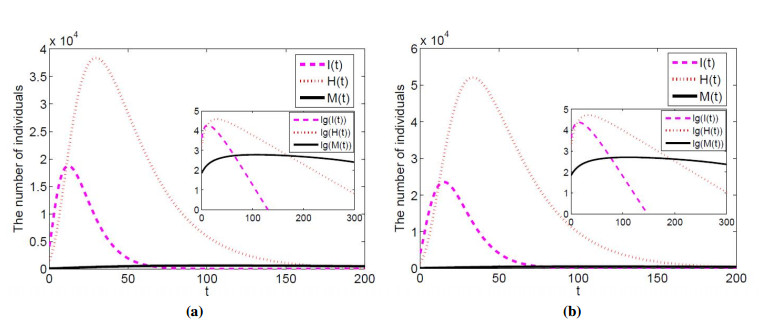
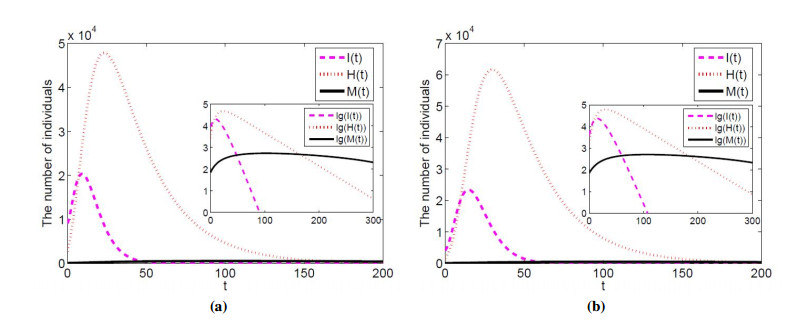
Comparing the different implementation rates of media coverage, the changes of potential patients and confirmed patients are shown in Figure 2. in Wuhan. When $u = 1$, it can be seen from Figure 2(a) that the number of confirmed patients in Wuhan will reach the maximum value of 38376 on the 31st day, and then it will gradually decrease. The subgraph is shown as logarithm values of the number of latent patients, confirmed patients and media coverage (the same below). It can be seen that with the passage of time, the number of latent patients will gradually decrease until die out under the retention of media coverage, which means that confirmed patients will also gradually die out. When $u = 0.8$, from Figure 2(b), the maximum value of confirmed patients in Wuhan will reach 52088 on the 34th day. With the amount of media coverage, it will gradually decrease over time, and eventually the latent patients and confirmed patients will die out. However, compared with $u = 1$, the peak time of the existed confirmed patients in Wuhan will be shifted back 3 days, and the number of confirmed patients will increase by 13712.

According to the psychological factors of the public under the epidemic situation, make appropriate assumptions: the whole Hubei Province pays less attention to media coverage than Wuhan, so the implementation rate of Hubei Province is set as $u = 0.9$ and $u = 0.7$. The impact of latent patients and confirmed patients is shown as Figure 3 by media coverage with different implementation rates in Hubei. When $u = 0.9$, from Figure 3(a), the maximum value of confirmed patients in Hubei Province will reach 48047 on the 28th day, and then it will gradually decrease. It can be seen from the subgraph that with the passage of time, the number of latent patients and confirmed patients will gradually decrease but not die out with the retention of media coverage, thus forming a local disease. This also illustrates that COVID-19 may exist on February 19th as a long-term flu like flu. When $u = 0.7$, from Figure 3(b), the maximum value of confirmed patients in Hubei will reach 81900 on the 39th day. With the retention of media coverage, the number of latent patients and confirmed patients will gradually decrease but not die out, thus forming a local disease. However, compared with $u = 0.9$, the peak time of confirmed patients in Hubei will be shifted back 11 days, and the number of confirmed patients will increase by 33853.

Simulation results 2:

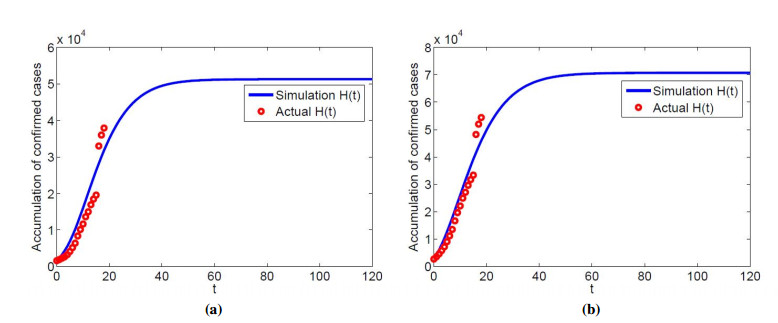
In simulation results 1, set the contact rate $c = 13$. But in practice, the contact rate is closely related to the media coverage. With the strengthening media coverage, the public will forwardly improve their awareness of self-protection, which will reduce the contact rate. Therefore, reference ^[7], the correlation function between contact rate and media coverage is $c = 18-log_2M(t)$. When $M(0) = 70$, $c = 12.87$. According to the data set $H_{Wuhan}$ and $H_{Hubei}$ as well as data fitting, the probabilities of each contact infection in Wuhan and Hubei was obtained. The fitting effect of confirmed cases accumulation in Wuhan is shown as the Figure 4(a). $\beta_{Wuhan}^c = 3.52\times 10^{-10}$ can be obtained. The fitting effect of confirmed cases accumulation in Hubei is shown as the Figure 4(b). $\beta_{Hubei}^c = 9.46\times 10^{-11}$ can be obtained. Because of the change of $c$, $R_0^{Wuhan}$ and $R_0^{Hubei}$ also changes.

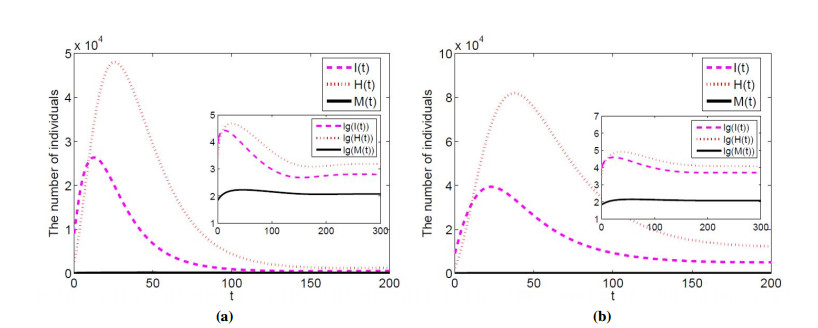
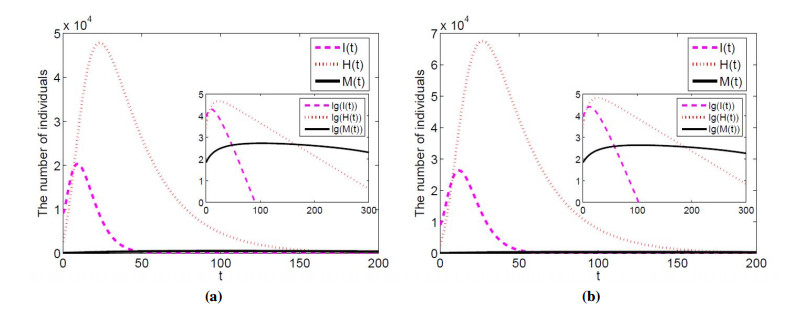
The impact of latent patients and confirmed patients is shown as Figure 5 by media coverage with different implementation rates $c = g(M)$ in Wuhan. When $u = 1$, it can be seen from Figure 5(a) that the number of confirmed patients in Wuhan will reach the maximum value of 39827 on the 27th day, and then it will gradually decrease. The subgraph is shown as logarithm values of the number of latent patients, confirmed patients and media coverage (the same below). It can be seen that the number of latent patients will gradually decrease with time until die out under the retention of media coverage, which means that confirmed patients will also gradually die out. When $u = 0.8$, from Figure 5(b), the maximum value of confirmed patients in Wuhan will reach 61671 on the 31st day. With the amount of media coverage, it will gradually decrease over time, and eventually the latent patients and confirmed patients will die out. However, compared with $u = 1$, the peak time of the existed patients in Wuhan will be shifted back 4 days, and the number of confirmed patients will increase by 21844.

As the whole Hubei Province pays less attention to media coverage than Wuhan, so the implementation rate of Hubei Province is set as $u = 0.9$ and $u = 0.7$. The impact of latent patients and confirmed patients is shown as Figure 6 by media coverage with different implementation rates in Hubei, when $c = f(M)$. When $u = 0.9$, from Figure 6(a), the maximum value of confirmed patients in Hubei Province will reach 47836 on the 24th day, and then it will gradually decrease. It can be seen from the subgraph that with the passage of time, the number of latent patients and confirmed patients will gradually decrease until die out. When $u = 0.7$, from Figure 6(b), the maximum value of confirmed patients in Hubei will reach 67595 on the 28th day. With the retention of media coverage, the number of latent patients and confirmed patients will gradually die out. However, compared with $u = 0.9$, the peak time of confirmed patients in Hubei will be shifted back 4 days, and the number of confirmed patients will increase by 19759.

5.   Conclusion and discussion

Based on the COVID-19 epidemic situation in various regions of Hubei, in this paper an SIHRS epidemic model was proposed with the effect of media coverage to analyze the impact of the spread of epidemic. Then, the globally asymptotically stable of a disease free equilibrium point and a unique endemic equilibrium point were proved. Then, based on the reported epidemic data of Hubei Province from January 26 to February 13^[23], the numerical simulation was used to verify the analysis results. The results shown that the latent patients and confirmed patients gradually decreased with time, under the retention of media coverage in Hubei. However, if the implementation rate of media coverage was reduced, the peak time of confirmed patients in Hubei would be shifted back, and the number of confirmed patients would increase significantly. It should be noted that under the condition of current prevention control measures and media coverage, COVID-19 may form a local epidemic. This situation are mainly caused by long incubation period, lack of vaccine and resumption of work. When the contact rate is a function of the effective accumulated information $M(t)$, the fitting effect and prediction effect of system should be better, which can better reflect the impact of media coverage on the model system.

It can be seen that although the direct effect of media coverage is not as good as that of vaccines, compulsory isolation and other measures, it is also a very necessary intervention. A large number of media coverage can enhance the ideology of public for epidemic situation, and that can form a situation in which the whole people participate in and fight against the epidemic together. Finally, on the premise of maintaining the media coverage and implementation rate, we should accelerate to research-develop the vaccines and specific drugs, and do a good job of epidemic prevention after returning to work.

Acknowledgment

The authors would like to thank the referees for helpful comments which resulted in much improvement of the paper. Project supported by National Nature Science Foundation of China (Grant No.11571324, 11701528), the Fund for Shanxi "1331KIRT", Shanxi Natural Science Foundation (Grant No.201801D121153, 20181D221171) and the distinguished young scholars fund of North University of China.

Conflict of interest

The authors declare there is no conflict of interest.