Low-frequency relationship between money growth and inflation in Turkey

1.   Introduction

High and chronic inflation has been one of the major problems in the Turkish economy since the 1970s. Despite various stabilization programs and structural reform efforts, the inflation rate had been stubbornly high until the early- to mid-2000s. The average year-on-year consumer price inflation was about 70% for the period 1986–1995, 54% for the period 1996–2005, and about 8.25% for the period 2006–2016. Although inflation has gradually declined to single-digit levels, it has generally fluctuated above the target level set by the central bank during the explicit inflation-targeting regime beginning in 2006. More recently, the annual consumer inflation rose to 11% in 2017 and about 16% in 2018, raising the concerns that these hikes may be persistent. There are also some signs that inflation uncertainty, as measured by the standard deviation, started to increase once again after 2015, meaning that it becomes particularly difficult to forecast future inflation. This development underlines the importance of finding a reliable leading indicator of inflation. A natural candidate for predicting the inflation rate is suggested by the quantity theory of money, which predicts that there is a one-to-one relationship between money growth and inflation in the long run.

In this paper, we ask the question of whether there is a stable and predictable relationship between money growth and inflation in the long run in Turkey, as suggested by the quantitative theory of money. In order to analyze the co-movements between the two variables in the long run, we employ frequency-domain methods to decompose the series and focus on the low-frequency components of the two series. As first suggested by Lucas (1980), the frequency-domain analysis offers a natural framework to examine the long-run relationship between money growth and inflation. As a complementary to the time-domain methods, the frequency domain approach, or spectral analysis, provides valuable information by decomposing the variability in a time series into its various longand short-term periodic components. This, in turn, allows researchers and policy-makers to determine relatively more important or prominent frequencies (and associated wavelengths) that contribute to fluctuations in that series. However, since the time resolution is lost, the spectral tools such as squared coherence are not informative about the changes in the relationship over time. The wavelet analysis can be helpful in such instances where we expect the co-movement between two variables across different frequencies (scale) may be time-dependent.

The discussion surrounding the nature of the long-term money growth-inflation relationship has been revived in the context of the European Central Bank’s (ECB) “two-pillar” monetary policy where monetary agammaegates still have a prominent role. For example, using band-spectrum regression and frequency-domain Granger causality tests, Assenmacher-Wesche and Gerlach (2008a) find that money growth Granger-causes inflation at low frequencies, while the output gap Granger-causes inflation at business-cycle frequencies. On the other hand, Schreiber (2009) argues that the low-frequency Granger-causality between money and inflation vanishes once controlled for additional variables such as unemployment and long-term interest rate. In the context of the ECB monetary policy framework, using wavelet analysis, Rua (2012) finds that the money growth-inflation relationship is stronger at low frequencies in the full sample, while there are some signs that money growth has lost its leading indicator status, especially after the early 1980s. Focusing on low-inflation OECD countries over the period 1970–2005, Teles et al. (2016) find that while the relationship between money growth and inflation is still strong and alive, especially after correcting for output growth and long-term interest rates, it becomes weaker in the implicit or explicit inflation targeting regime period of the sample. They argue that relatively low variability in the inflation rate across countries in the inflation targeting period makes it harder to find a low-frequency relationship between money growth and inflation. The money growth-inflation relationship has also been analyzed from a frequency-domain perspective using data from developing countries. For example, Rehman (2010) find an almost one-to-one relationship at low frequencies, but no significant relationship at high frequencies in Pakistan, using band-spectrum regressions. Similarly, Jiang et al. (2015) report a one-to-one relationship between money growth and inflation in the medium and long run in China, using wavelet analysis. Finally, Gallegati et al. (2019) use wavelet technique to analyze the relationship between the excess money growth rate and inflation in major developed countries including the US, the UK, Germany, and Japan in period 1871–2013 and find that there is a stable relationship between the two variables in the long run (specifically, at periods greater than 16–24 years). These results reinforce the idea that examining the money growth-inflation relationship from both time and frequency angles using wavelet tools may be highly useful when the relationship is expected to be both frequency- and time-dependent.

In this paper, we focus on the money growth-inflation relationship across both frequency and time dimensions in an emerging economy environment. More specifically, we examine the long-term predictive relationship between the growth rate of broadly defined money stock and the inflation rate in Turkey for the period 1986m1–2018m12. We use wavelet coherence based on the continuous wavelet transform to explore the nature of the co-movements between money growth and inflation. Along with spectral and wavelet coherence measures, we use a frequency domain decomposition of the Granger causality test within both bivariate and multivariate vector autoregression (VAR) system that contains additional variables besides inflation and money growth, namely, output growth, interest rate, exchange rate growth, and domestic government debt growth. In the case of monetary policy, this exercise may be useful to ascertain the variables that are relevant for predicting low-frequency movements of inflation, which is of primary importance for the monetary authorities. To accommodate the regime change in the conduct of monetary policy, we re-examine the relationship for two subsamples before and after 2006.

This paper is organized as follows. Section 2 presents a review of the relevant literature on the theoretical and empirical relationship between money growth rate and inflation. Section 3 describes the econometric methodology. Data, results, and discussions are presented in Sections 4, 5, and 6, respectively. Finally, Section 7 includes conclusions.

2.   Literature review

The relationship between monetary agammaegates and inflation has long been discussed in the literature. It would be fair to say that there was an absolute hegemony of the monetarist view in the 1960s, which regards inflation as "always and everywhere a monetary phenomenon" after the famous dictum of Milton Friedman (Friedman 1963). This view is based on the quantity theory of money and argues that any change in the quantity of money is directly and fully reflected at the price level.

In their book, Friedman and Schwartz (1983), using over a century-long data for the US and the UK, found that money demand and velocity of money are stable, and monetary changes are fully reflected in changes in price levels in both countries. Using the UK data between 1872–1996, Janssen et al. (2002) confirms their results, namely, monetary variables such as growth rate of real money base and excess money balances, can explain most of the variability in inflation. Recently, Su et al. (2016) presents that the excess money growth over output growth causes inflation in China, and Sasongko and Huruta (2018) shows that money growth Granger-causes inflation in Indonesia.

Following the quantity theory of money perspective, monetary agammaegates had been used by central banks as one of the main indicators in determining the stance of monetary policy. Notably, many central banks used "monetary targeting" for fighting inflation, especially after the oil price shocks and the collapse of the Bretton Woods system. Among them, maybe German Bundesbank was the most successful one in stabilizing the inflation at the low levels (Beck and Wieland, 2010; von Hagen and Hofmann, 2003).

However, the relevance of monetary agammaegates for the monetary policy decreased rapidly in the 1990s. Several factors have played a role in this development. Firstly, empirical studies found that the correlation between monetary agammaegates and inflation vanished in industrialized countries after having achieved low inflation (DeGrauwe and Polan, 2005; Svensson, 2002). More importantly, in his seminal paper, Taylor(1993) has shown that monetary policy decisions of the central banks can be approximated by a simple interest rate rule, which includes inflation and output gap. Although the Taylor rule was silent about the use of monetary agammaegates in the conduct of monetary policy, then-newly-emerged consensus on the use of New Keynesian models for explaining inflation has resulted in the abandonment of monetary agammaegates (Nelson, 2003).

New Keynesian models relied on an extended version of the Phillips curve (Phillips, 1958) for explaining inflation. Originally, the Phillips curve was a statement of simple statistical relationship, which implies a negative correlation between wage inflation and unemployment. This finding was popularized by Samuelson and Solow (1960) and started to be used as the primary explanation of the inflationary process in the 1960s. However, its incompetence in explaining the stagnation in the 1970s eroded its reliability and prevalence. Only after the so-called New Keynesians enriched the model with inflation expectations and nominal rigidities resulting from the optimization behavior of economic agents, it has revived as the New Keynesian Phillips Curve (NKPC) and has become the modern approach for explaining the inflation process. In essence, NKPC is the theoretical statement of that current inflation is determined by inflation expectations and real economic activity. Practically, either output gap or a measure of real marginal cost is used as a proxy for the real economic activity (Roberts, 1995). Recently, the lagged values of the inflation rate are also added to the model to account for inflation inertia. The new model, which includes both backward- and forward-looking components, is called the hybrid NKPC and being used along with the traditional NKPC (Gali and Gertler, 1999; Gali et al., 2001).

Many empirical studies have tested NKPC for diverse countries and periods. For example, Gali and Gertler (1999) tested NKPC for the US economy and found that while the backward-looking component of the inflation is statistically significant, it is quantitatively unimportant; therefore, traditional forward-looking NKPC is a good approximation for the US. Gali et al. (2001) replicated the same results with Euro-zone data, this time with an even stronger forward-looking component. Cespedes et al. (2005) and Ramos-Francia and Torres (2008) presented the validity of the hybrid NKPC for Chile and Mexico, respectively.

Currently, most of the central banks conduct monetary policy with a simple Taylor rule based on a form of the New Keynesian model. Central banks set an interest rate that affects the output gap, and it, in turn, determines the inflation rate through the NKPC (von Hagen and Hofmann, 2003).

Despite this apparent triumph of NKPC over the monetarist approach during the 1990s, the European Central Bank (ECB) announced that it would conduct a "two-pillar" monetary policy, which will give a "prominent role" for the growth rate of monetary agammaegates along with the output gap (ECB, 1999; Assenmacher-Wesche and Gerlach, 2008a). "Monetary analysis" comprises the first pillar, and the deviation of M3 growth from a reference value (4.5% then) was regarded as an indication of inflationary pressures (Gerlach-Kristen, 2006). This pillar follows the former monetary targeting approach of the Bundesbank and represents a reliable nominal anchor for the ECB's monetary policy (Jaeger, 2003). On the other hand, the second pillar is called the "economic analysis" and closely associated with the inflation targeting approach (Jaeger, 2003). Short-run fluctuations around the inflation trend are gauged with the output gap, along with cost-push factors such as changes in oil prices, exchange rates, unit labor costs, and tax changes (Assenmacher-Wesche and Gerlach, 2008a). The reason for such an eclectic policy is explained by ECB as "[in the Euro area] the inflation process can be broadly decomposed into two components, one associated with output gap at high frequency, and the other connected to more persistent trends, which is closely associated with the medium-term trend growth of money." (ECB, 2003).

Besides the ECB, monetary agammaegates play an essential role also in the monetary policy approach of the Swiss National Bank (SNB). The SNB conducted a monetary policy based on monetary targeting strategy until 1999. After 2000 it continued to use monetary agammaegates as an information source for future price developments, along with the indicators on the short-run price developments, such as output gap and the real exchange rate of the Swiss Franc (Gerlach-Kristen, 2006; Jordan et al., 2001).

As stated above, these two central banks’ use of monetary agammaegates and output gap together is based on the assumption that inflation has different determinants in the short- and long-run, and this argument has a long tradition in the monetary policy literature. Lucas (1980) may be considered as the pioneering study in this regard, in which he examined the relationship between annual M1 growth rate and consumer price inflation for the US in the period of 1955–1975 by means of graphical analysis. By using a two-sided moving average filter, he decomposed the two series into low- and high-frequency components and found the existence of an almost one-to-one relationship at low frequencies, but no relationship at high frequencies. However, McCallum (1984) and Whiteman (1984) criticized these results of Lucas (1980) for being vulnerable to the Lucas (1976) critique because of being based on reduced-form equations.

Gerlach (2002), Neumann (2003), and Neumann and Greiber (2004) have estimated an empirical two-pillar Phillips curve for the Euro area, which extends the NKPC with a low-frequency component of monetary growth rate. Their findings confirm that the low-frequency component of monetary agammaegates improves the prediction of future inflation. Gerlach-Kristen (2006) applies the same analysis to Switzerland and finds that the two-pillar Phillips curve is an accurate description of the inflationary process also in Switzerland. Assenmacher-Wesche and Gerlach (2008a) used band spectrum regression and frequency-domain Granger causality tests to determine the relationship between money growth and inflation at different frequencies in the euro area. They found that money growth Granger-causes inflation at low frequencies; on the other hand, output gap Granger-causes inflation at business-cycle frequencies. Assenmacher-Wesche and Gerlach (2008b) replicates the same results for Switzerland, using the same techniques. On the other hand, Schreiber (2009) investigates the Granger-causality relationship between money growth and inflation for the same data set as Assenmacher-Wesche and Gerlach (2008a) and replicates the same results for the bivariate case. However, when other variables such as unemployment and long-term interest rate are controlled, he observes that the low-frequency Granger-causality between money growth and inflation vanishes. Thus, he concludes that the results of Assenmacher-Wesche and Gerlach (2008a) are flawed with an omitted variable bias

For the case of Turkey, many studies empirically investigated the determinants of inflation in general and the relationship between money growth and inflation in particular. Time-domain analysis methods such as VAR/ECM, cointegration analysis, and Granger causality tests seem to dominate the empirical literature. For example, Lim and Papi (1997) argued that inflation is predominantly a monetary phenomenon over the period 1970–1995, influenced directly by money stock, exchange rates, and public deficits. Using an error correction model, they also found that inertial factors are important in the inflationary process, as evidenced by statistically significant lagged inflation. Akcay et al. (1996) detected a cointegration relationship between money growth, budget deficits, and inflation for the post-WWII period, but these links are weakened after 1986 when the public deficit started to be financed with domestic borrowing. They also underlined the importance of the inertial component in the inflationary process. Tekin-Koru and Ozmen (2003) detected a cointegration relationship between money growth, inflation, and budget deficits for the period of 1983–1999. Also, Us (2004) found that monetary growth is not a cause of inflation using Granger causality tests, variance decomposition, and impulse-response analyses.

Several studies have also investigated the NKPC approach in explaining inflation dynamics in Turkey. Yazgan and Yilmazkuday (2005) found evidence supporting the traditional forward-looking NKPC. Celasun (2006) and Agenor and Bayraktar (2008) asserted that the hybrid NKPC model fits Turkish data well and forward- and backward-looking components weigh approximately equal; therefore, inflation is partially sticky. Bastav (2015) examined the inflation dynamics in Turkey within an NKPC framework and showed that inflation is not sensitive to the output gap but to the growth rate of the output. Saz (2011) estimated both traditional and hybrid versions of the NKPC model by calculating a marginal cost index, instead of the widely used income share of labor as a proxy variable, and found evidence in favor of the model. Baser-Andic et al. (2014) also suggested that hybrid NKPC is valid for Turkish data, by estimating the model with Bayesian methods, instead of the General method of moments (GMM). On the other hand, Catik and Martin (2008) presented that Turkish data does not support NKPC between 1996 and 2007.

3.   Econometric methodology

Unlike the bulk of the literature, in this paper, we employ frequency-domain and wavelet tools to examine the relationship between the money stock growth rate and inflation. In this section, we briefly review the standard measures in the spectral and wavelet analysis and introduce the frequency domain Granger-causality test.

3.1.   Spectral and wavelet coherence

Cross-spectral tools such as cospectrum and coherence-squared (or spectral coherence) can be used to describe the nature of the frequency-wise correlation between inflation and the growth rate of the money stock. The spectral coherence measures how much of the variation in a variable, $x$, can be explained by the variations in another variable, $y$, at a given frequency. It is defined as

where $f_{xy}(\omega)$ is the cospectrum between $x$ and $y$, $q_{xy}(\omega)$ is the quadrature spectrum, $f_x(\omega)$ is the spectrum of $x$, and $f_y(\omega)$ is the spectrum of $y$. $\kappa^2(\omega)$ only takes values between 0 and 1 and may be thought of as the frequency-domain analog of the correlation coefficient (squared). Since coherence-squared can only take positive values, it cannot give information on the direction of the relationship. The sign of the relationship can be determined by the sign of the cospectrum at a given frequency.

Another useful spectral tool is the gain spectrum, which measures the impact of the input variable ($x$) on the output variable ($y$) over spectral frequencies. The gain spectrum is defined as

$G(\omega)$ is the same as the absolute value of the slope coefficient from the regression of the Fourier transformation of an output series on the Fourier transformation of an input series. Consider the model

where $y$ is the inflation rate, $x$ is the money growth rate, and $y^*(\omega)$ and $x^*(\omega)$ are the Fourier transformations. The quantity theory of money predicts that there is a one-to-one relationship between inflation and money growth at $\omega = 0$.

Although the spectral coherence is a valuable tool to decompose the strength of the relationship between two variables into various spectral frequencies, it cannot provide information on the time dimension because the time resolution is lost once the series is represented in the frequency domain. This drawback may not be a problem in practice if we have a stationary and stable time series without breaks, regime changes, outliers, and temporary or permanent changes in the power spectra. In those instances, wavelet analysis may be employed as an alternative, because it can detect localized changes in a signal.

One of the central concepts in wavelet analysis is the continuous wavelet transform (CWT). CWT gives us information on scale (frequency) and time simultaneously and defined as

where $\psi(.)$ is a mother wavelet function, $s$ is a scaling or dilation factor that controls the width of the wavelet and $\tau$ is a translation parameter controlling its location. Scaling a wavelet simply means stretching it (if $|s| > 1$) or compressing it (if $|s| < 1$), while translating it simply means shifting its position in time. Although there are several alternative wavelet functions, we use the Morlet wavelet which is widely used in cross-wavelet analysis in the literature.

One of the advantages of the Morlet wavelet is that the inverse of the scale can be interpreted approximately as a Fourier frequency. Once CWT is computed, it can be depicted as a contour plot to see the changes in the periodic behavior along the time dimension. Analogous to cross-spectral Fourier analysis, the cross-wavelet analysis provides a decomposition of the relationship between two series over the time-scale domain. The wavelet (squared) coherence allows simultaneous analysis of the co-movement between two series in both time and frequency domains. It may be considered as an extension of the concept of spectral coherence into the time-frequency domain. Thus, one can infer not only the important frequencies (periods) but also the time that they occur. The wavelet coherence between two time series $x$ and $y$ is defined as

where $W_{x y}(\tau, s)$ is the cross-wavelet power and $S(.)$ is a smoothing function defined on both time and scale.

3.2.   Granger causality in the frequency domain

Our primary econometric tool is based on the concept of Granger causality in the frequency domain. In a bivariate system consisting of inflation and money growth, the general testing procedure may be described as follows. Let $y_t$ be the inflation rate and $x_t$ be the growth rate of monetary agammaegates. Consider Equation (7) for $y_t$ in the context of a bivariate VAR($p$) model.

The null hypothesis of no Granger-causality from money growth to inflation can be stated as (Granger, 1969)

which can be tested using the standard F or Wald tests. Non-rejection of this null will imply that once we control for lagged inflation, history of money growth does not matter. In other words, lagged money growth rates do not help to predict the inflation rate in the next period. A closely related concept of linear feedback and associated measures has been introduced by Geweke (1982) in which informational content is decomposed into reciprocal feedbacks between two variables plus instantaneous or contemporaneous feedback. If $x$ does not Granger-cause $y$, then the Geweke measure of linear feedback from $x$ to $y$ will be zero.

Recognizing that the predictive ability between the two time series (or blocks of time series) can also vary across different frequencies, Geweke (1982) and Geweke (1984) introduced the frequency domain versions of the linear feedback measures. Geweke's measure may also be interpreted as a frequency domain version of the Granger causality test. However, the test turns out to be difficult to implement as one needs to use bootstrap or numerical differentiation. As an alternative, Breitung and Candelon (2006) suggested a simpler procedure (BC test, hereafter) by reformulating the null hypothesis in terms of two restrictions in the bivariate VAR(p) system. Using the representation in Equation (7) the null hypothesis of $M_{m\rightarrow \pi}(\omega) = 0$ is equivalent to:

where $\boldsymbol \beta = [\beta_1, \ldots, \beta_p]'$ and $\boldsymbol R(\omega)$ is $2\times p$ restriction matrix:

Let $\boldsymbol \gamma = [c_1, \alpha_1, \ldots, \alpha_p, \beta_1, \ldots, \beta_p]'$ be $q = (2p+1)\times 1$ vector of parameters and let $\boldsymbol V$ be $q \times q$ covariance matrix from the unrestricted regression (equation 7). Then the Wald statistic is

where $\boldsymbol Q$ is $2\times q$ restriction matrix such that

In practice, the model in Equation (7) can be augmented by conditioning on additional variables, as suggested by Geweke (1984)¹. Furthermore, the model for inflation can be extended to include a measure of the growth rate of real economic activity (output growth), interest rates, the growth rate of exchange rates, and the growth rate of government debt stock. For example, the equation for the inflation rate in the VAR system can be written as

¹ A related conditional measure has been suggested by Hosoya1991 and Hosoya2001 in which contemporaneous information on a third series was also included.

where $\boldsymbol Z_{t-j}$ is the vector of additional (lagged) conditioning variables in the system.

It should be noted that the null hypothesis of no Granger causality is tested at a single frequency, $\omega$, which is assumed to be known and specified a priori. For practical purposes, one may compute test statistics for a sequence of frequencies and plot them to examine the pattern. However, the joint interpretation over a frequency band is not possible. To overcome that difficulty and to allow for joint interpretation, Breitung and Schreiber (2018) suggested an extension to the BC test. For a given frequency band $[\omega_L, \; \omega_U]$ defined in $0 < \omega < \pi$, they showed that the smallest BC test statistic within the band could be used to test the joint significance of Granger-causality. To ascertain if money growth is Granger-causal for inflation in a given frequency band, we compute the BC test statistics over all Fourier frequencies $\omega = 2\pi f$ and focus on the lower frequencies with wavelengths ² larger than 1.5 years or 18 months, corresponding to frequencies $\omega\in [0.01, 0.35]$. Following Yildirim_Tastan2012, we further decompose longer wavelengths into the medium and long run. The medium run corresponds to business-cycle periodicities that are between 18 to 60 months (approximately $\omega\in (0.1, 0.35]$). On the other hand, the long run corresponds to periodicities larger than 60 months (approximately $\omega\in [0.01, 0.1]$).

² The wavelength or the period is defined as $2\pi/\omega$ which is the inverse of the fundamental frequency $f\in (0, 1/2)$.

4.   Data

The inflation rate series is calculated as the monthly growth rate of the consumer price index (CPI) covering the period 1986m1–2018m12. The CPI series is retrieved from the Electronic Data Delivery System (EDDS) of the Central Bank of the Republic of Turkey (CBRT). Since the definition of the CPI has been changed at the beginning of 2003, we extended the new series with the growth rates of the old series. The money growth series is calculated as the monthly growth rate of M3 agammaegate for the same period, which is retrieved from the FRED system of the St.Louis Fed. Industrial production index (IPI), domestic debt stock, and exchange rate data (Turkish Liras per US dollar) data were obtained from the EDDS of the CBRT. We used the average annualized 3-month deposit interest rates, which was retrieved from the International Financial Statistics Database of the IMF. To eliminate the seasonal movements in the data that might obscure the analysis in the frequency domain, we seasonally adjusted money growth, inflation, and IPI series using the Census-X13 method.

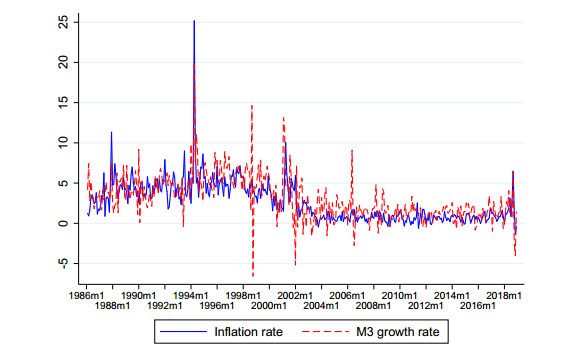
The inflation and money growth series are plotted in Figure 1. The visual inspection of this figure suggests that the two series move closely with each other with an apparent change in the levels of the series, especially after the early 2000s.

According to the standard ADF tests, all variables are stationary except inflation and interest rates. On the other hand, the Enders and Lee (2012) supF statistics for inflation and interest rates indicate that the deterministic components are nonlinear, possibly as a result of structural breaks and smooth regime changes. Flexible Fourier ADF test results indicate that when we account for the nonlinear trend, inflation and interest rates can be accepted as stationary processes.³

³ The results of the unit root tests are presented in Appendix A.

5.   Results

5.1.   Bivariate analysis

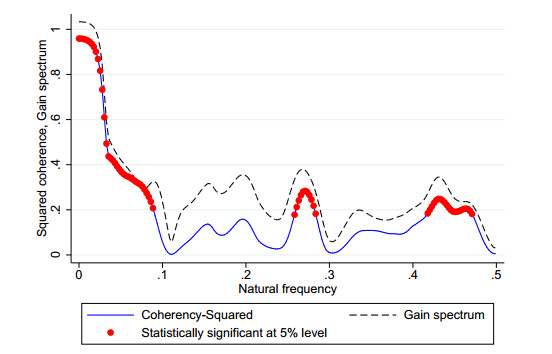
First, we start with the bivariate analysis of the relationship between inflation and money growth in the frequency domain. Figure 2 displays the estimates of spectral coherence and the gain spectrum between inflation and money growth across frequencies over the full sample. In this figure, red dots on the squared coherence estimates represent statistically significant values at 5% level.⁴ As can be seen in Figure 2, the squared coherence between inflation and money growth is statistically significant at low and medium frequencies (including business cycle frequencies). Permanent changes in the growth rate of money can explain a significant portion of the long-run variations in inflation. The gain spectrum at the vicinity of zero frequency is equal to unity implies that there is a one-to-one relationship between money growth and inflation in the long run.

⁴ For a review of spectral analysis and also for the threshold formula see (Bloomfield, 2000).

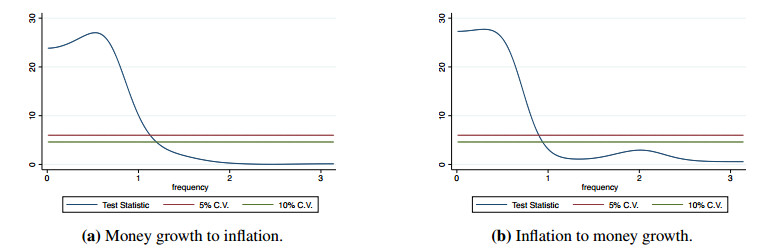
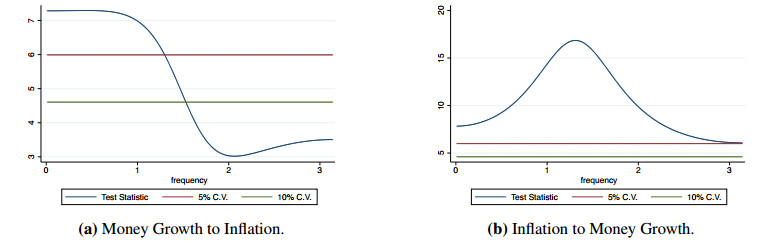
As part of our baseline bivariate analysis of the relationship between money growth and inflation, we use the frequency-domain Granger-causality tests to determine if either variable is useful in predicting the long-run movements in the other variable. The test results are summarized in Figure 3 across all Fourier frequencies.⁵ We specify a bivariate VAR($p$) and identify the lag order using the Akaike Information Criterion (AIC), which suggests a lag order of $p = 5$. The time-domain Granger-causality tests⁶ indicate that there is a bidirectional predictive relationship between inflation rate and money growth. The frequency decomposition of the Granger causality test, depicted in Figure 3a, suggests that money growth can predict the movements in inflation rate at frequencies lower than $1.12$, corresponding approximately to wavelengths longer than 6 months. Similarly, the inflation rate can also predict the movements in money growth at frequencies lower than $0.89$, corresponding approximately to wavelengths longer than 7 months (see Figure 3b).

⁵ We used the Stata command written by Tastan2015 to compute and draw the frequency-domain Granger causality tests.

⁶ Not reported to save space but available upon request.

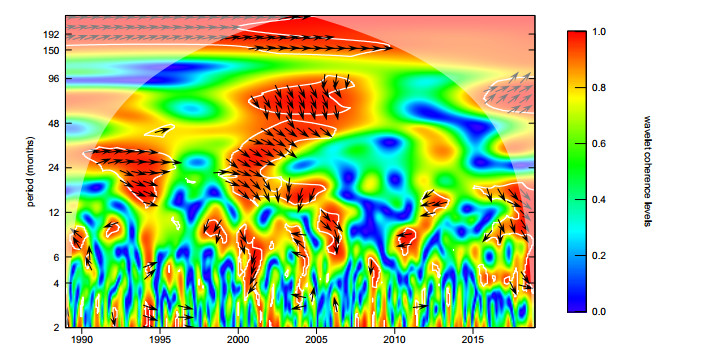
The analysis so far suggests that money growth rate and inflation are highly correlated in the long run. As we mentioned previously, the spectral tools may not be appropriate if there are regime changes or structural breaks in the variables. To explore this further, we computed the wavelet coherence between money growth and inflation. Figure 4 depicts the wavelet coherence between inflation and money growth rate for the full sample period. The wavelet coherence, obtained using the Morlet wavelet, is a contour plot over the frequency (converted into periods in months) in the vertical axis and time on the horizontal axis. The areas inside the white strips indicate statistically significant coherence levels (obtained from Monte Carlo simulations using white noise series). The pale-colored area represents regions outside the cone of influence arising from the cyclical imputation of the wavelet coherence levels. The arrows summarize the direction and the lead-lag relationship between the two series based on the phase difference. The phase difference between two variables, say $x$ and $y$, describes how far series $x$ leads series $y$ along the circumference of the unit circle. An arrow pointing right indicates that the two series are positively correlated (in-phase), and vice-versa.

In the very long run, represented by periods larger than $150$ months (about $12$ years), money growth and inflation are positively correlated (see Figure 4). In the short run covering the periods less than one year, we observe that the relationship between money growth and inflation is rather mixed, with leads and lags on both directions. Focusing on the intermediate frequencies corresponding to cycles of $18$ to $96$ months (including the business cycle frequencies), we see that the two series are highly correlated in the 1990s and the early 2000s. Money growth leads inflation in those frequencies. The linear positive association is particularly strong during the financial crises of 1994 and 2001, as indicated by the phase difference arrows pointing to the right. However, for the post-2001 crisis period, especially during 2006–2015, the linear association becomes somewhat weaker in the medium to long run. The wavelet coherence also shows signs of high correlation towards the end of the period. Although it must be cautiously interpreted at the ridges, inflation and money growth tend to become highly correlated at periods of $12$ to $24$ months.

The findings from the wavelet coherence indicate that there might be a structural break in the nature of the inflation-money growth relationship in the medium and long run after 2005. The fact that the beginning of the year 2006 corresponds to a critical monetary policy shift for Turkey provides a rationale for such a change. The CBRT has switched to explicit inflation targeting regime after this date.

To further evaluate the impact of policy change on the low-frequency money growth-inflation relationship, we compute the spectral coherence and gain spectrum for the two subperiods before and after 2006m1 and display the results in Figure 5. For the first subsample (1986m1–2005m12), inflation and money growth are highly correlated at low frequencies, including cycles of length larger than 12 months. The gain spectrum is very close to 1, as predicted by the quantity theory of money. The cross-spectral measures for the second period (2006m1–2018m12) present a slightly different picture. While the cross-spectral coherence between inflation and money growth indicates that the correlation at low frequencies has become relatively weaker (and statistically significant at 5% level), the gain spectrum at around zero frequency is still equal to unity, which supports the quantity theory of money. Overall, spectral coherence and gain spectrum at zero frequency imply that there is a one-to-one relationship between the two variables in both subperiods.

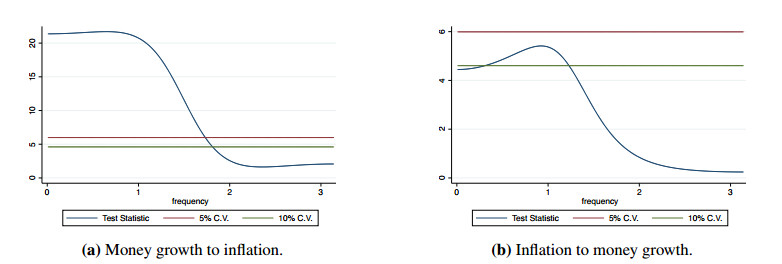
We repeat the subperiod exercise for the BC Granger causality tests between inflation and money growth. As can be seen in Figure 6, money growth Granger-causes inflation at low frequencies in the first subperiod, whereas inflation is not Granger-causal (at 5% significance level) for money growth. On the other hand, there is a bidirectional Granger-causal relationship between money growth and inflation at low frequencies in the period 2006m1–2018m12 (Figure 7).

5.2.   Multivariate analysis

In order to avoid spurious results, we estimate a multivariate VAR($p$) model and compute the BC Granger-causality test statistics conditional on a set of real and financial factors that potentially have a significant influence on both variables. First, we define a measure of output growth to control for the changes on the demand side. Since GDP is only available quarterly, we used the IPI as a proxy. Second, we used an interest rate series that reflect both the liquidity conditions and inflation expectations in the economy. Third, to account for the important role that the government has played in the Turkish economy, the growth rate of the domestic debt stock series is added to the system. Finally, we also included the growth rate of the exchange rate in the VAR system. As manufacturing is highly dependent on imported intermediate goods in Turkey, production costs generally tend to be sensitive to the variations in exchange rates. Besides, as indicated by over 50% of the bank deposits being denominated in US Dollars, it is the most important asset for economic units to store wealth. Therefore, the growth rate of the exchange rate controls for both the cost side pressure on inflation and wealth effect on expenditures. As the data for the domestic government debt was only available since 1988m12, we conducted the multivariate analysis for the period 1988m12–2018m12.

We start by estimating a VAR($p = 5$) model for the full sample where the lag order is selected using the AIC. We first compute frequency-wise Granger causality BC test statistics over all frequencies and then test the joint significance of the frequency bands corresponding to long and medium run as defined previously. In addition to Granger causality links between money growth and inflation, a visual depiction of the links among the rest of the variables in the system may provide further information regarding the nature of the inflation dynamics. To ease the exposition, we summarize the long- and medium-term Granger-causal relationships in Figure 8 by a "directed graph" as suggested by Eichler2007. In these figures, arrows with a straight line represent a Granger causality relationship over the frequency bands that is significant at $5\%$ level, and those with a dashed line represent a relationship that is significant at $10\%$ level. If there is no link between two variables, it implies that there is no Granger causality between them. Granger causality graph, depicted in Figure 8, is based on Table 1 which presents corresponding numerical results for statistically significant Granger-causal links over long and medium-term frequency bands using the minimum BC test statistics.⁷

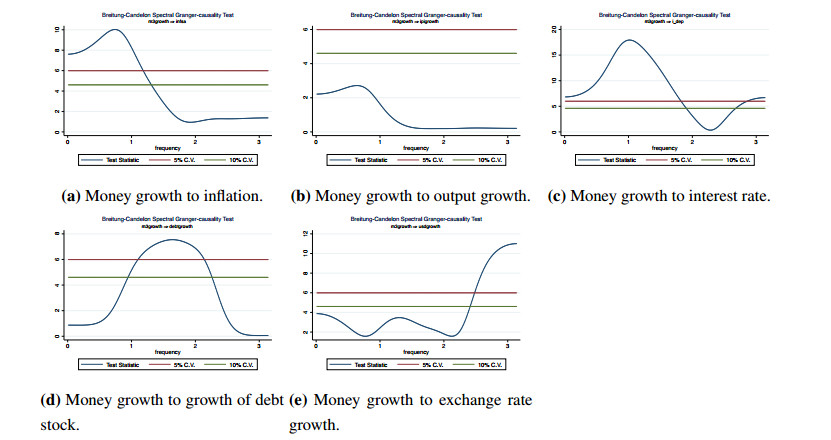
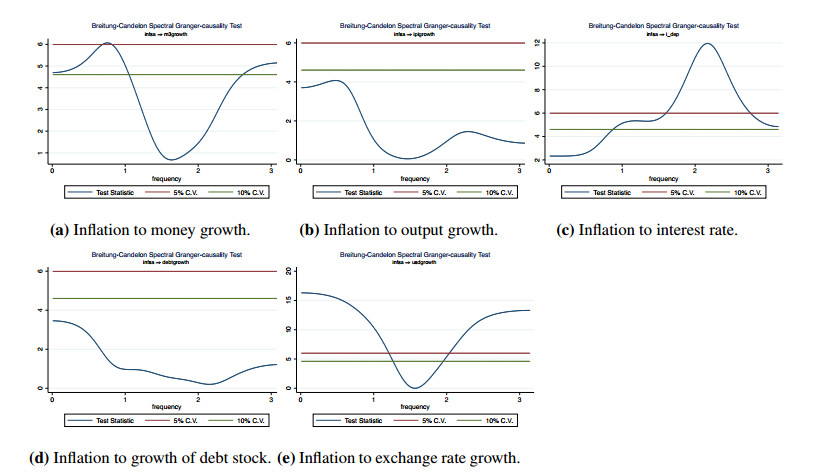
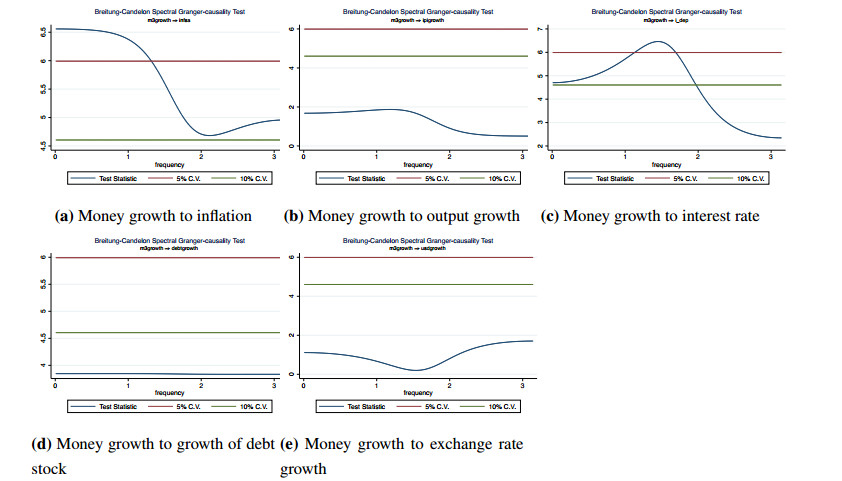
⁷ Detailed Granger-causality test results from money growth and from inflation to the other variables in the system are displayed in graphical form in Appendix (Figure 10 and Figure 11, respectively). We have not included full results to save space but available upon request.

As in the bivariate system, money growth Granger-causes inflation in both medium and long run, corresponding to the frequency band $0.01 \leq \omega \leq 0.1$.⁸ However, unlike the bivariate case, the link from inflation to money growth is only significant at 10% level. There is some evidence that inflation Granger-causes money growth at $5\%$ level in the short run just between the frequencies $0.69$ and $0.82$, which roughly correspond to the wavelengths of $9-10$ months.⁹

⁸ In fact, as can be seen in Figure 10 in Appendix, money growth Granger-causes inflation at $5\%$ level at the frequencies up to $1.19$, which roughly corresponds to the movements longer than $6$ months (at $10\%$ level, it is at the frequencies up to $1.32$, corresponding to the movements roughly longer than 5 to 6 months).

⁹See Figure 11 in Appendix.

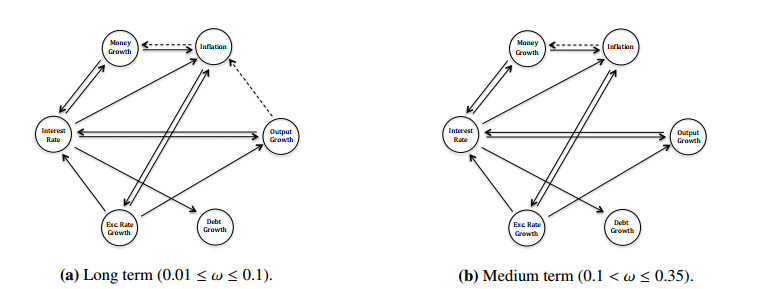
Results depicted in the Granger causality graph in Figure 8 for the frequency band $(0.01 \leq \omega \leq 0.1)$ (see Panel (a)) suggest that money growth, interest rate, exchange rate growth, and output growth (albeit weakly at $10\%$ significance level) Granger-causes inflation in the long term. There is a bidirectional Granger causality at low frequencies between money growth and interest rate and also between the interest rate and output growth.

Besides money growth, inflation Granger-causes the exchange rate in the long run. Although there is weak evidence for the direct Granger causality from inflation to money growth, the relationship between inflation and exchange rate growth provides another channel for inflation to predict money growth indirectly. There are also bidirectional Granger-causality relationships between money growth and interest rate, and between the interest rate and output growth. These relationships constitute many indirect links among the variables, apart from the direct relationships between them. The only exception in this landscape is debt growth, as it is not Granger-causal for any other variable. However, long-term movements of debt growth can be predicted by interest rate, and, therefore, the other variables in the system are linked to debt growth indirectly through the interest rate. When we look at the results for the medium term (Figure 8, Panel (b)), we see that all the relationships in the long-term among the variables are preserved, except for the one running from output growth to inflation.

As we did in the bivariate analysis, we now re-run the BC Granger causality tests separately for the two subperiods before and after 2006m1. Based on AIC, the lag order is chosen as $p = 5$ in the first subperiod and $p = 3$ in the second subperiod. Figure 9 summarizes Granger causality graphs over the two subsamples.¹⁰

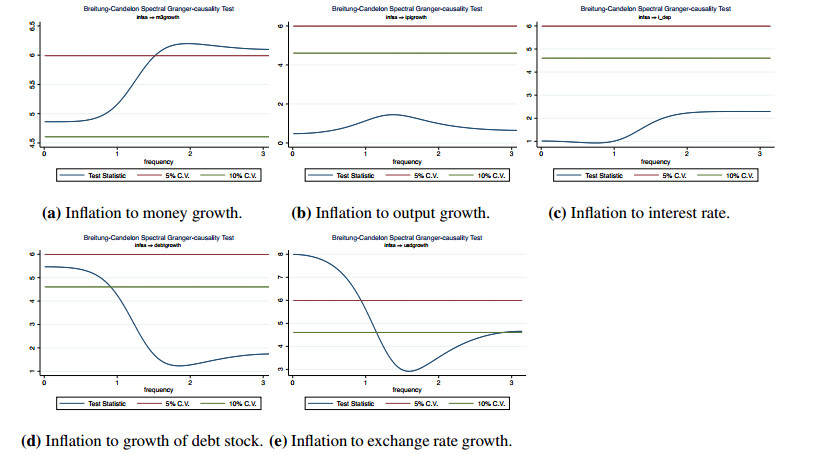
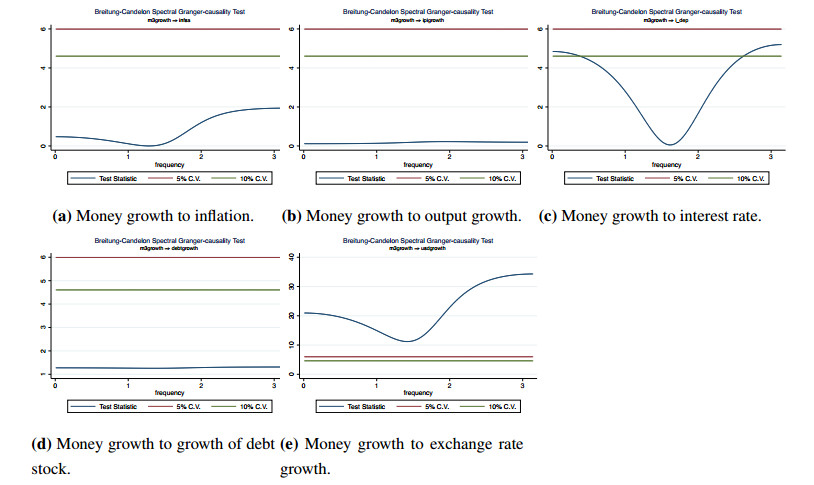
¹⁰ Detailed Granger-causal results from money growth and from inflation to the other variables in the system are displayed in graphical form in Appendix.

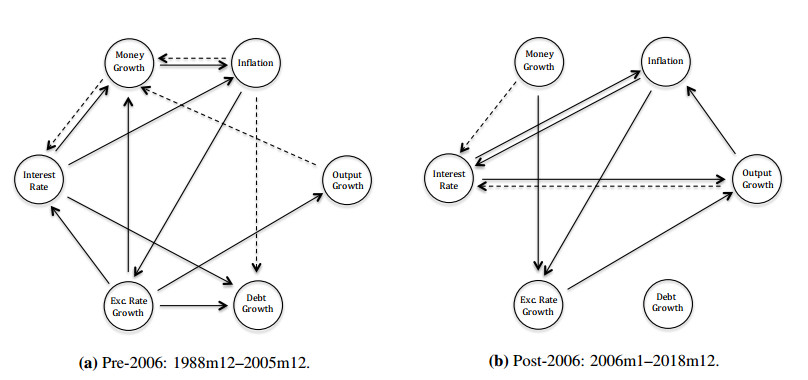
As can be seen in Figure 9 and in Tables 2 and 3, there are significant differences between the two subperiods in terms of Granger-causal links. Since the linkage patterns for the long- and medium-term are the same for each subperiod, we present one figure for each. Test statistics and corresponding p-values for the relationships significant at $10\%$ level are given in Tables 2 and 3. A quick look at the figures suggests that while there is a bidirectional Granger-causality link at low frequencies between money growth and inflation in the period before 2006, this relationship disappears after 2006. Although money growth Granger-causes or is Granger-caused by other variables in the system except for debt growth in the first subperiod, it is not Granger-caused by any variable and Granger-causes just interest rate and exchange rate growth in the second subperiod.

The interest rate is Granger-causal for inflation in both subperiods. However, in the second subperiod, the relationship between the two turns into a bidirectional one, suggesting that interest rate can also be useful to predict long-term movements in the inflation rate. The predictive relationship between the interest rate and output growth is also worth mentioning. While there are no direct links between output growth and interest rate in the pre-2006 period, we observe that interest rate may be a helpful predictor for the output growth in the second subsample. Albeit weak at a 10% level, there is also a Granger-causal link from output growth to interest rate, suggesting a feedback relationship.

Regarding the demand side, which is represented by output growth, we see that it is not important in predicting low-frequency movements in inflation in the pre-2006 period. However, it Granger-causes inflation at low frequencies in the post-2006 period. Conditional frequency-domain Granger causality test results imply that exchange rate growth is not informative for predicting long-term movements in inflation. In contrast, in both subperiods, inflation help predict the low-frequency components in exchange rates. On the other hand, the exchange rate is Granger-causal for output growth in both periods. While there are predictive links from the exchange rate to both interest rate and money growth in the pre-2006 period, this is no longer the case in the second period. In contrast, money growth and interest rate (albeit weakly at a 10% level) may help predict long-run movements in exchange rates in the second period.

The place of the government debt growth in the low-frequency Granger-causal links is also striking. While government debt growth is not Granger-causal for any other variables, it is Granger-caused by inflation, interest rate, and exchange rate growth in the pre-2006 period. However, all these relationships vanish in the post-2006 period, and debt growth seems to be turned into a stand-alone variable.

6.   Discussion

When we compare the predictors of inflation in the two subperiods, we see that while inflation is Granger-caused by interest rate and money growth in the first subperiod, it is Granger-caused by interest rate and output growth in the second subperiod. This change can be interpreted as a result of the change in the inflationary process in Turkey. The first subperiod, particularly before the crisis of 2001, is marked by high levels of government deficits and the CBRT's financing of these deficits with monetization. The resulting excessive level of money growth was the main driver of inflation in this period. With the structural measures taken in the aftermath of the 2001 crisis, the CBRT has become relatively independent and switched to explicit inflation targeting regime after 2006. As is well-known, in the inflation targeting regime, the interest rate is the primary tool used by central banks to control inflation. If inflation deviates from the targeted level, central banks adjust the interest rate independently in order to achieve the target level. The bidirectional link between inflation and interest rate in the second subperiod suggests that the CBRT adjusted interest rates according to the level of inflation and, the interest rate was effective for controlling inflation. Therefore, albeit CBRT could not hit its target level of inflation except for two years –2009 and 2010– under the explicit inflation targeting regime, it was successful in bringing the interest rate in such a central position in the inflation process after 2006. Also, the disappearance of the Granger-causal link between money growth and inflation in the second subperiod may be a reflection of the fact that the CBRT did not have to finance government deficits in this subperiod. Indeed, as a result of the measures taken by the government after the crisis of 2001, the government established a tight fiscal discipline, reducing its fiscal dominance in the economy drastically. Hence, there was no political pressure on the CBRT to monetize the government deficits, and it could maintain its independence, at least in the significant part of the second subperiod.

The direction of Granger-causality runs from the exchange rate to money growth in the first subperiod; however, it reverses in the second subperiod. This reversal of direction may be interpreted as a result of the "unconventional monetary policy framework" applied by the CBRT in the period 2010–2016. In this framework, the CBRT used unconventional tools such as interest rate corridor, differentiated required reserve ratio, and reserve option mechanism in order to actively manage both the amount of liquidity and short-term interest rates in the market. The rationale behind this policy was to prevent potential financial instability in the form of excess credit growth (hence, money growth) and "over-appreciation" of Turkish Lira induced by short-term capital flows from developed countries to emerging market economies in the wake of the Global Financial Crisis of 2008–2009 (Kara, 2015). Hence, our findings for the second subperiod may be interpreted as evidence for the effectiveness of the CBRT's "unconventional monetary policy" to control exchange rate growth.

Finally, the occurrence of the Granger-causal link from the interest rate to output growth in the second period may indicate the effectiveness of interest rates on inducing consumption and investments. In particular, both the households (Karaçimen, 2014) and small-and-medium-sized enterprises (Terzi, 2015) had greater access to credit finance in the relevant period. By increasing the part of durable consumption and housing investment for households and of investment for small-and-medium-sized enterprises, the relaxation of the financial constraint might have increased the sensitivity of consumption and investment, therefore, output growth, to changes in interest rates. On the other hand, as crystallized in the Taylor rule, central banks can follow a target level of output, besides the inflation target while determining interest rates. In the second subperiod, albeit weak, the Granger-causal link from output growth to interest rate might indicate that the CBRT took into consideration the level of output besides inflation (at least in some part of the period). We note that as our analysis is not based on a structural model, these arguments need to be further examined in future studies.

7.   Conclusion

Motivated by the quantity theory of money, in this paper, we analyzed the low-frequency predictive relationship between inflation and money growth in Turkey for the period 1986m1–2018m12. Bivariate spectral coherence analysis and the BC Granger causality tests provided evidence for the existence of a two-way predictive relationship between the long and medium-run movements of the two variables over the full sample period. However, the wavelet coherence analysis indicated a potential structural break in the relationship after 2006, the year that marks the switch to the explicit inflation targeting policy. Thus, we replicated the analysis for the subperiods before and after 2006m1 separately. Again, spectral coherence and gain spectrum indicated a one-to-one relationship between the two variables in both subperiods. While the direction of the long run Granger-causality runs from money growth to inflation before 2006, there is a bidirectional relationship between money growth and inflation after 2006.

In order to check the robustness of our results, we rerun the Granger causality tests with a multivariate VAR model where we controlled for output growth, interest rate, domestic debt growth, and exchange rate growth, all of which may potentially contain predictive information on both money growth and inflation in the case of Turkey. In the full sample, we found a bi-directional predictive relationship between money growth and inflation in the long run. When we analyzed the subperiods separately, we find that while there was a long-run predictive relationship between money growth and inflation before 2006, this relationship disappears in the second subperiod. Besides, the one-way Granger-causal relation from interest rate to inflation turns into a bidirectional one in the second subperiod. We argue that the differences between the two periods may indicate a change in the inflationary process of Turkey resulting from the decrease in fiscal dominance of the government, the CBRT's switch to the explicit inflation targeting regime, and the CBRT's "unconventional monetary policy framework".

Acknowledgements

The authors are grateful to the anonymous referees for their helpful comments and suggestions. Usual disclaimers apply.

Conflict of interest

The authors declare no conflict of interest.

Supplementary

A.   Unit root tests

ADF unit root tests may be less powerful in the presence of nonlinear trends resulting from regime changes and structural breaks. To remedy that problem, several extensions have been suggested in the literature. Enders and Lee (2012) suggested an extended version of the ADF test, which does not make any assumptions on the type, number, and location of the break. In this approach, it is assumed that the deterministic component has a nonlinear structure that can be captured by the appropriate number of flexible Fourier components. For example, the flexible Fourier ADF test regression with only a single component can be written as follows (Enders and Lee, 2012):

Trigonometric terms in this equation provides a flexible way to capture unknown type and number of breaks. Under the null hypothesis of $\alpha_2 = 0, \alpha_3 = 0$, the model reduces to the standard ADF test regression. The rejection of the null hypothesis $H_0: \rho = 0$ implies that $y_t$ is stationary around a nonlinear trend. Enders and Lee (2012) show that under the null hypothesis, the ADF test statistic ($t$ ratio) has an asymptotic distribution that depends on the number of frequency components $k$ and the number of observations, $T$. In practice, $k$ is usually unknown, but it can be determined by estimating all test regressions for all possible $k$ under a maximum value (e.g., 5) and then choosing the model with the smallest sum of squared residuals (RSS).

Enders and Lee (2012) also suggested a test for the nonlinearity of the deterministic components which can be applied before the flexible Fourier test. They suggested testing $H_0: \alpha_2 = 0, \alpha_3 = 0$ using the usual F test statistic that has a non-standard distribution under the unit root null. Also, since $k$ is unknown as well, one needs to compute all possible F statistics for each $k < k_{max}$ and use supremum of these (supF). Enders and Lee (2012) provides an approximation of the distribution of supF statistic and its critical values. If the supF statistic is less than the critical value at a given significance level, one can conduct the usual ADF unit root tests as it implies that the deterministic components are linear.

The results for the FFADF tests along with those for the standard ADF tests for the series used in our analysis are presented in Table 4.

B.   Multivariate frequency domain Granger causality test results