Multi-scale modeling of cholera dynamics in a spatially heterogeneous environment

1.   Introduction

Infectious diseases remain a serious public health burden in developing countries, leading to high morbidity and mortality every year. Mathematical modeling has long been a useful theoretical tool to investigate the mechanisms of infectious diseases and provide input for the design of control strategies. Although traditional mathematical epidemic models are focused on disease transmission and spread at the population level, there is increasing interest in connecting the between-host transmission dynamics and the within-host immunological dynamics ^[1,2,3,4,5]. These studies, however, are mainly concerned with directly transmitted or vector-borne diseases, and typically involves only a single population setting in a homogeneous environment.

The goal of the present paper is to conduct multi-scale modeling for cholera, a severe waterborne infection, in a spatially heterogeneous environment. Although cholera is an ancient disease, it continues to devastate impoverished populations that have limited access to clean water, hygiene and sanitation resources. The persistence of cholera has been highlighted by large outbreaks in Yemen (2016–2018), South Sudan (2014), Haiti (2010–2012), and many other places, with millions of cases reported in recent years ^[6,7].

The causative agent of cholera is the bacterium Vibrio cholerae, which can survive and multiply both in the aquatic environment and within the human body. Individual hosts can catch the pathogen from ingestion of contaminated water through the indirect (i.e., environment-to-human) transmission route, or from close contact with infected individuals through the direct (i.e., human-to-human) transmission route ^[8,9]. Once entering the body of a host, the pathogenic bacteria go through complicated processes of biological, chemical and genetic interactions, leading to large amounts of watery diarrhea and other symptoms (such as vomiting, muscle cramps and low blood pressure) that characterize human cholera. Thus, the dynamics of cholera normally involve dual transmission pathways, different time scales happening for the between-host transmission and within-host interaction, and could vary significantly from place to place due to the heterogeneity in environmental, geographic, and socioeconomic conditions.

Mathematical modeling of cholera could play an important role in understanding the infection and designing effective strategies for disease prevention and intervention. A large number of cholera models have been published in recent years; see, for example, ^{[8,10,11,12,13,14,15,16,17,18,19,20]}. Despite the many progresses made in these studies, our current knowledge in the fundamental mechanisms of cholera remains limited.

In a study of the 2008–2009 Zimbabwe cholera outbreak ^[12], basic reproduction numbers were estimated for the 10 provinces in Zimbabwe. The results were highly heterogeneous, an indication that the underlying transmission pattern varied widely throughout the country. Similarly, an investigation of the 2010–2012 Haiti cholera outbreak produced very different reproduction numbers for different administrative departments of Haiti ^[17]. Although relatively simple mathematical models were used in these studies, they did imply that spatial heterogeneity plays an important role in cholera transmission. Consequently, the effects of the movement of human hosts and the dispersal of pathogenic bacteria may also contribute to the overall pattern of cholera epidemics and endemism.

In order to represent the spatial movement of hosts and pathogens, simple partial differential equation (PDE) models were developed in ^[18,19] to account for cholera epidemic spreading along a theoretical river, where only the environment-to-human transmission route was considered. In ^[21], a PDE cholera model based on reaction-diffusion equations was proposed that represents the spatial diffusion of the pathogens and human hosts while incorporating both the direct and indirect transmission routes. This work was later extended in ^[22] to include a convection process for the pathogenic bacteria, and in ^[23] to incorporate seasonal fluctuation into the spatiotemporal dynamics of cholera. For all these PDE studies, the spatial domain is restricted to a one-dimensional (1D) space. Meanwhile, multi-patch models based on ordinary differential equations are also proposed ^[24,25] to study the spread of cholera from one patch to another due to human and/or water movement.

In spite of these efforts and related findings, some difficulties remain in the investigation of the spatial dynamics of cholera. For example, it is still a nontrivial task to model and analyze cholera epidemics in a realistic setting that incorporates spatial variations and multiple transmission pathways of cholera. It also remains a challenge to quantify the infection risk of cholera in a spatially heterogeneous environment.

Another limitation in current modeling studies of cholera is the insufficient understanding of the within-host disease dynamics. Most of the published cholera models are concerned with the between-host transmission and spread at the population level. On the other hand, experimental measurements ^[26] show that cholera infection involves complicated within-host dynamics that are distinct from many other infections such as vector-borne or directly transmitted diseases. In particular, the pathogenesis of the vibrios inside the human body involves a special type of virus, referred to as the cholera toxin phage (CTX$\phi$). This phage is originally present as an integrated section of the genome of the V. cholerae bacterium, and it remains silent within V. cholerae in the natural environment. However, when the vibrios are ingested into the human body and reach the intestinal area, the viruses within some vibrios are activated and, through a horizontal gene transfer, transduces the vibrios ingested from the environment into another type of vibrios, which we refer to as human vibrios, that have a much higher infectivity (up to 700-fold compared to that of the environmental vibrios) ^[8,9,27]. The released viruses then attach to and enter other vibrios, and such bacterial-viral interaction leads to the production of large amounts of toxin causing severe diarrhea. Eventually, through shedding, these highly infectious vibrios get out of the human body and remain active for a period of several hours, during which time these vibrios may significantly impact the disease transmission among human hosts. Therefore, the within-host interaction constitutes an essential part of cholera dynamics and is closely related to the between-host transmission and spread of the disease.

A mathematical model that links the between-host and within-host dynamics of cholera was proposed in ^[28], which involved two time scales: the fast scale for the pathogen dynamics inside the human body, and the slow scale for the disease transmission among hosts and the time evolution of the environmental vibrios. In a related study ^[29], the within-host dynamics of cholera were investigated in more detail, where the vibrios ingested from the environment (with lower infectivity) and those transformed inside the human body (with higher infectivity) are distinguished, and their interaction with the virus (CTX$\phi$) is taken into account. More recently, a multi-scale cholera model was proposed in ^[30] that couples the between-host transmission, the within-host interaction and the temporal evolution of the bacteria in the environment. Particularly, the within-host subsystem in this model involves the interaction among the cholera vibrios, the virus, and the host immune response.

In the present study, we aim to partially fill the knowledge gaps in the two aforementioned challenges in cholera modeling, by integrating multi-scale modeling of cholera into a spatially heterogeneous setting. The motivations for this study are threefold: (1) to better understand the spatial dynamics of cholera; (2) to gain more knowledge in cholera dynamics at different time scales; and (3) to connect the between-host transmission, the within-host interaction and the time evolution of the environmental bacteria for cholera in a heterogeneous spatial domain. We will employ the multi-group modeling technique, which is one of the most successful approaches to investigate spatial heterogeneity in mathematical epidemiology ^[31,32]. Other modeling studies to deal with spatial heterogeneity include the Lagrangian and Eulerian approaches (see ^[33] and references therein) which explicitly describe the population dispersal. Some of the existing cholera models have already utilized the multi-group technique; see, e.g., ^[17,34]. In the multi-group framework, the entire population is divided into multiple groups and disease transmission may occur within the same group and between different groups, reflecting the movement of human hosts and/or the pathogen from one region to another. For each group, we will investigate cholera dynamics at multiple scales by coupling the between-host transmission and within-host interaction. The within-host dynamics remain the same for individuals in the same group, allowing for a level of homogeneity for each group (i.e., a subset of the total population), but they differ from group to group, reflecting the heterogeneity in terms of environmental conditions, medical resources, individual contact patterns, etc., in different subsets of the host population. To our knowledge, this study represents the first effort in integrating multi-scale and multi-group frameworks for cholera modeling.

We will start from a general multi-group setting, where disease transmission occurs both within each group and across different groups with distinct transmission rates. A common water source is shared by all host groups, so that all hosts may contribute (e.g., through shedding) to the time evolution of the pathogenic bacteria in the environment while they are exposed to the pathogens from the contaminated water shared by the entire population. We will then focus our attention on two special, but biologically important, cases. For each case, we conduct careful analysis on the equilibrium solutions and their stabilities, and complement the analytical findings with some numerical simulation results.

The remainder of this paper proceeds as follows. In Section 2, we present the general formulation of our multi-group, multi-scale model. In Section 3, we consider the first special case where the host groups are connected with semi-uniform disease transmission. In Section 4, we study the second special case where the host groups are isolated so that there is no cross-transmission among different groups. Finally, we conclude the paper with some discussion in Section 5.

2.   General formulation

We consider a human population in a spatially heterogeneous environment. The total population is divided into $m$ distinct groups that reside in different locations. Each host group is partitioned into a susceptible compartment $S_i$, an infected (and infectious) compartment $I_i$, and a recovered compartment $R_i$, where the population in each group is assumed to be a constant and given by $N_i = S_i + I_i + R_i$, for $i = 1, \ldots, m$. Meanwhile, we assume that all the host groups share the same water source, and we let $B$ denote the concentration of the bacterium Vibrio cholerae in the common water supply.

We then describe the between-host transmission dynamics of cholera in this setting by the following system of differential equations:

for $i = 1, \cdots, m$, together with the equation for the time evolution of the pathogenic vibrios in the environment:

Here we assume that the natural birth and death rates for all the human hosts are the same, denoted by $\mu \,$, considering the relatively short duration of a typical cholera epidemic (compared to the average human lifespan) and the generally low lethality rate of cholera ^[6,7]. For each $i = 1, \cdots, m$, susceptible individuals in group $i$ contract cholera either through direct (i.e., human-to-human) transmission from infectives in group $k$ at the rate $\beta_{H_{ik}}$ ($1 \leq k \leq m$), or through indirect (i.e., environment-to-human) transmission from the contaminated water at the rate $\beta_{L_i} \,$. Meanwhile, an infected individual in group $i$ recovers at the rate $\gamma_i \,$, and contributes (via shedding) to the growth of the bacteria in the aquatic environment at the rate $\xi_i(Z_i)$ depending on the within-host pathogen load $Z_i$, defined in system (2.3). We assume that the environmental bacterial growth is predominantly refueled by the infected hosts. In addition, $\, \delta$ denotes the natural removal rate of the vibrios.

After the vibrios from the environment are ingested by a human host, they interact with the virus CTX$\phi$ in the small intestine. Consequently, the environmental vibrios are transformed into highly toxic and infectious vibrios ^[9,27]), which we refer to as the human vibrios. Meanwhile, the host immune system responds to the invasion by trying to eliminate the pathogenic vibrios and viruses as a means to protect the human body. Hence, we use the following system of differential equations (an extension of the model from ^[30] for homogeneous host settings) to describe the within-host dynamics of an average infected individual in the $i$th group

Here $Z_i$, $V_i$, and $M_i$ ($i = 1, \cdots, m$) represent the concentrations of human vibrios, viruses (i.e., CTX$\phi$), and host immune cells, respectively. The parameters $c_{1_i}$ and $c_{2_i}$ denote the generation rates, and $d_{1_i}$ and $d_{2_i}$ denote the immune killing rates, for human vibrios and viruses respectively; $\zeta_i$ is the removal rate of human vibrios (due to natural death or shedding), $\tau_i$ is the removal rate of viruses, and $p_i$ is the removal rate of the immune cells; $e_{1_i}$ and $e_{2_i}$ represent the immune stimulation rates from the human vibrios and viruses, respectively. We have assumed in systems (2.2) and (2.3) that the environmental vibrios are only produced in the aquatic environment, whereas the human vibrios are only generated inside the human body and, after being shed out by infected individuals, lose their high infectivity and eventually become part of the environmental vibrios.

The within-host dynamics, represented by system (2.3) for each group, take place on a fast time scale, ranging from several hours to a few days. In contrast, the between-host dynamics, represented by system (2.1) for each group, are on a much slower scale, typically lasting several months or even a few years. Thus, cholera dynamics in each host group are modeled by a multi-scale process, involving both within-host interaction and between-host transmission. Note that all the host groups interact with the common water source in the sense that they are exposed to the pathogenic bacteria while they also contribute to the bacterial growth in the environment. Note also that the within-host dynamics are dependent on the environmental bacterial concentration. Therefore, the temporal evolution of the environmental bacteria, represented by Eq (2.2), plays an important role by not only connecting all the host groups, but also linking the between-host and within-host dynamics inside each group.

Equations (2.1)–(2.3) constitute our multi-group, multi-scale model for cholera dynamics in a spatially heterogeneous environment. This general formulation, however, makes mathematical analysis difficult. As a means to demonstrate the application of this framework, in what follows we focus our attention on two simplified (yet biologically meaningful) scenarios of the model and conduct careful analysis to each.

3.   Case one: Semi-uniform transmission

Since all the host groups share the same water source, it may be reasonable to assume that all individuals are equally exposed to the pathogen in the contaminated water and have an equal chance to contract cholera from the environment-to-human route. Consequently, the indirect transmission rates are assumed to be the same for all groups:

Meanwhile, we assume that an infected individual in group $i$ has an equal probability to contact a susceptible individual from any group; that is, the direct transmission rates satisfy the following condition:

This could happen when all the host groups are adjacent to each other and have similar population size, and people regularly move from one place to another. Though, in general, we assume that $\beta_{Hi} \neq \beta_{Hj}$ when $i \neq j$, so that we retain some degree of heterogeneity in direct transmission patterns for different host groups. We refer to this setting as a multi-group model with semi-uniform transmission.

Our between-host system (including the environmental pathogen equation) now takes a simpler form, given below

The within-host system, on the other hand, remains the same as given in Eq (2.3).

We first investigate the between-host dynamics described in Eq (3.3) using the separation of scales; that is, the fast variable $Z_i$ for each group $i$ is regarded at its steady state when analyzing the slow system (3.3). Consequently, $\xi_i(Z_i)$ is treated as a constant in this process and we may simply write $\xi_i = \xi_i(Z_i)$ for $i = 1, 2, \cdots, m$.

3.1.   Between-host reproduction number

The disease-free equilibrium (DFE) of system (3.3) is given by $(\textbf{S}, \textbf{I}, \textbf{R}, B) = (\textbf{N}, 0, 0, 0)$ where $\textbf{S} = (S_1, S_2, \dots, S_m)$, $\textbf{I} = (I_1, I_2, \dots, I_m)$, $\textbf{R} = (R_1, R_2, \dots, R_m)$, and $\textbf{N} = (N_1, N_2, \dots, N_m)$. To compute the basic reproduction number $R_0$ for system (3.3), we employ the standard next-generation matrix technique ^[35]. We separate the right-hand side of the infection subsystem (i.e., $\textbf{I}$ and $\textbf{B}$) into the generation of new infection, denoted by $\mathcal{F}$, and the transfer among compartments, denoted by $\mathcal{V}$. Then the next-generation matrix is given by $FV^{-1}$ where $F$ and $V$ denote the Jacobian matrices associated with $\mathcal{F}$ and $\mathcal{V}$, respectively, evaluated at the DFE. Specifically,

The basic reproduction number is defined as the spectral radius of the next-generation matrix; i.e., $R_0 = \rho(FV^{-1})$. Note that the matrix $FV^{-1}$ can be expressed as a product $AB$ where

Since $\rho(AB) = \rho(BA)$, we obtain

where, again, $\xi_i = \xi_i(Z_i)$ is treated as a constant ($i = 1, 2, \cdots, m$). The expression in (3.5) can also be obtained by observing that the next-generation matrix has rank one and so $R_0 = {\rm tr}(FV^{-1})$.

Remark 3.1.1. In Eq (3.5), each term $R_0^i \triangleq \frac{N_i}{\gamma_i + \mu}\left(\beta_{Hi} + \xi_i\frac{\beta_L}{\delta}\right)$ represents the individual reproduction number for group $i$ ($i = 1, 2, \cdots, m$), where the first part (associated with $\beta_{Hi}$) depicts the contribution of the human-to-human transmission, and the second part (associated with $\beta_L$) describes the contribution of the environment-to-human transmission. Thus, the direct and indirect transmission routes, combined together, determine the disease risk for each group $i$, and the overall infection risk for the multi-group system (3.3) is shaped by the summation of the individual risk factors from all the host groups. Biologically, this result indicates a collective impact of individual communities on the entire population for the onset of a cholera epidemic. For example, even if there is only one host group with high risk (so that its individual reproduction number is larger than unity), then $R_0 > 1$ for the whole population and a cholera epidemic would take place and spread to all groups, due to the inter-group connections. Similarly, even if the risk factor $R_0^i < 1$ for each group $i$, there is still a possibility for the collective value $R_0$ to be higher than unity which triggers a cholera outbreak. Hence, to effectively control cholera in such a closely connected population, efforts should be made to weaken both the direct and indirect transmission modes, for each host group, so as to reduce the overall $R_0$ below unity.

When $R_0 < 1$, it follows that the DFE is locally asymptotically stable ^[35]. To explore the global stability of the DFE, we employ the method described in ^[36] to construct a Lyapunov function. Let us first introduce the following function:

where $F, \; V, \; \mathcal{F}$ and $\mathcal{V}$ are defined as in the computation of $R_0$, and $\mathbf{x} = (I_1, I_2, ..., I_m, B)^T$ and $\mathbf{y} = (S_1, S_2, ..., S_m)^T$ denote the infection and non-infection compartments, respectively. Note that the infection subsystem of (3.3) can be written as

We first show that $f(\mathbf{x}, \mathbf{y}) \geq 0$ and $f(\mathbf{0}, \mathbf{y}) = 0$. In fact, we have

Then

and $f(\mathbf{0}, \mathbf{y}) = 0$.

Let $w^T$ be the left eigenvector of the matrix $V^{-1}F$ corresponding to the eigenvalue $\rho(V^{-1}F) = \rho(FV^{-1}) = R_0$. It is straightforward to observe that $F \geq 0$, $V^{-1} \geq 0$, and $V^{-1}F$ is non-negative and irreducible. Thus, we obtain $w^T \gg 0$ by the Perron-Frobenius theorem. We are now ready to prove the following result.

Theorem 3.1. When $R_0 < 1$, the DFE of system (3.3) is globally asymptotically stable.

Proof. We construct a Lyapunov function $L = w^T V^{-1} \mathbf{x}$. Differentiating $L$ along the vector field of system (3.3) yields

where we have used Eq (3.7). When $R_0 < 1$, we have $L' \leq 0$, and $L' = 0$ if and only if $\mathbf{x} = \mathbf{0}$ (since $w^T \gg 0$). Meanwhile, it is straightforward to verify that $\mathbf{y} = \mathbf{y_0} \triangleq (N_1, N_2, \cdots, N_m)^T$ is globally asymptotically stable in the disease-free subsystem of (3.3). Thus, the only invariant set that contains $\mathbf{x} = \mathbf{0}$ is the singleton $\{(\mathbf{0}, \mathbf{y_0})\}$; i.e., the DFE. Based on LaSalle's invariance principle, the DFE is globally asymptotically stable.

Theorem 3.1 confirms our observation in Remark 3.1. That is, when the overall between-host reproduction number $R_0$ is reduced below unity, the disease would be eliminated from the whole population.

3.2.   Between-host endemic equilibrium

We now consider the existence and uniqueness of a nontrivial equilibrium for system (3.3). Solving $\frac{dB}{dt} = 0$ for $B^*$ gives

Solving $\frac{dS_k}{dt} = 0$ for $S_k^*$ ($k = 1, 2, \cdots, m$) and substituting for $B^*$ give

Solving $\frac{dI_k}{dt} = 0$ for $I_k^*$ ($k = 1, 2, \cdots, m$) and substituting for $S_k^*$ give

Letting $f(\textbf{I}^*) = \sum\limits_{j = 1}^{m}\left(\beta_{Hj} + \xi_j\frac{\beta_L}{\delta}\right)I_j^*$ yields

for $1 \leq k \leq m$. This establishes the following relation for all $k$:

where

We may now rewrite $I_1^*$ in the following manner:

where

Assuming $I_1^* \neq 0$, we divide both sides by $I_1^*$ and obtain, after some algebraic manipulation,

Clearly, as long as $I_1^* > 0$, then $I_k^* > 0$ for all $k$; consequently, $B^* > 0$ and $S_k^* > 0$ for all $k$. Thus, in order to achieve a unique positive endemic equilibrium, the inequality

must hold. Upon inspection, the above inequality is equivalent to the inequality $R_0 > 1$, where $R_0$ is defined in (3.5). Therefore, system (3.3) has a unique endemic equilibrium when $R_0 > 1$.

In what follows we establish the global asymptotic stability of the endemic equilibrium with $(S_i^*, I_i^*, B^*)$, $1 \leq i \leq m$. Our proof is inspired by the approach of constructing Lyapunov functions on networks using graph theory ^[37]. We define

for $1\leq i \leq m$, and

Then

Note that

and

Combining (3.10) and (3.11) yields

where we have used the property that $1 -x + \ln x \leq 0$ for all $x > 0$, with the equality holding if and only if $x = 1$. Similarly, we find

Adding (3.12) and (3.13), we obtain

for $1 \leq i \leq m$, where

Meanwhile, we have

where we have used $1 - \dfrac{B^*I_i}{BI_i^*} \leq \ln\dfrac{BI_i^*}{B^*I_i} = \ln\dfrac{B}{B^*} - \ln\dfrac{I_i}{I_i^*}$. Thus,

with

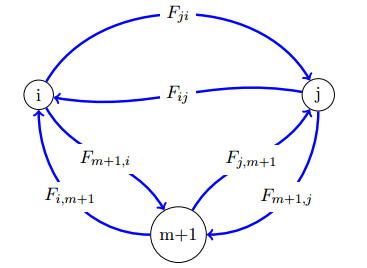
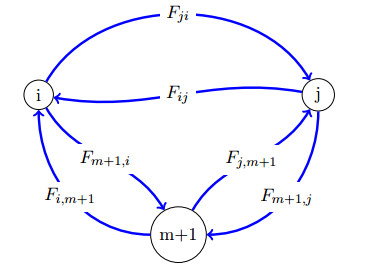
Now, for any $1\leq i \leq m$ and $1\leq j \leq m$, we have a graph structure illustrated in Figure 1 with three vertices $i$, $j$ and $m+1$.

It can be easily verified that on each directed cycle the following hold:

We now have a weighted digraph $\mathcal{G}$ with $m+1$ vertices and an associated $(m+1) \times (m+1)$ weight matrix $A = (a_{ij})$ whose entry $a_{ij}$ equals the weight of arc $(j, i)$. We denote this weighted digraph with its associated weight matrix as $(\mathcal{G}, A)$. We note that $(\mathcal{G}, A)$ is strongly connected, and $A$ is irreducible. Furthermore, we define $c_i$ as the cofactor of the $i$-th diagonal element of the Laplacian matrix of $(\mathcal{G}, A)$. Equivalently,

where $\mathbf{T}_i$ is the set of all spanning trees $\mathcal{T}$ of $(\mathcal{G}, A)$ that are rooted at vertex $i$, $w(\mathcal{T})$ is the weight of $\mathcal{T}$, and $c_i > 0$ ^[37].

The following general result was established in ^[37]:

Theorem 3.2. Consider a system of differential equations on a graph $\mathcal{G}$ with $n$ vertices

where $t > 0$ and $u_i \in D_i$ with $D_i$ being an open set in $\mathbb{R}^{m_i}$, $i = 1, 2, \cdots, n$. Assume that:

(1) There exist functions $V_i(t, u_i)$, $F_{ij}(t, u_i, u_j)$ and constants $a_{ij} \geq 0$ such that

(2) Along each directed cycle $\mathcal{C}$ of the weighted digraph $(\mathcal{G}, A)$, $\, A = (a_{ij})$,

Let constants $c_i$ ($1\leq i \leq n$) be defined in the same way as in (3.15). Then the function

satisfies $V'(t, \mathbf{u}) \leq 0$ for $t > 0$ and $\mathbf{u} = (u_1, u_2, \cdots, u_n) \in D_1 \times D_2 \times \cdots \times D_n$; namely, $V$ is a Lyapunov function for system (3.16).

We have already shown that the conditions in Theorem 3.2 hold in our case, and thus we may conclude that

with $c_i$ given in (3.15) and $V_i$ defined in (3.8) and (3.9) for $1\leq i \leq m+1$, is a Lyapunov function for the system (3.3) satisfying $\, V' \leq 0$. It can also be easily verified that $V' = 0 \iff (S_i, I_i, B) = (S_i^*, I_i^*, B^*)$ for $i = 1, 2, ..., m$. Hence, by LaSalle's invariance principle, the endemic equilibrium of system (3.3) is globally asymptotically stable. We have established the following result.

Theorem 3.3. When $R_0 > 1$, the between-host transmission system (3.3) has a unique endemic equilibrium that is globally asymptotically stable.

Theorems 3.1 and 3.3 show that at the between-host level (without incorporating the within-host dynamics), the basic reproduction number defined in (3.5) serves as a threshold quantity to characterize the global dynamics of system (3.3): the disease is eliminated when $R_0 < 1$ and is persistent when $R_0 > 1$.

3.3.   Full system

Based on the separation of scales, a standard equilibrium analysis can be conducted to the fast-scale, within-host system (2.3), where the slow variable $B$ is treated as a constant. Defining $R_{0i}^{\rm F} = \frac{c_{2_i} B}{\tau_i}$ as the basic reproduction number for the within-host dynamics associated with each group $i$ ($1 \leq i \leq m$). It is easy to show that when $R_{0i}^{\rm F} < 1$, there is a unique and stable trivial equilibrium $(Z_i, V_i, M_i) = (0, 0, 0)$; when $R_{0i}^{\rm F} > 1$, the trivial equilibrium is unstable, and there is a unique and stable positive equilibrium.

Remark 3.3.1. Biologically, this implies that when the concentration of the environmental vibrios $B$ (treated as a constant) is sufficiently low, the within-host dynamics may be trivial. In contrast, when the environmental bacterial concentration $B$ is higher than a certain threshold, then the within-host dynamics become non-trivial and could potentially impact the between-host disease infection at the population level. Note also that the within-host reproduction number $R_{0i}^{\rm F}$ ($i = 1, 2, \cdots, m$) is generally distinct from each other, reflecting the heterogeneity among different host groups.

Next, we proceed to consider the full system of our multi-scale model that couples the between-host dynamics, described by Eq (3.3), and the within-host dynamics, described by Eq (2.3). The slow scale and fast scale are then linked together in the analysis below. In particular, the fast variable $Z_i$ is no longer a constant in the slow-scale system (3.3), and the slow variable $B$ is no longer a constant in the fast-scale system (2.3).

3.3.1.   Basic reproduction number

We will again utilize the next-generation matrix technique to calculate the basic reproduction number of the full system. First, note that a unique disease-free equilibrium of the system (2.3) and (3.3) is given by

We separate the vector of unknowns $\mathbf{X}$ of the system into the infection and non-infection related compartments as follows:

where

We can then compute the next-generation matrix $FV^{-1}$, and subsequently obtain the basic reproduction number of the full system

Remark 3.3.2. The expression in (3.18) shows that when the between-host and within-host dynamics are linked, the cholera infection risk for the entire population can still be represented as a combination of the individual risk factors from all host groups, an interpretation similar to that made to the between-host reproduction number $R_0$ defined in Eq (3.5). Although the expression of $\widetilde{R_0}$ is similar to that of $R_0$ in (3.5), the distinction is that the fast variable $Z_i$ for each group $i$ is treated as a constant in Eq (3.5) at the slow time scale, whereas $Z_i$ does not appear in Eq (3.18) since the slow and fast variables are coupled in the full system. Instead, the host shedding term $\xi_i(0)$ in Eq (3.18) represents the role played by the fast-scale dynamics in shaping the overall disease risk.

3.3.2.   Endemic equilibrium

Next we seek the existence and uniqueness of a positive endemic equilibrium. For any group $i$, we may solve the within-host system at the equilibrium given by $(Z_i', \, V_i', \, M_i')^T = 0$. The result is

Substituting the last two equations in (3.19) into the first one, and defining

we can modify the endemic equilibrium from Section 3.2 to include the shedding function $\xi(Z_i^*)$. Then for any $1\leq k \leq m$ we have

where

with the solutions for $S_k^*$ following directly from here. Note that the between-host and within-host systems are coupled through the environmental bacterial equation. Utilizing the relationship between $I_k^*$ and $I_1^*$, we have the following system in $I_1^*$ and $B^*$:

If a solution exists for this system, then it also determines a positive equilibrium for the full system. Equivalently, an intersection of the two equations

determines an endemic equilibrium. To proceed, we introduce the following assumptions regarding the functions $\xi_k$ and the model parameters for $1 \leq k \leq m \,$:

(A1) $\xi_k > 0$, $\; \xi_k^{'} > 0$, and $\; \xi_k^{''} < 0$

(A2) $\dfrac{\zeta_k}{\tau_k} < \dfrac{d_{1_k}}{d_{2_k}}$

(A3) $\beta_L < \delta$, $\;$ and $\, \max \xi_k < \dfrac{\beta_{H_k}}{1 - \frac{\beta_L}{\delta}}$

(A4) $\xi_k\big(q_k(B) \big)^{'} \, \big|_{B = 0} < \frac{\delta^2}{\mu \beta_L} \xi_k\big(q_k(0) \big)$

Remark 3.3.3. Assumptions (A1), (A3) and (A4) provide biologically meaningful characterizations for the host shedding functions $\xi_k$. Specifically, we regulate $\xi_k$ as positive, monotonically increasing with the within-host pathogen load but remaining below a certain threshold, and subject to a saturation effect (when the pathogen load is high, the shedding rate would increase more slowly than linearly).

Theorem 3.4. Under assumptions (A1) and (A2) , there exists a positive endemic equilibrium for the coupled system (3.3) and (2.3) when $\widetilde{R_0} > 1$. Such an endemic equilibrium is unique if additional assumptions (A3) and (A4) hold.

Proof. First, we show the existence of an endemic equilibrium under assumptions (A1) and (A2). Consider the function $q_k(B^*)$ and its first and second derivatives:

Additionally,

Next, we consider $f(B^*)$:

where

Since $\xi_k'(Z^*) > 0$ and $q_k'(B^*) > 0$ we have $R_0^* > \widetilde{R_0}$ for all $B^*$. Therefore, when $\widetilde{R_0} > 1$,

Now,

Also,

and

Finally, we observe that $f(0) > 0$, $\; g(0) = 0$, and

Thus, there exists at least one point of intersection between the curves of $f$ and $g$.

To guarantee that this intersection is unique, we assume (A3) and (A4) hold. Note that

where

Meanwhile, we have

By assumption (A3),

Let

Note that $\, h(0) > 0$ and

Therefore $h(B^*)$ is a positive increasing function. By assumption (A4), we have $\sigma(0) > \dfrac{\mu \beta_L}{\delta^2} \sigma'(0)$; i.e., $h(0) > \dfrac{\mu \beta_L}{\delta^2}$, which yields $h(B^*) > \dfrac{\mu \beta_L}{\delta^2}$. Consequently, we have

Combining equations (3.23), (3.24) and (3.25), we obtain $g'(B^*) > f'(B^*)$ for all $B^* > 0$. Hence, there is only one intersection between $f$ and $g$, which guarantees a unique endemic equilibrium.

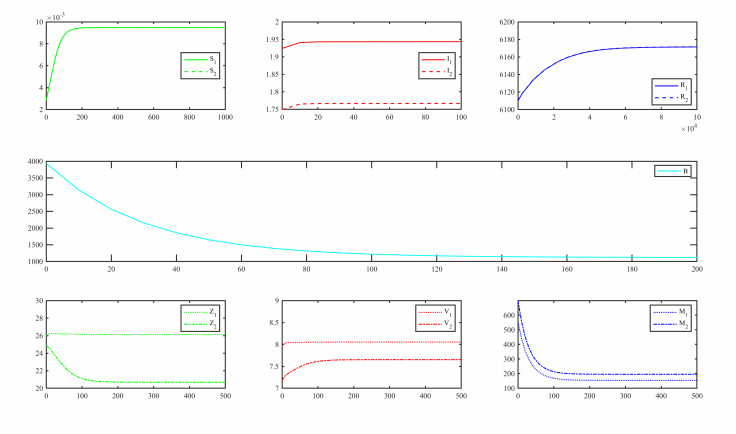
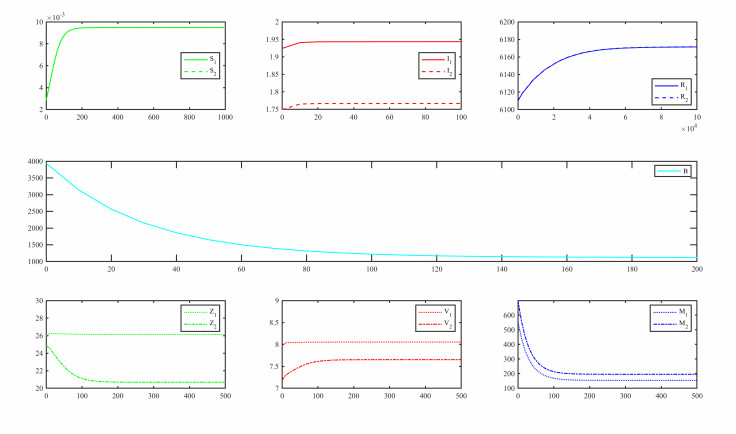
Theorem 3.4 provides sufficient conditions to ensure the existence and uniqueness of the endemic equilibrium for the full system (2.3) and (3.3). Due to the complexity of this coupled system, we have not resolved the stability of the endemic equilibrium. Nevertheless, it is reasonable to expect that this equilibrium is at least locally asymptotically stable when $\widetilde{R_0} > 1$. We have conducted numerical simulation to the full system and the numerical results are consistent with our expectation. We find that when $\widetilde{R_0} > 1$, all solution orbits starting sufficiently close to the endemic equilibrium will eventually converge to it. A typical scenario is shown in Figure 2 with $m = 2$ that demonstrates the local asymptotic stability of the endemic equilibrium.

4.   Case two: Isolated host groups

Now we consider another special case for the general model in (2.1)–(2.3), and assume that these $m$ host groups are isolated from each other so that there is no direct communication among groups. Consequently, the cross-transmission rates in the direct transmission route would become zero; i.e.,

This would be feasible for a large spatial domain with a common water source (such as a long river or a large lake), where the host groups reside in different locations that are remote from each other. Meanwhile, we make the same assumption as in (3.1) regarding the indirect transmission rates.

The between-host system under this setting is given by

while the within-host system (2.3) remains the same.

4.1.   Between-host system

We again start the analysis by separating the between-host system (4.2) from the within-host system. Subsequently, we treat the fast variable $Z_i$ as a constant in the slow-scale system (4.2) so that $\xi_i = \xi_i(Z_i)$ is a constant ($1\leq i \leq m$).

The disease-free equilibrium is given by $S_i = N_i$ and all other variables equal to zero. The next-generation matrix of system (4.2) is found as

The basic reproduction number $R_0 = \rho(FV^{-1})$, however, cannot be analytically determined in this case. Nevertheless, with some further simplifications, an explicit form can be reached. For example, if we assume that the direct transmission quantity, $\beta_{Hi} N_i$, and the recovery rate, $\gamma_i$, are the same for all the host groups; i.e., $\beta_{Hi} N_i \triangleq p$ and $\gamma_i \triangleq \gamma$ for $1 \leq i \leq m$, then $R_0$ can be found as

Remark 4.1.1. We may compare the results in equations (4.3) and (3.5) for the basic reproduction numbers associated with the two different settings. In Eq (3.5), if we make the same assumptions that $\beta_{Hi}N_i \triangleq p$ and $\gamma_i \triangleq \gamma$ for $1 \leq i \leq m$, then the equation is reduced to

Obviously the indirect transmission parts are identical in equations (4.3) and (4.4). This is certainly expected as the indirect transmission follows the same pattern in these two cases. The difference between the two reproduction numbers, then, is the direct transmission part. For the current case characterized by isolated groups (but each group sharing the same direct transmission quantity), the risk factor based on direct transmission is the same for each group, and also for the entire population (since there is no cross-transmission between groups). In contrast, for the previous case characterized by frequent and regular communications among all groups, the risk factor based on direct transmission for the entire population is the summation of the individual factors from all $m$ groups, leading to the multiplication of $m$ in Eq (4.4). Due to such a difference in direct transmission pattern, the current case, represented by (4.3), exhibits a lower infection risk than that of the previous case, represented by (4.4).

A cholera transmission model similar to our between-host system (4.2) has been studied in detail in ^[34] and the results are applicable to our case. Specifically, Theorems 4.1 and 4.2 in ^[34] lead to the result below that characterizes the global dynamics of system (4.2).

Theorem 4.1. Let the between-host reproduction number $R_0$ be defined in (4.3).

(ⅰ) If $R_0 \leq 1$, then the disease-free equilibrium of system (4.2) is globally asymptotically stable.

(ⅱ) If $R_0 > 1$, then the disease-free equilibrium is unstable, and system (4.2) admits a unique endemic equilibrium that is globally asymptotically stable.

4.2.   Full system

We proceed to link systems (4.2) and (2.3) to study the coupled between-host and within-host dynamics for the current isolated group model. With similar algebraic manipulation as before, we can obtain the next-generation matrix $FV^{-1}$ and then define the basic reproduction number $\widetilde{R_0} = \rho(FV^{-1})$. Note that the disease-free equilibrium is still given by $S_i = N_i$ ($i = 1, 2, \cdots, m$) and all other variables equal to zero. As a special case, when $\beta_{Hi}N_i = p$ and $(\gamma_i + \mu) = v$ for $1 \leq i \leq m$, we have

The term $\xi_i(0)$ again reflects the feedback of the within-host dynamics to the between-host transmission. Indeed, the interpretation of the relationship between equations (4.5) and (4.3) is similar to that between equations (3.18) and (3.5).

To analyze the positive endemic equilibrium for the coupled system, we set all equations in (4.2) and (2.3) to zero. The equilibrium solutions for the within-host system (2.3) remain the same as derived before. The between-host system (4.2) leads to the following ($i = 1, 2, \cdots, m$):

which yields a quadratic equation for $I_i^*$

For any $B^* > 0$, Eq (4.6) has one and only one positive root:

Meanwhile, setting $B' = 0$ in system (4.2) yields

where the function $q_k(B^*)$, defined in Eq (3.20), represents the equilibrium solution from the within-host system. Substituting Eq (4.7) into (4.8), we obtain

Hence, a nontrivial solution of (4.9), or equivalently, a positive intersection between the two curves $B^*$ and $F(B^*)$, determines a positive endemic equilibrium. To proceed, we need additional assumptions given below, for $1\leq k \leq m$:

(A5) $\beta_{H_k} N_k < \gamma_k + \mu$

(A6) The function $F_k(B^*) \triangleq \xi_k(q_k(B^*))g_k(B^*)$ is a concave function; i.e., $F_k^{''}(B^*) \leq 0$.

Remark 4.2.1. Condition (A5) sets an upper bound for the total direct transmission involved within each host group. Alternatively, it can be interpreted as prescribing a maximum for the individual community size $N_k$ (when the direct transmission rate is fixed), or the direct transmission rate $\beta_{H_k}$ (when the community size is fixed), for each group. Condition (A6) implies that $F_k(B^*)$ is subject to a saturation effect, which is a common assumption for a biologically feasible function.

Theorem 4.2. Let the basic reproduction number for the coupled system (4.2) and (2.3) be defined in Eq (4.5). Then, under assumption (A5) , the system has at least one positive endemic equilibrium. Additionally, if assumption (A6) holds, then the endemic equilibrium is unique.

Proof. Based on Eq (4.7) and assumption (A5), it is easy to observe

Hence, it follows that

Meanwhile, direct calculation yields

Subsequently, using $g_k(0) = 0$ and $q_k(0) = 0$ we obtain

With the simplifications $\beta_{H_k}N_k = p$ and $\gamma_k + \mu = v$ ($1 \leq k \leq m$) incorporated in Eq (4.5), we have

Note that $v - p > 0$ based on assumption (A5). It is now straightforward to verify that

would yield $F'(0) > 1$. Combining this fact with (4.10), we obtain that the two curves $B^*$ and $F(B^*)$ must have at least one intersection for $B^* > 0$. Furthermore, if assumption (A6) holds, then

and thus the intersection point between $B^*$ and $F(B^*)$ must be unique.

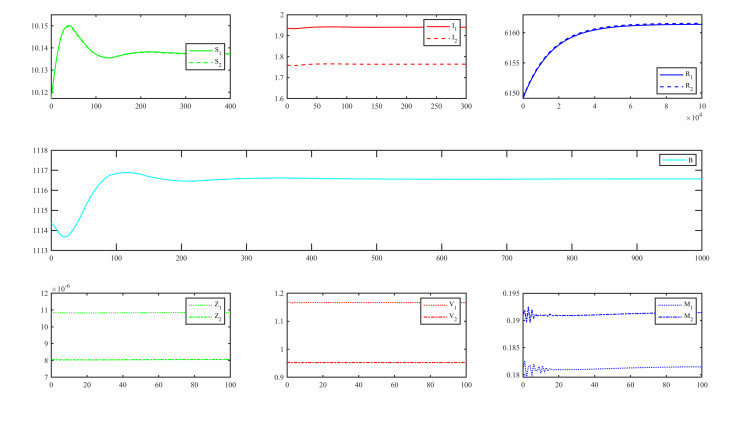
With similar difficulty as in the full system of the previous case, we have not analytically worked out the stability property of the endemic equilibrium. Our numerical results, nevertheless, demonstrate that the endemic equilibrium is at least locally asymptotically stable when $\widetilde{R_0} > 1$; that is, all solution orbits starting in a small neighborhood of the endemic equilibrium will eventually converge to the endemic equilibrium. A typical result is illustrated in Figure 3 (other results are similar and not shown here).

5.   Discussion

We have presented a multi-group, multi-scale model to investigate cholera dynamics. Each group has its own susceptible, infected, and recovered compartments linked together through direct and indirect transmission routes. Each group also has its own system governing the within-host dynamics, coupled together through the environmental equation. The study integrates multi-scale modeling and multi-group modeling, traditionally seen as two distinct and unrelated realms in mathematical epidemiology, into one single framework.

Cholera dynamics are complex, involving a wide variety of biological, environmental, genetic, geographic, and socioeconomic factors and spanning a number of temporal and spatial scales. In order to gain deeper understanding of such dynamics, our work has emphasized the interplay among the multiple routes of disease transmission, the multiple scales of disease dynamics, and the multiple host groups that represent the spatial heterogeneity.

We have specifically focused on two types of spatial settings: one with connected groups and semi-uniform transmission representing a host population who are in regular, consistent contact and communication, and the other with isolated groups and no cross-transmission representing a population who are divided and remotely located from one another. For each case, we have derived the basic reproduction numbers associated with the decoupled and coupled systems, analyzed the equilibria and stabilities of the multi-scale model, and conducted some numerical simulation to complement the analytical results. In particular, we have found that under biologically feasible conditions, the system dynamics and global stability at the between-host level exhibit a sharp threshold at $R_0 = 1$, where $R_0$ is the between-host reproduction number that is shaped by the collection of the disease risk factors from all the individual host groups. Our findings highlight the importance of a whole-population approach for cholera prevention and intervention; that is, reducing the overall reproduction number below unity for cholera elimination at the entire population level. Toward that goal, specific cholera control measures should target both the environment-to-human and human-to-human transmission routes, and be strategically implemented in different groups/communities taking into account the spatial heterogeneity and host characteristics.

When the within-host dynamics are linked to the between-host transmission, the analysis of the model becomes more challenging due to the complexity, strong nonlinearity and high dimension of the overall system. We have obtained results on the existence and uniqueness of the endemic equilibrium in each case, indicating the persistence of the infection when the basic reproduction number $\widetilde{R_0}$ is higher than unity, but have not resolved the endemic stability of the fully coupled system. Nevertheless, our numerical results indicate that the endemic equilibrium is at least locally asymptotically stable when $\widetilde{R_0} > 1$, as naturally expected.

Further development of the modeling framework could involve more detailed description of the within-host dynamics (e.g., by distinguishing the innate and adaptive immune responses and including both into the pathogen-host interaction), as well as more sophisticated spatial settings (e.g., by considering both shared and isolated aquatic environments). We may also consider different ways of defining host groups (e.g., based on age, gender and health conditions, instead of locations) to extend our modeling framework. Such future study may benefit from numerical simulation based on efficient implementation of a multi-scale algorithm. Meanwhile, it may be worthwhile to explore a multi-scale PDE modeling approach, where the spatial dynamics of cholera are represented by a PDE system, and possibly compare with our current multi-scale, multi-group model, to gain a more complete picture of cholera dynamics. In addition, agent-based modeling techniques for within-host and between-host disease dynamics (e.g., ^{[38,39,40,41]}) might offer useful insight that complements the results from our deterministic modeling approaches. Finally, these modeling efforts would benefit from realistic case studies where the models are used to fit field data to estimate real risks of cholera and to guide disease control and management.

Acknowledgments

This work was partially supported by the National Science Foundation (under Grant Nos. 1557739 and 1520672). The authors are grateful to the editor for handling this paper and to the three anonymous referees for their helpful comments that have significantly improved this paper.

Conflict of interest

The authors declare there is no conflict of interest.